Mis-sizing of stent promotes intimal hyperplasia: impact of endothelial shear and intramural stress

Abstract

Stent can cause flow disturbances on the endothelium and compliance mismatch and increased stress on the vessel wall. These effects can cause low wall shear stress (WSS), high wall shear stress gradient (WSSG), oscillatory shear index (OSI), and circumferential wall stress (CWS), which may promote neointimal hyperplasia (IH). The hypothesis is that stent-induced abnormal fluid and solid mechanics contribute to IH. To vary the range of WSS, WSSG, OSI, and CWS, we intentionally mismatched the size of stents to that of the vessel lumen. Stents were implanted in coronary arteries of 10 swine. Intravascular ultrasound (IVUS) was used to size the coronary arteries and stents. After 4 wk of stent implantation, IVUS was performed again to determine the extent of IH. In conjunction, computational models of actual stents, the artery, and non-Newtonian blood were created in a computer simulation to yield the distribution of WSS, WSSG, OSI, and CWS in the stented vessel wall. An inverse relation (R² = 0.59, P < 0.005) between WSS and IH was found based on a linear regression analysis. Linear relations between WSSG, OSI, and IH were observed (R² = 0.48 and 0.50, respectively, P < 0.005). A linear relation (R² = 0.58, P < 0.005) between CWS and IH was also found. More statistically significant linear relations between the ratio of CWS to WSS (CWS/WSS), the products CWS × WSSG and CWS × OSI, and IH were observed (R² = 0.67, 0.54, and 0.56, respectively, P < 0.005), suggesting that both fluid and solid mechanics influence the extent of IH. Stents create endothelial flow disturbances and intramural wall stress concentrations, which correlate with the extent of IH formation, and these effects were exaggerated with mismatch of stent/vessel size. These findings reveal the importance of reliable vessel and stent sizing to improve the mechanics on the vessel wall and minimize IH.

percutaneous coronary interventions, such as stents [bare metal and drug-eluting stents (DES)], have revolutionized coronary artery disease (CAD) treatment in the past three decades (2). There are nearly 1 million stents used annually for the treatment of CAD, but the risks of in-stent restenosis (ISR) and late thrombosis remain as complications requiring revascularization and, in some cases, can result in acute coronary syndrome (1, 2, 12). Because of their ability to substantially attenuate neointimal formation after stenting, the DES was projected to largely eliminate the ISR problem. Restenosis with DES remains significant (1, 2), however, particularly in complex lesion subsets. Furthermore, there is an increased risk of late thrombosis with DES (7, 39). Finally, DES does not address the fundamental flow disturbances before endothelization or compliance mismatch associated with stent to artery size mismatch, which can significantly contribute to ISR (34).

Experimental and clinical evidence suggests that alterations of fluid wall shear stress (WSS) contribute to the occurrence of ISR. Specifically, it has been observed clinically that the sites of neointimal hyperplasia (IH) highly correlate with sites of low WSS (33). Furthermore, nonuniform WSS spatial distribution [higher WSS gradient (WSSG)] and a higher oscillatory shear index (OSI) were also found to contribute to cell migration and differentiation (40, 46). After stent deployment, the struts compress the vessel wall and cause flow disturbance at the intima acutely. The circumferential wall stress (CWS) concentrations are likely to provoke inflammatory responses that may initiate cell migration, proliferation, and atherogenesis (42).

A number of studies have simulated either stent fluid mechanics (4, 25, 30) or solid mechanics (3, 31). For example, He et al. (25) investigated the effect of stent strut design patterns on fluid WSS. La Disa et al. (30) simulated alteration of the local fluid environment after stent implantation. Additionally, Berry et al. (4) performed in vitro experimental flow evaluations of stents. Lally et al. (31) and Bedoya et al. (3) investigated the effects of stent design parameters on artery wall mechanics. Timmins et al. (43) found that stents with larger strut spacing and axial amplitude impose less stress on the vessel wall, which may lead to less IH development. Although these previous studies provided insightful findings, the following were not considered: 1) non-Newtonian blood properties, which become significant at the stent struts where WSS is low; 2) the roles of WSSG and OSI in addition to WSS, as well as the combined solid/fluid effects; 3) the role of mis-sizing on the fluid and solid mechanics of the coronary vessel wall; and 4) superimposition of these fluid/solid mechanical forces on IH in a coronary artery porcine model. Here, we address these and other limitations.

The objective of this study was to investigate the role of both stent fluid and solid mechanics on the development of IH. The hypothesis was that both fluid and solid disturbances significantly contribute to IH, i.e., there are direct relations between stresses on the endothelium surface (WSS, WSSG, and OSI) and within the vessel wall (CWS) and IH due to a stent implant. Accordingly, we developed a physics-based computational model to predict the fluid and solid disturbances created by the stent in a swine animal model and studied the IH response at a 1 mo followup. To vary the ranges of mechanical stresses, we intentionally over- and undersized the stents relative to the vessel diameter. The relation between mechanical stresses and the biological response may provide insights into the mechanism of IH development.

MATERIALS AND METHODS

Animal experiments.

A total of 10 swine were used in the present study. Four healthy male swine (55–60 kg) were used for the correct sizing (match diameter of stent and vessel lumen) and −10%, +10%, and +20% cases (1 animal for each case using a Guidant Multi-link Penta stent with a strut thickness of 96 μm). Six healthy male swine (55–60 kg) were used for the +10% and +30% cases as well as the correct sizing cases (1, 2, and 3 animals for the correct size, +10%, and +30% cases, respectively). The stent used in these animals was J&J Cordis Bx Velocity with a strut thickness of 86 μm. The strut thicknesses of the two stents used in the present study were similar (86 vs. 96 μm), and, hence, no significant differences in IH were identified due to these two particular stents. The stents used were deployed using standard balloon inflation to the appropriate pressure as done clinically. The remodeling of vessel wall in the stented region was evaluated at 1 mo for the 10 animals. All animals were imaged at the time of stenting and at the time of termination. This animal study was approved by the Institutional Animal Care and Use Committee of Indiana University and complied fully with the National Institutes of Health Guide for the Care and Use of Laboratory Animals (35).

At a scheduled time, animals were fasted overnight. A preanesthetic induced with ketamine (20 mg/kg) and atropine (0.05 mg/kg) was administered intramuscularly before endotracheal intubation. Animals were ventilated using a mechanical respirator, and general anesthesia was maintained with 1–2% isoflurane and O₂. Intravascular ultrasound (IVUS) was used to size the coronary arteries and stents as previously described (19). Briefly, the guiding catheter was attached to a manifold assembly that allows continuous blood pressure monitoring, saline flush, drug injection, and contrast (Omnipaque, Mallinckrodt Medical, St. Louis, MO) injection. An angioplasty guidewire (diameter: 0.014 in.) was placed into the arteries under fluoroscopic guidance. Standard anterior-posterior, right anterior oblique 30°, and left anterior oblique 30° angiographic images were obtained to verify placement.

Stent sizing and IH.

An IVUS catheter (3.2-Fr, 35-MHz Ultra-cross, or 2.9-Fr, 40 MHz Discovery, Boston Scientific on a Hewlett-Packard Sonos console) was advanced 4–8 cm through the coronary arteries to obtain “serial sections” of ultrasound images along the artery to quantify the size of the artery and stent. Various-sized stents were deployed into the arteries for the respective groups, i.e., for a 3-mm-diameter vessel, the correctly sized stent outer diameter, and for −10%, +10%, +20%, and +30% cases, stents were 3, 2.7, 3.3, 3.6, and 3.9 mm, respectively. The stents were deployed at appropriate balloon pressures to the desired dimensions. The sizing was accurate provided that the vessel sizing with IVUS and stent deployment were reliable, which were performed by an interventional cardiologist. Even in the 10% undersized case, there was strut apposition with the vessel wall because there was some degree of curviness to the vessel and the stents were not perfectly centered in the vessels. Hence, no stent migration was observed, and the IH growth covered and embedded the struts over time.

Angiograms were used to confirm the absence of thrombus in the experiments. Stents were placed in the proximal left circumflex (LCx) and right coronary artery vessels to minimize the effects of tapering present in the left anterior descending coronary artery. After stent placement, repeat IVUS was performed to ensure the deployment of the stent at the respective diameter. At the scheduled terminal date, the stented arteries were reimaged with IVUS. The IVUS catheter was advanced 5 mm distal to the stented regions of the LCX and right coronary artery and pulled back automatically at a rate of 0.5 mm/s and stopped at 5 mm proximal to the stent.

IH was quantified by the IH area/stent area at each of the cross-sections along the length of the artery/stent. IH was defined as the fibrous or soft plaque less echogenic than the adventitia. Examples of IVUS images showing stent struts and IH are shown in Fig. 1, where the metal struts are seen as bright short line segments on the image. Hence, it was possible to distinguish the new tissue growth (IH) from the struts toward the lumen and original vessel wall outward of the struts. Intra-/interobserver repeatability was performed, and the results confirmed accuracy within IVUS variability. The stent area was determined by the area of a polygon whose vertices were the edges of the struts to ensure close approximation of the area (Fig. 1, A and B).

Fig. 1.

Intravascular ultrasound (IVUS) images showing the extent of neointimal hyperplasia (IH) covering the struts. The red outlines show the lumen area and the area bounded by the struts. A: correctly sized stent. B: 10% oversized stent. C: representative histology of a stented coronary artery (left circumflex) shows that both the internal elastic lamina (IEL) and external elastic lamina (EEL) were intact, without any disruption or tearing for 30% oversizing. The arrow points to the IEL. The arrowhead points to the lumen.

The stented arteries were analyzed at 14 cross-sections/vessel (8 cross-sections at the stented region and 3 cross-sections at each side beyond the stent edge). The severity of IH at each cross-section was quantified as the percent area stenosis calculated as follows: (IH area/stent area) × 100%. SigmaScan Pro imaging software was used to quantify the IVUS image measurements (IH area and stent area) and the percentage of cross-sectional area stenosis. These measurements were then superimposed on the fluid (WSS, WSSG, and OSI) and solid (CWS) fields.

To evaluate the role of injury, histology was performed on the 30% oversize case. Vessels containing stents were embedded in methyl methacrylate, cut into sections using a diamond knife, and then stained with Verhoeff-Van Gieson's stain to delineate the internal elastic lamina (IEL) and external elastic lamina (EEL).

Physics-based computational models.

Three-dimensional (3-D) computational models of stents and blood were created in Pro/Engineer, which is a computer-assisted design package. The models were then interfaced, meshed, and solved in validated finite element and computational fluid dynamic packages ANSYS and FLOTRAN, respectively. Correctly sized, 10%, 20%, and 30% oversized stent models, and 10% undersized stent models were created for the simulations. The stent geometry simulated was a design with the general pattern similar to commercial stents (J&J Cordis Bx Velocity and Guidant-Boston Scientific Multi-link Penta stents). Because of the symmetry of the stent, quarter symmetry models were developed to reduce computational costs. About 1.5 million mesh elements were used in the simulations. A mesh convergence test showed that doubling the number of elements only resulted in a <2% difference in WSS and CWS. Hence, the mesh density was sufficient for the simulations.

The governing equations for blood were the Navier-Stokes (conservation of momentum) and continuity (conservation of mass) equations (20), namely:

$$\frac{\partial \overrightarrow{V}}{\partial t}+\overrightarrow{V}·\overrightarrow{\nabla }\overrightarrow{V}+\frac{\overrightarrow{\nabla }\mathrm{p}}{\rho }-2\frac{\eta }{\rho }\overrightarrow{\nabla }·D=\overrightarrow{0}$$ (1)

$$\overrightarrow{\nabla }·\overrightarrow{V}=0$$ (2)

where V is blood velocity, t is time, P is blood pressure, ρ is blood mass density, η is blood dynamic viscosity, $\overrightarrow{\nabla }$ is the gradient operator, and D is the blood rate of deformation tensor.

The governing equations for the vessel wall and stent were the momentum and equilibrium equations (21), i.e., Newton's laws of mechanics:

$$\rho a_i-{\sigma }_{ij·j}-\rho f_i=0\hspace{0.17em}\text{in}\hspace{0.17em}{{\displaystyle }}^s\Omega \left(t\right)$$ (3)

$${\sigma }_{ij}{n}_j-t_i=0\hspace{0.17em}\text{on}{}^s\mathrm{\Gamma }\left(t\right)$$ (4)

where a_i is acceleration, f_i is force per unit mass, ^sΩ(t) is the vessel domain at time t, n_j is the normal vector, t_i is the surface traction vector, σ_ij is stress, and ${}^s\mathrm{\Gamma }\left(t\right)$ is interface boundary.

The Carreau model was used to account for the shear thinning behavior of blood (a non-Newtonian property). The model has been known to accurately describe the behavior of red blood cell suspensions, and the viscosity matched closely with experimental measurements (15):

$$\mu ={\mu }_{\infty }+\left({\mu }_0-{\mu }_{\infty }\right){\left[1+{\left(\lambda \dot{\gamma }\right)}^2\right]}^{\left(n-1\right)/2}$$ (5)

where μ is the effective blood viscosity; μ_∞ (equal to 0.0035 kg·m⁻¹·s) and μ₀ (equal to 0.25 kg·m⁻¹·s) are the blood viscosities at infinite and zero shear rates, respectively; γ̇ is the shear rate; λ (equal to 25 s) is a time constant associated with the viscosity changes with shear rate; and n (equal to 0.25) is a power law index (15, 37). WSSG and OSI were computed once the respective stress components were calculated from the computational fluid dynamics analysis. The formulations of WSSG and OSI were described in previous publications (8, 11). The combined parameters CWS × WSSG and CWS × OSI were compared with IH. The product of these parameters was used because CWS, WSSG, and OSI all promote IH. Since WSS has an inverse relation with IH, the ratio (e.g., CWS/WSS) was used. To combine the solid and fluid parameters, addition or subtraction is not appropriate, as the solid and fluid stresses are orders of magnitude different (i.e., kPa vs. Pa).

Blood was modeled as incompressible with pulsatile flow based on coronary artery velocity measurements over the cardiac cycle, applied at the inlet of vessel (26). Velocity measurements were obtained using a pressure-flow combo wire (Volcano). For the outlet of the vessels, a zero traction boundary condition was imposed (30). Flow was assumed to be nonturbulent since the Reynolds number in the coronary artery is an order of magnitude lower than that for turbulence (Reynolds number > 4,000).

At the wall interface, no slip was assumed between blood and the endothelium, and the vessel wall was considered to be impermeable. Computed WSS values were averaged circumferentially and temporally for comparison with the extent of IH. The vessel wall was modeled as a nonlinear anisotropic hyperelastic material based on experimental measurements as described in detail in previous publications (9, 11, 45). The dynamic process of stent deployment was modeled by a displacement-driven time function imposed on the struts to expand the stent to the desired size. The stent struts interact and deform the compliant vessel wall by a contact algorithm. The augmented Lagrange algorithm was applied. Penetration between the stent and vessel elements was not allowed by the contact algorithm. If penetration was detected, the overlapping elements were returned to their positions at the previous time step.

RESULTS

Ten stented animals and corresponding simulations produced the IH (percent cross-sectional area stenosis) relation with WSS, WSSG, OSI, and CWS as presented below. Reynolds numbers, a measure of likelihood for turbulent flow, were calculated. The average Reynolds numbers for the computational models and stented animal vessels of the various sizing cases ranged from 100 to 130. This range is an order of magnitude smaller than the Reynolds number for the transition to turbulence (2,300–4,000) and fully turbulent (>4,000) (14); hence, the simulations were nonturbulent. The simulation results were independent of the computational time steps, as the resulting WSS patterns and magnitudes were very similar for various time steps. Although some of the figures appeared two-dimensional, they were side views of the fully 3-D models.

IVUS images showed the extent of IH covering the struts (Fig. 1). The red outlines in Fig. 1 show the lumen area and the area bounded by the struts. Correctly sized stents resulted in minimal IH, whereas the 10% oversized stent resulted in more extensive IH. The histology of a stented coronary artery (LCx) showed that even in the worst case (30% oversizing), both the IEL and EEL were intact, without any tearing or apparent injury (Fig. 1C).

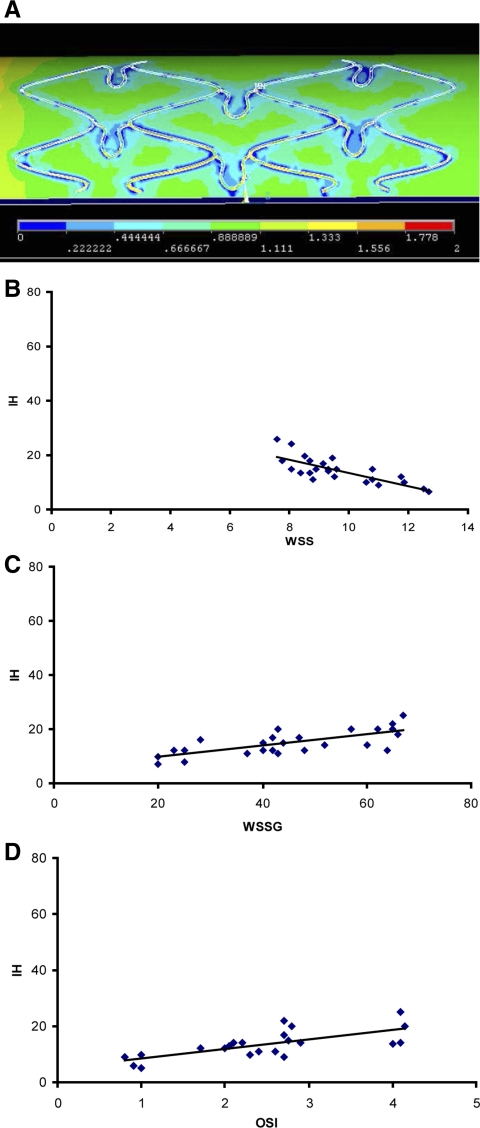
The correlations between WSS, WSSG, and OSI and IH along the axial cross-sections were statistically significant, as shown in Table 1 and Figs. 2–5. The regions of lower WSS and higher WSSG and OSI resulted in more extensive IH. As shown in Figs. 2–5, the regions closely surrounding the struts had lower WSS (1 Pa = 10 dyn/cm²). The WSS distribution and correlation with IH, in the case of a correctly sized stent, are shown in Fig. 2, A and B, respectively (linear relation). WSS values at the struts, between the struts, and in the unstented region ranged from 4–6, 7–9, and 10–12.5 dyn/cm², respectively. Figure 2, C and D, shows a linear relation between WSSG, OSI, and IH, respectively.

Table 1.

Summary of correlation relations between the various parameters and IH

	WSS, dyn/cm2	WSSG, dyn/cm3	OSI, %	CWS, kPa	CWS/WSS, ×104	CWS × WSSG, ×104 kPa·dyn/cm3	CWS × OSI, ×104 kPa·%
m	−4.75	0.41	4.80	0.06	0.28	4.54	74.04
b	71.25	6.76	8.21	1.26	8.87	19.23	18.82
R2	0.59	0.48	0.50	0.58	0.67	0.54	0.56

WSS, wall shear stress; WSSG, WSS gradient; OSI, oscillatory shear index; CWS, circumferential wall stress. Shown are the average values of R² and the following correlation equation coefficients: the slope (m) and y-intercept (b). IH = mx +b. For example, IH = −4.75WSS + 71.25. P < 0.005 for all of the above correlations.

Fig. 2.

A: wall shear stress (WSS) distribution (1 Pa = 10 dyn/cm²) with a correctly sized stent. The presence of stent struts lowers the WSS. B: a linear least-squares fit between WSS (dynes/cm²) and IH (percent area) is shown (R² = 0.61, P < 0.005). C and D: positive correlations between WSS gradient (WSSG; dyn/cm³) and the oscillatory shear index (OSI; %) and IH (percent area).

Fig. 3.

A: WSS distribution (in Pa) with a −10% undersized stent (frontal view of a three-dimensional model). The presence of stent struts lowers the WSS. B: an inverse correlation between the WSS (dyn/cm²) and IH (percent area) is shown in the case with an undersized stent. This trend was consistent with that of the stent oversizing case (R² = 0.54, P < 0.005). C and D: positive correlations between WSSG and OSI and IH.

Fig. 4.

A: WSS distribution (in Pa) with a 10% oversized stent. The presence of stent struts lowers the WSS. B: a linear least-squares fit between WSS and IH is shown (R² = 0.56, P < 0.005). C and D: positive correlations between WSSG and OSI and IH.

Fig. 5.

A: WSS distribution (in Pa) with a 30% oversized stent. The presence of stent struts lowers the WSS. B: a linear least-squares fit between WSS and IH is shown (R² = 0.62, P < 0.005). C and D: positive correlations between WSSG and OSI and IH.

For the case of an undersized stent, Fig. 3A shows the WSS distribution. WSS values near the submerged struts, between the struts, and in the unstented region ranged from 5–7, 7–8.5, and 10–11.5 dyn/cm², respectively. Figure 3B shows an inverse correlation between the WSS and IH (percent area), whereas C and D show a linear relation between WSSG and OSI and IH, respectively. This trend was consistent with that of the stent oversizing cases. Figure 4A shows the WSS distribution with a 10% oversized stent. WSS values near the struts, between the struts, and in the unstented region ranged from 3–4.5, 6–9, and 10–12 dyn/cm², respectively. Figure 4B shows an inverse correlation between the WSS and IH (percent area), and C and D show a similar linear relation between WSSG and OSI and IH, respectively. Figure 5A shows the WSS distribution with a 30% oversized stent. Generally, the stent struts lowered the WSS near the struts. WSS values near the struts, between the struts, and in the unstented region ranged from 2–3.5, 4.5–7, and 10–12 dyn/cm², respectively. Figure 5B shows an inverse correlation between the WSS and IH (percent area), whereas C and D show a similar linear relation between WSSG, OSI, and IH, respectively. For the WSS and IH data of various sizing cases, the average R² = 0.59 (P < 0.005).

The relation between CWS and IH varied linearly, as shown in Fig. 6, A and B, for the +10% and +20% stent oversized cases, respectively. Peak CWS occurred at the struts, whereas the minimum CWS occurred in the nonstented region. The ratio of maximum CWS between the +10% and +20% cases was ∼2. The regions of higher CWS resulted in more extensive IH. For the CWS and IH data of the oversized cases, the average R² = 0.58 (P < 0.005).

Fig. 6.

A: a positive correlation between solid wall stress [circumferential wall stress (CWS)] and IH is shown in the +10% sizing case (R² = 0.61, P < 0.005). B: a positive correlation between CWS and IH is shown in the +20% sizing case (R² = 0.56, P < 0.005).

A regression analysis of CWS/WSS and IH showed a highly significant linear relation for the +10% and +20% stent oversized cases (Fig. 7, A and B, respectively). For the CWS/WSS and IH data of the oversized cases, the average R² = 0.67 (P < 0.005). For the product of solid and fluid mechanical parameters (i.e., CWS × WSSG and CWS × OSI) and IH data of the oversized cases, the average R² = 0.54 and 0.56, respectively (P < 0.005; Table 1). Figure 7C shows the effect of stent sizing on the extent of IH, which was quantified as the maximum percent area stenosis.

Fig. 7.

A: a positive correlation between CWS/WSS and IH is shown in the +10% sizing case (R² = 0.68, P < 0.005). B: a positive correlation between CWS/WSS and IH is shown in the +20% sizing case (R² = 0.64, P < 0.005). C: effect of stent sizing on the extent of IH quantified as the maximum percent area stenosis in the stented region for all the data.

DISCUSSION

A significant correlation was found between WSS, WSSG, OSI, CWS, and IH along the length of the stent implant. A linear relation was found between solid (vessel wall) CWS and fluid WSSG, OSI, and IH, whereas an inverse relation was found between fluid WSS and IH. An even more highly significant linear relation was found between the ratio of CWS/WSS and the products CWS × WSSG and CWS × OSI and IH, suggesting that the effects of both strut flow disturbances and radial wall force on IH are synergistic.

The stent struts lower WSS and create an unsmooth distribution of WSS, thereby elevating WSSG, which has been found to expand intracellular gap junctions and disrupt intracellular junctions, making the vessel wall more vulnerable to the infiltration of inflammatory cells and LDL (46). Compared with the correctly sized case, oversized and undersized stents resulted in higher OSI, a measure of the extent of oscillatory behavior of flow that has been found to promote pathological processes in arteries.

Stent undersizing.

The low WSS pattern corresponding to the strut pattern may induce thrombosis, particularly in undersizing, where small gaps may be present between struts and the endothelium (Fig. 3) (16). Low WSS can cause red blood cells to adhere to each other, which may initiate the clotting cascade. Lin et al. (32) found that an initiator of the coagulation cascade, tissue factor, was upregulated by low WSS. Tissue factor catalyzes the conversion of prothrombin to thrombin. In addition, nonuniform WSS has been found to contribute to cell migration and differentiation (46). For undersized and malapposed stents, the unfilled gaps between the struts and vessel wall are highly inducive for the accumulation of red blood cells, platelets, and lipids, all of which are thrombogenic. Additionally, flow obstruction and disturbance due to the undersized struts protruding into the lumen may be inducive to thrombosis. Stent undersizing and malapposition have been recently recognized to promote stent thromosis (7).

Stent oversizing.

In the case of oversized stents, the struts were in contact with the vessel wall immediately after deployment, but they did not get embedded acutely into the wall. The embedding observed occurs weeks after stenting as IH grew over the struts. The low-WSS regions at the stent step up regions (stent edges) persist, especially in the case of DES, due to the lack of filling and smoothing effects of IH (Figs. 4 and 5). The low-WSS regions may predispose the stented vessel to thrombosis, as the adverse effects on fluid mechanics resulting from incorrect sizing may persist.

Oversizing can significantly alter WSS distributions and increase CWS, which, in turn, contributes to IH. As shown in Figs. 4 and 5, the regions closely surrounding the struts had lower WSS. The reason that the +30% sized stent had low-WSS and high-WSS regions near each other at the stent edges is most likely due to the flow diverging and then converging, altering the velocity gradient near the wall, which determines the WSS (Fig. 5). The low-WSS patterns caused by the struts may induce thrombosis as discussed earlier. Platelets and inflammatory cells can be triggered into activated states by stagnant flow and particularly low WSS (5, 44). The thrombosis associated with stent deployment may also provide a scaffold for IH, and the platelets may release PDGF, which attracts inflammatory cells. Stent oversizing creates higher intramural stresses in the vessel wall. Solid wall stresses are stimuli for inflammatory responses, contributing to the atherogenesis process (42). A significant linear relation between CWS and IH was observed (Fig. 6), especially at higher stresses. It is known that altered stress and strain within tissue (i.e., hypertension) can stimulate remodeling and cellular proliferation (21). The stent struts increase CWS, which may lead to inflammation and vessel injury. This is consistent with the recent study by Timmins et al. (44) in the femoral artery, i.e., the greater CWS, the greater IH. Arterial adventitia fibroblasts migrate to the neointima, where they differentiate into myofibroblasts and secret various extracellular matrix proteins. The highly significant linear relations between CWS/WSS, CWS × WSSG, CWS × OSI, and IH suggest that fluid and solid mechanics both influence the extent of IH (Fig. 7 and Table 1). It is plausible that the stresses (fluid and solid) act in synergy. The initial fluid WSS poststenting initiates the signal transduction for tissue remodeling. Studies by Sheehy et al. (40) and Cejna et al. (7) found that the reendothelization process takes 4–8 wk, beyond the time frame of the present study (4 wk). Therefore, the effect of the fluid forces persists. Even with the embedding process at the struts, the solid wall stress and strain still persist, i.e., the media are still affected by large strain and compression even as the neointimal tissue grows between the IEL and lumen.

An important determinant of the vessel health after stent placement is the rate and extent of in-stent reendothelialization. This is due to the fact that the new endothelial layer prevents thrombosis by isolating the thrombogenic metallic stent struts and the underlying plaque from the circulating prothrombotic factors. A possible mechanism for circulating endothelial progenitor cell deposition is that the stent deployment causes vessel wall injury, which may provoke the inflammatory response and homing of circulating endothelial progenitor cell to the injury site to deposit on the stent surface. This is analogous with smooth muscle precursor cells homing to the site of inflammation surrounding vascular plaques.

Comparison with clinical studies.

In a large clinical trial, the effect of residual stenosis (various degrees of oversizing) after stent implantation on the rate of stent restenosis was evaluated in >2,000 patients (41). They found that even 10% oversizing led to excessive IH. Both 20% and 10% oversizing led to a higher restenosis rate than 10% undersizing (residual stensosis). The IH in the various sizing cases are highly consistent with the present study (maximum area stenosis of 64.9% vs. 62% in 20% oversizing, 47.7% vs. 55% in 10% oversizing and 33.3% vs. 38% in 10% undersizing; Fig. 7C). Although the immediate lumen area after stenting was larger, the present study shows that oversizing results in significantly more IH. Interestingly, a clinical trial study by Gibson et al. (23) found that oversizing was associated with significantly increased cardiovascular events such as infarction and thrombosis.

Effect of strut thickness on IH.

A clinical trial of thick struts versus thin struts stents found a significant difference in IH (36). The difference was attributed to the large difference in strut thickness: 140 μm for Cordis BX Velocity, nearly three times as thick as the Guidant RX Multilink stents (50 μm thickness). A previous clinical trial compared different strut thicknesses of the same stent design (both of Guidant Multilink, 140 vs. 50 μm) and found similar ISR rates as the trial with Cordis vs. Guidant stents (28). Therefore, it was concluded that the strut thickness was the main factor for the difference in IH. In the present study, the strut thicknesses of the Cordis and Guidant stents were similar, 96 vs. 86 μm, and hence no significant differences in IH due to these two particular types of stents were identified.

Role of injury versus mechanotransduction.

Although IH may be caused by both cellular injury (due to overstretch) and stretch-mediated mechanotransduction due to altered mechanical forces, the primary interplay between oversizing and IH in this study is likely due to the latter. For the endothelium and vascular smooth muscle cells, the increased CWS due to stent oversizing is likely to cause injury, which promotes IH (24). Cellular or tissue injury, however, is not necessary for IH development. We performed histology on stented vessels to determine the extent of injury. We found that, even in the worst case (30% oversizing), both the IEL and EEL were intact, without any apparent disruption or tearing (Fig. 1). The IEL was stretched and the media compressed, but there was no perforation or tearing. Injury to the IEL and EEL are typically associated with extensive inflammation (47). A study by Gunn et al. (24) found that stretch of the vessel alone in stent oversizing (without any apparent wall injury) was sufficient to cause IH. They suggested that the stretch of media stimulated smooth muscle cell proliferation and migration and, thus, IH development. This is consistent with our observations stressing the media stimulated smooth muscle cell proliferation and migration.

Both low fluid shear and high solid stresses are inducive to inflammation. Low fluid shear enables inflammatory cells, such as leukocytes, to adhere to the endothelium and initiate the inflammatory process (13, 18). High solid stresses stretch the endothelium and cell gap junctions, making it easier for inflammatory cells to infiltrate into the vessel wall (42). The relationship between stresses and inflammation should be investigated in future atherosclerotic animal studies.

The effects of WSS on IH and atherogenesis have been established in the literature, where WSS has an inverse relation with IH (as determined here along the length of the stent). Furthermore, the disturbances in CWS and WSS act in synergy, as shown for the first time in this study, since the combination of these two stresses due to stent radial stretch and strut flow disturbances resulted in more highly significant correlations to IH than each individual effect.

The findings of this study suggest that an optimization of current stents may be desirable to minimize the biological response. The geometric models in the present study were created using Pro-Engineer, a 3-D CAD software based on parametric model construction. Design optimizations are possible using parametric software such as Pro-Engineer and optimization software (43). In future studies, response surface and gradient-based methods may be used to optimize various stent designs to minimize the flow disturbance and vessel wall stress.

Limitations.

One limitation of the study is that the stent deployments were operator dependent and may lead to variable injury at the time of implantation. The specifics of the stenting procedure require interventional skills and experience. An interventional cardiologist with extensive experience with stenting performed the vascular procedures consistently. Two different stent geometries were used, i.e., Guidant Multi-link Penta stent with a strut thickness of 96 μm and J&J Cordis Bx Velocity with a strut thickness of 86 μm. As the strut thicknesses of these two stents used in the present study were similar, no significant differences in IH were identified due to these two particular stents.

It is not possible to determine medial injury by IVUS, and only 30% oversizing had histological assessment. Medial injury with 30% overexpansion to the media may also have contributed to the greater neointimal response. The histology of 30% oversizing demonstrated compression of the media. This compressed state and associated stress and strain are likely to stimulate smooth muscle cell immigration from the media toward the lumen, as suggested by Gunn et al. (24). Histology of 30% oversizing was performed as this was the most severe case likely to result in vascular injury. Undersizing of 10% did not result in nearly as much IH as 30% oversizing. The reason is likely that, in undersized cases, the solid wall stress is minimal, whereas in the 30% oversized case, the solid wall stress is maximal, whereas fluid WSS is the lowest. The compression of media and potential injury is directly related to solid wall stress (CWS).

Another limitation of the present model is the assumption that the undersizing or oversizing occurs uniformly along the length of the stent. In reality, some portions of the stent may be well apposed, whereas others may not, along a nonuniform plaque. Oversizing may occur at the narrow stenotic region, and undersizing is more likely in the expanded region outside the stenosis. Given the level of complexity of such models, it is necessary to take a step-by-step approach. Since the animals used in the present study were healthy, plaque components were not modeled. The multilayer and plaque structures can be modeled in future studies.

Furthermore, arteries may be tortuous but become straight once the stent is implanted. Since the clinically observed restenosis mainly occurs within the stented region, a straight segment was simulated here. Stent tapering was not considered in the present model as the lack of tapering was confirmed by IVUS imaging. Prolapse of tissue between the struts was not modeled, which may influence intrastrut WSS. This effect is not expected to be nearly as significant as the effect of stent struts.

Finally, bare metal stents were used in this study to avoid the suppression of IH as with DES. These findings may also be relevant for DES, however, since when drug elution is completed, IH can still occur due to the presence of mechanical disturbances created by the stent. Paradoxically, the lack of tissue remodeling and filling in the case of DES may make the low WSS profile persists longer than in the case of bare metal stent and may predispose the stented region to late thrombosis.

Summary.

This study underscores the role of CWS and WSS in IH. These direct relations between CWS, WSS, and IH provide a basis for future additional experiments to connect vessel biology and function to stent biomechanics. One major finding is that optimal stenting requires correct sizing of the stents, as both oversizing and undersizing are highly inducive to IH and may additionally create local conditions that predispose to thrombosis. These findings may also lead to improved stent designs that reduce strut-induced flow disturbances as well as solid wall stresses.

GRANTS

This research was supported in part by National Heart, Lung, and Blood Institute Grants HL-087235 and HL-084529 (to G. S. Kassab) and HL-062552 (to M. Sturek).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: H. Y. C., A. K. S., J. S. C., H. Z., and D. B. performed experiments; H. Y. C., J. S. C., H. Z., M. S., B. B., and D. B. analyzed data; H. Y. C., A. K. S., J. S. C., M. S., B. B., D. B., and G. S. K. interpreted results of experiments; H. Y. C. and G. S. K. edited and revised manuscript; H. Z. and B. B. prepared figures; M. S. conception and design of research; G. S. K. approved final version of manuscript.