Role of intra-abdominal pressure in the unloading and stabilization of the human spine during static lifting tasks

Abstract

The role of intra-abdominal pressure (IAP) in unloading the spine has remained controversial. In the current study, a novel kinematics-based approach along with a nonlinear finite-element model were iteratively used to calculate muscle forces, spinal loads, and stability margin under prescribed postures and loads measured in in vivo studies. Four coactivity levels (none, low, moderate, and high) of abdominal muscles (rectus abdominis, external oblique, and internal oblique) were considered concurrently with a raise in IAP from 0 to 4 kPa when lifting a load of 180 N in upright standing posture and to 9 kPa when lifting the same load in forward trunk flexions of 40° and 65°. For comparison, reference cases with neither abdominal coactivity nor IAP were investigated as well. A raise in IAP unloaded and stabilized the spine when no coactivity was considered in the foregoing abdominal muscles for all lifting tasks regardless of the posture considered. In the upright standing posture, the unloading action of IAP faded away even in the presence of low level of abdominal coactivity while its stabilizing action continued to improve as abdominal coactivity increased to moderate and high levels. For lifting in forward-flexed postures, the unloading action of IAP disappeared only with high level of abdominal coactivities while its stabilizing action deteriorated as abdominal coactivities increased. The unloading and stabilizing actions of IAP, hence, appear to be posture and task specific.

Introduction

An estimation of spinal loads, trunk-muscle forces, and stability of the human trunk during various activities, especially lifting that has been associated with higher incidence of back disorders [23, 39], is essential to properly assess the risk of injury in various loading conditions and postures. The prevention, treatment, and rehabilitation programs would subsequently benefit from such improved knowledge. One parameter with the potential to influence spinal mechanics and stability is intra-abdominal pressure (IAP) that has been reported to increase during static and dynamics lifting tasks [1, 5, 24, 27, 34, 45, 46, 52, 54]. For years, it has been argued that an increase in IAP could unload the spine both directly by pressing upwards on the rib cage via diaphragm and indirectly by generating an extensor moment on the lumbar spine that decreases the back-muscle activities [5, 20–22, 31, 36–38, 41, 54]. This relief mechanism has also been suggested as a remedy to the paradox in biomechanical model predictions in which the spinal loads exceed tissue-tolerant limits during heavy lifts [9, 19]. Accordingly, abdominal belts have been recommended with the objective to increase IAP and unload spine [36, 43].

Experimental studies, however, have found that IAP increase is associated with a concurrent increase in the intradiscal pressure during Valsalva maneuvers [55] and no reduction in erector spinae activity in lifting [42, 52]; thus raising questions on the unloading role of IAP. The co-contraction of abdominal muscles occurring along with an increase in IAP produces a flexor moment, large enough to offset or even exceed the IAP-generated extensor moment [11, 49, 52]. Large cross-sectional area of the diaphragm and the moment arm of the net IAP force considered in biomechanical model studies have been suggested to be the reason for overestimation of auxiliary extensor moment generated by IAP [49, 51].

The controversy on the unloading role of IAP [14, 22] is partly due to uncertainties about the magnitude and pattern of abdominal muscle coactivities that occur with an increase in IAP. Studies that advocate the unloading effect of IAP usually consider a raise in IAP to be primarily due to the activity of transverse abdominis (TA) whose fibers are mostly oriented in the transverse plane thus imposing little or no compression penalty on the lumbar spine [20–22, 37]. On the other hand, others insist that appreciable increase in IAP cannot develop without simultaneous coactivity of all the abdominal muscles including internal oblique (IO), external oblique (EO), and rectus abdominis (RA) whose activity would counterbalance the upward unloading force and generated extensor moment due to IAP [11, 14]. Inability of biomechanical models to accurately partition the loads among the trunk active–passive components and evaluate spinal loads remains as another reason for the existing controversy. The predictions of EMG-driven models on the effect of IAP on spinal loading and stability [11, 49] are only as accurate as the many underlying assumptions made in their formulation and the spine model used. Moreover, model studies advocating unloading role of IAP during maximum back exertions have considered the TA as the only abdominal muscle that generates IAP and have neglected spinal passive moment even in forward-flexed postures [21].

Normal function of IAP in the unloading of the spine cannot adequately be investigated during the Valsalva maneuver or maximum voluntary strength exertions in which the concurrent presence of abdominal coactivities and IAP at high levels likely offset one another [37]. The current study was set to delineate the role of IAP on muscle forces and spinal loads during regular static lifting activities involving standing and forward-flexed postures. The kinematics-based approach combined with a nonlinear finite-element model of spinal active–passive components was applied to estimate trunk-muscle forces, spinal loads, and stability [3, 30, 67]. This realistic nonlinear finite-element model circumvents many shortcomings in other biomechanical models by accounting for kinematics and kinetics conditions as well as passive–active synergies at all the spinal levels. Direct in vivo measurements under the same postures and loads are used to both provide prescribed kinematics into the model and validate model predictions with measured EMG activities. It is hypothesized that (a) the beneficial role of IAP in unloading the spine would depend on the magnitude of IAP and relative coactivity of the abdominal muscles and (b) an increase in IAP with or without concurrent abdominal co-activation would stabilize the spine. Determination of the extent of abdominal coactivity beyond which the beneficial unloading and stabilizing effects of IAP disappear is the objective of this work.

Methods

In vivo measurement

More details for both in vivo and finite-element model studies can be found elsewhere [3, 30, 67]. Kinematics of the spine under standing posture as well as trunk flexions of 40° and 65° with 180 N in hands were measured in fifteen healthy males (age 30±6 years, height 177±7 cm, mass 74±11 kg) using infrared light-emitted markers, LED, attached on the skin at the tip of T1, T5, T10, T12, L1, L3, L5, and S1 spinous processes. Three extra LED markers were placed on the posterior–superior iliac spine and ilium (left/right iliac crests) for evaluation of pelvic rotation, and one on the load to track the position of weights in hands. A three-camera Optotrak system (NDI International, Waterloo, ON, Canada) was used to collect the 3D coordinates of the LED markers. Simultaneously, five pairs of surface electrodes were positioned bilaterally over longissimus dorsi (~3 cm lateral to midline at the L1), iliocostalis (~6 cm to midline at the L1), multifidus (~2 cm to midline at the L5), EO (~10 cm to midline above umbilicus and aligned with muscle fibers), and RA (~3 cm to midline above the umbilicus). The raw EMG signals were amplified, band-pass filtered at 10–400 Hz by a second order Butterworth filter, rectified over 4 s trial duration and averaged for both sides. For normalization, EMG data at maximum voluntary contraction (MVC) was collected in standing (in cardinal planes while loaded via a strapped harness), prone, and supine positions.

Thoracolumbar finite element model

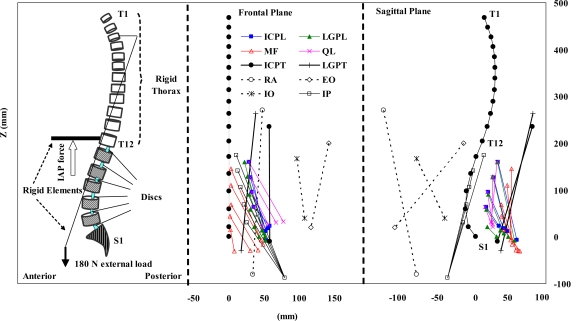
A sagittally symmetric T1–S1 beam rigid-body model consisting of six deformable beams to represent T12–S1 segments and seven rigid elements to represent T1–T12 (as a single body) and lumbosacral vertebrae (L1–S1) was used (Fig. 1). The nonlinear load–displacement response under single and combined axial/shear forces and moments along with the flexion versus extension differences were represented in this model based on numerical and measured results of previous single- and multi-motion segment studies [59, 60, 66, 67, 75]. In all cases, based on the mean body weight of our subjects and percentage of body weight at each motion segment level reported elsewhere [62, 70], a gravity load of 387 N was distributed eccentrically at different segmental levels. To simulate the external load carried symmetrically in hands, 180 N was applied at the location measured in vivo via a rigid element attached to the T3 vertebra (Fig. 1).

Fig. 1.

The FE model as well as global and local musculatures in the sagittal and frontal planes (only fascicles on one side have been shown). ICPL iliocostalis lumborum pars lumborum, ICPT iliocostalis lumborum pars thoracic, IP iliopsoas, LGPL longissimus thoracis pars lumborum, LGPT longissimus thoracis pars thoracic, MF multifidus, QL quadratus lumborum, IO internal oblique, EO external oblique, and RA rectus abdominus

Prescribed postures

Mean measured sagittal rotations at the upper torso (evaluated based on the change in the inclination of the line attaching the T1 marker to the T12 one) and pelvis (evaluated based on the change in the orientation of the normal to the plane passing through the markers on the pelvis) were prescribed onto the model at the T12 and S1 levels, respectively. As for the individual lumbar vertebrae, the total lumbar rotation, calculated as the difference between the foregoing two rotations, was partitioned in accordance with the proportions reported in earlier investigations; i.e., 8% at T12–L1, 13% at L1–L2, 16% at L2–L3, 23% at L3–L4, 26% at L4–L5, and 14% at L5–S1 [29, 61, 63, 64, 75].

Intra-abdominal pressure

The magnitude of IAP while holding 180 N in hands was taken as 4 kPa in the standing posture [53] and 9 kPa at trunk flexions of 40° and 65° [31, 53] (Table 1). The diaphragm areas and total force magnitudes/lever arms considered in different cases are also listed in Table 1. The IAP was represented by an upward force applied to the thorax via a rigid element attached to the T12 level. The direction of this force was taken in the vertical direction in the case simulating the upright posture. For the forward-flexion simulations, however, this force changed the direction to follow the thorax rotation (Fig. 1).

Table 1.

Characteristics considered for the application of IAP in the model

Task (+180 N in hands)	IAP (kPa)	Area (cm2)a	Total force (N)	Lever arm at T12 (cm) *	Extensor moment (N m) at T12
Standing posture	4	200	80	4.0	3.2
Flexion 40° and 65°	9	250	225	5.0	11.25

^aDaggfeldt and Thorstensson [21]

Abdominal muscle coactivity

Among the abdominal muscles (IO, EO, and RA), the largest and smallest coactivity during lifting tasks has been observed in IO and RA, respectively [15, 28, 31, 57, 68]. To simulate a wide range of likely situations in the model, therefore, three different levels of relative coactivity were considered in the abdominal muscles: (1) low level: RA 0.5%, EO 1%, IO 2%; (2) intermediate level: RA 1%, EO 2%, IO 4%, and (3) high level: RA 2%, EO 4%, IO 8%. These activities were considered as a percentage of the maximum active force, which in turn was calculated for each abdominal muscle as its physiological cross-section area (PCSA) (Table 2) times the maximum active stress (taken as 0.6 MPa) (see Table 3). Additional cases were also studied in which the above coactivities were neglected altogether in which cases, IAP was assumed to be solely generated by the TA activation. Moreover, reference cases were considered for comparison where neither IAP nor abdominal coactivity was represented.

Table 2.

Physiological cross-sectional area (PCSA, mm²) and initial length (in parentheses, mm) for muscles on each side of the spine at different insertion levels

Local muscles	ICPL	IP	LGPL	MF	QL
L1	108 (170)	252 (276)	79 (172)	96 (158)	88 (137)
L2	154 (118)	295 (241)	91 (132)	138 (135)	80 (104)
L3	182 (84)	334 (206)	103 (88)	211 (106)	75 (74)
L4	189 (50)	311 (169)	110 (52)	186 (82)	70 (46)
L5	–	182 (132)	116 (25)	134 (51)	–

Global muscles	RA	EO	IO	ICPT	LGPT
T1-T12	567 (353)	1576 (239)	1345 (135)	600 (250)	1100 (297)

ICPL iliocostalis lumborum pars lumborum, ICPT iliocostalis lumborum pars thoracic, IP iIliopsoas, LGPL longissimus thoracis pars lumborum, LGPT longissimus thoracis pars thoracic, MF multifidus, QL quadratus lumborum, IO internal oblique, EO external oblique, RA rectus abdominus

Table 3.

Three levels of abdominal muscle coactivity and the generated force/flexor moment

Level	% Coactivity	Force on each side (N)a	Lever arm at T12 (mm)		Flexor moment (N m) at T12
1—Low	RA: 0.5	1.7	S	140.0	0.48
			F40	150.0	0.51
			F65	151.2	0.51
	EO: 1	9.5	S	17.7	0.33
			F40	12.0	0.23
			F65	10.9	0.21
	IO: 2	16.1	S	98.7	3.19
			F40	98.4	3.18
			F65	98.8	3.19
2—Moderate	RA: 1	3.4	S	139.9	0.95
			F40	150.0	1.02
			F65	151.2	1.03
	EO: 2	18.9	S	17.7	0.67
			F40	12.0	0.45
			F65	10.9	0.41
	IO: 4	32.3	S	98.8	6.38
			F40	98.5	6.36
			F65	98.9	6.38
3—High	RA: 2	6.8	S	140.0	1.91
			F40	149.9	2.04
			F65	151.1	2.06
	EO: 4	37.8	S	17.6	1.33
			F40	12.0	0.91
			F65	10.9	0.82
	IO: 8	64.6	S	98.7	12.75
			F40	98.6	12.74
			F65	99.0	12.79

S standing posture, F40 flexion posture at 40°, F65 flexion posture at 65°

^a(0.6 MPa)×PCAS×(% Coactivity)

Muscle model and muscle force calculation

A sagittally symmetric muscle architecture with 46 local (attached to lumbar vertebrae) and 10 global (attached to thoracic cage) muscle fascicles was used (Fig. 1; Table 2) [8, 69]. To evaluate muscle forces, kinematics-based algorithm was employed to solve the redundant active–passive system subjected to the prescribed measured kinematics and external loads. In this manner, the calculated muscle forces at each instance of loading were compatible with the prescribed kinematics (i.e., posture) and external loading while accounting for the realistic nonlinear stiffness of the passive system. Each sagittal rotation applied a priori at all the spinal levels of the model generated an equilibrium equation at that level in the form of 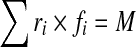(r muscle lever arm, f muscle force, and M the required sagittal moment due to the applied rotation). To resolve the redundancy problem, an optimization approach with the cost function of minimum sum of cubed muscle stresses was used along with inequality equations of unknown muscle forces remaining positive and greater than their passive force components (calculated based on muscle strain and a tension–length relationship [25]) but smaller than the sum of their respective maximum forces (i.e., 0.6 PCSA) and the passive force components. Once muscle forces were calculated, the axial compression and horizontal shear penalties of these muscle forces were fed back into the finite-element model as additional updated external loads. This iterative approach was continued till convergence was reached. The finite-element program ABAQUS (Hibbit, Karlsson & Sorensen, Inc., Pawtucker, RI, version 6.5) was used to carry out nonlinear structural analyses while the optimization procedure was analytically solved using an in-house program based on lagrange multipliers method [65].

Stability analyses

In each simulation case, after the muscle forces were calculated, the model was modified with uniaxial elements replacing the muscles between their insertion points. Stiffness of each uniaxial element, k, was assigned using the linear stiffness–force relationship k=qF/l (F known muscle force, l instantaneous muscle length, q muscle-stiffness coefficient chosen a priori) [6, 18]. Nonlinear analyses under same external loads and prescribed pelvic tilt were performed for different q values thus identifying the critical q below which the system ceased to be stable. These nonlinear analyses under applied forces serve as the gold standard to evaluate the system stability and to verify the validity of the calculated muscle forces under the prescribed kinematics performed in the earlier stage of the analysis. In addition to the nonlinear analyses, linear buckling and perturbation analyses at loaded, deformed, configurations were also carried out as complementary approaches to estimate trunk stability margin as a function of q.

Results

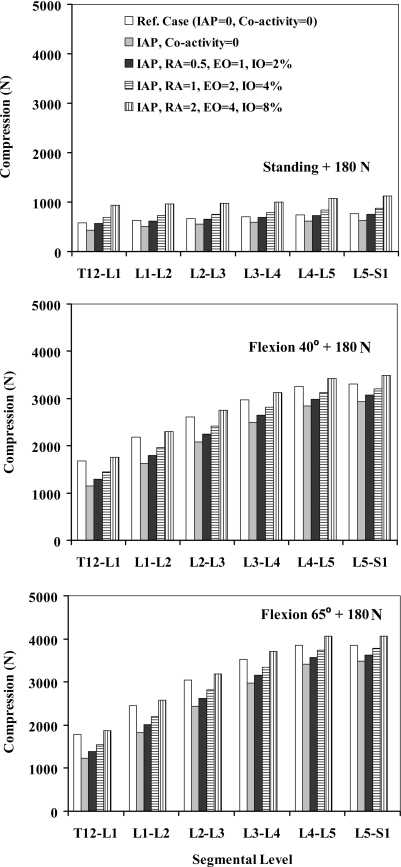
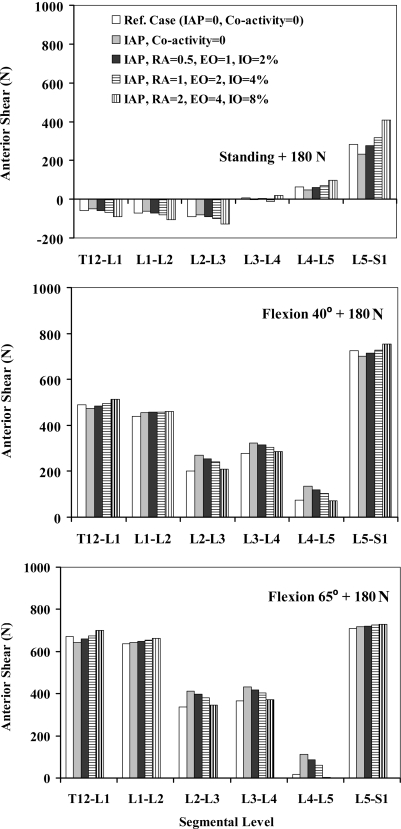
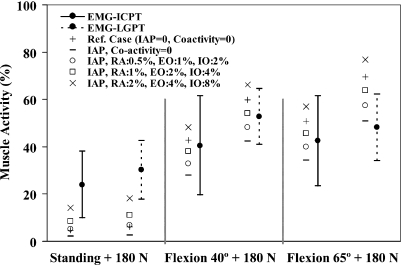
Forces in abdominal muscles and associated moments at the T12 level were calculated based on the prescribed percentage of coactivities, muscle PCSAs, and lever arms at deformed configurations (Table 3). In all the tasks, when IAP was introduced into the model without any concurrent coactivity in abdominal muscles, the spine was markedly unloaded in compression at all the levels and in all the tasks considered (Fig. 2). Shear forces decreased at all the levels in upright posture whereas they generally increased in flexion tasks (Fig. 3). Furthermore, the activity of thoracic (global) extensor muscles considerably dropped due to the extensor moment generated by IAP (Fig. 4).

Fig. 2.

Axial compression (N) acting normal to different intervertebral disc levels (T12/S1) in reference cases (no IAP and no abdominal coactivity) and four cases with different abdominal coactivities along with IAP of 4 kPa when lifting a load of 180 N in upright standing posture and of 9 kPa when lifting the same load in forward trunk flexions of 40° and 65°

Fig. 3.

Anterior–posterior shear force (N) acting parallel to mid-planes of different intervertebral disc levels (T12/S1) in reference cases (no IAP and no abdominal coactivity) and four cases with different abdominal coactivities along with IAP of 4 kPa when lifting a load of 180 N in upright standing posture and of 9 kPa when lifting the same load in forward trunk flexions of 40° and 65° °

Fig. 4.

Normalized in vivo measured EMG activity (mean ± SD) of thoracic extensor muscles (LGPT and ICPT) for different lifting tasks. Predictions have also been shown in reference cases (no IAP and no abdominal coactivity) and four cases with different abdominal coactivities along with IAP of 4 kPa when lifting a load of 180 N in upright standing posture and of 9 kPa when lifting the same load in forward trunk flexions of 40° and 65°

When coactivity of abdominal muscles was also introduced into the model along with IAP, the foregoing decreasing trend in the axial compression reversed at all spinal levels and under all tasks (Fig. 2). As a result of changes in global extensor muscle activity (Fig. 4), the beneficial role of IAP actually disappeared and even reversed in upright standing posture for all coactivity levels and in flexion postures under the highest activity considered. Although larger abdominal coactivity increased the segmental shear forces in the standing posture, the effect was less pronounced in flexion tasks (Fig. 3).

Neglecting IAP and abdominal coactivity (i.e., in reference cases), the spinal stability substantially improved as the trunk flexed forward from upright standing (critical q=17) to 40° and 65° positions (critical q=0). Introduction of IAP alone into the model without any abdominal coactivity improved spinal stability in all the tasks considered (e.g., q decreased from 17 to 14 in the standing posture). The presence of abdominal (RA, EO, and IO) coactivity consistently increased the spinal stability in standing posture (e.g., q decreased to 10 and further to 8 for the low and intermediate levels of abdominal coactivities, respectively). In flexion tasks, critical q remained always equal to 0 while linear stability analyses demonstrated a slight decrease in the system stability margin. The stability margin in flexion tasks, however, slightly improved in all the cases when compared with the reference cases in which neither IAP nor abdominal coactivity were considered.

Discussion

The main objective of this study was to investigate the effect of IAP in concurrence with different activity levels of abdominal muscles on extensor muscle forces, spinal loads, and system stability during static lifting tasks in both upright standing and forward-flexed postures carrying 180 N in hands. A novel kinematics-based finite-element approach was used in which the a priori measured kinematics of the spine were prescribed into a nonlinear finite-element model to evaluate muscle and internal loads resulting in a synergistic solution of the active–passive system [3, 30, 67]. This iterative approach not only satisfied the equilibrium equations in all the directions along the entire length of the spine but also yielded spinal postures in full accordance with IAP/external/gravity loads, muscle forces, and nonlinear ligamentous stiffness properties. The stability margin of the spine under muscle forces, kinematics, and IAP/gravity/external loads considered were subsequently determined.

In agreement with other studies [21], the IAP values considered in this study (i.e., 4 kPa in standing and 9 kPa in flexion tasks) unloaded the compression on the spine by a mean value of ~19% at all the levels when no concurrent coactivity was considered in the abdominal muscles (RA, EO, and IO). In these cases, the activity of both the thoracic extensor muscles (LG and IC) decreased by ~55% in standing and ~30% in flexion tasks. In the presence of low coactivity in abdominal muscles (level 1: RA 0.5%, EO 1%, IO 2%), the unloading effect of IAP in the standing posture faded away while that in flexion tasks reduced to a mean of ~13% at all the levels (Fig. 2). In this case, in the standing posture, the activity of thoracic extensors very slightly exceeded their reference values computed under no IAP and no abdominal coactivity (Fig. 4). In flexion tasks, as the abdominal coactivity further increased to the moderate level, the IAP unloaded the spine by an average of only ~7% (level 2: RA 1%, EO 2%, IO 4%) while at the highest level of abdominal coactivity (level 3: RA 2%, EO 4%, IO 8%), compression on the spine actually increased on an average by ~5% at all the levels (Fig. 2). Accordingly, the activity in extensor muscles increased beyond that in the reference case only in the case with the highest abdominal coactivity (Fig. 4). These results confirm the first hypothesis of the study that IAP has the potential to substantially unload the spine in standing and flexion tasks, a role that depends directly on the IAP magnitude and concurrent level of coactivity in abdominal muscles in such tasks. That is, IAP could indeed even increase the back-muscle forces when large coactivity is generated in the IO, EO, and RA muscles. The hypothesis of the study regarding the stabilizing effect of abdominal coactivities in various tasks in presence of IAP, however, was only confirmed in standing postures and not in flexion tasks in which a slightly lower stability margin was predicted when higher levels of abdominal coactivity were considered.

Methodological remarks

The assumption of rigid body motion at the T1–T12 segments (upper torso) was confirmed, in agreement with others [58], by measuring nearly equal rotations at lines attaching either the markers T12–T5 or markers T12–T1. The assumption of global extensor muscles as straight lines attaching the pelvis to the upper thorax may be a crude one when the lumbar spine approaches full flexion in which case, these muscles wrap around the surrounding tissues. Although the simulated tasks in this study involved rotations of the thorax much smaller than those at full flexion, determination of the extent of such a consideration on the results needs additional studies. The Latissimus dorsi, lumbodorsal fascia, and intersegmental/multisegmental muscles were neglected. Latissimus dorsi has been known to produce trunk extensor moment via the lumbodorsal fascia; a contribution suggested not being sizable during the lifting tasks [7, 50]. For the reference cases in which no coactivity was assumed in concurrence with IAP, the IAP was assumed to be generated solely by TA coactivity. In this case, fascicles of TA were considered to be oriented in the transverse plane without having any axial compressive force penalty despite the fact that some of its fascicles especially in the middle and lower regions are somewhat oblique [72]. Other abdominal muscles (RA, EO, and IO) were all modeled by a single fascicle. A consideration of several fascicles instead of just one for oblique muscles (EO and IO) has influenced the estimated spinal loads significantly in asymmetric lifting tasks but only slightly in symmetric ones [26]. The values for IAP, intra-abdominal area, and the level arm of the intra-abdominal force were all selected from those reported in the literature for the tasks similar to the ones considered in this study (Table 1).

For qualitative comparison of predicted extensor muscle activities with EMG data (Fig. 4) as well as to calculate the abdominal muscle forces, the maximum allowable muscle stress of 0.6 MPa was assumed for all the muscles, which is in the mid-range of those in the literature (0.3–1.0 MPa) [26, 33]. It is important to emphasize that any changes in this maximum stress value would directly influence the forces considered in the abdominal muscles for different cases. The passive tension–length relationship was also assumed to be the same for all the muscles despite the fact that the specific architecture of each muscle could influence this relationship [74]. The passive tension–length curve used in the current study was adapted from recent experimental data [25], which is in the range of those reported by others [48, 58, 74]. It is important to emphasize that the passive force–length and stiffness relations considered for muscles in the current study have absolutely no bearing at all on the predicted spinal loads and muscle forces. The partitioning of the calculated muscle forces into active and passive components in post-processing of the data (Fig. 4) would, however, be influenced by the choice of passive force–length relationship. The cost function of the minimum sum of cubed muscle stresses used in the optimization algorithm has been recognized to predict muscle activities in agreement with the EMG data [40, 73].

IAP and abdominal coactivity values

The IAP during maximum voluntary exertion or Valsalva manoeuvre has reached as high as 26.2 ± 9.6(mean±SD) kPa [11], 28 kPa [32], ~19 ± 6 kPa [21], 26.6 ± 6.7 kPa [35], and 38.8 ± 5.2 kPa [31]. It has been reported to reach 50 kPa in power-competitive lifters wearing belt [52]. In neutral standing posture without carrying any load in hands, IAP has been measured as low as 0.2 kPa [2], 0.3 kPa [46], and 0.98 kPa [55]. The magnitude of 4 kPa considered in this study for IAP in the standing posture with 180 N in hands is in the upper range of reported values (~0.5–4 kPa) [2, 53, 55]. Different IAP measurement techniques could influence the recorded data [2]. Although the choice of this value would undoubtedly influence the predictions but the conclusion regarding the ineffectiveness of IAP in unloading the spine in standing postures based on the assumed value of 4 kPa would remain unchanged. This is due to the large flexor moment produced by abdominal muscles, especially IO, even in the presence of low coactivity levels.

Large scatter also exists in the magnitude of IAP reported for forward-flexed postures; however, there is a general consensus that IAP increases as trunk flexion and moment increase [2, 9, 21, 49, 53, 55]. The magnitude of 9 kPa considered in this study for IAP in flexion tasks with load in hands is at the middle range of mean values reported in the literature (1–21 kPa) [2, 31, 36, 44, 52, 53, 55].

Despite general accord in the literature that IO is much more active than RA in lifting tasks; there is a large variation in the reported normalized activity in the abdominal muscles [15, 28, 31, 57, 68]. This discrepancy could partly be due to different techniques used to measure MVC activities required for EMG normalization. In the present study, the forces considered in abdominal muscles could correspond to much greater muscle activity levels; had a smaller allowable stress been assumed; the same forces would correspond to abdominal activities increased by twofold when the maximum stress of 0.6 MPa is replaced by 0.3 MPa.

Unloading effect of IAP in standing postures

Our results suggest that IAP could hardly unload the spine in standing postures unless if no or very low coactivity occurs in the abdominal muscles. The lowest abdominal activity in this study (RA 0.5%, EO 1%, and IO 2%) generated ~4 N m flexor moment (Table 3) that exceeded 3.2 N m extensor moment due to IAP (Table 1). To compensate this additional flexor moment, slightly larger forces were needed in the extensor muscles, which exceeded those in the reference case with no IAP/coactivity (Fig. 4). This, in turn, resulted in an increase in spine compression at all the levels that offset almost all the beneficial unloading action of IAP (Fig. 2).

The foregoing flexor moment of 4 N m is mainly produced by IO (~3.2 N m) due to its relatively large level arm with respect to the thorax and large PCSA. In vivo studies demonstrate that TA and IO are the most active muscles during back-extension activities [5, 15, 28, 31, 49, 57, 68]. Fascicles of IO are suggested to be primarily oriented transversely in which case, similar to TA, they would not cause appreciable flexor moment and axial compression penalties on the spine [20, 22]. Although this might be true for IO fascicles at lower regions [56, 72] the remaining fascicles attaching iliac crest and rib cage are oriented obliquely at ~50–75° to the horizontal plane [69, 72] which can generate considerable flexor moment and axial compression on the spine. Those fascicles of IO which are oriented more transversely may redirect their force to the RA sheath via linea semilunaris to enhance their effective moment arm [47].

Using a biomechanical model of the lumbar spine in which IAP was introduced with no concurrent abdominal coactivities, it was claimed that IAP can unload the spine at all levels by ~400 N (34–40% of total compression) during maximal back extension in an extended posture when lying on the side [21]. In direct contrast, in another biomechanical model study in which only the coactivity of abdominal muscles was incorporated into the model without IAP, abdominal coactivities were found to overload the spine by ~500 N at the L5–S1 level (22% of total compression) when holding 22.5 kg in hands in the erect posture [28]. Our results demonstrate that it is extremely important to consider both abdominal coactivities and IAP into a biomechanical model of upright standing postures. In support of others [11], our results refute the unloading role of IAP in standing postures in the presence of even low coactivity in IO acting alone or along with other abdominal muscles.

Unloading effect of IAP in flexion tasks

Based on the results of this study, it appears that the unloading effect of IAP is more prevalent in flexion tasks in which only the highest abdominal coactivity level (RA 2%, EO 4%, IO 8%) erased the beneficial unloading effect of IAP (Fig. 2). This relative effectiveness in flexion as compared with the upright posture is mainly due to the larger IAP, greater IAP area, and lever arm in flexion which generate ~11.3 N m extension moment. Given that the coactivity of IO, as the primary flexor generating abdominal muscle flexion, decreases in the forward flexion as reported in the literature [28, 48], the possible unloading effect of IAP under flexion could then become more important. The coactivity of both RA and EO has been measured by some to decrease in forward-flexion tasks compared to the standing postures [3, 10, 71] while others report an opposite trend [28, 55]. If indeed a fall in abdominal muscle (RA, EO, and IO) coactivities occur from standing to flexed postures, then the increase in IAP from standing posture to flexed posture should be provided mainly by contraction of the TA, diaphragm and pelvis floor muscles. Intra-muscular EMG measurements [15–17] as well as model studies [4, 21] have also provided evidence that the TA is the most significant contributor to raising IAP during back extension.

Stability

There is a general consensus that an increase in IAP stabilizes the spine; however, the mechanism behind this stabilizing action is not yet well understood. One such mechanism is based on the premise that any increase in IAP is accompanied by the co-contraction of abdominal muscles, which in turn increase the spinal stiffness and stability [12, 13]. In this case, it is assumed that the generated flexor moment due to abdominal coactivities cancel out the extensor moment produced by IAP thus requiring no additional activity in extensor muscles. Our results demonstrate that, in the upright standing posture, the combination of IAP and abdominal coactivity generates a net flexion moment that is offset by additional back-muscle activity. Therefore, the associated improvement in stability observed in the current study is due to increases in both abdominal and extensor muscle activities in the presence of IAP. On the other hand, such was not the case for lifting tasks in flexion in which spinal stability slightly deteriorated as abdominal coactivities increased. In these postures, since no muscle stiffness was needed to provide the stability (critical q=0), any increase in muscle activities would augment compression on the spine causing a drop in the critical load of the structure.

Conclusion

The unloading and stabilizing actions of IAP seem to be posture and task specific. While the stabilizing effect of IAP and the concurrent abdominal coactivity in the upright standing posture is evident, the ability of IAP to unload the spine holds true only for very low abdominal coactivities or for the case in which only TA is responsible for any increase in IAP. In contrast, the unloading action of IAP appears more effective in forward-lifting tasks while its stabilizing role disappears. This study is the first to satisfy all requirements: kinetics, kinematics, and stability at all spinal levels in the presence of gravity, external load, extensor/flexor muscle activations, and IAP.