Abstract
Studies of intermanual transfer have been used to probe representations formed during skill acquisition. We employ a new method that provides a continuous assay of intermanual transfer, intermixing right- and left-hand trials while limiting visual feedback to right-hand movements. We manipulated the degree of awareness of the visuomotor rotation, introducing a 22.5° perturbation in either an abrupt single step or gradually in ∼1° increments every 10 trials. Intermanual transfer was observed with the direction of left-hand movements shifting in the opposite direction of the rotation over the course of training. The transfer on left-hand trials was less than that observed in the right hand. Moreover, the magnitude of transfer was larger in our mixed-limb design compared with the standard blocked design in which transfer is only probed at the end of training. Transfer was similar in the abrupt and gradual groups, suggesting that awareness of the perturbation has little effect on intermanual transfer. In a final experiment, participants were provided with a strategy to offset an abrupt rotation, a method that has been shown to increase error over the course of training due to the operation of sensorimotor adaptation. This deterioration was also observed on left-hand probe trials, providing further support that awareness has little effect on intermanual transfer. These results indicate that intermanual transfer is not dependent on the implementation of cognitively assisted strategies that participants might adopt when they become aware that the visuomotor mapping has been perturbed. Rather, the results indicate that the information available to processes involved in adaptation entails some degree of effector independence.
Keywords: awareness, motor adaptation, motor learning, motor skills, transfer
people flexibly use either hand to execute simple movements, such as reaching for a cup of coffee or opening a door, and do so with seemingly equal precision. In contrast, skilled movements, especially those involving tools, are performed much more proficiently with the dominant limb. Indeed, we may rarely use the nondominant limb to hold a toothbrush, swing a squash racquet, or cut with scissors. However, when required to use the nondominant limb, perhaps while recovering from a broken bone, people show a reasonable degree of competence. How does the nondominant limb become proficient with these skilled movements? Does it learn from observing years of dominant hand use, or are aspects of the skilled transferred from the right hand to the left hand at the time of execution?
Previous studies have investigated the transfer of motor learning between limbs. A common method is to train participants to overcome a visuomotor perturbation with one limb and then examine performance with the untrained limb. After adaptation to a visuomotor rotation with one limb, a substantial benefit is observed during testing with the untrained limb (Cunningham and Welch 1994; Imamizu and Shimojo 1995; Sainburg and Wang 2002). Adaptation to novel inertial loads (Wang and Sainburg 2004) and force fields (Criscimagna-Hemminger et al. 2003; Dizio and Lackner 1995; Malfait and Ostry 2004) also exhibits transfer between the limbs.
The pattern of intermanual transfer suggests that the motor system learns to adapt movements to offset an environmental perturbation. After training with the right arm on a leftward visual shift, the left arm will show rapid learning for leftward shifts and greater interference for rightward shifts (Cunningham and Welch 1994; Imamizu and Shimojo 1995; Sainburg and Wang 2002). Learning to a move in a novel force field also exhibits transfer in extrinsic coordinates (Criscimagna-Hemminger et al. 2003; Dizio and Lackner 1995; Malfait and Ostry 2004). For example, to counteract a rightward force on a reaching movement with the right arm, the motor system may increase flexion/adduction of the biceps, anterior deltoids, and pectoralis major. However, when moving with the left limb, one observes increased extension/abduction of the triceps and posterior deltoids, indicating that the system has learned to anticipate a rightward force. This latter finding is surprising given that intralimb adaptation appears to occur mainly in intrinsic coordinates (Shadmehr and Mussa-Ivaldi 1994).
This difference in reference frames raises the possibility that at least some of the processes underlying intermanual transfer may be unrelated to processes involved in adaptation. Cognitive processes have been suggested, since participants are aware of the experimental perturbations, which results in large performance errors (Malfait and Ostry 2004). The role of awareness in adaptation, or more specifically, strategies that could be developed in response to awareness, has proven to be a controversial topic (Martin et al. 1996; Mazzoni and Krakauer 2006; Sülzenbrück and Heuer 2009; Taylor et al. 2010; Taylor and Ivry 2011). Awareness of experimental manipulations leads to numerous changes in performance such as rapid improvements in performance (Kagerer et al. 1997; Hwang et al. 2006; Heuer and Hegele 2008), increased trial-by-trial variance, increased reaction times, and decreased aftereffects (Benson et al. 2011; Fernandez-Ruiz et al. 2011; Saijo and Gomi 2010). These features suggest participants may be exploring strategies that could offset movement errors.
Performance changes arising from strategy use are quite distinct from what is seen in normal adaptation. In the latter, trial-by-trial changes are generally monotonic and become smaller over time, reaction times are minimally altered, and aftereffects are prominent. Indeed, although strategic processes can change performance, the evidence suggests that over the course of learning, strategies make a negligible contribution to adaptation of a sensorimotor mapping. Sensorimotor adaptation representations have been shown to be isolated from strategy-based representations, even at the cost of overall performance, when the two systems are put in competition with one another (Mazzoni and Krakauer 2006; Sülzenbrück and Heuer 2009; Taylor et al. 2010; Taylor and Ivry 2011).
Nonetheless, it is possible that the benefits observed in tests of intermanual transfer reflect strategic processes. The benefit in tests of intermanual transfer may not reflect transfer of a newly acquired sensorimotor mapping per se. Instead, participants may adopt a strategy to offset the perturbation: for example, if a rightward force field is imposed on right arm movements during training, the participant may produce a nonspecific counteracting leftward force during the initial transfer trials with the left arm, or, during visuomotor adaptation, participants might alter the aiming direction of a movement in anticipation of the perturbation (see Heuer and Hegele 2008). This hypothesis may provide an account of the reference frame discrepancy between sensorimotor adaptation and intermanual transfer: the former is, at least for force fields, expressed in intrinsic space (due to adaptation), whereas the latter is expressed in extrinsic coordinates (due to strategy).
The role of awareness on intermanual transfer was directly tested by Malfait and Ostry (2004), who manipulated the saliency of the error signal in force field learning. In separate conditions, the perturbation was introduced either abruptly or gradually. With their gradual condition, the trial-by-trial increase was selected to be sufficiently small such that the participants were unaware of the force field. At the end of training, performance with the right arm was similar in the two conditions, with the participants generating a counteracting force such that the limb moved in a relatively straight path to the target. However, the pattern of intermanual transfer was strikingly different for the two conditions. In the abrupt condition, the initial errors with the left hand were substantially reduced compared with a control condition. In contrast, there was no benefit from right-hand training in the gradual condition. This dissociation suggests that the positive transfer observed in the abrupt condition may reflect an effect of awareness (Malfait and Ostry 2004). The precise underlying cause of this benefit of awareness is unclear in this study, but it is possible that participants may have adopted a strategy by which they opted to plan left arm movements in a direction opposite the (expected) force field. Alternatively, they might have simply been prepared to push harder to counteract the force field.
Wang et al. (2011) employed a similar manipulation in a recent study of intermanual transfer during visuomotor adaptation, introducing a 32° rotation either in a single step or over the course of 32 trials. Interestingly, they observed similar levels of transfer in both conditions, leading them to argue that awareness is irrelevant to the factors underlying intermanual transfer. However, adaptation of the left hand was incomplete at the end of training, with participants producing a consistent error exceeding 10°. Moreover, based on the debriefing reports, participants were aware that the visuomotor mapping had been perturbed, even if they could not describe the perturbation. Thus, with this blocked design, it remains possible that awareness contributed to right-hand transfer, even when the perturbation had been introduced in a gradual manner.
As exemplified by the Wang et al. study, studies of intermanual transfer have relied on a block design in which training is initially done with one limb and transfer is then tested with the other limb. This type of design precludes an analysis of the time course of transfer: learning within the nontrained limb is only probed following massed training. A block design may be especially problematic when evaluating the relevance of awareness. In an abrupt condition, awareness may be especially pronounced at the start of training but become reduced as performance improves (Beilock et al. 2004; Beilock 2007). In a gradual condition, awareness may become more pronounced over time if learning is incomplete (Wang et al. 2011). Moreover, given that learning and consolidation processes occur over different timescales (Brashers-Krug et al. 1996; Shadmehr and Brashers-Krug 1997; Smith et al. 2006), the degree of intermanual transfer may vary over the course of training. Transfer once a new sensorimotor state has been established may differ from that observed during the early stages of learning. Indeed, intermanual transfer is much stronger following distributed rather than massed practice, suggesting that there may important temporal constraints (Taub and Goldberg 1973).
An alternative method to probe intermanual transfer is a mixed-limb design. In such designs, movements of the two limbs are intermixed throughout the experiment. If feedback is given on each trial, it becomes difficult to separate intralimb learning and interlimb transfer (Galea and Miall 2006; Galea et al. 2010). In this study we introduced a novel variant of a mixed-limb task, one designed to provide a continuous assessment of intermanual transfer. On each trial, the participant reached to a target with either the right or left hand. After an initial training period, a visuomotor rotation was introduced. The critical experimental manipulation was that feedback was only provided after right-hand movements. We assumed that right-hand trials would exhibit adaptation. By continuously probing left-hand performance, this method allowed us to track the time course of intermanual transfer. Performance changes on left-hand trials must be driven by right-hand learning given that feedback is withhold on the left-hand trials.
This design is particularly useful for assessing the effects of awareness on intermanual transfer. As noted above, the persistent visual error observed at the end of training with a rotation that is introduced gradually (Kagerer et al. 1997; Klassen et al. 2005; Saijo and Gomi 2010) may induce some level of awareness that the environment has been perturbed (Wang et al. 2011). By using the gradual manipulation with our mixed-limb design, we obtain a continuous probe of transfer, one in which learning, at least in the early stages of training, is unlikely to be contaminated by awareness. As such, our method should provide a strong test of whether intermanual transfer is altered by awareness of the experimental perturbation. We employed this novel mixed-limb design method in experiments 1 and 2 and compared the results from this approach with those obtained in a traditional block design in experiment 3.
Awareness can also be problematic if participants adopt strategies to explicitly respond to a perturbation. Such strategies are idiosyncratic across individuals, as well as variable across trials for a given individual. To minimize this variability, we conducted a fourth experiment in which we provided the participants with an explicit strategy, one that counteracts the visuomotor rotation (Mazzoni and Krakauer 2006). That is, after the introduction of a large, 45° rotation, participants were told about the perturbation and told to aim to a location a corresponding distance in the opposite direction. Implementation of this strategy leads to immediate success on the task. Interestingly, performance deteriorates over subsequent trials, reflecting the operation of an implicit adaptation system that does not have access to the strategy (Mazzoni and Krakauer 2006; Sülzenbrück and Heuer 2009; Taylor et al. 2010). In effect, this procedure puts strategic and adaptation processes in opposition to one another (Taylor and Ivry 2011). By using this procedure with our mixed-limb design, we sought to examine the contribution of these two processes to intermanual transfer when participants are fully aware of a visuomotor rotation.
METHODS
Participants
Seventy-six right-handed participants (age 18–30, 27 males) were recruited from the research participation pool maintained by the Department of Psychology at University of California, Berkeley. The protocol was approved by the University's Institutional Review Board, and participants provided informed consent. Handedness was verified using the Edinburgh handedness inventory (Oldfield 1971).
Experimental Apparatus and General Procedures
Participants made reaching movements by sliding either the left or right hand over a smooth table surface to visually presented targets. Hand movements were tracked by a three-dimensional motion tracking system (miniBIRD; Ascension Technology, Burlington, VT). The movement sensor was sewn into the tip of the index finger of a glove, and the participant wore left- and right-hand gloves during the experiment. The motion tracking system sampled position information at 138 Hz, with approximate spatial resolution of 0.05 cm.
An overhead mirrored projection system was used such that the visual stimuli appeared on the surface of the table (Oliveira et al. 2010). The mirror occluded vision of the hands; thus feedback, when provided, was in the form of a small red circular “cursor” that indicated the position of the index finger.
The participant sat at a table with both hands resting on the surface. At the beginning of each trial, a cue (“left hand” or “right hand”) was presented at center of the display for 500 ms. Immediately following the offset of the cue, an empty blue circle (8 pixels/7 mm) appeared, indicating the start position. The participant was required to move the cued hand into the start position. To assist the participant, an empty white ring with a diameter equal to the distance of the hand from the starting position was displayed. By moving toward the starting position, the diameter of this ring became smaller. When the hand was within 10 pixels (8.8 mm) of the starting position, the ring changed to a small iconic left or right hand, and the participant moved this icon into the start location. This method allowed us to guide the participants to the start position without having these movements influenced by ongoing adaptation.
Experiment 1.
In experiment 1 (n = 24), after the start position was maintained for 500 ms, a filled green circle (8 pixels) appeared at one of eight possible locations at a 10-cm radial distance (Fig. 1). This target appeared within a wedge region centered in front of the start position. Four target locations were to the left of the center and four to the right, with a 2° separation between locations (range: 82–98° excluding 90°). The participant was instructed to make a horizontal reaching movement to the target by sliding their hand along the surface of the table. Participants were trained to move quickly (movement duration < 250 ms) and were not provided with online visual feedback during the movement. Endpoint feedback was provided on some trials (see below). On these trials, a stationary red cursor appeared as soon as the hand crossed the virtual ring (10-cm radial amplitude). This feedback cursor remained present for 1,000 ms.
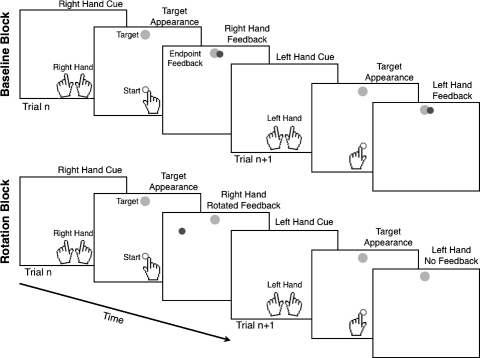
Fig. 1.
Task design. A cue indicated which hand should be moved to the start circle. Once the cued hand was appropriately positioned, the target appeared (gray circle). Participants reached to the target. Feedback was limited to information about the endpoint of the movement, signaled by a red circle (indicated by black circle). During the baseline block (top), the left hand was given endpoint feedback. During the rotation block (bottom), the endpoint feedback for the right hand was rotated by 22.5° in the counterclockwise direction. No feedback was provided on left-hand trials.
Testing began with an initial block of 128 movements during which participants reached to targets with the appropriately cued hand. Each hand was used on 50% of the trials (64 trials/hand). During this block, endpoint feedback was provided for both hands. The target locations were selected in a pseudorandom manner such that all 16 conditions (2 hands × 8 locations) were presented before any condition repeated.
Participants next completed a block in which feedback was limited to right-hand trials. This block consisted of 40 trials, 5 per target location. The right hand was cued on 32 of the trials (and feedback provided); the left hand was cued on the remaining 8 trials. On left-hand trials, participants were instructed to maintain movement speed and try to be as accurate as possible, even in the absence of feedback.
After these two baseline blocks, the visuomotor rotation was introduced. For half the participants, a 22.5° counterclockwise (CCW) rotation was introduced abruptly. With this degree of rotation, participants are aware that the displays have been altered. For the other half of the participants, the rotation was introduced gradually, increasing by ∼1° every 10 movements. The rotation block consisted of 240 trials, with 80% of the movements made with the right hand (192 movements) and 20% with the left hand (48 movements). Within these constraints, the cued hand was determined randomly. Feedback was only provided on right-hand trials.
The experiment concluded with a washout block of 96 trials in which the rotation was abruptly turned off for both groups. Fifty percent of the movements were made with each hand during this block (48 movements/hand), and endpoint feedback was again limited to right-hand trials.
Experiment 2.
Experiment 2 (n = 20) was identical to experiment 1 except that the left hand was used as frequently as the right hand throughout the experiment. There were only 32 trials in the second baseline block in which participants were introduced to moving with the left hand without feedback. The rotation block had the same number of total trials as in experiment 1 (240), although 50% of these were now performed with each hand. The washout block was identical to that used in experiment 1. Two groups were again tested, one in which the rotation was introduced abruptly and one in which the rotation was introduced gradually.
Experiment 3.
Experiment 3 (n = 22) was designed to provide a between-experiment comparison of our mixed-limb design and the more traditional block design in which intermanual transfer is only tested after training with one arm. We modified the structure of the session to segregate right- and left-hand blocks. During the baseline blocks, participants first used only the right hand, making 48 movements with veridical endpoint feedback. After this, they made 48 reaches with the left hand. For the first 24 movements, veridical endpoint feedback was presented; for the last 24 movements, the feedback was eliminated. After completing these baseline blocks, the participants made an additional 24 reaches with the right hand with veridical endpoint feedback. The rotation was then introduced with half of the participants exposed to the abrupt imposition of a 22.5° CCW rotation in a single step and the other half exposed to small incremental rotations that increased gradually to 22.5°. The rotation block consisted of 120 trials, all performed with the right hand. At the end of this block, the participants were instructed, both by a visual cue on the screen and by the experimenter, to now switch and reach with the left hand. We sought to minimize the delay between the right-hand training block and left-hand transfer given that sensorimotor adaptation is subject to time-dependent memory decay (Brashers-Krug et al. 1996). Eighty left-hand movements were performed without visual feedback, providing a probe of intermanual transfer following blocked training.
Two participants in the abrupt group did not appear to understand or follow the instructions, with right-hand reaches always directed at the target even when the feedback indicated a large error. These individuals were excluded from the analysis, yielding 10 participants in the abrupt and gradual groups.
Experiment 4.
In experiment 4 (n = 10), we employed a method developed to examine the effect of strategic instructions on visuomotor rotation (Mazzoni and Krakauer 2006; Taylor et al. 2010; Taylor and Ivry 2011). The eight target locations now spanned a full circle around the start position, separated by 45° (beginning at 22.5°). At the start of each trial, blue circles appeared to indicate these positions. One immediately turned green to indicate the target location for that trial.
Testing began with an initial block of 64 movements in which the left and right hands were each cued on 50% of the trials. Endpoint feedback was provided on all trials. Participants then completed a block in which they were trained to use a 45° strategy. On these trials, the green target appeared at one of the eight locations and the participants were instructed to reach to the empty blue circle located 45° in the clockwise (CW) direction from the green target. Participants practiced this strategy for 48 trials, 40 requiring movements with the right hand and 8 requiring movements with the left hand. Feedback was again provided on both right- and left-hand trials, allowing the participants to become familiar with the use of a 45° strategy.
After completing this strategy-only block, participants were instructed to resume reaching directly to the cued green target. During this block, we introduced changes in hand probability and feedback. The block consisted of 40 trials, 32 with the right hand and 8 with the left hand. Feedback was only provided on right-hand trials.
Immediately following these 40 trials, a 45° CCW rotation was abruptly introduced (the gradual condition was not included in experiment 4). The first two trials were always performed with the right hand. As expected, the endpoint error was very large (∼45°) and participants were aware of the large perturbation. We then instructed the participants to implement a strategy to offset this perturbation. Specifically, they were told that they should move to the blue circle located 45° in the CW direction from the cued green target. This strategy would offset the rotation and ensure that the endpoint feedback appeared near the green target. A total of 160 trials were tested in the rotation+strategy block, 128 with the right hand and 32 with the left hand.
The rotation was turned off in a final washout block. Participants were instructed to stop using the strategy and reach directly to the green target. The first 16 trials included 8 with the right hand and 8 with the left hand, one for each target with each hand. No feedback was presented for either hand. After these 16 trials, 160 additional washout trials (80 trials/hand) were conducted, but now with feedback presented on all trials.
Movement Analysis
Reaction time was defined as the time between the appearance of the target and time at which movement amplitude exceeded 1 cm. Movement time was calculated when the hand passed through the virtual target ring (10-cm radial amplitude). Note that this is not a true measure of movement time, since the movements terminated beyond the virtual ring. However, keeping distance constant allows a comparison of kinematics during the period of interest.
To analyze the effects of the visuomotor rotation, we looked at the angular difference between the target position and the position of the hand when it crossed the virtual ring, a dependent measure we refer to as endpoint hand angle. For this calculation, 0° was defined as movement directly to the target, independent of the actual target location. Thus, if a rotation of 22.5° CCW were imposed, a fully adapted movement would have a hand angle of 22.5° CW. To determine movement curvature, each trajectory was rotated with respect to the target location such that the y-component of the movement was parallel to the line connecting the start position and target, and the x-component was perpendicular to this line. Curvature, or movement area, was defined as the absolute area between the x- and y-components.
Since movements were pseudorandomly distributed to the targets such that each target was visited before a movement was repeated to a target, we averaged right-hand movements into bins of eight movements for all of the blocks. In experiment 1, left-hand movements in the first baseline block and the washout block were averaged into eight-movement bins. However, for the rotation block, we used bins of just two trials for the left-hand movements, since only 20% of the movements involved the left hand. In experiment 2, left-hand movements were averaged across eight-movement bins, since these occurred at the same frequency as right-hand movements.
We performed a secondary analysis on the data from the gradual conditions in experiments 1 and 2, utilizing an assessment that should have minimal contamination from awareness. Over time, the participants may have become aware that the environment had been perturbed, especially if their rate of adaptation did not match the rate at which the rotation was increased. We fit the right-hand time series of hand angles for each participant with a line to determine the slope of adaptation and fit this function to the slope of the gradual rotation. We computed the residual error between these two functions using bins of eight movements. For each bin, we computed a series of one-sample t-tests (Bonferroni corrected for multiple comparisons) to determine bins in which the residual error was significantly different from zero. The first bin at which there was a significant residual was operationalized to define the time point in training at which the participant's error was sufficiently large to induce awareness of the perturbation. We took the average of the endpoint hand angles from all the left-hand trials preceding this point to assess intermanual transfer. We recognize that this analysis may be prone to type 1 errors. Nonetheless, we adopted this secondary analysis as a conservative way to estimate intermanual transfer in the absence of awareness. This analysis could not be applied to the data from experiment 3, because transfer was only probed after training.
Statistical analyses were performed in Matlab. We report the degrees of freedom for the t values when paired t-tests were performed and the degrees of freedom for the F values when analysis of variance (ANOVA) was performed. To evaluate intermanual transfer, we first assessed whether changes in hand angle for the left hand were significantly different from zero. We then compared the hand angle changes between the two limbs to assess the degree of transfer. For these analyses, we used a Bonferroni correction by setting the α-value criterion to 0.025 to account for the fact that we were performing two comparisons of the same data sets. This correction did not change the significance in any of these tests. We report the means and 95% confidence interval of the mean for the dependent variables.
State-Space Modeling of Experiments 1–3
The abrupt and gradual visuomotor rotations, by definition, induce different errors. In the abrupt condition, the introduction of the visuomotor rotation produces a large error; in the gradual condition, an incremental error is added every 10 trials. Whereas adaptation in the abrupt condition generally follows an exponential function, adaptation in the gradual condition follows a more linear function matched to the ramping input. Although conventional methods of fitting adaptation rates with an exponential or linear function are applicable to each condition, the adaptation rates cannot be compared between conditions.
State-space modeling allows for a comparison of adaptation rates between the abrupt and gradual conditions because it is iterative in design and fits the data on a trial-by-trial basis. We used this technique in this study, not in a predictive manner but as a tool to estimate two measures: 1) the adaptation rate for the right hand across training trials and 2) the adaptation rate for the left hand across transfer trials. For clarity, we refer to the latter as the transfer rate.
On a given trial (n), participants were cued to move either their right (R) or left (L) hand. The motor output (y) for that trial is defined as
| (1) |
In this formalization, the right hand has an internal model state (xR) and the left hand has (a distinct) internal model state (xL). When the current trial is a right-hand movement, R is set to 1 and L is set to 0; when the current trial is a left-hand movement, R is set to 0 and L is set to 1. During the rotation block, the motor output (y) is rotated on right-hand trials, a value (rot) that is fixed in the abrupt condition and increases over time in the gradual condition. The rotation produces an error (e):
| (2) |
This error is then used to update the internal model state for each limb for the next trial (n + 1):
| (3) |
| (4) |
where AR characterizes the retention of the previous state of the right hand (xR) and is updated by the adaptation rate BR using the error e from the previous trial (n). The left hand has its own set of parameters. However, left-hand movements are always performed without visual feedback. Thus it can only be updated by errors observed on right-hand trials; we consider the adaptation rate for the left hand (BL) as a measure of the rate of transfer. The internal model states for both the right (xR) and left hand (xL) are updated following each trial regardless of which hand was used on the previous trial. Note that since there is no visual error on left-hand trials, changes to the internal model states after these trials are solely due to the forgetting term.
The model (Eqs. 1–4) was fit, on an individual basis, to the time series of the right and left hand angles with the Nelder-Mead method, or simplex method (Nelder and Mead 1965), implemented in Matlab. We fit the time series data from the last block of the baseline movements, the rotation block, and the washout block. The retention parameter A was bounded between 0 and 1, whereas the adaptation rate B was bounded between −1 and 0. The goodness of fit of the model was measured by the root mean square error (RMS) and Pearson's correlation coefficient (r) between the expected and observed endpoint hand angle.
The simplex method can be sensitive to initial conditions, especially when the model is overparameterized. When we had distinct retention parameters for the right and left hand, we occasionally obtained bimodal parameter solutions such that the retention parameter for the left hand (AL) would be zero and the transfer rate for the left hand (BL) would be unrealistically large, achieving values greater than the adaptation rate for the right hand. To eliminate this problem, we fixed the retention rate to be identical between the hands: AR = AL. This reduced the number of free parameters to three (A, BR, and BL), stabilizing the parameter solutions across a range of initial conditions.
We used the Bayesian information criterion (BIC) and Akaike information criterion (AIC) to determine whether the constraint on A had a significant impact on the goodness of fit. Across all of the participants, the BIC values were 3.09 ± 0.15 and 3.17 ± 0.20 for the four- and three-parameter models, respectively. For AIC, the comparable values were 2,941 ± 155 and 3,378 ± 75. These small differences indicate that the inclusion of separate A terms for the right and left hands is not essential.
We did not fit the data in experiment 4. Although it is possible to model strategy use during adaptation (Taylor and Ivry 2011), the procedure is considerably more complex and superfluous to the specific question we ask presently concerning intermanual transfer when adaptation occurs in the face of a strategy.
RESULTS
Experiment 1
The first baseline block provides a comparison of kinematics and accuracy for left- and right-hand movements, since each hand was cued 50% of the time and feedback was provided for both hands. In the analyses of these data, we combined the data for the abrupt and gradual groups (n = 24), since the rotation had not yet been introduced. Movements were fast and of comparable duration for the left (287 ms) and right hands (283 ms). On average, movements were very accurate (Fig. 2, black) and comparable for left- and right-hand movements. The endpoint angle was 0.1 ± 0.8° and −0.3 ± 0.8° for the left and right hands, respectively (t23 = 0.61, P = 0.55). Given the absence of online feedback, participants produced approximately straight movements toward the target. Signed movement curvature was not significantly different from zero during the first baseline block for either hand (t23 = 0.47, P = 0.64).
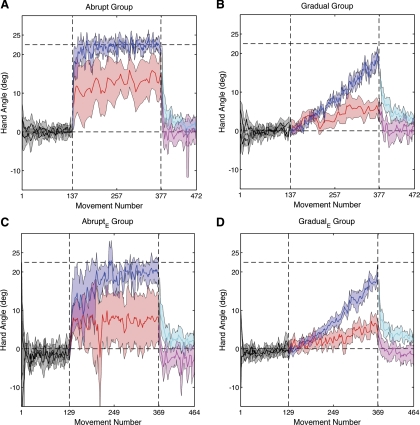
Fig. 2.
A and B: average hand angle over the course of experiment 1 for the abrupt (A) and gradual (B) groups. The rotation was introduced on trial 137 and removed on trial 377. C and D: average hand angle over the course of experiment 2 for the equated abrupt (abruptE; C) and equated gradual (gradualE; D) groups. The rotation was introduced on trial 129 and removed on trial 369. Black, baseline trials (no rotation); blue, right-hand trials during rotation phase; red, left-hand trials during rotation phase; cyan, right-hand trials during washout phase; magenta, left-hand trials during washout phase. Shading represents the 95% confidence interval around the means. The data were smoothed using a 3-movement window.
Interestingly, removal of endpoint feedback for the left hand in the second baseline block did not affect accuracy. Mean endpoint angle remained comparable for the left and right hands (t23 = 0.55, P = 0.58). Consistent with the instructions, participants were able to maintain similar kinematics for the left hand in the absence of feedback. Comparing left hand-only performance between the first and second baseline blocks showed no difference in endpoint hand angle (t23 = 0.27, P = 0.79), movement time (t23 = 0.86, P = 0.40), and movement curvature (t23 = 0.77, P = 0.45).
The introduction of a −22.5° CCW rotation for the abrupt group resulted in a substantial error in visual space for right-hand movements. Participants rapidly adapted to the visuomotor transformation, adjusting their right-hand movements to reach in the CW direction with respect to the target (Fig. 2A, blue). The average right-hand endpoint angle for the first 8 movements was 13.9 ± 2.4°; this value increased to 22.3 ± 1.1° for the last 8 movements (t11 = 6.68, P < 0.001). Indeed, the participants were fully adapted, as indicated by the fact that the endpoint error (mean endpoint hand angle minus rotation) was not significantly different from zero (t11 = 0.43, P = 0.68). Removal of the CCW rotation produced an aftereffect, measuring 9.0 ± 3.7° when averaged over the first 8 movements of the washout block. This value was significantly greater than zero (t11 = 4.82, P < 0.001), providing further evidence of sensorimotor adaptation.
Left-hand movements also showed “adaptation” during the rotation block, even though participants never saw any feedback on these trials (Fig. 2A, red). The average endpoint angle was 8.3 ± 6.2° over the first two left-hand trials and increased to 13.8 ± 1.1° by the end of training (t11 = 5.37, P < 0.001). The magnitude of adaptation for the left hand was less than that observed for the right hand (end of training: t11 = 3.41, P = 0.006). We also examined the left-hand angle at peak velocity to check whether intermanual transfer was more pronounced near the end of the movement (Sainburg and Wang 2002). By the end of the rotation block, the angle of the left hand at peak speed was 15.5 ± 5.2°, a value that is not statistically different when the dependent variable is the angle at the end of movement (t11 = 0.42, P = 0.68).
For the gradual group, the visuomotor rotation was introduced incrementally, ∼1° CCW every 10 movements. A postexperiment interview revealed that most participants were unaware of the rotation; the few who reported noticing the rotation only became aware late in the rotation block. Nevertheless, the participants showed gradual adaptation with the right hand moving in the CW direction to counter the rotation (Fig. 2B, blue). The endpoint angle of the right hand was 18.4 ± 1.5° for the last 8 movements of the rotation block. This value is significantly greater than that observed over the first 8 movements of the rotation block (t11 = 24.6, P < 0.001) but falls short of complete adaptation to 22.5° (t11 = 5.48, P < 0.001). The aftereffect of 9.7 ± 1.2° was significant (t11 = 15.5, P < 0.001).
The gradual group also showed significant transfer to left-hand movements. By the end of the rotation block, the left-hand endpoint angle was 6.0 ± 1.8°, a value larger than that observed at the start of the rotation block (averages over 2 trials at start and end: t11 = 6.69, P < 0.001). The left hand also exhibited a small but significant aftereffect of 2.7 ± 2.0° (t11 = 2.66, P = 0.02). Adaptation of the left hand was attenuated compared with that observed in the right hand, both at the end of the rotation block (t11 = 13.2, P < 0.001) and in terms of the size of the aftereffect (t11 = 6.85, P < 0.001).
Experiment 1 introduced a new method to assess intermanual transfer, providing continuous probes of left-hand performance over the course of a rotation block in which feedback was limited to the right hand. The right hand showed near-complete adaptation when the rotation was introduced abruptly. Adaptation was also substantial when the rotation was introduced incrementally. As inferred from the change in left-hand performance, intermanual transfer was observed in both the abrupt and gradual conditions. The finding of left-hand transfer in the gradual condition is especially interesting, since the participants had little or no awareness of the rotation. This observation indicates that intermanual transfer is not limited to explicit knowledge about task constraints. We will return to a direct comparison of the degree of intermanual transfer between the abrupt and gradual groups following the results for experiment 2, using a state-space model to analyze the data.
In both the abrupt and gradual groups, the magnitude of adaptation was less than that observed in the right hand. This effect may reflect incomplete transfer of learning from the right to left hand. However, it is important to keep in mind that during the rotation block, 80% of the trials were performed by the right hand. This not only provides the right hand with more learning opportunities but also may affect performance if consolidation and retention factors are time dependent as well as repetition dependent. We address this issue in experiment 2.
Experiment 2
Two new groups of participants were tested on the abrupt and gradual rotations (abruptE and gradualE). Unlike experiment 1, the left and right hands were selected with equal probability during all of the blocks, including the rotation block. Thus differences in left-hand adaptation during the rotation block, as well as aftereffects in the washout block, should reflect factors related to transfer, rather than asymmetries in hand use.
As with experiment 1, there were no differences between left- and right-hand performance during the baseline blocks, including the second baseline block in which feedback was limited to right-hand trials (endpoint accuracy: t19 = 1.12, P = 0.28; curvature: t19 = 1.67, P = 0.11; movement time: t19 = 0.98, P = 0.34).
Right-hand adaptation was again rapid following the abrupt introduction of the 22.5° CCW visuomotor rotation (Fig. 2C, blue). By the end of the rotation block, the endpoint angle of the right hand for the abruptE group was 20.1 ± 2.5°, a value not significantly different from the imposed rotation of −22.5° (t9 = 1.86, P = 0.10). Adaptation was also evident for left-hand trials (Fig. 2C, red). The endpoint angle was significantly different from baseline block (t9 = 2.84, P = 0.02) and increased over the course of the rotation, reaching a value of 8.2 ± 6.2° at the end of the rotation block. The magnitude of left-hand adaptation was less than that observed in the right hand (t9 = 4.42, P = 0.002).
Participants in the gradualE group adapted with their right hand in response to the incrementally introduced rotation (Fig. 2D, blue). As in experiment 1, the adaptation was incomplete, reaching a final endpoint angle of 17.5 ± 1.1°, a value that was short of complete adaptation compared with the final rotation amount of 22.5° (t9 = 8.62, P < 0.001). Adaptation was again observed in left-hand trials. By the end of the rotation block, the endpoint angle of the left hand was 5.0 ± 2.7° (t9 = 3.61, P = 0.001). This value is considerably less than that that observed for the right hand (t9 = 9.48, P < 0.001).
In summary, the results of experiment 2 are similar to those observed in experiment 1. Intermanual transfer was observed during visuomotor learning under conditions in which participants were aware of the environmental perturbation and, more importantly, when awareness of the rotation was minimal or absent. The degree of transfer remained incomplete in experiment 2, even though the number of right and left hand trials was equated.
Experiment 3
Experiment 3 served as a point of comparison with experiments 1 and 2, evaluating the degree of transfer in a traditional block design. For this experiment, left-hand transfer was only assessed after a block of 120 right-hand reaches with the rotation. Similar to experiments 1 and 2, right-hand adaptation was rapid following the abrupt introduction of −22.5° CCW visuomotor rotation (Fig. 3A, solid line). By the end of the rotation block, the endpoint angle of the right hand for the blocked abrupt group was 17.9 ± 3.0°, a value that falls short of full adaptation to the imposed rotation of −22.5° (t9 = 2.95, P = 0.01). Transfer to the left hand was modest (Fig. 3A, dashed line). If we average over the first 8 movements in the transfer block, the aftereffect is only 0.6 ± 2.5°, a value that is not significantly different from that for the left-hand baseline reaches (t9 = 1.46, P = 0.17). However, if we restrict our analysis to the first reach with the left hand, then positive transfer is observed. The endpoint angle of the left hand was 3.1 ± 2.3°, indicating a significant shift compared with baseline (t9 = 2.65, P = 0.02).
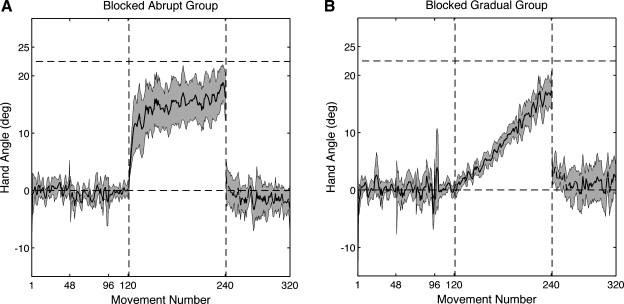
Fig. 3.
A and B: average hand angle over the course of experiment 3 for the blocked abrupt (A) and blocked gradual (B) groups. The rotation was introduced on trial 120 and removed on trial 240. Solid and dashed lines indicate the right- and left-hand trials, respectively. Shading represents the 95% confidence interval around the means. The data were smoothed using a 3-movement window.
Participants in the blocked gradual group adapted with their right hand in response to the incremental rotations (Fig. 3B, solid line). The mean hand angle was 16.8 ± 2.4° at the end of training, a value short of complete adaptation (t9 = 4.59, P = 0.001). Transfer was also observed in the left-hand movements (Fig. 3B, dashed line) and, in fact, was more robust than that observed in the blocked abrupt condition. When the analysis included the first 8 left-hand movements in the transfer block, the aftereffect was 3.0 ± 1.53°, significantly different from the hand angle at the end of the baseline block (t9 = 4.45, P = 0.002). For completeness, we also performed a restricted analysis, using only the data from the first left-hand trial. In this case, too, significant transfer was observed (4.3 ± 2.1°, t9 = 4.06, P = 0.003).
The block design of experiment 3 allowed a direct comparison of the degree of transfer between the abrupt and gradual conditions. When limited to the first trial, the difference was not reliable (t18 = 0.72, P = 0.48). However, the absolute degree of transfer in experiment 3 appears to be significantly less than the degree of transfer in experiments 1 and 2. A direct comparison is problematic, since feedback was present during the washout block for experiments 1 and 2. We did not provide feedback in the transfer block in experiment 3 because we wished to preclude learning. Thus this post hoc, between-experiment analysis was restricted to the first trial (a left-hand trial) in the washout block from experiments 1 and 2 and the first transfer trial in experiment 3. When these data were analyzed with a two-way ANOVA, rotation format was not reliable (F1,63 = 1.3, P = 0.26), but the effect of mixing the limbs was marginally significant (F1,63 = 3.08, P = 0.08). The degree of transfer was numerically larger in the two experiments in which the hands were mixed during training compared with when the two hands were tested in a sequential fashion. The interaction was not significant (F2,63 = 1.55, P = 0.22).
Awareness in the Gradual Conditions in Experiments 1 and 2
On the basis of our postsession questionnaires, most of the participants in the gradual groups of experiments 1 and 2 reported little awareness of the visuomotor rotation (4 of 22 participants). Interestingly, more participants in the gradual, blocked version of experiment 3 reported being aware of the perturbation (7 of 10 participants). Mixing movements of the right and left hands may lead to more uncertainty in motor execution and lead the participants to be more tolerant of movement errors (rather than attributing the error to a change in the environment).
We recognize that reports of awareness are problematic, subject to demand characteristics and variable criterion/response biases (Curran and Keele 1993; Perruchet and Amorim 1992; Willingham et al. 1989). To provide a performance-based criterion of awareness in experiments 1 and 2, we analyzed the data to identify, for each participant, the point within the session at which the visual error might be of sufficient magnitude such that the participants might suspect that the environment has been perturbed. To this end, we used a regression analysis to determine when the residual error on hand angle from right-hand trials was significantly greater than what would be expected based on normal variation in performance.
For this analysis, we first compared the slopes of the induced gradual rotation with the slopes obtained from the time series of hand angles. Given that the rotation was increased by ∼1° every 10 movements, the slope of the rotation in experiment 1 was −0.0992° per right-hand movement and in experiment 2, −0.0995°. (The rates are different between experiments because there were different numbers of right-hand movements in the 2 experiments.) A linear function provided a good fit of the participants' time series of hand angles (experiment 1: r2 = 0.72 ± 0.05, P < 0.001; experiment 2: r2 = 0.76 ± 0.05, P < 0.001), with mean slope values of 0.081 ± 0.008° and 0.083 ± 0.008° for experiments 1 and 2, respectively. Both of these values are less than the rate of adaption (experiment 1: t11 = 5.44, P < 0.001; experiment 2: t9 = 3.99, P = 0.003), consistent with the fact that adaptation at the end of the rotation block was incomplete (see Fig. 2).
We then examined the residuals between the actual rotation and performance functions to identify the first bin at which the residuals were significantly different from zero. This occurred at movement 77 ± 18.02 for experiment 1 and at movement 37 ± 10.20 for experiment 2. The earlier value for experiment 2 presumably reflects the fact that there were fewer right-hand trials, thus slowing down the rate of learning. Given the assumption that the potential for awareness might occur at or after this point, we examined the average of all the left-hand trials prior to this bin. Averaging over these trials, the hand angle on left-hand movements was 2.17 ± 1.38° in experiment 1 and 1.50 ± 1.30° in experiment 2. Although these averaged values are small, they are significantly greater than the average left-hand angles in the baseline block in experiment 1 (t11 = 3.88, P = 0.002) and in experiment 2 (t11 = 2.26, P = 0.048). In summary, even when we restrict the analysis to the early stages of training, epochs in which the observed error falls within the boundary of normal movement variability, transfer is already evident in the movements of the left hand.
State-Space Model Estimation of Right-Hand Adaptation and Left-Hand Transfer
As described in methods, we fit the hand angle time series with a state-space model. For each individual, we fit the right- and left-hand data sets in a combined fashion, using the error observed on right-hand trials to update the internal models for both hands after each trial. Overall, the state-space model provided a good fit for the participants in all six groups (abrupt and gradual groups in experiments 1–3: mean r = 0.81 ± 0.03). The goodness-of-fit values for each individual, along with the parameter estimates, are presented in Table 1.
Table 1.
State-space model parameters
| Subject | A | BR | BL | RMS | r | BIC | AIC | Subject | A | BR | BL | RMS | r | BIC | AIC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abrupt group (experiment 1) | Gradual group (experiment 1) | ||||||||||||||
| 1 | 1.000 | −0.742 | −0.642 | 5.813 | 0.879 | 3.536 | 3.559 | 1 | 0.997 | −0.057 | 0.001 | 4.158 | 0.845 | 2.897 | 3.298 |
| 2 | 0.909 | −0.474 | −0.364 | 7.549 | 0.706 | 4.087 | 3.756 | 2 | 0.994 | −0.030 | −0.005 | 3.327 | 0.824 | 2.454 | 3.121 |
| 3 | 1.000 | −0.635 | −0.109 | 7.798 | 0.836 | 4.145 | 3.758 | 3 | 0.979 | −0.065 | −0.016 | 3.714 | 0.800 | 2.673 | 3.222 |
| 4 | 0.947 | −0.721 | −0.036 | 8.458 | 0.741 | 4.304 | 3.841 | 4 | 0.996 | −0.043 | −0.001 | 4.846 | 0.747 | 3.196 | 3.422 |
| 5 | 1.000 | −0.918 | −1.000 | 4.494 | 0.933 | 3.055 | 3.366 | 5 | 0.984 | −0.142 | −0.057 | 4.095 | 0.809 | 2.844 | 3.296 |
| 6 | 0.991 | −0.135 | −0.103 | 10.062 | 0.644 | 4.666 | 3.949 | 6 | 0.997 | −0.026 | −0.016 | 4.331 | 0.729 | 2.979 | 3.308 |
| 7 | 0.990 | −0.101 | −0.028 | 4.854 | 0.867 | 3.204 | 3.413 | 7 | 0.970 | −0.056 | −0.013 | 3.514 | 0.765 | 2.562 | 3.181 |
| 8 | 1.000 | −0.436 | −0.322 | 6.970 | 0.874 | 3.933 | 3.696 | 8 | 0.989 | −0.066 | −0.053 | 4.375 | 0.747 | 2.974 | 3.345 |
| 9 | 1.000 | −0.474 | −0.317 | 4.107 | 0.929 | 2.875 | 3.298 | 9 | 0.985 | −0.068 | −0.038 | 2.949 | 0.865 | 2.209 | 3.049 |
| 10 | 0.994 | −0.089 | −0.060 | 4.540 | 0.867 | 3.045 | 3.373 | 10 | 0.970 | −0.214 | −0.107 | 4.345 | 0.799 | 2.981 | 3.340 |
| 11 | 1.000 | −0.489 | −0.366 | 5.169 | 0.910 | 3.335 | 3.461 | 11 | 0.997 | −0.151 | −0.037 | 3.578 | 0.882 | 2.594 | 3.194 |
| 12 | 0.995 | −0.111 | −0.012 | 4.252 | 0.923 | 2.944 | 3.324 | 12 | 0.989 | −0.099 | −0.039 | 3.734 | 0.832 | 2.666 | 3.226 |
| Mean | 0.986 | −0.444 | −0.280 | 6.172 | 0.842 | 3.594 | 3.566 | 0.987 | −0.085 | −0.032 | 3.914 | 0.803 | 2.752 | 3.250 | |
| 95% CI | 0.015 | 0.153 | 0.161 | 1.056 | 0.051 | 0.329 | 0.122 | 0.005 | 0.031 | 0.017 | 0.290 | 0.027 | 0.149 | 0.057 | |
| AbruptE group (experiment 2) | GradualE group (experiment 2) | ||||||||||||||
| 1 | 0.992 | −0.506 | −0.399 | 6.284 | 0.874 | 3.697 | 3.533 | 1 | 0.994 | −0.052 | −0.025 | 3.741 | 0.702 | 2.629 | 3.151 |
| 2 | 0.988 | −0.262 | −0.085 | 3.322 | 0.924 | 2.414 | 3.055 | 2 | 0.995 | −0.095 | −0.027 | 3.085 | 0.867 | 2.301 | 3.009 |
| 3 | 0.994 | −0.038 | −0.009 | 5.493 | 0.730 | 3.453 | 3.403 | 3 | 0.995 | −0.072 | −0.034 | 3.350 | 0.793 | 2.407 | 3.274 |
| 4 | 0.999 | −0.488 | −0.510 | 7.639 | 0.812 | 4.117 | 3.677 | 4 | 1.000 | −0.049 | 0.000 | 4.355 | 0.796 | 2.991 | 3.070 |
| 5 | 0.997 | −0.072 | −0.073 | 5.981 | 0.838 | 3.625 | 3.455 | 5 | 0.990 | −0.074 | −0.049 | 3.816 | 0.719 | 2.659 | 3.263 |
| 6 | 0.992 | −0.199 | −0.067 | 5.818 | 0.832 | 3.571 | 3.476 | 6 | 0.957 | −0.572 | −0.218 | 4.420 | 0.872 | 2.871 | 3.166 |
| 7 | 0.984 | −0.480 | −0.043 | 6.088 | 0.826 | 3.654 | 3.510 | 7 | 0.974 | −0.175 | −0.011 | 3.852 | 0.811 | 2.730 | 3.264 |
| 8 | 0.714 | −0.869 | −0.064 | 5.469 | 0.787 | 3.436 | 3.431 | 8 | 0.992 | −0.052 | −0.018 | 3.812 | 0.710 | 2.717 | 3.163 |
| 9 | 0.991 | −0.019 | 0.018 | 14.544 | 0.483 | 5.389 | 4.184 | 9 | 0.981 | −0.135 | −0.071 | 3.218 | 0.813 | 2.373 | 3.165 |
| 10 | 0.991 | −0.050 | 0.010 | 6.292 | 0.810 | 3.697 | 3.559 | 10 | 0.997 | −0.029 | 0.002 | 3.658 | 0.799 | 2.626 | 3.031 |
| Mean | 0.964 | −0.298 | −0.122 | 6.693 | 0.791 | 3.705 | 3.528 | 0.988 | −0.131 | −0.045 | 3.731 | 0.788 | 2.630 | 3.156 | |
| 95% CI | 0.052 | 0.165 | 0.106 | 1.740 | 0.070 | 0.431 | 0.165 | 0.008 | 0.095 | 0.038 | 0.257 | 0.036 | 0.129 | 0.056 | |
| Blocked abrupt group (experiment 3) | Blocked gradual group (experiment 3) | ||||||||||||||
| 1 | 0.972 | −0.021 | −0.009 | 3.412 | 0.740 | 2.525 | 1.982 | 1 | 0.967 | −0.225 | 0.000 | 5.874 | 0.822 | 3.508 | 2.252 |
| 2 | 0.973 | −0.298 | 0.000 | 4.741 | 0.944 | 3.038 | 2.141 | 2 | 1.000 | −0.173 | −0.007 | 4.309 | 0.858 | 2.991 | 2.098 |
| 3 | 1.000 | −0.056 | −0.008 | 4.811 | 0.894 | 3.243 | 2.151 | 3 | 0.995 | −0.027 | −0.008 | 3.095 | 0.779 | 2.330 | 1.934 |
| 4 | 0.898 | −0.291 | 0.000 | 8.318 | 0.740 | 4.346 | 2.427 | 4 | 0.998 | −0.036 | −0.015 | 5.357 | 0.544 | 3.383 | 2.206 |
| 5 | 0.944 | −0.154 | −0.057 | 4.045 | 0.902 | 2.871 | 2.071 | 5 | 1.000 | −0.066 | −0.004 | 3.151 | 0.903 | 2.360 | 1.943 |
| 6 | 0.887 | −0.100 | −0.036 | 4.240 | 0.818 | 2.938 | 2.093 | 6 | 1.000 | −0.024 | −0.008 | 4.344 | 0.667 | 3.003 | 2.102 |
| 7 | 0.990 | −0.033 | 0.000 | 4.047 | 0.916 | 2.786 | 2.058 | 7 | 0.892 | −0.315 | −0.077 | 3.943 | 0.828 | 2.806 | 2.054 |
| 8 | 0.998 | −0.043 | −0.003 | 4.130 | 0.906 | 2.951 | 2.088 | 8 | 1.000 | −0.094 | −0.022 | 2.727 | 0.906 | 2.077 | 1.871 |
| 9 | 0.940 | −0.330 | 0.000 | 5.631 | 0.916 | 3.449 | 2.237 | 9 | 0.898 | −0.139 | −0.003 | 3.334 | 0.773 | 2.472 | 1.971 |
| 10 | 0.983 | −0.010 | −0.007 | 5.517 | 0.276 | 3.501 | 2.229 | 10 | 0.911 | −0.174 | 0.000 | 4.080 | 0.858 | 2.732 | 2.071 |
| Mean | 0.958 | −0.133 | −0.012 | 4.889 | 0.805 | 3.165 | 2.148 | 0.966 | −0.127 | −0.014 | 4.021 | 0.794 | 2.766 | 2.050 | |
| 95% CI | 0.025 | 0.079 | 0.012 | 0.860 | 0.109 | 0.307 | 0.082 | 0.029 | 0.056 | 0.011 | 0.957 | 0.100 | 0.386 | 0.108 | |
Parameter values are given for each participant in experiments 1–3 from the best-fitting state-space model (Eqs. 1–4). A, retention term of the internal model, fixed to be identical for each hand; BR, adaptation rate for the internal model of the right-hand state; BL, transfer rate for the internal model of the left-hand state (both BR and BL are updated with the visual error from right-hand movement trials); RMS, root mean square error between the model and the actual time series; r, correlation coefficient for the model; BIC, Bayesian information criterion; AIC, Akaike information criterion (in 1,000s); 95% CI, 95% confidence interval.
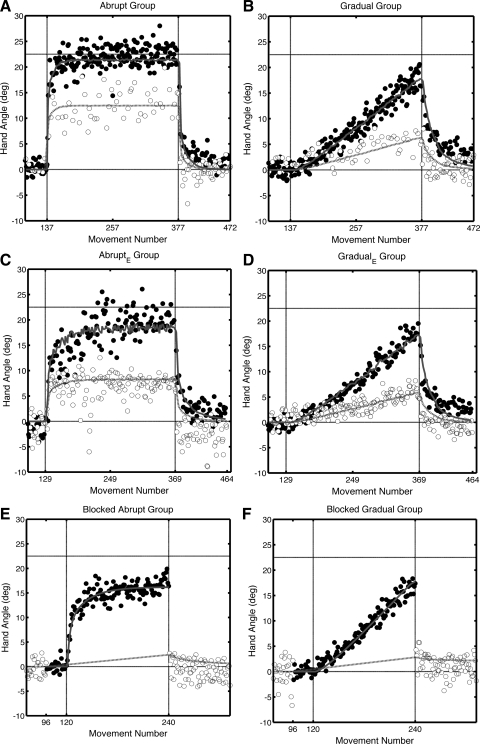
The fits for the group-averaged data are shown in Fig. 4. A few points should be noted concerning the modeling results for experiments 1 and 2. First, in the abrupt conditions (Fig. 4, A and C), left-hand transfer reaches near asymptotic values after just a few trials, despite the fact that left-hand performance never approaches the level of adaptation observed in the right hand. This occurs because updating of the left-hand internal model is based on error signals generated on right-hand trials. When the hand angle for the right hand approaches the rotation (22.5°), the error is small, and thus left-hand transfer (adaptation) stops or is greatly attenuated. Second, a different pattern is observed in the gradual conditions (Fig. 4, B and D). In these conditions an error signal persists across the training block, and left-hand transfer continues. Third, during the washout block, a large error is again generated on right-hand trials, producing rapid de-adaptation in both the right and left hands.
Fig. 4.
State-space model fit of experiments 1–3. The model (Eqs. 1–4) was fit to the last baseline block, the rotation block, and the washout block. Solid and dotted lines indicate the estimate of right- and left-hand adaptation and transfer, respectively, based on the model. Filled and open circles indicate the group-averaged hand angles for right- and left-hand movements, respectively. A: experiment 1, abrupt group. B: experiment 1, gradual group. C: experiment 2, abruptE group. D: experiment 2, gradualE group. E: experiment 3, blocked abrupt group. F: experiment 3, blocked gradual group.
For experiment 3, the transfer of adaptation to the left hand cannot be observed during training because the experiment used a blocked design. However, if we assume that an internal model underlying (potential) left-hand performance is updated on each trial, then we can infer the output of this model across the experiment. As shown in Fig. 4, E and F, the model assumes there would be modest learning across the training block, resulting in positive transfer at the time of the transfer block.
In terms of the parameters estimates, we did not observe any difference in the memory retention term A between the abrupt and gradual condition. A two-way ANOVA failed to reveal a main effect of rotation format (abrupt/gradual) (F1,63 = 0.71, P = 0.40) or a main effect of experiment (F2,63 = 1.63, P = 0.20). These null results are consistent with the hypothesis that the trial-by-trial rate of forgetting the hand state (1 − A) was similar in all conditions, regardless of the relative proportion of limb use of whether the changes in the internal state arise because of experienced error due to movement or via transfer.
Given the radical difference in format of the mixed and blocked designs, we first compared the parameter estimates for experiments 1 and 2. We performed a three-way ANOVA on the estimated rate of adaptation with the factors frequency of left-hand movements, rotation format, and hand. The main effect of frequency was not reliable (F1,43 = 1.82, P = 0.18), indicating that the relative proportion of right- and left-hand movements did not change the rate of adaptation. A main effect was observed for the factor hand (F1,43 = 7.76, P = 0.006). The change in hand angle is faster for the right hand, perhaps because the error signal is given more weight when used to adjust an internal model of the hand producing the error. The effect of rotation format was also reliable (F1,43 = 26.4, P < 0.001), with higher adaptation rates for both hands in the abrupt condition. The latter result is especially interesting given that the parameter estimates from the state-space model are based on trial-by-trial changes in performance: the error is weighted more heavily when the perturbation is introduced abruptly, resulting in both faster adaptation of the right-hand internal model and greater transfer to the left hand. None of the interaction terms approached significance.
The preceding analysis indicates that awareness of the perturbation may increase the rate of adaptation of the right hand. This raises the question of whether the faster rate of transfer in the left hand is secondary to the faster rate of adaptation, or whether there is also a change in the rate of transfer with the abrupt introduction of the rotation. In the model, the degree of left-hand transfer is dependent on the degree of adaptation; as such, greater left-hand transfer in the abrupt conditions could be due to an increased rate of adaptation. To assess this hypothesis, we normalized the data by dividing the left-hand transfer rate by the right-hand adaptation rate for each participant. We submitted these normalized estimates of transfer to a two-way ANOVA with the factors experiment and rotation format. Neither factor was reliable (experiment: F1,43 = 1.15, P = 0.29; rotation format: F1,43 = 2.58, P = 0.12). Thus the normalized transfer rates show no differences between the groups, suggesting that the amount of transfer was only dependent on the amount of adaptation, and unrelated to awareness.
Turning to experiment 3, we performed a two-way ANOVA with the factors rotation format and hand. In contrast to experiments 1 and 2, the main effect of rotation format was not significant (F1,39 = 0.01, P = 0.94). The effect of hand was reliable (F1,39 = 21.6, P < 0.001). Similar to experiments 1 and 2, adaptation for the right hand was faster than transfer to the left hand.
Finally, we used the parameter estimates to evaluate the effect of mixing or blocking the two hands in assessing intermanual transfer. Since our previous analysis suggested that left-hand transfer was dependent on the right-hand adaptation rate, we focused on the normalized values of transfer (left-hand adaptation divided by right-hand adaptation). We submitted these normalized transfer values to a two-way ANOVA to test for the effect of rotation format and mixing limbs. Again, there was no effect of rotation format (F1,63 = 2.81, P = 0.10). However, there was a main effect of mixing limbs (F1,63 = 9.18, P = 0.004), with lower rates of transfer in the blocked design of experiment 3.
Experiment 4
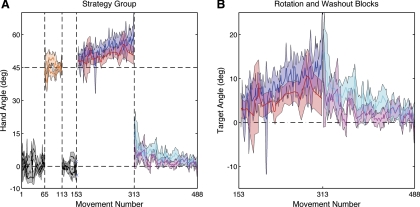
In experiments 1–3, a considerable degree of intermanual transfer was observed when a visuomotor rotation was introduced abruptly or gradually. This indicates that transfer is not dependent on awareness that the environment has been perturbed or arises from the implementation of an endogenously, generated strategy. We took a different tack in experiment 4: we instructed participants to implement a strategy that would compensate for an imposed rotation. Specifically, participants were told to aim 45° CW to the target location to offset a 45° CCW rotation. Previous studies have shown that people are able to immediately negate the error introduced by the visuomotor rotation. However, a paradoxical increase in error is observed over the course of training (Mazzoni and Krakauer 2006; Taylor and Ivry 2011). This effect is attributed to the operation of a motor adaptation process, one that is based on the difference between the planned trajectory and the feedback. As such, this procedure effectively isolates an adaptation process from a strategy, since the two are put in opposition to each other. We exploited this procedure to ask whether intermanual transfer was observed for the component restricted to adaptation.
During the baseline block, the average endpoint angles for right- and left-hand movements were −1.1 ± 1.5° and 1.3 ± 1.9°, respectively (Fig. 5A, black and gray). These values were not different from one another (t9 = 1.66, P = 0.13). No differences were observed between the two hands in terms of movement curvature (t9 = 1.21, P = 0.26) and movement time (t9 = 2.16, P = 0.06). Participants had no difficulty following instructions to reach 45°CW from the green target when endpoint feedback was veridical (Fig. 5A, orange). In the second baseline block, participants resumed reaching to the green target and endpoint feedback was only provided on right-hand trials. Compared with the first baseline block, eliminating left-hand feedback slightly worsened endpoint accuracy (t9 = 2.34, P = 0.04) but did not change movement time (t9 = 1.22, P = 0.25) or movement curvature (t9 = 1.84, P = 0.10).
Fig. 5.
A: average hand angle over the course of experiment 4. Solid and dashed black lines indicate right- and left-hand trials, respectively, for the baseline blocks. Participants practiced using the strategy in the strategy-only block with the right (solid orange) and left hand (dashed orange). Participants experienced the 45° rotation on the first 2 movements of the rotation before being instructed to use the strategy. In the rotation+strategy block, participants were instructed to aim at the 45° clockwise aiming target (right-hand trials are shown in blue and left-hand trials in red). The rotation was removed, and participants were instructed to stop using the strategy on trial 313 (right-hand trials are shown in cyan and left-hand trials in magenta). B: average target angle during the rotation+strategy and washout blocks. The difference between the hand angle and the target angle was always 45° due to the rotation. Colors are as defined in A.
The introduction of the 45° CCW visuomotor rotation resulted in substantial endpoint error. The first two movements, always performed with the right hand, resulted in a visual target error of −45.9°, reflecting the fact that the movements were directed toward the green target. Participants were then instructed to use the 45° CW aiming strategy. Even though feedback was only provided on right-hand trials, the participants were instructed to adopt this strategy on both right- and left-hand trials. Implementation of the strategy resulted in an immediate reduction of visual target error. Calculated over the first two right-hand trials, the mean error was −6.4°. The participants were also successful in implementing the strategy with the left hand (mean visual target error of 2.8° on the first left-hand trial).
As the rotation+strategy block continued, the endpoint angle for the right hand began to drift in the direction of the strategy (Fig. 5, A and B, blue), consistent with previous studies (Mazzoni and Krakauer 2006). Our focus in this study was on whether this drift is also observed in the left hand. For each hand, we compared the endpoint angle between the beginning and end of the rotation+strategy block. For the right hand, the endpoint angle over the first 8 trials was 38.7 ± 13.2°. When calculated over the last 8 trials, this value increased to 57.1 ± 4.6° (t9 = 2.60, P = 0.03). A similar drift was observed on left-hand trials (Fig. 5, A and B, red): the endpoint angle rose from 47.8 ± 3.9° to 53.5 ± 4.2°, an effect that was significant (t9 = 3.07, P = 0.02). Note that right-hand performance was much more variable during the initial rotation+strategy trials as participants adjusted their aiming direction to bring the feedback cursor close to the target location. However, by the end of the rotation+strategy block, the mean endpoint angle was similar for the right and left hands (t9 = 1.87, P = 0.09).
During the washout block, participants were instructed to stop using the strategy and aim directly to the green target. To obtain a learning-free measure of the aftereffect, we did not provide feedback for the first eight trials with each hand. The average endpoint angles for the right and left hands were 12.1 ± 5.2° and 5.8 ± 3.2°, respectively (Fig. 5B, cyan and magenta). Both of these values were significantly different from baseline condition (right hand: t9 = 4.81, P < 0.001; left hand: t9 = 2.8, P = 0.02). The initial aftereffect for the right hand was larger than the aftereffect for the left hand (t9 = 4.20, P = 0.002). Feedback was then introduced on right-hand trials, allowing this aftereffect to washout. Similar to that observed during the learning phase, washout was also observed for left-hand movements.
DISCUSSION
We employed a novel method to examine intermanual transfer over the course of visuomotor adaptation, interleaving reaches performed with either the right or left hand. By limiting feedback to right-hand trials, we could assess the development of transfer in the left hand. In the first two experiments, we compared visuomotor adaptation under conditions in which the rotation was introduced abruptly or gradually. Significantly intermanual transfer was observed under both conditions. The magnitude of adaptation in the left hand was less than that observed in the right hand, even when the two hands were used equally often (experiment 2). Intermanual transfer was also observed with a more traditional blocked design (experiment 3), although a between-experiment comparison indicated that the degree of transfer was lower compared with our mixed design. A state-space model was used to fit the time series of the movements on a trial-by-trial basis. The results of this analysis indicated that the degree of transfer to the left hand was dependent on the degree of adaptation of the right hand. Moreover, the parameter estimates of the rate of adaptation confirmed that transfer was greater when probed over the course of learning, rather than at the completion of learning. We also observed intermanual transfer when we used a manipulation in which motor adaptation actually hinders performance (experiment 4). Together, the data presented demonstrate that visuomotor adaptation is not restricted to the limb receiving feedback concerning the visual perturbation. Moreover, intermanual transfer is not dependent on awareness of the perturbation. Rather, it develops on a trial-by-trial basis, dependent on the previously experienced error.
Intermanual Transfer and Awareness
Experiments 1–3 included conditions in which the visuomotor perturbation was introduced either abruptly or gradually. There are substantial differences between these two manipulations. In the gradual condition, successive rotations add only a small error and participants rarely are aware of the accumulating perturbation. In the abrupt condition, there is a large initial error that rapidly becomes small. In contrast, participants are aware of the altered environment in the abrupt condition, indicating some degree of surprise on the first trials after the rotation is introduced. Adaptation is faster when the perturbation is introduced abruptly, both in visuomotor adaptation (Kagerer et al. 1997) and in force field learning (Malfait and Ostry 2004). Studies of intramanual adaptation suggest that the faster rate of learning likely reflects differences in how error signals are treated, rather than a boost from the deployment of an explicit strategy (Berniker and Kording 2008; Criscimagna-Hemminger et al. 2010; Smith et al. 2006). Nonetheless, it is possible that awareness may be relevant for intermanual transfer, even if it contributes in a negligible manner to the final state of adaptation of the trained limb.
To date, only two studies have employed the gradual/abrupt contrast in studies of intermanual transfer. In the Malfait and Ostry (2004) study, transfer was only observed following force field adaptation when the perturbation was introduced abruptly, leading the authors to hypothesize that a cognitive strategy was responsible for transfer. In contrast, in the Wang et al. (2011) study, transfer was observed in both the abrupt and gradual conditions during visuomotor rotation adaptation. Their results would indicate that awareness has a negligible role on intermanual transfer.
As noted in the Introduction, one limitation with the Wang study is that participants developed some degree of awareness of the perturbation in their gradual condition. This awareness would likely be most salient right around the start of transfer given that incomplete adaptation yielded an error of ∼10° at the end of training. Our approach minimized this problem by probing transfer throughout training. Although we did not directly assess awareness during training (Perruchet and Amorim 1992), our continuous probe of intermanual transfer allowed us to examine the transfer function to determine whether there were any discontinuities. Our reasoning was that if a participant became aware of the rotation and developed a strategy to offset the rotation, we would see an abrupt onset of “transfer” at some point over the course of training.
Contrary to this prediction, we did not observe the sudden emergence of transfer in the gradual conditions of experiments 1 and 2 (or any such changes in performance with the trained limb). The time course of transfer evolved in a near-identical manner to that observed for right-hand learning, although the level of adaptation was reduced. The results from the abrupt condition also argue against a role for cognitive strategies in intermanual transfer. Similar to the gradual conditions, the magnitude of left-hand transfer reached an asymptotic level that is considerably below that reached by the right hand. If participants were employing a strategy to aim in a clockwise direction, we would expect that the same strategy would have been employed with either hand (or limited to just the right hand). It does not seem reasonable that they would attenuate the strategy on left-hand trials.
Previous experiments in which participants are given a cognitive strategy to compensate for a visuomotor rotation have revealed a striking degree of independence between strategic and motor processes (Mazzoni and Krakauer 2006; Sülzenbrück and Heuer 2009; Taylor and Ivry 2011). When participants use a strategy, the rotation is immediately counteracted. However, as training continues, the movements begin to drift in the direction of the strategy, revealing the continued operation of an adaptation process that does not have access to the strategy. In the current study, we exploited this phenomenon as a further test of the effect of awareness on intermanual transfer. Drift was present, not only in the movements of the right hand but also in those produced with the left hand.
Together, the current results provide compelling evidence that motor adaptation processes are largely driving intermanual transfer, consistent with the conclusions of Wang et al. (2011). It remains unclear why Malfait and Ostry (2004) only observed intermanual transfer during force field learning when the perturbation was introduced in an abrupt manner. We note that in their study, participants were given considerably more training trials in the gradual condition. Given that consolidation processes occur at multiple timescales (Shadmehr and Brashers-Krug 1997; Smith et al. 2006), the absence of transfer in the gradual condition may be related to the degree of consolidation achieved at the time of test. High levels of transfer that may be evident during the early stages of learning may give way to effector specificity as skills become more consolidated (Karni et al. 1998). It is also possible that the discrepancy between our results and those of Malfait and Ostry reflect differences in the control operations required for learning novel force fields or novel visuomotor transformations.
Mechanisms of Intermanual transfer
Recognizing the limitations in directly comparing the abrupt and gradual conditions, we employed a state-space model to parameterize the process of right-hand adaptation and transfer to the left hand. The model was designed to have separate internal models for the right and left hand, with the visual error information from right-hand trials used to update both internal models. Previous accounts of intermanual transfer have focused on the idea that movements with either limb share a common internal model. One notable example is the callosal model of Taylor and Heilman (1980), developed, in large part, to account for hand dominance as well as asymmetries observed with apraxia. In the strong version of this model, internal models are only stored for movements produced with the dominant limb. When movements are produced with the nondominant limb, this single internal model must be accessed and transferred over the corpus callosum. Information loss will arise during transcallosal transmission, thus rendering poorer control for movements with the nondominant limb. Applying this idea to the current context, the information loss would occur in the transfer of an adapted internal model across limbs.
There are various problems with this hypothesis. For example, split-brain patients have minimal difficulty using either limb to make reaching movements (Franz et al. 1996), arguing against the reliance of an internal model isolated to a single hemisphere. Moreover, people can simultaneously learn opposing visuomotor rotations with the left and right arms (Galea and Miall 2006; Galea et al. 2010). It is hard to understand how the left arm could learn a clockwise rotation while the right arm learns a counterclockwise rotation if there is just a single internal model, controlling movements with either arm.
These observations led us to consider an alternative architecture in which there are separate internal models for each hand (e.g., see Sainburg and Wang 2002) and, most critically, the two models are updated by a common error term. In our task, errors experienced on right-arm trials are used to update not only the internal model for the right arm but also an internal model associated with the left arm. The model provided reasonable fits of the data for both hands in all of the experiments. Moreover, an analysis of the parameter estimates is consistent with the conclusion that a common process underlies intermanual transfer in both the abrupt and gradual conditions. The rates of adaptation and transfer were greater when the rotation was introduced abruptly due to the fact that the error was larger in the abrupt conditions. However, when the rate of transfer was normalized by the rate of adaptation, we observed no difference between the abrupt and gradual conditions.
It remains to be seen if this common error updating is only restricted to conditions in which feedback is limited to movements with one hand, the constraint applied in the current study. We do note that a generic updating process would be especially adaptive for transformations defined in extrinsic coordinates. For example, a tennis player who switches hands to avoid backhand shots would want to incorporate the environmental conditions into his or her strokes with either hand.
Degraded Intermanual Transfer
The behavioral data show that transfer from the right hand to the left hand was incomplete. The degree of adaptation in the left hand was always less than that observed in the right hand. This difference is especially striking at asymptote. Regardless of whether the rotation was introduced abruptly or gradually, the angular shift in left hand reaching was 33–50% of that evidenced by the right hand in our mixed design experiments. Interestingly, this difference was present even when the left hand was used as frequently as the right hand (experiment 2). Moreover, a small, albeit significant, degree of transfer was observed when we used a blocked design (experiment 3). These observations suggest that incomplete left-hand transfer is not related to memory decay. Indeed, a single memory retention parameter was sufficient to produce good fits with our state-space model for both the mixed and blocked designs. This modeling work suggests that incomplete transfer is due to a loss of information concerning the error signal. That is, the weight given to the error is larger for updating the right-hand internal model, the hand that produced the error, compared with the weight given to the error for updating the left-hand internal model.
We can think of a number of reasons why there may be a loss of error information. The sharing of error information across the limbs may be similar to the processes that underlie observational learning (Brown et al. 2010; Mattar and Gribble 2005). As in the present study of intermanual transfer, observation learning does not appear to depend on the development of cognitive strategies (Mattar and Gribble 2005). Moreover, the rate of learning via action observation is less than that found during action execution, consistent with what we observe in left-hand transfer. At a neural level, there may simply be information loss arising from the added signal processing required during observational learning or transfer. This may relate to noise arising in interhemispheric communication in general or asymmetries related to hand dominance. For example, an error signal broadcast to the nondominant hand may produce less change than one broadcast to the dominant hand given differences in the relative salience of these signals. Moreover, the gain of learning and transfer may be a function of the perceived proficiency or confidence attributed to the two limbs (Berniker and Kording 2008).
Another possibility is that the degraded transfer may be reflect a state dependency for the incorporation of error information. When an error arises from a right-arm movement, the right arm is in the appropriate state to incorporate that error information. That is, the right arm, by definition, is task relevant: it has produced the movement that led to the error. In contrast, the (resting) left arm is not in a state that is appropriately suited to incorporate this information. Thus an error signal, even if broadcast equally well to controllers for both arms, may be less effective when applied to a controller that is not fully engaged. Indeed, studies using choice reaction time tasks have shown that fluctuations in cortical excitability of a stationary limb are modulated by task relevance (Duque and Ivry 2009).
This hypothesis may also explain, in part, the reduced rate of transfer in the blocked design of experiment 3 compared with the mixed design of experiments 1 and 2 (see also Balitsky Thompson and Henriques 2010; Malfait and Ostry 2004; Sainburg and Wang 2002; Wang and Sainburg 2004). Wang et al. (2011) also observed a modest level of right-hand transfer with a blocked design, reporting a figure of ∼25%. This value is likely inflated by the fact that they provided feedback during transfer, allowing for some adaptation to occur during on the right-hand trials. The task irrelevance during training of the transfer limb may have produced attenuated levels of transfer.
A final possibility is that during transfer, the motor system has to combine multiple sources of conflicting error information. In visuomotor learning, the mapping between proprioception and vision is altered during adaptation. This can result in a recalibration of both visual and proprioceptive space (Cressman and Henriques 2011; Ostry et al. 2010). It is possible that only the recalibrated visual map is shared between the limbs, whereas the recalibrated proprioceptive map remains restricted to the trained limb. As such, when transfer is tested, the motor system combines a recalibrated visual mapping with an unaltered proprioceptive mapping. This combination would result in a lower degree of adaptation, even if there was full transfer of the modified visual map. Future research should employ methods that provide separate probes of changes in visual and proprioceptive mappings to evaluate this hypothesis.
GRANTS
J. Taylor was supported by National Institutes of Health (NIH) National Research Service Award F32NS064749. R. Ivry was supported by NIH Grants R01HD060306 and P01NS040813.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
J.A.T. and R.B.I. conception and design of research; J.A.T. and G.J.W. performed experiments; J.A.T. and G.J.W. analyzed data; J.A.T., G.J.W., and R.B.I. interpreted results of experiments; J.A.T. prepared figures; J.A.T. drafted manuscript; J.A.T. and R.B.I. edited and revised manuscript; J.A.T. and R.B.I. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Christina Gee and Azeen Ghorayshi for help with data collection. We thank John Schlerf for setting up the experimental equipment and Jing Xu for help with statistical analysis.
REFERENCES
- Balitsky Thomson AK, Henriques DY. Visuomotor adaptation and intermanual transfer under different viewing conditions. Exp Brain Res 202: 543–554, 2010 [DOI] [PubMed] [Google Scholar]
- Beilock SL, Bertenthal BI, McCoy AM, Carr TH. Haste does not always make waste: expertise, direction of attention, and speed versus accuracy in performing sensorimotor skills. Psychon Bull Rev 11: 373, 2004 [DOI] [PubMed] [Google Scholar]
- Beilock SL. Understanding skilled performance: memory, attention, and choking under pressure. In: Sport and Exercise Psychology: International Perspectives, edited by Morris T, Terry P, Gordon S. Morgantown, WV: Fitness Information Technology, 2007, p. 153–166 [Google Scholar]
- Benson BL, Anguera JA, Seidler RD. A spatial explicit strategy reduces error but interferes with sensorimotor adaptation. J Neurophysiol 105: 2843–2851, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berniker M, Kording K. Estimating the sources of motor errors for adaptation and generalization. Nat Neurosci 11: 1454–1461, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brashers-Krug T, Shadmehr R, Bizzi E. Consolidation in human motor memory. Nature 18: 252–255, 1996 [DOI] [PubMed] [Google Scholar]
- Brown LE, Wilson ET, Obhi SS, Gribble PL. Effect of trial order and error magnitude on motor learning by observing. J Neurophysiol 104: 1409–1416, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cressman EK, Henriques DT. Motor adaptation and proprioceptive recalibration. J Neurophysiol 191: 91–99, 2011 [DOI] [PubMed] [Google Scholar]
- Criscimagna-Hemminger SE, Donchin O, Gazzaniga MS, Shadmehr R. Learned dynamics of reaching movements generalize from dominant to nondominant arm. J Neurophysiol 89: 168–176, 2003 [DOI] [PubMed] [Google Scholar]
- Criscimagna-Hemminger SE, Bastian AJ, Shadmehr R. Size of error affect cerebellar contributions to motor learning. J Neurophysiol 103: 2275–2284, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham HA, Welch RB. Multiple concurrent visual-motor mappings: implications for models of adaptation. J Exp Psychol Hum Percept Perform 20: 987, 1994 [DOI] [PubMed] [Google Scholar]
- Curran T, Keele SW. Attentional and nonattentional forms of sequence learning. J Exp Psychol Learn Mem Cogn 19: 189, 1993 [Google Scholar]
- Dizio P, Lackner JR. Motor adaptation to Coriolis force perturbations of reaching movements: endpoint but not trajectory adaptation transfers to the nonexposed arm. J Neurophysiol 74: 1787–1792, 1995 [DOI] [PubMed] [Google Scholar]
- Duque J, Ivry RB. Role of corticospinal suppression during motor preparation. Cereb Cortex 19: 2013–2024, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Ruiz J, Wong W, Armstrong IT, Flanagan JR. Relation between reaction time and reach errors during visuomotor adaptation. Behav Brain Res 219: 8–14, 2011 [DOI] [PubMed] [Google Scholar]
- Franz EA, Eliassen JC, Ivry RB, Gazzaniga MS. Dissociation of spatial and temporal coupling in the bimanual movements of callosotomy patients. Psychol Sci 7: 306–310, 1996 [Google Scholar]
- Galea JM, Miall RC. Concurrent adaptation to opposing visual displacements during an alternating movement. Exp Brain Res 175: 676–688, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galea JM, Sami SA, Albert NB, Miall RC. Secondary tasks impair adaptation to step- and gradual-visual displacements. Exp Brain Res. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heuer H, Hegele M. Adaptation to visuomotor rotations in younger and older adults. Psychol Aging 23: 190–202, 2008 [DOI] [PubMed] [Google Scholar]
- Hwang EJ, Smith MA, Shadmehr R. Dissociable effects of the implicit and explicit memory systems on learning control of reaching. Exp Brain Res 173: 425–437, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imamizu H, Shimojo S. The locus of visual-motor learning at the task or manipulator level: implications from intermanual transfer. J Exp Psychol Hum Percept Perform 21: 719–733, 1995 [DOI] [PubMed] [Google Scholar]
- Kagerer FA, Contreras-Vidal JL, Stelmach GE. Adaptation to gradual as compared with sudden visuo-motor distortions. Exp Brain Res 115: 557–561, 1997 [DOI] [PubMed] [Google Scholar]
- Karni A, Meyer G, Rey-Hipolito C, Jezzard P, Adams MM, Turner R, Ungerleider LG. The acquisition of skilled motor performance: fast and slow experience-driven changes in primary motor cortex. Proc Natl Acad Sci USA 95: 861–868, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klassen J, Tong C, Flanagan JR. Learning and recall of incremental kinematic and dynamic sensorimotor transformations. Exp Brain Res 164: 250–259, 2005 [DOI] [PubMed] [Google Scholar]
- Kluzik J, Diedrichsen J, Shadmehr R, Bastian AJ. Reach adaptation: what determines whether we learn an internal model of the tool or adapt the model of our arm? J Neurophysiol 100: 1455–1464, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malfait N, Ostry DJ. Is interlimb transfer of force-field adaptation a cognitive response to the sudden introduction of load? J Neurosci 24: 8084–8089, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin TA, Keating JG, Goodkin HP, Bastian AJ, Thach WT. Throwing while looking through prisms: II. Specificity and storage of multiple gaze-throw calibrations. Brain 119: 1199, 1996 [DOI] [PubMed] [Google Scholar]
- Mattar AAG, Gribble PL. Motor learning by observing. Neuron 46: 153–160, 2005 [DOI] [PubMed] [Google Scholar]
- Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci 26: 3642–3645, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Comput J 7: 308–313, 1965 [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9: 97–113, 1971 [DOI] [PubMed] [Google Scholar]
- Oliveira FTP, Diedrichsen J, Verstynen T, Duque J, Ivry RB. Transcranial magnetic stimulation of posterior parietal cortex affects decisions of hand choice. Proc Natl Acad Sci USA 107: 17751–17756, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostry DJ, Darainy M, Mattar AA, Wong J, Gribble PL. Somatosensory plasticity and motor learning. J Neurosci 30: 5384–5393, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perruchet P, Amorim M. Conscious knowledge and changes in performance in sequence learning: evidence against dissociation. J Exp Psychol Learn Mem Cogn 18: 785–800, 1992 [DOI] [PubMed] [Google Scholar]
- Saijo N, Gomi H. Multiple motor learning strategies in visuomotor rotation. PLoS One 5: e9399, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Wang J. Interlimb transfer of visuomotor rotations: independence of direction and final position information. Exp Brain Res 145: 437–447, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Brashers-Krug T. Functional stages in the formation of human long-term motor memory. J Neurosci 17: 409–419, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4: e179, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sülzenbrück S, Heuer H. Functional independence of explicit and implicit motor adjustments. Conscious Cogn 18: 145–159, 2009 [DOI] [PubMed] [Google Scholar]
- Taub E, Goldberg LA. Prism adaptation: control of intermanual transfer by distribution of practice. Science 180: 755–757, 1973 [DOI] [PubMed] [Google Scholar]
- Taylor HG, Heilman KM. Left-hemisphere motor dominance in righthanders. Cortex 16: 587–603, 1980 [DOI] [PubMed] [Google Scholar]
- Taylor JA, Ivry RB. Flexible cognitive strategies during motor learning. PLoS Comput Biol 7: e1001096, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor JA, Klemfuss NM, Ivry RB. An explicit strategy prevails when the cerebellum fails to compute movement errors. Cerebellum 9: 580–586, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. Limitation in interlimb transfer of visuomotor rotations. Exp Brain Res 55: 1–8, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Joshi M, Lei Y. The extent of interlimb transfer following adaptation to a novel visuomotor condition does not depend on awareness of the condition. J Neurophysiol 106: 259–264, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willingham DB, Nissen MJ, Bullemer P. On the development of procedural knowledge. J Exp Psychol Learn Mem Cogn 15: 1047–1060, 1989 [DOI] [PubMed] [Google Scholar]