New Perspectives on Iron–Ligand Vibrations of Oxyheme Complexes

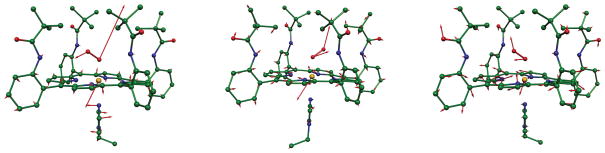
Abstract

We report our studies of the vibrational dynamics of iron for three imidazole-ligated oxyheme derivatives that mimic the active sites of histidine-ligated heme proteins complexed with dioxygen. The experimental vibrational data are obtained from nuclear resonance vibrational spectroscopy (NRVS) measurements conducted on both powder samples and oriented single-crystals, and which includes several in-plane (ip) and out-of-plane (oop) measurements. Vibrational spectral assignments have been made through a combination of the oriented sample spectra and predictions based on density functional theory (DFT) calculations. The twoFe–O₂ modes that have been previously observed by resonance Raman spectroscopy in heme proteins are clearly shown to be very strongly mixed and are not simply either a bending or stretching mode. In addition, a third Fe–O₂ mode, not previously reported, has been identified. The long-sought Fe–Im stretch, not observed in resonance Raman spectra, has been identified and compared with the frequencies observed for the analogous CO and NO species. The studies also suggest that the in-plane iron motion is anisotropic and is controlled by the orientation of the Fe–O₂ group and not sensitive to the in the in-plane Fe–N_p bonds and/or imidazole orientations.

Introduction

Diatomic molecules make essential contributions to the processes of life. The best known is the role of molecular oxygen, which transformed Earth’s biosphere and is central to complex biomolecular networks.^[1] Myoglobin and hemoglobin are examples of proteins containing heme molecules that perform their biochemical functions by reversibly binding and releasing dioxygen. In spite of a long history of study on the interactions of dioxygen with the oxygen-carrying and -storing heme proteins, there are a number of scientific debates concerning the geometric, electronic, and biophysical properties, many of which continue to the present time. These issues include the geometry of the bound dioxygen,^[2] the perplexing nature of the (diamagnetic) electronic structure,^[3] the assignment of the vibrational modes of the Fe–O₂ unit,^{[4, 5]} the dynamics of the Fe–O₂ group in the heme environment,^[6] the relative orientation of the bound dioxygen with respect to the plane of the trans histidine,^[7] and the importance of the Fe–N(histidine) bond strength,^[8] especially with respect to the mechanism of hemoglobin cooperativity.^[9] Only the first of these issues has been completely resolved initially with the “picket fence porphyrin” O₂ structures^[10], and then with the structures of oxymyoglobin^[11] and oxyhemoglobin^[12] that showed a dioxygen molecule bonded end-on and bent.

We have investigated the vibrational and dynamical nature of [Fe(TpivPP)(RIm)(O₂)]^[13] complexes with nuclear resonance vibrational spectroscopy (NRVS)^[14] and multi-temperature X-ray and Mössbauer measurements.^[16] NRVS is a synchrotron-based spectroscopic technique that provides direct experimental access to all Fe vibrations.^[17] For diatomic ligated hemes such as [Fe(Porph)(RIm)(XO)] (X = O, C, or N), the vibrations involving the six covalent bonds to the iron contribute prominently to the NRVS signal, and include the imidazole and pyrrole nitrogens as well as the Fe–XO vibrations. This is in contrast to other vibrational techniques e.g. resonance Raman spectroscopy which, although observing Fe–XO vibrations, have not observed the Fe–Im vibration(s) trans to Fe–X–O, critical to assessing the Fe–Im bond strength, inherent in the low frequency region with weak signal, spectral congestion and low sensitivity to isotopic substitution.^[18]

Both powder and polarized single-crystal measurements can be made with NRVS. For many samples, the crystal can be oriented so that the NRVS measurement is made with the incident X-ray beam either parallel to the porphyrin planes or perpendicular to them. Such orientations lead to intensity enhancements in the in-plane (ip) or out-of-plane (oop) modes respectively. A single crystal measurement allows the unambiguous identification of many modes as either having in-plane or out-of-plane character. Even more detail can be obtained by aligning crystals with the probe beam in-plane and along selected directions corresponding to significant molecular features. The application of this more detailed experiment to the five-coordinate complex [Fe(OEP)(NO)]^[19] gave observed anisotropic vibrational spectra. Analysis of the spectra led to the conclusion that the axial nitrosyl ligand was controlling the direction of the in-plane iron motion.

In this paper, we report detailed NRVS measurements on oxyheme derivatives with the different axial imidazoles 1-MeIm, 1-EtIm or 2-MeHIm. Besides powder measurements, we utilized oriented single-crystal measurements to acquire in-plane and out-of-plane vibrations, to study the effects of hindered vs. unhindered imidazoles, and afford new insight of the iron dynamics. DFT calculations are conducted to predicted the vibrational dynamics. We compare the vibrational predictions on the amplitude and direction of the Fe motion, as well as mode frequencies with the experimental spectra. This comparison provides a rigorous and successful test of the predictions, which describe vibrational modes observed in the experimental spectra.^[20]

Experimental Section

General Information

All reactions and manipulations were carried out under argon using a double-manifold vacuum line, Schlenkware and cannula techniques. Benzene and heptane were distilled over sodium/benzophenone. Chlorobenzene was washed with concentrated sulfuric acid, then with water until the aqueous layer was neutral, dried with MgSO₄, and distilled twice over P₂O₅ under argon. Research grade oxygen (99.999%) was purchased from PRAXAIR and used as received. [H₂(TpivPP)] was prepared according to a local modification of the reported synthesis.^[21] Metalation of 95% ⁵⁷Fe enriched samples was prepared by a method similar to that of Landergren.^[22] Mössbauer measurements were performed on a constant acceleration spectrometer with optional small field (Knox College). Samples for Mössbauer spectroscopy were prepared by immobilization in Apiezon M grease.

Synthesis of [⁵⁷Fe(TpivPP)(1-RIm)(O₂)] (R = Me or Et) (powder and single crystal)

[⁵⁷Fe(TpivPP)(1-RIm)₂] was obtained by a local modification of the reported synthesis.^{[21, 23]} [⁵⁷Fe(TpivPP)(1-RIm)₂] (30 mg) was dried in vacuum for 30 mins. Drops of the imidazole and benzene (~5 mL) were then transferred into the Schlenk by cannula. This mixture was gently heated with stirring and cooled to room temperature to give a clear red solution. Oxygen was then bubbled into this solution to yield the oxygenated species. A dark-red powder sample was obtained from the reaction solution by addition of heptane and filtered. The purity of the powder samples were confirmed by a Mössbauer measurement. X-ray quality crystals of [⁵⁷Fe(TpivPP)(1-EtIm)(O₂)] were obtained in 8 mm × 250 mm sealed glass tubes by slow liquid diffusion using heptane as nonsolvent.

Synthesis of [⁵⁷Fe(TpivPP)(2-MeHIm)(O₂)] (powder and single crystal)

Moderate-sized (0.3–0.5 mm) single crystals of [⁵⁷Fe(TpivPP)(2-MeHIm)] were freshly isolated.^[24]a The crystals were exposed to 1–2 atm of pure dioxygen gas that was saturated with ethanol vapor at room temperature. The dioxygen adduct [⁵⁷Fe(TpivPP)(2-MeHIm)(O₂)] was obtained after 3 days reaction and used immediately for the spectroscopic experiment. A powder sample was prepared by crushing these crystals and the purity was confirmed by a Mössbauer measurement.

Crystal alignment and NRVS measurements

A detailed crystal alignment and NRVS measurement program has been developed.^[19] The crystal alignment procedures described previously were used for all O₂ single-crystal samples on a Bruker-Nonius Kappa CCD diffractometer. For the dioxygen complexes, the porphyrin plane defined by four porphyrin nitrogen atoms is determined by the crystallographic symmetry of the problem with Miller indices 0,1,0. With this plane parallel to the goniometer axis, rotation of the aligned crystal will give both the in-plane (ip) and out-of-plane (oop) measurements. All NRVS measurements were made at Sector 3–ID of the Advanced Photon Source, Argonne National Laboratory. All crystal orientations were confirmed to remain valid after the NRVS measurements. The Fe-weighted vibrational density of states (VDOS) is obtained from the data with the program PHOENIX^{[25, 26]} that removes temperature factors, multiphonon contributions, and an overall factor proportional to inverse frequency. Complete details have been given in Leu et al.^[27]

Vibrational Predictions

Predictions of the vibrational spectra were obtained from DFT calculations using the Gaussian 09 program package.^[28] [Fe(Porphine)(1-MeIm)(O₂)] and [Fe(TpivPP)(RIm)(O₂)] (RIm = 1-MeIm or 2-MeHIm) have been calculated. Initial unconstrained calculations using all atoms of the porphyrin derivative were performed. The unrestricted B3LYP functional,^[29] the TZVP basis set for iron,^[30] and 6–31G* for the remaining atoms were used and, for the picket fence derivatives, initial calculations were based on the molecular geometry from the crystal structure. These calculations converged to a closed-shell singlet configuration. Open-shell calculations were also performed. The open-shell singlet states were obtained by orbital swapping from the converged triplet states to ensure that they do not converge to closed-shell singlet states.

Predicted Mode Composition Factors and Vibrational Density of States

The DFT calculations can predict mode composition factors.^[31] The mode composition factor ${\text{e}}_{j\alpha }^2$ is equal to the fraction of the kinetic energy in frequency α due to the motion of atom j (here ⁵⁷Fe, a NRVS active nucleus). The mode composition factors provide a convenient quantitative comparison between the observed spectra and DFT predictions.^[31] The normal mode calculations describe vibrational eigenvectors with atomic displacements r_i, which directly determine the mode composition factors as shown in equation (1):

$$e_{j\alpha }^2=\frac{m_j{r}_j^2}{\sum m_i{r}_i^2}$$ (1)

where the sum over i runs over all atoms of the molecule, m_i is the atomic mass of atom i, and r_i is the absolute length of the Cartesian displacement vector for atom i. The mode composition factors in the different directions are defined as in-plane and out-of-plane. The in-plane component can be calculated from a projection of the atomic displacement vectors x and y, which lie in the porphyrin plane (eq. 2). The out-of-plane component, which is perpendicular to the porphyrin plane for a normal mode, is obtained from a projection of the atomic displacement vector z (eq. 3).

$$e_{j\alpha ,\text{inplane}}^2=\frac{m_j(r_{jx}^2+r_{jy}^2)}{\sum m_i{r}_i^2}$$ (2)

$$e_{j\alpha ,\text{outofplane}}^2=\frac{m_j{r}_{jz}^2}{\sum m_i{r}_i^2}$$ (3)

The predicted mode composition factors can also be compared to the integrated spectral areas obtained from NRVS.^[18] NRVS VDOS intensities can be simulated from the mode composition factors using the normal Gaussian distribution function, where the full width at half height (FWHH) is defined appropriately by considering the experimental resolution (FWHH=7.5 cm⁻¹ in this paper). The x, y, and z components of iron energy for normal modes with total ${\text{e}}_{Fe}^2$ above 0.01 for [Fe(TpivPP)(1-EtIm)(O2)] and [Fe(TpivPP)(2-MeHIm)(O2)] are given in Tables S1–S3 of the Supporting Information.

Results

NRVS

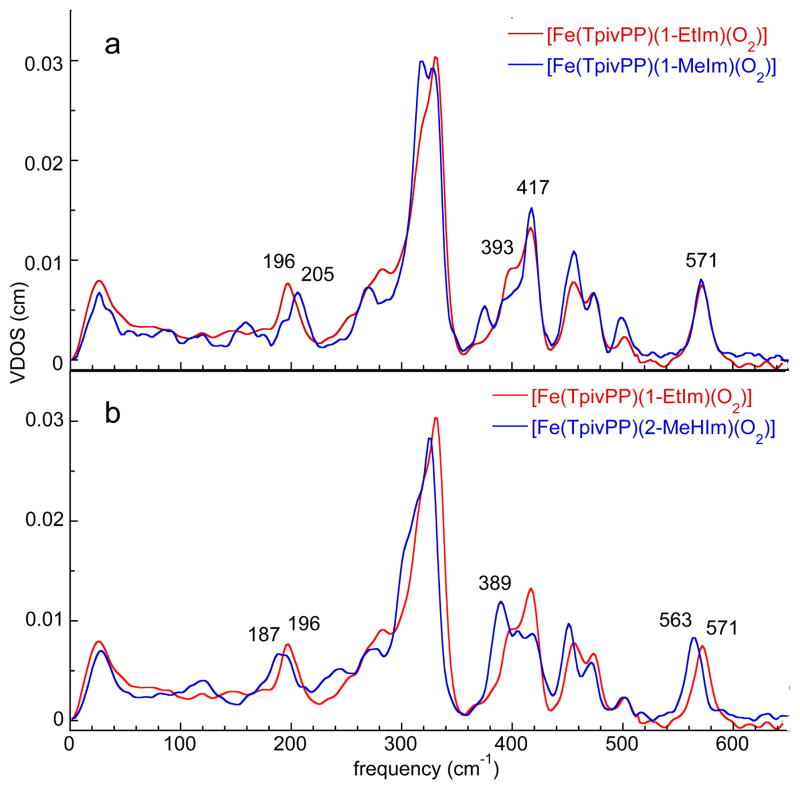
Three oxyheme complexes, [Fe(TpivPP)(RIm)(O₂)] (RIm = 1-MeIm, 1-EtIm, or 2-MeHIm), have been characterized as powder samples by NRVS. Single crystals adequate for oriented crystal NRVS experiments were available for 1-EtIm and 2-MeHIm derivatives; both the in-plane and out-of-plane orientations have been measured. The experimental spectra will be displayed as appropriate in the Discussion and the Supporting Information. The powder samples were measured at ~25 K with a helium cryostat, whereas the single-crystal spectra were measured at higher temperatures with a nitrogen flow cryocooler. The in-plane spectra were taken at the experimental temperature of 148 K (1-EtIm derivative) and 128 K (2-MeHIm derivative). The out-of-plane spectra were taken at the experimental temperature of 120 K (1-EtIm derivative) and 129 K (2-MeHIm derivative). The in-plane and out-of-plane components are scaled to show their relative contributions to the powder spectrum. The small difference observed in the value of the highest frequency mode for 1-EtIm (571 cm⁻¹ powder and 566 cm⁻¹ oriented crystal) and 2-MeHIm (563 cm⁻¹ powder and 559 cm⁻¹ oriented crystal) derivatives are believed to be a temperature effect.

Closed-shell vs. Open-shell calculations

Model calculations on [Fe(Porphine)(1-MeIm)-(O₂)] for the closed-shell and open-shell singlet states were performed in order to explore whether such ground state differences would effect the vibrational predictions. The open-shell singlet is predicted to have lower relative energy by B3LYP; the axial Fe–O bond distance is longer in the open-shell singlet than in the closed-shell singlet (1.860 Å vs. 1.762 Å, respectively). There are significantly different predictions for the nominal Fe–O stretch: a predicted lower than observed frequency from the open-shell results and a higher than observed frequency from the closed-shell prediction as well as other differences. Similar geometric differences between open-shell and closed-shell singlets have been noted previously,^{[3]d, [32, 33]} but to our knowledge no vibrational predictions have been made.

We then conducted closed-shell and open-shell calculations for the picket fence porphyrin derivatives which gave similar results. The open-shell singlet prediction for [Fe(TpivPP)(1-EtIm)(O₂)] gave a lower relative energy and longer axial Fe–O bond distance than in the closed-shell singlet (1.873 Å vs. 1.753 Å, respectively). These results together with the experimental structural parameters are given in Table 1. The calculated energetics of the spin states are sensitive to the DFT method employed.

Table 1.

Calculated and experimental structural parameters for [Fe(TpivPP)(1-EtIm)(O₂)], [Fe(TpivPP)-(2-MeHIm)(O₂)] and [Fe(Porphine)(1-MeIm)(O₂)].^[a]

	[Fe(TpivPP)(1-EtIm)(O2)]			[Fe(TpivPP)(2-MeHIm)(O2)]		[Fe(Porphine)(1-MeIm)(O2)]
	B3LYP (cs)[b]	B3LYP (os)[b]	X-ray	B3LYP (cs)[b]	X-ray	B3LYP (cs)[b]	B3LYP (os)[b]
Fe–O2	1.753	1.873	1.798(3)	1.749	1.804(3)	1.762	1.860
Fe–NIm	2.107	2.122	2.043(3)	2.171	2.087(5)	2.101	2.076
Fe–Np	2.000	2.007	1.989(3)	1.992	1.993(2)	2.009	2.030
	2.003	2.008		1.990		2.033	2.019
	2.031	2.023	1.990(3)	2.022	1.997(2)	2.036	2.017
	2.031	2.022		2.018		2.011	2.028
O–O	1.277	1.294	1.166(8)	1.278	1.130(6)	1.264	1.249
			1.111(12)		1.206(19)
Fe–O–O	121.8	118.0	126.6(4)	121.5	129.9(3)	121.7	126.9
			132.4(7)		129.6(11)

^[a]Basis set for iron: TZVP; Distance values in Å, Angle values in deg.

^[b]cs: closed-shell; os: open-shell

The measured and two predicted VDOS (open-shell and closed-shell) for [Fe(TpivPP)(1-EtIm)(O₂)] are presented in Figure S1. Substantial similarity in the lower frequency region (< 340 cm⁻¹) is found for the two calculated configurations. In the higher frequency region (>360 cm⁻¹), the closed-shell calculation predicted seven major features, which are apparent in the same region of the experimental powder VDOS. These bands are comparable to the experiment in both frequencies and intensities. In contrast, the open-shell calculation predicted only five features in the same region. We thus conclude that the predictions we have obtained for the full closed-shell picket fence calculation will be the most useful in understanding the modes of the experimental spectra even though the predicted Gibbs Free Energy is lower for the open-shell result.

Discussion

The powder spectra of [Fe(TpivPP)(1-MeIm)(O₂)] and [Fe(TpivPP)(1-EtIm)(O₂)] are shown in Figure 1a. General features of the O₂ NRVS spectra are similar to the analogous NO^[20] and CO^[27] species. Three spectral regions command attention: i) the region above 360 cm⁻¹, ii) the region below 220 cm⁻¹, and finally iii) the region between 220–360 cm⁻¹. The high frequency region, >360 cm⁻¹, which must contain the Fe–O₂ bending and stretching modes, is seen to be nearly identical for the two complexes. Similarly, the ~220–360 cm⁻¹ region, primarily due to ip iron motion, also shows only minor differences. The spectral region below ~220 cm⁻¹, which is responsive to iron doming and iron/imidazole motions, displays more significant spectral differences. We conclude that only features that involve imidazole motion will be characteristic of 1-EtIm and 1-MeIm differences.

Figure 1.

The measured VDOS for powder samples of [Fe(TpivPP)(Im)(O₂)].

Replacing 1-EtIm with 2-MeHIm leads to interesting changes in the >360 and 0–220 cm⁻¹ regions (Figure 1b). The 8 cm⁻¹ difference in the highest frequency band (Figure 1b) could suggest differences in the Fe–O₂ bond strength between the derivatives. Resonance Raman studies of [Fe(TpivPP)(RIm)(O₂)] where RIm is either a hindered or unhindered imidazole often showed such differences^[34] but not always.^[35] However, crystal structures of [Fe(TpivPP)(1-EtIm)(O₂)] and [Fe(TpivPP)(2-MeHIm)(O₂)] at 100 K show the same Fe–O₂ bond distance (1.798(4) and 1.804(3) Å). ^[36] We suggest that differences in normal mode composition, a possible result of the differing trans Fe–N_Im interactions^[37] play a role in the frequency differences. Note that other high frequency modes also show similar shifts (Figure 1b).

Resonance Raman spectra of oxyheme proteins have been measured by several investigators.^{[4, 5]} An oxygen isotope sensitive band at ~568 cm⁻¹ is seen in all studies, whereas an additional band at ~425 cm⁻¹ is only seen in some.^[38] There has been substantial controversy concerning the assignment of the bands, particularly that of the 568 cm⁻¹ band. Although this band was initially assigned as the Fe–O₂ stretch,^[4]a spectra taken with the mixed ¹⁶O¹⁸O isotope showed relatively little sensitivity to the mass of the terminal oxygen atom,^[4]b leading to the conclusion that the band is better described as the Fe–O₂ bending mode.^[5]a

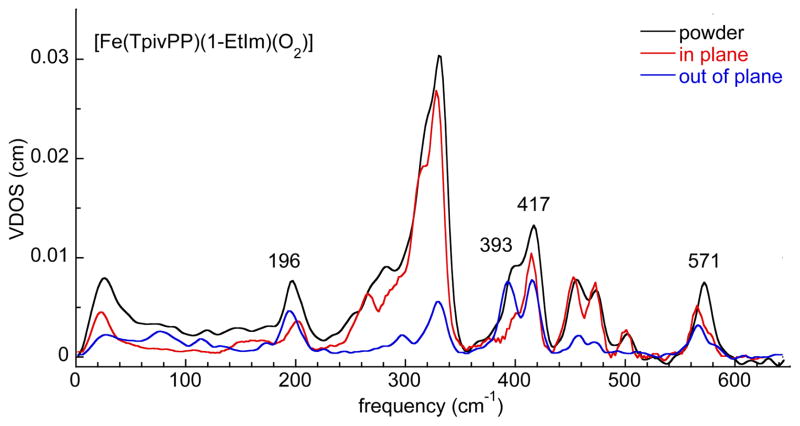
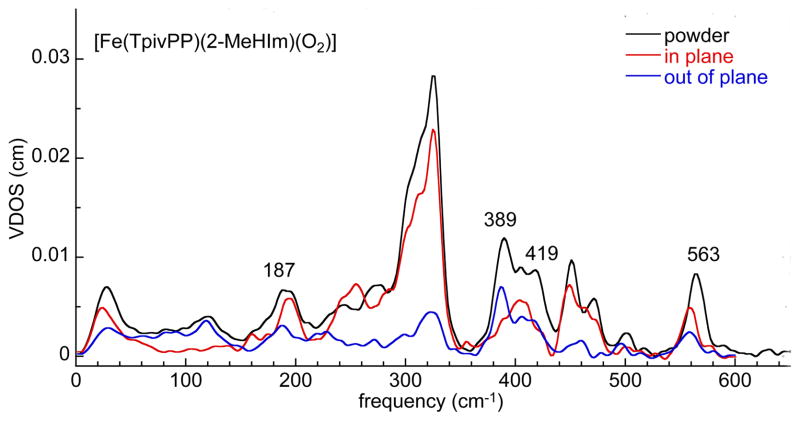
We have carried out oriented single-crystal NRVS measurements^{[19, 20, 27, 39]} to clarify the Fe–O₂ mode assignments. Single crystals adequate for the oriented NRVS experiment were available for the 1-EtIm and 2-MeHIm derivatives. Figures 2, 3, S2, and S3 display the ip and oop spectra. Three relatively intense out-of-plane modes with frequencies of 571, 417 and 393 cm⁻¹ are seen in the 1-EtIm derivative (Figure 2) and 563, 419 and 389 cm⁻¹ in the 2-MeHIm derivative (Figure 3). The two at highest frequency (571 and 417 cm⁻¹ or 563 and 419 cm⁻¹) are similar to the oxygen isotope sensitive bands (568 and 425 cm⁻¹) observed in resonance Raman. In both derivatives, these two bands have both ip and oop contributions, both are thus significantly mixed modes and assignments as either bending or stretching is problematic. The strongly mixed stretching and bending character of the Fe–O₂ modes indicate that Raman assignments based on isotope sensitivity will have substantial uncertainty. It should be noted that the Fe–O₂ mode mixing is at least as pronounced as the Fe–NO mode mixing in the structurally similar {FeNO}⁷ nitrosyl complexes.^{[20, 39]}

Figure 2.

The measured VDOS for [Fe(TpivPP)(1-EtIm)(O₂)] (powder and single crystal) The experimental temperature for the powder sample was 25 K. The in-plane spectrum was taken with the porphyrin plane oriented parallel to the excitation beam at an experimental temperature of 148 K. The out-of-plane spectra were taken with the porphyrin plane oriented perpendicular to the excitation beam at an experimental temperature of 120 K. The in-plane and out-of-plane components are scaled to show their relative contributions to the powder spectrum. The small difference in the value of the highest frequency mode (571 cm⁻¹ powder and 566 cm⁻¹ oriented crystal) are believed to be a temperature effect.

Figure 3.

The measured VDOS for [Fe(TpivPP)(2-MeHIm)(O₂)] (powder and single crystal) The experimental temperature for the powder sample was 25 K. The in-plane spectrum was taken with the porphyrin plane oriented parallel to the excitation beam at an experimental temperature of 128 K. The out-of-plane spectra were taken with the porphyrin plane oriented perpendicular to the excitation beam at an experimental temperature of 129 K. The in-plane and out-of-plane components are scaled to show their relative contributions to the powder spectrum. The small difference in the value of the highest frequency mode (563 cm⁻¹ powder and 559cm⁻¹ oriented crystal) are believed to be a temperature effect.

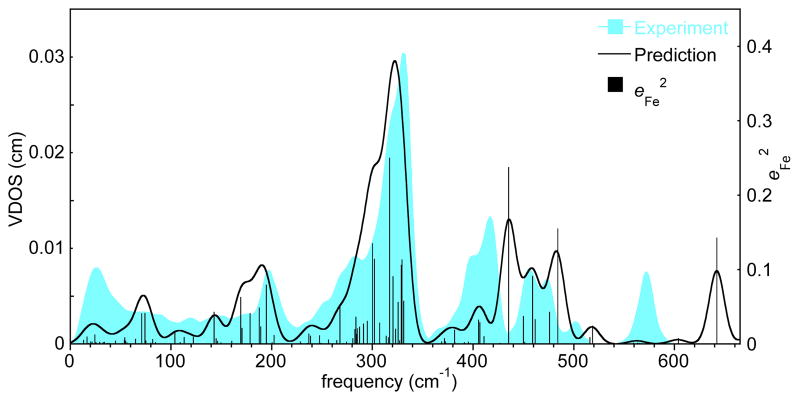
Vibrational predictions from DFT calculations^{[18, 40]} have helped in understanding the experimental vibrational spectra. Predicted frequencies and ${\text{e}}_{Fe}^2$ values are compared with the experimental spectrum in Figure 4. The diagram shows all predicted modes (black bars) and the predicted VDOS (black curve) obtained with a 15 cm⁻¹ Gaussian convolution. There are a total of seven major features (>360 cm⁻¹), all are apparent in the experimental powder VDOS (blue). Three of the modes are predicted to have significant concurrent iron and oxygen atom contributions; the character of the modes is shown in Figure 5; Figure S4 displays the relative energy contributions of Fe and the two oxygen atoms. Note the large difference in the relative motions of iron and proximal oxygen atom predicted for the highest frequency mode (Figure 5, left). Consistent with oriented single-crystal measurements, this mode is clearly a strongly mixed stretching and bending mode. The difference in the predicted and observed frequencies is similar to that seen for the highest frequency mode of nitrosyl species.^{[20, 41]} The second observed mode is at 417 cm⁻¹; the predicted and observed character (Figure 5, middle) shows iron motion strongly mixed between stretching and bending, again consistent with the oriented single-crystal measurements. The third mode at 393 cm⁻¹ is observed to have iron oop character and the character of the predicted mode (Figure 5, right) is consistent with this. Note that the observed intensity is larger than that predicted (Figure 4). To our knowledge, the existence of this previously unrecognized mode has not been suggested by earlier vibrational studies, again demonstrating the unique capability of the NRVS technique. The occurrence of the three modes appears unrelated to the peripheral groups; calculations for [Fe(porphine)(1-MeIm)(O₂)] also predicts the same three Fe–O₂ modes.

Figure 4.

The measured (blue) and predicted (red) VDOS for [Fe(TpivPP)(1-EtIm)(O₂)] and the predicted Vibrational Kinetic Energy Distributions (KED) over Fe (black).

Figure 5.

Predicted vibrational modes of the Fe–O₂ fragment of [Fe(TpivPP)(1-EtIm)(O₂)] with frequency at 642, 435 and 405 cm⁻¹.

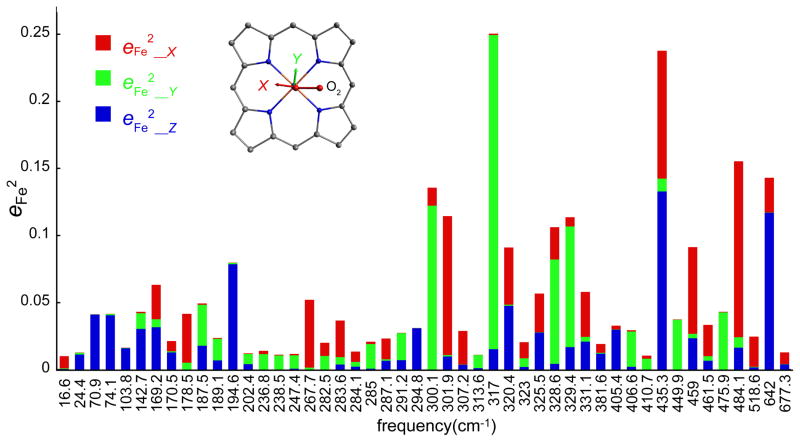
The theoretical calculations also suggest that the vibrations are strongly anisotropic and related to molecular structure details. Such molecularly defined anisotropy has been recently demonstrated for [Fe(OEP)(NO)].^[19] Figure S5 shows the predicted VDOS in three orthogonal directions and Figure 6 shows the predicted directional characteristics of each mode. In both diagrams, “z, blue” is along the heme normal, equivalent to the measured oop spectrum and the “x” and “y” directions correspond to the two ip Fe–C_methine vectors. In Figure 6, these are approximately parallel (x, red) and perpendicular (y, green) to the Fe–O₂ plane. All of the >360 cm⁻¹ modes, except the observed 393 cm⁻¹ band (predicted 405 cm⁻¹) have some ip character. The most intense bands in the spectrum also have oop character and for these, the motion is found to be only along the x and z directions, i.e., the iron motion is within the Fe–O₂ plane (Figures 5 and 6). The remaining bands have little O₂ motion and principally involve motion of the iron and the porphyrin ligand, nonetheless the ip iron motion is predicted to be either parallel or perpendicular to the Fe–O₂ plane. The predicted anisotropy is illustrated in Figure 6; the strong x, y anisotropy is apparent.

Figure 6.

The predicted directional characteristics of all modes with ${\text{e}}_{Fe}^2>0.01$. The values of the predicted frequencies are given at each tick mark, but the horizontal scale is only approximately linear in frequency to avoid overlaps. The color code for the plot shows the projection of iron motion along z (perpendicular to porphyrin plane, blue), x (along the Fe–O₂ projection, red) and y (perpendicular to the Fe–O₂ projection, green).

That the Fe–O₂ orientation is dominating the direction of the iron vibration was further shown by a calculation in which the Fe–O₂ and imidazole planes were constrained to be coplanar and lie along a Fe–C_methine vector (y). The calculations (Figure S6) show that the iron motion follows the change in the Fe–O₂ orientation; the imidazole orientation would appear to have little or no effect. The effect of the Fe–O₂ orientation is evidenced by a comparison of Figures 6 and S7. An experimental measurement in which crystals of [Fe(TpivPP)(1-EtIm)(O₂)] were aligned along the two independent Fe–O₂ directions is shown in Figure S8. These two directions approximately correspond to the directions parallel and perpendicular to the imidazole plane. Differences can be seen in the two spectra; the results do not contradict the expectation of anisotropy, but unfortunately, the O₂ disorder in the crystalline complex^{[10, 36]} does not allow us to demonstrate O₂ orientation effects conclusively.

In the spectral range below 220 cm⁻¹ (Figures 2 and 3), there are several recognizable oop and ip features as well as unresolved features. The calculations predict similar spectra for all three derivatives; the 11 predicted modes between 70 and 202 cm⁻¹ for [Fe(TpivPP)(1-EtIm)(O₂)] are depicted in Figures S9 and S10. We first consider the frequency region 120–200 cm⁻¹, with peaks that show sensitivity to imidazole identity (Figure 1). Figure S11 gives the KED for iron and 1-EtIm. All predicted modes in the range have simultaneous significant motion of iron and imidazole; all but two have significant oop iron motion. All modes also have significant motion of the porphyrin, peripheral pickets, and O₂. The oop mode observed at 196 cm⁻¹ in the single-crystal spectrum (predicted 195 cm⁻¹) is the mode with motions of iron and imidazole that most resembles that of a classical Fe–Im stretch (Figure S9). The remaining modes have motion of iron that are oblique to the heme plane and imidazole rocking motions either in or orthogonal to the imidazole plane as well as Fe–Im stretch character. These correspond to the features observed at 174 and 134 cm⁻¹ in the 1-EtIm derivative and 175(sh) and 130(sh) in the 2-MeHIm derivative. See oop spectra in Figure S3. The earlier tentative assignment of a weak feature at 272 cm⁻¹ in oxymyoglobin by resonance Raman^[4]e and later questioned by Kincaid and others^[4]c is clearly a porphyrin band and not an Fe–Im band.

The observed Fe–Im stretch shifts to lower frequencies in the sequence 1-MeIm > 1-EtIm > 2-MeHIm with values of <205,^[42] 196, and 187 cm⁻¹ (Table 2). The shifts are consistent with mass difference in 1-MeIm and 1-EtIm and the longer Fe–N_Im bond distance in 2-MeHIm as a result of steric hindrance, and thus in agreeement with an Fe–Im stretch assignment. However, this peak consists of more than one band as close inspection demonstrates and consistent with the DFT caclulations. Indeed, two resolved bands are clearly observable in the oriented crystal data of the 1-EtIm and 2-MeHIm derivatives (Figures 2 and 3). Note that the ip contribution is always observed at higher frequency.

Table 2.

Correlation of calculated and experimental mode frequencies for [Fe(Porph)(RIm)(XO)] (X = O, C or N) complexes. (All values in cm⁻¹.)

Complex	Method				Mode frequencies
		Fe–XO[a]			Fe–Im[b]			doming[c]		220–360 cm−1[d]
[Fe(TpivPP)(1-EtIm)(O2)]	NRVS[e]	571	417	393	196	174	134	118	78	296[f], 268, 282, 320, 330[g]
	DFT[h]	642	435	405	195	169	143	104	74/71	295[f], 268, 284, 302(2), 317, 329(2)
	rR[i]	~568	425[j]		Not observed			Not observed
[Fe(TpivPP)(2-MeHIm)(O2)]	NRVS[e]	563	419	389	187	175	130	119	80	300[f], 270, 278, 314, 325
[Fe(TpivPP)(1-MeIm)(O2)]	NRVS[k]	571	417	393	205	175	136	118	84	268, 286, 318, 327
[Fe(TPP)(1-MeIm)(CO)][l]	NRVS[e]	586	561	507	225	172		127	64	331[f], 241, 251, 320, 338
[Fe(TPP)(1-MeIm)(NO)][m]	NRVS[e]	565	473	440	149	175
tri-[Fe(TpFPP)(1-MeIm)(NO)][n]	NRVS	559	467	432	140	167
mono-[Fe(TpFPP)(1-MeIm)(NO)][n]	NRVS	560	474	433	153	177

^[a]These bands incorporate Fe–XO motions associated with bending and stretching modes.

^[b]The frequency with the motions that most closely resemble that of the classical Fe–Im stretch are bolded.

^[c]The frequency with the motion that most closely resembles that of the classical Fe doming mode is bolded.

^[d]Except as noted, these modes are in-plane.

^[e]Powder, in-plane, and out-of-plane measurements.

^[f]Out-of-plane.

^[g]Iron has in-plane and out-of-plane character.

^[h]Basis set for iron: TZVP; Closed-shell singlet.

^[i]Ref. 4, 5, 38.

^[j]Observed in some proteins only.

^[k]Powder data only.

^[l]Ref. 27.

^[m]Ref. 39.

^[n]Ref. 20.

An attractive feature of NRVS, which provides for the observation of all iron vibrational modes, is that it can allow the determination of the effects of a trans ligand on the iron–imidazole bond in six-coordinate species, [Fe(Porph)(RIm)(XO)], which is not accessible from resonance Raman. Conventionally, this would be the frequency of the Fe–Im stretch; which should be a measure of (sensitive to) the bond strength. An Fe–Im stretch has been unambiguously identified in [Fe(TPP)(1-MeIm)(CO)] and is found at 225 cm⁻¹, consistent with a strong Fe– N(Im) bond.^[27] There are additional bands in the CO spectra with significant Fe and imidazole motion (e.g. 172 cm⁻¹) similar to the 174 and 134 cm⁻¹ bands observed in [Fe(TpivPP)(1-EtIm)(O₂)] (Table 2). However, in several NO complexes there is only a very weak band observed at around 200 cm⁻¹; the oop bands with significant intensity and Fe and imidazole motion are at lower frequencies. The band that can be closely associated with the Fe–Im stretch is observed at 149 cm⁻¹ for [Fe(TPP)(1-MeIm)(NO)],^{[39, 44]} 140 cm⁻¹ for tri-[Fe(TpFPP)(1-MeIm)(NO)],^[20] and 153 cm⁻¹ for mono-[Fe(TpFPP)(1-MeIm)(NO)].^[20] The Fe–Im stretch observations are consistent with a much weaker bond and the known trans effect of the NO ligand.^[43] The Fe–Im frequencies observed in the three diatomic species is thus found to be in the order CO > O₂ > NO. Although this order may seem intuitive, to our knowledge, there has been no direct experimental evidence for this ordering in six-coordinate heme species.

The final observed band above 100 cm⁻¹ in [Fe(TpivPP)(1-EtIm)(O₂)] is the doming mode, predicted at 104 and observed at 118 cm⁻¹. A doming mode contribution is also strongly mixed in the broad band observed at about 78 cm⁻¹ and predicted at 74 and 71 cm⁻¹ (cf. Figure S10). These modes can be qualitatively described as motion of the center portion of the molecule including the iron, axial ligands and core in a direction perpendicular to the heme plane and opposed by motions of the pickets.

The 220–360 cm⁻¹ range is dominated by ip contributions. As seen in the oriented crystal measurements, the ip modes are much stronger than those of the oop modes (Figures 2 and 3). The predicted intense modes at 268, 284, 300, 302, 317 and 328.6 cm⁻¹ all present nearly pure ip iron motion, but only the 268 cm⁻¹ band is resolved. These modes are illustrated in Figure S12. The figure shows that all of these modes are predicted to have ip iron motion that is either parallel or perpendicular to the projection of the Fe–O₂ plane. Thus the orientation of the Fe–O₂ unit is controlling the ip iron dynamics and not the ip Fe–N_p interactions. The DFT calculation is consistent with this (Figures 6 and S7). However, there is also iron motion that has oop components. The modes at 320, 326, 329.4, and 331 cm⁻¹ have iron motion oblique to the porphyrin plane and contribute to the oop peak centered at ~330 cm⁻¹ (Fig. 2). In addition there is a pure oop mode predicted at 295 cm⁻¹, which is observed in the oop measurement at 296 cm⁻¹. This feature is also seen in the NRVS spectrum of [Fe(TpivPP)(2-MeHIm)(O₂)] (Figure 3). The predicted character of the observed 296 cm⁻¹ oop mode is illustrated in Figure S13. This is an unusual mode, with most of the motion in the oop motion of iron and the axial diatomic O₂ and with little motion of the trans imidazole. A similar mode, with oop motion of iron and CO but even less imidazole motion, has been observed at 331 cm⁻¹ in the CO complexes.^[27] Although the analysis of the NO complexes is incomplete, an analogous mode is likely in these species as well.

We have used NRVS, which provides all iron vibrational frequencies, to study three picket fence O₂ complexes with different imidazole ligands trans to O₂. Single-crystal spectra show that the two Fe–O₂ modes previously detected by resonance Raman have strongly mixed bending and stretching character. Neither mode can be described simply as the the bending mode and other as the stretching mode; this observation thus clearly resolves prior differing assignments. NRVS further reveals a third Fe–O₂ mode at 393 cm⁻¹ that had not been previously shown by other methods. Previously unidentified imidazole dependent iron–imidazole modes have now been identified. Six-coordinate iron porphyrinates with CO, O₂ or NO as the diatomic ligand show differences consistent with the Fe–Im interaction varying in the order CO > O₂ > NO. The Fe–O₂ orientation affects both in-plane and out-of-plane iron dynamics. The in-plane iron motion is either parallel or perpendicular to the Fe–O₂ plane. Table 2 summarizes a number of observed and predicted frequencies for the [Fe(TpivPP)(RIm)(O₂)] derivatives and provides comparisons with six-coordinate derivatives of CO and NO. A complete comparison for the NO derivatives is unavailable as the detailed analysis of these derivatives is still in progress. As in the O₂ case, the use of NRVS provides details of the vibrational spectra that have not been accessible by other techniques.

Supplementary Material

SI

Figure S1. A comparison of the measured and predicted (open-shell and closed-shell) VDOS for [Fe(TpivPP)(1-EtIm)(O₂)].

Figure S2. The measured in-plane VDOS for [Fe(TpivPP)(2-MeHIm)(O₂)] and [Fe(TpivPP)(1-EtIm)(O₂)]. The in-plane spectrum was taken with the porphyrin plane oriented parallel to the excitation beam.

Figure S3. The measured out-of-plane VDOS for [Fe(TpivPP)(2-MeHIm)(O₂)] and [Fe(TpivPP)(1-EtIm)(O₂)]. The out-of-plane spectra were taken with the porphyrin plane oriented perpendicular to the excitation beam.

Figure S4. The predicted vibrational kinetic energy distributions of the Fe–O₂ fragment in [Fe(TpivPP)(1-EtIm)(O₂)]. The heights of the individual bars equal the fraction of the kinetic energy associated with each atom or group. The lower panel shows the sum of the mode composition factors for Fe, O_bound, and O_terminal, and gives the fraction of mode energy localized on the Fe–O₂ fragment. Red bars indicate Fe–O₂ modes.

Figure S5. The predicted VDOS for [Fe(TpivPP)(1-EtIm)(O₂)] displaying the predicted anisotropy in the vibrational spectrum. The color code for the plot shows the projection of iron motion along z (perpendicular to porphyrin plane, blue), x (along the Fe–O₂ projection, red) and y (perpendicular to the Fe–O₂ projection green).

Figure S6. The predicted VDOS for [Fe(TpivPP)(1-EtIm)(O₂)] displaying the predicted anisotropy in the vibrational spectrum. The color code for the plot shows the projection of iron motion along z (perpendicular to porphyrin plane, blue), x (perpendicular to the Fe–O₂ projection, red) and y (along the Fe–O₂ projection, black).

Figure S7. The predicted directional characteristics of all modes with ${\text{e}}_{Fe}^2>0.01$. The values of the predicted frequencies are given at each tick mark, but the horizontal scale is only approximately linear in frequency to avoid overlaps. The color code for the plot shows the projection of iron motion along z (perpendicular to porphyrin plane, blue), x (perpendicular to the Fe–O₂ projection, red) and y (alone the Fe–O₂ projection, green).

Figure S8. Two O2 orienations

Figure S9. Edge and top views of the predicted vibrational modes of [Fe(TpivPP)(1-EtIm)(O₂)] at 195 cm⁻¹.

Figure S10. 11 predictions low frequency

Figure S11. The predicted vibrational kinetic energy distributions of the Fe–1-EtIm fragment (which includes all the 15 atoms of the 1-EtIm group) in [Fe(TpivPP)(1-EtIm)(O₂)]. The height of the individual bars equals the fraction of the kinetic energy associated with each atom or group. The lower panel shows the sum of the mode composition factors for Fe and 1-EtIm, and gives the fraction of mode energy localized on the Fe–1-EtIm fragment. Note the $e_{\text{Fe}}^2$ plot is on a different scale. Modes that involve simultaneously Fe and 1-EtIm motions are colored. Red and light blue bars indicate Fe–1-EtIm translation modes with 1-EtIm movement parallel or perpendicular to Fe–N_Im vector respectively; green bars indicate modes with strong imidazole rotation.

Figure S12. 200–300 region

Figure S13. The 295 band.

Table S1. x, y, z components of iron energy for normal modes with total iron energy above 0.01 of [Fe(TpivPP)(1-EtIm)(O₂)]. (optimized on a structure with Fe–O₂ near-perpendicular to imidazole plane).

Table S2. x, y, z components of iron energy for normal modes with total iron energy above 0.01 of [Fe(TpivPP)(1-EtIm)(O₂)]. (optimized on a structure with Fe–O₂ near-coplanar to imidazole plane).

Table S3. x, y, z components of iron energy for normal modes with total iron energy above 0.01 of [Fe(TpivPP)(2-MeHIm)(O₂)]. (optimized on a structure with Fe–O₂ near-perpendicular to imidazole plane).