A systems view of the protein expression process

Abstract

Many biological processes are regulated by changing the concentration and activity of proteins. The presence of a protein at a given subcellular location at a given time with a certain conformation is the result of an apparently sequential process. The rate of protein formation is influenced by chromatin state, and the rates of transcription, translation, and degradation. There is an exquisite control system where each stage of the process is controlled both by seemingly unregulated proteins as well as through feedbacks mediated by RNA and protein products. Here we review the biological facts and mathematical models for each stage of the protein production process. We conclude that advances in experimental techniques leading to a detailed description of the process have not been matched by mathematical models that represent the details of the process and facilitate analysis. Such an exercise is the first step towards development of a framework for a systems biology analysis of the protein production process.

Electronic supplementary material

The online version of this article (doi:10.1007/s11693-011-9088-1) contains supplementary material, which is available to authorized users.

Introduction

The concerted action of several factors governs the concentration of a given protein in a cell. The same is also true for the mRNA encoding the protein. Therefore, in order to study the distribution of mRNA and protein concentrations, it is important to consider the role of the constituent sub-processes of the protein production process, and estimate the net effect of the action of the regulators of these sub-processes. One of the means of such an analysis is through the formulation of a mathematical model that includes the entire pathway from DNA to functional protein. In this article, we review the mechanistic details of these sub-processes and their mathematical models as a necessary first step towards formulation of a comprehensive model for the protein production process.

There are several reviews which describe the biological machinery that constitutes parts of gene expression process. For instance, there are excellent reviews that describe the mechanistic details of transcription (Venters and Pugh 2009), and translation (Groppo and Richter 2009). Other papers present a ‘unified’ view of protein production (Orphanides and Reinberg 2002). Reviews of the mathematical models of gene expression (Smolen et al. 2000; Hasty et al. 2001) mainly discuss different approaches available and used for modelling gene expression, gene regulation and gene networks with specific examples. This paper systematically reviews the existing research on individual modules of the protein expression process, and discusses areas where the mathematical analysis lags the advances in the experimental investigations.

The protein production process

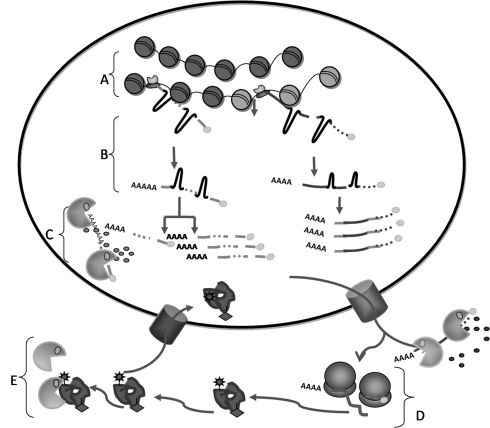
The process of protein production considered in this review includes all sub-processes that result in presence of the appropriate amount of protein molecules at a specific time and cellular location. The coordinated activity of multiple RNA and protein molecules is required to execute each sub-process. This coordination is achieved through regulation by other RNA and protein molecules, resulting in a very large and complex regulatory system. All the components of a particular step regulate the rate through their concentration. In several instances the output of the sub-process (RNA or protein) also regulates its own formation rate (feedback control). Here, due to space constraint we summarize experimental studies on the various processes involved in protein production and their open-loop and feedback control mechanisms with only one or two examples of each sub-process. The examples are summarized in Table 1. Since the scope of this review is limited to production of the protein, the extensive research in post translational protein modifications and regulation is not considered, except for ubiquitination that directly affects degradation. We divide the protein production process into five sub-processes (A–E in Fig. 1).

Table 1.

The references for steps in gene expression and the regulation at each step by protein and RNA

	Process
Regulator	Chromatin remodeling and histone modification	Transcription (initiation, elongation and termination)	Post-transcriptional processes (capping, poly-adenylation, splicing, interference and RNA degradation)	Translation (initiation, elongation and termination)	Post-translational modification (ubiquitinylation and protein degradation)
Protein	Peterson (2002), Kouzarides (2007)	Kerppola and Kane (1991), Thomas and Chiang (2006)	McCracken et al. (1997), Petersen-Mahrt et al. (1999) Guhaniyogi and Brewer (2001), Rozenblatt-Rosen et al. (2009)	Monnier et al. (2001), Sans et al. (2004) Wang and Proud (2008)	Vervoorts et al. (2006)
Protein feedback	Yang et al. (2009)	Cormack and Struhl (1992), Arigo et al. (2006)	Cheng et al. (2006)	Raney et al. (2002), Onouchi et al. (2005), Ivanova et al. (2010)	Hutti et al. (2007), Shembade et al. (2010)
RNA	Volpe et al. (2002), Barrandon et al. (2008), Gonzalez et al. (2008)	Brantl and Wagner (2002), Kwek et al. (2002), Mattick and Makunin (2006)	Bartel (2004), Storz et al. (2005), Ghildiyal and Zamore (2009)	Wang et al. (2002)
RNA feedback		Barrandon et al. (2008)	Xie et al. (2003)	Li et al. (1996), Ben-Asouli et al. (2002)

Fig. 1.

Sub processes in protein production: A chromatin remodelling and histone modification, B transcription and RNA processing, C RNA degradation, D translation, E protein degradation

Chromatin remodeling and histone modification

The activation of the promoter region such that it is competent for transcription factor and RNA polymerase binding can be considered as the first step in gene expression. The highly organized structure of chromatin has to be unpacked to facilitate such binding. This unpacking is achieved through binding of gene specific regulator(s) to the regulatory region of the gene. The regulator then recruits chromatin remodelling complexes and histone modifying enzymes to the site. The chromatin remodeling complexes [such as ATP dependent DNA helicase classes like SWI/SNF, ACF, CHRAC (Peterson 2002)] slide or peel off the nucleosomes from DNA. The histone modifying enzymes [such as histone acetyltransferase (HATs), deacetylases, lysine methyltransferases (Kouzarides 2007)] modify the histone proteins and thus change their affinity for DNA (Hirose 1998; Fry and Peterson 2001).

Other protein and RNA molecules can regulate gene expression by controlling the activity of these complexes. For example in case of skeletal muscle differentiation, the myogenic transcription regulatory factors Mef2 and myogenin interact with a SWI/SNF type of chromatin remodeling protein, Brg1, that alters the gene promoter region structure leading to myogenic late gene expression and terminal differentiation (Ohkawa et al. 2006). Examples of RNA controlling chromatin remodeling are Xist (X-inactive specific transcript) and roX (RNA on the X). The Xist RNA recruits chromatin remodeling enzymes which help to inactivate X chromosome. The roX RNA, on the other hand, helps in gene activation through the recruitment of NuRF (nucleosome remodeling factor) and MSL (male specific lethal) complex in male Drosophila X chromosome (Barrandon et al. 2008).

In addition to such regulation, promoter activation is also regulated through feedback regulation. In TH₂ cells, the protein Dec2 binds to the regulatory region of GATA-3 transcription factor and increases its expression by histone acetylation. GATA-3 in turn induces Dec2 mRNA expression, forming a positive feedback loop (Yang et al. 2009). To our knowledge, RNA mediated feedback control of chromatin remodeling or histone modification has not been reported.

Transcription

Transcription is generally divided into three multi-step phases: initiation, elongation and termination. Initiation involves the assembly of transcription factors and RNA polymerase at promoter site and start of transcription (Tjian 1996; Thomas and Chiang 2006). During elongation, the RNA polymerase synthesizes the RNA polymer (Kugel and Goodrich 2000; Saunders et al. 2006). Termination is the process where RNA polymerase ceases the synthesis of RNA and releases the pre-RNA (Kerppola and Kane 1991; Richardson and Roberts 1993).

Transcription is regulated by various protein and RNA molecules. For instance, the C terminal region of the protein BTAF1 induces dissociation of transcription factor TBP from promoter, and thus negatively regulates transcription initiation (Thomas and Chiang 2006). Another protein SII interacts with RNA polymerase II through C terminal domain of polymerase and stimulates elongation (Kerppola and Kane 1991). Rat1 protein encourages transcription termination by disrupting the contact between RNA polymerase and RNA (Kim et al. 2004). Transcription initiation is both positively and negatively influenced by RNA. FC RNA and B2 RNA competitively bind to RNA polymerase and inhibits pre-initiation complex assembly at promoter; whereas U1 snRNA activates transcription by interacting with transcription initiation factor TFIIH and stimulating the rate of first phosphodiester bond formation (Kwek et al. 2002). Transcription elongation is regulated by 7SK RNA, which inhibits the kinase activity of a subunit of elongation factor P-TEFb, leading to reduced transcription (Mattick and Makunin 2006). In E. coli, antisense RNA from control regions of pT181 and pIP501 inhibit transcription termination of rep-lacZ fusion gene by blocking the readthrough (Brantl and Wagner 2002).

Feedback regulation of transcription is mediated by both the transcription (RNA) and the translation (protein) products. The general transcription factor TATA binding protein (TBP) is required by all the three polymerases in eukaryotes (Cormack and Struhl 1992). This suggests a positive feedback loop in terms of requirement of TBP for its own transcription by RNA polII. The transcription factor Pit-1 binds to its own mRNA downstream of the transcription start site and hinders the elongation of the pit-1 mRNA (Smith and Sharp 1991). The yeast RNA binding protein NRD1 down-regulates its expression through premature termination by binding to NRD1 binding site in its premature transcript (Arigo et al. 2006). An example of RNA regulating transcription at initiation step is DHFR non coding RNAs. A short transcript obtained from minor promoter of DHFR gene, forms a triple helix with double stranded DNA for DHFR gene which interacts with the transcription factor TFIIB resulting in transcription repression (Barrandon et al. 2008). An example of cis-acting RNA regulation is CCATT sequence in the major late promoter region of SV40 virus, which directs termination of its own transcription (Connelly and Manley 1989).

RNA processing and degradation

Transcription results in formation of a ‘pre-RNA’ which is processed to form a mature RNA molecule. RNA processing includes 5′ capping, splicing and 3′ polyadenylation. 5′ capping is a three step process in which GMP is added to 5′ end and methylated at N7 position with the help of three enzymes, viz, RNA 5′ triphosphatase, guanylyltransferase and methyltransferase. Splicing is also a multistep process in which two exon sequences are fused and the intron in-between these sequences is spliced out. It is catalysed by a complex called spliceosome which consists of five small nuclear RNAs and many proteins (Padgett et al. 1986). 3′ end polyadenylation is carried out by multimeric protein factors that include cleavage and polyadenylation specificity factors (CPSF), cleavage stimulatory factor (CstF), cleavage factor I and II, and poly(A) polymerase (Proudfoot et al. 2002). Once the mature RNA molecules are formed they are transported from nucleus to the cytoplasm. A protein complex Mex:Mtr2 is required for transport of mRNA from the nuclear pore complexes to cytoplasm (Stewart 2007). In the cytoplasm RNA molecules are degraded depending upon their stability, secondary structure and regulation imposed by other protein and RNA components. Degradation involves shortening of polyA tail, decapping, and then 5′–3′ exonucleolytic cleavage of mRNA by the enzymes, mainly XRN1. After shortening of the polyA tail, 3′ exonucleolytic cleavage can also take place (Beelman and Parker 1995; Houseley and Tollervey 2009).

Protein and RNA molecules regulate steps in RNA processing to modulate gene expression. C-terminal Domain (CTD) of RNA polymerase II stimulates 5′ capping (McCracken et al. 1997). Protein p32 interacts with and inhibits ASF/SF2 proteins that act as splicing repressors in context dependent manner and hence activates splicing in concentration dependent manner (Petersen-Mahrt et al. 1999). 3′ end formation is regulated by the protein Cdc73 which facilitates the recruitment of CPST and CstF and hence positively regulates production of the transcript of its target gene INTS6 (Rozenblatt-Rosen et al. 2009). The enzyme RNase L controls stability of mRNA of transcription factor MyoD (Guhaniyogi and Brewer 2001). Antisense RNA can regulate splicing of mRNA leading to alternate splice variants. For example, Rev-ErbAα RNA found in B lymphocytes controls the ratio of two splice forms of the thyroid hormone receptor (Storz et al. 2005). miRNA and siRNA bind to their target mRNA and change their stability by regulating their degradation (Bartel 2004; Ghildiyal and Zamore 2009).

Feedback regulation of RNA processing and degradation has also been reported, for instance in the Ras activation pathway. One of the variable exon 6 (v6) of the transmembrane glycoprotein CD44 is a co-receptor that binds to the human growth factor (HGF), activating the Ras pathway. Ras signaling in turn leads to alternative splicing of the CD44 variants resulting in the enhanced production of the co-receptor (Cheng et al. 2006). miRNA mediated feedback of mRNA degradation is observed in case of miR162, whose target mRNA includes the transcript for the plant protein Dcl1, which is required for formation of miRNAs including miR162 (Xie et al. 2003).

Translation

Like transcription, translation is divided into three phases, viz, initiation, elongation and termination. During initiation, the 5′ cap of mRNA recruits ribosomal subunits and other initiation factors (eIFs) forming an initiation complex. During elongation, elongation factors (eEFs) help to recruit the charged tRNA molecule and form peptide bond with the previous amino acid. During termination the release factor eRF recognizes stop codon and helps to release ribosome and the polypeptide chain (Pain 1996; Groppo and Richter 2009).

An example of the translation initiation regulation by protein is eIF2Bε, which controls the GTP-GDP exchange of eIF2 (Wang and Proud 2008). Proteins also control elongation, for instance Cyclin dependent kinase 1 (CDK1) activates eEF1B through phosphorylation of its subunit eEF-1γ which in turn leads to the activation of eEF-1A and hence an increase of elongation rate (Monnier et al. 2001; Sans et al. 2004). An example of trans-acting RNA regulating translation initiation is BC1 RNA, which interacts with eIF4A and Poly A binding protein resulting in inhibition of translation initiation (Wang et al. 2002). We could not find any reports of RNA molecules regulating translation elongation or termination.

Feedback regulation of translation is mediated by both proteins and RNA. The protein eIF1 negatively autoregulates itself during initiation of the translation step (Ivanova et al. 2010). In Arabidopsis, the first exon of the cystathionine -γ-synthase mRNA codes for a short peptide that causes stalling at the translational elongation step (Onouchi et al. 2005). Proteins (such as the MAGDIS peptide obtained from upstream ORF of AdoMetDC enzyme gene of polyamine synthesis pathway (Raney et al. 2002) can regulate synthesis of its own peptide by regulating translation termination. An example of feedback mediated by RNA effect on translation is seen in IFN-γ mRNA which forms a pseudo-knot with the 5′ UTR of PKR (a protein kinase) and activates its translation. PKR in turn inhibits translation of IFN-γ by phosphorylating the initiation factor eIF2α (Ben-Asouli et al. 2002).

Protein degradation

Degradation of proteins is a spatio-temporally controlled process. Generally the protein to be degraded is tagged by addition of ubiquitin proteins with the help of three enzymes, viz, E1 Ub-activating enzyme, E2 Ub-conjugating enzyme and E3 Ub-protein ligase. These tagged proteins then associate with the proteasome system where the protein is unfolded and translocated to the catalytic core of proteasome. Before translocation the ubiquitin is removed with the help of de-ubiquitinylating enzymes. The proteasome degrades the unfolded protein to give peptides in range of 7–9 amino acids (Baumeister et al. 1998; Ravid and Hochstrasser 2008).

Expression level of proteins is mediated by protein and RNA regulators through control of degradation. The enzyme GSK3 regulates MYC protein stability by phosphorylation, which induces ubiquitinylation (Vervoorts et al. 2006). Feedback regulation of degradation is seen for instance in NF-κB signalling. When stimulated by NF-κB agonist, IKKβ leads to the transcription of NF-κB as well as A20 genes. IKKβ phosphorylates A20, thereby increasing A20 activity (Hutti et al. 2007). A20 down regulates the NF-κB through ubiquitination and proteosome mediated degradation of the components in the NF-κB activation pathway (Shembade et al. 2010). There are no reports to our knowledge of regulation of protein degradation by RNA molecules.

Mathematical models of processes in gene expression

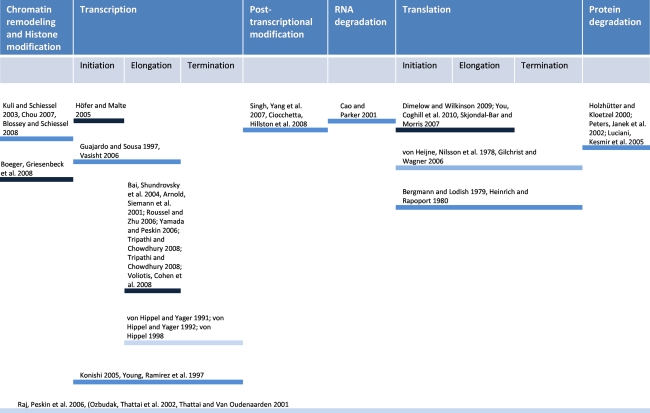
It is very difficult to capture the vast amount of detail of the protein production process summarized in the previous section in the form of a single mathematical model. As most mathematical models are designed for a specific purpose, for instance to analyse a particular sub-process, or to help suggest an explanation for a particular experiment, this level of detail is usually not required for most models. However in order to understand the contribution of different sub-processes to the overall dynamics of gene expression, their inclusion in a comprehensive model is necessary. In this section we review mathematical models for gene expression. The models are summarized in Table 2 with more details listed in Supplementary File 1. There are different kinds (stochastic/deterministic, discrete/continuous, steady-state/dynamic) of mathematical models formulated for different processes in gene expression. Some of them consider the overall process but at lesser details while others focus on a part of whole process and include details. As with the previous section, we discuss models that focus on specific steps of the protein production process. However, as most models include at least a lumped model for one or more of the other sub-processes, it is difficult to have a clear demarcation. The mathematical models are summarized in Fig. 2, which gives a visual representation of the subprocesses considered and the degree of detail considered for several models.

Table 2.

Mathematical models for steps in gene expression and the regulation at each step by protein and RNA

	Process
Regulator	Chromatin remodeling and histone modification	Transcription (initiation, elongation and termination)	Post-transcriptional processes (capping, poly-adenylation, splicing, interference and RNA degradation)	Translation (initiation, elongation and termination)	Post-translational modification (ubiquitinylation and protein degradation)
Protein	Kim and O’Shea (2008), Luca Mariani (2010)	Kugel and Goodrich (2000)	Cao and Parker (2001), Singh et al. (2007)	Nayak et al. (2011)	Holzhütter and Kloetzel (2000), Peters et al. (2002), Luciani et al. (2005)
Protein feedback	Sedighi and Sengupta (2008), Narula et al. (2010)	Bernard et al. (2006), Rajala et al. (2010)	Model needed	Bar (2009), De Silvaa et al. (2010)	Lee et al. (2010)
RNA	Model needed	Model needed	Levine et al. (2007)	Model needed	Model needed
RNA feedback	Model needed	Model needed	Aguda et al. (2008)	Model needed	Model needed

Fig. 2.

Some models for the protein production process organised in terms of breadth and level of detail included. The intensity of the bar qualitatively indicates the relative level of details included in the model

Models for chromatin remodeling and histone modification

A few mathematical models for chromatin remodeling and histone modification have been reported. A deterministic model (Blossey and Schiessel 2008) considers chromatin remodeling in terms of histone tails modifiers, chromatin remodelers and transcription factors. It considers different histone states and shows that the mechanism of chromatin modification can help in kinetic proofreading to differentiate right genes to be activated. The model by Kuli and Schiessel (2003) is a discrete model which considers nucleosome sliding along DNA due to thermally induced one base pair twist. The model identifies the mobility of the nucleosomes and estimates that majority of nucleosomes are highly mobile while <5% show very low mobility. Such nucleosomes require active remodeling activity and can be considered as switching elements for global chromatin rearrangements. Chou (2007) has modeled passive histone sliding as well as active protein driven histone unwrapping using a stochastic model and has considered competition between sliding and peeling off a histone. The model calculates mean histone detachment time and mean detachment distance. The study by Boeger et al. (2008) considers stochastic transitions of nucleosomes between different configurations and linked the dynamic chromatin structure to the transcription process. The model specifically considers PHO5 promoter and proposes that disassembly of nucleosomes is the rate limiting step in PHO5 gene expression. The model by Raj et al. (2006) is a stochastic model which does not consider the detailed mechanism but considered the effect of gene activation and inactivation kinetics on the gene expression. The model explains the statistical properties of transcriptional burst and studies the effect of gene activation kinetics on burst size and burst frequency.

A deterministic model for chromatin remodeling is formulated (Kim and O’Shea 2008) to quantitatively study expression in yeast for PHO5, a gene for acid phosphatase regulated by Pho4. This model quantitatively relates the affinity as well as accessibility of the Pho4 binding in the promoter leading to induction of the gene expression. It considers four possible nucleosome positions that can be achieved for the activation of the gene, some open and some opened after rearrangement. A stochastic model considering a two step gene induction process for IL-4 gene expression (Luca Mariani 2010) considers opening and closing of chromatin as a binary process. Other processes considered in the model include chromatin rearrangement, transcription and translation.

Several models describe feedbacks operating at the chromatin remodelling level. In a deterministic model for the Scl-Gata-Fili1 triad for hematopoietic stem cells, it is assumed that distant enhancers increase the transcriptional rate via adjusting the chromatin states rather than having direct effect on transcriptional components. Change in the level of transcriptional regulators leads to dynamic equilibrium between the closed and the open state. It has also been shown that the Scl-mediated positive feedback plays an important role in affecting the signal of the triad (Narula et al. 2010). A stochastic model of stepwise chromatin remodeling using mean field description is formulated by Sedighi and Sengupta (2008). The model considers positive feedback by the silenced information regulators (SIR) proteins involved in the silencing of the DNA. The model predicts existence of two stable states, the hyper-acetylated state and silenced state of DNA.

Models for transcription

Most mathematical models for the protein production process include transcription and its regulation. A smaller number focus exclusively on transcription. Young et al. (1997) formulated a deterministic kinetic model of in vitro synthesis of RNA for batch RNA production. The model considers the effect of nucleotide and Mg²⁺ ion concentration on RNA production and predicts the optimal conditions in terms of NTP and Mg²⁺ ion concentration. A kinetic model of transcription in phage T7 is formulated by Arnold et al. (2001). In this model RNA synthesis rate is considered to be dependent on polymerase, promoter and nucleotide concentration. The model considers initiation and elongation processes. The model formulated by Bai et al. (2004) is a sequence dependent kinetic model of elongation by RNA polymerase. Sequence information is considered by calculating the kinetic rates for elongation based on sequence dependent NTP incorporation rates. The model explains back-tracking and pauses during elongation.

There are also a large number of stochastic models for transcription. They consider different sub-processes. The model by Höfer and Malte (2005) considers details of transcription initiation process emphasizing promoter activation and polymerase recruitment. The effect of kinetics of transcription complex assembly, mRNA synthesis and degradation on mRNA noise and ability of transcription regulators to control mRNA abundance is studied. A discrete kinetic model of transcription elongation process is formulated by Yamada and Peskin (2009) which considers the look-ahead feature of polymerase and estimates the window size for RNA polymerase. But the model considers only one directional movement of RNA polymerase. In the model proposed by Roussel and Zhu (2006) transcription elongation is modeled as a polymerization process. The model identifies the probability distribution of transcriptional delay and elongation rate by using chemical master equation and stochastic simulations. The model by Voliotis et al. (2008) is a detailed one which considers transcription initiation and elongation with pauses and backtracking of polymerase and derives a analytical expression for transcription time. The models by Tripathi and Chowdhury (2008a, b) focus on the elongation phase of transcription. One model considers RNA traffic on DNA strand by taking into account the steric interaction of RNA polymerase. Using analytical and numerical methods mRNA synthesis rate and RNA polymerase average density is calculated. This model studied effect of RNA pol concentration on intrinsic noise of mRNA. The other model of transcription considers gene activation and inactivation. Using analytical method, an expression for distribution of burst size in terms of parameters of transcription, is obtained. The mechanical aspect of the transcription process (force generation by polymerase) is considered in two models (Jülicher and Bruinsma 1998; Galburt et al. 2007).

Several models for transcription adopt the thermodynamics approach. The models by von Hippel and Yager (1991, 1992; von Hippel 1998) consider the free energy of DNA–DNA, DNA–RNA, RNA–RNA and the elongation complex in prokaryotic system. Considering the free energy of these complexes at each nucleotide position the models predict elongation and termination phases of transcription. The models also predict pause during elongation, backward sliding of RNA pol and termination efficiency. The model by Guajardo and Sousa (1997) is a thermodynamic model for RNA polymerase translocation along DNA strand for prokaryotic systems. The model considers primer extension by polymerase and energy partitioning between the 3′ NMP and new NTP as competitive binding equilibrium. The model proposed by Vasisht (2006) uses statistical mechanics approach to predict RNA polymerase pauses and back-tracking. It considers thermodynamic stability of the elongation complex at each nucleotide position. A thermodynamic model for transcriptome formation is formulated by Konishi (2005). It considers the transcript level as balance between the rate of synthesis and degradation. The rate is related to the free energy of the polymerase and regulator complex.

A deterministic model describing the different stages of initiation complex of the adenovirus major late promoter (AdMLP) has been studied by Kugel and Goodrich (2000). This model describes preinitiation complex formation, initiation, escape commitment, promoter escape and transcript elongation. It proposes that the TFIIH enhances the promoter escape over the aborted complex formation and shows it to be the rate limiting step in the RNA polymerase II transcription initiation.

Many models include feedback at the transcriptional level. A deterministic model that considers delay due to transcription and translation is formulated for Hes1 protein mediated transcriptional self repression. The model is then extended for feedback by the protein Gro. The feedback loop leads to steady oscillatory protein variation. A key idea used is that of characteristic turnaround duration which introduces the time delay between the transcription initiation and repression (Bernard et al. 2006 ). A delayed stochastic model to show the effect of RNA pausing on unregulated gene expression and a repressilator in prokaryotic system is developed by Rajala et al. (2010). In genetic repressilator, changing pause rate and time duration within practical parameter, influence the bursting dynamics and the noise in the transcript and protein level. Raising the occurrence level or the extent of pausing increases the period length but does not affect the robustness of the periodicity.

Models for RNA processing and degradation

Compared to the vast number of models for transcription there are relatively very few models for RNA processing. A deterministic model for rRNA processing is formulated by Singh et al. (2007). The model considers four steps: transcription, pre-mRNA splicing, pre-mRNA turnover and mRNA degradation. However the model does not consider alternate splicing. Another model formulated by Ciocchetta et al. (2008) is a stochastic model for co-transcriptional cleavage of rRNA in yeast. Two alternate pathways of rRNA processing are modeled and relative frequency of these pathways is determined.

There are a few models for mRNA degradation. A deterministic kinetic model for mRNA turnover in eukaryotes is formulated by Cao and Parker (2001). The model considers mRNA synthesis and has modeled the degradation pathways in detail. It studies the effect of change of reaction rate parameters on mRNA level and decay rate. The study suggests that experimentally obtained half-life of mRNA generally underestimates its stability. Carrier and Keasling (1997) have formulated a stochastic model for mRNA degradation in prokaryotes. The model considers both degradation by endonuclease and protection by ribosomes. RNA mediated post-transcriptional regulation is modeled by Khanin and Higham (2007). The model considers mRNA and miRNA binding leading to mRNA degradation and inhibition of translation. The models by Levine et al. are models for siRNA mediated post transcriptional regulation (Levine et al. 2007; Jost et al. 2011).

There are relatively few models that include feedback at the transcript processing or mRNA degradation stage. A deterministic kinetic model formulated by Aguda et al. (2008) considers miR-17 and E2F mediated feedback loop, in which E2F activates miR-17 while miR-17 inhibited E2F synthesis. The model studies the oscillatory behaviour resulting from the presence of the feedback loop.

Models for translation

There are many models formulated for the translation process. A deterministic kinetic model for translation that considers initiation, elongation and termination (von Heijne et al. 1978) predicts that the elongation rate varies along mRNA which can be due to coupling between ribosome movement and mRNA secondary structure. Bergmann and Lodish (1979) has formulated a deterministic kinetic model for protein synthesis in eukaryotes and applied it to hemoglobin synthesis. The model studies relationship between total protein synthesis rates and size of polysome. The model investigates effect of limiting amount of certain tRNA on total protein synthesis rate. A detailed kinetic model for translation in eukaryotic cell is developed by Heinrich and Rapoport (1980). The model considers initiation, elongation and termination. It suggests that total protein synthesis rate is dependent on initiation and elongation while termination did not influence the rate of protein synthesis. It also studies the ribosome distribution along mRNA and effect of ribosome concentration. The model by Dimelow and Wilkinson (2009) is a detailed model for translation initiation. Using PCA the model identifies flux controlling steps in translation initiation. The model by You et al. (2010) is a deterministic kinetic model for translation initiation. The model studies the effect of initiation factor concentration on protein synthesis rates. The model also studies cell population by considering Gaussian distribution for molecular abundance and parameter values and investigates the effect of noise on translation rate. The model formulated by Skjondal-Bar and Morris (2007) focuses on translation initiation and elongation and includes details such as regulation of initiation factors. A discrete kinetic model of translation is formulated by Gilchrist and Wagner (2006). The model considers different features such as ribosome recycling, codon bias and nonsense errors. The model shows that heterogeneity observed in translation rates due to codon bias leads to spikes and dips in probability of ribosome occupancy.

There are a couple of models for the prokaryotic translation process. Drew (2001), Heyd and Drew (2003) formulated stochastic models for translation, which also considers mRNA synthesis and protein degradation steps. The model considers differential codon usage in case of plasmids.

An ensemble of deterministic kinetic models of translation initiation is formulated by Nayak et al. (2011). Using these models the essential features of translation initiation are identified. A deterministic model for the translation using detail mechanism of elongation has been formulated to study the steady state properties of the E. coli trpR gene translation. Protein synthesis is taken to be a function of polysome size. It is suggested that polysome organization forces the translation rate to maximum levels which are dependent on the complex relationship between the ribosomal possession in the elongation cycle intermediate step (rate limiting step in elongation) and the ribosome distribution with respect to codon position along the length of the mRNA (Zouridis and Hatzimanikatis 2007).

A deterministic model to incorporate initiation control via eIF-2 subunit is developed by Bar (2009). The model considers feedback on 48S initiation complex. The model predicts that by controlling the levels of 48S initiation complex the rate of the protein synthesis can be controlled. A mathematical model to study the feedback involved in translation of translation release factors (eRF) is formulated by De Silvaa et al. (2010). The model studies both positive and negative feedbacks mediated by translation release factors.

Models for protein degradation

A deterministic mathematical model for protein degradation is formulated by Holzhütter and Kloetzel (2000) analyzed the pattern of peptide fragments. The model describes time evolution of average probabilities of specific fragment. Another deterministic model is formulated by Peters et al. (2002) which considers cleavage by 20s proteasome. The process of cleavage is modeled by Michaelis–Menten kinetics and the cleavage rates are estimated. Proteasomal degradation is also considered in a model by Luciani et al. (2005), which assumes that the rate of reaction depends upon proteasomal gate size. This model studies the length distribution of the protein fragments.

Feedback control of protein degradation has also been modeled for some systems. A deterministic model is formulated to study TNFR and A20 mediated negative feedback, where active TNFR activates protein A20; and A20 in turn negatively regulates TNFR signalling through ubiquitinylation (Lee et al. 2010).

Discussion

Through rigorous experimentation, details of the mechanisms of the protein production process are emerging almost on a daily basis. The increasing sophistication of experimental techniques has resulted in the ability to carry out simultaneous high throughput experiments for multiple sub-processes (Lu et al. 2006; Taniguchi et al. 2010). However mathematical models have not been able to match this frenetic pace of advance. This is not unexpected given the relative number of investigators working on the experimental and mathematical aspects of biology. This leads to lacunae at two levels: missing detailed models for sub-processes, and missing models for the whole protein production. In this section, such specific subareas where a modelling approach may offer insight are listed, and a strategy for organising the mathematical modelling and analysis in terms of usable modules is suggested.

An analysis of the existing models shows that the number of models developed for transcription and translation far exceeds the number of models developed for RNA processing, degradation and protein degradation. To our knowledge, model considering mechanistic details for transport of mRNA from nucleus to cytoplasm has not yet been developed. A comparison of Tables 1 and 2 suggests areas where experimental data is available but there are no mathematical models developed to our knowledge. There are several interesting observations where a mathematical model may offer a possible explanation of the mechanism. For instance, in a study (Bar-Even et al. 2006) of the concentrations of 43 proteins of Saccharomyces cerevisiae under 11 different conditions, it is observed that (as expected) at low abundance the noise decreases as the inverse square of protein mean while at high abundance the noise is not correlated with the mean. This unexpected lack of correlation at high abundance levels is also seen in another study of S. cerevisiae proteomics (Newman et al. 2006). There are conflicting reports on the correlation of mRNA levels with protein levels, with some studies (Lu et al. 2006; Schwanhausser et al. 2011) supporting the conclusion that protein abundance can be explained by mRNA abundance, and others (Taniguchi et al. 2010) suggesting that there is no correlation between the mRNA and protein copy numbers.

In order to plan the effort to develop a model for the protein production process, a modular organization may be the best. In this approach, detailed models for a particular sub-process are developed in ‘usable’ form with clearly defined inputs and outputs. This enables a plug-and-play operation where modules can be used with minimum customisation. For instance a researcher working on the one module can use other modules for sub-processes interacting with the working module. Models that span multiple sub-processes can be constructed by linking all the relevant modules. The problem then reduces to defining the nature of the modules. Given the intricate nature of the regulation of various sub-processes by both RNA and protein products, one possible division is the temporal order, from activation to transcription to translation. This is the approach adopted in this review for organising the available information. Another equally logical division is on the basis of unit operations such as polymerization, transport, initiation, termination, degradation. Analysis of regulation may be organised in terms of unit processes such as autocatalysis (Gadgil and Kulkarni 2009). Once such a subdivision is agreed upon, an organised effort towards developing a comprehensive and usable mathematical model for the protein production process can be initiated. Besides the implications in understanding the native cellular process, mathematical models have proved complementary to the synthetic biological developments right from the first synthetic toggle switch (Gardner et al. 2000) to the riboswitches which provide predictable tuning of gene expression (Babiskin and Smolke 2011). A comprehensive mathematical model will help to understand the basic design principles and will lead to new, more complex circuit designs having the desired properties and fine tuneable control.