Abstract
Many sequencing studies are now underway to identify the genetic causes for both Mendelian and complex traits. Via exome-sequencing, genes harboring variants implicated in several Mendelian traits have already been identified. The underlying methodology in these studies is a multistep algorithm based on filtering variants identified in a small number of affected individuals and depends on whether they are novel (not yet seen in public resources such as dbSNP), shared among affected individuals, and other external functional information on the variants. Although intuitive, these filter-based methods are nonoptimal and do not provide any measure of statistical uncertainty. We describe here a formal statistical approach that has several distinct advantages: (1) it provides fast computation of approximate p values for individual genes, (2) it adjusts for the background variation in each gene, (3) it allows for incorporation of functional or linkage-based information, and (4) it accommodates designs based on both affected relative pairs and unrelated affected individuals. We show via simulations that the proposed approach can be used in conjunction with the existing filter-based methods to achieve a substantially better ranking of a gene relevant for disease when compared to currently used filter-based approaches, this is especially so in the presence of disease locus heterogeneity. We revisit recent studies on three Mendelian diseases and show that the proposed approach results in the implicated gene being ranked first in all studies, and approximate p values of 10−6 for the Miller Syndrome gene, 1.0 × 10−4 for the Freeman-Sheldon Syndrome gene, and 3.5 × 10−5 for the Kabuki Syndrome gene.
Introduction
Spurred by recent advances in high-throughput sequencing technologies, sequencing studies for varied Mendelian and complex traits are currently underway. Such studies will provide an unprecedented view of the genetic variation, rare and common, that influences the risk of these diseases. Genes for several Mendelian diseases have already been identified1, 2, 3 via exome-sequencing of a small number of affected individuals and additional information from public resources such as dbSNP and the 1000 Genomes Project.
The large number of genetic variants in the human genome and the low population frequency of the majority of these variants create challenges for the computational and statistical analysis of these data. In particular, traditional testing strategies based on individual variant testing can have low power, and new statistical methods that aggregate information across multiple variants in a genetic region have been proposed.4, 5, 6, 7, 8, 9, 10, 11, 12, 13
For Mendelian diseases, traditional methods for gene mapping range from candidate gene studies (where candidates were selected based, for example, on functional similarity to already established genes, and in many situations their exons were sequenced in a small number of subjects) to positional cloning strategies (where small regions discovered via linkage analysis were followed-up with denser genotyping that led to the identification of haplotypes thought to harbor causal mutations). Recently, several studies have been published on the use of whole-exome sequencing data on a small number of (mostly unrelated) affected individuals to identify the genes containing disease variants in several Mendelian traits.1, 2, 3 Unlike traditional linkage methods, the underlying gene could be identified directly and by using unrelated subjects. More precisely, in each case the relevant gene was identified via a filter-based methodology, where variants identified in cases were checked for novelty (not identified before), functionality (e.g., nonsynonymous variants), and sharing among affected (and possibly related) individuals. Such an approach is intuitive and reasonable; however, from an inferential perspective it has several disadvantages including: (1) it does not produce any measure of statistical uncertainty (e.g., gene-level p values), making it unfeasible to assess consistency with the null hypothesis; (2) it does not adjust for background variation in each gene, therefore allowing large genes to rank high on the basis of their size alone; and (3) it does not properly account for the different levels of variant sharing expected among relatives of different types, which can affect the rank of the genes. Although the filter-based approach can take into account external information such as functional predictions or linkage scores, such information needs to be provided in a dichotomized fashion (e.g., linkage or no linkage) rather than original scores (or transformations thereof).
In what follows, we discuss a formal statistical framework that aims to address the aforementioned limitations of the filter-based approach and show applications to simulated data and recent studies for three Mendelian traits. For these previously published Mendelian studies, we show that the proposed approach ranks the gene relevant for disease first in all three studies and assigns significant p values to the respective genes.
We assume the disease mutations in Mendelian diseases are rare, as is strongly suggested by the data available on Mendelian mutations.14 We also assume that disease mutations are deleterious, a reasonable assumption for Mendelian disorders.
Material and Methods
We start by reviewing the filter-based approach that is currently being used to map genes harboring disease variants for Mendelian traits from sequence data. Then we propose a weighted sum statistic and an analytical approximation of the p value for a gene. We then discuss an omnibus method that combines this weighted sum approach with the currently-used filter-based method to achieve a more sensible gene ranking procedure.
Filter-Based Approach
The filter-based approach is based on computing for each gene a statistic equal to the number of affected individuals that are carriers of at least one nonsynonymous variant that is novel, that is, not seen in controls.1 For unrelated affected individuals, computing this statistic is straightforward. Let G be a gene of interest and MU be the number of novel variant positions observed in a set of A affected individuals sequenced at gene G. Let Xij be the coded genotype (i.e., the number of the minor allele) for affected individual i ≤ A at novel variant position j ≤ MU. Then for each affected individual i, we calculate the load (or burden) of novel nonsynonymous variants as:
where wj is 1 for nonsynonymous variant and is 0 otherwise. Then the filter-based method is based on the following statistic:
| (Equation 1) |
where I(·) is an indicator function. Genes are then ranked according to the value of Sfilter.
For affected relative pairs and Mendelian diseases, it is reasonable to assume that both affected individuals in a pair share the disease variant. If each pair of affected relatives is treated as a unit, the score for each unit (i.e., the equivalent of I{Li>0} above) is taken to be 1 if there is at least one novel, nonsynonymous variant in gene G shared between both relatives, and is 0 otherwise. However, this definition fails to account for the different levels of expected sharing among relatives of different types. Ideally, one would like to assign a higher score if two cousins share such a variant versus two siblings. Later we discuss such an alternative scoring scheme.
As the number of sequenced controls increases, restricting attention to only the novel variants runs the risk of disregarding rare disease mutations that are in fact present in control individuals as well (possibly because of reduced penetrance and/or a recessive mode of inheritance). A simple extension of the filter-based approach is to also consider variants that have a frequency in controls less than some threshold, say 0.01, rather than only the novel ones. We refer to this approach as Filter-R (all rare variants are included), and the existing filter-based approach based on novel variants only is referred to as Filter-N.
Weighted Sum Statistic for Mendelian Traits
We describe here a weighted sum statistic that resembles statistics that have been proposed before for case-control designs.6 However, unlike existing weighted sum statistics, for the proposed statistic (1) an approximate analytical p value can be calculated for each gene, and (2) both affected relative pairs and unrelated affected individuals can be accommodated.
Let G be a gene of interest and M be the number of rare variant positions observed in a set of individuals (both affected and unaffected) sequenced at gene G. We assume for now that all individuals are unrelated. A rare variant is defined as a variant with a population frequency less than some prespecified threshold, e.g., 0.01. The optimal threshold is not known and necessarily depends on the underlying frequency spectrum for disease mutations in Mendelian diseases. However, extensive data available on the frequency spectrum for Mendelian mutations suggest that the total mutation frequency is <<1% for most Mendelian diseases.14 For each rare variant position j, with j ≤ M, let T (j) be the total number of variants in affected individuals (note that this corresponds to an additive model). One simple statistic we can define is:
Moreover, incorporation of external weights such as those from Polyphen15 or SIFT16 can be done easily. For example,
where wj is the weight for variant j, which can be any real positive number (derived independently of the data). For example, if only nonsynonymous variants are to be included, then wj = 1 for such variants and is 0 otherwise. A similar weighting scheme works if only variants that are not in dbSNP are to be considered.
Let Na be the total number of chromosomes in affected individuals, and Nu be the corresponding number for controls. For variant j let be the estimated frequency based on controls. If we assume that the underlying frequency distribution of the variants in a region can be approximated by Beta (α,β), then we estimate fj by:
where xj is the observed number of occurrences of the minor allele in controls at variant position j (The parameters α and β can be estimated from data available on controls with standard maximum likelihood estimation.17 We also note that results are robust to the choice of α and β, especially as Nu becomes large.). If we assume for now that the rare variants under consideration are in linkage equilibrium, then we show in Appendix A (Expectation and Variance of T(j) and Expectation and Variance of Sw) that:
In the general case when variants are allowed to be correlated, a suitable variance estimator has also been derived (Expectation and Variance of Sw).
We use the following gamma-based approximation for the probability density function of the weighted sum statistic of Poisson-like random variables (Table A6; see also Fay and Feuer18):
| (Equation 2) |
where and Q is the incomplete gamma function:
This approximation becomes very accurate as the observed number of variants M in a region increases. It can however be slightly conservative when M is small (Table A6).
Only Novel Variants in Cases are Considered
Previous studies on several Mendelian traits1, 2, 3 have used public resources such as dbSNP and 1000 Genomes Project data as well as sequence data on a small number of controls to filter out variants that are common and only keep those that are novel (do not appear in these existing databases). This is indeed a reasonable approach if disease mutations are assumed to be very rare and highly penetrant. We can modify our weighted sum statistic above as follows:
where MU is the number of novel variants in affected individuals. Note that MU is a subset of M and that and . In order to calculate and one would need to estimate the number of novel variants in cases based on the observed variants in controls, and both parametric and nonparametric methods can be applied to obtain such estimates.17, 19 However, it can be difficult to obtain accurate estimates on the number of novel variants in a gene if only a small number of variants is observed in controls, as would be the case for many genes of small to moderate length. Therefore, we use the same gamma-based approximation as in Equation 2 to obtain an upper bound on the p value for this scenario.
In what follows we refer to the weighted sum approach with all rare variants as WS-R and to the above approach with only the novel variants as WS-N.
Affected-Relative Pairs
For Mendelian diseases data on affected relatives, for example affected siblings or affected cousins, might be available. It would be desirable to extend both the filter-based approach and the weighted sum approach discussed above to be able to handle relative pairs. A simple solution adopted in the current filter-based approach is to score each pair of affected relatives as 1 if they share at least one novel and nonsynonymous variant and is 0 otherwise. A potential weakness of such a scoring scheme is that it fails to account for the different levels of expected sharing among relatives of different types. In particular, we would like to assign a higher score when such sharing happens between more distant relatives, for example cousins, compared with siblings.
In Ionita-Laza and Ottman20 we have developed such a scoring scheme. Namely, for a pair of relatives, we derive an effective number of variants in the pair, that is, the number of variants at a fixed segregating or variant position adjusted for the familial correlation. We have denoted this number by keff and showed there that for a pair of relatives keff can be calculated as follows:
where f is the frequency of the variant at the given position, φ is the kinship coefficient; δ is 0 if the two relatives can share a maximum of one allele identical by descent (e.g., first cousins) and 1 if they can share two alleles identical by descent (e.g., siblings).
When two heterozygous individuals are unrelated, φ = 0, and we obtain the expected result that keff = 2. For identical twins φ = 0.5, δ = 1, and keff = 1. For two sibs, when f = 0.01 we obtain keff = 1.17. Similarly for two second cousins, keff = 1.76. These and other examples are summarized in Table A1. With this scoring scheme, the filter-based approach can be modified to assign higher scores to sharing among cousins compared with siblings.
It is also possible to extend the weighted sum approach to take into account data on affected relatives in addition to unrelated affected individuals. For a variant position and a pair of relatives, instead of the observed number of variants we use the effective number keff defined above. Then for variant position j we replace T(j), the total number of variants at position j in the affected individuals, with Teff(j), and the weighted sum statistic is correspondingly defined as:
As for the scenarios with only unrelated individuals, we derive a gamma-based approximation for the distribution of Sw (Expectation and Variance of Sw When Affected Individuals Are Related).
For Mendelian diseases, it is reasonable to assume that affected relatives within the same family are likely to share the disease mutation. The approach discussed above can be modified easily to reflect this assumption by setting keff to be zero unless both relatives share a variant (that can be, for example, nonsynonymous and novel). More precisely,
This is the default setting in our handling of affected relatives, and the one illustrated in the examples that follow.
Joint-Rank Approach
We describe here how the weighted sum approach above can be combined with the currently-used filter-based method to produce an overall better ranking for the gene(s) containing disease variants in a study. Both approaches discussed in the previous sections attempt to quantify the increase in rare variant burden in affected individuals, although in slightly different ways. The weighted sum approach aggregates information across all affected individuals and adjusts for the underlying variation in controls, but does not always distinguish whether the variants that enter the calculation of Sw occur in many or just a few of the individuals. On the contrary, the existing filter-based approach essentially exploits the information on the number of affected individuals that carry at least one novel variant but fails to distinguish whether variants occur recurrently at the same position, or different positions, and does not take into account the number of novel variants an individual carries, unlike the weighted sum approach.
For the purpose of ranking genes, we propose to combine the two approaches to calculate for each gene a combined rank, henceforth called the Joint-Rank, that represents the average of the ranks from the weighted sum and filter-based approaches. For a gene that contains variants implicated in disease, both ranks should be high, and the Joint-Rank approach might lead to an overall better ranking of that gene. The filter-based rank is not adjusted for the background variation, and hence the Joint-Rank can be viewed as adjusting the filter-based rank for the length of the gene and the background variation in each gene.
The various approaches discussed in this section are summarized in Table 1.
Table 1.
Summary of Methods Discussed in Text
| Approach | Description |
|---|---|
| WS-R | weighted sum with all rare variants (e.g., minor allele frequency [MAF] ≤ 0.01) |
| WS-N | weighted sum with only novel variants (not seen before) |
| Filter-R | filter-based approach with all rare variants (e.g., MAF ≤ 0.01) |
| Filter-N | filter-based approach with only novel variants (not seen before) |
| Joint-Rank-R | for each gene: the average of the ranks from approach WS-R and Filter-R |
| Joint-Rank-N | for each gene: the average of the ranks from approach WS-N and Filter-N |
Software
Software implementing the proposed approaches is available freely on I.I.-L.'s website.
Results
Next, we investigated via simulations the properties of the proposed approaches. We also used real high-coverage sequence data on 310 control individuals randomly selected from the large collection of unaffected individuals that have been sequenced as part of the American Recovery and Reinvestment Act (ARRA) Autism Project (see Sequence Data for more details on these data) to illustrate applications to three Mendelian disease examples recently reported in the literature: Miller Syndrome2 [MIM 264750], Freeman-Sheldon Syndrome1 [MIM 193700], and Kabuki Syndrome3 [MIM 147920].
Simulated Data
We first used simulations to investigate the underlying properties of the proposed approaches. We simulated 10 independent genomic regions each 1 Mb long under a coalescent model by using the software package COSI.21 The model used in the simulation was the calibrated model for the European population and was an option available in the COSI package. A total of 10,000 haplotypes were generated for each region. We then randomly sampled small subregions of the size of individual genes. The size of each gene was sampled from the length distribution of real exonic regions (as available from the refGene table; see Web Resources).
Type 1 Error
We evaluated the type 1 error of the proposed approaches for several different scenarios, including two different designs: (1) case-control and (2) affected sib pairs and unrelated controls. The results for the case-control design are shown in Table 2. We show there that the proposed gamma-based approximation is valid and leads to a good control of the type 1 error when rare variants (not necessarily novel) are considered.
Table 2.
Type 1 Error for the Case-Control Design
| Aa | Ub |
α |
|||
|---|---|---|---|---|---|
| 10−4 | 10−3 | 10−2 | 5 × 10−2 | ||
|
WS-R | |||||
| 5 | 100 | 1.5 × 10−4 | 6.0 × 10−4 | 4.0 × 10−3 | 1.7 × 10−2 |
| 500 | 1.3 × 10−4 | 7.0 × 10−4 | 5.0 × 10−3 | 2.1 × 10−2 | |
| 1000 | 1.1 × 10−4 | 5.7 × 10−4 | 5.0 × 10−3 | 2.1 × 10−2 | |
| 10 |
100 | 1.0 × 10−4 | 4.0 × 10−4 | 3.0 × 10−3 | 1.6 × 10−2 |
| 500 | 1.2 × 10−4 | 7.1 × 10−4 | 4.8 × 10−3 | 2.3 × 10−2 | |
| 1000 |
1.1 × 10−4 | 8.0 × 10−4 | 5.0 × 10−3 | 2.3 × 10−2 | |
| WS-N | |||||
| 5 | 100 | 7.8 × 10−5 | 3.0 × 10−4 | 1.5 × 10−3 | 6.7 × 10−3 |
| 500 | 2.6 × 10−5 | 7.4 × 10−5 | 4.3 × 10−4 | 3.0 × 10−3 | |
| 1000 | 2.1 × 10−5 | 1.2 × 10−4 | 2.9 × 10−4 | 1.1 × 10−3 | |
| 10 | 100 | 3.3 × 10−5 | 1.4 × 10−4 | 1.1 × 10−3 | 6.1 × 10−2 |
| 500 | 7.0 × 10−6 | 5.2 × 10−5 | 2.5 × 10−4 | 2.0 × 10−3 | |
| 1000 | 1.3 × 10−5 | 3.0 × 10−5 | 1.1 × 10−4 | 8.6 × 10−4 | |
Number of unrelated affected individuals.
Number of unrelated unaffected individuals.
When only novel variants (i.e., not seen in a set of independent controls) are considered, the approximation can be very conservative. Despite this conservativeness, because the magnitude of the effect at genes with variants implicated in Mendelian diseases is expected to be large, the approximation is expected to be powerful for such effects. Permutation-based methods can be employed for the genes with smallest p values to obtain better approximations for the p values (see Permutation Testing).
Similar results hold for data sets containing affected relative pairs (Table A2).
Gene Ranking
We investigated here the performance of the various approaches as measured by the overall ranking of the gene relevant for disease in a genome scan with 20,000 genes. A genome scan was simulated by sampling 20,000 regions with region length selected from the gene (exonic) length distribution in refGene table. The genes were sampled independently from the ten 1 Mb regions we have simulated. We assumed ten affected individuals and a number of controls between 100 and 500. One gene at random was selected, and a small number of affected individuals (between two and six) were assumed to each carry a different novel disease mutation in that gene. We simulated 1,000 such genome scans, and calculated the median rank for the implicated gene across the 1,000 simulations.
We show in Figure 1 that the Joint-Rank-N approach outperforms both the WS-N and the Filter-N methods in terms of the rank assigned to the implicated gene. The performance of the filter-based approach decreases with increasing genetic heterogeneity, and it is in these situations that a formal approach such as the weighted sum method discussed in this paper becomes particularly necessary.
Figure 1.
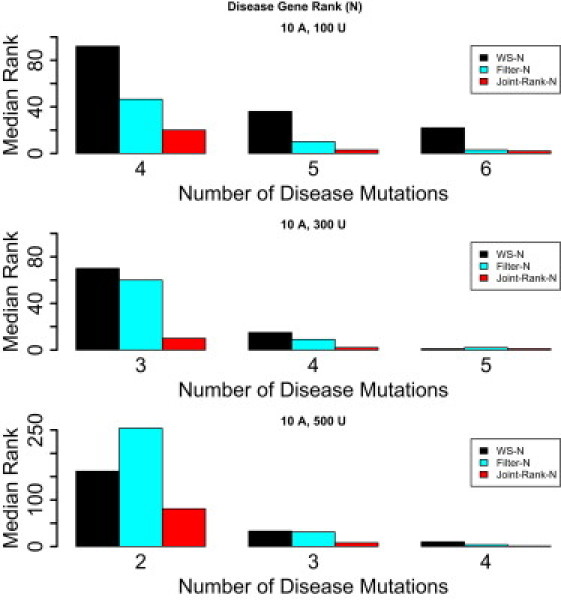
The Median Rank, with Novel-Variants Only, of a Gene with Variants Implicated in Disease in Genome Scans with 20,000 Genes, with Gene Length Sampled from the Real Gene Length Distribution
One thousand such genome scans are simulated. Two to six of 10 affected individuals are assumed to carry a novel disease mutation in the implicated gene (with fewer mutations for larger number of controls). The following methods are compared: WS-N, Filter-N, and Joint-Rank-N.
Filtering out variants that have been seen before could become problematic in the near future as the number of sequenced controls continues to grow because disease variants can potentially be present in controls as well (in the case of reduced penetrance and/or a recessive mode of inheritance). The extension of the filter-based approach to include rare variants rather than only novel variants (i.e., Filter-R) does not perform very well, especially as the number of affected individuals that carry a disease mutation at a disease locus decreases (Figure A1). In such situations the proposed weighted sum approach (WS-R) alone is expected to perform better. We also note here that the performance of all methods improves substantially as the number of sequenced controls increases.
Results for affected sib pairs are shown in Figure A2 and are similar to those for the case-control design.
Applications to Three Mendelian Diseases
For these applications, we used real high-coverage sequence data with spiked-in mutations to resemble the original disease studies as closely as possible. In particular, we assumed that the same number of affected individuals as in the original studies are carriers of novel nonsynonymous disease mutations, and these mutations are artificially added to the corresponding gene for each study above and beyond the existing variation in our real data. We also disregarded variants with a known rs number by simply setting their weights to 0. The next set of results are based on these spike-in data sets.
Miller Syndrome
In Ng et al.2 the authors performed exome-sequencing of four affected individuals, two siblings and two unrelated affected individuals, with Miller Syndrome. All four affected individuals were compound heterozygotes for novel and nonsynonymous mutations in one gene, DHODH [MIM 126064], and the two siblings shared the disease mutations. Because the sequence data available to us contained only unrelated individuals, we emulated the original study by using data on only three unrelated individuals as cases and 300 unrelated individuals as controls; all individuals were part of the same exome-sequencing study (Sequence Data). For the implicated gene DHODH we made the additional assumption that each of the three affected individuals was compound heterozygote for unique mutations in this gene.
In Figure 2 we plot the p values (WS-N) for all genes, as well as the value of the filter-based statistic (i.e., the number of affected individuals carriers of novel nonsynonymous variants). With only three affected individuals, we identify gene DHODH as the leading gene, with an approximate p value of 10−6 (WS-N). The permutation p values are 3.0 × 10−7 for both WS-R and WS-N.
Figure 2.
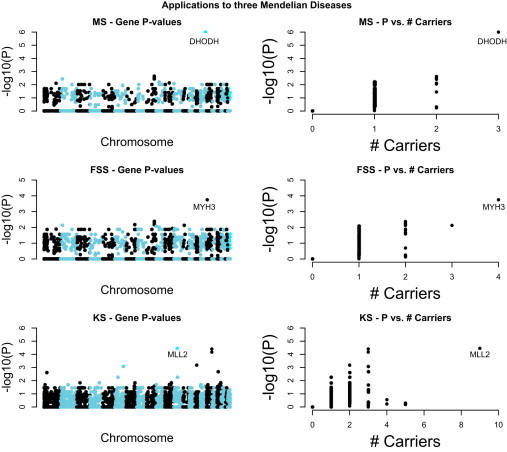
Applications to Three Mendelian Diseases: Miller Syndrome, Freeman-Sheldon Syndrome, and Kabuki Syndrome
Left: The p values (WS-N) for 19,811 genes surveyed (Manhattan plot). Right: For each gene the number of affected individuals that are carriers of novel disease variants and the gene p value are shown.
Freeman-Sheldon Syndrome
For the Freeman-Sheldon syndrome example, Ng et al.1 performed exome-sequencing of four unrelated affected individuals. Two different novel and nonsynonymous variant positions in the same gene, MYH3 [MIM 160720], were detected in all four individuals. Three individuals had a mutation at the first variant position, whereas the fourth individual had a mutation at the second variant position. Based on our spike-in data set, the resulting approximate p value (WS-N) in this case is 1.0 × 10−4. This was the highest ranked gene in the study (Figure 2). The permutation p values are 5.7 × 10−5 for WS-R and 6.0 × 10−7 for WS-N.
Kabuki Syndrome
For the Kabuki Syndrome example, exome-sequencing was performed in ten unrelated affected individuals (Ng et al.3). Nine different novel and nonsynonymous mutations in gene MLL2 [MIM 602113] were identified in the ten affected individuals. Based on our spike-in data set, the resulting approximate p value (WS-N) is 3.5 10−5, and again this is the highest ranked gene (Figure 2). The permutation p values are 3.4 × 10−6 for WS-R and 4.0 × 10−7 for WS-N.
Results for these three Mendelian diseases are summarized in Table 3 and Table A7.
Table 3.
Summary Results for the Applications to Three Mendelian Traits
| Syndrome | Gene Length (kb) |
Data Set |
MOIa | P valueb(WS-N) | |
|---|---|---|---|---|---|
| Ac | Ud | ||||
| Miller | 16.0 | 3 | 300 | CH | 1.0 × 10−6 |
| Freeman-Sheldon | 28.7 | 4 | 300 | D | 1.0 × 10−4 |
| Kabuki | 36.3 | 10 | 300 | D | 3.5 × 10−5 |
Mode of Inheritance: compound heterozygote (CH) or dominant (D).
Analytical p value.
Number of unrelated affected individuals.
Number of unaffected individuals.
Discussion
Recent studies have shown how genes harboring variants implicated in Mendelian diseases can be identified with whole-exome sequence data for a small number of affected individuals. The underlying approach is based on filtering variants based on novelty, functionality, and sharing among multiple affected individuals. Such filter-based approaches are intuitive and powerful for Mendelian diseases but suffer from several shortcomings. Notable among them are (1) the lack of statistical uncertainty assessment (e.g., in the form of p values) and (2) the lack of adjustment for the background variation in each gene, so that large genes can rank high on the basis of their size alone. We have shown here that such a filter-based approach can be complemented by a formal statistical procedure that has several distinct advantages: (1) it evaluates statistical significance by calculating approximate p values, (2) it can handle both related and unrelated affected individuals, (3) it can incorporate external weights about the functionality of variants or linkage-based scores, and importantly, (4) it adjusts for background variation so that more variable regions do not rise to the top based on noise alone. The resulting procedure leads to an overall better ranking of the relevant gene and allows for untying genes that otherwise have the same number of affected individuals that carry a novel mutation in the gene. The proposed method is particularly useful (compared with the filter-based approach) when there is locus heterogeneity and more complex inheritance, a scenario likely to happen as more and more Mendelian diseases are being studied.22
We have investigated two distinct scenarios: one that considers all rare variants in the population, regardless of whether they have been seen before or not (WS-R); and a second scenario where only novel variants in cases are included (WS-N). We have derived a gamma-based approximation for the null distribution of the weighted sum statistic WS-R and have shown that this approximation is good. Also, we have shown that the same approximation can be used for WS-N to derive an upper bound on the p value (although more precise approximations can be obtained by random permutations, especially on the genes with the smallest p values). Via applications to both simulated and real data, we have shown that a combination of the weighted sum approach and the filter-based approach, a procedure we call Joint-Rank, provides a more robust way to rank genes in Mendelian diseases compared with filter-based approaches alone. In particular, the Joint-Rank approach adjusts for the background variation in each gene (as does the weighted sum approach) and at the same time favors genes with a larger number of affected individuals that are carriers of novel variants (as does the filter-based approach).
Throughout most of our examples, we have assumed that causal variants are novel and hence not present in unaffected individuals. Under such a scenario, the optimal approach is indeed to only consider novel variants. However, if causal variants could be present in unaffected individuals (for example, for a recessive mode of inheritance, or reduced penetrance scenarios), the weighted sum approach WS-R should also be considered. This is particularly important as the number of control exomes available increases when even very rare variants can be identified in control individuals. The availability of a large number of sequenced controls will be important, because, as we have shown, the power of the proposed approach increases with the number of controls.
We revisited recent exome-sequencing studies on several Mendelian diseases and showed how the approach works concretely in these examples. The proposed approach produced significant p values for each of the genes that harbor disease variants for the three Mendelian traits while properly adjusting for the background variation in each gene, as estimated from exome-sequencing data available to us for 300 controls. Because of the lack of even modest-sized sequence data sets in the past, the filter-based approach used a variety of variant databases to filter out already discovered variants, including dbSNP and 1000 Genomes Project data. With the proposed approach, it is still possible to use these databases to filter out variants by simply setting the weights for variants in the databases to 0, and this is especially useful when the number of controls available is rather small. For our own examples, we have presented results based on a relatively small number of controls (i.e., 300); however, increasing the number of controls will naturally lead to smaller p values and improved overall ranking for the gene harboring disease variants.
As with any association study, good experimental design is essential. The validity of the p values obtained from the weighted sum approach, and of the Joint-Rank procedure overall, is contingent on having a control data set that is comparable to the affected individuals for both ethnic background as well as sensitivity and specificity for variant detection. Other potential issues, such as hidden relatedness among individuals, can lead to an inflated type 1 error. Principal component analysis or mixed-model methods can be used to adjust for relatedness of subjects by extending the current method to a regression-framework, such as sequence kernel association test.13 Adjustment for covariates, when available, is also straightforward in such a framework.
One strength of the proposed weighted sum approach is that the p values can be obtained in an analytical fashion. This fact makes the proposed approach to be computationally very fast compared to a permutation-based procedure, and also allows inclusion of affected relative pairs, situations where resampling-based procedures are nontrivial. Our applications to the three Mendelian disease examples each took ∼45 seconds on a regular desktop.
The proposed methods implicitly assume an additive model for the effect of mutations at a position. This model is optimal for additive, and expected to be powerful for dominant, compound heterozygous and recessive modes of inheritance.
For Mendelian diseases, results from previous linkage-based scans might be available. In that case, Roeder et al.23 proposed an exponential weighting scheme, whereby linkage scores are translated into weights that can be used to weight the gene-level p values calculated with the proposed approach, as in a weighted hypothesis testing procedure.24
In summary, we have discussed an analytic framework to identify genes that contain variants implicated in Mendelian diseases and have shown that it performs well in simulations and applications to previous exome-sequencing studies for three Mendelian traits.
Acknowledgments
The research was partially supported by National Science Foundation grant DMS-1100279 and National Institutes of Health grant 1R03HG005908 (to I.I.-L.), and grants R37-CA076404 and P01-CA134294 from the National Cancer Institute (to X.L.). Control exomes were sequenced as part of an ongoing ARRA-funded autism exome-sequencing grant (MH089025, Mark Daly, communicating principal investigator, Joseph Buxbaum, Bernie Devlin, Richard Gibbs, Gerard Schellenberg, James Sutcliffe, collaborating principal investigators). The authors gratefully acknowledge two referees for their valuable comments that substantially improved the paper.
Published online: December 1, 2011
Appendix A
Expectation and Variance of Sw for Unrelated Cases
Expectation and Variance of T(j). We assume we have sequenced Nα / 2 affected individuals, and Nu / 2 unaffected individuals. For an observed variant position j, let be the estimated frequency of fj based on Nu chromosomes. Then we use the following to estimate the expected value of T(j).
For the variance, we have:
Expectation and Variance of Sw. We recall here that for each gene we calculate the following weighted sum statistic:
Then . For the variance of Sw we have:
The covariance can be estimated as follows.25 Let Ve be the M×M empirical variance estimator with , where N = A + U is the total number of individuals (affected and unaffected). Let D be the M×M diagonal matrix with . Also, we define an adjusted variance matrix: . Then an estimate for Var (Sw) is
Expectation and Variance of Sw When Affected Individuals Are Related
Expectation and Variance for T(j). We show here how to derive the expected value and variance of Teff at a variant position when affected relatives are considered. Let A be the total number of affected relative pairs (of same type). If f is estimated based on Nu chromosomes, then we can get for
where
Note that above we replace f by when calculating keff|2. Through simulation experiments we have shown that there is small variability in the values of keff|2 for any fixed value of . If one assumes that f follows, for example, a Beta(0.1 + x, 10 + N – x) where x is the observed number of occurrences of the minor allele in controls, and N is the number of control chromosomes, then we show in Table A3 that the variability in keff is quite small.
To assess the covariance between Teff at two different positions, we need to know the joint distribution of genotypes at two positions in two relatives. Lange26 has derived the relative-to-relative transition probabilities for two linked genes, and we make use of these transition probabilities and the observed genotype distribution at two positions in unrelated controls to derive the joint distribution in relatives that we need. We then use a gamma-based approximation for the weighted sum of Poisson random variables.
We claim here that the distribution of Teff under the null hypothesis of no association with disease can be approximated by an overdispersed Poisson distribution with mean , and an index of dispersion very close to 1. It is easy to verify this claim by simple simulation experiments. We have simulated data sets of affected sib pairs and controls at one single variant position of frequency 0.001 ≤ f ≤ 0.01. For each data set, we calculate Teff assuming (1) the true value of f and (2) the estimated value of f from controls. We report the mean and variance for Teff(f) and based on 10,000 random simulations as well as the correlation between Teff(f) and . Results are shown in Table A4. For more distant relatives, such as first and second cousins, we only report the theoretical mean and variance for Teff(f) (Table A5). As shown, the theoretical and empirical results match very well. There is a slight inflation in the variance over the mean for sib pairs and when f = 0.01 (dispersion index < 1.06), although this inflation disappears for more distant relatives. In Figure A3 we also show the distribution of Teff against a Poisson with the same mean for a scenario with 100 affected sib pairs and 500 controls and f = 0.005.
Gamma-Based Approximation for a Sum of Weighted Poisson Random Variables
We have done some simple calculations in R to assess the accuracy of the gamma-based approximation for the weighted sum of Poisson random variables. We assume M Poisson random variables are included, and for each a weight wi is chosen from U(0,1). The results for different values for M are shown in Table A6.
Quantile-Quantile Plots for Three Mendelian Diseases
In addition to the Manhattan-type plots in Figure 2 we also show here the Quantile-Quantile (Q-Q) plots (Figure A4). Note that the observed p values refer to analytical p values calculated based on WS-R. We remove genes with little information, namely those genes with no observed variant in affected individuals. The resulting distribution of p values is, however, not uniform (0,1) because of the bias induced by selecting only genes with at least one variant in cases. Therefore, we only consider observed p values that are less than 0.2.
Permutation Testing
It is possible to obtain empirical p values for the weighted sum approach by random permutations of case/control status for each of the three Mendelian diseases considered. For the permutation approach the usual procedure is to randomly reassign case/control status to the individuals in the data set and then calculate the p value from the gamma-based approximation (Equation 2 in text). The empirical p value is calculated as the proportion of permuted data sets for which the gamma-based p value is at most as large as the p value observed in the original data. Results for the three Mendelian disease are shown in Table A7.
Sequence Data
To illustrate applications to real sequence data, we used exome-level data on 310 control individuals randomly selected from the large collection of unaffected individuals that have been sequenced as part of the ARRA Autism Project (AAP). The AAP involves whole-exome sequencing of 1,000 autism cases, 1,000 controls, and several hundred trios. Whole-exome sequencing of controls was carried out at the Broad Institute and at Baylor College of Medicine with standard approaches. Following quality control (QC), variants were called with several approaches (including the Genome Analysis Toolkit27), and variant call files with all variants and relevant QC metrics were made available to us. For our applications we considered data on 310 randomly chosen control individuals.
Figure A1.
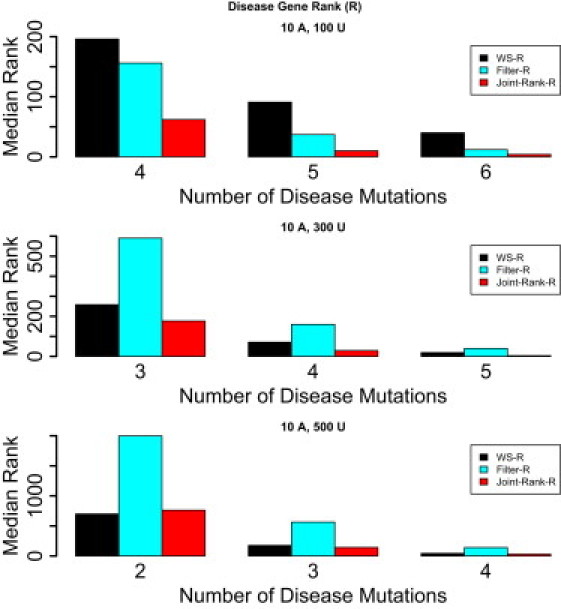
The Median Rank, with All Rare Variants Considered. of a Gene with Variants Implicated in Disease in Genome Scans with 20,000 Genes, with Gene Length Sampled from the real Gene Length Distribution
One thousand such genome scans are simulated. Two to six of ten affected individuals are assumed to carry a novel disease mutation in the implicated gene. The following methods are compared: WS-R, Filter-R, and Joint-Rank-R.
Figure A2.
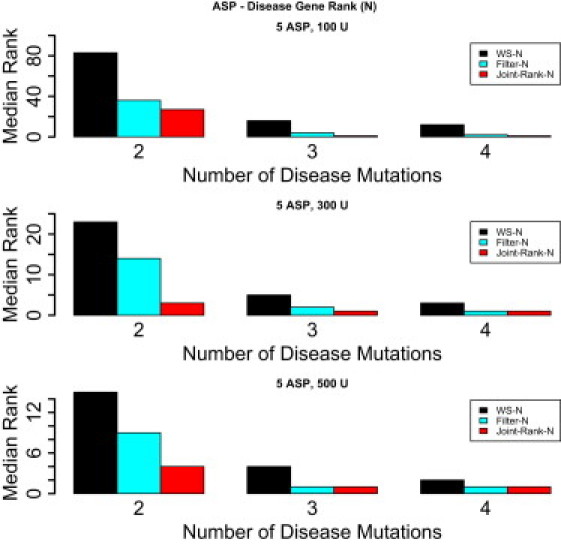
The Median Rank of a Gene with Variants Implicated in Disease in Genome Scans with 20,000 Genes and Gene Length Sampled from the Real Gene Length Distribution
One thousand genome scans are simulated. Two to four of five affected sib pairs (ASP) are assumed to share a novel disease mutation in the gene. The following methods are compared: WS-N, Filter-N, and Joint-Rank-N.
Figure A3.
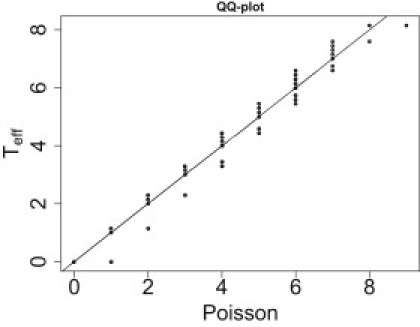
Q-Q plot showing distribution of Teff versus Poisson[E (Teff)]
One hundred ASPs and 500 controls are simulated for a total of 30,000 simulations.
Figure A4.
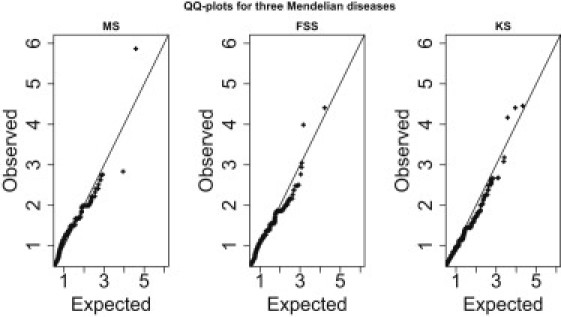
Q-Q plots showing the distributions of observed p values versus expected p values for three Mendelian diseases
Analytical p values are based on WS-R.
Table A1.
The Effective Number of Variants at a Rare Variant Position in Two Related Heterozygous Individuals as Defined in the Text
| Relationship | φ | keff |
|---|---|---|
| Identical twins | 1 / 2 | 1.00 |
| Parent-child | 1 / 4 | 1.17 |
| Sibs | 1 / 4 | 1.17 |
| Half sibs | 1 / 8 | 1.34 |
| Uncle-nephew | 1 / 8 | 1.34 |
| First cousins | 1 / 16 | 1.50 |
| First cousins once removed | 1 / 32 | 1.64 |
| Second cousins | 1 / 64 | 1.76 |
| Unrelated individuals | 0 | 2.00 |
φ is the kinship coefficient. Results for f = 0.01 are shown.
Table A2.
Type 1 Error for the Sib Pair Design
| Aa | Ub |
α |
|||
|---|---|---|---|---|---|
| 10−4 | 10−3 | 10−2 | 5 × 10−2 | ||
| WS-R | |||||
| 5 | 100 | 1.7 × 10−4 | 8.0 × 10−4 | 4.7 × 10−3 | 2.0 × 10−2 |
| 500 | 1.0 × 10−4 | 7.4 × 10−4 | 5.5 × 10−3 | 2.6 × 10−2 | |
| 1000 | 1.4 × 10−4 | 7.0 × 10−4 | 4.9 × 10−3 | 2.5 × 10−2 | |
| 10 |
100 | 1.0 × 10−4 | 5.0 × 10−4 | 3.8 × 10−3 | 1.8 × 10−2 |
| 500 | 1.1 × 10−4 | 9.8 × 10−4 | 6.0 × 10−3 | 2.7 × 10−2 | |
| 1000 | 1.5 × 10−4 | 9.9 × 10−4 | 5.9 × 10−3 | 2.7 × 10−2 | |
| WS-N | |||||
| 5 | 100 | 1.0 × 10−4 | 4.5 × 10−4 | 2.2 × 10−3 | 8.0 × 10−3 |
| 500 | 2.7 × 10−5 | 2.7 × 10−4 | 4.9 × 10−4 | 2.4 × 10−3 | |
| 1000 | 2.4 × 10−5 | 5 × 10−5 | 3.0 × 10−4 | 1.5 × 10−3 | |
| 10 | 100 | 4.9 × 10−5 | 2.5 × 10−4 | 1.4 × 10−3 | 6.7 × 10−3 |
| 500 | 2.0 × 10−5 | 1.0 × 10−4 | 3.8 × 10−4 | 1.7 × 10−3 | |
| 1000 | 4.9 × 10−5 | 1.0 × 10−4 | 2.9 × 10−4 | 1.4 × 10−3 | |
Number of affected sib pairs.
Number of unrelated unaffected individuals.
Table A3.
Mean and Standard Deviation for keff|2 Assuming and f Is Sampled from the Corresponding Posterior Distribution
| Number of Controls | Mean | Standard Deviation |
|---|---|---|
| 0.01 | ||
| 100 | 1.17 | 0.03 |
| 500 | 1.17 | 0.01 |
| 1000 | 1.17 | 0.01 |
| 0.005 | ||
| 100 | 1.14 | 0.03 |
| 500 | 1.14 | 0.01 |
| 1000 | 1.14 | 0.01 |
Table A4.
Simulation Results for Teff
| Nsibs | Ncontrols |
f |
|
Cora |
Theoretical |
|||
|---|---|---|---|---|---|---|---|---|
| μ | var | |||||||
| f = 0.01 | ||||||||
| 5 |
100 | 0.152 | 0.163 | 0.152 | 0.163 | 0.999915 | 0.156 | 0.161 |
| 500 | 0.153 | 0.151 | 0.153 | 0.151 | 0.999968 | 0.156 | 0.161 | |
| 1000 | 0.162 | 0.168 | 0.162 | 0.168 | 0.999986 | 0.156 | 0.161 | |
| f = 0.001 | ||||||||
| 5 | 100 | 0.017 | 0.018 | 0.017 | 0.018 | 0.999864 | 0.016 | 0.016 |
| 500 | 0.014 | 0.015 | 0.014 | 0.015 | 0.999984 | 0.016 | 0.016 | |
| 1000 | 0.016 | 0.017 | 0.016 | 0.017 | 0.999985 | 0.016 | 0.016 | |
Correlation between Teff(f) and .
Table A5.
Theoretical Results for Teff
| f | N |
Theoretical |
|
|---|---|---|---|
| μ | var | ||
| Siblings | |||
| 0.01 | 5 | 0.156 | 0.161 |
| 0.001 | 0.016 | 0.016 | |
| First cousins | |||
| 0.01 | 5 | 0.191 | 0.194 |
| 0.001 | 0.019 | 0.019 | |
| Second cousins | |||
| 0.01 | 5 | 0.197 | 0.196 |
| 0.001 | 0.019 | 0.020 | |
Table A6.
Gamma-Based Approximation of Weighted Sum of M Poisson RVs
| M |
α |
||||
|---|---|---|---|---|---|
| 10−5 | 10−4 | 10−3 | 10−2 | 0.05 | |
| 3 | 4.7 × 10−6 | 5.3 × 10−5 | 4.3 × 10−4 | 6.3 × 10−3 | 2.8 × 10−2 |
| 5 | 1.0 × 10−5 | 9.3 × 10−5 | 8.3 × 10−4 | 7.0 × 10−3 | 3.3 × 10−2 |
| 20 | 1.0 × 10−5 | 9.3 × 10−5 | 8.4 × 10−4 | 8.0 × 10−3 | 3.9 × 10−2 |
| 40 | 1.0 × 10−5 | 9.7 × 10−5 | 8.8 × 10−4 | 8.4 × 10−3 | 4.1 × 10−2 |
Table A7.
Analytical versus Permutation p Values for Three Mendelian Traits
| Syndrome |
WS-R |
WS-N |
||
|---|---|---|---|---|
| Analytical P | Permutation P | Analytical P | Permutation P | |
| Miller | 1.0 × 10−6 | 3.0 × 10−7 | 1.0 × 10−6 | 3.0 × 10−7 |
| Freeman-Sheldon | 1.0 × 10−4 | 5.7 × 10−5 | 1.0 × 10−4 | 6.0 × 10−7 |
| Kabuki | 3.1 × 10−5 | 3.4 × 10−6 | 3.5 × 10−5 | 4.0 × 10−7 |
Web Resources
The URLs for data presented herein are as follows:
1000 Genomes Project, http://www.1000genomes.org/
I.I.-L's website, http://www.columbia.edu/∼ii2135/
Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/
PolyPhen-2, http://genetics.bwh.harvard.edu/pph2/
SIFT, http://sift.jcvi.org/
References
- 1.Ng S.B., Turner E.H., Robertson P.D., Flygare S.D., Bigham A.W., Lee C., Shaffer T., Wong M., Bhattacharjee A., Eichler E.E., et al. Targeted capture and massively parallel sequencing of 12 human exomes. Nature. 2009;461:272–276. doi: 10.1038/nature08250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ng S.B., Buckingham K.J., Lee C., Bigham A.W., Tabor H.K., Dent K.M., Huff C.D., Shannon P.T., Jabs E.W., Nickerson D.A., et al. Exome sequencing identifies the cause of a mendelian disorder. Nat. Genet. 2010;42:30–35. doi: 10.1038/ng.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ng S.B., Bigham A.W., Buckingham K.J., Hannibal M.C., McMillin M.J., Gildersleeve H.I., Beck A.E., Tabor H.K., Cooper G.M., Mefford H.C., et al. Exome sequencing identifies MLL2 mutations as a cause of Kabuki syndrome. Nat. Genet. 2010;42:790–793. doi: 10.1038/ng.646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li B., Leal S.M. Methods for detecting associations with rare variants for common diseases: Application to analysis of sequence data. Am. J. Hum. Genet. 2008;83:311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Madsen B.E., Browning S.R. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5:e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Price A.L., Kryukov G.V., de Bakker P.I., Purcell S.M., Staples J., Wei L.J., Sunyaev S.R. Pooled association tests for rare variants in exon-resequencing studies. Am. J. Hum. Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu D.J., Leal S.M. A novel adaptive method for the analysis of next-generation sequencing data to detect complex trait associations with rare variants due to gene main effects and interactions. PLoS Genet. 2010;6:e1001156. doi: 10.1371/journal.pgen.1001156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.King C.R., Rathouz P.J., Nicolae D.L. An evolutionary framework for association testing in resequencing studies. PLoS Genet. 2010;6:e1001202. doi: 10.1371/journal.pgen.1001202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bhatia G., Bansal V., Harismendy O., Schork N.J., Topol E.J., Frazer K., Bafna V. A covering method for detecting genetic associations between rare variants and common phenotypes. PLoS Comput. Biol. 2010;6:e1000954. doi: 10.1371/journal.pcbi.1000954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Han F., Pan W. A data-adaptive sum test for disease association with multiple common or rare variants. Hum. Hered. 2010;70:42–54. doi: 10.1159/000288704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ionita-Laza I., Buxbaum J.D., Laird N.M., Lange C. A new testing strategy to identify rare variants with either risk or protective effect on disease. PLoS Genet. 2011;7:e1001289. doi: 10.1371/journal.pgen.1001289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Neale B.M., Rivas M.A., Voight B.F., Altshuler D., Devlin B., Orho-Melander M., Kathiresan S., Purcell S.M., Roeder K., Daly M.J. Testing for an unusual distribution of rare variants. PLoS Genet. 2011;7:e1001322. doi: 10.1371/journal.pgen.1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wu M.C., Lee S., Cai T., Li Y., Boehnke M., Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am. J. Hum. Genet. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pritchard J.K., Cox N.J. The allelic architecture of human disease genes: Common disease-common variant…or not? Hum. Mol. Genet. 2002;11:2417–2423. doi: 10.1093/hmg/11.20.2417. [DOI] [PubMed] [Google Scholar]
- 15.Adzhubei I.A., Schmidt S., Peshkin L., Ramensky V.E., Gerasimova A., Bork P., Kondrashov A.S., Sunyaev S.R. A method and server for predicting damaging missense mutations. Nat. Methods. 2010;7:248–249. doi: 10.1038/nmeth0410-248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kumar P., Henikoff S., Ng P.C. Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nat. Protoc. 2009;4:1073–1081. doi: 10.1038/nprot.2009.86. [DOI] [PubMed] [Google Scholar]
- 17.Ionita-Laza I., Lange C., M Laird N. Estimating the number of unseen variants in the human genome. Proc. Natl. Acad. Sci. USA. 2009;106:5008–5013. doi: 10.1073/pnas.0807815106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fay M.P., Feuer E.J. Confidence intervals for directly standardized rates: A method based on the gamma distribution. Stat. Med. 1997;16:791–801. doi: 10.1002/(sici)1097-0258(19970415)16:7<791::aid-sim500>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 19.Efron B., Thisted R. Estimating the number of unknown species: How many words did Shakespeare know? Biometrika. 1976;63:435–437. [Google Scholar]
- 20.Ionita-Laza I., Ottman R. Study designs for identification of rare disease variants in complex diseases: The Utility of Family-based Designs. Genetics. 2011 doi: 10.1534/genetics.111.131813. in press. Published online August 11, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schaffner S.F., Foo C., Gabriel S., Reich D., Daly M.J., Altshuler D. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chakravarti A. Genomic contributions to Mendelian disease. Genome Res. 2011;21:643–644. doi: 10.1101/gr.123554.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roeder K., Bacanu S.A., Wasserman L., Devlin B. Using linkage genome scans to improve power of association in genome scans. Am. J. Hum. Genet. 2006;78:243–252. doi: 10.1086/500026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ionita-Laza I., McQueen M.B., Laird N.M., Lange C. Genomewide weighted hypothesis testing in family-based association studies, with an application to a 100K scan. Am. J. Hum. Genet. 2007;81:607–614. doi: 10.1086/519748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rakovski C.S., Xu X., Lazarus R., Blacker D., Laird N.M. A new multimarker test for family-based association studies. Genet. Epidemiol. 2007;31:9–17. doi: 10.1002/gepi.20186. [DOI] [PubMed] [Google Scholar]
- 26.Lange K. Relative-to-relative transition probabilities for two linked genes. Theor. Popul. Biol. 1974;6:92–107. doi: 10.1016/0040-5809(74)90033-1. [DOI] [PubMed] [Google Scholar]
- 27.McKenna A., Hanna M., Banks E., Sivachenko A., Cibulskis K., Kernytsky A., Garimella K., Altshuler D., Gabriel S., Daly M., DePristo M.A. The Genome Analysis Toolkit: A MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 2010;20:1297–1303. doi: 10.1101/gr.107524.110. [DOI] [PMC free article] [PubMed] [Google Scholar]


