High activity and Lévy searches: jellyfish can search the water column like fish

Abstract

Over-fishing may lead to a decrease in fish abundance and a proliferation of jellyfish. Active movements and prey search might be thought to provide a competitive advantage for fish, but here we use data-loggers to show that the frequently occurring coastal jellyfish (Rhizostoma octopus) does not simply passively drift to encounter prey. Jellyfish (327 days of data from 25 jellyfish with depth collected every 1 min) showed very dynamic vertical movements, with their integrated vertical movement averaging 619.2 m d⁻¹, more than 60 times the water depth where they were tagged. The majority of movement patterns were best approximated by exponential models describing normal random walks. However, jellyfish also showed switching behaviour from exponential patterns to patterns best fitted by a truncated Lévy distribution with exponents (mean μ = 1.96, range 1.2–2.9) close to the theoretical optimum for searching for sparse prey (μ_opt ≈ 2.0). Complex movements in these ‘simple’ animals may help jellyfish to compete effectively with fish for plankton prey, which may enhance their ability to increase in dominance in perturbed ocean systems.

1. Introduction

There is growing concern that jellyfish may proliferate in the World's oceans as a result of over-fishing and other human impacts [1]. A number of life-history features of jellyfish help them to increase in perturbed systems, including their short generation times, high reproductive output, lack of predators, broad prey spectrum and, owing to their tactile rather than visual feeding, an ability to feed efficiently in turbid water and during both night and day [2,3]. Once this switch to a jellyfish-dominated system has occurred, there is concern that by consuming large amounts of plankton prey, including fish eggs and larvae, high densities of jellyfish may impede the recovery of fish stocks even if fishing pressure is then reduced [4,5]. Certainly, it is widely recognized that the plankton feeding phase for developing fish plays a key role in fisheries recruitment, with high feeding success leading to good recruitment [6]. Fish larvae of a wide range of species feed on plankton with their prey spectra often driven by gape limitation, so that as fish larvae grow their prey size increases, e.g. from micro- to mesozooplankton [6]. Equally, many jellyfish feed predominantly on a range of plankton prey, including phytoplankton, microzooplankton and mesozooplankton [7]. Hence, dietary overlap between jellyfish and developing fish will be a general feature where these taxa co-occur rather than an unusual occurrence. Consequently, competition for plankton between jellyfish and fish is expected and plankton consumption by high densities of jellyfish may directly impact fisheries recruitment. However, in contrast to the situation with marine fish, very little is known about foraging movements and behaviour of jellyfish even though understanding such activity is relevant to population demographic processes such as changes in distribution and abundance.

This lack of information about the movements of free-living jellyfish contrasts with the resurgence in interest in the movement ecology of vertebrates driven by the fusion of high resolution tracking datasets for free-living animals with robust statistical procedures for analysing these data [8,9]. The field has also seen the development of themes that cut across disciplines from ecology to theoretical physics [10]. Arising from recent analysis is strong empirical evidence that a range of both air-breathing divers (e.g. turtles, penguins) as well as diverse fish show Lévy-flight movement patterns [11] that theoretically optimize encounters with prey that are sparsely distributed [12,13]. Lévy flight describes a power-law distributed pattern of movement step lengths in which short movement steps are interspersed with much longer ‘relocation’ steps, and where the exponent (μ) of the power law lies within the range 1 < μ ≤ 3. Conversely, when prey are more uniformly distributed it is expected that Brownian movement may optimize prey encounter rates [14]. More recently, it has been demonstrated that the movement patterns of a number of marine fish, including sharks, tunas as well as the ocean sunfish (Mola mola), change systematically between habitats presumably to optimize foraging success in differing prey fields [15]. However, although movements approximated by Lévy flights have been identified in diverse taxa, from amoebae to mammals [13], it has not been demonstrated whether these movement patterns are caused by innate behaviours of the foraging predators themselves [11,15], or are instead an emergent property caused by the prey field distribution, with predators simply curtailing movement steps in response to prey encounters [16,17]. Some empirical studies have questioned whether organisms adopt Lévy flight behaviour (e.g. [18]), but experimental studies on Drosophila in the absence of external cues show power-law distributed movement patterns that suggest such movements arise from flexible, innate behaviours [19–21].

Because of the relative ease with which vertebrates can be equipped with electronic tags, this previous work has focused on these animals. The extent to which individual pelagic marine invertebrates move vertically remains poorly resolved. Traditionally, pelagic invertebrates that form part of the plankton have been considered to have relatively simple vertical movements associated with populations moving en-masse in association with diel or tidal cycles [22,23]. This view pervades because sampling techniques integrate the vertical distribution of populations rather than allowing individuals to be followed [22]. However, information about the movements of individual pelagic marine invertebrates, including cephalopods and jellyfish, is now starting to emerge [24–27]. One advantage that fish might be presumed to have over jellyfish is their higher active prey search using highly developed eyes, with the general assumption that jellyfish are passive hunters and, by chance, simply drift into prey occasionally (e.g. [28]). Here, we challenge this view by equipping jellyfish with pressure-sensitive data-loggers to record their patterns of vertical movements over periods of several weeks during their summer feeding period.

2. Material and methods

(a). Jellyfish tracking

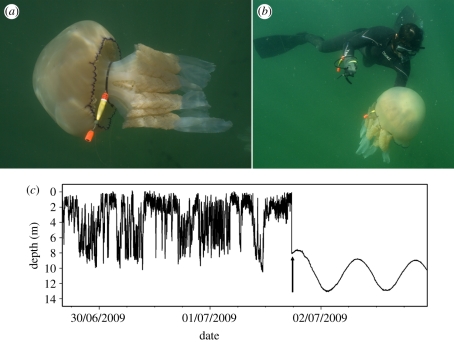
We attached time-depth recorder tags (CEFAS Technologies G5, Lowestoft UK, physical dimensions, cylinders 3.1 by 0.8 cm) to scyphozoan jellyfish (Rhizostoma octopus) in Carmarthen Bay, Wales (51.72° N 4.63° W) in September 2008 and 2009 and June 2009. Water depth at the time of tagging was less than 10 m. Deeper water (more than 20 m) further offshore was located approximately 11 km from the tagging locations. The size of all tagged jellyfish was estimated to be between 0.40 and 0.50 m bell diameters corresponding to wet weights of between 5 and 10 kg [29]. Tags were programmed to record depth every minute (depth precision, 0.03 m) and temperature every 5 min. Aerial surveys (for details, see [30]) were used to locate aggregations of jellyfish in the bay and then to direct the location of subsequent ship-borne tagging work. Once jellyfish were spotted from boat observers, snorkel divers entered the water and deployed the tags in situ. Tags were attached to the jellyfish using a plastic cable tie loosely fitted around the peduncle that joins the swimming bell to the oral arms of the jellyfish (figure 1a,b). A small plastic float was used to ensure that the entire attachment was very slightly positively buoyant. Tag attachment took a few seconds. The peduncle of the jellyfish is very robust, hence, we expected that the tag would only detach when the jellyfish died and was physically broken up, at which time the tag would float to the sea surface. We planned to recover tags when they washed ashore and were found by members of the public, either still attached to stranded jellyfish, or detached if the jellyfish had died and broken up at sea. A local publicity campaign was conducted to try to maximize return rates and people returning tags were offered a nominal reward (£25) and provided with information about the deployment data for that tag.

Figure 1.

(a,b) Images showing attachment of data-loggers to jellyfish by looping a cable tie around the peduncle that connects the swimming bell to the oral arms. (c) An example of how the death of a jellyfish was evident in the tag's depth record. The jellyfish was inferred to die at sea and then sink to the seabed, following which a clear tidal signal was evident with very little residual depth variation. Inferred time of death indicated by the vertical arrow.

On return of tags, data were downloaded to a PC and visual exploration of each dataset was performed in Multitrace Dive (Jensen Software Systems, Laboe, Germany). We first determined the time of jellyfish death in each dataset. Death of the jellyfish could be inferred in several ways. Jellyfish can strand ashore and indeed several tags were found in this way as part of mass jellyfish strandings. In this case, the time of stranding could be seen by (i) the tag being at the surface, and (ii) a temperature spike when the tag came out of the water. Second, a jellyfish might die at sea. In this case, the depth data revealed a rapid ascent of the tag to the surface, sometimes preceded by a protracted time when the tag appeared to be on the seabed as indicated by very little depth variation and a clear tidal signal. In one case, this tidal signal, indicative of a tag on the seabed, continued for an entire summer (greater than three months; figure 1c). We suspect that in this case, the tag was tangled up with other material on the seabed (e.g. seaweed) which prevented it from rising to the surface. Serendipitously, this tag allowed us to assess the extent of tag-recorded ‘vertical movement’ caused simply by waves and tides.

(b). Integrated vertical movement

Once datasets were cut only to include the time when they were attached to live jellyfish (as confirmed by vertical movements), we assessed the pattern of vertical movement in several ways. First, the integrated vertical movement (IVM) was calculated as the sum of the absolute differences in depth between readings n and n + 1. For example, if depth readings over 5 min were 4.6, 5.2, 1.7, 2.6 and 3.6 m, this equates to absolute changes in depth of 0.6, 3.5, 0.9 and 1 m, which sum to an IVM of 6 m. Owing to the irregular and nonlinear trends in IVM over time, we analysed the IVM patterns within a generalized additive model framework (GAM). All analyses were carried out in R [31], using the mgcv package [32].

(c). Split-moving window matrix analysis/model selection

Ten of the longest depth time-series data were subjected to quantitative analysis of the frequency distribution of movement steps following the recently developed robust statistical procedures [15]. First, split-moving window matrix analysis (SMWMA) was applied to each of the 10 time series and average dissimilarities in depth use across different ‘window’ sizes were calculated at a significance level of p < 0.01. This analysis identifies boundaries in the dataset that occur when the average dissimilarity between the two halves of the split-moving window is statistically significant (see [15]). This was undertaken to separate each time series into sections where the movement pattern was likely to be more behaviourally consistent than the whole. The time-stamped depth records from each section were then converted into vertical move steps by coalescing intermediate points. An intermediate point is one where the vertical direction of the movement to and from this point is the same, i.e. this is a part of a continuous movement artificially interrupted by a sampling event. So, for example, the series of depth readings 4.1, 3.7, 2.9, 2.5, 2.7, 3.4 and 3.6 m, would equate to vertical steps of 1.6 m (4.1–2.5 m) followed by 1.1 m (2.5–3.6 m). Finally, maximum-likelihood estimation (MLE) was employed to fit exponential, power law (Lévy) and truncated power law (truncated Pareto-Lévy) models to the data, and Akaike Information Criteria (AIC) weights were calculated for model comparisons [15]. Briefly, for each track section, parameters for power law, exponential and truncated Pareto distributions were calculated using MLE [33]. Ranked move step-length plots combining empirical and best-fit plots were used to reject sections that were a poor fit to all distributions. Log-likelihoods and Akaike weights were calculated for the remaining sections and were used to determine which distribution (model) best fit the data (for detailed methodology used, see [15]).

(d). Jellyfish gut analysis

During tag deployments in June 2009, we assessed the gut content of R. octopus. Jellyfish were collected with a hand net by snorkellers and brought onboard. Jellyfish were then up-ended into a large plastic bowl and the oral arms removed at the peduncle with a scalpel. This exposed the internal canal system containing ingested material which was then flushed. This material was immediately preserved in 8 per cent Lugol's iodine in 125 ml darkened glass jars and kept in a cool environment until return to the laboratory. All samples were analysed within 4 days. Small prey items (less than 100 µm long) were identified and counted using an Olympus CH binocular microscope at 100×magnification. Large prey items (greater than 100 µm long) were identified and counted using an Olympus SZ40 dissecting binocular microscope at 30×magnification. A sufficient sample was analysed to count at least 100 prey items in both the small and large size classes, which was typically 1 per cent and 10–20% of the total volume, respectively. A selection of prey items was measured to the nearest 5 µm using an eyepiece graticule calibrated with a stage micrometer. Equivalent spherical volume or biovolume calculations were carried out based on basic shapes of prey items in each category [34,35].

3. Results

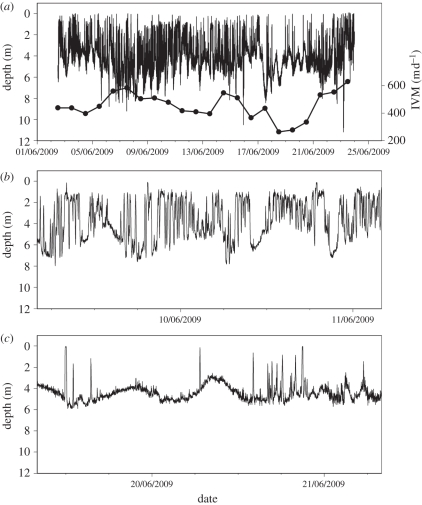
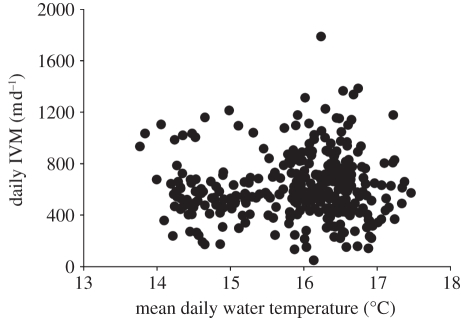
Between September 2008 and 2009, we deployed 72 tags on R. octopus, of which 25 were recovered (as of 1 April 2011), providing dive data for between 2 and 28.5 days (mean 13.0 days, s.d. = 8.46) prior to the death of the jellyfish (figure 1). In our initial analysis, we looked at the depth data from all the recovered tags. All the jellyfish showed a high level of IVM (figure 2). The mean daily IVM was 619.2 m d⁻¹ (s.d. = 249, n = 327 calendar days on which data were collected for the 25 jellyfish). On most days, jellyfish had IVMs of between 350 and 800 m d⁻¹ (80% of days). Visual inspection showed near-continuous up and down movements on these days (figure 2b), while on the days with the lowest values for IVM (less than 350 m d⁻¹), the jellyfish remained predominantly at the same depth with occasional vertical excursions (figure 2c). At such times, visual inspection of the depth trace showed there was occasionally a tidal signal in depth that was consistent with the jellyfish maintaining position close to the seabed. Essentially, when the jellyfish were less active, then the depth logger behaved more like a water depth gauge. The highest values for daily IVM (greater than 800 m d⁻¹), again corresponded with near-continuous vertical movements, but in these cases the difference between the maximum and minimum depth increased, presumably reflecting the fact that the jellyfish were in deeper water. Deployments occurred in different seasons (September 2008 and 2009 and June 2008) and hence tagged jellyfish experienced different water temperatures, with mean daily ambient water temperatures ranging from 13.8°C–17.5°C. High daily IVM occurred across this range of temperatures, i.e. IVM appeared not to be influenced by water temperature across this temperature range (figure 3).

Figure 2.

(a) A 22 day record of depth (2–23 June 2009) for jellyfish no. 2032 and (symbols right axis) the integrated vertical movement (IVM) each day. (b,c) Examples of the type of depth versus time trace corresponding to different integrated daily movement values: 507 and 341 m d⁻¹, respectively, for these sections. The apparent spikes in the depth data (e.g. (c)) are real and not some kind of measurement artefact, as evidenced by several successive values showing the descent and ascent phases, with typical vertical movement rates of 1 m min⁻¹.

Figure 3.

For all tag recoveries (n = 25 jellyfish), the daily integrated vertical movement (IVM) plotted against ambient water temperature. High daily IVMs were recorded across a range of temperatures and the magnitude of the daily IVM did not change with temperature (F_1,325 = 0.7, p = 0.42).

The magnitude of this IVM was not caused simply by the effect of waves or tides moving over jellyfish resulting in depth changes. For example, for one tag which remained on the seabed throughout most of July–October 2009 (figure 1c) the IVM was, on average, 82.0 m d⁻¹ (s.d = 43.2, n = 114 days), approximately 13 per cent of the mean daily IVM recorded for jellyfish. The magnitude of IVM was also not simply caused by a large diel change in the depth occupied by the jellyfish. For example, for the 25 jellyfish, the mean difference between the maximum and minimum depths recorded each day was only 10.8 m (s.d. = 5.8, n = 327 days), less than 2 per cent of the average daily IVM.

The extent of vertical movement also changed with time (e.g. figure 2). To examine if the daily IVM of different jellyfish co-varied through time, we selected seven long datasets for jellyfish tagged on the same day (minimum of 13 different days over which depth data were collected from tagging to death of the jellyfish). This selection ensured that we had sufficient data to examine potential drivers of temporal changes in daily IVM. The fit of the regression splines to each individual daily IVM time series is shown in the electronic supplementary material, figure S1. We fitted a GAM model for daily IVM time series using the variables ‘jellyfish ID’, day, maximum depth and ‘time until death’. We found significant autocorrelation for daily IVM levels on successive days and therefore applied an auto-regressive moving average model for the residuals. We found highly significant differences between individual jellyfish IVM patterns (p < 0.001), that also showed significant interaction with day (p < 0.001). We also found a significant effect of maximum depth (p = 0.002) that shows a strong positive relationship with daily IVM. Therefore, between individuals there were differing changes in IVM across the same period of days, that is, each individual changed its behaviour with respect to date (elapsed time) in its own way. The daily IVM was not related to the number of days until the jellyfish expired. The key findings from the analysis of daily IVM of (i) generally continuous up and down movements, and (ii) changes in behaviour through time, were also evident in the quantitative analysis of movement step-length frequencies.

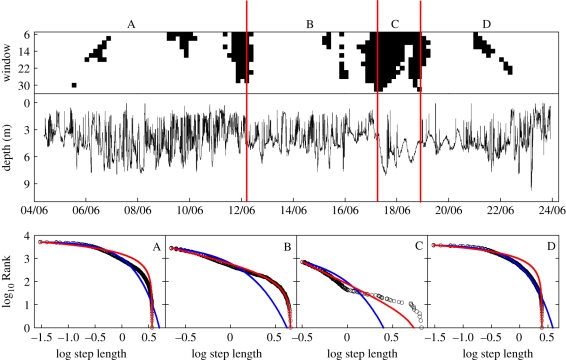
For the analysis of vertical step-length frequency distributions, we selected the longest 10 datasets available which ranged from 12.5 to 28.5 days (mean 21.0, s.d. = 4.6) prior to the death of the jellyfish. This selection was made so that there was the maximum possible amount of data upon which to perform the SMWMA. The 10 jellyfish selected covered the range of vertical movements shown in the IVM analysis (figure 2). This analysis of step-length frequency distributions showed a range of movement patterns. For example, for jellyfish no. 2219, the SMWMA analysis highlighted five significantly different sections within the track with respect to the proportion of time spent at different depths. The calculated exponents (μ) from MLE analysis on individual sections were not within the Lévy range for sections A–C and E, with AIC weights (wAIC) favouring the exponential model for three sections (B–D) and evidence of good visual fits to the exponential for sections A and E (see the electronic supplementary material, table S1). Switching behaviour between movement patterns best approximated by exponential and truncated Lévy models was observed for both jellyfish nos 2211 and 2032. For no. 2211, six separate sections were analysed (A–F) and truncated Lévy model fits were supported for two sections (A and E; electronic supplementary material, table S1). For these sections, μ-values were calculated to be 1.72 and 2.22, respectively, indicating specialized random-walk movement patterns close to the theoretical optimum (μ_opt ≈ 2.0) [36]. Exponential model best fits were supported for the other sections (C,D,F) indicating movements consistent with normal random walks that approximate Brownian motion. Section B was not best fit by either model distribution using wAIC values for model selection (electronic supplementary material, table S1), although visually the exponential appeared to fit well. For jellyfish no. 2032 the track separated into four sections (A–D). The move-step distributions for sections A and D were best fitted by the exponential model, whereas for sections B and C a truncated Lévy model with μ exponents 1.91 and 2.91 provided the best fit (wAIC = 1) (figure 4). The movement pattern in section B was close to theoretically optimal Lévy searching for sparse prey, whereas section C, although Lévy, was approximated by a best-fit model with an exponent close to 3; above this exponent value a movement pattern emerges as Brownian motion [7]. This alternating pattern of an exponential best fit followed by a truncated Lévy fit, and back again, is indicative of jellyfish nos 2211 and 2032 changing movement responses to the environment during the tracking periods. Likewise within the depth data for the remaining seven jellyfish, 16 different sections were identified, of which three sections had best model fits described by a truncated power law with μ values of 2.56, 1.18 and 1.20. These analyses confirm that Lévy fits and theoretically optimal Lévy fits (μ values close to 2.0) occur within the data, but are not frequent. There were also sections having low μ-values, describing ballistic (straight-line movement) tracks that are indicative of near-continuous movements from near the sea bottom to the surface and back.

Figure 4.

For jellyfish no. 2032 (top panel) the split-moving window analysis plot showing the identification of movement pattern discontinuities. Middle panel, the complete depth versus time trace spanning 22 days. Vertical lines delineate sections (A–D) for which significant differences in the vertical step-length frequency distributions were identified using SMWMA. Lower panel, rank-frequency plots of the move-step length distribution for sections A–D (black circles) showing model fits to data of the truncated Lévy (red line) and exponential (blue line) distributions. Akaike weights support truncated Lévy model fits to data in sections B and C, with exponents (μ) of 1.91 and 2.91, respectively, and exponential best fits in sections A and D.

In summary, the MLE analysis of vertical move-step lengths shows: (i) a predominance of normal random walks (described by exponential model fits that approximate Brownian motion) across different sections within and between individuals; (ii) evidence in some sections for near-continuous surface to depth/seabed movements described by move distributions with low exponents (μ) characteristic of straight-line (ballistic) tracks; (iii) significant support for movement patterns in several sections conforming to a truncated Lévy flight with exponents close to a theoretical optimum for efficient search for sparse prey; and (iv) individuals showed switching between Brownian and Lévy behaviour, perhaps in response to changes in the environment, such as different prey densities encountered.

Gut contents were assessed for nine individuals. All individuals had an appreciable amount of material in their guts which included phytoplankton, heterotrophic protists (ciliates and flagellates), crustacean larvae (barnacle and copepod nauplii, copepodites, crab zoea), mollusc larvae, copepods, hydrozoans and chaetognaths. The mean number of prey items was more than 5000 per individual. Small microzooplankton and phytoplankton (less than 100 µm long) contributed 66 per cent of the gut biovolume.

4. Discussion

The first clear finding from our study is that jellyfish in the wild do not simply drift at a fixed depth, but rather they perform extensive vertical movements that equate to moving up and down through the entire water column dozens of times a day. Our findings clearly pertain to a single species, R. octopus, and a useful goal of future studies will be to examine the generality of our findings across other jellyfish species. The wide availability of a range of small data-loggers for protracted animal tracking (e.g. [37]) provides the potential for an expansion of jellyfish tracking work. In an evolutionary context, it is also interesting that jellyfish in the wild can also sometimes exhibit movement patterns approximated by theoretically near-optimal Lévy flights, as has been demonstrated for turtles, fish and penguins [11,15]. The most parsimonious explanation for the jellyfish vertical movements we recorded is that they were associated with prey searching. Implicit in this explanation is the fact that the jellyfish were foraging and not exclusively engaged in other potential activities such as reproduction. Our stomach analysis probably under-represented soft-bodied, easily digested prey items such as hydrozoans, but certainly the jellyfish were feeding on a variety of prey types, including both phytoplankton and zooplankton. This evidence from stomach contents supports our inference of active feeding by the tracked animals.

There are other reasons why animals may move vertically in the water that might potentially account for some of the vertical activity seen in the jellyfish. For example, vertical movement often occurs associated with a diel cycle (diel vertical migration or DVM) [38]. However, we saw no evidence of a systematic day–night shift in depth. Furthermore, any repositioning in shallow water (the water depth in our study area was generally less than 10 m) will not produce appreciable IVM. For example, a diel movement from 4 to 10 m would only produce an IVM of 12 m per day (6 m at dawn and 6 m at dusk). Some plankton may reposition vertically associated with the tidal cycle, but as with DVM this systematic repositioning will only produce a small IVM because there is only a one-step movement associated with each change from low to high tide. It is conceivable that jellyfish vertical movements might be a predator evasion tactic. However, it is hard to imagine that the relatively slow descent and ascent speeds (ca 1 m min⁻¹) might allow escape from fast moving predators such as the leatherback turtle (Dermochelys coriacea) and the ocean sunfish (M. mola). Plankton, including jellyfish, may reposition in the water column depending on weather. For example, aerial surveys tend to reveal Rhizostoma jellyfish near the surface on calm days [30]. However as with DVM, in shallow water any vertical repositioning associated with weather conditions will only produce very low levels of daily IVM. We recorded high levels of daily IVM across different seasons and water temperatures which suggest that this level of activity is a general behaviour of this species of jellyfish rather than something unusual that only occurs in specific circumstances. Furthermore, jellyfish tracked simultaneously showed different patterns of daily IVM over time. This analysis suggests that the variability in daily IVM is not a common response to the same external drivers (e.g. weather conditions or tidal cycle), but rather the behaviour of each jellyfish is a reflection of its own unique and immediate environment.

Waves constantly passing over a submerged jellyfish will also produce depth excursions which when summed might conceivably lead to high daily IVM. However, we were able to quantify this effect and certainly waves only accounted for a very small proportion of the daily IVM that we observed by jellyfish. We conclude that the high levels of vertical activity recorded for jellyfish are not a consequence of diel vertical movement, movements associated with tidal cycles, weather or a consequence of constant wave action over a tag.

Some observations of hunting behaviour of jellyfish support the view of a cruising predator. For example, complex movements that change in line with prey density have been recorded through detailed video recordings of jellyfish swimming in aquaria, i.e. they can perceive prey and change their behaviour accordingly [39–41]. In 2.3 m deep tanks, the jellyfish Chrysaora quinquecirrha was observed to change depth over a range of up to 1.5 m within a few minutes, presumably in search of prey [39]. Prey search is certainly one of the principal reasons underlying vertical movements in marine vertebrates [40]. Micro-patches of plankton are now well defined across a range of systems [42–44]. Our results imply that strata of high densities of Rhizostoma prey are rare so that the jellyfish spend long periods searching for high prey densities. The small-scale distribution of plankton prey is hypothesized to be one of the key determinants of the foraging success by fish larvae and hence a key influence on fisheries recruitment [45]. Known as the ‘Lasker's stable ocean hypothesis’, the prediction is that when plankton prey are localized in high density in discrete depth layers, then fish larvae focus on these layers and achieve high foraging success compared with when plankton prey are more dispersed, for example, after storm events. Lévy-type movements presumably function to maximize the probability that jellyfish encounter sparsely distributed, high density micro-patches of prey [11,15,36]. However, we also observed significant variation in the exponents of the movement fitted by a Lévy distribution (μ = 1.2–2.9). The exact adaptive nature of this variation is not known, yet they may represent a response to foraging within environments which differ in their biotic factors, such as patch size and quality [15]. For example, when prey is more uniformly distributed, models predict that a more Brownian-type movement pattern will optimize prey encounters and indeed this was a movement pattern also exhibited by the jellyfish. Jellyfish can orient to olfactory cues from prey [46] and so, additionally, vertical movements will be useful in sampling olfactory trails that tend to disperse horizontally because of current shear. In some periods (when IVM was low), vertical excursions were followed by a vertical return to the depth occupied prior to the excursion. This pattern of ‘bounce’ movements has also been seen in some fish [47,48] and presumably represents an animal prospecting away from a preferred depth, not finding an improvement in conditions elsewhere and so returning to the original depth. Such behaviour sits outside the Lévy search paradigm where it is assumed that a prey patch is not purposefully revisited once deserted. Again this finding of ‘vertical return’ behaviour, points to jellyfish movements, at least on occasions, being fine-tuned to prey resources.

One key goal for future work is to track predators as they move through known prey fields. To date, studies have tracked a range of predators but only made inferences about the probable prey fields [15,49]. It will certainly be very difficult to measure prey fields in certain situations (e.g. pelagic sharks feeding on fish and cephalopods), but the jellyfish–zooplankton complex, like that of planktivorous sharks and zooplankton [50,51], is one where techniques are available (e.g. plankton pumps) for measuring the prey field in some detail. Hence jellyfish may be a good model group for future studies that aim to unravel the drivers of different movement patterns by predators.

Overall, the key finding that emerges from our study is that the vertical movement behaviour of jellyfish is complex and most probably serves to maximize foraging success in a prey field that changes in space and time. Previously complex vertical search patterns have been reported in marine vertebrates, such as Lévy flight searching [11,15], and might be thought to give vertebrates a competitive foraging advantage over invertebrates. The finding of complex vertical movement patterns in jellyfish suggests that they may compete more strongly with fish for plankton prey than first thought. This insight could play an important role in our understanding of how, in the future, jellyfish may come to dominate perturbed ocean systems.