Abstract
In this paper we study the error rate of RNA synthesis in the look-ahead model for the random walk of RNA polymerase along DNA during transcription. The model’s central assumption is the existence of a window of activity in which ribonucleoside triphosphates (rNTPs) bind reversibly to the template DNA strand before being hydrolyzed and linked covalently to the nascent RNA chain. An unknown, but important, integer parameter of this model is the window size w. Here, we use mathematical analysis and computer simulation to study the rate at which transcriptional errors occur as a function of w. We find dramatic reduction in the error rate of transcription as w increases, especially for small values of w. The error reduction method provided by look-ahead occurs before hydrolysis and covalent linkage of rNTP to the nascent RNA chain, and is therefore distinct from error correction mechanisms that have previously been considered.
Keywords: transcription modeling, elongation dynamics of transcription, error-correcting mechanisms, Gillespie simulation, chemical master equation
1. Introduction
The elongation phase of transcription is the stage in which RNA polymerase incorporates ribonucleoside triphosphates (rNTPs) into the nascent RNA chain. In bacteria, the rate of chain elongation ranges from ~ 30 – 80 bases/second, and may depend on the rate at which the cell is growing [36]. The error rate of transcription in vitro is ~ 1 to 2 per 100,000 basepairs [30, 5, 18], but the error rate of transcription in vivo is much debated. Although RNA polymerase is highly conserved in all living organisms, the two most studied polymerases are bacterial polymerase from Escherichia coli and eukaryotic RNA polymerase II (Pol II). Almost all current data for studying errors in transcription are from studies of these two polymerases.
Of all the steps in transcription, the elongation stage is most amenable to a physical description [10]. Recent experimental advances in single molecule microscopy have produced high quality dynamic data [2, 11, 28] on the elongation dynamics of transcription. These advances have aided in developing accurate quantitative models of elongation. These models have mainly focused on transcription pausing and backtracking [3, 4, 27, 33, 37, 39, 40, 41]. The look-ahead model of transcription elongation dynamics proposed by Yamada and Peskin [40, 41] assumes that there exists a window of activity in which rNTPs bind reversibly to the template DNA strand before being hydrolyzed and linked covalently to the nascent RNA chain. An important parameter of the model is the window size, in bases, denoted by w. In the present paper, we study the influence of the window size w on the error rate of transcription.
Transcriptional fidelity is clearly important for the survival of cells and organisms. Several error-correcting mechanisms involving proofreading to maintain fidelity in transcription have been proposed [7, 13, 20, 42]. It has also been hypothesized that transcription elongation factors play an important role in enhancing transcriptional fidelity, including factors such as GreA, GreB and NusA [26, 31] in bacteria and TFIIS in eukaryotes [16, 29]. Several investigators have studied mutations of Pol II and their effects on transcriptional elongation rate, control and fidelity [6, 15, 17,21,22,23]. Here we investigate an error reduction mechanism that is inherent in the look-ahead model.
The distinction between error reduction and error correction is that error reduction occurs before an incorrect rNTP has been hydrolyzed and incorporated into the nascent RNA chain, whereas error correction occurs afterwards. Error reduction is thus inherently more economical than error correction. The two mechanisms are by no means mutually exclusive, and nature may well employ both of them. In this paper, however, we limit our considerations to the study of an error reduction mechanism that is inherent in the look-ahead concept.
2. The Model
This section contains a complete statement of the look-ahead model [41], as well as a description of the special case of the look-ahead model that is used in the present paper to assess the influence of look-ahead on the error rate of transcription. The model description here is in verbal form; the equations that govern the model appear in the following sections as needed, see also [41],
The look-ahead model assumes that there is a window of activity (subset of the transcription bubble formed by RNA polymerase) within which ribonucleoside triphosphates (rNTPs) can bind reversibly to the template strand of the DNA prior to being linked covalently to the nascent RNA chain. The sites within the window of activity where such reversible binding may occur are numbered j = 1,2, …, w. We assume that the binding and unbinding of rNTP to these different sites occur independently of whether any of the other sites are occupied or unoccupied, and also that the rate constants for these reactions depend only upon the chemical identity of the DNA base that is present at a site and upon the chemical identity of the rNTP that is binding or unbinding there, but not upon the location of the site within the window of activity.
Site #1 of the window of activity is special. We assume that it is the only site at which covalent linkage of an rNTP to the nascent RNA chain may occur. Therefore, covalent linkage of an rNTP can only occur when site #1 of the window of activity is occupied. The rate constant for covalent linkage may depend on which DNA base is present at site #1 and also on which rNTP is reversibly bound there.
When such covalent linkage does occur, we assume that this causes the RNA polymerase, and with it the transcription bubble and the window of activity, to move forward a distance of one basepair along the DNA. The result from the point of view of the window of activity is downward shift in the state of its sites. Let s(j) denote the state of site j immediately before the covalent linkage event, and let s′(j) denote the state of site j immediately afterwards. By “state” of a site we mean the following: (1) the identity of the template strand DNA base that is located at that site, (2) whether or not that DNA base has an rNTP reversibly bound to it, and finally (3) the identity of that rNTP if there is one present. The downward shift of the states of the sites within the window of activity that accompanies a forward move of the RNA polymerase is described as follows: s′(j) = s(j + 1) for j = 1,2, …, w − 1. Note that s(1) plays no role here, since the prior content of site #1 leaves the window of activity during a forward move of the RNA polymerase. In fact, the rNTP at site #1 is the one that is incorporated into the nascent RNA chain during (or immediately prior to) that forward move. Also, note that the above formula does not specify s′(w). Since site w is a new one that has just been drawn into the window of activity by the forward move, its DNA base is the one that was immediately downstream of the window of activity on the template strand immediately prior to the forward move, and we know that there cannot be any rNTP bound to the DNA base at site #w immediately following a forward move. This is because there has not been any time for such binding to occur.
In general, the look-ahead model as defined above has a large number of parameters. Specifically, there are 16 rate constants for reversible binding of an rNTP to a DNA base within the window of activity, 16 rate constants for the corresponding unbinding reactions, and 16 rate constants for the covalent linkage to the nascent RNA chain of an rNTP that is reversibly bound to the DNA base at site #1 of the window of activity. (The number 16 = 4 × 4 arises in each case because the rate constant in question depends on the chemical identity of the DNA base and also on the chemical identity of the rNTP, with 4 choices for each.) The window size w, which of course is a positive integer, is yet another parameter of the look-ahead model.
Since our purpose here is not to make realistic parameter choices, but rather to study the potential of look-ahead as an error-reduction mechanism, we restrict the parameters in such a way as to highlight the issue of fidelity of transcription in its simplest possible form. This is accomplished by treating all Watson-Crick base pairs as equivalent to each other, and likewise all non-Watson-Crick base pairs as equivalent to each other, while of course maintaining the distinction between a Watson-Crick and a non-Watson-Crick base pair. We regard any Watson-Crick base pair as “correct,” and therefore we use the subscript “C” on any rate constant that pertains to a Watson-Crick base pair. Similarly, we regard a non-Watson-Crick base pair as “incorrect,” and use the subscript “I” to denote any rate constant pertaining to such a miss-matched pair.
The parameters of the model are as follows:
w = window size in bases (a positive integer)
αC,αI = rate constants for binding (association) of the correct (C) or any particular incorrect (I) rNTP to an available DNA base at any particular site within the window of activity
βC,βI = rate constants for unbinding (dissociation) of a correct (C) or incorrect (I) rNTP that is reversibly bound within the window of activity
kC,kI = rate constants for hydrolysis and covalent linkage to the nascent RNA chain of an rNTP that is correctly (C) or incorrectly (I) bound at the site of incorporation (site #1) in the window of activity.
Note that for any given DNA base, there is only one correct rNTP that can bind to it, but there are three incorrect choices of rNTP. Therefore, the overall rate constant for incorrectly filling an empty site is 3αI. This factor of 3 is significant, since it biases the system in favor of errors and makes the problem of achieving high-fidelity transcription all the more difficult.
The six rate constants defined above are all first-order rate constants, with units of reciprocal time. By the law of mass action, the binding rate constants αC and αI are each proportional to the concentrations of their respective rNTPs. We assume here that the concentrations of the four rNTPs are equal, so that the symmetry stated above in which all Watson-Crick pairs are equivalent, and all non-Watson-Crick pairs are equivalent, is not disturbed by unequal ambient concentrations of the different rNTPs.
Although w may be any positive integer, it should be kept in mind that the look-ahead feature of the model is only present when w > 1. When there is more than one site within the window of activity, the model has a parallel-processing or assembly-line character, in which rNTPs can be lined up along the template strand of the DNA, so that with high probability an rNTP is already present when the RNA polymerase is ready to incorporate it into the nascent RNA chain. This parallel-processing feature obviously accelerates transcription. Its impact on the fidelity of transcription, if any, is not so readily apparent. We study this issue by comparing the error rate of the model with w = 1, which may be called the non-look-ahead case, to the error rate when w > 1.
3. Analysis of the Model
Analysis of the Error Rate when w = 1
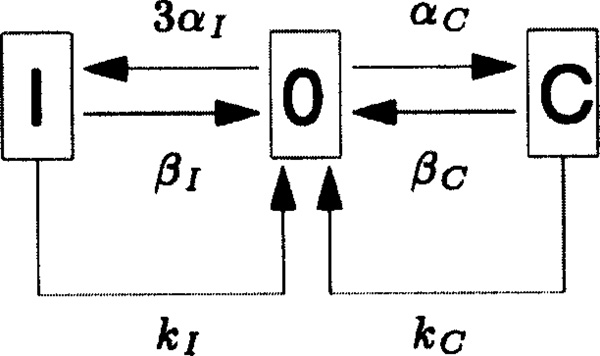
The case in which w = 1 is the special case of the look-ahead model in which there is no look-ahead feature. In this case, the window of activity contains a single site which may be in one of three states: it may have no rNTP bound, it may have the correct rNTP bound, or it may have an incorrect rNTP bound to the DNA base that is located within the window. The transitions among these possible states, together with their rate constants, are depicted in Figure 1. Note in particular the arrows with rate constants kI and kC in Figure 1. These depict the hydrolysis and irreversible covalent linkage to the nascent RNA chain of the incorrect or correct rNTP that is reversibly bound at the site. According to our assumptions, such covalent linkage is accompanied by a forward shift of the RNA polymerase molecule by one basepair along the DNA. Immediately after this forward move, there cannot be any rNTP bound to the DNA base that has just been brought into the window of activity. This explains why the arrows labeled by kI and kC point back to the empty site in Figure 1.
Figure 1.
The kinetic scheme of the look-ahead model in the special case w = 1. This is the case in which the model has no look-ahead feature, since there is only one site in the window of activity. The parameters αC and αI are the rate constants for binding a correct (C) or incorrect (I) rNTP to an empty site. The parameters βC and βI are the rate constants for unbinding of a correct (C) or incorrect (I) rNTP that is reversibly bound at that site, thus leaving the site empty again (state 0). The parameters kC and kI are the rate constants for the hydrolysis and covalent linkage to the nascent RNA chain of a correct (C) or an incorrect (I) rNTP that was reversibly bound at the site in question. Like an unbinding reaction, covalent linkage also results in an empty site, since it involves a forward move of the RNA polymerase to the next location along the DNA. Note that the rate constant for incorrectly filling an empty site is 3αI since there are always 3 possible incorrect choices for an rNTP.
We analyze the steady state of the kinetic scheme depicted in Figure 1. Let
pI = probability that an incorrect rNTP is reversibly bound
pC = probability that a correct rNTP is reversibly bound
1 − (pI + pC) = probability no rNTP is bound.
The steady state equations can be read directly from Figure 1. They are:
Putting these equations in standard form, we obtain:
The determinant is:
and we have:
Having solved for pI and pC, we can evaluate the error rate in the following way. By definition, the error rate E is given by
| (3.1) |
where υ is the number of bases transcribed per second, and υI is the number of bases transcribed incorrectly per second. From the kinetic scheme of Figure 1, it is clear that
For window size w = 1, we therefore have the following results:
where
Analysis of the Error Rate when w → ∞
Of course, the window size cannot be infinite, but it is instructive to consider this case, as it presents the look-ahead effect in its most pure form. Later on we shall use numerical methods to study the error rate as a function of w.
To analyze the limit of infinite window size, we adopt a different point of view from the one used in the previous section, and we think about the transient from one incorporation event to the next. Suppose that such an event has occurred at t = 0. We focus attention on first site of the window of activity. It has three possible states which we will denote by I, 0, and C where 0 denotes an empty site, i.e., a site to which no rNTP is bound. Because we are considering the limit w → ∞, the site in question has had plenty of time to equilibrate during its journey through the window. Throughout this journey, for all t < 0, the site in question has been at some location other than location #1. Because of this, the only reactions that could have occurred at this site during t < 0 are those of binding or unbinding of correct or incorrect rNTP. Therefore, the probabilities of the different states at the site which has just become site #1 immediately after a forward move are given by:
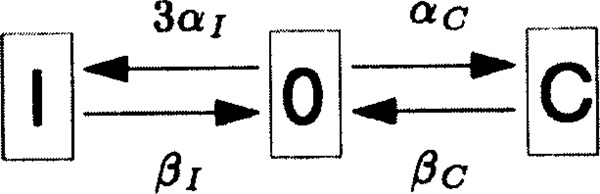
It is easy to check that the above probabilities are the normalized steady state of the kinetic scheme found in Figure 2. It is a special case of the one we considered above for w = 1; we can just set kC = kI = 0 and obtain the needed results.
Figure 2.
The kinetic scheme for any site other than site #1 of the window of activity. Here the only reactions are binding (α) and unbinding (β) of correct (C) or incorrect (I) rNTP. The state labeled 0 has no rNTP bound. In the limiting case of infinite window size, it may be assumed that the kinetic scheme shown here is in its steady state.
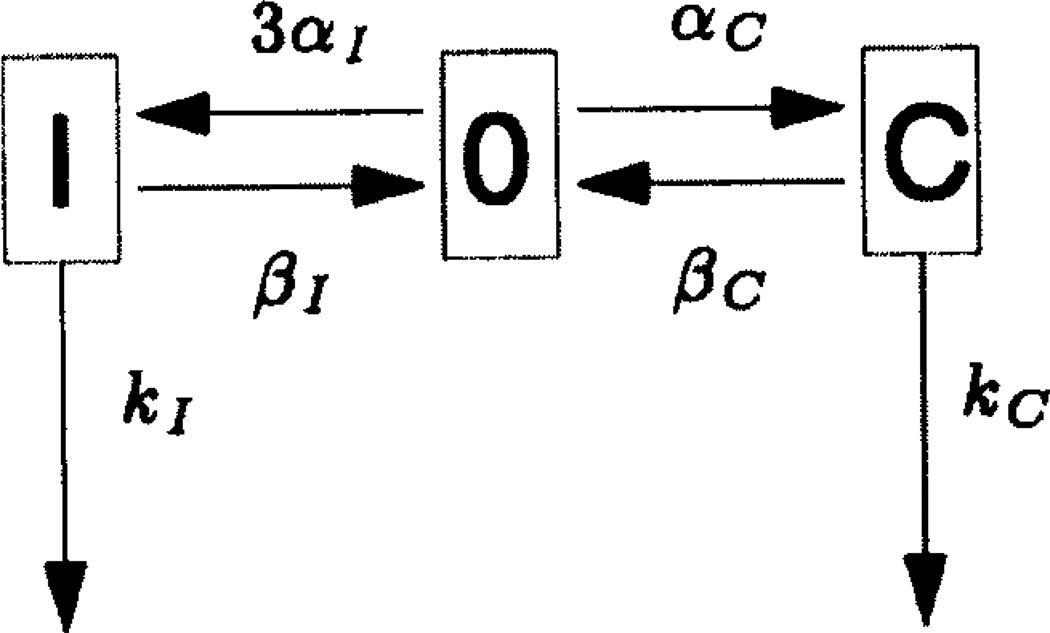
Now that we have the probabilities for the different states of the first site immediately after a forward move, we have to consider the time-dependent evolution of these probabilities. This evolution is governed by the transient kinetic scheme illustrated in Figure 3.
Figure 3.
The kinetic scheme of site #1 of the look-ahead model. The process shown here terminates when either of the vertical arrows is traversed, since this describes the hydrolysis and covalent linkage of a correct (C) or incorrect (I) rNTP to the nascent RNA chain. This causes the RNA polymerase to move forward along the DNA, and the state (I, 0, or C) of the site that was previously site #2 becomes that of site #1.
The differential equations of this scheme are given by:
The initial data have been given above. There are two ways to exit, i.e., by the covalent-linkage reactions with rate constants kI and kC, and the error rate E∞ is exactly equal to the probability of exit from state I, by the route with rate constant kI. It follows that
We do not actually need to solve the full initial-value problem in order to evaluate E∞. Instead, we can integrate all three equations from 0 to ∞ with respect to time. Since exit by one route or the other eventually occurs, pI(∞) = p0(∞) = pC(∞) = 0, and we get:
where . In matrix form, the above equations are as follows:
The determinant of this system is:
Of special interest is:
Since pI(0) + p0(0) + pC(0) = 1, the above result reduces to:
The error rate for w = ∞ is then given by:
Comparison with the w = 1 case shows that the first term is E1. Factoring this, we get:
| (3.2) |
Substituting our previous results for pC(0) and pI(0), this equation becomes:
Note that
We note in passing that the formula for the error rate in Eq. 3.2 is actually correct for any window size, provided that one substitutes into it the appropriate values of pC(0) and pI(0). These are the probabilities that, immediately after a forward move of the RNA polymerase molecule, the site that has just become site #1 of the window of activity already contains a correct or an incorrect rNTP, respectively. (These probabilities do not, in general, add up to 1, since the site may also be empty.) Unfortunately, the probabilities pC(0) and pI(0) are not easy to evaluate analytically for an arbitrary window size w. In the special case w = 1, we have pC(0) = PI(0) = 0, and the right-hand side of Eq. 3.2 reduces to E1, thus confirming the consistency of our analysis. In the special case w = ∞, we can also evaluate these probabilities from steady-state considerations, as has been done above.
Before turning to the case of general window size, for which numerical methods are needed, we summarize what can be learned about the effect of look-ahead on error rate by comparing the cases w = 1 and w = ∞. Recall that w = 1 is the non-look-ahead case, whereas w = ∞ is the case of maximal look-ahead.
An instructive special case is obtained by taking the limit βC → 0. This is the case in which a correct Watson-Crick pair is very stable and for practical purposes does not dissociate (within the time-scales that are relevant for transcription). Taking this limit in the formulae for E1 and E∞, we find that E1 has a nonzero limit but that E∞ → 0. In this special case, then, the limiting error rate at infinite window size is zero, even though the error rate remains non-zero with the same parameters in the absence of look-ahead. The reason for this effect is clear. When the window size is 1, there is always the possibility that an incorrect rNTP will bind and be incorporated before the correct rNTP happens to bind. With look-ahead, however, there is more time for the incorrect rNTP to dissociate and be replaced by a correct rNTP. Once the correct rNTP binds, it remains in place until it is incorporated (under the assumption that βC = 0). As the window size increases, the probability that any particular DNA base will already have the correct rNTP bound by the time it enters site #1 of the window of activity becomes overwhelming, since the binding of the correct rNTP is irreversible (under the assumption that βC = 0).
More generally, suppose that the six rate constants of the model fall into two groups that we shall call “fast” and “slow”. Let the fast rate constants be kC, αC, and βI, and let the slow rate constants be kI, αI, and βC. Thus, we assume that the fast reactions are the binding and incorporation of correct rNTP and the unbinding of incorrect rNTP, whereas the slow reactions are the binding and incorporation of incorrect rNTP and the unbinding of correct rNTP. These are certainly plausible assumptions. Let us assume, moreover, that there is a significant gap in the speeds of the fast and slow reactions, such that any reaction in the fast group is much faster than any reaction in the slow group. Under these conditions we can derive approximate expressions for the error rates when w = 1 and when w = ∞, as follows:
| (3.3) |
According to our assumptions about fast and slow reactions, the error rate is already small in the case w = 1, but it is further reduced by look-ahead as w → ∞ by the small factor the multiplies E1 on the right-hand side of the above equation.
Numerical Evaluation of the Error Rate of Transcription for Arbitrary Window Size w
Because of the limitations of mathematical analysis of the model for an arbitrary window size, we employed numerical methods to investigate the relationship between window size and error rate. We used two independent methods so that each would provide a check on the other.
Stochastic Simulation
The dynamics of the look-ahead model are described by a discrete-state continuous-time stochastic process, which can be simulated directly by an event-driven methodology that is often called the Gillespie method [8,9]. The details of the application of this methodology to the look-ahead model are described in [41].
Event-driven simulation jumps from one event to the next, where an event is the occurrence of one of the reactions of the model (binding, unbinding, or covalent linkage of an rNTP). Immediately after an event has occurred, the state of the model is ascertained, and a list of reactions that are possible in that state is constructed. The sum, K, of the rate constants of the possible reactions is then used to in the determination of the time interval until the next event by choosing that time interval at random with probability density K exp(−Kt). The particular event that next occurs is chosen (independently of the inter-event time interval) according to the rule that a reaction with rate constant k will be chosen with probability k/K.
In the computational experiments reported here, we simulated the transcription of a DNA strand 300,000 base pairs in length. The DNA sequence to be transcribed was chosen randomly, but note that the sequence actually has no significance when the rate constants of the model are chosen in the manner described above, such that all Watson-Crick base pairs are equivalent, all non-Watson-Crick base pairs are equivalent, and all rNTPs are present in equal concentrations. Results will be presented below, along with those obtained from the master-equation formulation, which is described next.
Master-Equation Formulation
The state of the system at any given time is given by a vector
where
Let δj be a vector of length w with components
Then the possible transitions of the system starting from state s are as follows. For binding events we have:
For unbinding events we have:
For forward movement (i.e. covalent linkage) we have:
In the expressions for the rate constants, factors like (Sj = 0) are Boolean expressions that evaluate to 1 if they are true, and 0 if they are false. They express the condition under which the transition may occur.
Next we define:
where
It is important to define R in this additive manner (instead of defining individual elements separately) since there may be more than one transition connect a given pair of states. For example,
In such cases, we want R to contain the sum of the rates of the different possible transitions from s → s′. This situation will happen automatically if we initialize R to 0 and then update R by adding the relevant element for each possible transition.
The size of R is 3w × 3w. In practice, we must assign an integer from 1, ⋯, 3w to each state. This is done according to the rule:
. Thus s1, ⋯, sw are the ternary digits of i − 1, but in the opposite of the usual order, since s1 is the least significant digit.
Note that the diagonal elements of R are zero. The rows of R give the rate constants for leaving a given state, and the columns give the rate constants for entering a given state.
In terms of R, the master equation is:
Let
Then,
and the steady-state solution, which we wish to obtain, is the normalized solution of
where the normalization is given by the following condition:
Once we have the normalized solution, we may evaluate:
Here υC is the rate at which bases are correctly incorporated into the nascent RNA chain, and υI is the rate at which bases are incorrectly incorporated into the nascent RNA chain. The forward velocity of the RNA polymerase (in bases transcribed per unit time) is:
and the error rate is:
Numerical Results
The parameters used to obtain the results reported here are stated in Table 1. These parameters are not meant to be realistic; they were chosen to illustrate the error-reduction capability of look-ahead. In particular βC is chosen much smaller than βI. This choice is motivated by the idea that a Watson-Crick base pair should be more stable (and hence, slower to dissociate) than a non-Watson-Crick base pair. The quantitative strength of this effect may be influenced by the local environment within the RNA polymerase molecule, and cannot therefore be estimated from physical-chemical measurements on the unbinding of rNTP from single stranded DNA in solution. The assumed smallness of βC is what makes look-ahead particularly effective as an error-reduction mechanism.
Table 1.
Parameter values used in the model simulations. These parameter values were chosen arbitrarily to illustrate the possible influence of look-ahead on the error rate of transcription.
| Parameter Symbol | Description of Parameter | Value |
|---|---|---|
| αC | Binding of Correct rNTP to empty site | 2 |
| αI | Binding Incorrect rNTP to empty site | 2 |
| βC | Unbinding of Correct rNTP from occupied site | 0.01 |
| βI | Unbinding of Incorrect rNTP from occupied site | 20 |
| kC | Hydrolysis and Covalent Linkage of Correct rNTP | 1 |
| kI | Hydrolysis and Covalent Linkage of Incorrect rNTP | 0.10 |
It should also be noted that we have chosen kI an order of magnitude smaller than kC. This is based on the assumption that the RNA polymerase molecule can detect whether the rNTP at site #1 of the window is correctly matched to the DNA base at that site, and will proceed to link the rNTP covalently to the nascent RNA chain at a higher rate if that rNTP is correct as opposed to incorrect. The assumed disparity between kI and kC is an error-reduction mechanism that operates independently of look-ahead.
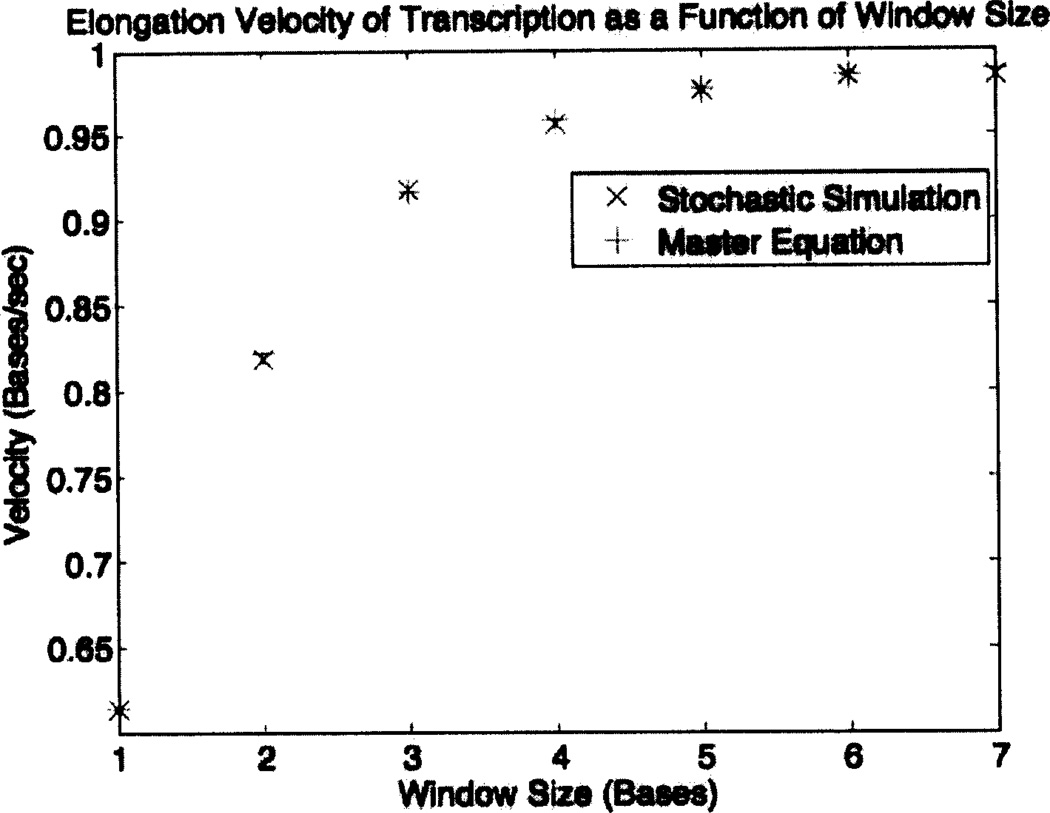
We have used the two computational methodologies described above to obtain the overall transcription rate and also the error rate of transcription, each as a function of the window size w, with all of the other parameters of the look-ahead model held fixed. The results concerning the overall rate of transcription are presented in Table 2 and Figure 4. They show, as expected, that transcription proceeds faster as the size of the look-ahead window increases. This is an expression of the parallel processing aspect of look-ahead. The larger the size of the look-ahead window, the higher the probability that an rNTP will already be present at site #1 of the window of activity immediately following a forward move of the RNA polymerase molecule. When this occurs, incorporation of that rNTP can proceed without waiting for the site to fill.
Table 2.
Transcription velocity (bases transcribed per unit time) as a function of window size. Comparison of the results of master-equation computations and stochastic simulations using a random DNA sequence comprised of 300,000 basepairs. In both cases, the parameters are those shown in Table 1. Because of the arbitrariness of these parameters, the absolute velocities are not significant. Note the agreement of the results obtained by the two methods, and the upward trend of the velocity as the window size increases.
| Window Size | Master-Equation Velocity | Stochastic Velocity |
|---|---|---|
| 1 | 0.613061 | 0.613510 |
| 2 | 0.822285 | 0.818836 |
| 3 | 0.916041 | 0.917765 |
| 4 | 0.958165 | 0.956782 |
| 5 | 0.976547 | 0.975784 |
| 6 | 0.984337 | 0.986362 |
| 7 | 0.987563 | 0.984162 |
Figure 4.
The elongation velocity of transcription is an increasing function of the size of the look-ahead window. This is an expression of the parallel processing feature of the look-ahead model [41]. Note the agreement of the results of the two methods of computation.
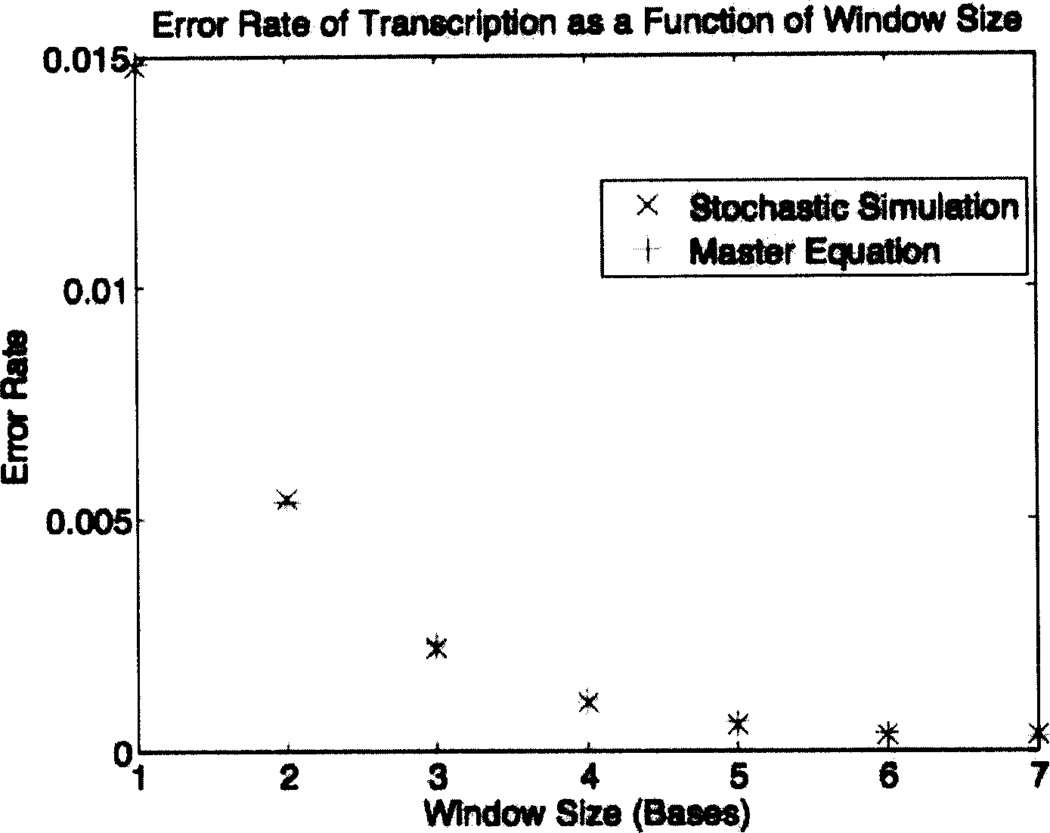
In many processes of everyday life, speed and accuracy are inversely related. One might expect on this basis that the increase in speed described above would be accompanied by a decrease in fidelity, but this is not the case. The results in Table 3 and Figure 5 show that the error rate of transcription decreases dramatically as the size of the look-ahead window increases. Note that most of this improvement in fidelity occurs for small window sizes, with saturation of the effect as the window size becomes large. It is quite remarkable that no price in terms of speed is paid for this improvement in fidelity. On the contrary, as discussed above, look-ahead increases the velocity of transcription.
Table 3.
Error rate of transcription as a function of window size. Comparison of the results of master-equation computations and stochastic simulations using a random DNA sequence comprised of 300,000 basepairs. In both cases, the parameters are those shown in Table 1. Note the agreement of the results obtained by the two methods, and the strongly downward trend of the error rate as the window size increases, especially for small window sizes.
| Window Size | Master-Equation Error Rate | Stochastic Error Rate |
|---|---|---|
| 1 | 0.014850 | 0.014700 |
| 2 | 0.005378 | 0.005423 |
| 3 | 0.002284 | 0.002193 |
| 4 | 0.001083 | 0.001023 |
| 5 | 0.000591 | 0.000536 |
| 6 | 0.000388 | 0.000393 |
| 7 | 0.000305 | 0.000316 |
Figure 5.
The error rate of transcription is a strongly decreasing function of the size of the look-ahead window, especially for small window sizes. This is because the look-ahead mechanism allows time for the correct complementary rNTP to be selected by a DNA base before that DNA base reaches site #1 of the window of activity, where hydrolysis and covalent linkage of the rNTP to the nascent RNA chain occur. Note the agreement of the results of the two methods of computation.
The two drastically different methods of calculation employed here (stochastic simulation and solution of the steady-state master equation) give essentially the same results. This strongly suggests that the speed and error rate of transcription are being calculated correctly (within the framework of the assumptions of the look-ahead model).
Discussion, Conclusions, and Future Work
In this paper, we have studied the influence of look-ahead [41] on the error rate of transcription, and have shown that dramatic reduction in the error rate can be achieved by making the number of sites within the look-ahead window larger than one. Large look-ahead windows are not needed for this purpose. Indeed, the improvement as the window size increases is greatest for small window sizes and the fidelity gradually saturates (i.e., stops improving) as the window size increases further. The predicted improvement in fidelity is achieved by the look-ahead mechanism with no reduction in speed; on the contrary, the speed of transcription is also enhanced by look-ahead.
The error-reduction mechanism enabled by look-ahead is different from error-correcting mechanisms that have been considered previously. The fundamental difference is that the look-ahead mechanism, as its name implies, acts before the metabolically costly steps of hydrolysis and covalent linkage of an rNTP to the nascent RNA chain. In this sense, look-ahead is an economical mechanism that prevents errors so that they do not need to be corrected after the fact. Error reduction (e.g., via look-ahead) and error-correction are by no means incompatible, and one would guess that nature would exploit both possibilities in order to make the error rate of transcription as low as possible.
The look-ahead model is fundamentally a chemical-kinetic scheme, and the error-reduction mechanism of look-ahead accordingly resembles kinetic proofreading, which was independently proposed by Hopfield and Ninio [14, 25]. The concept of kinetic proofreading has been invoked to explain the low error rate of translation as well as other physiological processes such as T-cell receptor signal transduction, signal transduction specificity and RecA protein binding dynamics [1, 24, 12, 32, 35]. A distinctive feature of look-ahead, however, is the use of several sites, assembly-line fashion, to allow more time for discrimination to occur.
Concerning the elongation dynamics of transcription, recent papers by Voliotis et. al. [37, 38] have explored the implications of a hypothesized kinetic proofreading mechanism. Specifically, the backtracking of the RNA polymerase can reverse the covalent linkage of an incorrect base in the nascent chain. Another variation of this mechanism was proposed by [18, 19, 20] in which error correction occurs after the hydrolysis but before the covalent linkage of the rNTP into the nascent RNA chain. For comparison, note that no distinction is made in the current form of the look-ahead model between the hydrolysis step and the covalent linkage step. A summary of various mechanisms that have been proposed either to correct or to reduce errors during transcription can be found in Table 4.
Table 4.
Possible fidelity mechanisms during transcriptional elongation. This table summarizes mechanisms that have been proposed either to reduce or to correct errors during transcriptional elongation. The look-ahead model is an example of an error reduction mechanism, in which errors are avoided before the incorrect ribonucleotide triphosphate (rNTP) is hydrolyzed and incorporated into the nascent RNA chain. This mechanism is in contrast to error-correcting mechanisms such as kinetic proofreading [14, 25] and hydrolysis rejection. In hydrolysis rejection, the rejection of an incorrect rNTP is done after the hydrolysis step, but before the covalent linkage. Finally, there are proposed error-correcting mechanism that operate after the incorrect rNTP has already been incorporated into the nascent RNA chain. The polymerase expends energy in the form of ATP to actively correct for such an error. The precise mechanism for this kind of correction remains unknown but is thought to involve additional enzymes [28].
An important project for future work is to devise experiments and mathematical/computational methods to determine realistic parameters for the look-ahead model. This will almost certainly require departure from the idealized case considered in the present paper, in which the only distinction made was that between a Watson-Crick base pair and a non-Watson-Crick base pair. In reality it is more likely that each of the 16 possible base pairs (one choice of DNA base and one choice of rNTP) has its own particular binding rate constant, unbinding rate constant, and covalent linkage rate constant. Although parameter fitting was done in [41], that paper considered only a special case in which unbinding was neglected and only correct Watson-Crick pairs were ever allowed to form. The problem of parameter fitting in the general case is of course much more difficult. The task may be somewhat eased, however, by the experimental ability to control the DNA sequence that is being transcribed as well as the ambient concentrations of the different rNTP, and to count the errors of transcription that actually occur.
Acknowledgements
We thank the organizers of the 2009 Shanks Conference on Mathematical Sciences in Biology and Biomedicine at Vanderbilt University for the opportunity to present this research. We would like to acknowledge the support and advice of Professor Daniel B. Forger. The first author was supported on an NSF-IGERT Grant DGE-033366, and the second author was supported in part by NIH Grant 1P50GM071558-01A2 to the Systems Biology Center in New York. Soli Deo Gloria.
References
- 1.Alon A. An introduction to systems biology: design principles of biological circuits. Boca Raton: Chapman and Hall; 2007. [Google Scholar]
- 2.Abbodanzieri E, Greenleaf W, Shaevitz J, Landick R, Block S. Direct observation of base-pair stepping by RNA polymerase. Nature. 2005;438:460–465. doi: 10.1038/nature04268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bai L, Fulbright R, Wang M. Mechanochemical kinetics of transcription elongation. Phys. Rev. Lett. 2007;98(No. 6):068103. doi: 10.1103/PhysRevLett.98.068103. [DOI] [PubMed] [Google Scholar]
- 4.Bar-Nahum G, Epshtein V, Ruckenstein A, Rafikov R, Mustaev A, Nudler E. A ratchet mechanism of transcription elongation and its control. Cell. 2005;120(No. 2):183–193. doi: 10.1016/j.cell.2004.11.045. [DOI] [PubMed] [Google Scholar]
- 5.Blank A, Gallant J, Burgess R, Loeb L. An RNA polymerase mutant with reduced accuracy of chain elongation. Biochemistry. 1986;25(No. 20):5920–5928. doi: 10.1021/bi00368a013. [DOI] [PubMed] [Google Scholar]
- 6.Chen Y, Chafin D, Price D, Greenleaf A. Drosophila RNA polymerase II mutants that affect transcription elongation. Jour. Biol. Chem. 271;1996(No. 11):5993–5999. [PubMed] [Google Scholar]
- 7.Eichhorn G, Chuknyisky P, Butzow J, Beal R, Garland C, Janzen C, Clark P, Tarien E. A structural model for fidelity in transcription. Proc. Natl. Acad. Sci. 1994;91(No. 16):7613–7617. doi: 10.1073/pnas.91.16.7613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gillespie D. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comp. Phys. 1976;22(No. 4):403–434. [Google Scholar]
- 9.Gillespie D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81(No. 25):2340–2361. [Google Scholar]
- 10.Greive S, von Hippel P. Thinking quantitatively about transcriptional regulation. Nat. Rev. Mol. Cell Biol. 2005;6:221–232. doi: 10.1038/nrm1588. [DOI] [PubMed] [Google Scholar]
- 11.Herbert K, Greenleaf W, Block S. Single-molecule studies of RNA polymerase: motoring along. Annu. Rev. Biochem. 2008;77:149–176. doi: 10.1146/annurev.biochem.77.073106.100741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hlavacek W, Redondo A, Metzger H, Wofsy C, Goldstein B. Kinetic proofreading models for cell signaling predict ways to escape kinetic proofreading. Proc. Natl. Acad. Sci. 2001;98(No. 13):7295–7300. doi: 10.1073/pnas.121172298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Holmes S, Santangelo T, Cunningham C, Roberts J, Erie D. Kinetic investigation of Escherichia coli RNA polymerase mutants that influence nucleotide discrimination and transcription fidelity. Jour. Biol. Chem. 2006;281(No. 27):18677–18683. doi: 10.1074/jbc.M600543200. [DOI] [PubMed] [Google Scholar]
- 14.Hopfield J. Kinetic proofreading: a new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl. Acad. Sci. 1974;71(No. 10):4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Howe K, Kane C, Ares A. Perturbation of transcription elongation influences the fidelity of internal exon inclusion in saccharomyces cerevisiae. RNA. 2003;9(No. 8):993–1006. doi: 10.1261/rna.5390803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jeon C, Agarwal K. Fidelity of RNA polymerase II transcription controlled by elongation factor TFIIS. Proc. Natl. Acad. Sci. 1996;93(No. 24):13677–13682. doi: 10.1073/pnas.93.24.13677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kireeva M, Nedlialkov Y, Cremona G, Purtov Y, Lubkowska L, Malagon F, Burton Z, Strathern J, Kashlev M. Transient reversal of RNA polymerase II active site closing controls fidelity of transcription elongation. Mol. Cell. 2008;30(No. 5):557–566. doi: 10.1016/j.molcel.2008.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Libby R, Gallant J. The role of RNA polymerase in transcriptional fidelity. Mol. Microbiol. 1991;5(No. 5):999–1004. doi: 10.1111/j.1365-2958.1991.tb01872.x. [DOI] [PubMed] [Google Scholar]
- 19.Libby R, Gallant J. Phosphorolytic error correction during transcription. Mol. Microbiol. 1994;12(No. 1):121–129. doi: 10.1111/j.1365-2958.1994.tb01001.x. [DOI] [PubMed] [Google Scholar]
- 20.Libby R, Nelson L, Calvo J, Gallant J. Transcriptional proofreading in escherichia coli. EMBO Jour. 1989;8(No. 10):3153–3158. doi: 10.1002/j.1460-2075.1989.tb08469.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Malagon F, Kireeva M, Shafer B, Lubkowska L, Kashlev M, Strathern J. Mutations in the saccharomyces cerevisiae RPB1 gene conferring hypersensitivity to 6-Azauracil. Genetics. 2006;172(No. 4):2201–2209. doi: 10.1534/genetics.105.052415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mason P, Struhl K. Distinction and relationship between elongation rate and processivity of RNA polymerase II in vivo. Mol. Cell. 2005;17(No. 6):831–840. doi: 10.1016/j.molcel.2005.02.017. [DOI] [PubMed] [Google Scholar]
- 23.de la Mata M, Alonso C, Kadener S, Fededa J, Blaustein M, Pelisch J, Cramer P, Bentley D, Kornblihtt A. A Slow RNA Polymerase II Affects Alternative Splicing in Vivo. Mol. Cell. 2003;12(No. 2):525–532. doi: 10.1016/j.molcel.2003.08.001. [DOI] [PubMed] [Google Scholar]
- 24.McKeithan T. Kinetic proofreading in T-cell receptor signal transduction. Proc. Natl. Acad. Sci. 1995;92(No. 11):5042–5046. doi: 10.1073/pnas.92.11.5042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ninio J. Kinetic amplification of enzyme discrimination. Biochimie. 1975;57(No. 5):587–595. doi: 10.1016/s0300-9084(75)80139-8. [DOI] [PubMed] [Google Scholar]
- 26.Roberts J, Shankar S, Filter J. RNA polymerase elongation Ffactors. Annu. Rev. Microbiol. 2008;62:211–233. doi: 10.1146/annurev.micro.61.080706.093422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Roussel J, Zhu R. Stochastic kinetics description of a simple transcription model. Bull. Math. Biol. 2006;68(No. 7):1681–1713. doi: 10.1007/s11538-005-9048-6. [DOI] [PubMed] [Google Scholar]
- 28.Shaevitz J, Abbondanzieri E, Landick R, Block S. Backtracking by single RNA polymerase molecules observed at near-base-pair resolution. Nature. 2003;426:684–687. doi: 10.1038/nature02191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sims R, Belotserkovskaya R, Reinberg D. Elongation by RNA polymerase II: the short and long of it. Genes Dev. 2004;18:2437–2468. doi: 10.1101/gad.1235904. [DOI] [PubMed] [Google Scholar]
- 30.Springgate C, Loeb L. On the fidelity of transcription by escherichia coli ribonucleic acid polymerase. J. Mol. Biol. 1975;97(No. 4):577–591. doi: 10.1016/s0022-2836(75)80060-x. [DOI] [PubMed] [Google Scholar]
- 31.Stepanova E, Lee J, Ozerova M, Semenova E, Datsenko K, Wanner B, Severinov K, Borukhov S. Analysis of promoter targets for Escheichia coli transcription elongation factor GreA in vivo and in vitro. J. Bateriol. 2007;189(No. 24):8772–8785. doi: 10.1128/JB.00911-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Swain P, Siggia E. The role of proofreading in signal transduction specifity. Biophys. J. 2007;82(No. 6):2928–2933. doi: 10.1016/S0006-3495(02)75633-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tadigotla V, O’Maoileidigh D, Sengupta A, Epshtein V, Ebright R, Nudler E, Ruckenstein A. Thermodynamic and kinetic modeling of transcriptional pausing. Prof. Natl. Acad. Sci. 2006;103(No. 12):4439–4444. doi: 10.1073/pnas.0600508103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Thomas J, Platas A, Hawley D. Transcriptional fidelity and proofreading by RNA polymerase II. Cell. 1998;93(No. 4):627–637. doi: 10.1016/s0092-8674(00)81191-5. [DOI] [PubMed] [Google Scholar]
- 35.Tlusty T, Bar-Ziv R, Libchaber A. High-fidelity DNA sensing by protein binding fluctuations. Phys. Rev. Lett. 2004;93(No. 25):2581031. doi: 10.1103/PhysRevLett.93.258103. [DOI] [PubMed] [Google Scholar]
- 36.Vogel U, Jensen K. The RNA chain elongation rate in escherichia coli depends on the growth rate. J. Bacteriol. 1994;176(No. 10):2807–2813. doi: 10.1128/jb.176.10.2807-2813.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Voliotis M, Cohen N, Molina-Paris C, Liverpool T. Fluctuations, pauses, and backtracking in DNA transcription. Biophys. J. 2008;94(No. 2):334–348. doi: 10.1529/biophysj.107.105767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Voliotis M, Cohen N, Molina-Paris C, Liverpool T. Backtracking and error correction in DNA transcription in The Art and Science of Statistical Bioinformatics. Leeds: Leeds University Press; 2008. pp. 104–107. [Google Scholar]
- 39.Xie P. A dynamic model for transcription elongation and sequence-dependent short pauses by RNA polymerase. BioSystems. 2008;93:199–210. doi: 10.1016/j.biosystems.2008.04.013. [DOI] [PubMed] [Google Scholar]
- 40.Yamada Y, Peskin C. A chemical kinetic model of transcriptional elongation. LANL ArXiv. 2006 q-bio.BM/0603012. [Google Scholar]
- 41.Yamada Y, Peskin C. A look-ahead model for the elongation dynamics of transcription. Biophys. J. 2009;96(No. 8):3015–3031. doi: 10.1016/j.bpj.2008.12.3955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zenkin N, Yuzenkova Y, Severinov K. Transcript-assisted transcriptional proofreading. Science. 2006;313(No. 5786):518–520. doi: 10.1126/science.1127422. [DOI] [PubMed] [Google Scholar]