Abstract
In this article, we use longitudinal morphometry (shape and size) measures of hippocampus in subjects with mild dementia of Alzheimer type (DAT) and nondemented controls in logistic discrimination. The morphometric measures we use are volume and metric distance measures at baseline and follow-up (two years apart from baseline). Morphometric differences with respect to a template hippocampus were measured by the metric distance obtained from the large deformation diffeomorphic metric mapping (LDDMM) algorithm. LDDMM assigns metric distances on the space of anatomical images, thereby allowing for the direct comparison and quantization of morphometric changes. We also apply principal component analysis (PCA) on volume and metric distance measures to obtain principal components that capture some salient aspect of morphometry. We construct classifiers based on logistic regression to distinguish diseased and healthy hippocampi (hence potentially diagnose the mild form of DAT). We consider logistic classifiers based on volume and metric distance change over time (from baseline to follow-up), on the raw volumes and metric distances, and on principal components from various types of PCA analysis. We provide a detailed comparison of the performance of these classifiers and guidelines for their practical use. Moreover, combining the information conveyed by volume and metric distance measures by PCA can provide a better biomarker for detection of dementia compared to volume, metric distance, or both.
Keywords: computational anatomy, dementia of Alzheimer Type, hippocampus, large deformation diffeomorphic metric mapping (LDDMM), logistic discrimination, morphometry, principal component analysis
1 Introduction
Alzheimer’s disease (AD) at its early stages is characterized by the accumulation of neurofibrillary tangles and amyloid plaques within the hippocampus [1–5]. Neuronal damage and death associated with this accumulation [6] may manifest as macroscopic gray matter losses, which are detectable in living subjects using currently available magnetic resonance imaging (MRI). Specifically, volume losses within the hippocampus have been reported in individuals with mild AD [7–12], and hippocampal volume losses have been shown to correlate with AD neuropathology [13]. Progressive atrophy of the entire brain has been observed in AD cases [14]. However, due to the complexity of the human brain and the non-uniform distribution of AD neuropathology early in the course of disease, detailed examination of specific brain regions (e.g., hippocampus) known to be affected early in the AD disease process may be preferred for distinguishing preclinical and very mild forms of AD from normal aging [15–17].
The development of Computational Anatomy (CA) has enabled us to quantify and compare brain volumes and shapes in neurological diseases [18–23]. These methods combine image-based diffeomorphic maps between MR scans with representations of brain structures as smooth manifolds using mathematical principles of general pattern theory [16–17, 21, 24–25] and may be especially sensitive to changes in brain structures associated with early forms of AD. Using such methods, we previously demonstrated that the combined assessment of hippocampal volume loss and shape deformity optimally distinguished individuals with very mild dementia of the Alzheimer type (DAT) from both cognitively normal elderly individuals [8, 26]. These methods were also extended to quantify changes in neuroanatomical volumes and shapes within the same individuals over time [27].
Other longitudinal neuroimaging analyses of hippocampal structures in individuals with AD have also emerged [28–39]. In particular, studies of shape have been carried out by comparison of anatomical structures via vector field displacements generated by large deformation diffeomorphic metric mapping (LDDMM) between two shapes [40–41]. The construction of such a metric space allows one to quantify similarities and differences between anatomical shapes [42–43]. This is the vision laid out by D’Arcy W. Thompson almost one hundred years ago [44].
In this paper, we present an analysis based on generating metric distances of shapes relative to a template [40–41]. This approach could provide us a powerful tool in analyzing subtle shape changes over time with considerably less computational load. In previous work [27, 45], we compared rates of change in hippocampal volume and shape in subjects with very mild DAT and age and gender matched cognitively normal elderly individuals. The change in hippocampal shape over time was defined as a residual vector field resulting from rigid-body motion registration, and changes in patterns were analyzed via a principal components analysis (PCA) of these residual vectors. In this study, we compute and analyze metric distances based on the data used in [27] and [26]. We provide the details of mathematical methodology to obtain the metric distances in the Appendix section and statistical methodology for our analysis in [26]. For two groups of hippocampi, we estimate their metric distances to a template. These distances are computed on baseline and follow-up scans in both groups. We then implement PCA on the morphometric measures of volume and metric distances in order to extract salient features of morphometry. We use the principal components obtained from PCA in logistic discrimination and compare the performance of the logistic classifiers and provide guidelines for diagnostic purposes. We demonstrate that the logistic classifier based on principal components from PCA analysis has the best performance in discrimination of diseased hippocampi from healthy ones. We briefly describe the data set in Section 2.1, statistical methods we employ in Section 2.2, results in Section 3, discussion in Section 4, and computation of metric distances via LDDMM in the Appendix.
2 Methods
2.1 Subjects and Data Acquisition
A detailed description of subject recruitment can be found in [27]. Briefly, semi-structured interviews were conducted annually by experienced clinicians with informants and the subjects to assess each subject’s cognitive and functional performance; neurological examinations were also obtained. The clinician determined 3 the presence or absence of dementia and, when present, its severity with the clinical dementia rating (CDR). Overall CDR score of 0 indicates no dementia, while CDR scores of 0.5, 1, 2, and 3 indicate very mild, mild, moderate, and severe dementia, respectively [46]. CDR assessments have been shown to have an inter-rater reliability of κ =0.74 (weighted kappa coefficient [47] κ of 0.87) [48], which has been confirmed in multi-center dementia studies [49]. Elderly subjects with no clinical evidence of dementia (i.e., CDR0) have been confirmed with normal brains at autopsy with 80% accuracy; i.e., approximately 20% of such individuals show evidence of AD [50]. CDR0.5 subjects have subtle cognitive impairment, and 93% of them progress to more severe stages of illness (i.e., CDR score larger than 0.5) and show neuropathological signs of AD at autopsy [50–52]. Although elsewhere the CDR0.5 individuals in our sample may be considered to have mild cognitive impairment (MCI) [53], they fulfill our diagnostic criteria for very mild DAT and at autopsy overwhelmingly have neuropathological AD [54].
This study included previously generated longitudinal hippocampal surface data from 18 DAT subjects (CDR 0.5, 11 male, 7 female, 74±4.4 years old) and 26 age-matched nondemented subjects (CDR 0, 12 male and 14 female, 73±7.0 years old) ([55]). These data were generated at 2 (range 1–2.6) and 2.2 (range 1.4–4.1) years apart, respectively. MR data from an additional nondemented subject (male, age = 69, same scanning protocol) was used as a neuroanatomical template; for details see [55]. Expert-produced manual outlines of the left and right hippocampus in the template scan created from using methods previously described [56–57] were used as binary templates.
For the left and right hippocampal surfaces of each subject generated at baseline and follow-up, binary volumetric images were created by flood filling the inside of the surfaces, followed by smoothing with a Gaussian filter of 9×9×9 -voxel window and one voxel standard deviation. Before converting to volumetric binary images, each individual hippocampal surface was first scaled by a factor of 2 and aligned with the template surface, which was also scaled by a factor of 2, by a rigid-body rotation and translation. We showed that mapping accuracy could be enhanced at higher resolutions because of smaller voxels – voxels at the periphery of the structure (i.e., surface) account for much more of the structural volume at 1 mm3 voxel resolution versus 0.5 mm3 [56]. The left hippocampi at baseline for CDR0.5 subjects are labeled as LB-CDR0.5 and those at follow-up are labeled as LF-CDR0.5; CDR0 subjects are labeled as LB-CDR0 and LF-CDR0 accordingly. Similar labeling is done for the right hippocampi.
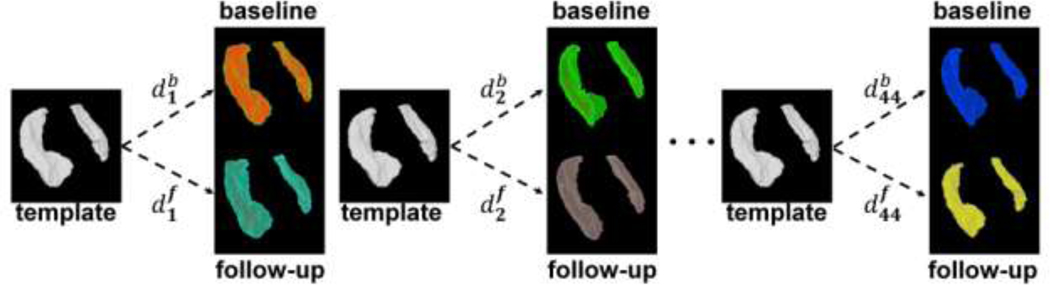
The LDDMM algorithm yields metric distances in left hemisphere at baseline (b) and at follow-up (f) denoted , respectively, and in the right hemisphere at baseline (b) and at follow-up (f) denoted , respectively, for k =1,…,44, as illustrated in Figure 1 (see also Appendix). We also have the volume measures of hippocampi similarly labeled as for k = 1,…,44. The metric distance measures the morphometric difference between a given hippocampus and a known healthy one.
Figure 1.
Generation of metric distances based on binary images for subjects k = 1,2,…,44 at baseline (b) and at follow-up (f).
2.2 Statistical Methods
We apply logistic discrimination with metric distances and volumes, since the diagnosis has only two levels, namely CDR0 and CDR0.5. We use logistic regression to estimate the risk or probability of having DAT (for more on logistic regression and logistic discrimination, see [58] and [59], respectively). We consider the logistic model with the response logit p = log[p/(1−p)] where p = P(Y = 1) (i.e., the probability that the subject is diagnosed with CDR0.5). First we model logit p with all volume and metric distance measures as the predictor variables (called the full model). On this full model, we choose a reduced model by a two-step model selection procedure: First an Akaike Information Criteria (AIC) in a stepwise algorithm, and a stepwise backward elimination procedure on the resulting model [60]. We stop the elimination procedure when all the remaining variables are significant at α = 0.05 level. Based on the final model with significant predictors, we apply logistic discrimination as follows: If the estimated probability is larger than a prespecified value p0, the subject is classified as CDR0.5, otherwise the subject is classified as CDR0 (i.e., healthy). This threshold probability p0 can also be optimized with respect to a cost function which incorporates correct classification rates, sensitivity, and/or specificity [61]. We apply the same model selection procedure and construct the logistic classifier as described above in each of the models we consider.
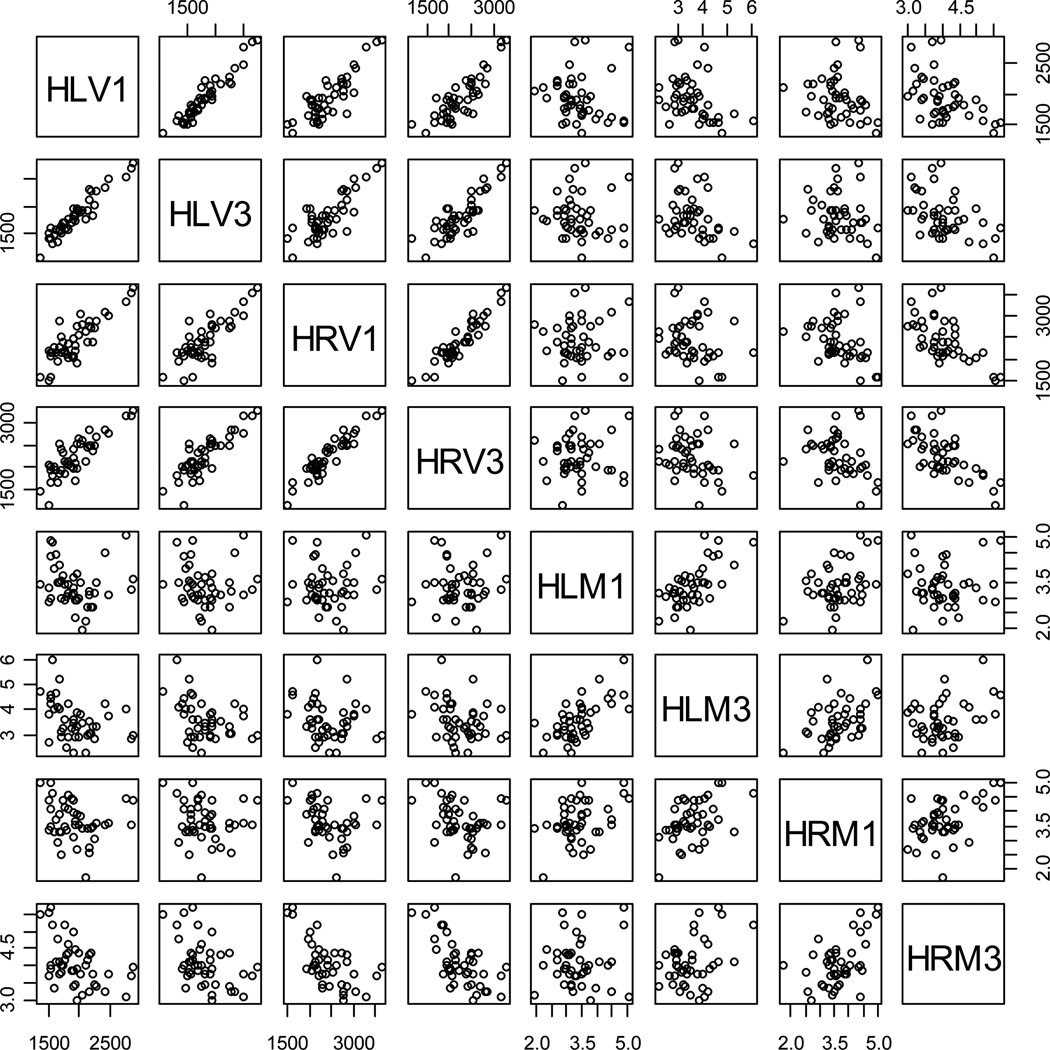
The volume and metric distance measures tend to be correlated, since they measure related (but not the same) aspects of morphometry. See Figure 2 for the scatter plot matrix for each pair of the variables where the volume measures seem to be highly correlated with each other and metric distance measures are also correlated with each other but to a smaller extent. We perform PCA to obtain a set of uncorrelated variables that represent some identifiable aspect of the morphometry [59, 62]. We apply three types of PCA on these variables. In the first one, we perform PCA on the metric distances and volumes of hippocampi with eigenvalues based on the covariance matrix. However, since the volumes are in mm3 and metric distances are unitless, the data are not to scale (the volumes are recorded in thousands while metric distances in unitary digits and variance of volumes is much larger than that of metric distances). To remove the influence of the scale, we apply two transformations on the variables. First, we multiply the metric distance values by 1000 to make the location and scale of the metric distance to be on the same order with those of volumes. Secondly, we standardize each variable so that each variable has the same scale, that is, PCA is applied with eigenvalues based on the correlation matrix. Then we perform logistic regression based on the principal components obtained from these PCA types.
Figure 2.
Pair plots of the volume and metric distance measures for the hippocampi at baseline and follow-up. HLV: volume of left hippocampus; HRV: volume of right hippocampus; HLM: metric distance for left hippocampus; HRM: metric distance for right hippocampus. The numbers 1 and 3 stand for year 1 (i.e., baseline) and year 3 (i.e., follow-up), respectively.
We also estimate the empirical cumulative distribution functions (cdf) of the metric distances and compare them pairwise (i.e., compare the cdfs of metric distances for two independent groups at a time) by Kolmogorov-Smirnov (K-S) test [63]. In all the two-sample comparisons, when a test yields significant result we also provide its direction, hence report a p -value based on the one-sided version of the test. On the contrary, when a test yields insignificant results, then there is no direction to indicate (i.e., there is no significant difference between the two groups) and hence the two-sided p -value is reported.
3 Results
3.1 Principal Component Analysis on Metric Distances and Volumes
When PCA is applied on the volumes and metric distances (i.e., on the variables ), we find that the first principal component accounts for almost all (~ 91%) of the variation (see Table 1). Let PCi stand for principal component i, for i = 1,2,…,8. Considering the variable loadings, we see that PC1 seems to be the volume (i.e., size) component, PC2 is the contrast between left and right hippocampal volumes, PC3 is the contrast between baseline and follow-up hippocampal volumes, PC4 is the volume contrast between baseline left hippocampi and follow-up left hippocampi, PC5 is the metric distance (i.e., shape) component, PC6 is the contrast between left and right hippocampus distances, PC7 is the contrast between baseline and follow-up metric distances, and PC8 is the contrast between baseline left and follow-up right metric distances with baseline right and follow-up left distances. There seems to be a clear distinction between principal components associated with volume and metric distances: the first four principal components are associated with the volume measures and account for almost all the variation, while the last four principal components are associated with metric distances, and explain only a negligible portion of the variation.
Table 1.
The importance of principal components and variable loadings from the principal component analysis (PCA) with eigenvalues based on the covariance matrix. HLV1 (3): volume of left hippocampus at baseline (follow-up); HLM1 (3): metric distance of left hippocampus at baseline (follow-up); HRV1 (3): volume of right hippocampus at baseline (follow-up); HRM1 (3): metric distance of right hippocampus at baseline (follow-up); PCj stands for principal component j for j = 1,2,…,8 ; Prop. Var: proportion of variance explained by the principal components; Cum. Prop: cumulative proportion of the variance explained by the particular principal component.
| PCA with Covariance (for volume and metric distances) | ||||||||
| Importance of Components | ||||||||
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | |
| Prop. Var | .9091 | .0637 | .0196 | .0075 | ~ .0 | ~ .0 | ~ .0 | ~ .0 |
| Cum. Prop. | .9091 | .9729 | .9924 | ~1 .0 | ~1 .0 | ~1 .0 | ~1 .0 | 1 .0 |
| Variable Loadings | ||||||||
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | |
| HLV1 | 0.42 | 0.50 | 0.23 | 0.72 | ~ . 0 | ~ .0 | ~ .0 | ~ .0 |
| HLV3 | 0.43 | 0.62 | −0.10 | −0.65 | ~ . 0 | ~ .0 | ~ .0 | ~ .0 |
| HRV1 | 0.58 | −0.50 | 0.62 | −0.18 | ~ . 0 | ~ .0 | ~ .0 | ~ .0 |
| HRV3 | 0.55 | −0.34 | −0.75 | 0.16 | ~ .0 | ~ .0 | ~ .0 | ~ .0 |
| HLM1 | ~ .0 | ~ .0 | ~ .0 | ~ .0 | −0.56 | 0.43 | −0.24 | 0.67 |
| HLM3 | ~ .0 | ~ .0 | ~ .0 | ~ .0 | −0.64 | 0.25 | 0.50 | −0.52 |
| HRM1 | ~ .0 | ~ .0 | ~ .0 | ~ .0 | −0.48 | −0.55 | −0.63 | −0.28 |
| HRM3 | ~ .0 | ~ .0 | ~ .0 | ~ .0 | −0.21 | −0.67 | 0.55 | 0.45 |
When we perform PCA on metric distances and volumes of hippocampi with eigenvalues based on the correlation matrix, the first three principal components account for 90% of the variation (see Table 2). Comparing the variable loadings (not presented), we do not have a clear separation between volume and metric distance components, but, for example, the PC6 is the contrast between left and right volumes, and PC7 is the contrast between baseline and follow-up distances. When we perform PCA on volumes and scaled metric distances (i.e., 1000 × metric distances) of hippocampi with eigenvalues based on the covariance matrix, the first three principal components account for 87% of the variation (see Table 2). Similar to the PCA on correlation, we do not have a clear distinction of factors in principal components, but PC1 is the contrast between volume and metric distances. The variable loadings in the PCA analysis suggest that volume is mostly a measure of size and partly related to shape and metric distance is mostly a measure of shape and partly related to size. Hence, one should use both of volume and metric distance in morphometric analysis of brain tissues in order not to lose any relevant information, which is in agreement with [26].
Table 2.
The importance of principal components from the PCA with eigenvalues based on the correlation matrix (top) and on the covariance matrix with volume and scaled distances (bottom). Variable labeling and abbreviations are as in Table 1.
| Importance of Components PCA with Correlation (for volume and metric distances) | ||||||||
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | |
| Prop. Var | .5461 | .2291 | .1154 | .0474 | .0321 | .0184 | .0070 | .0045 |
| Cum. Prop. | .5461 | .7751 | .8906 | .9379 | .9700 | .9885 | .9955 | 1 .0 |
| Importance of Components PCA with Covariance (for volume and scaled (by 1000) metric distances) | ||||||||
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | |
| Prop. Var | .4856 | .2663 | .1234 | .0608 | .0469 | .0105 | .0043 | .0020 |
| Cum. Prop. | .4856 | .7520 | .8754 | .9362 | .9832 | .9937 | .9980 | 1 .0 |
We also compare the cdfs of metric distances by K-S test which requires independence between the groups compared. Hence we only compare the cdf of LB-CDR0.5 with cdf of LB-CDR0 groups, cdf of RB-CDR0.5 with cdf of RB-CDR0 groups, cdf of LF-CDR0.5 with cdf of LF-CDR0 groups, and cdf of RF-CDR0.5 with cdf of RF-CDR0 groups. But we cannot compare, e.g., cdfs of LB-CDR0 and LF-CDR0 groups or cdfs of LB-CDR0 and RB-CDR0 groups due to dependence between the groups. At α = 0.05 level, the cdf of RF-CDR0.5 distances is significantly smaller than the cdf of RF-CDR0 distances (p=0.0259). That is, metric distances RF-CDR0.5 are stochastically larger than RF-CDR0 metric distances. The cdf of LF-CDR0.5 distances is almost significantly smaller than the cdf of LF-CDR0 distances (p=0.0604), but the cdfs of LB-CDR0.5 and LB-CDR0 are not significantly different (p=0.6932) and the cdfs of RB-CDR0.5 and RB-CDR0 are not significantly different either (p=0.8997).
3.2 Logistic Discrimination Analysis
We have applied logistic discrimination with metric distances only and demonstrated that discrimination with metric distances is better than chance (i.e., the correct classification rate is significantly larger than 50%, in particular the optimal threshold value is p0 = 0.38, the correct classification rate is 70%, sensitivity is 72%, and specificity is 69%), and using metric distances and volumes (for each year and each hemisphere) improves the performance of the discrimination (the optimal threshold value is p0 = 0.48, and the correct classification rate, sensitivity, and specificity are 84%, 83%, and 85%, respectively) [26]. In this article, we also apply logistic discrimination on the volume and metric distance differences over time, and also to the principal components obtained from the three types of PCA. For a more detailed discussion of logistic discrimination with various other models, see [61].
When we apply the logistic discrimination using both volume and metric distance differences over time (from baseline to follow-up) as predictors, the model selection procedure yields . The optimal threshold value is p0 = 0.48, and the correct classification rate, sensitivity, and specificity are 77%, 67%, and 85%, respectively. Notice that logistic classifier with these differences only performs slightly better than the models based on metric distances only.
In the above analysis, we are considering subjects with hippocampus measurements for both baseline and follow-up for left and right hemisphere. However, in practice for this method to be useful in detecting mild DAT, first a new patient’s hippocampus at about the same age of our subjects (around 75 years old) should be scanned (which would just be the baseline measurements for this subject), and then if possible rescanned about two years later (which would be the follow-up measurements for this subject). Hence, to be able to use some type of classifier with just the baseline measurements, we need a logistic regression model and a classifier based on baseline measurements only. Therefore, we perform logistic regression on the baseline variables (i.e., on ), and our model selection procedure yields (denoted as Model I in Table 3). With the logistic classifier based on this model, the optimal threshold value is p0 = 0.30–0.31, and the correct classification rate, sensitivity, and specificity are 80%, 81%, and 78%, respectively.
Table 3.
The correct classification rates (CCR), sensitivity, and specificity values with optimal p0 = popt for the logistic classifiers based on the models in the first column. In Models IIa–c, PCi are obtained from PCA on the baseline measures, and in Models Iva-c, PCi are obtained from PCA on all measures. In Models IIa–c, and IIIa–c, “a” is for PCA on the raw variables, “b” is for the PCA on volume and scaled metric distances, and “c” is for PCA on standardized variables.
| Model | popt | CCR | sensitivity | specificity | |
|---|---|---|---|---|---|
| .30–.31 | 80% | 81% | 78% | ||
| IIa : logit pk = β0 + β1PC1 + β2PC2 | .43–.46 | 77% | 81% | 77% | |
| IIb : logit pk = β0 + β1PC2 + β2PC3 | .36–.37 | 75% | 83% | 69% | |
| IIc : logit pk = β0 + β1PC1 + β2PC2 + β3PC3 | .35–.38 | 80% | 89% | 73% | |
| .34–.44 | 86% | 94% | 81% | ||
| IVa: logit pk = β0 + β1PC1 + β2PC2 + β3PC3 + β4PC4 | .35–.37 | 86% | 94% | 81% | |
| IVb: logit pk = β0 + β1PC1 + β2PC2 + β3PC3 + β4PC7 + β5PC8 | .44–.45 | 86% | 89% | 85% | |
| IVc: logit pk = β0 + β1PC1 + β2PC4 + β3PC7 | .60 | 86% | 72% | 96% |
We also apply logistic discrimination using the principal components obtained from the PCA on baseline volume and metric distance measures. After the PCA procedure, we keep all the principal components instead of just the first few (which explain a large portion of the variation) for the full model and then apply the model selection procedure that yields only the principal components that have the most discriminatory power. Notice that by this procedure, we might end up with a subset of the original principal components some of which explains only a small portion of the variation. When PCA is performed on these baseline variables with the covariance matrix, we see that the first two principal components explain almost all the variation, and PC1 is the volume component, while PC2 is the volume contrast between left and right hippocampi at baseline (details omitted). When we perform logistic regression on the principal components with this PCA, our model selection procedure yields logit pk = β0 + β1PC1 + β2PC2 (denoted as Model IIa in Table 3). With the logistic classifier based on this model, the optimal threshold value is p0 = 0.43–0.46, and the correct classification rate, sensitivity, and specificity are 77%, 81%, and 77%, respectively. When PCA is performed on the volumes and scaled (by 1000) metric distances at baseline with the covariance matrix, we see that the first three principal components explain almost all the variation. When we perform logistic regression on the principal components with this PCA, our model selection procedure yields logit pk = β0 + β1PC2 + β2PC3 (denoted as Model IIb in Table 3). With the logistic classifier based on this model, the optimal threshold value is p0 = 0.36–0.37, and the correct classification rate, sensitivity, and specificity are 75%, 83%, and 69%, respectively. Finally, we perform logistic regression on the principal components with the PCA with the correlation matrix. Our model selection procedure yields logit pk = β0+ β1PC1 + β2PC2 + β3PC3 (denoted as Model IIc in Table 3). With the logistic classifier based on this model, the optimal threshold value is p0 = 0.35–0.38, and the correct classification rate, sensitivity, and specificity are 80%, 89%, and 73%, respectively.
We apply the logistic discrimination using both volumes and metric distance as predictors. The model selection procedure yields (denoted as Model III in Table 3). With the classifier based on this logistic regression model, the optimal threshold value is p0 = 0.34–0.44, and the correct classification rate, sensitivity, and specificity are 86%, 94%, and 81%, respectively.
We also apply logistic discrimination using the principal components obtained from the PCA on volume and metric distance measures. When logistic regression is applied to the eight principal components from the PCA on the covariance matrix, we see that only the first four principal components are significant yielding the model logit pk = β0+ β1PC1 + β2PC2 + β3PC3 + β4PC4 (denoted as Model IVa in Table 3). That is, only the first four principal components which are the volume component of the morphometry have significant coefficients. In the discrimination, the optimal threshold value is p0 = 0.35–0.37 with the correct classification rate, sensitivity, and specificity being 86%, 94%, and 81%, respectively. When the principal components from the PCA based on the covariance matrix with volume and scaled (by 1000) metric distances are used in logistic regression, only PC1, PC2, PC3, PC7, and PC8 are kept after the model selection procedure yielding the model logit pk = β0+ β1PC1 + β2PC2 + β3PC3 + β4PC7 + β5PC8 (denoted as Model IVb in Table 3). In the logistic discrimination based on these principal components, the optimal threshold value is p0 = 0.44–0.45 with the correct classification rate, sensitivity, and specificity being 86%, 89%, and 85%, respectively. When the principal components from the PCA based on the correlation matrix are used in logistic regression, only PC1, PC4, and PC7 are kept after the model selection procedure yielding the model
(denoted as Model IVc in Table 3). In the logistic discrimination based on these principal components, the optimal threshold value is p0 = 0.44 with the correct classification rate, sensitivity, and specificity being 86%, 72%, and 96%, respectively.
Notice that with volume and distance being used together, there is an increase in performance (i.e., in correct classification rate, sensitivity, and specificity values) compared to the models based on distance only or volume and distance change over time. However these increases are slightly significant. Classifying baseline and follow-up metric distances independently, and calling the result CDR0.5 even if the baseline and follow-up classifications are divergent is a reasonable approach, since it will increase the chances of detecting a demented subject. Furthermore, when principal components from PCA are used, correct classification rate, sensitivity, and specificity values are higher compared to the values based on the raw volumes and metric distances. In particular, with principal components based on the PCA with covariance matrix, we get the highest sensitivity, while with principal components based on PCA with correlation matrix, we get the highest specificity. Moreover, if volume and metric distances are measured over time as in this study, they constitute better indicators of mild form of DAT, compared to the case which uses only the baseline measurements.
4 Discussion and Conclusions
In this study, we use the hippocampal volumes and metric distances obtained by using the large deformation diffeomorphic metric mapping (LDDMM) algorithm to construct logistic classifiers that discriminate subjects with mild form of Dementia of Alzheimer type (DAT) from healthy subjects. The volume and metric distance measures were obtained in a longitudinal study in groups of subjects with and without mild DAT (labeled as CDR0.5 and CDR0 patients, respectively) at baseline and at follow-up (two years apart from baseline). The subjects in this paper have been previously analyzed using related but different tools. As a single scalar measure, volumes were used for diagnosis group comparisons at baseline and follow-up [27] and displacement, momentum vector fields based on LDDMM were used for discrimination only at baseline [55]. Volumes and metric distances are analyzed for diagnosis group comparisons and for the logistic discrimination procedure [26]. But principal component analysis (PCA) on only volumes and metric distances has not been performed and the principal components obtained from PCA on volumes and metric distances and the volume and metric distance differences over time from baseline to follow-up have not hitherto been used in diagnostic classification (with logistic discrimination). The metric distance gives a single number reflecting the global morphometry (i.e., the size and shape) while volume measurements only provide information on size. So, metric distances provide morphometric information that is not conveyed by volume. The results might completely differ if another template was selected, due to the confounding nature of size for the metric distance. The metric distance will provide meaningful shape comparisons if the same template is used for new data as well. The choice of template that yields optimal discrimination results is a topic of ongoing research.
Differences in morphometry between diagnosis groups or morphometric changes over time can be detected by metric distances computed via LDDMM and could potentially serve as a biomarker for the disease. The morphometric changes in the left hippocampus in CDR0.5 subjects from baseline to follow-up are not significantly different from those in the CDR0 subjects (p=0.134), while the morphometric changes in the right hippocampus in the CDR0.5 group from baseline to follow-up are significantly larger than those in the CDR0 group (p=0.0070).
In this study we apply logistic discrimination based on volumes and metric distances, as logistic regression not only provides a means for classification, but also yields a probability estimate for having very mild dementia. Furthermore, one can optimize the threshold probability with respect to a particular cost function for the entire training data set, or by a cross-validation technique. Differences and changes (over time) in morphometry can also be used for diagnostic discrimination of subjects in non-demented (i.e., CDR0) or demented (i.e., CDR0.5) groups. When logistic classifier was based on metric distance only, the correct classification rate was about 70% in our logistic regression analysis (with 72% sensitivity and 69% specificity). Metric distances can be used to distinguish AD from normal aging quantitatively; however, to be able to use it for diagnostic purposes, the method should be improved to a greater extent [26]. Metric distances increase and volumes decrease by time and when the logistic classifier is based on the metric distance and volume differences over time (from baseline to follow-up) do not provide much additional benefit in logistic discrimination over the discrimination based on metric distances only (correct classification rate is 77%, sensitivity is 67%, and specificity is 85%).
Since our goal is to classify or discriminate the demented hippocampi from healthy hippocampi, and when a subject is scanned for the first time, then we only would have the baseline measures (i.e., ). So we also construct logistic classifiers based on the baseline measurements. We perform logistic regression on the baseline raw variables and principal components from the three types of PCA we consider (see Models I and IIa–c in Table 3). Each of these classifiers performs better in discrimination compared to the model based on distance only or based on the volume and metric distance change over time. The best performing model is the logistic classifier based on the PCA with the correlation matrix (i.e., Model IIc) when correct classification rate, sensitivity, and specificity are all considered.
When the subject is also scanned about two years later, we would have both baseline and follow-up measures, so we also construct logistic classifiers based on all these measures (i.e., ). When (raw) volume and metric distances are used together (see model III), the classification results improve (correct classification rate is 84%, sensitivity is 83%, and specificity is 85%) compared to results based on distance only or on volume and metric distance differences over time. We also construct logistic classifiers based on the principal components from the three versions of the PCA analysis. With PCA on the covariance matrix (i.e., Model IVa) correct classification rate is 86%, sensitivity is 94%, and specificity is 81%, with PCA on volume and scaled distances (i.e., Model IVb) correct classification rate is 86%, sensitivity is 89%, and specificity is 85%, and with PCA on the correlation matrix (i.e., Model IVc) correct classification rate is 86%, sensitivity is 72%, and specificity is 96%. Notice that when the longitudinal measures are used in logistic discrimination, the classification performance increases compared to the models based on the baseline measures only. Furthermore, in terms of sensitivity, Model III and Model IVa are the best performers, while in terms of specificity Model IVc is the best performer, and with respect all three criteria Model IVb is the best performer. That is, in our logistic discrimination analysis on the principal components, highest sensitivity values are obtained when the volume-related principal components (from PCA with covariance matrix) are used, and highest specificity is obtained when the variables are standardized and their linear combinations are used (i.e., principal components from PCA with the correlation matrix). When PCA on volumes and scaled metric distances, all three measures of correct classification rate, sensitivity, and specificity are simultaneously high and this might also be desirable in practice. Therefore, we recommend logistic discrimination with principal components from all three versions of the PCA analysis, and depending on the goal of the analysis one might prefer one over the others.
When principal components from PCA are used in logistic discrimination, we obtain better results compared to the raw volumes and metric distances. However in PCA, we recommend keeping all the principal components (instead of the usual practice of keeping only the first few components), because some principal component with a low contribution to the total variation might still be significant in discriminating the two diagnostic groups. Such principal components are kept after the model selection procedure in our logistic regression. If the PCA is applied with the covariance matrix (i.e., PCA is applied on the variables in the original scale), then the size measures (such as volumes) dominate the PCA analysis, and the first few principal components account for most of the variation. On the other hand, if PCA is applied with the correlation (i.e., PCA is applied on the standardized variables), principal components will usually be linear combinations of both volume and metric distance measures. The same holds for PCA on volumes and scaled metric distances.
In practice, if our classifiers were to be used, first a new subject at age about 75 will have scans in the baseline, and the logistic discrimination based on the baseline models (Models I and IIa–c) should be used. Since we will have the baseline measurements only, one can apply the logistic classifier with raw variables (i.e., Model I in Table 3) or with principal components from PCA with the correlation matrix. If the subject is scanned roughly two years later, then we will have the longitudinal measurements, so one can apply the logistic classifier with the raw variables (i.e., Model III in Table 3) and with principal components from PCA models (i.e., Models IVa–c in Table 3). The principal components for the new subject will be obtained using the variables loadings (i.e., the linear combination formulae that form the principal components) in each PCA type analysis, and these principal components should be used in the logistic regression modeling.
Changes within a subject may produce a more sensitive measure of shape change. However, because the template is different for each longitudinal computation (i.e., each subject’s own baseline), parallel transport analysis of the vector fields is required for statistical comparison of group change [64–65], which is beyond the scope of this work. Also, alternative average template computed from the actual populations as in [66] may also result in more sensitive metric distances. Likewise, metric distances derived from surfaces rather than binary images via LDDMM-Surface [67] may yield better sensitivity. The advent of large scale multi-site neuroimaging studies of AD such as the Alzheimer's Disease Neuroimaging Initiative (ADNI), European-ADNI, Japanese-ADNI and Australian Imaging, Biomarker and Lifestyle Flagship Study of Ageing (AIBL) [68–69] may provide a useful test bed for a more refined analysis of metric distances. Furthermore, we have not accounted for structural deformations in MRI data, which has likely reduced the power. The effects of gradient warping of structural data are also topic of prospective research.
We provide evidence that LDDMM (together with volumes) can be used for diagnostic purposes for mild DAT based on structural changes in the hippocampus of the subjects. In conclusion, volumes and metric distances have the potential to be biomarkers in detecting morphometric changes in the hippocampus in subjects with very mild dementia. In particular, when logistic discrimination and PCA are used together, these measures are more powerful in discrimination of diseased and healthy subjects. Further theory and application are needed to see how metric distances combined with other biomarkers can be used in clinical diagnosis of dementia as well as neurological and psychiatric disorders.
Acknowledgements
We would like to acknowledge support from NIH (P01 AG03991, P50 AG05681, AG05684, P41-RR15241, P50 MH71616, and MH 56584), NSF DMS-0456253, NSERC 31-611387 and the Pacific Alzheimer Research Foundation. The authors thank the Clinical Core of the Alzheimer's Disease Research Center at Washington University for the clinical and cognitive assessments of the participants.
APPENDIX: Computing Metric Distance via LDDMM
Metric distances between the binary images and the template image are obtained by computing diffeomorphisms between the images. For any pair I, J ∈ ℐ there exists a flow of diffeomorphisms gt, t ∈[0 1]transforming one shape to the other g ·I ~ J. The metric distance between any pair I,J is given by the length of the shortest or geodesic curve through the space of shapes connecting them. The diffeomorphisms are constructed as a flow of ordinary differential equations ġt = vt(gt), t ∈[0,1] with g0 = id the identity map, and associated vector fields vt,t ∈[0,1] [56, 70]. The metric distance between two shapes I, J takes the form,
such that g transforms I to J. The norm ‖·‖V is chosen to ensure that the vector fields are smooth in space (derivatives exist in the squared-energy sense). To calculate the norm we use LDDMM [40] by introducing a cost function measuring correspondence between mapped anatomical objects C(g ·I,J) and then computing the geodesic connection to minimize the cost. Here, we solve the inexact matching problem forcing one shape to map onto the other, obtaining a matching cost C which is small but not identically zero. Correspondence is based on the intensity data at the voxel level; reliability has been demonstrated [40]. Vector fields connecting each template-subject pair is then used to compute metric distances in each hemisphere at baseline and at follow-up (see Figure 1).
References
- 1.Davis DG, et al. Alzheimer neuropathologic alterations in aged cognitively normal subjects. Journal of Neuropathology and Experimental Neurology. 1999;58(4):376–388. doi: 10.1097/00005072-199904000-00008. [DOI] [PubMed] [Google Scholar]
- 2.Haroutunian V, et al. Regional distribution of neuritic plaques in the nondemented elderly and subjects with very mild Alzheimer Disease. Archives of Neurology. 1998;55(9):1185–1191. doi: 10.1001/archneur.55.9.1185. [DOI] [PubMed] [Google Scholar]
- 3.Braak H, Braak E. Staging of Alzheimer's disease-related neurofibrillary changes. Neurobiol Aging. 1995;16(3):271–278. doi: 10.1016/0197-4580(95)00021-6. discussion 278-84. [DOI] [PubMed] [Google Scholar]
- 4.Braak H, Braak E. Staging of Alzheimer-related cortical destruction. Int Psychogeriatr. 1997;9(Suppl 1):257–261. discussion 269-72. [PubMed] [Google Scholar]
- 5.Braak H, Braak E, Bohl J. Staging of Alzheimer-related cortical destruction. Eur Neurol. 1993;33(6):403–408. doi: 10.1159/000116984. [DOI] [PubMed] [Google Scholar]
- 6.Price JL, et al. Neuron number in the entorhinal cortex and CA1 in preclinical alzheimer disease. Archives of Neurology. 2001;58(9):1395–1402. doi: 10.1001/archneur.58.9.1395. [DOI] [PubMed] [Google Scholar]
- 7.Convit A, et al. Hippocampal atrophy in early Alzheimer's disease: anatomic specificity and validation. Psychiatric Quarterly. 1993;64(4):371–387. doi: 10.1007/BF01064929. [DOI] [PubMed] [Google Scholar]
- 8.Csernansky JG, et al. Early DAT is distinguished from aging by high-dimensional mapping of the hippocampus. Neurology. 2000;55(11):1636–1643. doi: 10.1212/wnl.55.11.1636. [DOI] [PubMed] [Google Scholar]
- 9.Krasuski JS, et al. Relation of medial temporal lobe volumes to age and memory function in nondemented adults with Down's syndrome: Implications for the prodromal phase of Alzheimer's disease. American Journal of Psychiatry. 2002;159(1):74–81. doi: 10.1176/appi.ajp.159.1.74. [DOI] [PubMed] [Google Scholar]
- 10.Mega MS, et al. Hippocampal atrophy in persons with age-associated memory impairment: Volumetry within a common space. Psychosomatic Medicine. 2002;64(3):487–492. doi: 10.1097/00006842-200205000-00013. [DOI] [PubMed] [Google Scholar]
- 11.Mu Q, et al. A quantitative MR study of the hippocampal formation, the amygdala, and the temporal horn of the lateral ventricle in healthy subjects 40 to 90 years of age. American Journal of Neuroradiology. 1999;20(2):207–211. [PMC free article] [PubMed] [Google Scholar]
- 12.Scheltens P, Barkhof F. Structural neuroimaging outcomes in clinical dementia trials, with special reference to disease modifying designs. Journal of Nutrition, Health and Aging. 2006;10(2):123–128. [PubMed] [Google Scholar]
- 13.Gosche KM, et al. Hippocampal volume as an index of Alzheimer neuropathology: findings from the Nun Study. Neurology. 2002;58(10):1476–1482. doi: 10.1212/wnl.58.10.1476. [DOI] [PubMed] [Google Scholar]
- 14.Fox NC, et al. Imaging of onset and progression of Alzheimer's disease with voxel-compression mapping of serial magnetic resonance images. Lancet. 2001;358(9277):201–205. doi: 10.1016/S0140-6736(01)05408-3. [DOI] [PubMed] [Google Scholar]
- 15.Chan D, et al. Rates of global and regional cerebral atrophy in AD and frontotemporal dementia. Neurology. 2001;57(10):1756–1763. doi: 10.1212/wnl.57.10.1756. [DOI] [PubMed] [Google Scholar]
- 16.Christensen GE, Rabbitt RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Transactions on Image Processing. 1996;5(10):1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
- 17.Miller MI, et al. Mathematical textbook of deformable neuroanatomies. Proceedings of the National Academy of Sciences of the United States of America. 1993;90(24):11944–11948. doi: 10.1073/pnas.90.24.11944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hogan RE, et al. MRI-based high-dimensional hippocampal mapping in mesial temporal lobe epilepsy. Brain. 2004;127(8):1731–1740. doi: 10.1093/brain/awh197. [DOI] [PubMed] [Google Scholar]
- 19.Miller MI. Computational anatomy: Shape, growth, and atrophy comparison via diffeomorphisms. NeuroImage. 2004;23:S19–S33. doi: 10.1016/j.neuroimage.2004.07.021. [DOI] [PubMed] [Google Scholar]
- 20.Thompson PM, et al. Mapping cortical change in Alzheimer's disease, brain development, and schizophrenia. Neuroimage. 2004;23:S2–S18. doi: 10.1016/j.neuroimage.2004.07.071. [DOI] [PubMed] [Google Scholar]
- 21.Grenander U, Miller MI. Computational anatomy: An emerging discipline. Quarterly of Applied Mathematics. 1998;56(4):617–694. [Google Scholar]
- 22.Toga AW, Thompson PM. Brain atlases of normal and diseased populations. Int Rev Neurobiol. 2005;66:1–54. doi: 10.1016/S0074-7742(05)66001-1. [DOI] [PubMed] [Google Scholar]
- 23.Toga AW. Computational biology for visualization of brain structure. Anatomy and Embryology. 2005;210(5–6):433–438. doi: 10.1007/s00429-005-0040-6. [DOI] [PubMed] [Google Scholar]
- 24.Grenander U. General Pattern Theory. Oxford: Clarendon Press; 1993. [Google Scholar]
- 25.Grenander U, Miller MI. Representations of knowledge in complex systems. J. R. Statist. Soc. B. 1994;56(3):549–603. [Google Scholar]
- 26.Ceyhan E, et al. Quantization and Analysis of Hippocampal Morphometric Changes due to Dementia of Alzheimer Type Using Metric Distances Based on Large Deformation Diffeomorphic Metric Mapping. Computerized Medical Imaging and Graphics. 2011 doi: 10.1016/j.compmedimag.2011.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang L, et al. Changes in hippocampal volume and shape across time distinguish dementia of the Alzheimer type from healthy aging. NeuroImage. 2003;20(2):667–682. doi: 10.1016/S1053-8119(03)00361-6. [DOI] [PubMed] [Google Scholar]
- 28.Fox NC, Freeborough PA. Brain atrophy progression measured from registered serial MRI: Validation and application to Alzheimer's disease. Journal of Magnetic Resonance Imaging. 1997;7(6):1069–1075. doi: 10.1002/jmri.1880070620. [DOI] [PubMed] [Google Scholar]
- 29.Fox NC, Freeborough PA, Rossor MN. Visualisation and quantification of rates of atrophy in Alzheimer's disease. Lancet. 1996;348(9020):94–97. doi: 10.1016/s0140-6736(96)05228-2. [DOI] [PubMed] [Google Scholar]
- 30.Killiany RJ, et al. MRI measures of entorhinal cortex vs hippocampus in preclinical AD. Neurology. 2002;58(8):1188–1196. doi: 10.1212/wnl.58.8.1188. [DOI] [PubMed] [Google Scholar]
- 31.Wang D, et al. MR image-based measurement of rates of change in volumes of brain structures. Part II: Application to a study of Alzheimer's disease and normal aging. Magnetic Resonance Imaging. 2002;20(1):41–48. doi: 10.1016/s0730-725x(02)00472-1. [DOI] [PubMed] [Google Scholar]
- 32.Yamaguchi S, et al. Five-year retrospective changes in hippocampal atrophy and cognitive screening test performances in very mild Alzheimer's disease: The Tajiri project. Neuroradiology. 2002;44(1):43–48. doi: 10.1007/s002340100688. [DOI] [PubMed] [Google Scholar]
- 33.Crum WR, Scahill RI, Fox NC. Automated hippocampal segmentation by regional fluid registration of serial MRI: validation and application in Alzheimer's disease. Neuroimage. 2001;13(5):847–855. doi: 10.1006/nimg.2001.0744. [DOI] [PubMed] [Google Scholar]
- 34.Leow AD, et al. Longitudinal stability of MRI for mapping brain change using tensor-based morphometry. Neuroimage. 2006;31(2):627–640. doi: 10.1016/j.neuroimage.2005.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Apostolova LG, et al. Conversion of mild cognitive impairment to alzheimer disease predicted by hippocampal atrophy maps. Archives of Neurology. 2006;63(5):693–699. doi: 10.1001/archneur.63.5.693. [DOI] [PubMed] [Google Scholar]
- 36.Mungas D, et al. Longitudinal volumetric MRI change and rate of cognitive decline. Neurology. 2005;65(4):565–571. doi: 10.1212/01.wnl.0000172913.88973.0d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dickerson BC, Sperling RA. Neuroimaging biomarkers for clinical trials of disease-modifying therapies in Alzheimer's disease. NeuroRx. 2005;2(2):348–360. doi: 10.1602/neurorx.2.2.348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ewers M, Teipel SJ, Hampel H. Update of structural MRI-based methods for the early detection of Alzheimer's disease [Aktuelle entwicklungen der strukturellen MRT zur fru?hdiagnostik der Alzheimer-demenz] Nervenheilkunde. 2005;24(2):113–119. [Google Scholar]
- 39.Barnes J, et al. Does Alzheimer's disease affect hippocampal asymmetry? Evidence from a cross-sectional and longitudinal volumetric MRI study. Dementia and Geriatric Cognitive Disorders. 2005;19(5–6):338–344. doi: 10.1159/000084560. [DOI] [PubMed] [Google Scholar]
- 40.Beg MF, et al. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision. 2005;61(2):139–157. [Google Scholar]
- 41.Miller MI, Trouve A, Younes L. On the metrics and Euler-Lagrange equations of computational anatomy. Annual Review of Biomedical Engineering. 2002;4:375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]
- 42.Glaunès J, et al. Large Deformation Diffeomorphic Curve Matching. International Journal of Computer Vision (online) 2008 doi: 10.1007/s11263-008-0141-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Trosset M, et al. Semisupervised learning from dissimilarity data. Computational Statistics and Data Analysis. 2008;52:4643–4657. doi: 10.1016/j.csda.2008.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thompson DW. In: On Growth and Form: The Complete Revised Edition. Bonner JT, editor. Cambridge, UK: Cambridge University Press; 1992. Canto (1st ed., 1917) ed, [Google Scholar]
- 45.Wang L, et al. Abnormalities of hippocampal surface structure in very mild dementia of the Alzheimer type. NeuroImage. 2006;30(1):52–60. doi: 10.1016/j.neuroimage.2005.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Morris JC. The Clinical Dementia Rating (CDR): current version and scoring rules. Neurology. 1993;43(11):2412–2414. doi: 10.1212/wnl.43.11.2412-a. [DOI] [PubMed] [Google Scholar]
- 47.Cohen J. A coefficient for agreement for nominal scales. Educational and Psychological Measurement. 1960;20:37–46. [Google Scholar]
- 48.Burke WJ, et al. Reliability of the Washington University Clinical Dementia Rating. Archives of Neurology. 1988;45(1):31–32. doi: 10.1001/archneur.1988.00520250037015. [DOI] [PubMed] [Google Scholar]
- 49.Morris JC, et al. Clinical dementia rating training and reliability in multicenter studies: the Alzheimer's Disease Cooperative Study experience. Neurology. 1997;48(6):1508–1510. doi: 10.1212/wnl.48.6.1508. [DOI] [PubMed] [Google Scholar]
- 50.Berg L, et al. Clinicopathologic studies in cognitively healthy aging and Alzheimer disease: Relation of histologic markers to dementia severity, age, sex, and apolipoprotein E genotype. Archives of Neurology. 1998;55(3):326–335. doi: 10.1001/archneur.55.3.326. [DOI] [PubMed] [Google Scholar]
- 51.Morris JC, et al. Cerebral amyloid deposition and diffuse plaques in "normal" aging: Evidence for presymptomatic and very mild Alzheimer's disease. Neurology. 1996;46(3):707–719. doi: 10.1212/wnl.46.3.707. [DOI] [PubMed] [Google Scholar]
- 52.Price JL, Morris JC. Tangles and plaques in nondemented aging and 'preclinical' Alzheimer's disease. Annals of Neurology. 1999;45(3):358–368. doi: 10.1002/1531-8249(199903)45:3<358::aid-ana12>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 53.Petersen RC, et al. Current concepts in mild cognitive impairment. Archives of Neurology. 2001;58(12):1985–1992. doi: 10.1001/archneur.58.12.1985. [DOI] [PubMed] [Google Scholar]
- 54.Storandt M, et al. Longitudinal course and neuropathologic outcomes in original vs revised MCI and in pre-MCI. Neurology. 2006;67(3):467–473. doi: 10.1212/01.wnl.0000228231.26111.6e. [DOI] [PubMed] [Google Scholar]
- 55.Wang L, et al. Large Deformation Diffeomorphism and Momentum Based Hippocampal Shape Discrimination in Dementia of the Alzheimer Type. IEEE Trans. Medical Imaging. 2007;26:462–470. doi: 10.1109/TMI.2005.853923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Haller JW, et al. Three-dimensional hippocampal MR morphometry with high-dimensional transformation of a neuroanatomic atlas. Radiology. 1997;202(2):504–510. doi: 10.1148/radiology.202.2.9015081. [DOI] [PubMed] [Google Scholar]
- 57.Wang L, et al. Statistical analysis of hippocampal asymmetry in schizophrenia. NeuroImage. 2001;14(3):531–545. doi: 10.1006/nimg.2001.0830. [DOI] [PubMed] [Google Scholar]
- 58.Dalgaard P. Introductory Statistics with R. Springer-Verlag: 2002. [Google Scholar]
- 59.Johnson DE. Applied Multivariate Methods for Data Analysis. California: Duxbury Press; 1998. [Google Scholar]
- 60.Burnham KP, Anderson D. Model Selection and Multi-Model Inference. New York: Springer; 2003. [Google Scholar]
- 61.Ceyhan E, et al. Technical Report # KU-EC-08-3: Analysis of Metric Distances and Volumes of Hippocampi Indicates Different Morphometric Changes over Time in Dementia of Alzheimer Type and Nondemented Subjects. Koç University; 2008. [Google Scholar]
- 62.Mardia KV, Kent JT, Bibby JM. Multivariate Analysis. London: Academic Press; 1979. [Google Scholar]
- 63.Conover W. Practical Nonparametric Statistics. 3rd ed. New York: John Wiley & Sons; 1999. [Google Scholar]
- 64.Younes L. Jacobi fields in groups of diffeomorphisms and applications. Quart. Appl. Math. 2007;65:113–134. [Google Scholar]
- 65.Qiu A, et al. Parallel transport in diffeomorphisms distinguishes the time-dependent pattern of hippocampal surface deformation due to healthy aging and the dementia of the Alzheimer's type. Neuroimage. 2008;40(1):68–76. doi: 10.1016/j.neuroimage.2007.11.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ma J, et al. Bayesian Template Estimation in Computational Anatomy. NeuroImage. 2008;42:252–261. doi: 10.1016/j.neuroimage.2008.03.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Vaillant M, et al. Diffeomorphic Metric Surface Mapping in Subregions of the Superior Temporal Gyrus. Neuroimage. 2007;34:1149–1159. doi: 10.1016/j.neuroimage.2006.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Butcher J. Alzheimer’s researchers open the doors to data sharing. The Lancet Neurology. 2008;6:480–481. doi: 10.1016/S1474-4422(07)70118-7. [DOI] [PubMed] [Google Scholar]
- 69.Jack CR, Jr, et al. The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods. J Magn Reson Imaging. 2008;27:685–691. doi: 10.1002/jmri.21049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Trouve A. Diffeomorphisms groups and pattern matching in image analysis. International Journal of Computer Vision. 1998;28(3):213–221. [Google Scholar]