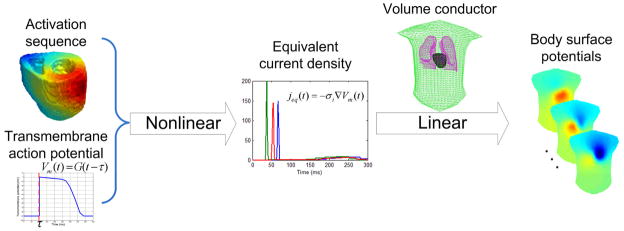
Abstract
A new algorithm for three-dimensional (3D) imaging of the activation sequence from noninvasive body surface potentials is proposed. After formulating the nonlinear relationship between the 3D activation sequence and the body surface recordings during activation, the extended Kalman filter (EKF) is utilized to estimate the activation sequence in a recursive way. The state vector containing the activation sequence is optimized during iteration by updating the error covariance matrix. A new regularization scheme is incorporated into the “predict” procedure of EKF to tackle the ill-posedness of the inverse problem. The EKF based algorithm shows good performance in simulation under single-site pacing. Between the estimated activation sequences and true values, the average correlation coefficient (CC) is 0.95, and the relative error (RE) is 0.13. The average localization error (LE) when localizing the pacing site is 3.0 mm. Good results are also obtained under dual-site pacing (CC = 0.93, RE = 0.16, LE = 4.3 mm). Furthermore, the algorithm shows robustness to noise. The present promising results demonstrate that the proposed EKF-based inverse approach can noninvasively estimate the 3D activation sequence with good accuracy and the new algorithm shows good features due to the application of EKF.
Index Terms: Extended Kalman filter, Inverse problem, Three-dimensional electrocardiographic imaging
I. Introduction
Mapping of the cardiac activation sequence could facilitate diagnosis and treatment of cardiac arrhythmias. By analyzing the activation sequences, abnormal cardiac activation can be revealed and critical pathways/substrates of the arrhythmias can be found. In electrophysiological labs, cardiac electrograms on the heart surface can be recorded/reconstructed by invasive sensors and the local activation time is picked up at the point of the maximum negative derivative or the maximum negative peak of the electrogram [1]–[2]. Noninvasive methods have also been developed to obtain the activation sequence from body surface potential maps (BSPMs) by solving the inverse problem. A popular trend of the cardiac inverse approach is estimating the epicardial potentials from the BSPMs [3]–[6], and the epicardial activation sequence can be subsequently derived from the estimated potentials [7]. On the other hand, direct estimation of the heart surface (both the endocardium and epicardium) activation sequence has been reported by applying the so-called “critical point” theory [8] or nonlinear optimization procedures [9]–[11]. The heart surface activation times estimated with the “critical point” theory are often used as initial values of other nonlinear optimization methods. The BSPM-based estimation of the activation sequence has been investigated in clinical settings for managing arrhythmias, such as localizing the accessory pathway of Wolff-Parkinson-white (WPW) syndrome [12] and assisting cardiac resynchronization therapy [13]. Though promising results have been reported, the inverse solutions by those inverse approaches are on the heart surface and the intramural activities in the three-dimensional cardiac volume cannot be directly revealed [14]. Transmural three-dimensional imaging of cardiac electrical activity is thus expected to facilitate the research on the mechanisms of arrhythmias and also to guide the clinical management of cardiac arrhythmias in a more efficient way. In order to noninvasively estimate intramural cardiac activity, a heart-model-based three-dimensional (3D) activation sequence imaging approach has been proposed [15] and validated on animal models [16]–[17]. Most recently, a physical-model-based 3D activation sequence imaging approach was reported [18] and validated in a rabbit model [19].
One major difficulty of solving the inverse problem is its ill-posed nature, which is due to the smoothing and attenuation effects when the cardiac electrical signals travel through the torso volume conductor. As a result, slight measurement noise on body surface potentials may induce large perturbation to the inverse solution. The ill-posed nature of the 3D inverse problem is even more challenging. One way of circumventing this difficulty is by employing an excitable heart model incorporating a priori physiological knowledge [15]. The inverse scheme was performed by iteratively optimizing the parameters of the heart model to obtain the expected physiological/pathological characteristics corresponding to the measured BSPMs. Alternatively, in our physical-model-based approach, regularization methods were employed to deal with the ill-posedness. The spatial-temporal equivalent current densities were inversely derived from BSPMs and from them spatial activation sequences were then determined. In the present study, we have further investigated the methodology of the 3D inverse problem. The forward problem from the 3D activation sequence to the BSPMs is nonlinear and we try to solve the corresponding inverse problem using the extended Kalman filter.
The Kalman filter is a set of mathematical equations that estimate the state of a process in a recursive way by minimizing the estimated error covariance [20]. It can incorporate all available information and provide an optimal estimation, even when the precise nature of the modeled system is unknown. Regarding the cardiac inverse problem, the Kalman filter has been applied to estimate epicardial potentials from recorded BSPMs [21]–[22] and to estimate endocardial potentials from recorded intracavitary potentials by a noncontact multi-electrode array [23], in which a linear relationship between the estimated sources and the recordings exists if the volume conductor is assumed quasi static. On the other hand, if the system is nonlinear, the Kalman filter would not be available and the extended Kalman Filter (EKF) has been developed to tackle the nonlinearity [20]. It has been reported that the EKF was used to reconstruct the activation wavefront curve on the epicardium from the BSPMs [24].
The aim of the present study is to estimate the 3D activation sequence from noninvasive BSPMs by using the Kalman filter. Noting that the transfer function from the 3D activation sequence to the BSPMs is nonlinear, the EKF is employed in the algorithm to handle non-linearity. The original contributions of the present study include: 1) defining and numerically modeling the nonlinear relationship between the 3D activation sequence and BSPMs, and then applying the EKF on this nonlinear inverse problem; 2) using a novel and cost-efficient regularization method in the EKF to handle the ill-posedness of the inverse problem. Simulation studies with a realistic human model are performed to evaluate the performance of the proposed inverse approach. The merits of the proposed algorithm are then discussed.
II. Methods
A. From three-dimensional activation sequences to body surface potentials
The relationship between 3D activation sequences and body surface potentials was defined in the forward problem. First, based on the bidomain theory [25], the equations governing the quasi-static volume conductor were as follows,
| (1) |
| (2) |
where σi and σe are the intracellular and extracellular conductivity tensor, φ(t) the field potential at time instant t, jeq(t) the equivalent current density at t, Vm(t) the transmembrane potential at t, Ω the human body volume conductor, and n the outward unit normal to the body surface S. By applying the finite element method [26], equation (1) was numerically solved and the linear relationship between the equivalent current density and the body surface potentials was built as
| (3) |
where φB(t) is an N × 1 vector containing the body surface potentials at time instant t, N is the number of recording electrodes on the body surface. Jeq(t) is a 3M × 1 vector containing equivalent current densities at M grid points in the myocardium at time instant t. Each of the equivalent current densities is represented by an orthogonal triple of dipoles. A is an N × 3M transfer matrix relating the equivalent current densities to the body surface potentials.
Second, based on the physiological knowledge of the cardiac transmembrane action potential, at location r in the myocardium, a nonlinear relationship between the activation time and the transmembrane potential could be defined as
| (4) |
where G represents the waveform of the transmembrane action potential at r, as shown in Fig. 1. In practice, G could be simulated using the equation introduced in [10], where the action potential was simulated with an inverse tangent equation. In the present study, a universal waveform of the action potential was assigned to every cellular unit in the ventricles, which started with the very steep phase 0 and was followed by a plateau, as shown in Fig. 1. Since only the activation period of the heart was simulated and utilized in the present study, the diversity of phase 2 as well as phase 3 had little effect and was neglected in the present study. Substituting equation (4) into equation (2), and then substituting equation (2) into equation (3), we arrived at
Fig. 1.
The nonlinear modeling from the 3D activation sequence to the body surface potentials.
| (5) |
where φB is an N × Nt matrix containing the body surface potentials recorded by N electrodes at Nt time instants covering the entire activation of the heart, τ is the vector of activation times at M points in the 3D myocardium, and h is the nonlinear operator relating the activation sequence to the body surface potentials. The temporal resolution of the activation time and the corresponding BSPMs was set as 1 ms.
B. The state space model and the extended Kalman filter
In order to apply the Kalman filter to solve (5), a state-space model was established and governed by the following equations:
| (6) |
| (7) |
where τk is the state vector at step k and here it is the vector containing the activation sequence of the 3D heart, f is a processor that predicts the current state from the previous state, φB,k is the measured body surface potentials corresponding to the kth state, h is the nonlinear operator defined in (5), and w, v are process noise and measurement noise, respectively, which are both assumed as independent Gaussian white noise with the following normal distribution:
| (8) |
It was noteworthy that in this approach, each step did not correspond to a time instant; instead, each step corresponded to an entire beat during activation. The input of each step was the measured body surface potentials over the activation of the heart. In practice, if the body surface potentials during a series of beats were available, and those beats corresponded to the same cardiac event, then the BSPMs during each of the beats were sequentially employed in each step of iteration. If BSPMs from only one beat were available, then those BSPMs could be repeatedly employed in each step of iteration. Employing multiple beats could incorporate more information regarding measurement noise. For obtaining the best performance by using the proposed approach, it was assumed in the present study that data from multiple beats under the same cardiac event were available.
In other researchers’ work regarding the cardiac inverse problem, f can be defined linearly, such as scalar multiple of the identity [21], [23]. The f can also be determined by using a regularized least-square approach [21] or using a maximum likelihood approach [22]. In their work, temporal evolution of the state vector (the heart surface potentials) exists. On the contrary, the state vector of the proposed algorithm (the activation sequence of an entire cardiac cycle) does not evolve in temporal domain. In the present approach, a nonlinear predicting procedure was utilized to regularize the inverse solutions, and the nonlinear f was determined by the following rule:
| (9) |
where τj,k is the updated activation time in the kth step of iteration, τi,k−1 is among the n activation times in the k−1th step whose locations are within a pre-defined spatial distance to the location of τj,k, and ε is a pre-defined threshold determining the method of updating τj,k. The index set for each τj,k was determined by the pre-defined constant of distance l. This constant was chosen by experience to let the average value of n be about 8. The actual value of n for each activation time varied due to the geometry of the heart. In practice, the value of ε was chosen to be equal to l divided by the conduction velocity inside the myocardium.
The Kalman filter is a linear recursive estimator, while both f and h are nonlinear in the present study. Thus the extended Kalman filter (EKF) was employed to handle the non-linearity by linearizing the estimation around the current estimate using the partial derivatives of the process function and measurement function. Equation (6) and (7) were rewritten as
| (10) |
| (11) |
where τk and φB,k are the actual state vectors and measurement vectors, τ̂k is an a posteriori estimate of the state at step k, F is the Jacobian matrix of partial derivatives of f with respect to τ, H is the Jacobian matrix of partial derivatives of h with respect to τ, W is the Jacobian matrix of partial derivatives of equation (6) with respect to w, V is the Jacobian matrix of partial derivatives of equation (7) with respect to v. W and V were calculated from equation (6) and (7), respectively. F was derived from equation (9) by calculating its partial derivative with respect to τ. F needed to be calculated in every step because equation (9) changed in every step. H was calculated by using the following scheme:
| (12) |
where M is the number of myocardial locations at which the activation times are sampled, and the ρ is the temporal resolution of the activation times. The subscript k indicating the kth updating step is omitted for all variables.
The EKF then used (10) and (11) to recursively update the state vector in an attempt of minimizing the error variance/covariance matrix. The detailed implementation of EKF is shown in Appendix. The initial value of the error variance/covariance matrix was set as P0 = I. During the iteration, the estimated error variance/covariance matrix would be updated and eventually converge. The initial value of the state vector could be obtained by using one of the following methods: 1) to get the initial guess on the activation sequence from the simulation using an excitable physiological heart model [27]; 2) to pick up the initial guess of the activation sequence using the inversely reconstructed current density [18]. In the present study, the second scheme was used. As mentioned above, a series of beats were employed in the EKF approach; the BSPMs from the first beat of them was used to derive the initial state vector by using the weighted minimal norm (WMN) method in [18].
C. Computer simulation
A realistic human heart-torso model built from computed tomography (CT) images was employed in the present study [28]. The torso, lungs and blood mass were assumed to be isotropic conductors. A generalized cardiac anisotropy was incorporated into the heart model as described in detail in [15]. The myocardial fiber orientations rotated counterclockwise over 120° from the outermost layer (epicardium, −60°) to the innermost layer (endocardium, 60°) with uniform increment between the consecutive layers. The conductivities of different tissues were set as follows: torso (0.20 S/m), lungs (0.08 S/m), blood mass (0.6 S/m), cardiac tissue (interstitial: 0.6 S/m along the fiber orientation and 0.15 S/m transverse to the fiber orientation; intercellular: 0.3 S/m along the fiber orientation and 0.075 S/m transverse to the fiber orientation). The “true” activation sequence was generated by a cellular-automaton heart model [27] and then equivalent current densities were subsequently obtained using equation (4) and (2). A 128-electrode array was employed to represent the body surface potential map. The forward calculation from equivalent current density to body surface potentials was performed using the finite element method [26].
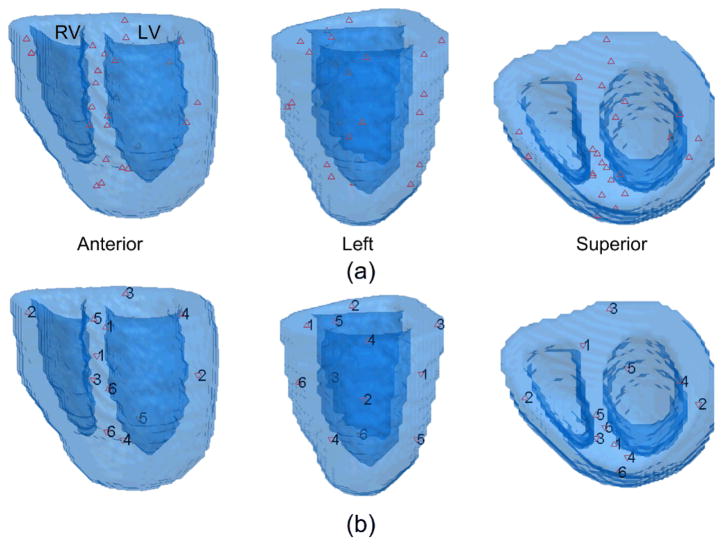
In this simulation, pacing was performed in the ventricles and the simulated “true” 3D activation sequence in the activation cycle and the corresponding body surface potential maps (BSPMs) were calculated. The forward model used for simulating the “measured” BSPMs was the same with that used in the inverse procedure. A Gaussian white noise was added onto the BSPMs to simulate the noise contaminated measurements. The proposed inverse approach was then applied to the “measured” BSPMs, and the performance was evaluated by comparing the estimated activation sequences to the simulated activation sequences throughout the entire myocardial volume. The single-site pacing study was conducted at 24 pacing sites from different regions of the ventricles. The ventricular longitudinal section was divided into five regions: anterior, left wall, posterior, right wall and septum. The whole ventricle from base to apex was divided into three regions: basal, middle and apical. Thus the ventricles were segmented into 12 regions: basal-anterior (BA), basal-right-wall (BRW), basal-posterior (BP), basal-left-wall (BLW), basal-septum (BS), middle-anterior (MA), middle-posterior (MP), middle-left-wall (MLW), middle-septum (MS), apical-anterior (AA), apical-posterior(AP) and apical-septum (AS). Two pacing sites were chosen from each of the regions.
Dual-site pacing study was also employed to simulate the condition of cardiac excitation originating from two centers in an ectopic beat. In each study, a pair of pacing sites was chosen from different regions and then pacing was conducted from both of the sites. The other settings were the same with the single-site pacing study. In total, 6 pairs of pacing sites were chosen from the following regions: BA-MP, BRW-MLW, BP-MS, BLW-AA, BS-AP and MA-AS. The locations of the pacing sites in the heart are shown in Fig. 2.
Fig. 2.
The locations of the pacing sites shown in three views. (a) the 24 single pacing sites; (b) the 6 pairs of dual pacing sites.
In order to evaluate the performance of the proposed approach, the correlation coefficient (CC) and relative error (RE) were calculated between the estimated and the “true” activation sequence. The CC was defined as
| (13) |
where τ̂i is the estimated activation time at the ith myocardial location, is the average activation time over the N myocardial locations throughout the 3D heart, τi is the true activation time at the ith myocardial location and τ̄ is the average true activation time. The RE was defined as
| (14) |
The CC can evaluate the similarity regarding the global pattern between the estimated and the true 3D activation sequence, while the RE quantify the dissimilarity in the estimated results.
Since single-pacing and dual-pacing protocols were used, the EKF’s performance on localizing the origin(s) of the activation was evaluated by picking up the earliest activated site(s) according to the inversely estimated activation sequence. The localization error (LE) was reported.
III. Results
Both single-site pacing and dual-site pacing studies were conducted. In each of the studies, the iteration of the EKF always converged. Fig. 3 shows the change of the CC and RE between the estimated and the true 3D activation sequence during iteration when the heart is paced at the BLW region. The increase of CC and decrease of RE indicate that the estimated activation sequence is optimized during iteration. Both CC and RE eventually converge because the error covariance matrix has converged and become stable after enough iteration steps.
Fig. 3.
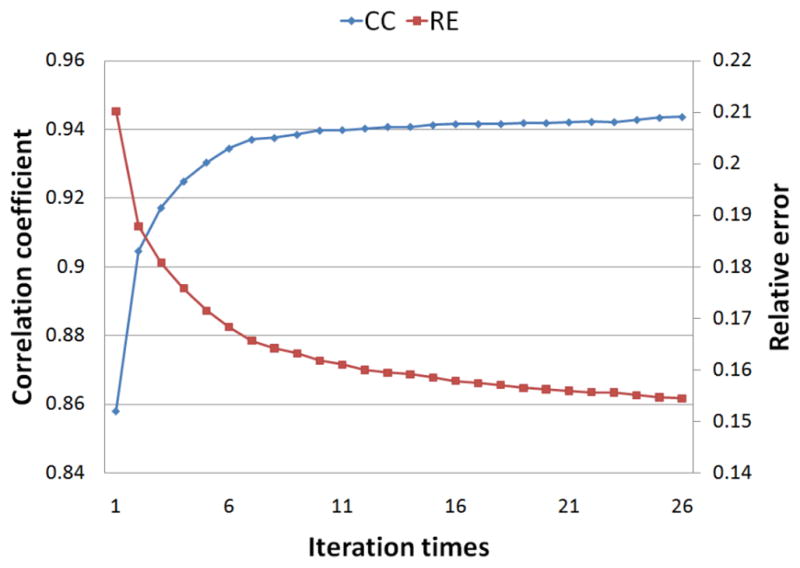
The convergence of the correlation coefficient and the relative error between the estimated and the true activation sequence during iteration. The heart is paced in the basal-left-wall region.
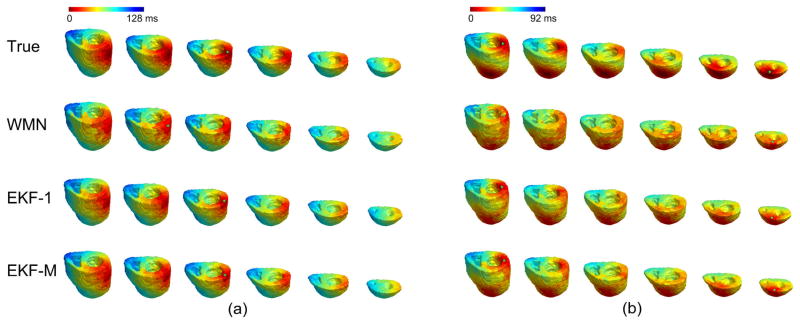
The single-site pacing studies were first conducted at 24 sites throughout the ventricles when the measured BSPMs were contaminated with a 20 μV level Gaussian white noise (assuming the peak-peak value of the BSPMs was 3 mV). Fig. 4(a) depicts an example of an inversely estimated 3D activation sequence when the heart is paced at the MLW region. When using the activation sequence obtained by the WMN method (the second row) and the picking-up principle proposed in [18] as the initial value of the EKF iteration, the final output of EKF (the 3D activation sequence shown in the third row) has shown significant improvement with higher consistency with the “true” activation sequence. The evaluation results of the 24 single-pacing studies are shown in Table I. Regarding the initial estimates by using the WMN method in [18], the average CC between the estimated 3D activation sequence and the true results over the 24 pacing studies was 0.90±0.04. After applying the EKF, the average CC increased to 0.95±0.03. Furthermore, the average relative error was 0.13±0.04. The earliest activated site was localized and compared to the true pacing site. Over the 24 pacing sites, the average localization error was 3.0±0.8 mm. In order to test the robustness of the algorithm regarding noise, a 60 μV level noise was also employed in the single-site pacing studies. The other settings were the same. The results over the 24 pacing sites are summarized in Table II. Though the noise level is 200% higher, the average CC slightly decreased by only 0.005 and RE increased by 0.006. The similar results in Table I and Table II suggests that the increased noise level has little effect on the inverse results.
Fig. 4.
The inverse results in simulation when (a) single-site pacing at middle-left-wall; (b) dual-site pacing at basal-left-wall and anterior-apex. In each panel, the first row is the true 3D activation sequence shown by 6 horizontal sections, arranged from base to apex; the precise pacing site(s) is indicated with green star(s). The second row is the estimated 3D activation sequence picked up from the reconstructed current densities; the current densities are inversely calculated with the weighted minimal norm (WMN) method; the estimated origin(s) of activation is indicated by green star(s). The third row is the estimated 3D activation sequence with the extended Kalman filter (EKF) when BSPMs from one beat are employed; the estimated origin(s) of activation is indicated by green star(s). The fourth row is the estimated 3D activation sequence with the extended Kalman filter (EKF) when BSPMs from multiple beats are employed; the estimated origin(s) of activation is indicated by green star(s).
TABLE I.
Evaluation of inverse solutions during single-site pacing (20 μV noise)
| Pacing region | BA | BRW | BP | BLW | BS | MA |
|---|---|---|---|---|---|---|
| (1) CC/RE | 0.972/0.090 | 0.982/0.075 | 0.978/0.096 | 0.958/0.134 | 0.974/0.092 | 0.962/0.122 |
| LE (mm) | 1.87 | 1.54 | 3.12 | 2.79 | 3.87 | 2.38 |
| (2) CC/RE | 0.983/0.081 | 0.982/0.079 | 0.957/0.130 | 0.944/0.155 | 0.909/0.178 | 0.959/0.133 |
| LE (mm) | 3.48 | 3.85 | 3.82 | 3.60 | 1.62 | 3.75 |
|
| ||||||
| Pacing region | MP | MLW | MS | AA | AP | AS |
|
| ||||||
| (1) CC/RE | 0.980/0.096 | 0.910/0.198 | 0.936/0.147 | 0.945/0.154 | 0.908/0.194 | 0.941/0.142 |
| LE (mm) | 2.19 | 4.09 | 2.47 | 2.81 | 3.55 | 3.33 |
| (2) CC/RE | 0.975/0.116 | 0.982/0.083 | 0.891/0.218 | 0.965/0.147 | 0.973/0.120 | 0.898/0.196 |
| LE (mm) | 3.25 | 3.40 | 2.59 | 2.61 | 3.77 | 2.57 |
CC: correlation coefficient; RE: relative error; LE: localization error.
BA: basal-anterior; BRW: basal-right-wall; BP: basal-posterior; BLW: basal-left-wall; BS basal-septum; MA: middle-anterior; MP: middle-posterior; MLW: middle-left-wall; MS: middle-septum; AA: apical-anterior; AP: apical-posterior; AS: apical-septum.
TABLE II.
Evaluation of inverse solutions during single-site pacing (60 μV noise)
| Pacing region | BA | BRW | BP | BLW | BS | MA |
|---|---|---|---|---|---|---|
| (1) CC/RE | 0.968/0.094 | 0.978/0.080 | 0.976/0.102 | 0.957/0.141 | 0.973/0.093 | 0.956/0.134 |
| LE (mm) | 1.87 | 1.54 | 3.12 | 2.79 | 3.87 | 2.38 |
| (2) CC/RE | 0.982/0.082 | 0.981/0.081 | 0.953/0.139 | 0.939/0.165 | 0.899/0.190 | 0.956/0.138 |
| LE (mm) | 3.48 | 3.85 | 3.82 | 3.60 | 1.62 | 3.75 |
|
| ||||||
| Pacing region | MP | MLW | MS | AA | AP | AS |
|
| ||||||
| (1) CC/RE | 0.981/0.095 | 0.903/0.214 | 0.933/0.151 | 0.942/0.158 | 0.901/0.202 | 0.929/0.157 |
| LE (mm) | 2.19 | 4.09 | 2.47 | 2.81 | 3.55 | 3.33 |
| (2) CC/RE | 0.974/0.117 | 0.981/0.090 | 0.888/0.230 | 0.961/0.151 | 0.963/0.128 | 0.896/0.198 |
| LE (mm) | 3.25 | 3.40 | 2.59 | 2.61 | 3.77 | 2.57 |
CC: correlation coefficient; RE: relative error; LE: localization error.
BA: basal-anterior; BRW: basal-right-wall; BP: basal-posterior; BLW: basal-left-wall; BS basal-septum; MA: middle-anterior; MP: middle-posterior; MLW: middle-left-wall; MS: middle-septum; AA: apical-anterior; AP: apical-posterior; AS: apical-septum.
In the dual-site pacing studies, the 20 μV level noise was added onto the simulated BSPMs. One example of dual-pacing studies is shown in Fig. 4(b), where the heart is paced from BLW and AA simultaneously. Compared to the initial value in the second row, the result obtained with EKF better localizes both of the earliest activated sites in the complex dual-pacing condition. The pacing site in BLW region is near the endocardium, while the other one in AA region is near the epicardium. As shown in Fig. 4(b), in the inverse result by WMN method, it is hard to tell the depth of the earliest activated sites, but the result by EKF clearly indicates the depth of the localized sites, which proves the proposed algorithm’s ability to reveal 3D information beyond the heart surface. The results of dual-site pacing studies are shown in Table III. In summary, the average CC of the 6 studies was 0.93±0.02, and the average RE was 0.16±0.02. Both of the origins of activation in each study were localized, and the average localization error over 12 sites in 6 studies was 4.3±1.6 mm.
TABLE III.
Evaluation of inverse solutions during dual-site pacing
| Pacing region | BA-MP | BRW-MLW | BP-MS | BLW-AA | BS-AP | MA-AS |
|---|---|---|---|---|---|---|
| CC | 0.942 | 0.912 | 0.920 | 0.935 | 0.910 | 0.965 |
| RE | 0.158 | 0.161 | 0.180 | 0.141 | 0.192 | 0.129 |
| LE (mm) | 3.48/4.33 | 3.28/5.08 | 1.79/6.33 | 3.24/4.40 | 6.60/2.57 | 4.51/6.37 |
IV. Discussion
In the present study, a new method of inversely estimating the three-dimensional activation sequence has been proposed and evaluated in simulation studies. We have reported: 1) formulating the nonlinear relationship between the three-dimensional transmural activation sequence and the body surface potentials, and employing the extended Kalman filter to solve the 3D activation sequence from BSPMs; 2) applying a new nonlinear regularization scheme in the predicting procedure of EKF. The present computer simulation results are promising. When the initial estimate was obtained employing the algorithm reported in [18], the proposed EKF algorithm was able to converge to a better solution than the initial estimate in all simulations studied.
An interesting work of applying Kalman filter in the cardiac inverse problem was presented in [23], where the Duncan and Horn formulation of a Kalman filter was employed to estimate the endocardial potentials from the intracavitary potential mapping. By applying KF on the linear problem defined in their work, temporal information was incorporated and stable inverse results were reported. Most recently, a novel algorithm was proposed to noninvasively estimate the epicardial activation wavefront curve employing the extended Kalman filter [24]. They modeled the nonlinear relationship between the epicardial activation wavefront curve and the BSPMs, and set up the state space model by incorporating general physiological knowledge, e.g. conduction velocity. In comparison, our goal was estimating the cardiac activation in the 3D myocardium, instead of on the heart surface, from the noninvasive body surface measurement. Similar to [24], the forward relationship from the 3D activation sequence to the body surface potential maps was nonlinear, so the EKF was chosen to tackle the nonlinearity in the present study.
EKF has brought some interesting features. Firstly, the simulation shows that the EKF-based approach is robust to the measurement noise. When the noise level increased from 20 μV to 60 μV, the accuracy of inverse solutions did not significantly become worse, because information regarding noise level was incorporated into the EKF calculation by estimating the noise variance/covariance matrix. The merit of EKF is that even if our estimate on noise is not accurate, the iterative approach may still find optimal solutions, while the iteration speed may be affected. That means that when measurements are severely contaminated by noise, the EKF-based inverse approach may still have good performance, which has been demonstrated in the present study when the white noise was present.
Secondly, the EKF-based approach can incorporate all information that can be provided to it. The Kalman filter is theoretically an optimal data processing algorithm, which processes all available measurements to seek the optimal estimate of the state based on them [29]. The EKF is a suboptimal estimator which utilizes the first-order Taylor series of the system to transfer the nonlinear problem into linear, and EKF also incorporates all available information. Specifically, when estimating the activation sequence, BSPMs covering the entire activation period of the ventricles have been used as input in the present approach. Thus the temporal information in the body surface measurements has been naturally incorporated into the EKF. Other methods have also been developed to take advantage of the temporal nature of the electrocardiographic inverse problem, such as using the Twomey regularization [4], using the structural constraints [30] or using the spatio-temporal multiple regularization scheme [31]–[32]. Improvement has been reported by using temporal regularization methods. In the proposed algorithm, temporal regularization on the inverse solution is not available, since the state vector itself is the activation times. Instead, temporal information is contained in the BSPMs in each step’s input, and has been incorporated into the proposed approach to benefit the inverse calculation.
Lastly, the ill-posedness of the inverse approach has been handled in the predicting procedure. Overcoming the ill-posedness of the inverse problem is critical for obtaining informative and physiological reasonable solutions. Many efforts have been reported. The truncated singular value decomposition method removes very small singular values to minimize the effect of measurement noise. The popular Tikhonov regularization scheme balances the residual with a measure of some undesirable property of the solution, such as the unreasonable large value of the expected solution. The “critical points” theory determines the activation time at a critical point by looking for the “jump” from the first order derivative of the ECG signals, and thus overcomes the ill-posedness [8]. In the present study, a new regularization scheme has been incorporated into the predicting procedure. The activation time is updated from the estimated activation times in previous step at nearby sites, or at the original site only. The determination is made according to nonlinear criteria (details in equation (9)). By using this scheme, the updated activation times in the “correct” procedure are filtered: the unreasonable change in the activation times is removed, while the reasonable update is processed. This regularization scheme facilitates the convergence of the iteration and at the same time, the useful information obtained in the “correct” procedure is well preserved in the updated results.
A sequence of beats which are under the same cardiac event are employed as the input of the proposed algorithm. On the other hand, a single beat can be repeatedly used as input to update the error variance/covariance matrix and to obtain the inverse solution. We have found that in simulation, a little worse but still good inverse results can be obtained by using data from only one beat. Under 20 μV level noise, the average CC of the 24 single-site pacing studies when employing one beat is 0.951, only decreased by 0.002 compared to the value when employing multiple beats. In the dual-site pacing studies, the decrease of average CC under 20 μV level noise is only 0.003. Fig. 4 shows examples of inverse results when employing only one beat, which are very similar to the results when employing multiple beats. It is not surprising because ideal model and white noise are used in the present study. When tackling real data, employing multiple beats may better suppress the effects caused by the variation of the beats, such as measurement noise.
The present simulation protocol has some limitations. The forward model for generating the “measured” BSPMs is identical to what is used in the inverse approach, which would benefit the inverse approach. When employing data from multiple beats as input, the “measured” BSPMs of each beat are calculated from the same activation sequence, and so the study is assumed to be conducted in an ideal condition. In dual-site pacing, the distance between each pair of pacing sites are relatively far. While beyond the scope of the present study, more complicated simulation protocols and the evaluation with real human/animal data shall address those limitations in future studies.
It is worthy of noting that the EKF is in fact a sub-optimal estimator since the higher-order information is neglected when linearizing the system. The efficiency of the EKF depends on the linearity of the system around the true value of the unknown state vector. Furthermore, the solution of the 3D activation sequence may be nonunique. To tackle the possible nonuniqueness, we have 1) incorporated the knowledge about the electrocardiophysiology into the modeling procedure; 2) considered the spatial correlation of the activation times in the 3D space in the state update of EKF. Besides those efforts, a high-quality initial value for the iteration would help the convergence to the expected solution. A guess far from the true value may result in an incorrect solution. Regarding our problem, that doesn’t mean the initial guess of the 3D activation sequence will be fairly accurate at every site; instead, the global pattern is more critical. In the present study, the activation sequence picked up from the inversely estimated equivalent current densities using weighted minimal norm method was used and satisfactory results were reported. On the other hand, the activation times obtained on the heart surface’s critical points by using the “critical points” theory may also be a good initial estimate for the EKF approach.
Acknowledgments
This work was supported in part by NIH RO1HL080093 and NSF CBET-0756331. C. Liu was supported in part by a Doctoral Dissertation Fellowship from the Graduate School of the University of Minnesota.
The authors are grateful to Chengzong Han for useful discussions.
Biographies

Chenguang Liu (S’05–M’10) received the B.S. and M.S. degrees in biomedical engineering from Tsinghua University, Beijing, China, in 2001 and 2003, respectively, and the Ph.D. degree in biomedical engineering from the University of Minnesota, Twin Cities, in 2010.
He is currently a Postdoctoral Associate at Department of Biomedical Engineering, University of Minnesota. His research interests include biological signal processing, system modeling, interventional electrophysiology, electrocardiography forward and inverse problem, and animal experimentation.

Bin He (S’87–M’88–SM’97–F’04) received the BS degree (Highest Honors) in electrical engineering from Zhejiang University, Hangzhou, China, and the Ph.D. degree (Highest Honors) in bioelectrical engineering from Tokyo Institute of Technology, Japan.
He completed the Postdoctoral Fellowship in biomedical engineering from Harvard University – Massachusetts Institute of Technology, Cambridge, MA. He is currently a Distinguished McKnight University Professor and Professor of biomedical engineering at the University of Minnesota, Twin Cities, where he is also currently the Director of the Center for Neuroengineering.
He has pioneered the development of electric source imaging, and made significant contributions to functional neuroimaging, cardiac electrical tomography, brain – computer interface, and magnetoacoustic tomography. His research interests include neuroengineering, functional biomedical imaging, and bioelectromagnetism.
Prof. He is a Fellow of the American Institute for Medical and Biological Engineering, the Institute of Physics, and the International Society for Functional Source Imaging. He was the recipient of the National Science Foundation CAREER Award and the American Heart Association Established Investigator Award.
Appendix
The implementation of the extended Kalman filter The error variance/covariance matrix of the state vector is defined as
| (A1) |
where τ is the true activation sequence, and τ̂ is the estimated result. The EKF approach includes “predict” and “correct”. In “predict” procedure, the a priori estimate of the state vector and the error variance/covariance matrix are projected from the estimate in last step:
| (A2) |
| (A3) |
In the “Correct” procedure, the Kalman gain K is calculated, and then the a posteriori estimate of the state vector and error variance/covariance matrix are updated with the measured body surface potentials and the Kalman gain:
| (A4) |
| (A5) |
| (A6) |
Then the τ̂k and Pk are used in the next step of update.
References
- 1.Gepstein L, Hayam G, Ben-Haim SA. A novel method for nonfluoroscopic catheter-based electroanatomical mapping of the heart: in vitro and in vivo accuracy results. Circulation. 1997;95:1611–1622. doi: 10.1161/01.cir.95.6.1611. [DOI] [PubMed] [Google Scholar]
- 2.Gornick CC, Adler SW, Pederson B, Hauck J, Budd J, Schweitzer J. Validation of a new noncontact catheter system for electroanatomic mapping of left Ventricular Endocardium. Circulation. 1999;99:829–835. doi: 10.1161/01.cir.99.6.829. [DOI] [PubMed] [Google Scholar]
- 3.Barr RC, Spach MS. Inverse calculation of QRS-T epicardial potentials from normal and ectopic beats in the dogm. Circ Res. 1978;42:661–675. doi: 10.1161/01.res.42.5.661. [DOI] [PubMed] [Google Scholar]
- 4.Oster HS, Rudy Y. The use of temporal information in the regularization of the inverse problem of electrocardiography. IEEE Trans Biomed Eng. 1992;39:65–75. doi: 10.1109/10.108129. [DOI] [PubMed] [Google Scholar]
- 5.Shahidi AV, Savard P, Nadeau R. Forward and inverse problems of electrocardiography: modeling and recovery of epicardial potentials in humans. IEEE Trans Biomed Eng. 1994;41:249–256. doi: 10.1109/10.284943. [DOI] [PubMed] [Google Scholar]
- 6.Greensite F, Huiskamp G. An improved method for estimating epicardial potentials from the body surface. IEEE Trans Biomed Eng. 1998;45:98–104. doi: 10.1109/10.650360. [DOI] [PubMed] [Google Scholar]
- 7.Ramanathan C, Raja NG, Jia P, Ryu K, Rudy Y. Noninvasive electrocardiographic imaging for cardiac electrophysiology and arrhythmia. Nature Medicine. 2004;10:422–428. doi: 10.1038/nm1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huiskamp G, Greensite F. A new method for myocardial activation imaging. IEEE Trans Biomed Eng. 1997;44:433–446. doi: 10.1109/10.581930. [DOI] [PubMed] [Google Scholar]
- 9.Oostendorp T, Macleod RS, van Oosterom A. Non-invasive determination of the activation sequence of the heart: validation with invasive data. Proc. 19th Ann. Int. Conf. IEEE EMBS; Chicago, IL. 1997. pp. 335–337. [Google Scholar]
- 10.Modre R, Tilg B, Fischer G, Wach P. Noninvasive myocardial activation time imaging: a novel inverse algorithm applied to clinical ECG mapping data. IEEE Trans Biomed Eng. 2002;49:1153–1161. doi: 10.1109/TBME.2002.803519. [DOI] [PubMed] [Google Scholar]
- 11.van Dam PM, Oostendorp TF, Linnenbank AC, van Oosterom A. Non-invasive imaging of cardiac activation and recovery. Ann Biomed Eng. 2009;37:1739–1756. doi: 10.1007/s10439-009-9747-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Berger T, Fischer G, Pfeifer B, Modre R, Hanser F, Trieb T, Roithinger FX, Stuehlinger M, Pachinger O, Tilg B, Hintringer F. Single-beat noninvasive imaging of cardiac electrophysiology of ventricular pre-excitation. J Am Coll Cardiol. 2006;48:2045–2052. doi: 10.1016/j.jacc.2006.08.019. [DOI] [PubMed] [Google Scholar]
- 13.Jia P, Ramanathan C, Ghanem RN, Ryu K, Varma N, Rudy Y. Electrocardiographic imaging of cardiac resynchronization therapy in heart failure: observation of variable electrophysiologic responses. Heart Rhythm. 2006;3:296–310. doi: 10.1016/j.hrthm.2005.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Avari JN, Rhee EK. Cardiac resynchronization therapy for pediatric heart failure. Heart Rhythm. 2008;5:1476–1478. doi: 10.1016/j.hrthm.2008.05.024. [DOI] [PubMed] [Google Scholar]
- 15.He B, Li G, Zhang X. Noninvasive three-dimensional activation time imaging of ventricular excitation by means of a heart-excitation model. Phys Med Biol. 2002;47:4063–4078. doi: 10.1088/0031-9155/47/22/310. [DOI] [PubMed] [Google Scholar]
- 16.Zhang X, Ramachandra I, Liu Z, Muneer B, Pogwizd SM, He B. Noninvasive three-dimensional electrocardiographic imaging of ventricular activation sequence. Am J Physiol — Heart Circulatory Physiol. 2005;289(6):H2724–2732. doi: 10.1152/ajpheart.00639.2005. [DOI] [PubMed]
- 17.Liu C, Skadsberg N, Ahlberg S, Swingen C, Iaizzo PA, He B. Estimation of global ventricular activation sequences by noninvasive 3-dimensional electrical imaging: validation studies in a swine model during pacing. J Cardiovasc Electrophysiol. 2008;19:535–540. doi: 10.1111/j.1540-8167.2007.01066.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu Z, Liu C, He B. Noninvasive reconstruction of three-dimensional ventricular activation sequence from the inverse solution of distributed equivalent current density. IEEE Trans Med Imaging. 2006;25:1307–1318. doi: 10.1109/tmi.2006.882140. [DOI] [PubMed] [Google Scholar]
- 19.Han C, Liu Z, Zhang X, Pogwizd SM, He B. Noninvasive three-dimensional cardiac activation imaging from body surface potential maps: a computational and experimental study on a rabbit model. IEEE Trans Med Imaging. 2008;27:1622–30. doi: 10.1109/TMI.2008.929094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Grewal MS, Andrews AP. Kalman Filtering Theory and Practice Using MATLAB. 2. New York: John Wiley & Sons; 2001. [Google Scholar]
- 21.Joly D, Goussard Y, Savard P. Time-recursive solution to the inverse problem of electrocardiography: A model-based approach. Proc. 15th Ann. Int. Conf. IEEE EMBS; San Diego, CA. 1993. pp. 767–768. [Google Scholar]
- 22.El-Jakl J, Champagnat F, Goussard Y. Time-space regularization of the inverse problem of electrocardiography. Proc. 17th Ann. Int. Conf. IEEE EMBS; Montreal, QC, Canada. 1995. pp. 213–214. [Google Scholar]
- 23.Berrier KL, Sorensen DC, Khoury DS. Solving the inverse problem of electrocardiography using a Duncan and Horn formulation of the Kalman filter. IEEE Trans Biomed Eng. 2004;51:507–515. doi: 10.1109/TBME.2003.821027. [DOI] [PubMed] [Google Scholar]
- 24.Ghodrati A, Brooks DH, Tadmor G, MacLeod R. Wavefront-based models for inverse electrocardiography. IEEE Trans Biomed Eng. 2006;53:1821–1831. doi: 10.1109/TBME.2006.878117. [DOI] [PubMed] [Google Scholar]
- 25.Miller WT, Geselowitz DB. Simulation studies of the electrocardiogram. I. The normal heart. Circ Res. 1978;43:301–315. doi: 10.1161/01.res.43.2.301. [DOI] [PubMed] [Google Scholar]
- 26.Zhang Y, Zhu S, He B. A high-order finite element algorithm for solving the three-dimensional EEG forward problem. Phys Med Biol. 2004;49:2975–2987. doi: 10.1088/0031-9155/49/13/014. [DOI] [PubMed] [Google Scholar]
- 27.Li G, He B. Localization of the site of origin of cardiac activation by means of a heart-model-based electrocardiographic imaging approach. IEEE Trans Biomed Eng. 2001;48:660–669. doi: 10.1109/10.923784. [DOI] [PubMed] [Google Scholar]
- 28.He B, Liu C, Zhang Y. Three-dimensional cardiac electrical imaging from intracavity recordings. IEEE Trans Biomed Eng. 2007;54:1454–1460. doi: 10.1109/TBME.2007.891932. [DOI] [PubMed] [Google Scholar]
- 29.Maybeck PS. Stochastic models, estimation and control volume 1. Academic press. 1979 [Google Scholar]
- 30.Greensite F. The temporal prior in bioelectromagnetic source imaging problems. IEEE Trans Biomed Eng. 2003;50:1152–1159. doi: 10.1109/TBME.2003.817632. [DOI] [PubMed] [Google Scholar]
- 31.Zhang Y, Ghodrati A, Brooks DH. An analytical comparison of three spatio-temporal regularization methods for dynamic linear inverse problems in a common statistical framework. Inverse Problems. 2005;21:357–382. [Google Scholar]
- 32.Brooks DH, Ahmad GF, MacLeod RS, Maratos GM. Inverse electrocardiography by simultaneous imposition of multiple constraints. IEEE Trans Biomed Eng. 1999;46:3–18. doi: 10.1109/10.736746. [DOI] [PubMed] [Google Scholar]