ASYMPTOTIC AND BIFURCATION ANALYSIS OF WAVE-PINNING IN A REACTION-DIFFUSION MODEL FOR CELL POLARIZATION

Abstract

We describe and analyze a bistable reaction-diffusion (RD) model for two interconverting chemical species that exhibits a phenomenon of wave-pinning: a wave of activation of one of the species is initiated at one end of the domain, moves into the domain, decelerates, and eventually stops inside the domain, forming a stationary front. The second (“inactive”) species is depleted in this process. This behavior arises in a model for chemical polarization of a cell by Rho GTPases in response to stimulation. The initially spatially homogeneous concentration profile (representative of a resting cell) develops into an asymmetric stationary front profile (typical of a polarized cell). Wave-pinning here is based on three properties: (1) mass conservation in a finite domain, (2) nonlinear reaction kinetics allowing for multiple stable steady states, and (3) a sufficiently large difference in diffusion of the two species. Using matched asymptotic analysis, we explain the mathematical basis of wave-pinning, and predict the speed and pinned position of the wave. An analysis of the bifurcation of the pinned front solution reveals how the wave-pinning regime depends on parameters such as rates of diffusion and total mass of the species. We describe two ways in which the pinned solution can be lost depending on the details of the reaction kinetics: a saddle-node or a pitchfork bifurcation.

1. Introduction

In a recent reaction-diffusion (RD) model for biochemical cell polarization proposed in [21] we found a wave-based phenomenon whereby a traveling wave is initiated at one end of a finite, homogeneous 1D domain, moves across the domain, but stalls before arriving at the opposite end. We refer to this behavior as wave-pinning. We observed that this phenomenon was obtained from a two-component RD system obeying a modest set of assumptions: (1) Mass is conserved and limited, i.e. there is no production or removal, only exchange between one species and the other. (2) One species is far more mobile than the other, e.g. due to binding to immobile structures, or embedding in a lipid membrane. (3) There is feedback (autocatalysis) from one form to further conversion to that form.

The biological motivation for studying our specific system comes from polarization of a living eukaryotic cell, such as a white-blood cell, amoeba, or yeast in response to a signal. Resultant chemical asymmetry then organizes the downstream response of the cell (e.g. shape change, motility, division, etc). Explaining the basis for such symmetry breaking has become an important question in cell biology over the past decade, motivating such mathematical models as [20, 35, 24, 26, 6]. Our own work [18, 3, 12] has focused on switch-like polarity proteins, Rho GTPases, that are conserved in eukaryotic cells from amoebae to humans. Rho GTPases are activated by guanine exchange factors (GEFs) and inactivated by GTPase-activating proteins (GAPs). Upon stimulation, levels of Rho GTPase activity rapidly redistribute across a cell with some (e.g. Rac, Cdc42) becoming strongly activated at one end (to form the front of the cell [15, 23]) whereas others (such as RhoA) dominate at the opposite end (to form the rear [42]). In [21], we investigated a minimal system for the initial symmetry breaking, consisting of a single active-inactive pair of GTPases. From a mathematical perspective, this yields an opportunity for deeper analysis. It also clarifies minimal necessary conditions for symmetry breaking. The purpose of this paper is to investigate the mathematical properties of this model and its wave-pinning behaviour.

The model is based on a caricature of Rho proteins: (1) The protein has an active (GTP-bound) and an inactive (GDP-bound) form. (2) The active forms are only found on the cell membrane; those in the fluid interior of the cell (cytosol) are inactive. (3) There is a 100-fold difference between rates of diffusion of cytosolic vs membrane bound proteins [27]. (4) Continual exchange of active and inactive forms (mediated by GEFs and GAPs) and unbinding from the cell membrane (aided by GDP dissociation inhibitors, GDIs) is essential for polarization [10]. Because the cell edge is thin, this exchange is rapid and not diffusion limited. (5) On the time-scale of polarization (minutes), there is little or no protein synthesis in the cell (timescale of hours), so that the total amount of the given protein is roughly constant. (6) Feedback from an active form to further activation are common, e.g. see [10]. A schematic diagram of our model is given in Fig. 2.1, but many other competing mechanisms are likely at play in real cells.

Fig. 2.1.

(a) Our 1D model represents a strip across a cell diameter (L ≈ 10µm), shown top-down and side view. (b) Side view of a cell (top) showing membrane (shaded) and cytosol (white) and a cell fragment (bottom) ≈ 0.1µm thick, see [38]. Active (u(x, t), black dots) and inactive (v(x, t), white dots) protein redistributes along this axis during polarization. (c) Enlarged rectangle from (b) showing exchange between membrane and cytosol (u ↔ v), unequal rates of diffusion, inactivation by (GAPs), and activation by GEFs with positive feedback (+ arrow). (Schematic not drawn to scale).

We formulate the model (Section 2), and apply matched asymptotics (Section 3) to show how the wave speed, shape and stall positions are affected by the parameters. In Section 4, we describe the bifurcation structures for various reaction kinetics and discuss biological implications in the Discussion.

2. Model formulation

Consider a one dimensional domain Ω = {x : 0 ≤ x ≤ L} along a cell diameter (shaded bar, Fig 2.1a). Every value of x includes both membrane and cytosol. Denote by u(x, t) and v(x, t) the concentrations of active and inactive protein respectively at position x and time t. Cell fragments (e.g. keratocyte fragments, typical thickness 0.1–0.2µm and diameter 10µm, Fig 2.1b) can polarize and crawl. We thus assume that appreciable chemical gradients do not develop in the thickness direction, and hence consider a single coordinate, x. We also approximate both u and v as residing in the same 1D domain Ω. The concentrations u and v satisfy the following equations

$$\frac{\partial u}{\partial t}=D_u\frac{{\partial }^{2}u}{\partial x^2}+f(u,v),$$ (2.1a)

$$\frac{\partial v}{\partial t}=D_v\frac{{\partial }^{2}v}{\partial x^2}-f(u,v),$$ (2.1b)

where f(u, v) is the rate of interconversion of v to u, and the rates of diffusion satisfy D_u ≪ D_v, reflecting the fact that the membrane bound species u diffuses much more slowly than the cytosolic species v. The boundary conditions are

$$\begin{array}{cc}\frac{\partial u}{\partial x}=\frac{\partial v}{\partial x}=0,\hfill & x=0,L.\hfill \end{array}$$ (2.1c)

It is clear that system (2.1) leads to mass conservation, i.e. that

$${\displaystyle {\int }_{\mathrm{\Omega }}}(u+v)\mathit{\text{dx}}=K_{\text{total}}=\text{constant}.$$ (2.2)

The model is easily reformulated on a 1D domain with periodic boundary conditions where the “membrane” is the perimeter, with cytosol in the interior. The phenomena and analysis is essentially identical (doubling the domain of the no-flux problem produces such a periodic domain), so we can directly transfer the insights obtained for the no-flux problem to the periodic case. We shall henceforth focus primarily on the no-flux problem, with reaction term f(u, v) as proposed in [21]:

$$f(u,v)=(\text{activation rate})·v-(\text{inactivation rate})·u=\eta (\delta +\frac{\gamma u^2}{m^2+u^2})v-\eta u,$$ (2.3)

where η, γ, m > 0, δ ≥ 0 are constants. The activation of Rho proteins by GEFs (first term, v → u) is not fully deciphered biologically, but experimental evidence points to feedback from downstream signals and/or from direct binding to Rho GTPases. In this single-Rho protein caricature, we assumed direct positive feedback from the active form, u to its own GEF-mediated activation rate (+ arrow, Fig 2.1b), modeled as a Hill function [22, 37]. In more detailed models, we based the feedback on experimental evidence, e.g. for neutrophils [18, 3, 12]. For the rate of inactivation by GAPs (second term, u → v), we take the simplest possible form, i.e. a constant. As discussed in [12], whether positive feedback is assumed in GEF activity or negative feedback in GAP activity is, to some extent, arbitrary in the caricature.

For suitable choices of γ, m and δ, f(u, v) has the following property. The expression f(u, v) = 0, seen as an equation for u with v fixed over a suitable range, has three roots u₋(v) < u_m(v) < u₊(v). Moreover, u_±(v) are stable fixed points of the ODE $\frac{\mathit{\text{du}}}{\mathit{\text{dt}}}=f(u,v)$ whereas u_m(v) is an unstable fixed point. In other words, the function f(u, v) is a bistable function of u over a range of v values. Much of the analysis to follow applies not only to the specific form of f(u, v) given in (2.3) but to a family of reaction terms satisfying a number of properties including bistability. A precise characterization of this family will be given shortly.

We now make our equations dimensionless. We scale concentrations with m and the reaction rate with η, both of which are dictated by the form of the reaction term (see (2.3)). Take the domain length L to be the relevant length scale. Equations (2.1) can be rescaled using

$$\begin{array}{cccc}u=m\tilde{u},\hfill & v=m\tilde{v},\hfill & x=L\tilde{x},\hfill & t=\frac{L}{\sqrt{\eta D_u}}\tilde{t},\hfill \end{array}$$ (2.4)

where ũ, ṽ, x̃, and t̃ are dimensionless variables. The scaling in time is chosen so that we obtain a distinguished limit appropriate for the analysis of wave-pinning (see next Section). We define:

$$\begin{array}{cc}{\epsilon }^2=\frac{D_u}{\eta L^2},\hfill & D=\frac{D_v}{\eta L^2}.\hfill \end{array}$$ (2.5)

The value of the diffusion coefficient D_v is affected by the time the inactive Rho GTPases spent in the cytosol and depends on the presence of Rho GDI. (Inhibiting GDI can reduce that time, thus reducing the diffusion coefficient of the inactive forms, which is discussed later on.) For typical normal conditions, the diffusion coefficients are D_u = 0.1 µm²s⁻¹ and D_v = 10 µm²s⁻¹ Given D_u ≪ D_v, we let ε be a small quantity. We let D = 𝒪(1) with respect to ε. This assumption may be written as $\sqrt{D_v/\eta }\approx L$, i.e. on the timescale of the biochemical reaction, the inactive substance can diffuse across the domain. In the context of cell polarization, we have a typical cell diameter L ≈ 10µm, reaction timescale η ≈ 1 s⁻¹. The dimensionless constants are then ε ≈ 0.03 and D ≈ 0.1. One time unit in the dimensionless system is approximately 30 s, although we also discuss the behaviour of the system on a fast timescale (t_s = 1s) and on a slow timescale (τ ≈ 1000 s).

Substituting the relationships (2.4) and (2.5) into (2.1) dropping the ˜ and using the same symbol f for the dimensionless reaction term, we obtain:

$$\epsilon \frac{\partial u}{\partial t}={\epsilon }^2\frac{{\partial }^{2}u}{\partial x^2}+f(u,v),$$ (2.6a)

$$\epsilon \frac{\partial v}{\partial t}=D\frac{{\partial }^{2}v}{\partial x^2}-f(u,v),$$ (2.6b)

with boundary conditions:

$$\begin{array}{cc}\frac{\partial u}{\partial x}=\frac{\partial v}{\partial x}=0,\hfill & x=0,1.\hfill \end{array}$$ (2.6c)

Note that our domain is now 0 ≤ x ≤ 1. The (dimensionless) total amount of protein satisfies

$${\displaystyle {\int }_0^1}(u+v)\mathit{\text{dx}}=K.$$ (2.7)

where K = K_total/m. We shall henceforth work almost exclusively with the dimensionless system.

The reaction term (2.3) assumes the following dimensionless form:

$$f(u,v)=(\delta +\frac{\gamma u^2}{1+u^2})v-u.$$ (2.8)

As mentioned earlier, we shall consider not only (2.8) but a family of reaction terms satisfying the following properties:

1. (Bistability Condition) In some range v_min ≤ v ≤ v_max (bistable range), the equation f(u, v) = 0 has three roots, u₋(v) < u_m(v) < u₊(v). Keeping v fixed within the bistable range, u_±(v) are stable fixed points and u_m(v) is an unstable fixed point of the ODE $\frac{\mathit{\text{du}}}{\mathit{\text{dt}}}=f(u,v)$. That is:

   $$\frac{\partial f}{\partial u}(u_{\pm }(v),v)<0,\frac{\partial f}{\partial u}(u_m(v),v)>0.$$ (2.9)

2. (Homogeneous Stability Condition) The homogeneous states, (u, v) ≡ (u_±(v), v), v_min < v < v_max are stable states of the system (2.6).

3. (Velocity Sign Condition) There is one value v = v_c, v_min < v_c < v_max at which the following integral I(v) vanishes:

   $$I(v)={\displaystyle {\int }_{u_{-}(v)}^{u_{+}(v)}}f(u,v)\mathit{\text{du}}.$$ (2.10)

   We assume in addition that I > 0 for v > v_c and I < 0 for v < v_c.

We shall see in Section 3.1 that the second condition can be reduced to the following:

$$(\frac{\partial f}{\partial u}-\frac{\partial f}{\partial v}){|}_{(u,v)=(u_{\pm }(v),v)}<0.$$ (2.11)

Assuming this result, we can check that (2.8) satisfies the above properties for the following parameter values. For γ > 0 and δ ≥ 0, (2.8) satisfies the above conditions if and only if γ > 8δ. The corresponding bistable range is given by v_min = κ₊ < v < κ₋ = v_max where:

$${\kappa }_{\pm }=\frac{1}{\gamma }{(\frac{\rho }{{\omega }_{\pm }}+\frac{{\omega }_{\pm }}{1+{\omega }_{\pm }^2})}^{-1},{\omega }_{\pm }=\sqrt{\frac{1-2\rho \pm \sqrt{1-8\rho }}{2(1+\rho )}},\rho =\frac{\delta }{\gamma }.$$ (2.12)

When δ = 0, v_min = 2/γ and v_max = ∞. In our computational examples, we shall make use of (2.8) with δ = 0 and γ = 1, which we record here for future reference:

$$f(u,v)=\frac{u^{2}v}{1+u^2}-u.$$ (2.13)

We shall often make use of a caricature of (2.8) that satisfies all of the above properties:

$$f(u,v)=u(1-u)(u-1-v).$$ (2.14)

and whose bistable range is 0 < v < ∞. For (2.14), algebraic manipulations are easier than (2.8) or (2.13). In Section 4, we shall also make use of another cubic that satisfies the above conditions:

$$f(u,v)=-(u-1)(u-u_m)(u+1),u_m=-\frac{\mathit{\text{av}}}{\sqrt{1+{(\mathit{\text{av}})}^2}},a>0.$$ (2.15)

The bistable range for the model with kinetics (2.15) is −∞ < v < ∞. At least one of the roots of this polynomial is always negative, and thus, it is no longer possible to interpret u and v as being concentrations of chemicals. The arguments to follow, however, never require that u and v be positive. Both (2.14) and (2.15) will prove useful in understanding the bifurcation structure of our system.

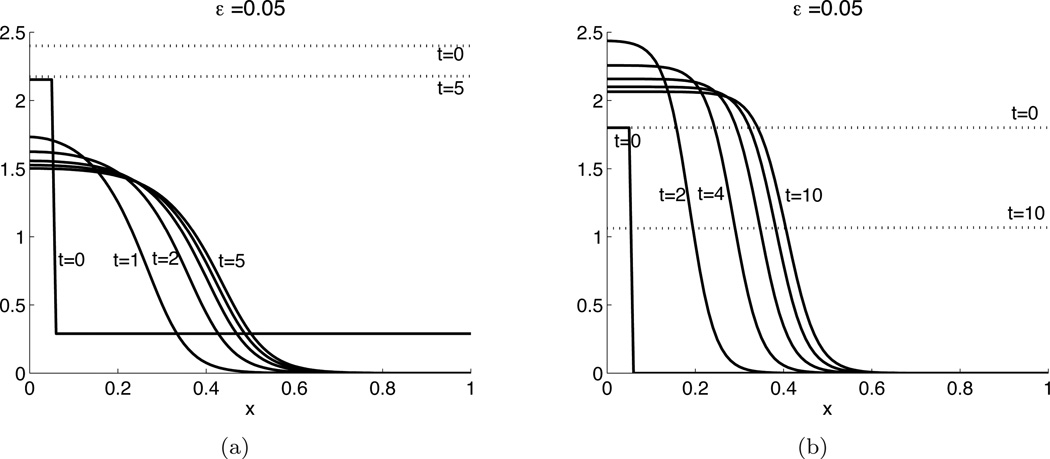
We now describe the behavior of interest: As a stand-alone equation for fixed v, (2.6a) is a scalar reaction diffusion equation of bistable type, known to support propagating front solutions on an infinite domain. Coupling this with (2.6b) on a finite domain gives rise to wave-pinning. We simulated the dimensionless (2.6) with kinetics (2.13) and (2.14), using initial conditions with u high close to x = 0 and v spatially uniform (Fig. 2.2). This represents a stimulus at the left end of the domain. The initial profile of u develops into a steep front that propagates into the domain, losing some of its height, and eventually comes to a halt. The concentration of active species u is then high on the left and low on the right portion of the domain. The spatially localized stimulus has been amplified to produce a stable spatial segregation of the domain into a “front” and a “back”, achieving polarization. (On a periodic domain −1 ≤ x ≤ 1 initialized with a rectangular pulse in u centered at x = 0, the solution satisfies no-flux BCs on 0 < x < 1 for all t, and produces the same dynamics.)

Fig. 2.2.

Wave-pinning behavior for the reaction diffusion model (2.6) with ε = 0.05, D = 1. (a) Hill function reaction kinetics (2.13) with δ = 0, γ = 1, m = 1, K = 2.8. (b) Cubic reaction kinetics (2.14) and K = 1.9. Solutions to u (solid) and v (dashed) are shown at the indicated times. The wave is initiated as the square pulse in u at t = 0.

3. Asymptotic Analysis of Wave-Pinning

3.1. Stability of the Homogeneous State

Let (u_s(v), v) be a steady state of (2.6), where u_s = u_± or u_m. Linearize (2.6) about (u_s, v):

$$\begin{array}{cc}\hfill \epsilon \frac{\partial }{\partial t}\left(\begin{array}{c}\hfill u\hfill \\ \hfill v\hfill \end{array}\right)=ℒ\left(\begin{array}{c}\hfill u\hfill \\ \hfill v\hfill \end{array}\right)\equiv J\left(\begin{array}{c}\hfill u\hfill \\ \hfill v\hfill \end{array}\right)+\frac{{\partial }^2}{\partial x^2}\left(\begin{array}{c}\hfill {\epsilon }^{2}u\hfill \\ \hfill \mathit{\text{Dv}}\hfill \end{array}\right),\hfill & \hfill J=\left(\begin{array}{cc}\hfill f_u\hfill & \hfill f_v\hfill \\ \hfill -f_u\hfill & \hfill -f_v\hfill \end{array}\right){|}_{(u,v)=(u_s(v),v)}\hfill \end{array}.$$ (3.1)

where f_u and f_v denote partial derivatives of f with respect to u and v respectively. Here, the Jacobian matrix of the reaction terms, J, is evaluated at (u_s, v). To study linear stability, we study the spectral properties of the operator ℒ under boundary conditions (2.6c). We must also respect the mass constraint (2.7) so that the perturbations satisfy:

$${\displaystyle {\int }_0^1}(u+v)\mathit{\text{dx}}=0.$$ (3.2)

Since we are on a bounded domain, we need only consider eigenvalues. It is clear that all eigenfunctions of ℒ are of the form:

$$\left(\begin{array}{c}u\hfill \\ v\hfill \end{array}\right)=\left(\begin{array}{c}{\alpha }_u\hfill \\ {\alpha }_v\hfill \end{array}\right)\text{cos}\mathit{\text{kx}}$$ (3.3)

where k = nπ, n = 0, 1, 2, … where α_u and α_v are constants such that (α_u, α_v) ≠ (0, 0). When k ≠ 0, α_u and α_v are arbitrary, whereas when k = 0, α_u + α_v = 0 to satisfy (3.2). The eigenvalues satisfy the quadratic equation:

$${\lambda }^2-{\tau }_k\lambda +{\mathrm{\Delta }}_k=0,{\tau }_k=\text{tr}{ℒ}_k,{\mathrm{\Delta }}_k=\text{det}{ℒ}_k,{ℒ}_k=\left(\begin{array}{cc}\hfill -{\epsilon }^2{k}^2+f_u\hfill & \hfill f_v\hfill \\ \hfill -f_u\hfill & \hfill -{\mathit{\text{Dk}}}^2-f_v\hfill \end{array}\right)$$ (3.4)

where trℒ_k and detℒ_k denote, respectively, the trace and determinant of the 2 × 2 matrix ℒ_k. When k = 0, the two solutions to the above quadratic equation are:

$$\begin{array}{cc}\lambda =0,\hfill & \text{or}\lambda ={\tau }_0=f_u-f_v.\hfill \end{array}$$ (3.5)

If τ₀ < 0, the second eigenvalue is negative. If we assume τ₀ = f_u − f_v ≠ 0, the eigenfunction associated with λ = 0 ceases to satisfy the mass constraint. Thus, if we assume τ₀ < 0 we have stability for k = 0. When k ≠ 0 both roots of (3.4) have negative real part if and only if τ_k < 0 and Δ_k > 0. Since

$${\tau }_k=-(D+{\epsilon }^2)k^2+{\tau }_0<{\tau }_0$$ (3.6)

τ_k < 0 so long as τ₀ < 0.

$${\mathrm{\Delta }}_k=D{\epsilon }^2{k}^4-f_u(D-{\epsilon }^2)k^2-{\tau }_0{\epsilon }^2{k}^2.$$ (3.7)

Therefore, Δ_k > 0 so long as f_u < 0 and D > ε². The condition D > ε² is always met since we are assuming that ε is small. For u_s = u_±, f_u < 0 is met by the bistability condition (2.9). Thus, for f satisfying the bistability condition, the homogeneous stability condition of the last Section is equivalent to τ₀ < 0. This is condition (2.11). It is interesting that the stability condition of the ODE system with fixed v (f_u < 0) together with the stability condition for spatially homogeneous perturbations (τ₀ < 0) implies stability for all wave numbers.

For u_s = u_m, f_u > 0 by (2.9). For fixed k, (3.7) can be made negative by making ε sufficiently small, and thus (u_m(v), v) is always an unstable steady state for small enough ε. This does not preclude the possibility that (u_m(v), v) be a stable steady state for some finite ε value. Suppose f_u > 0 and τ₀ < 0. Let us consider the positivity of Δ_k, k ≥ π:

$$\frac{{\mathrm{\Delta }}_k}{k^2}=D{\epsilon }^2{k}^2-f_u(D-{\epsilon }^2)-{\tau }_0{\epsilon }^2\ge D{\epsilon }^2{\pi }^2-f_u(D-{\epsilon }^2)-{\tau }_0{\epsilon }^2.$$ (3.8)

Therefore, (u_m(v), v) is a stable steady state of the system so long as the right-most quantity is positive. This is the case if ε satisfies the following bound:

$${\epsilon }^2>\frac{f_{u}D}{D{\pi }^2+f_v}.$$ (3.9)

Since τ₀ < 0 by assumption, f_u < f_v and thus the right hand side of the above inequality is less than D. Therefore, if τ₀ < 0, there is a range of values satisfying ε² < D (i.e. diffusion coefficient of u is smaller than that of v) for which (u_m(v), v) is a stable steady state of (2.6). On the other hand, if τ₀ > 0, (u_m(v), v) is always unstable.

For (2.14), labeling the roots u₋ = 0, u_m = 1, u₊ = 1 + v, it is easily seen that (u_m(v), v) is always unstable since f_v = 0 at u = u_m and thus τ₀ = f_u > 0. For (2.15), (u_m(v), v) can be stable for a range of ε values if a > 1 and v is in a suitable range. The stability of this middle stationary plays a role in determining the bifurcation structure of the system as we shall see in Section 4.3.

3.2. Detailed Asymptotic Analysis of Wave-Pinning

Model (2.6) has dynamics on three time scales, short, long, and intermediate with the latter of greatest interest to us. We start with the short time scale and defer discussion of the long time scale to the next section. Accordingly, introduce the short time variable t_s = t/ε. (This corresponds to t_s = 1 s). Rescaling t to t_s in (2.6) and assuming the ansatz u = u₀ + εu₁, v = v₀ + εv₁, we find that u₀ and v₀ satisfy the equations:

$$\frac{\partial u_0}{\partial t_s}=f(u_0,v_0),$$ (3.10a)

$$\frac{\partial v_0}{\partial t_s}=D\frac{{\partial }^2{v}_0}{\partial x^2}-f(u_0,v_0).$$ (3.10b)

Suppose v₀ satisfies v_min < v₀ < v_max so that f(u₀, v₀) is bistable in u₀. Eqn. (3.10a) implies that u₀ will evolve towards either u₊(v₀) or u₋(v₀) depending on whether u₀(v₀) > or < u_m(v₀). At the end of the short time scale, v₀ will have a spatial profile that is uniform whereas u₀ will assume the values of u₊(v₀) or u₋(v₀) depending on position. The domain will thus have segregated into regions where u₀ = u₊(v₀) or u₋(v₀). An important implication of this is that a localized or graded stimulus that raises u(x, t) above the value u_m(v₀) at one end of the cell will give rise to macroscopic difference in levels of u at opposite poles of the cell, i.e. u₊ vs u₋ on this short timescale. This rapid timescale contrasts with the relatively slow symmetry breaking dynamics near a Turing diffusion-driven instability [21].

The profile arising at the short timescale could typically include multiple transition layers where u switches between u₊ and u₋ (e.g. in response to noisy, rather than graded input). That profile serves as initial condition for the intermediate time scale, (In absence of such transitions, this is the stable steady state already characterized.)

Consider a single transition layer in the intermediate time scale (t ≈ 30 s). (Multiple transition layers are discussed in the next Section.) We will show how the location of the pinned front depends on the mean concentration of material K, and not on the details of the reaction kinetics. Let ϕ(t) be the position of the transition layer or the front, which is time-dependent. We perform a matched asymptotic calculation, expanding u = u₀ + εu₁ … and likewise for v. Substituting these expansions into (2.6) and retaining leading order terms we have:

$$0=f(u_0,v_0),$$ (3.11a)

$$0=D\frac{{\partial }^2{v}_0}{\partial x^2}-f(u_0,v_0).$$ (3.11b)

Eqs. (3.11) are valid in the outer region 0 ≤ x < ϕ(t) − 𝒪(ε) and ϕ(t) + 𝒪(ε) ≤ x < 1, that is, at some small distance away from the sharp transition zone at the front. Note that it is impossible to solve the above system with most initial data for u₀ and v₀ (justifying the need to consider a short time scale.) During the short time scale, the arbitrary initial condition evolves into an initial profile that is admissible as an initial condition for the intermediate time scale analysis. Adding (3.11a,b), we find that $\frac{{\partial }^2{v}_0}{\partial x^2}=0$. Combining this with the no-flux boundary condition (2.6c), we see that:

$$v_0(x,t)=\{\begin{array}{cc}{v}_{<}(t)\hfill & 0\le x<\varphi (t)-𝒪(\epsilon ),\hfill \\ v_{>}(t)\hfill & \varphi (t)+𝒪(\epsilon )<x\le 1,\hfill \end{array}$$ (3.12)

where the values of v to the right and to the left of the front, v_> and v_<, do not depend on x. From (3.11a), u₀ takes on one of the values u₊, u₋ or u_m in the outer regions. Assuming a front solution, such that (without loss of generality) u transitions from u₊ to u₋ for increasing x as we traverse ϕ(t), let:

$$u_0(x,t)=\{\begin{array}{cc}{u}_{+}(v_{<})\hfill & 0\le x<\varphi (t)-𝒪(\epsilon ),\hfill \\ u_{-}(v_{>})\hfill & \varphi (t)+𝒪(\epsilon )\le x<1.\hfill \end{array}$$ (3.13)

Introduce a stretched coordinate ξ = (x − ϕ(t))/ε to study the inner layer near the front. The inner solution is denoted by U, V, where

$$\begin{array}{cc}U(\xi ,t)=u((x-\varphi (t))/\epsilon ,t),\hfill & V(\xi ,t)=v((x-\varphi (t))/\epsilon ,t)\hfill \end{array}.$$ (3.14)

Note that (3.14) is not a traveling front solution in the strict sense, as the wave speed dϕ/dt is not constant. As the amplitudes of U and V also change with time, we do not assume u(x, t) = U(ξ), but rather u(x, t) = U(ξ, t), and likewise for V.

Rescale (2.6) using the ξ spatial variable and substitute the ansatz U = U₀ + εU₁ + … and likewise for V and ϕ. We obtain, to leading order,

$$\frac{{\partial }^2{U}_0}{\partial {\xi }^2}-\frac{d{\varphi }_0}{\mathit{\text{dt}}}\frac{\partial U_0}{\partial \xi }+f(U_0,V_0)=0,$$ (3.15a)

$$\frac{{\partial }^2{V}_0}{\partial {\xi }^2}=0.$$ (3.15b)

From (3.15b), it follows that

$$V_0=a_1(t)\xi +a_2(t),$$ (3.16)

where a₁(t), a₂(t) are functions of t determined by matching the inner (V₀) and outer (v₀) solutions, i.e.

$$\begin{array}{cc}\underset{\xi \to -\mathrm{\infty }}{\text{lim}}{V}_0(\xi )=v_{<},\hfill & \underset{\xi \to \mathrm{\infty }}{\text{lim}}{V}_0(\xi )=v_{>}.\hfill \end{array}$$ (3.17)

For these limits to exist, V₀ must be a constant in the inner layer (see (3.16)), i.e. v₀ = V₀. Thus, V₀ is spatially uniform throughout the domain, and is equal to the outer solution v₀. We thus recover the observation that v₀ is uniform on the intermediate time scale. Biologically, this says that v is well mixed in the cytosol at intermediate time. We drop the dependence of v₀ on x (and V₀ on ξ).

We next consider a solution for U₀ in the inner layer. Since V₀ is spatially constant in the inner layer, (3.15a) is an equation in U₀ only, where V₀ is a (time varying) parameter. We must solve the boundary value problem (3.15a) with the matching conditions from (3.13) as boundary conditions at ±∞:

$$\begin{array}{cc}\underset{\xi \to -\mathrm{\infty }}{\text{lim}}{U}_0(\xi )=u_{+}(V_0),\hfill & \underset{\xi \to \mathrm{\infty }}{\text{lim}}{U}_0(\xi )=u_{-}(V_0)\hfill \end{array}.$$ (3.18)

Such a heteroclinic solution $U_0^{\varphi }(\xi ,V_0)$, unique up to translation, exists for general bistable reaction terms f(U, V) [14, 22]. Multiplying (3.15a) by $\partial U_0^{\varphi }/\partial \xi$ and integrating from ξ = −∞ to ξ = ∞, we obtain:

$$\frac{d{\varphi }_0}{\mathit{\text{dt}}}\equiv c(V_0)=\frac{{\displaystyle {\int }_{u_{-}(V_0)}^{u_{+}(V_0)}}f(s,V_0)\mathit{\text{ds}}}{{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{(\partial U_0^{\varphi }(\xi ,V_0)/\partial \xi )}^{2}d\xi }.$$ (3.19)

An explicit analytical expression for c(v) cannot in general be obtained. An exception is when the reaction kinetics is of the form f(u, v) = −(u − u₊(v))(u − u_m(v))(u − u₋(v)), where u₋ < u_m < u₊. In this case c(v) is given by [22]:

$$c(v)=\frac{1}{\sqrt{2}}(u_{+}(v)-2u_m(v)+u_{-}(v)).$$ (3.20)

The sign of the velocity, however, is determined by the numerator of the fraction in (3.19) and can thus be easily determined given the reaction term f(u, v). By the velocity sign condition (see equation (2.10)) we see that dϕ₀/dt is positive when V₀ > v_c and negative when V₀ < v_c.

By (2.2), we see that u₀ and V₀ = v₀ satisfy the relation:

$$v_0+{\displaystyle {\int }_0^1}{u}_0\mathit{\text{dx}}=K.$$ (3.21)

The integral of u₀ can be approximated by contributions from the two outer regions (to the left and the right of the front) and a 𝒪(ε) contribution from the inner region:

$${\displaystyle {\int }_0^1}{u}_0\mathit{\text{dx}}={\displaystyle {\int }_0^{\varphi (t)-𝒪(\epsilon )}}{u}_0\mathit{\text{dx}}+{\displaystyle {\int }_{\varphi (t)+𝒪(\epsilon )}^1}{u}_0\mathit{\text{dx}}+𝒪(\epsilon )=u_{+}(v_0){\varphi }_0(t)+u_{-}(v_0)(1-{\varphi }_0(t))+𝒪(\epsilon ),$$

where we have used (3.13) in the second equality. Discard terms of 𝒪(ε). The reaction-diffusion system is then reduced to the following ordinary-differential-algebraic system:

$$\begin{array}{cc}\frac{d{\varphi }_0}{\mathit{\text{dt}}}=c(v_0),\hfill & v_0=K-u_{+}(v_0){\varphi }_0-u_{-}(v_0)(1-{\varphi }_0),\hfill \end{array}$$ (3.22)

where c(v₀) is given by (3.19). In (3.22), the total amount of material, K, is allocated to a band of width ϕ₀ at level u₊, a band of width 1 − ϕ₀ at level u₋, and a homogeneous level of v₀ across the entire interval.

We now show that the front speed, dϕ₀/dt, and the rate of change dv₀/dt, have opposite signs. Differentiating the relation f(u_±(v), v) = 0 with respect to v and using (2.11) leads to

$$0={(\frac{\partial f}{\partial u}\frac{{\mathit{\text{du}}}_{\pm }}{\mathit{\text{dv}}}+\frac{\partial f}{\partial v})|}_{u=u_{\pm }(v)}>(1+\frac{{\mathit{\text{du}}}_{\pm }}{\mathit{\text{dv}}}){\frac{\partial f}{\partial u}|}_{u=u_{\pm }(v)}.$$ (3.23)

Using (2.9) we conclude that:

$$1+\frac{{\mathit{\text{du}}}_{\pm }}{\mathit{\text{dv}}}>0.$$ (3.24)

Differentiating the second relation in (3.22) with respect to t results in:

$$(1+\frac{{\mathit{\text{du}}}_{+}(v_0)}{\mathit{\text{dv}}}{\varphi }_0+\frac{{\mathit{\text{du}}}_{-}(v_0)}{\mathit{\text{dv}}}(1-{\varphi }_0))\frac{{\mathit{\text{dv}}}_0}{\mathit{\text{dt}}}=-(u_{+}(v_0)-u_{-}(v_0))\frac{d{\varphi }_0}{\mathit{\text{dt}}}.$$ (3.25)

Since the front position must reside within a domain of unit length, we have 0 < ϕ₀ < 1. Using this and (3.24), we see that the factor multiplying dv₀/dt in (3.25) is positive. Since (u₊ − u₋) > 0, we conclude from (3.25) that dv₀/dt and dϕ/dt have opposite signs. Thus, v₀ is depleted as the wave progresses across the domain. This result also implies that the stalled front position is stable. It is interesting that this conclusion was obtained using the two conditions, bistability and homogeneous stability.

Suppose v is sufficiently large initially, i.e., v₀ > v_c at t = 0. Since dϕ₀/dt is positive for v₀ > v_c, dv₀/dt < 0. Thus, v₀ decreases as the front ϕ₀ advances. If v₀ approaches v_c the front will come to a halt, i.e. will become pinned. Suppose the front is pinned at ϕ_p. Then ϕ_p can be determined as follows. When the wave pins, we have

$$v_c=K-u_{+}(v_c){\varphi }_p-u_{-}(v_c)(1-{\varphi }_p).$$ (3.26)

We can interpret (3.26) as a relation between ϕ_p and K. We must have 0 < ϕ_p < 1. This leads to a condition on K for wave-pinning to occur:

$$v_c+u_{-}(v_c)<K<v_c+u_{+}(v_c)$$ (3.27)

that is, for wave-pinning to occur, the total concentration of chemical in the domain must fall within a range given by (3.27). The pinned front is stable; if the front is perturbed, it will relax back to the pinned position ϕ_p as can be seen from the velocity sign condition and the fact that $\frac{d{\varphi }_0}{\mathit{\text{dt}}}\text{ and }\frac{{\mathit{\text{dv}}}_0}{\mathit{\text{dt}}}$ have opposite signs.

We now illustrate the above theory with the reaction term (2.14). In this case, the reaction term is a cubic polynomial in u, and we may apply (3.20) to find an explicit expression for c(v). The leading order equations (3.22) become:

$$\begin{array}{cc}\frac{d{\varphi }_0}{\mathit{\text{dt}}}=\frac{v_0-1}{\sqrt{2}},\hfill & v_0=K-(1+v_0){\varphi }_0.\hfill \end{array}$$ (3.28)

From (3.28), we find that the wave stops when v₀ = 1 ≡ v_c. Condition (3.27) reduces to:

$$1<K<3.$$ (3.29)

Solving (3.28) for v₀, we obtain

$$\begin{array}{cc}\frac{d{\varphi }_0}{\mathit{\text{dt}}}=\frac{1}{\sqrt{2}}(\frac{K-\varphi }{1+\varphi }-1),\hfill & v_0=\frac{K-{\varphi }_0}{1+{\varphi }_0}.\hfill \end{array}$$ (3.30)

The position at which the wave stalls, is therefore ${\varphi }_p=\frac{K-1}{2}$. Fig. 3.1 shows that predictions of the ODE (3.30) agree with numerical solutions to the full PDE system (2.6) using the cubic reaction kinetics, (2.14). The exact front position is calculated from the numerical solution of the PDE system by tracking the position ϕ_num at which u = u_m(v) (u_m = 1 for reaction kinetics (2.14)). ϕ_num(t₀) is used as an initial condition, where t₀ ≈ 0 is a time at which the solution to the PDE system has relaxed to the form assumed in the asymptotic calculations. The error decreases with time as the wave becomes pinned. Based on the numerical evidence, we find that the leading order approximation is accurate to order ε. To get a measure of the error of the leading term approximation, we can calculate the next term in the asymptotic expression. We refer the reader to [11].

Fig. 3.1.

(a) Evolution of the front position ϕ_num from a numerical solution to (2.6)–(2.14) with ε = 0.05, D = 1 (solid), and from the zero order asymptotic order approximation, ϕ₀ from Eq. (3.30) (dashed). (b) The error (×10⁻³), ϕ_num − ϕ₀ vs time. (c) The effect of ε on the error ϕ_num − ϕ₀.

3.3. Multiple Layers, Long Time Behavior and Higher Dimensions

In the previous section, we discussed the behavior of system (2.6) in the intermediate time scale under the assumption that the initial profile consists only of a single front. We discuss what happens when the initial profile has multiple fronts or layers. Let ϕ_k(t), k = 1, ⋯ n be the front positions so that ϕ_k(t) < ϕ_k+1(t). For notational convenience, we let ϕ₀(t) = 0 and ϕ_n+1(t) = 1. If u transitions from u₊ to u₋ as we cross a front in the positive x direction, we shall call this a positive front. If the transition is from u₋ to u₊, we call this a negative front. In the sequel, we shall assume that ϕ₁(t) is a positive front. The case in which ϕ₁(t) is a negative front can be treated in an analogous fashion. If ϕ₁(t) is a positive front, all fronts with odd k are positive fronts and all fronts with even k are negative fronts. Through an analysis similar to the one in the previous Section, we may conclude that the dynamics of the fronts can be tracked by the following ODE system, similarly to (3.22):

$$\frac{d{\varphi }_k}{\mathit{\text{dt}}}=c(v)\text{ if }1\le k\le n\text{is odd},$$ (3.31)

$$\frac{d{\varphi }_k}{\mathit{\text{dt}}}=-c(v)\text{ if }1\le k\le n\text{is even},$$ (3.32)

$$\begin{array}{cc}K=u_{+}(v)L_{+}+u_{-}(1-L_{+}),\hfill & L_{+}={\displaystyle \sum _{0\le 2l\le n}}({\varphi }_{2l+1}-{\varphi }_{2l}).\hfill \end{array}$$ (3.33)

For simplicity of notation, we have dropped the additional subscript showing that the above are leading order approximations. As the fronts evolve, it is possible that adjacent fronts will collide. In this case, two fronts will disappear, and the dynamics can be continued by renaming the fronts and applying the above ODE system with n − 2 fronts instead of n fronts. If front ϕ₁(t) or ϕ_n(t) hits either x = 0 or x = 1 respectively, one can again write down an ODE for the front positions with n − 1 fronts valid after this incident.

As t → ∞ in the above ODE system, it is possible that the final configuration will still consist of multiple fronts, despite possible annihilations of fronts that may have occurred. At this point, v = v_c, and all fronts have velocity 0. As far as the intermediate time scale is concerned, these multiple front solutions are stable.

A natural question is whether these multiple front solutions will slowly evolve beyond the intermediate time scale. In this long time scale, v is almost exactly equal to v_c everywhere. Asymptotic calculations show that the evolution of multiple fronts are very similar to that of the mass-constrained Allen Cahn model, whose long time behavior has been studied extensively [39, 28, 36]. In the mass-constrained Allen Cahn model, multiple front solutions are known to slowly evolve to a single front solution. Thus, multiple front solutions are metastable, and the only genuinely stable solutions are the single front solutions. The time scale of this evolution is, however, “exponentially slow” [36].

It is possible to write down higher dimensional versions of the model present system, in which with u diffusing on a surface and v in the interior. The behavior of such a model is essentially the same to leading order as the one-dimensional model in the short and intermediate time scales. In the long time scale, the dynamics reduces, again, to that of mass-constrained Allen Cahn. Here, the curvature of the transition layer will play a role in the long-time evolution, a feature not seen in the one-dimensional model [29, 39]. Effects of interface curvature are observed in 2D simulations of the RD system with (2.3) (Vanderlei et al). In related, more biochemically detailed models for cell motility (Marée et al, personal communication) such effects provide feedback from cell shape to dynamics of the RD regulatory system.

4. Bifurcation Structure of the Wave-Pinning System

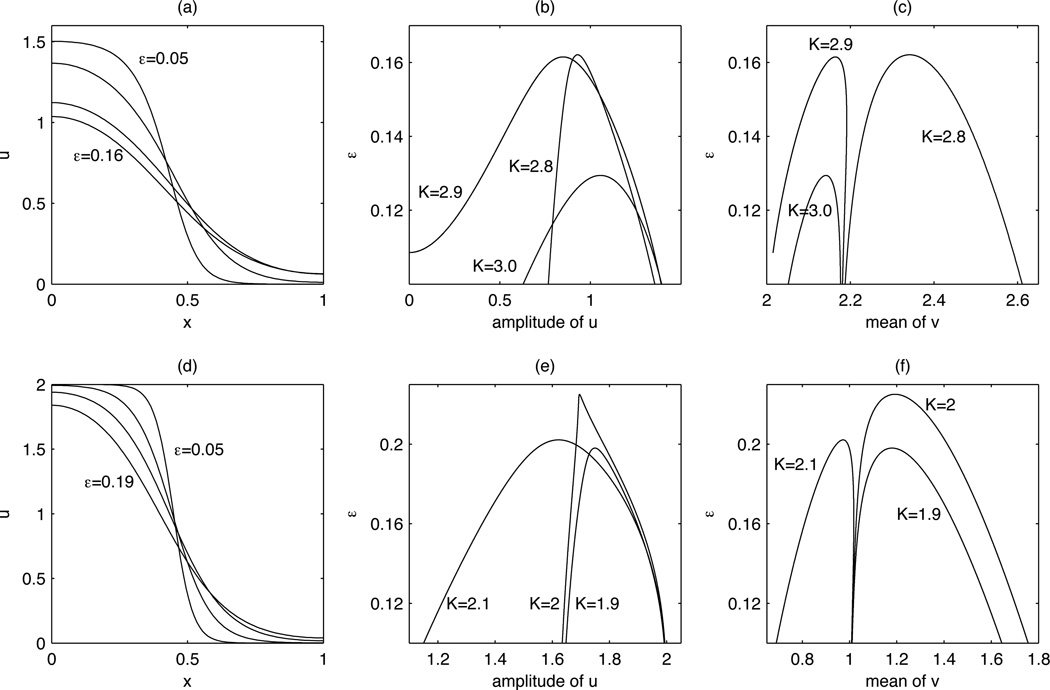
As we saw in the previous section, wave-pinning behavior occurs for small values of ε. In this regime, the pinned single front solution (which we shall hence forth refer to as the pinned solution or pinned front) is a stable stationary solution of the system. A natural question is whether this pinned solution persists as the value of ε is increased. If ε² = D in (2.6), such stable front solutions cannot exist. We thus expect that there is some value of ε above which the pinned solution ceases to exist. We simulated (2.6) to steady state and gradually increased the value of ε. Fig. 3.2(a) and (d) show the results of sample computations when (2.13) and (2.14) are used for the reaction term. As ε increases from a small value, there is a gradual change in the wave shape and stall position. Beyond some ε_c, the pinned front disappears and is replaced by a stable spatially homogeneous solution. An interesting feature of this transition is that it is “abrupt”: the amplitude of the front (the difference between the maximum and minimum values of u) does not vanish gradually as ε approaches ε_c. In Section 4.1, we shall explore the bifurcation structure for (2.13) and (2.14). In Section 4.2, we focus on obtaining detailed information on the bifurcation structure for (2.14). In Section 4.3, we indicate other possible bifurcations we may expect of the pinned solution.

Fig. 3.2.

The effect of ε on wave shape and existence/stability for reaction terms (2.13) (a–c) and (2.14) (d–f) with D = 1. (a, d): the shape of the pinned wave with (a) K = 2.8 for ε = 0.05, 0.1, 0.15, 0.16 and (d) K = 1.9 for ε = 0.05, 0.1, 0.15, 0.19. The front gets shallower and broader as ε increases, losing stability at (a) ε_c ≈ 0.1621 (d) ε_c ≈ 0.1980. We plot the amplitude of u (in b, e) and the mean of v (in c, f) as the pinned solution is continued for K = 2.8, 2.9, 3.0 for (b, c) and K = 1.9, 2, 2.1 for (e, f). The peaks correspond to saddle-node bifurcations. In (b), the amplitude approaches u₊(v_c) ≈ 1.5150 for the pinned front and decreases as the solution is continued. For K = 2.9, the amplitude reaches 0, at which there is a pitchfork bifurcation (see Section 4.3). In (c), the mean of v is close to v = v_c = 2.17506 for the pinned solution. In (e), the amplitude is close to 2 for the pinned front. In (f), the mean of v is close to 1 for the pinned solution. Note the similarity of (f) with Fig. 4.2.

4.1. Bifurcation at finite D

For fixed D > 0 and K chosen in a suitable range, there is a stable front solution to system (2.6) (i.e., the pinned front) for ε sufficiently small. As discussed, there is a value ε = ε_c above which this pinned solution cannot be continued. Thus, ε_c is a function of D and K.

We compute ε_c by numerically continuing the pinned front solution as we vary ε. The details of the method we use can be found in [11]. Computational results are given in Fig. 3.2 (panels b, c for reaction terms (2.13) and panels e, f for reaction terms (2.14)). For all values of D and K tested, the numerical results indicated a fold (saddle-node) bifurcation at ε_c. The pinned solution is stable until ε = ε_c is reached, and this merges with an unstable front solution (saddle point).

The dependence of ε_c on D and K is plotted in Figure 3.3, illustrating the possibility that for fixed ε and K (e.g. ε = 0.22, K = 2.1 in (b)), varying D (e.g. by sequentially inhibiting the GDIs that make Rho proteins cytosolic), could lead to gain/loss of polarity as the cusp in the εK plane gets displaced. For some D settings, the indicated point is inside the polarity region, and for other values it is outside.

Fig. 3.3.

Bifurcation diagrams showing the wave-pinning regimes (always below the displayed curve(s)) in the Kε plane for kinetics (2.13) (in a) and (2.14) (in b). The critical value of ε, ε_c, is plotted as a function of K for fixed D. The five solid lines correspond to D = 0.25, 0.5, 1, 2, 4. The dashed line in (b) is the D → ∞ curve (computed separately, see Section 4.2).

Recall from (3.29) that K_min = 1 < K < 3 = K_max is the wave-pinning regime for (2.14). For (2.13), the wave-pinning regime may be computed using (3.27) to yield K_min < K < K_max where K_min ≈ 2.1751, K_max ≈ 3.6901. For both (2.13) and (2.14), we sampled K between (3K_min + K_max)/4 < K < (K_min + 3K_max)/4. For both reaction terms, and fixed D, there is a value K = K_m at which ε_c reaches a sharp peak. (See discussion, end of next section.) The computed results indicate that ε_c is uniformly bounded in D and K. In particular, we observe that, for fixed K, ε_c(D, K) tends to some value as D is taken large. This serves as one motivation for studying the limit D → ∞, to which we shall now turn.

4.2. Bifurcation Diagram in the limit D → ∞

Here, we study the bifurcation structure of the following system:

$$\begin{array}{ccc}\epsilon \frac{\partial u}{\partial t}={\epsilon }^2\frac{{\partial }^{2}u}{\partial x^2}+f(u,v),\hfill & v=K-{\displaystyle {\int }_0^1}\mathit{\text{udx}},\hfill & {\frac{\partial u}{\partial x}|}_{x=0,1}=0.\hfill \end{array}$$ (4.1)

This system can be obtained formally by letting D → ∞ in (2.6). From a biophysical standpoint, we are making the assumption that the cytosolic concentration v is well-mixed so that it is spatially constant, a common assumption in polarization models [17]. In Section 3.2, the well-mixed assumption emerged as a consequence of our asymptotic analysis. System (4.1) is often referred to as the shadow system of (2.6) [25, 5, 8] and captures the leading order behavior of system (2.6).

The steady state solution of (4.1) satisfies:

$$\begin{array}{ccc}{\epsilon }^2\frac{{\partial }^{2}u}{\partial x^2}+f(u,v)=0,\hfill & v=K-{\displaystyle {\int }_0^1}\mathit{\text{udx}},\hfill & {\frac{\partial u}{\partial x}|}_{x=0,1}=0.\hfill \end{array}$$ (4.2)

We shall view (4.2) as an ODE for u to be solved in the “time” variable x. It is slightly more convenient to use τ = x/ε as our “time” variable. Rewrite the first equation as a system of first order ODEs:

$$u_{\tau }=w,$$ (4.3a)

$$w_{\tau }=-f(u,v).$$ (4.3b)

For Eqs. (4.3) there is an “energy”. Multiplying (4.3b) by w = u_τ and integrating, we obtain

$$\begin{array}{ccc}\hfill w^2=F(u,v,B),& F(u,v,B)=-B+F_0(u,v),\hfill & F_0(u,v)=-{\displaystyle {\int }_0^u}2f(s,v)\mathit{\text{ds}}\hfill \end{array}$$ (4.4)

where B is an integration constant. Consider the uw phase plane that corresponds to system (4.3). The solution curves of (4.3) coincide with the level curves of the function w² = F₀(u, v) (see Fig. 4.1). Recall that the function f(u, v) is bistable in u for fixed v satisfying v_min < v < v_max (the bistability condition). We focus only on cases in which v falls within this bistable range. In this case, the function y = F₀(u, v) for fixed v has the form of a double well potential, whose local minima are at u = u₊, u₋ and whose local maximum is at u = u_m. A stationary solution corresponds to a solution trajectory in the uw phase plane that starts and ends at the u-axis (or w = u_τ = εu_x = 0), given the no-flux boundary conditions at x = 0, 1. It is clear that there can only be such a trajectory if B = F₀(u, v) as an equation for u has four distinct solutions (see Fig. 4.1). Let the two middle roots be u₀ and u₁ (we assume u₀ < u₁). Then, stationary single front solutions correspond to the “half loop” trajectory that connects (u, w) = (u₀, 0) and (u₁, 0). Such stationary single front solutions must be either monotone increasing or decreasing. In fact, the only stationary solutions (2.6) can have are multiple “half loop” trajectories that correspond to periodic multiple front solutions.

Fig. 4.1.

Typical shapes of the functions y = F₀(u, v) (panels a,c) and level curves of w² = F₀(u, v) (panels b, d) in the uw phase planes for kinetics (2.14) for v = 1 (right) and v = 9/8 (left). It is clear that there can only be a half-loop trajectory when F₀(u, v) = B has four distinct solutions. This happens when B_min < B < B_max. Note that, as B ↘ B_min, the half loop approaches either a heteroclinic or (half of) a homoclinic orbit. As B ↗ B_max, the half loop approaches the neutral center (u, w) = (u_m, 0).

For every (v, B) such that F(u, v, B) = 0 has four solutions in u, there is a corresponding half loop trajectory. These half loop trajectories form a two parameter family of possible stationary single front solutions (henceforth “fronts”). Let 𝒟_vB be the range of (v, B) values for which F(u, v, B) = 0 has four solutions. It is clear that (see Fig. 4.1):

$$\begin{array}{cc}\hfill {𝒟}_{\mathit{\text{vB}}}& =\{(v,B)\in {ℝ}^2|v_{\text{min}}<v<v_{\text{max}},B_{\text{min}}(v)<B<B_{\text{max}}(v)\}\hfill \\ B_{\text{min}}(v)\hfill & =\text{max}{F}_0(u_{\pm }(v),v),B_{\text{max}}(v)=F_0(u_m(v),v)\hfill \end{array}$$ (4.5)

The expression for B_max denotes the greater of the values F₀(u₊(v), v) and F₀(u₋(v), v). We thus have a correspondence between (v, B) values in 𝒟_vB and half-loop trajectories. The set 𝒟_vB exhausts all possible half-loop trajectories and this correspondence is expected to be one-to-one if the reaction term f is not pathological. For reaction terms (2.14), (2.15) or (2.8), this correspondence is indeed one-to-one. We shall henceforth assume this one-to-one correspondence.

The task of finding front solutions has now been reduced to finding the suitable half-loop trajectories that satisfy the two conditions:

$$u_x(x=0,1)=u_{\tau }(\tau =0,1/\epsilon )=0,$$ (4.6)

$$v=K-{\displaystyle {\int }_0^1}\mathit{\text{udx}}=K-\epsilon {\displaystyle {\int }_0^{1/\epsilon }}\mathit{\text{ud}}\tau .$$ (4.7)

First, consider (4.6). Half-loop solutions automatically satisfy w = u_τ = 0 and hence u_x = 0 at the endpoints, but this does not necessarily mean that the endpoints correspond to x = 0(τ = 0) and x = 1(τ = 1/ε). We must thus impose the condition that the domain length is 1. Suppose the front solution has value u₀ at x = 0 and u₁ at x = 1, u₀ < u₁ (and is monotone increasing w.l.o.g.) The domain length condition reduces to:

$$1={\displaystyle {\int }_0^1}\mathit{\text{dx}}={\displaystyle {\int }_{u_0}^{u_1}}\frac{\mathit{\text{dx}}}{\mathit{\text{du}}}\mathit{\text{du}}=\epsilon {\displaystyle {\int }_{u_0}^{u_1}}\frac{\mathit{\text{du}}}{\sqrt{F(u,v,B)}}\equiv \epsilon I(v,B)$$ (4.8)

where we used (4.4). The above change of variables is valid because the stationary front solution is monotone increasing. Note that u₀ and u₁, being the middle roots of the equation F(u, v, B) = 0, are functions of v and B. Condition (4.7) can, likewise, be written as

$$K=v+\epsilon {\displaystyle {\int }_{u_0}^{u_1}}\frac{\mathit{\text{udu}}}{\sqrt{F(u,v,B)}}\equiv v+\epsilon J(v,B).$$ (4.9)

We have thus reduced (4.2) to the two integral constraints (4.8) and (4.9). Furthermore, the integral constraints incorporate the fact that we seek single-front solutions; (4.2) is satisfied by any stationary solution. Given ε and the total mass K, we may solve (4.8) and (4.9) for v and B, which in turn uniquely determine the half-loop trajectory, and hence, the solution u.

Since ε ≠ 0, we may eliminate ε from (4.9) and (4.8). We have:

$$Q_K(v,B)\equiv (K-v)I(v,B)-J(v,B)=0.$$ (4.10)

If we can find the zero set of Q_K(v, B) where (v, B) ∈ 𝒟_vB, we will have obtained all single front stationary solutions for a fixed value of K (with v in the bistable range) regardless of whether it arises as a continuation of the wave-pinned solution.

Any point on this zero set corresponds to a different front solution, and the value of ε can be recovered by using (4.8). Consider the map:

$$ℳ:(v,B)\mapsto (M,\epsilon )=(M(v,B),{(I(v,B))}^{-1})$$ (4.11)

where the function M(v, B) is chosen so that the map ℳ defines a homeomorphism on 𝒟_vB. Note that the choice of M is far from unique; we shall see that M(v, B) = v works well for (2.14) and (2.15). Half-loop trajectories can then be parametrized by (M, ε) instead of (v, B). The zero-set of Q_K(v, B) in 𝒟_vB can be mapped by ℳ in a one-to-one fashion to yield a bifurcation curve on the Mε plane.

Up to now, the treatment has been fully general. We now apply this methodology to the case when the reaction term is given by (2.14). We shall be interested in obtaining the bifurcation diagram when 1 < K < 3, the wave-pinning regime (see (3.29)). First, we note that 0 < v is the bistable range. For fixed K, the range of possible values of v can be further restricted using the mass constraint:

$$v<v+{\displaystyle {\int }_0^1}\mathit{\text{udx}}=K<v+u_1<v+(1+v).$$ (4.12)

Therefore, we may restrict our search of the zero set of Q_K(v, B) to $\frac{K-1}{2}<v<K$.

We thus numerically evaluate Q_K(v, B) at sample points in the range ${𝒟}_{\mathit{\text{vB}}}^K={𝒟}_{\mathit{\text{vB}}}\cap \{\frac{K-1}{2}<v<K\}$ to find the zero set of Q_K(v, B). More specifically, we fix v and sample B uniformly within the admissible range. If there are adjacent sample B points for which Q_K(v, B) changes sign, a zero is obtained between these values by bisection. This procedure is repeated for v values uniformly sampled in (K − 1)/2 < v < K. Where the zero set has a complicated structure, sampling is refined to clarify this structure. Once the zero-set is obtained, we use the map ℳ with M(v, B) = v (see (4.11)) to obtain a bifurcation curve in the vε plane. Computational evidence indicates that ε = (I(v, B))⁻¹ is an increasing function of B for fixed v, and thus ℳ: (v, B) ↦ (v, ε) is a homeomorphism on 𝒟_vB. We note that the numerical evaluation of the integrals I(v, B) and J(v, B) needed in the evaluation of Q_K(v, B), is not entirely trivial, especially when B is close to B_min. This is related to the fact that the half-loop trajectories come very close to heteroclinic or homoclinic orbits on the uw phase plane. The techniques used to overcome this difficulty are discussed in [11].

We can explicitly obtain the region 𝒟_vε = ℳ(𝒟_vB) by studying the integral I(v, B). Assuming that I(v, B) > 0 is a decreasing function of B for fixed v, we have only to know the limiting values of I(v, B) as B → B_min(v) and B_max(v) (see (4.5)). As B → B_min for fixed v, the half loop trajectories approach (half of) a homoclinic orbit or a heteroclinic orbit in the uw plane (see Fig. 4.1). In either case, the total “time” it takes for the orbit to complete the half loop increases as B → B_min. Thus, I → ∞ as B → B_min. On the other hand, when B → B_max, the half-loop trajectory approaches the neutral center (u, w) = (u_m, 0) = (1, 0) in the uw phase plane. We may easily compute:

$$\underset{B\nearrow B_{\text{max}}}{\text{lim}}I(v,B)=\frac{\pi }{\sqrt{v}}.$$ (4.13)

Therefore:

$${𝒟}_{v\epsilon }=\{(v,\epsilon )\in {ℝ}^2|0<v,0<\epsilon <\sqrt{v}/\pi \}.$$ (4.14)

As one approaches the parabolic edge of 𝒟_vε, the amplitude(= u₁ − u₀) of the front solution tends to 0 and approaches the spatially homogeneous steady state (u, v) = (1, v). In fact, the parabolic edge is the only place where the amplitude tends to 0 in 𝒟_vε.

To study the stability of the stationary solutions corresponding to points on the zero set, we must compute u explicitly. Once we know v and B, we can find u₀ and u₁. We can then numerically solve the initial value problem (4.3) with u(0) = u₀ and w(0) = 0. Up to numerical error, the computed solution should, by design, satisfy u(τ = 1/ε) = u(x = 1) = u₁ and w(1/ε) = u_τ (τ = 1/ε) = εu_x (x = 1) = 0. We can then linearize about u the operator on the right hand side of (4.1). The spectrum of (the discretization of) this linearized operator, determines the linear stability of the steady state u.

The resulting bifurcation curves in the vε plane are given in Fig. 4.2. When K ≠ 2, there is at most one front solution that corresponds to each value of v (i.e., Q_K(v, B) = 0 has at most one solution in B for fixed v). For small values of ε, there are three front solutions. In order of increasing v, we denote these solutions $(u,v)=(u_{\epsilon }^{-}(x),v_{\epsilon }^{-}),(u_{\epsilon }^{\text{wp}}(x),v_{\epsilon }^{\text{wp}})\text{ and }(u_{\epsilon }^{+}(x),v_{\epsilon }^{+})$, which we call the minus, middle and plus branches respectively. We preserve this notation in our discussion of other cases in Figs 4.3–4.5.

Fig. 4.2.

Bifurcation diagrams for cubic kinetics (2.14) in the vε plane. Left to right: K < 2, K = 2, K > 2. When K ≠ 2, the middle branch is stable and the others are unstable, except for a small region 2 < K < K_p ≈ 2.00672 (see text and Fig. 4.3). When K = 2, middle and minus branches meet at a transcritical bifurcation (TC, (v_tc, ε_tc) ≈ (1, 0.23530)) and exchange stability. The values $v_{\epsilon }^{-}\text{ and }{v}_{\epsilon }^{+}$ tend to (K − 1)/2 and K, respectively, as ε → 0. The pitchfork bifurcation (PF) occurs at $(v_{\text{pf}},{\epsilon }_{\text{pf}})=(K-1,\sqrt{K-1}/\pi )$. The bifurcation diagram only shows the monotone increasing front solution. At PF, this meets with the monotone decreasing front as well as the spatially homogeneous state. SN: saddle-node bifurcation.

Fig. 4.3.

Bifurcation diagram for (2.14), K = 2.001,K_p ≈ 2.00672 (2 < K < K_p) in the vε plane. Right: magnified view. The (+, 1) and (+, 2) branches (labeled $v_{\epsilon }^{+,1}\text{ and }{v}_{\epsilon }^{+,2}$ respectively) come together at the saddle-node bifurcation denoted SN0 and the branches for (+, 2) and (+, 3) branches (labeled $v_{\epsilon }^{+,2}\text{ and }{v}_{\epsilon }^{+,3}$ respectively) come together at SN+. The (+, 2) branch is stable. At SN−, middle and minus branches come together. The dotted lines are the bifurcation curves at K = 2.

Fig. 4.5.

Bifurcation diagrams for the reaction term (2.15) in the vε plane with a = 2 and indicated values of K. Left: K = 0.1 < K_r ≈ 0.19498, Middle: K_r < K = 0.22 < K_q ≈ 0.22510, $v_{\epsilon }^{\text{pf}}$ is represented by the small portion of the curve between the pitchfork bifurcation (PF) and the saddle-node bifurcation (SN). Right: K = 0.3> K_q.

We first consider the case K < 2 (left panel). The pinned solution corresponds to the middle branch $(u_{\epsilon }^{\text{wp}}(x),v_{\epsilon }^{\text{wp}})$. The value $v_{\epsilon }^{\text{wp}}$ approaches 1 as ε → 0. We know from our asymptotic calculations that the integral ${\displaystyle {\int }_{u_0}^{u_1}}f(u,v)\mathit{\text{du}}$ vanishes to leading order when the wave stalls. This happens when the three roots u_±(v) and u_m(v) are equally spaced, which corresponds to v = 1. In the uw phase plane, $u_{\epsilon }^{\text{wp}}$ approaches a heteroclinic orbit that connects the two saddle points (u, w) = (0, 0) and (u, w) = (2, 0).

The other two front solutions are unstable with a one-dimensional unstable manifold. The values $v_{\epsilon }^{-}\text{ and }{v}_{\epsilon }^{+}$ approach v = (K − 1)/2 and v = K respectively as ε → 0. Let us consider the plus branch. As ε → 0, B approaches B_min. In the uw phase plane, $u_{\epsilon }^{+}$ approaches (half of) a homoclinic orbit that originates and ends at the saddle point (u, w) = (0, 0). As $u_{\epsilon }^{+}$ approaches this homoclinic orbit, the amount of “time” that the solution stays close to the saddle point increases, so that $u_{\epsilon }^{+}$ is very close to 0 for much of the interval 0 < x < 1. Near x = 1, there is a sharp transition zone in which $u_{\epsilon }^{+}$ makes a steep increase to u₁. This transition zone becomes increasingly narrow as ε → 0. We may say that the solution $(u_{\epsilon }^{+}(x),v_{\epsilon }^{+})$ approaches the stable homogeneous steady state (u, v) = (0, K) as ε → 0. The convergence of $u_{\epsilon }^{+}(x)$ to 0 is uniform outside of an arbitrarily small neighborhood of x = 1.

The situation for the minus branch is similar. As ε → 0, $v_{\epsilon }^{-}\to (K-1)/2$. In the uw phase plane, $u_{\epsilon }^{-}$ approaches half of the homoclinic orbit originating from the saddle point (u, w) = ((K + 1)/2, 0). The value of $u_{\epsilon }^{-}$ is close to (K + 1)/2 for most of 0 < x < 1 except for a small neighborhood around x = 0. The function $u_{\epsilon }^{-}$ converges uniformly to (K + 1)/2 on any set outside an arbitrarily small neighborhood around x = 0.

As ε is increased, there is a value $\epsilon ={\epsilon }_{\text{sn}}^{+}$ at which the middle and plus branches meet in a saddle-node bifurcation. At this point, the disappearance of the stable front solution (the middle branch) is “abrupt” in the sense that the amplitude of u is non-zero as the bifurcation is approached. This can be seen from the fact that this saddle-node bifurcation occurs in the interior of 𝒟_vε (see discussion after (4.14)).

The minus branch can be continued until it merges with a spatially homogeneous unstable steady state. This happens at the parabolic edge of 𝒟_vε (see (4.14)). Here, there is a pitchfork bifurcation at which the homogeneous steady state gives rise to two unstable front solutions, one that is monotone increasing and the other monotone decreasing. Note that, in Fig. 4.2, only the bifurcation diagram of the monotone increasing front solution is plotted. There is an identical bifurcation diagram for the monotone decreasing front, and these two solutions meet with a spatially homogeneous steady state at a pitchfork bifurcation. This homogeneous steady state corresponds to (u, v) = (1, K − 1). Using (4.14), the corresponding ε value ε_pf is equal to

$${\epsilon }_{\text{pf}}=\frac{\sqrt{v}}{\pi }=\frac{\sqrt{K-1}}{\pi }.$$ (4.15)

Linearize the operator on the right hand side of (4.1) around this homogeneous steady state, and call this operator ℒ. We can also obtain the above value by considering the spectrum of ℒ. At ε = ε_pf, one of the eigenvalues of ℒ corresponding to the wave number k = π becomes positive (see Section 3.1, in particular, equation (3.9) in the D → ∞ limit). For 1 < K < 3, expression (4.15) gives the least upper bound of the range of ε for which (not necessarily stable) single front solutions exist.

We now turn to the case K = 2. Consider (4.10) for If v = 1;

$$Q_2(1,B)={\displaystyle {\int }_{u_0}^{u_1}}\frac{1-u}{\sqrt{F(u,1,B)}}\mathit{\text{du}}=0.$$ (4.16)

Then the function F(u, 1, B) is symmetric about u = 1 and thus the same is true for u₀ and u₁ (i.e. (u₀ + u₁)/2 = 1). The above integral is therefore equal to 0 whenever it is well-defined. Therefore, all points such that v = 1 in 𝒟_vε (i.e., (v, ε) = (1, ε), 0 < ε < 1/π) are part of the bifurcation curve for K = 2. This v = 1 branch of solutions corresponds to the pinned front, which is thus stable for small ε. Denote this “middle branch” by $(u_{\epsilon }^{\text{wp}},v_{\epsilon }^{\text{wp}})$. As ε ↗ 1/π, we expect the middle branch to merge with an unstable homogeneous steady state at a pitchfork bifurcation, just like $u_{\epsilon }^{-}$ for K < 2. An unstable solution cannot give rise to two stable solutions in a pitchfork bifurcation. We conclude that the middle branch is unstable when ε is close to 1/π and that there must be an intermediate ε value between 0 and 1/π at which the middle branch loses stability.

For small ε, there are three single front solutions in the K = 2 case (labeled as in the K < 2 case). As we saw, $v_{\epsilon }^{\text{wp}}$ is always equal to 1. As ε is increased, the minus and middle branches meet in a transcritical bifurcation at ε = ε_tc ≈ 0.2353. Above ε_tc, the minus branch becomes stable and the middle branch loses stability. At $\epsilon ={\epsilon }_{\text{sn}}^{+}\approx 0.2419$, the minus and plus branches meet in a saddle-node bifurcation.

The K > 2 case is similar to the K <2 case except for fine details. When ε is small, we have three front solutions (named as before). The middle branch merges with the minus branch at $\epsilon ={\epsilon }_{\text{sn}}^{-}$ in a saddle-node bifurcation. The plus branch merges with the spatially homogeneous solution at ${\epsilon }_{\text{pf}}=\sqrt{K-1}/\pi$ in a pitchfork bifurcation.

An interesting detail in the K > 2 case is that there is a small window 2 < K < K_p ≈ 2.00672 for which the plus branch has a stable portion (see Fig. 4.3). The existence of such a portion is implied by the structure of the bifurcation diagram at K = 2. The saddle-node bifurcation at ${\epsilon }_{\text{sn}}^{+}$ should persist beyond K = 2 since saddle-node bifurcations are robust under perturbations. On the other hand, when a transcritical bifurcation is perturbed, it will generally give rise to zero or two saddle node bifurcations (see [16] for example). When K = 2 is perturbed to K < 2, the transcritical bifurcation does not give rise to any saddle node bifurcations. If perturbed to K > 2, it gives rise to two saddle node bifurcations, one of which occurs at $\epsilon ={\epsilon }_{\text{sn}}^{-}$. We shall name the other ε value $\epsilon ={\epsilon }_{\text{sn}}^0$. Both bifurcation points corresponding to $\epsilon ={\epsilon }_{\text{sn}}^0\text{ and }{\epsilon }_{\text{sn}}^{+}$ lie on the $(u_{\epsilon }^{+},v_{\epsilon }^{+})$ branch.

For 2 < K < K_p, there are three single front solutions over the range ${\epsilon }_{\text{sn}}^0<\epsilon <{\epsilon }_{\text{sn}}^{+}$, which we refer to as the (+, 1), (+, 2) and (+, 3) branches respectively in order of increasing v. The (+, 1) and (+, 2) branches meet in a saddle-node bifurcation at ${\epsilon }_{\text{sn}}^0$ and (+, 2) and (+, 3) branches meet at ${\epsilon }_{\text{sn}}^{+}$. The (+, 1) and (+, 3) branches are unstable whereas (+, 2) branch is stable. For 2 < K < K_p, therefore, there is a small window of ε values for which there is a stable front solution that cannot be reached by continuing the pinned front solution. For K ≥ K_p, the plus branch does not have a stable portion. At K = K_p, the saddle-node bifurcation points merge and disappear.

In Fig. 4.4, we show the K ε parameter region in which there is a stable single front solution. This should be seen as a refinement of the ε_c plot in Fig. 3.3 that we obtained for finite D. The region is peaked at approximately K = 2, but with some fine structure coming from the small window of front solutions that exist for 2 < K < K_p. The peaked geometry of this region comes from the fact that the saddle-node bifurcations at which the pinned solution loses stability are different for K > 2 and K < 2. At K = 2, we have a transcritical bifurcation that separates these two regimes. This explains the peaked appearance that we first saw in Figure 3.3.

Fig. 4.4.

Two parameter bifurcation plots for cubic kinetics (2.14). A stable front exists for values in the Kε parameter region bounded by the curve and the K-axis (left panel). Right: magnified “tip” of the curve. At (K_p, ε_p) ≈ (2.00672, 0.24474) the values ${\epsilon }_{\text{sn}}^{+}\text{ and }{\epsilon }_{\text{sn}}^0$ come together. At (2, ε_tc), ε_tc ≈ 0.23250, ${\epsilon }_{\text{sn}}^{-}\text{ and }{\epsilon }_{\text{sn}}^0$ come together at the transcritical bifurcation point.

4.3. Other Possible Bifurcation Structures

We now have a clear picture of the bifurcation structure for reaction term (2.14), especially when D → ∞. Given the broad similarity of the ε_c plots for (2.13) and (2.14) in Figure 3.3, it is natural to expect (2.13) to also have a bifurcation structure with features similar to (2.14). This raises the question of the generality of our findings. For other reaction terms that support wave-pinning, we may have other bifurcation scenarios. In particular, we can raise the following question. Except at K = 2, the pinned front was seen to undergo a saddle-node bifurcation in the case of (2.14), D → ∞. This bifurcation was “abrupt” in the sense that the front amplitude tends to a non-zero value as the bifurcation point is approached. Is the saddle-node bifurcation the only generic way in which the pinned front is lost? In particular, is it generically the case that the bifurcation is “abrupt”? The answers to both questions turn out to be negative. We briefly demonstrate this with a description of the bifurcation structure for the reaction term (2.15) where the pinned front can arise generically via a pitchfork bifurcation from a spatially homogeneous state. (Analysis is omitted, but proceeds along similar lines.) We here discuss the D → ∞ case, noting that computational examples can be produced in which such bifurcations occur for finite D.

For the reaction term (2.15), the middle homogeneous steady state (u_m, v) can be stable (Section 3.1). A similar conclusion is true in the D → ∞ case. This happens when a > 1, the case discussed here. (When a < 1, the full bifurcation diagram is quite similar to that of (2.14), i.e. the generic bifurcation is the saddle-node). As can be easily checked, −∞ < v < ∞ is the bistable range, and −1 < K < 1 is the range for which wave-pinning can occur. We focus on these values of K.

Consider first the spatially homogeneous steady states of the system for fixed K. For a given v, u must be either u = u₊, u₋ or u_m. There is one spatially homogeneous steady state each for u₋ and u₊: (u₋, v) = (−1, K + 1) and (u₊, v) = (1, K − 1). Consider the spatially homogeneous steady states that correspond to u = u_m. By conservation,

$$v+u_m(v)=v-\frac{\mathit{\text{av}}}{\sqrt{1+{(\mathit{\text{av}})}^2}}=K.$$ (4.17)

This equation can have three solutions in v for fixed K if a > 1 and K satisfies:

$$-K_q<K<K_q,K_q=\frac{1}{a}{(a^{2/3}-1)}^{3/2}.$$ (4.18)

It is clear that K_q is always smaller than 1. Let us call these three solutions $v_m^{-}<v_m^0<v_m^{+}$. We may adapt the calculations of Section 3.1 to the D → ∞ case. It can be checked that τ₀ = f_u − f_v < 0 at $(u_m^0,v_m^0)\equiv (u_m(v_m^0),v_m^0)$, and therefore, that this is a stable steady state so long as:

$$\epsilon >\frac{\sqrt{f_u(u_m^0,v_m^0)}}{\pi }\equiv {\epsilon }_{\text{pf}}^0.$$ (4.19)

Note that the above expression can be obtained by taking D → ∞ in (3.9). The other two homogeneous states are always unstable. When |K| > K_q (4.17) has only one solution.

The bifurcation diagram in the D → ∞ limit can be obtained as in the previous section. The possible bifurcation diagrams in the vε plane are given in Fig. 4.5, where we have taken a = 2 in (2.15). Only the case K ≥ 0 is shown. (The other case is a mirror image about the ε axis.)

For all values of −1 < K < 1, there are three single front solutions when ε is sufficiently small. Let us denote them by the minus, middle and plus branches with notation as before. There is a constant 0 < K_r < K_q (that depends on a) such that, when 0 ≤ K ≤ K_r the middle branch merges with the stable homogeneous solution $(u_m^0,v_m^0)$ in a pitchfork bifurcation. This happens at $\epsilon ={\epsilon }_{\text{pf}}^0$ defined in (4.19). The pinned front solution is stable up to this pitchfork bifurcation. Note that this is only possible since $(u_m^0,v_m^0)$ is a stable steady state for $\epsilon >{\epsilon }_{\text{pf}}^0$. The minus and plus branches are unstable and merge in pitchfork bifurcations, respectively, with the unstable homogeneous states $(u_m^{\pm },v_m^{\pm })$.

When K_r < K < K_q, the situation for the plus and minus branches does not change. However, the middle branch now loses stability in a saddle-node bifurcation with the solution branch $(u_{\epsilon }^{\text{pf}},v_{\epsilon }^{\text{pf}})$ that arises from a pitchfork bifurcation from the homogeneous state $(u_m^0,v_m^0)$. This branch is unstable. The difference between 0 ≤ K ≤ K_r and K_r < K < K_q is whether the pitchfork bifurcation at $(u_m^0,v_m^0)$ is subcritical or supercritical (see Fig. 4.5). In fact, we encountered a similar bifurcation for (2.13) when D = 1 and K = 2.9 (see Fig. 3.2 (b) and (c)).

For K > K_q, the middle branch loses stability in a saddle-node bifurcation with the minus branch. The plus branch merges with the unstable homogeneous solution $(u_m^{+},v_m^{+})$. The case K = K_q is highly degenerate and atypical, and we thus omit the details here.

Assuming that the above bifurcation picture is valid for all values of a > 1 (an observation supported by computational evidence), we can compute K_r as the value of K at which the pitchfork bifurcation at $(u_m^0,v_m^0)$ changes from being subcritical to supercritical. It is then possible to obtain an analytical expression for K_r as a function of a, using standard bifurcation theoretic calculations, a computation we do not include here in the interest of brevity (see, for example, [13] for a similar computation). From this expression, one can see that K_r → 1 as a → ∞. In other words, the range of K over which the pinned solution merges with a stable homogeneous solution increases with a, covering the entire wave-pinning regime (−1 < K < 1) as a → ∞.

For reaction term (2.14), the only generic bifurcation through which the pinned solution is lost was of saddle-node type. Reaction term (2.15) is an example in which the pinned solution can be generically lost by merging with a stable spatially homogeneous state. As a → ∞, this is the case for most values of K in the wave-pinning regime. Our study in the present section suggests a general connection between the stability of homogeneous states of type (u_m(v), v) and the type of bifurcation at which the pinned solution is lost.

5. Discussion

The simplicity of our model and the universality of reaction-diffusion systems in biology, chemistry, and physical settings suggests that wave-pinning phenomena may be quite ubiquitous [19, 31, 34, 41]. In this paper, our motivation stems from cell polarization and the biochemistry of Rho proteins, and the variables u and v correspond to active and inactive forms of one Rho protein. While there is no direct visualization of Rho GTPase wave propagation, there is experimental evidence of wave phenomena and bistability in polarized cells [30, 2, 40].

In our model, conservation of total amount of protein K_total (and in dimensionless form, mean concentration K) stems from the fact that there is no net production nor loss of total protein on the timescale of interest. Bistability arises from positive feedback in the GEF-mediated activation term. The appearance of a small parameter, ε in this problem stems from membrane confinement of one species (the active protein), reducing its rate of diffusion by orders of magnitude, relative to the rapidly diffusing inactive form (D = O(1)). The three key properties of the reaction term (bistability, homogeneous stability and the velocity sign conditions, see Section 2) are necessary and sufficient to produce the stalling wave, as shown here mathematically. Furthermore, as shown, the stalled wavefront position is stable.

Exploiting the smallness of ε using matched asymptotic analysis, we showed that both (2.3), as well as the simpler (2.14) satisfies these properties and thus supports wave-pinning. The analysis allowed us to determine the range of K values for which wave-pinning is possible. Furthermore, we were able to reduce the RD system to a simple differential algebraic system for the front position, whose explicit form could be calculated in the case of (2.14). This reduction gives an excellent approximation of the original system as ε is made small (Fig. 3.1). We briefly discussed the long-time behavior of our system as well as its higher dimensional generalizations. We argued that the long-time behavior is analogous to that of the mass-constrained Allen-Cahn model, whose properties have been well-characterized [29, 39, 28, 36].

As ε is increased, the matched asymptotic calculations are no longer valid, and the pinned front is eventually lost. This led us to examine the bifurcation structure of the system. For finite D, we did so using pseudoarclength continuation on the full PDE system (Figs. 3.2–3.3). Reaction terms (2.13) and (2.14) revealed a similar bifurcation structure. We found that the pinned front was always lost in a saddle-node (fold) bifurcation, and delineated the parameter region in the K ε plane for which wave-pinning was possible (Fig. 3.3). We obtained a complete bifurcation picture for single front solutions in the limit D → ∞ for the reaction term (2.14), using a method related to the “time map” technique [33, 7]. We found that there is a transcritical bifurcation at K = 2 (Fig. 4.2). This value acts as a “watershed”, explaining the cusp-like form seen in Fig. 3.3. Other bifurcation pictures are possible. In the case of (2.15), the pinned front solution can be lost through a pitchfork bifurcation (Fig. 4.5). The possibility of such a bifurcation depends on the stability of the “middle” homogeneous steady states.

Many other proposed models for cell polarization are based on diffusion-driven, Turing-type instabilities [35, 24, 26], in which a state that is stable in the absence of diffusion is destabilized in its presence, a mechanism fundamentally different from the wave-pinning mechanism considered here in the following ways: first, as noted in Section 3.1 and in [21], our model is not destabilized by small amplitude noise of any wavenumber, i.e. there is no Turing bifurcation in the model. Second, the timescales of polarization in our model and in Turing RD systems is vastly different (see [21]), being driven by slow growth of critical modes in the Turing systems versus moving wave propagation in ours. There are also more detailed models for the dynamics of Rho proteins [12, 18, 3]. These show similar phenomena, but their complexity interferes with a full mathematical analysis.

We conclude with a discussion of possible biological implications. The small parameter ε exploited in our analysis depends on several biological parameters including rates of diffusion D_u, reaction η, and domain size L. The necessary condition ε ≪ 1,D ≈ O(1) is satisfied by virtue of the large difference in diffusion of the membrane-bound active Rho protein and inactive form that diffuses freely in the cytosol when normal GDI protein levels occur. Normally, these rates of diffusion differ by 100-fold. Assuming a typical cell diameter of 10 µm, reaction timescale η = 1 s⁻¹, and diffusion coefficients D_u = 0.1 µm²s⁻¹ and D_v = 10 µm²s⁻¹, the dimensionless constants are ε ≈ 0.03 and D ≈ 0.1. This is within the wave-pinning regime for the Hill function kinetics (2.3). However, increasing the diffusion coefficient of the active form tenfold to D_u = 1µm²s⁻¹, or slowing down the rate of interconversion η to 0.1 s⁻¹, or decreasing the cell size to L ≈ 3 µm leads to ε ≈ 0.1 and D ≈ 1, putting the Hill function kinetics system into the bifurcation regime where wave-pinning and hence polarization would be lost.

Such predictions are experimentally testable. Cell fragments capable of polarization [38] could be made successively smaller to test the effect of domain size. The amount of Rho protein in a cell can be manipulated (see, e.g. Cdc42 variation, [1]) to investigate our prediction that polarity is present in some intermediate range of values of total Rho protein. Our results also suggest that overexpression of Rho protein, which is a standard tool to study Rho protein functions, can have the unintended effect of eliminating polarization. The mobility of cytosolic Rho proteins can be changed in various ways [9] directly, or by inhibiting GDIs [4]. We also showed (Fig 3.3) that changes in the diffusion coefficient D_v (affected by the GDI level) may also lead to gain/loss of wave-pining polarity, as the border between wave-pinning and homogeneous regimes is shifted. Experiments in budding yeast show that non-functional GDIs can result in dissipation of polarity [32], which supports our predictions.