Continuous Locomotion-Mode Identification for Prosthetic Legs Based on Neuromuscular–Mechanical Fusion

Abstract

In this study, we developed an algorithm based on neuromuscular–mechanical fusion to continuously recognize a variety of locomotion modes performed by patients with transfemoral (TF) amputations. Electromyographic (EMG) signals recorded from gluteal and residual thigh muscles and ground reaction forces/moments measured from the prosthetic pylon were used as inputs to a phase-dependent pattern classifier for continuous locomotion-mode identification. The algorithm was evaluated using data collected from five patients with TF amputations. The results showed that neuromuscular–mechanical fusion outperformed methods that used only EMG signals or mechanical information. For continuous performance of one walking mode (i.e., static state), the interface based on neuromuscular–mechanical fusion and a support vector machine (SVM) algorithm produced 99% or higher accuracy in the stance phase and 95% accuracy in the swing phase for locomotion-mode recognition. During mode transitions, the fusion-based SVM method correctly recognized all transitions with a sufficient predication time. These promising results demonstrate the potential of the continuous locomotion-mode classifier based on neuromuscular–mechanical fusion for neural control of prosthetic legs.

I. Introduction

Lower limb amputation is a major impairment that can interfere with basic activities of daily living [1]. One of the major functions of prosthetic legs is to restore the locomotion of lower limb amputees [2]. Focusing on transfemoral (TF) prostheses, most of commercially available prosthetic knees are passive devices, which are mainly designed to fulfill two major functions during level-ground walking: 1) generating smooth knee flexion and, then, extension through the swing phase and 2) creating stable stance phase [1]. However, leg amputees wearing passive devices cannot negotiate uneven terrains, such as stairs and ramps, in a natural and efficient way due to the lack of active net torque in artificial knees. Advancements in embedded electronics and electromechanical actuators have propelled the recent development of powered artificial legs [3]–[5]. Powered TF prostheses usually employ a finite-state machine (FSM) to control the knee joint impedance or knee position in each gait phase (i.e., state in the FSM) [3], [4]. The desired impedance of powered knees also depends on the locomotion mode [4], [5], as the dynamics and kinematics of the knee joint varies across different locomotion modes (e.g., level-ground walking and stair ascent/descent). Therefore, in order to perform seamless and safe locomotion-mode transitions, the user must “tell” the prosthesis the intended function before executing the transitions so that the controller of the artificial knee can switch the control mode in time.

Various intent recognition strategies have been developed to enable intuitive prosthetic leg control. One method is called “echo control” [6], [7], in which the prosthetic leg simply repeats the motion of the sound leg. The user must use the sound leg to lead task transitions. Such an approach has been adopted to allow for smooth prosthesis control during gait initiations and terminations; however, the assumption of this approach is that the motions of two legs are symmetric during locomotion, which is not always valid. For example, the motions of lower limbs are different in the transition from level-ground walking to stepping over an obstacle. In addition, this method requires the user to don and doff an instrumented orthotic on the unimpaired leg and cannot be used by bilateral leg amputees. A recent study reported an intent recognition algorithm based on data from mechanical sensors mounted on a powered prosthesis [8]. One TF amputee performed sitting, standing, and level-ground walking, while wearing the powered prosthesis. The algorithm recognized gait initiations, terminations, and transitions between sitting and standing based on ground reaction forces (GRF) and the kinematic patterns of the prosthesis. The study reported 100% accuracy in recognizing task transitions and only three false identifications in a 570-s trial period. These results demonstrated the potential of intent recognition based on mechanical information for control of prosthetic legs. However, only a young TF amputee was tested. The initiation and termination of level-ground walking were the only locomotion transitions tested in this study. In addition, a 500-ms system delay was reported, which may be inadequate for smooth control of prosthetic legs during transitions between dynamic walking modes. Promptly recognizing transitions between locomotion modes, such as level-ground walking and stair descent, is very important to ensure patient safety. Furthermore, as additional ambulation modes are incorporated into the control system, the permutations between mode transitions increase, which makes identifying mode transitions much more difficult in comparison to only identifying gait initiation and termination.

The mechanical sensors respond to the patient's movements, whereas electromyographic (EMG) signals precede movement onset and may be used to help predict task transitions. Surface EMG signals are one of the major neural-control sources for powered upper limb prostheses, experimental motorized orthoses, and rehabilitation robots. Although proportional myoelectric control and advanced EMG pattern-recognition-based control have been used in upper limb prostheses for decades [9]–[12], no EMG-controlled lower limb prostheses are commercially available. This is because these prosthetic legs have been passive and have performed reasonably well. With the advent of powered lower limb prostheses, a much greater scope of capabilities is now possible, i.e., to fully exploit their dexterity, a neural source of user intent is now required. Our research group has developed a phase-dependent EMG pattern recognition strategy for locomotion-mode identification [13]. This strategy was tested on eight able-bodied subjects and two subjects with long TF amputations. Four discrete gait phases were considered in this study. Around 90% accuracy for identifying seven locomotion modes was obtained when EMG signals from thigh muscles of able-bodied subjects or residual thigh muscles of amputee subjects were used as input to the system. Although the results were promising, an increase in classification accuracy is warranted to ensure safe and robust operation.

One potential solution is data fusion—a field of study that integrates data from multiple sensors to achieve improved accuracy for detection, estimation, or classification [14]. Data fusion has been successfully applied in a variety of fields, including communications, medical, and robotics applications [14]–[16]. Data fusion has been also used with EMG and acoustic speech to enhance speech recognition in noisy environments [17]. Since promising results for user intent identification have been reported using EMG signals from residual muscles [13] or mechanical measurements from prosthetic legs [8], fusing both data sources may further improve the accuracy of locomotion-mode identification. We call such a design neuromuscular–mechanical fusion.

In this study, we developed an interface based on neuromuscular–mechanical fusion to continuously recognize a variety of ambulation tasks and predict task transitions. This study extends previous research as follows.

1. This paper reported a well-conceived application of data fusion in a novel biomedical problem, i.e., identification of amputees' locomotion modes for intuitive control of prosthetic leg.

2. The designed pattern recognition scheme interprets a combination of neural and mechanical inputs and provided continuous decisions, aimed for real-time implementation.

3. This study considered six ambulation modes and five mode transitions, which are commonly encountered in the daily life and are less studied than the transitions at gait initiations and terminations.

4. A new evaluation approach and metrics were designed and applied in quantifying the performance of the designed locomotion-mode identification system.

5. Data collected from five patients with TF amputations were used to evaluate the potential of the fusion algorithm for neural control of artificial legs.

The results of this study may aid the further development of neurally controlled powered artificial legs to enhance the mobility of leg amputees.

II. Methods

A. Participants and Measurements

This study was conducted under Institutional Review Board (IRB) approval with the informed consent of all subjects. Five subjects with unilateral TF amputations (TF01–05) were recruited; their demographic information is shown in Table I. All five subjects wore prosthetic legs on a daily basis.

Table I. Summary of Demographic Information for Five Subjects With TF Amputations (TF01–TF05).

	Age	Weight (kg)	Height (cm)	Gender	Years post-amputation	Residual limb length ratio*	Prosthesis for daily use
TF01	51	80.3	177.8	M	32	82%	SNS Knee
TF02	56	75.2	173.4	M	38	62%	SNS Knee
TF03	26	53.4	160.2	F	25	40%	Total Knee
TF04	42	66.1	165.8	F	11	77%	C-Leg
TF05	57	75.8	175.3	M	31	51%	RHEO

^*Residual limb length ratio: the ratio between the length of the residual limb (measured from the ischial tuberosity to the distal end of the residual limb) to the length of the non-impaired side (measured from the ischial tuberosity to the femoral epicondyle).

Surface EMG signals from two gluteal muscles (gluteus maximus and gluteus medius) on the amputated side and the thigh muscles of the residual limb were monitored. The number of EMG electrodes (7–9) placed on the residual limb depended on the residual limb length. The targeted thigh muscles were sartorius (SAR), rectus femoris (RF), vastus lateralis (VL), vastus medialis (VM), gracilis (GRA), biceps femoris long head (BFL), semitendinosus (SEM), biceps femoris short head (BFS), and adductor magnus (ADM). Note that the locations for electrode placements were approximate and guided by palpation and EMG recordings when the subjects were instructed to perform hip flexion/extension and hip adduction/abduction and to imagine and execute knee flexion/extension. Since the designed algorithm in this study searches the patterns of EMG signals, precisely targeting specific surface muscle is not necessary, but recording neuromuscular control information for the motions of hip and knee joints is required. A ground electrode was placed on the bony area near the anterior iliac spine. The EMG electrodes were embedded in customized gel liners (Ohio Willow Wood, OH) for both comfort and reliable electrode–skin contact. A 16-channel EMG system (Motion Lab System, LA) was used to collect EMG signals from all subjects. The EMG system filtered signals between 20 and 420 Hz with a pass-band gain of 1000 and, then, sampled at 1000 Hz. Mechanical GRF and moments were measured by a 6-DOF load cell (Bertec Corporation, OH) mounted on the prosthetic pylon. The six measurements from the load cell were also sampled at 1000 Hz. Gait events were detected by insole pressure sensors under both feet (Pedar-X, Novel Electronics Inc., Germany). Experiments were videotaped. All data recordings were synchronized.

B. Experimental Protocol

During the experiment, the TF subjects wore a hydraulic passive knee. Experimental sockets were duplicated from each subject's ischial containment socket with suction suspension. In addition, total elastic suspension belts were used to reinforce socket suspension. The subjects received instructions and practiced the tasks several times prior to measurement.

Six locomotion modes and five mode transitions were investigated. The locomotion modes were level-ground walking (W), stepping over an obstacle (O), stair ascent (SA), stair descent (SD), ramp ascent (RA), and ramp descent (RD). The investigated task transitions were level-ground walking to stair ascent, ramp ascent, and stepping over an obstacle (i.e., W→SA, W→RA, and W→O) and stair descent and ramp descent to level-ground walking (i.e., SD→W and RD→W). Note that the experimental obstacle course in the laboratory did not have enough platform length to capture SA/RA→W and W→SD/RD.

During testing, subjects were instructed to walk at a comfortable speed. Level-ground walking was tested on a straight walkway. For the task of stepping over an obstacle, subjects were asked to step over a box 15-cm high and 30-cm wide during ambulation. All subjects used the amputated side as the leading limb to cross the obstacle. When negotiating the five-step stairs or 10-foot ramp, subjects were allowed to use railings if necessary. Subjects began with level-ground walking, transited to stair/ramp ascent, turned 180°, performed stair/ramp descent, and switched back to level-ground walking. During stair descent, TF01, TF02, and TF04 were able to use a normal alternating leg pattern, while TF03 and TF05 descended the staircase one step at a time. TF02 performed stair ascent with a normal alternating leg pattern, while the other subjects ascended the stairs one step at a time. The test on each locomotion mode was repeated 15 times. The order of the task modes was randomly assigned. Rest periods were allowed between trials to avoid fatigue.

C. Interface Architecture

The architecture of the neuromuscular–mechanical fusion-based interface is depicted in Fig. 1. The multichannel EMG signals and load measurements from the 6-DOF load cell are simultaneously streamed into this system and, then, segmented by continuous, overlapping analysis windows. In each analysis window, EMG features are extracted from each channel; the mechanical features are computed from individual DOFs. Then, both EMG features and mechanical features are fused into one feature vector for each analysis window. This feature vector is sent to a phase-dependent classifier, designed in our previous study [13] to efficiently deal with nonstationary input EMG signals. The phase-dependent classifier consists of multiple classifiers, each of which is built from data in one defined gait phase. The phase-detection model determines the current gait phase and switches on the corresponding classifier. The classifier decides the locomotion mode based on the feature vector. A postprocessing algorithm is, then, applied to produce a smooth, continuous decision stream.

Fig. 1.

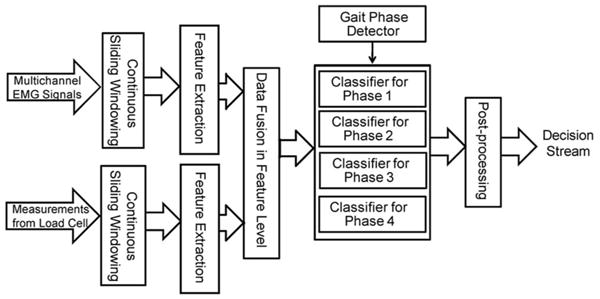
Architecture of the neuromuscular–mechanical fusion system for locomotion mode recognition.

D. Signal Processing Methods and System Design

1) Signal Preprocessing, Data Windowing, and Feature Extraction

The mechanical signals were filtered by a low-pass filter with a 45-Hz cut-off frequency. Sliding analysis windows were used to segment the EMG and force/moment data for continuous classification decision making. The length of the sliding windows was 150 ms, and the window increment was 12 ms (see Fig. 2). Features that characterized the data signals were extracted from each analysis window. For EMG signals, we used four EMG time-domain features (mean absolute value, number of slope sign changes, waveform length, and number of zero crossings), which have been shown to be very effective in EMG control of upper limb prostheses [11]. The detailed definition for computing these EMG features can be found in [11] and [12]. The maximum value, minimum value, and mean value of each direction of force or moment were chosen as the mechanical signal features.

Fig. 2.

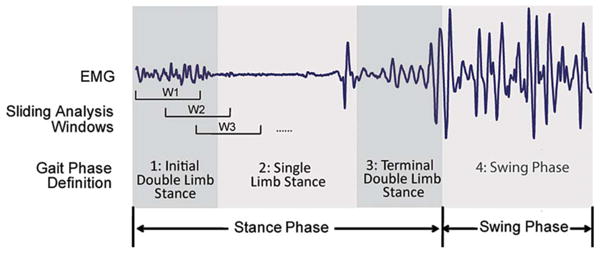
Data windowing scheme and definition of gait phases in one stride cycle.

For the fusion-based system, the EMG and mechanical features were concatenated into a feature vector x for each analysis window as

$$x=\{{\overline{f}}_1,{\overline{f}}_2,\dots ,{\overline{f}}_M,{\overline{g}}_1,{\overline{g}}_2,\dots ,{\overline{g}}_N\}$$ (1)

where f̄_m denotes the EMG features of channel m, and ḡ_n represents the mechanical features of the nth DOF. We also compared the performance of the system when only EMG features x = {f̄₁, f̄₂, …, f̄_M}, or mechanical features x = {ḡ₁, ḡ₂, …, ḡ_N}, were applied.

2) Locomotion-Mode (Class) Labeling

In order to train and test the performance of the classifier, we labeled each analysis window and its feature vector with a locomotion mode (a class index). It was difficult to label the analysis windows from transitions between locomotion modes, because there was no definitive moment of transition to serve as the separation between the two modes. Since one of the interface design goals was to predict mode transitions before a critical gait event to allow the prosthetic leg to smoothly and safely switch modes, we first define this critical timing for each type of transition. For all transitions from level walking (W→SA, W→RA, and W→O), the desired transition should be identified before the prosthetic foot leaves the ground to allow the knee to produce the proper flexion torque and prevent tripping over the obstacle, staircase, or incline. Therefore, the critical timing in these cases was defined at the beginning of the swing phase. For transitions to level walking (SD→W and RD→W), the critical timing was set at the initial contact of prosthetic foot on the level ground because the prosthetic side of the leg was still descending a staircase or ramp before this gait event. In order to allow the predicted task transitions of the designed system before the critical timings, we defined the beginning of the single-stance phase immediately prior to these critical gait events during the transition to be the separation between the two task modes.

3) Phase-Dependent Classification and Gait Phases Definition

The phase-dependent classification strategy designed in our previous study [13] was adopted. Unlike the previous study—in which we investigated four discrete gait phases (with a constant 200-ms duration)—we used continuous gait phases (phases 1–4 in Fig. 2) with durations ranging from 200 to over 800 ms. Note that the duration of a stride cycle for leg amputees was longer than that of able-bodied persons; the duration of the swing phase significantly increased for leg amputees because they preferred using the sound leg to support body weight. These gait phases were separated based on insole pressure sensor data and reaffirmed by the experimental video. The stance of one leg started from the foot–ground contact and terminated when the foot was off the ground. The data and resulting feature vector in each analysis window were labeled with a phase number. If an analysis window overlapped two gait phases (e.g., windows W2 and W3 in Fig. 2), it was labeled with the gait phase that contained more than half of the window's data. For example, window W2 in Fig. 2 was labeled with gait phase 1, while window W3 in Fig. 2 was labeled with gait phase 2. The features with the same phase label were grouped and used to train and test the classifier associated with the corresponding gait phase.

4) Pattern Classification Algorithm

A linear classification method, i.e., linear discriminant analysis (LDA), and a nonlinear approach, i.e., support vectors machine (SVM) with a nonlinear kernel [18], were investigated. Both algorithms have been studied for EMG pattern recognition for upper limb prosthesis control [11], [12], [19], [20]. The LDA classifier is the most frequently used and commonly suggested classifier for EMG pattern recognition because it has been reported as having a comparable classification performance to more complex types [21], [23] and as being computationally efficient for realtime myoelectric prosthesis control [12]. The detailed LDA algorithm and its application for EMG pattern recognition can be found in [19]. The SVM is a classification method that maps the features into a high-dimensional feature space using a kernel function and constructs a hyperplane with margins to separate binary classes [24]. The SVM has been reported to have better classification performance than LDA and artificial neural networks (ANN) in EMG pattern recognition for myoelectric prostheses, although no statistically significant differences were observed [20]. The SVM has also been successfully used in real-time EMG classification for robotic arm control [25]. Additional reasons for choosing the SVM with a nonlinear kernel were 1) a nonlinear classifier might accurately classify the data when the linear boundaries among classes are difficult to define and 2) the SVM is more computationally efficient than other nonlinear classifiers, such as the ANN.

In this study, a multiclass SVM with “one-against-one” (OAO) structure [18] and C-support vector classification (C-SVC) [24] was used. The applied kernel function was the radial basis function (RBF), which was defined as

$$k(x_i,x_j)=exp(-\gamma {\Vert x_i-x_j\Vert }^2),\gamma >0$$ (2)

where x_i and x_j are the feature vectors the of ith and jth classes, respectively, and γ = 1/n, where n is the dimension of the feature x. During the training procedure, all observed feature vectors x were nonlinearly mapped into a higher dimensional feature space based on the kernel function in (2). For the k-class classification problem, k(k − 1)/2 binary classifiers were constructed. In this study, there was a total of 6 classes, with a total of 15 binary classifiers for the classifier in each gait phase. To build each binary classifier, a hyperplane was found by simultaneously maximizing the boundary margin between two classes and minimizing the training classification errors. Fifteen hyperplanes between any two classes were computed after training. During the testing procedure, each observed feature vector x was nonlinearly transformed and sent to the individual binary classifiers built in the training procedure; therefore, a total of 15 classification decisions were made. A voting strategy was used to make the final decision. The class (mode) with the most votes out of the 15 decisions was considered to be the locomotion mode. If more than one class had the same number of votes, the class (mode) with the smaller class index was chosen as the final decision.

Leave-one-out cross-validation (LOOCV) [26] was used for training and testing the systems based on LDA or the SVM. In this procedure, data in one experimental trial were used as the testing dataset; data in all other trials were used as the training set. This procedure was repeated until each trial was used as the testing set.

5) Enhanced Majority Vote

A majority vote method was used to postprocess the classification decisions [27]. Rather than using the fixed-point majority vote, the voting scheme increased the number of voting decisions each time a rare transition was identified—such as the transition from stair ascent to stepping over an obstacle. Therefore, the probability of deciding on an unusual transition was low. In this study, the regular number of voting points was 5; the voting length increased to 15 when a rare transition was classified.

E. System Evaluation

As previously discussed, a transition between two locomotion modes is usually a dynamic process involving one or more steps. Therefore, it is difficult to define a moment that clearly separates two task modes. This makes system evaluation in mode-transition periods difficult. In this study, we separated data into static states and transitional periods and evaluated the system differently for the two states. Static states were defined as states when subjects continuously performed the same task. A transitional period was the period when subjects switched locomotion modes, which included a full stride cycle and two stance phases of the amputated leg. The transitional period began at initial prosthetic foot contact before switching the negotiated terrain and terminated at the end of the single-stance phase after the transition.

1) System Evaluation in Static States

The task modes (classes) studied in the static state included level-ground walking (W), stair ascent (SA), stair descent (SD), ramp ascent (RA), and ramp descent (RD). Note that stepping over an obstacle (O) was not included because this task only consisted of one stride cycle. The overall classification accuracy (CA) in the static states was quantified by

$$\text{CA}=\frac{\text{Number of correctly classified testing data}}{\text{Total number of applied testing data}}\times 100\%.$$ (3)

In addition, the confusion matrix M was computed to demonstrate the relationship between the target classes and the predicted classes:

$$M={\left[\begin{array}{cccc}{a}_{11}& a_{12}& ..& a_{15}\\ ..& a_{22}& ..& ..\\ ..& ..& ..& ..\\ a_{51}& ..& ..& a_{55}\end{array}\right]}_{5\times 5}$$ (4)

where each element in M is defined as

$$a_{ij}=\frac{\text{Number of testing data in class}i\text{predicted as class}j}{\text{Total number of testing data in tatget class}l}\times 100\%.$$ (5)

2) System Evaluation in Transitional Periods

To evaluate the performance of the interface in transitional periods, we quantified 1) the number of missed transitions and 2) the transition prediction time. These parameters were defined as follows.

1. The number of missed transitions: This parameter quantified the accuracy of the designed interface in identifying locomotion-mode transitions. A missed transition was identified if no correct transition or no stable task transition was recognized within the defined transitional period. A stable task transition was a correct transition decision recognized for at least 30 decisions without any other transition decisions.

2. Transition prediction time: This parameter evaluated the system response time for predicting the locomotion-mode transitions. The transition prediction time T_pred was defined as the time elapsed from the time for recognition of the last stable task transition t_d in the transitional period to the critical timing for the investigated task transition t_c. That is to say, T_pred = t_c − t_d. As discussed in Section II-D, for the transitions of W→SA, W→RA, and W→O, the critical timing t_c was the beginning of the swing phase (i.e., toe off) in the transitional periods. For the transitions of SD→W and RD→W, the critical timing t_c was the beginning of weight acceptance (i.e., heel contact) on the level ground. The positive T_pred represented the system responds before the critical event; A negative value indicated the system responds after the critical timing. A larger positive value of T_est corresponded to an earlier prediction of the mode transition.

III. Results

A. Mode-Recognition Accuracy in Static States

The average classification accuracy for each locomotion mode (static state) for the five subjects is shown in Fig. 3. The fusion-based method outperformed the classifiers with only EMG signals or GRF/moments. The EMG-based classifier produced slightly better accuracy than the mechanics-based classifier in the stance phase (phases 1, 2, and 3). During the swing phase (phase 4), the accuracy generated from the classifier based on mechanical measurements was only 50%–60%, because little information is recorded from the load cell during swing. In addition, a large cross-subject variation in the classification accuracy was observed for the classifier based on mechanical recordings. With fused data as the input, the SVM classifiers produced 1.5%–5.9% higher average accuracy in the four phases than the LDA classifiers; however, these differences were not statistically significant (one-way ANOVA, P > 0.05).

Fig. 3.

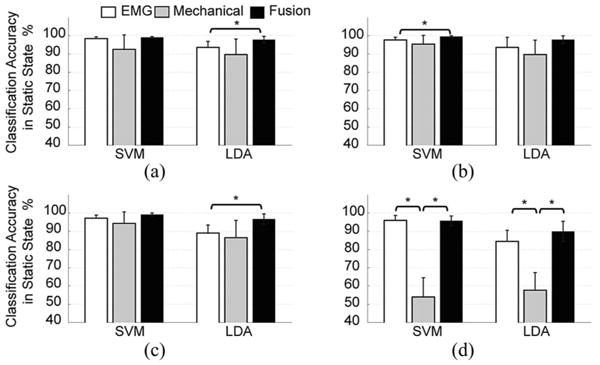
Classification accuracy in the static state averaged over five TF amputees. The classification accuracies derived from EMG signals only (white bars), GRF/moments only (gray bars), and fusion of both data sources (black bars) using the SVM and LDA classifiers are shown for individual gait phases. “*” indicates a statistically significant difference (one-way ANOVA, P < 0.05).

A confusion matrix derived from the fusion-based SVM classifier is shown in Table II. In the stance phase (phases 1, 2, and 3), the accuracy in identifying individual locomotion modes ranged from 97.6% to 100%. Most of the errors were due to confusion between level-ground walking and ramp ascent or descent. In the swing phase, the accuracy for recognizing level walking and ramp ascent decreased to 91.8% and 93.4%, respectively.

Table II. Confusion Matrix for Static State Derived From Fusion-Based SVM Classifier in Four Defined Phases.

Pha. 1	W	SA	SD	RA	RD	Targeted Classes	Pha.2	W	SA	SD	RA	RD
W	97.55	0.06	0	0.04	0.42		W	99.05	0.05	0	0.05	0.56
SA	0.30	99.88	0	0.08	0		SA	0.20	99.95	0	0.41	0
SD	0.09	0	99.61	0	0.03		SD	0	0	100	0	0
RA	0.70	0	0.39	99.87	0.03		RA	0.31	0	0	99.54	0
RD	1.36	0.06	0	0	99.52		RD	0.44	0	0	0	99.44
Estimated Classes							Estimated Classes
Pha. 3	W	SA	SD	RA	RD	Targeted Classes	Pha.4	W	SA	SD	RA	RD
W	97.81	0.26	0	0.13	0.01		W	91.79	0.05	0.62	2.92	1.71
SA	0.60	99.74	0	0.12	0		SA	1.30	99.49	0	0.88	1.08
SD	0.02	0	99.33	0.12	0		SD	2.46	0.19	98.48	0.24	0.75
RA	0.48	0	0.67	99.55	0.37		RA	2.28	0.10	0.49	93.44	0.88
RD	1.08	0	0	0.08	99.62		RD	2.17	0.17	0.40	2.53	95.57

Note: W, SA, RA, SD, and RD denote level walking, stair ascent, ramp ascent, stair descent, and ramp descent, respectively.

B. Transition Recognition Accuracy

Evaluation of system performance in the transitional periods was conducted on three combinations of classifier and data source (i.e., fusion-based SVM, fusion-based LDA, and EMG-based SVM), which outperformed the other studied combinations in the static state (see Fig. 2).

Table III lists the number of missed transitions among all tested transitional periods. The total number of tested task transitions was 75 for each subject. The fusion-based SVM classifiers accurately identified all types of transitions, while other methods failed to predict stable and correct transitions in the defined transitional periods.

Table III. Number of Missed Transitions Among all Tested Mode Transitions.

No. of Missed Transitions	TF01	TF02	TF03	TF04	TF05
SVM Fusion	0	0	0	0	0
SVM EMG	2	1	1	0	3
LDA Fusion	3	1	1	0	3

Note: The total number of tested task transitions was 75 for each subject.

The prediction time of stable mode transitions are demonstrated in Table IV. Based on the definition of prediction time, larger values (in milliseconds) corresponded to earlier prediction of task transition. The results were averaged across subjects and trials. Missed transitions were excluded from the calculation. The fusion-based SVM algorithm produced more accurate decisions and, therefore, showed earlier prediction of stable transitions than the EMG-based SVM algorithm and fusion-based LDA classifiers. The fusion-based SVM classifiers recognized stable transitions from level walking to stair ascent, ramp ascent, or stepping over an obstacle approximately 300–420 ms before the prosthetic foot left the ground (i.e., critical timing). These classifiers also identified transitions from stair descent or ramp descent to level-ground walking approximately 350–650 ms before the prosthetic foot contacted the ground (i.e., critical timing).

Table IV. Prediction Time of Mode Transitions before the Critical Event.

Unit: (ms)	W SA	W RA	SD W	RD W	W O
SVM Fusion	420±175	390±140	652±143	355±231	301±156
SVM EMG	254±132	221±96	415±162	209±177	150±146
LDA Fusion	226±116	254±121	432±179	252±154	256±105

Note: W, SA, RA, SD, RD, and O denote level walking, stair ascent, ramp ascent, stair descent, ramp descent, and stepping over an obstacle, respectively.

C. Representative Results of Continuous-Mode Selection

Fig. 4 shows the example performance of continuous-mode selection for the SVM classifiers based on EMG signals only, mechanical measurements only, and both EMG and mechanical signals. The corresponding gait phase was also demonstrated. The data were recorded from TF01. All the data sources can predict the transitions ahead of the critical events; however, the method based on merely mechanical load produced unstable decision and significant errors in the swing phase. The fusion-based classifier demonstrated the best performance in both static states and transitional periods. Specifically, in the transitional periods, the fusion-based algorithm demonstrated earlier prediction of the task transitions and stable classification decisions than the other two methods.

Fig. 4.

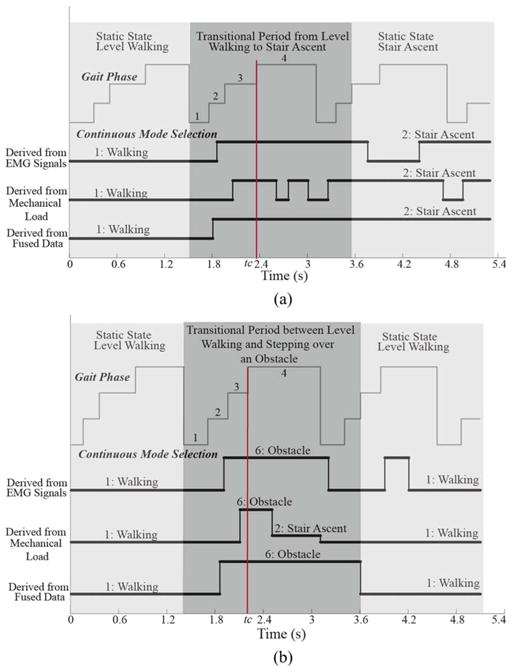
Example results of continuous-mode identification. (a) Results from a trial that recorded a transition between level-ground walking and stair ascent for subject TF01. (b) Results from a trial, where subject TF01 stepped over an obstacle during walking. Red vertical line indicates the critical timing t_c.

IV. Discussion

The mode-based control strategies in use for microcomputer-controlled passive or powered artificial legs do not result in smooth, safe prosthesis use. This is due to the lack of neural control. The prosthesis does not “know” the user's intent and, therefore, cannot automatically select the correct control mode. In this study, we developed a novel interface based on neuromuscular–mechanical fusion that could continuously classify a variety of locomotion modes performed by patients with TF amputations.

The designed interface, which combined neuromuscular–mechanical fusion with a previously developed phase-dependent pattern recognition strategy, could accurately identify locomotion modes and predict mode transitions. In both static states and transitions, the fusion-based approach outperformed the other approaches based on only one type of information source. In addition, the SVM classifiers produced better classification accuracy in static states and predicted stable task transitions 50–220 ms earlier than the LDA classifiers. These results indicate that the simple linear discriminant method may not be adequate for locomotion mode classification when using the long (often ≥200 ms) gait phases defined in this study. Impressively, the SVM classifiers based on neuromuscular–mechanical fusion could predict transitions between task modes before the critical gait event. For example, a smooth transition from level walking to stair ascent requires the switching decision to be made before the beginning of the swing phase so that the controller can promptly instruct the artificial joints and keep the prosthetic foot clear of the staircase during swing. For transitions from stair/ramp descent to level walking, correct mode transitions should be identified before weight acceptance so that the prosthetic controller can appropriately adjust the knee impedance or position. The success of our system in achieving these requirements (see Table IV) can be attributed to two strategies: 1) multisensor fusion improved classification accuracy, producing stable decisions for quick transition recognition and 2) data collected during transitions prior to critical gait events were categorized into the latter task mode during the training procedure for the classifier (see the task labeling method in Section II-D).

One of the challenges in this study was to find appropriate metrics for quantifying continuous-mode recognition. In myoelectric upper limb prosthesis control, transitions between two joint motions are quick and easy to define; however, transitions between locomotion modes involve one or more steps. This makes it impossible to define a clear boundary between two locomotion modes and precludes the use of quantification methods for upper limb EMG-based interfaces. In this study, we quantified system performance in static states (when the subjects continuously performed the same task) and transitions (when the subject switched from one mode to another) separately. During static states, the accuracy of locomotion-mode identification was quantified. During transitional periods, the ability of the system to accurately recognize stable transitions and the timing of transition identifications were evaluated. These evaluation methods proved useful for characterizing system performance with dynamic class transitions.

The study results demonstrated low classification accuracies in the swing phase compared to those of the stance phase for all investigated algorithms (see Fig. 3). This may be because 1) little force/moment information is recorded from the prosthetic pylon during swing and 2) the swing phase is longer than the three phases defined in the stance phase, possibly leading to larger variations in EMG features due to the nonstationary EMG signals [13]. Therefore, introducing other mechanical measurements—such as kinematics—or defining another phase in the swing phase might improve classification performance at the cost of increased system complexity.

Although the designed interface based on neuromuscular–mechanical fusion showed great potential for continuous locomotion-mode identification, several study limitations were identified. First, study results were based on a fairly simple fusion strategy. More sophisticated fusion structures should be investigated in future study. Second, the transitional periods were uniformly defined for all task transitions; these periods should be tailored to the transition type and the strategy used by individual leg amputees. Third, some of the methods used in this study may be difficult to implement in clinical applications. For instance, gait phases were defined based on information recorded from both the sound and amputated legs. This requires instrumentation of the sound leg, which is challenging for daily prosthesis use. Continuous detection of gait phases using mechanical information measured from the prosthesis has been successfully achieved [3] and should be considered for the clinical application of our designed system. Further investigation of data features is also necessary to optimize the system for practical use. Additionally, the evaluation of the designed system was based on offline analysis of experimental data conducted in the laboratory. The performance of mode identification system when the subjects walked in realistic environments with varied speed should be quantified in our future work. Furthermore, the system produced occasional errors in recognizing the locomotion modes and delays in predicting transitions based on offline analysis. In the next study phase, it would be important to understand the consequences of these errors and delays for real-time artificial knee control and optimize the interface for safe use of powered artificial legs in practice.

V. Conclusion

In this study, we developed a neuromuscular–mechanical fusion-based interface that could continuously classify locomotion modes and mode transitions performed by patients with TF amputations. The results showed that neuromuscular–mechanical fusion was superior to methods that took inputs from a single data source. The phase-dependent system based on neuromuscular–mechanical fusion and SVM classifiers produced over 99% accuracy in the stance phase and 95% accuracy in the swing phase for recognizing locomotion modes. In mode transitional periods, the fusion-based SVM method correctly identified all mode transitions with sufficient transition prediction time. These promising results may aid the future design of neurally controlled powered artificial legs and, therefore, enhance the mobility and quality of life of leg amputees.

Biographies

He Huang (S'03–M'06) received the B.S. degree from the School of Electronics and Information Engineering, Xi'an Jiao-Tong University, Xi'an, China and the M.S. and Ph.D. degrees from the Harrington Department of Bioengineering, Arizona State University, Tempe.

She was a Research Associate in the Neural Engineering Center for Artificial Limbs at the Rehabilitation Institute of Chicago, Chicago, IL. Currently, she is an Assistant Professor in the Department of Electrical, Computer, and Biomedical Engineering, University of Rhode Island, Kingston, RI. Her primary research interests include neural–machine interface, modeling and analysis of neuromuscular control of movement in normal and neurologically disordered humans, virtual reality in neuromotor rehabilitation, and design and control of therapeutic robots, orthoses, and prostheses.

Fan Zhang (S'11) received the B.S. degree in biomedical engineering from Tianjin Medical University, Tianjin, China, in 2006, and the M.S. degree in biomedical engineering from Tianjin University, Tianjin, China, in 2008. He is currently working the Ph.D. degree in biomedical engineering at the University of Rhode Island, Kingston, RI.

His research interests include signal processing, pattern recognition, and human motion analysis.

Levi J. Hargrove (S'05–M'08) received the B.Sc., M.Sc., and Ph.D. degrees in electrical engineering from the University of New Brunswick (UNB), Fredericton, NB, Canada, in 2003, 2005, and 2007, respectively.

He has been with the Center for Bionic Medicine at the Rehabilitation Institute of Chicago, Chicago, IL, since 2008. He is also a Research Assistant Professor in the Department of Physical Medicine and Rehabilitation (PM&R) and Biomedical Engineering, Northwestern University. Evanston, IL. His research interests include pattern recognition, biological signal processing, and myoelectric control of powered prostheses.

Dr. Hargrove is a member of the Association of Professional Engineers and Geoscientists of New Brunswick.

Kevin B. Englehart (S'86–M'99–SM'03) received the B.Sc. degree in electrical engineering and the M.Sc. and Ph.D. degrees all from the University of New Brunswick (UNB), Fredericton, NB, Canada, in 1989, 1992, and 1998, respectively.

He is currently a Professor in the Department of Electrical and Computer Engineering, UNB, where he is also the Associate Director of the Institute of Biomedical Engineering. His current research interests include neuromuscular modeling and biological signal processing using adaptive systems, pattern recognition, and time-frequency analysis.

Dr. Englehart is a Registered Professional Engineer and a member of the Canadian Medical and Biological Engineering Society.

Daniel R. Rogers received the B.Sc.E. degree from the University of New Brunswick, Fredericton, NB, Canada, in 2005, where he is currently working toward the Ph.D. degree in the Department of Electrical and Computer Engineering.

He is currently a Research Associate with the Institute of Biomedical Engineering, University of New Brunswick. His research interests include muscle fatigue assessment during dynamic contractions and control systems for powered prostheses.