Interfacial Orientation and Secondary Structure Change in Tachyplesin I: Molecular Dynamics and Sum Frequency Generation Spectroscopy Studies

Abstract

Recent advances in the collection and interpretation of surface-sensitive vibrational spectroscopic measurements have made it possible to study the orientation of peptides and proteins in situ in a biologically relevant environment. However, interpretation of Sum Frequency Generation (SFG) and Attenuated Total Reflectance – Fourier Transform Infrared (ATR-FTIR) vibrational spectroscopy is hindered by the fact that orientation cannot be inferred without some prior knowledge of protein structure. In this work, molecular dynamics (MD) simulations were used to study the interfacial orientation and structural deformation of the short β-sheet peptide tachyplesin I at the polystyrene/water interface. By combining these results with ATR-FTIR and SFG measurements, reasonable agreement was found with simulation results suggesting that tachyplesin I lies parallel to the surface, although simulation results imply a broader distribution of peptide twist angles than could be characterized using available experimental measurements. The interfacial structure was found to be deformable even when disulfide bonds were preserved, and these local deviations from a purely extended β-sheet conformation may be of importance to future developments in the interpretation of SFG and ATR-FTIR spectra.

Introduction

Interfaces are ubiquitous in biology, and the interaction of peptides or proteins with polymers, lipids, and other materials must be understood in order to address questions such as biocompatibility, biofouling, enzyme immobilization, and the behavior of membrane-active peptides and proteins.^1–4 However, few techniques possess the sensitivity and specificity to examine a thin layer of biomolecules at the interface in a biologically relevant environment, while also measuring quantitative information about biomolecular internal conformation and overall orientation. Although indisputably valuable, many biophysical techniques for the study of proteins have limitations such as interfering signals due to water absorption, the requirement for high vacuum, large sample requirements, or a lack of inherent surface specificity.^5–8

In recent years, sum frequency generation (SFG) vibrational spectroscopy has been applied to amino acids, peptides, and proteins, and numerous advantages have been demonstrated.^9–30 It has been found that SFG is capable of detecting even sub-monolayer amounts of protein in situ in aqueous environments at polymer or lipid interfaces.³¹ Previously, it has been shown that polarized SFG signal intensity ratios can be used to quantitatively determine the orientation of α-helical peptides.^{12, 15, 16} This was the first protein secondary structure motif for which SFG orientation measurements became possible, due to the fact that the well-ordered structure leads to strongly detectable signals, and because only a single orientation angle (tilt) needs to be characterized due to its inherited symmetry properties. Characterizing a single angle is feasible even with a small set of measurements. A similar approach was also used to determine the orientation of a 3₁₀ helical structures, as in alamethicin.³²

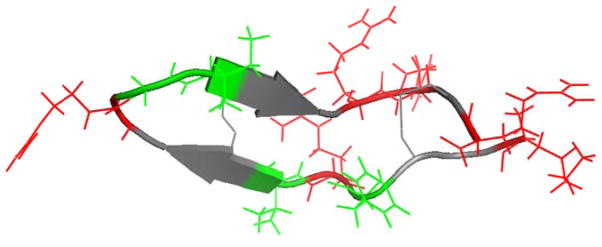
Recently, it has been shown that SFG is similarly capable of studying the orientation of antiparallel β-sheet secondary structures, which consist of two hydrogen bonded β-strands in an antiparallel orientation.^{12, 17, 23–25, 33–36} Since signal intensities are known to be related to the number of molecules at the interface, a recent study on β-sheet orientation ensured a high surface coverage of β-sheets by using the small peptide tachyplesin I (Figure 1), which consists of 17 residues (including six in the β-sheet conformation).

Figure 1.

Tachyplesin I is a 17-residue β-sheet peptide with both hydrophobic (green) and charged (red) residues.

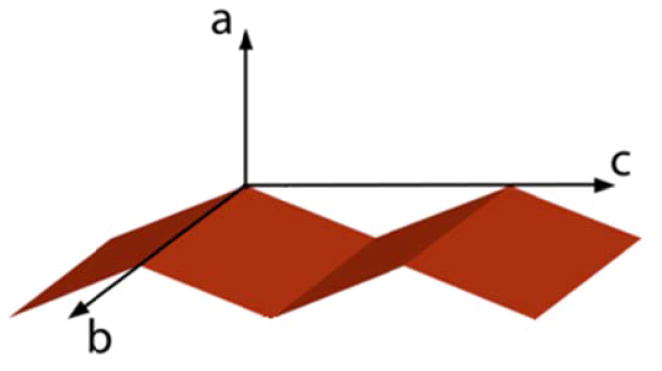
In order to apply SFG to the study of β-sheet orientation, a number of challenges remain that must be addressed. In particular, characterizing two angles (tilt and twist) with a limited set of measurements is only possible if one assumes that all molecules adopt the same orientation (δ distribution). In fact, the structure of tachyplesin I is not as inherently facially amphiphilic³⁷ as some previously studied helical peptides^{18, 20}, and so it is unclear whether a δ orientation distribution is actually realistic at a model hydrophobic/hydrophilic boundary such as the polystyrene (PS)/water interface. Second, although a small β-sheet peptide was chosen as a means to increase the surface coverage of the secondary structure of interest, the actual region of tachyplesin I that adopts that secondary structure is fairly short: three residues per β-strand.⁷ As a result, it is quite possible that the structure could deform significantly when adsorbed. This deformation is not taken into account in the SFG orientation analysis relations, which assume that the strands of the β-sheet are in the fully extended conformation. Third and lastly, although a combination of ATR-FTIR and SFG measurements was used in the previous study, the orientation relations used for ATR-FTIR were not capable of extracting the full range of information in the spectrum. This is a consequence of the fact that FTIR is only capable of obtaining one measurement, yet the orientation of β-sheets would be more accurately described using two angles (tilt and twist, as shown in Figure 2). Previous orientation analysis methodologies have therefore required assuming that one orientation angle can be averaged out^{38, 39} or held fixed.^{17, 40, 41}

Figure 2.

The molecular coordinate system used in this work. The long axis of the β-strands is oriented parallel to the c axis, while the plane of the β-sheet corresponds to the bc plane. The twist angle ψ represents rotation around the molecular c axis, and the tilt angle θ represents rotation around the molecular b axis.

It is well known that few β-sheet structures exist entirely in the extended conformation, and most sheets instead adopt a small twisting of the constituent strands.^42–46 This inherent deformation (which is not to be confused with the twist angle used to characterize molecular orientation) can vary depending on the structure, as it depends on a variety of factors including hydrogen bonding, the inherent chirality of the constituent amino acids, and side chain packing. To address questions about conformational flexibility, we used all-atom MD simulations aimed at addressing the above concerns and provide a more complete understanding of β-sheet orientation at interfaces. MD simulations have been widely used to study peptides and proteins on surfaces of varying charge and hydrophilicity, using force fields optimized to reproduce biomolecular structure and dynamic behavior. In recent years, early work using simple model surfaces and implicit solvent or simplified coarse grained models has given way to studies that increasingly employ polymer, inorganic, lipid, and SAM interfaces as model systems.^47–54 Due to the large amounts of computer processing time required for extensive characterization, the use of more detailed model systems requires a number of tradeoffs. Our simulations employed a simplified PS/water interface in a spherical boundary that balances the competing requirements of detail and computational performance. This model hydrophobic/hydrophilic interface is also amenable to characterization using a combination of SFG and MD. We believe that combining these techniques makes it possible to understand the interfacial orientation and structural flexibility of tachyplesin I in more detail, and will facilitate future studies of other peptides and proteins with β-sheet structures at interfaces.

Methods

SFG Data Analysis

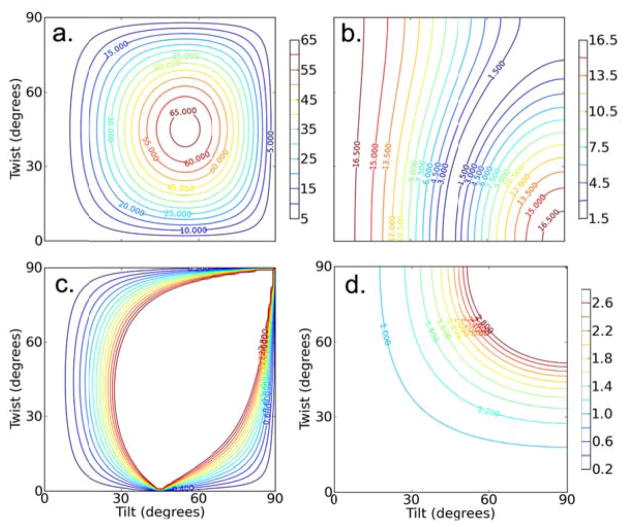
It has only recently become possible to analyze the orientation of β-sheets based on SFG measurements, following the derivation of the required molecular hyperpolarizability and surface susceptibility tensor components.^{17, 36} Although a range of polarizations and vibrational modes were found capable of producing SFG amide I signals, the B1 and B3 amide I vibrational modes are relatively weak. The most important SFG measurement available in SFG studies on β-sheets is the single intensity ratio $\frac{{\chi }_{\mathit{xxz}}^{(2)}}{{\chi }_{\mathit{yzx}}^{(2)}}$ of the B2 mode.^{17, 36} Plots of the most relevant experimental observables are shown in Figure 3, and the relevant equations are provided in the supporting information.

Figure 3.

For the B₂ mode: Calculated contour plots showing the relative magnitudes of a) ${\chi }_{\mathit{ssp}}^{(2)}$, b) ${\chi }_{\mathit{ssp}}^{(2)}$, and c) the fitted ssp/spp ratio (these ratios incorporate the Fresnel factors directly). d) Contour plot showing the FTIR dichroic ratio.

MD Simulations

The solvent/surface model system used for these simulations consists of an array of ethylbenzene molecules for the model PS surface and polymer bulk, solvated using TIP3 explicit solvent constrained in a spherical “droplet in a vacuum” system of 36Å radius using a spherical quartic boundary potential. Previous studies have shown that the presence of a water/vacuum boundary primarily affects the first few layers of water, so that the structure of the water in the center of the droplet remains reasonable. More details and discussion of this model system may be found in a previous publication.¹⁸ The structure of the tachyplesin I peptide was obtained from the Protein Databank (PDB ID 1ma2). Structure 9 of the 31-conformer NMR ensemble was extracted and used as the starting structure for all simulations. This starting structure was chosen due to the roughly parallel orientation of the two strands, particularly in the highly flexible disordered regions of the structure. This conformation therefore provides the best chance for all portions of the peptide to interact with the surface in a variety of initial simulation conditions. For a hydrophobic polymer surface, one would expect that hydrophobic interactions would dominate the adsorption behavior.^55–57 However, the structure of tachyplesin I does not possess the same strong facial amphilicity³⁷ as was present in magainin 2 or LK14 (studied previously).^{18, 20, 22} Therefore, a variety of simulations were performed with the peptides placed in different starting orientations.

The peptide was placed into the model solvent/surface system above the surface, so that the closest point of the peptide was ~2.5Å from the surface. The peptide was oriented along the x-axis of the coordinate system, then rotated into the respective coordinates for a variety of starting orientations as specified in Table 1. Overlapping water molecules were removed, and peptide coordinates were held fixed as an additional 500ps of equilibration was then performed for the solvent and surface in the presence of peptide. No counter-ions were included.

Table 1.

Initial conditions used for simulations.

Identifier	Length (ns)	PDB rotation		Euler Angles
		Tilt	Twist	Tilt	Twist
tachx270*	12 (18*)	90°	270°	100°	65°
tachx0*	4.8 (18*)	90°	0°	110°	−32°
tachx180*	12	90°	180°	76°	28°
tachx315*	12	90°	315°	119°	21°
tachx235*	6 (18*)	90°	235°	109°	42°
tachx90	2	90°	90°	77°	−75°

PDB rotation indicates the angles used to rotate the entire peptide molecule from coordinates in the PDB file (based on the backbone atoms in all 17 residues). Angles are also listed in a convention consistent with SFG analysis, determined based only on the 6 residues in the β-sheet portion of the peptide. The angles determined via these two methods differ because the sheet is not perfectly aligned with the plane of the peptide.

Simulation identifiers marked with an asterisk were also performed a second time with disulfide bonds removed.

For production runs, dynamics were performed using a Nosé-Hoover thermostat at 298K with the velocity-Verlet algorithm. The SHAKE algorithm was used to constrain all bonds involving hydrogen atoms, allowing the use of a 2fs timestep. All setup, equilibration, and dynamics were performed using version c34b1 of the CHARMM molecular dynamics package with the CHARMM22 all-atom parameter set.^{58, 59} These parameters were used for the water, protein, and surface residues. In the latter case, although not optimized for polymers, the CHARMM22 parameters should adequately represent the primarily hydrophobic interactions that dominate behavior of the polymer surface. A cutoff of 12.0Å was used when calculating the nonbonded interactions.

Experiments have shown that the presence of the two disulfide bonds in tachyplesin I is key to retention of the β-sheet structure⁶⁰. The loss of the two disulfide bonds may greatly affect the tachyplesin I – PS surface interactions. For comparison purposes, MD simulations were also performed on peptides with the disulfide bonds removed.

The most relevant exploratory simulations are summarized in Table 1, where the angles specified represent rotation of the entire PDB coordinate file to the lab coordinate system. To facilitate comparison to results from SFG spectroscopy, these initial positions were also calculated in terms of the Euler angles required to rotate a β-sheet from the molecular coordinate system to the specified position defined in the lab coordinate system. In Table 1, not all tilt angles (the angle between the β-sheet c-axis and the surface normal) determined using this latter procedure are exactly equal to 90° (peptide lying down). This is because the six β-sheet residues are not perfectly aligned with the overall peptide plane defined by all 17 total residues. The Euler angles θ and ψ are defined based on two vectors defined using backbone atoms. These vectors are oriented parallel and perpendicular to the sheet axis in the molecular coordinate system, respectively, and may be calculated from the rotation matrix elements based on the components of each of those vectors:

$$\begin{array}{c}\theta ={\mathit{cos}}^{-1}\left(\frac{z_{\left|\right|}}{\mid {\mathit{vec}}_{\left|\right|}\mid }\right)\\ \psi ={\mathit{sin}}^{-1}\left(\frac{z_{\perp }}{\mid {\mathit{vec}}_{\perp }\mid \ast \mathit{sin}\theta }\right)\end{array}$$ Equation 1

Where vec_|| refers to the vector running parallel to the long axis of the strands, and vec_⊥ refers to the vector running perpendicular to the long axis of the strands in the plane of the β-sheet.

For final data analysis, description of the resulting orientation is hampered by the fact that a significant portion of the peptide may be disordered. (At best, only 6 of the 17 residues comprise the β-sheet region) Thus, in all results reported, the orientation of the molecule was defined solely from the β-sheet portion of the molecule (residues 6–8 and 11–13) using the latter Euler angle convention described above.

Results

Molecular Dynamics

Including simulations in which the disulfide bonds were removed, a total of 11 molecular dynamics simulations spanning a total of ~120 ns were evaluated here. Of these, two initial conditions (tachx90 and tachx235) showed no or poor interaction with the surface, and were therefore excluded from the analysis. Since the peptide was allowed to move and diffuse freely to better accommodate formation of peptide-surface interactions, all windows presented were monitored carefully to ensure that the peptide did not randomly diffuse too close to the edges of the spherical model system (at the water/vacuum boundary) during the timescales studied.

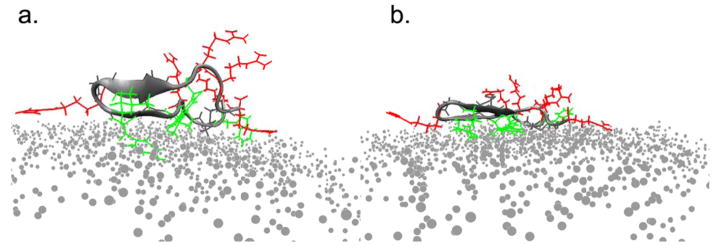
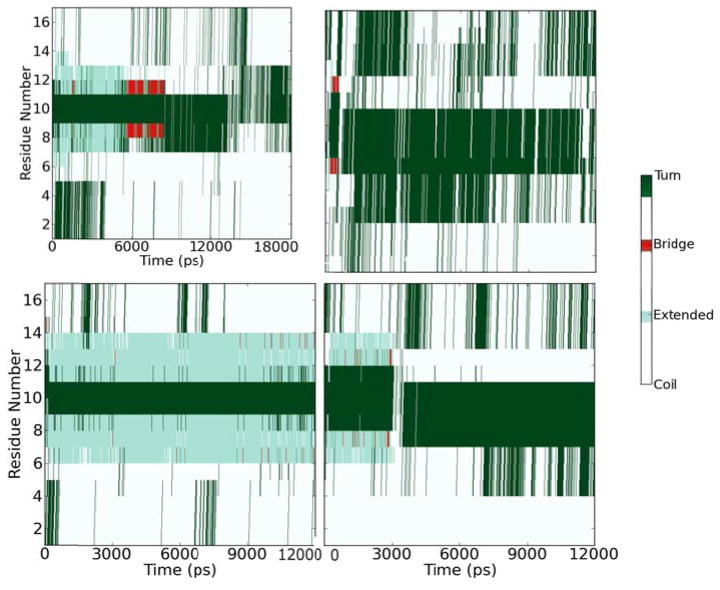
In general, all simulations ended with the long axis of the peptide lying roughly parallel to the plane of the surface (tilt of 90°), but a variety of twist angles were observed; the two most common local minima in time-dependent plots of orientation were twist angles centered around 0° and 45° (Figure 4). The changing angle between the β-strands (measured from vectors running through the backbone atoms of the two individual β-strands) also indicates that structural deformation of the β-sheet region occurs. Since analysis of molecular orientation in MD trajectories depends on the positions of selected backbone atoms (residues 6–8 and 11–13), it is important to note that the orientations listed will only have physical meaning if the peptide retains the β-sheet conformation at the end of the simulations.

Figure 4.

Two candidate final orientations of the peptide show qualitatively similar trends in surface area burial. Hydrophobic side chains are shown in green, and charged side chains are drawn in red. Surface residues are shown as grey dots, and water molecules are not shown. The peptide adopts a twist angle of a) ~50° (simulation tachx270) or b) ~10° (simulation tachx315).

Adsorption and Orientation

In order to understand the factors that affect adsorption of tachyplesin I, a variety of molecular dynamics simulations were performed in which the peptide was placed at different initial orientations. The results (Table 2) are striking for the variety of final orientations and structures observed. The simulations reported in Table 2 focus on the subset of ten trajectories that showed some interaction with the surface: five in which the disulfide bonds were kept intact, and five additional windows in which the disulfide bonds were removed initially. It is interesting to note that in one case (tachx235), the peptide only adsorbed when disulfide bonds were broken. This suggests that in this case reorganization of the backbone may help to accommodate rearrangements of side chains and alleviate unfavorable contacts with the surface.

Table 2.

Final orientation of the β-sheet section of the peptide when disulfide bonds were retained.

Name	With 3 residues			With 2 residues
	Tilt	Twist	Interstrand Angle	Tilt	Twist	Interstrand Angle
tachx270	107±2.8°	52±5.3°	12°	106±3.3°	28±3.9°	34°
tachx0	94±5.3°	60±6.9°	39°	92±5.5°	48±6.5°	12°
tachx180	88±4.2°	−8±7.2°	28°	102±5.3°	−5±7.5°	28°
tachx315	85±3.5°	12±4.8°	9°	83±3.3°	13±4.7°	23°

Angles are from the average of the last 50 frames in a rotation convention consistent with SFG data analysis. In order to account for deformation of the sheet structure, results for the entire sheet (residues 6–8 and 11–13) were compared to angles for a shorter segment (residues 6–7 and 12–13). The error bars quoted on tilt and twist angles represent one standard deviation.

Side chain rearrangements were also seen to dictate adsorption orientation and behavior in other simulation windows on the timescales studied. Reorganization of the bulky tyrosine side chains at residues 8 and 13 was found to influence the total disruption of secondary structure in the window tachx180. In the simulation window tachx270, bad side chain contacts were more transient, as the loss and recovery of secondary structure correlated to initial burial of the aliphatic chain of an arginine at the hairpin turn (residue 9). The adsorbed peptide eventually forms more (and more favorable) hydrophobic contacts, and recovery of the β-sheet structure in tachx270 coincides with release of arginine from the surface. In the analogous simulation without disulfide bonds, no such disruption of secondary structure was seen on the timescales studied, suggesting that flexibility of the peptide backbone allows side chains to reorganize more readily.

Structural Deformation

A variety of structural deformation metrics were applied in an attempt to better understand the behavior of the peptide at the interface:

1. Root-mean-squared displacement (RMSD) was evaluated as a metric for deformation of the β-sheet portion of the peptide (backbone atoms of residues 6 to 8 and 11 to 13), as well as for the backbone atoms of all residues.

2. In order to distinguish strands in the extended conformation from fully hydrogen-bonded β-sheets, the number of hydrogen bonds in the β-sheet and backbone was quantified over time. Hydrogen bonds were quantified using the default CHARMM cutoffs (4.5Å donor-acceptor distance and a donor-acceptor angle above 90°).

3. Secondary structure of each residue over time was monitored using the STRIDE algorithm for secondary structure assignment and the VMD Timeline plugin^{61, 62} to determine whether the peptide remained in the β-sheet conformation. STRIDE employs bond angles, hydrogen bonds, and other criteria to assign secondary structure.

These results are presented in Table 3, with the most direct visual comparison of secondary structure deformation presented in Figure 5 (and the expanded comparison in the supporting information).

Table 3.

Structural deformation metrics: Average number of hydrogen bonds and RMSD over the last 1 ns of each simulation trajectory.

Name	# hydrogen bonds		RMSD (Å)
	βsheet	Backbone	βsheet	Backbone
tachx270	2.6	3.5	0.6	2.5
No disulfide bonds	4.8	5.4	0.5	4.6
tachx0	1.5	1.6	1.1	3.0
No disulfide bonds	1.5	2.1	1.1	5.2
tachx180	2.8	4.0	1.9	2.1
No disulfide bonds	0.6	0.8	3.7	5.6
tachx315	4.1	4.3	0.75	3.2
No disulfide bonds	1.3	0.3	2.8	4.1
tachx235 (No disulfides, only)	1.8	2.7	1.1	3.5

Figure 5.

Secondary structure assigned to each residue of the peptide over time for simulation identifier tachx180 (top) and tachx315 (bottom). The left panels show structure over time with disulfide bonds present, and the right panels are for the same initial conditions with disulfide bonds removed. The color scheme used is presented as a sidebar.

Strikingly, we found that after 12–18 ns of simulation, the very short β-sheet region of the peptide can be deformed even when disulfide bonds are present (as in tachx180). Given that distinct B₂ mode signals from β-sheets are observed experimentally, the observed deformation may be an artifact of side-chain reorganizations on the short timescales studied in these simulations. When the disulfide bonds are removed, the β-sheet structure was only retained in window tachx270. In runs tachx0 and tachx235, only a single residue remained transiently in the bridged conformation. Experimentally, no β-sheet signals were observed in the absence of disulfide bonds.

When disulfide bonds were retained, secondary structure was generally retained in these simulations to a much higher degree. Only in one of the trajectories was secondary structure completely lost during ongoing reorganizations of side chain residues as the peptide reoriented from a non-optimal initial position (tachx180). Partial retention or even recovery of the secondary structure was observed in two of the four trajectories for which the peptide was found to adsorb to the surface (tachx270 and tachx0). The results in Figure 5 are in reasonable agreement with the hydrogen bond and RMSD quantification in Table 3. It is interesting to note that neither metric alone is sufficient to unequivocally indicate peptide folding, however. This is likely due to the fact that the β-sheet portion of tachyplesin I is very short, and so small local deformations are possible without loss of secondary structure. This highlights the importance of backbone dynamics in interpreting molecular orientation, as most orientation analysis methods require a known and fixed structure. Even when the β-sheet secondary structure is preserved (as for tachx315), our simulations show that the strands are not arranged in a completely ideal and extended conformation, with inter-strand angles of 10° or higher.

The Stability of the Final Adsorbed State

The highly deformable peptide backbone of tachyplesin I prevents the use of constrained sampling methods to calculate a free energy profile as a function of peptide orientation. It appears that backbone deformation is important to the initial adsorption process, but addition of an artificial constraint might lead to other less meaningful disruption of the structure rather than restraining peptide orientation. Based on the assumption that hydrophobic surface area burial drives a change in free energy upon adsorption^55–57, solvent accessible surface area was calculated for all windows in the simulation based on the surface area of the selected residues plus the polystyrene surface, minus the surface area of the selected residues in solvent and the surface area of the polystyrene surface in the absence of peptide.⁶³ The surface area module in CHARMM did not directly provide the surface area of the residue as it contributes to the surface area of the overall protein, and as a result, the values measured are a relative metric that may not add up to 100%.

In all but one simulation window (tachx315), the removal of disulfide bonds leads to greater surface area burial (Table 4). Yet since simulation windows that showed high hydrophobic surface area burial were accompanied by higher burial of other residues as well, it is unclear how much of an enthalpic driving force is involved, and calculations of the total potential energy of the system were inconclusive. By contrast, the strong facial segregation of residues in previously studied peptides^{20, 22} created a clear driving force for adsorption via burial of hydrophobic surface area. In tachyplesin I, residues are poorly segregated, and side chains are free to reorganize. This leads to a variety of candidate orientations with tradeoffs between favorable and unfavorable peptide-surface interactions. Other factors, such as structural deformation and entropic considerations, likely therefore play a significant role in determining the overall free energy of adsorption.⁶⁴ A single unambiguously most stable twist angle or backbone arrangement could not be determined on the timescales studied by MD simulations, suggesting that both enthalpic and entropic considerations contribute to a diverse free energy landscape.

Table 4.

Burial of solvent accessible surface area by residue type.

Name	Change in solvent accessible surface area (SASA)- units of Å2
	Overall	Hydrophobic	Hydrophilic	Charged
tachx270	887	639	466	277
No disulfides	1659	850	1110	894
tachx0	1273	800	765	719
No disulfides	1582	862	852	651
tachx180	1295	614	696	632
No disulfides	1411	931	772	769
tachx315	1458	792	786	593
No disulfides	1147	589	690	670
tachx235 (No disulfides, only)	1287	304	872	726

Individual tallies do not add up to 100% due to limitations in the algorithm used.

SFG and ATR-FTIR Spectra

Spectra obtained from tachyplesin I at the PS/water interface were presented previously¹⁷. As discussed above, SFG data analysis and orientation determination was focused on the B₂ mode peak at 1635 cm⁻¹, since other signals were too weak to ensure reliable ratios for analysis. These spectra were fit as described in a previous publication.¹⁷ For total internal reflection geometry, and taking $n^{\prime }=\frac{n_1+n_2}{2}$ as the corrected index of refraction at the interface^{65, 66}, the normalized Fresnel factors L_xxz, L_yxz, and L_yzx are 10.1, 3.5, and 1.0, respectively.⁶⁷

Combined Spectroscopies for Orientation Determination

Orientation analysis may be performed by considering the ratio of the SFG experimental observables ${\chi }_{\mathit{eff}}^{(2)}$ in the polarizations of interest. The SFG measured quantity for the B₂ mode peak centered at 1635 cm⁻¹ is:

$$\frac{{\chi }_{\mathit{ssp}}^{(2)}}{{\chi }_{\mathit{spp}}^{(2)}}=\frac{L_{\mathit{yyz}}}{L_{\mathit{yxz}}}\frac{N_s\langle {\mathit{cos}}^3\theta \mathit{cos}\psi \mathit{sin}\psi -\mathit{cos}\theta \mathit{cos}\psi \mathit{sin}\psi \rangle {\beta }_{\mathit{acb}}}{-\frac{1}{2}{N}_s\langle {\mathit{cos}}^2\theta -{\mathit{sin}}^2\theta {\mathit{cos}}^2\psi \rangle {\beta }_{\mathit{acb}}}$$ Equation 2

In order to characterize both of the required orientation angles (tilt and twist), a second measurement was obtained from polarized Attenuated Total Reflection Fourier Transform Infrared (ATR-FTIR) Spectroscopy. Orientation relations for β-sheet structures have been published previously for ATR-FTIR^{40, 68}, and were employed in a previous study to characterize the orientation of tachyplesin I by considering only the tilt angle (θ)¹⁷:

$${\text{R}}^{\text{ATR}}(\text{amide}\text{I})=\frac{{\text{E}}_{\text{x}}^2}{{\text{E}}_{\text{y}}^2}+\frac{2\langle {cos}^2\theta \rangle }{3-\langle {cos}^2\theta \rangle }·\frac{{\text{E}}_{\text{z}}^2}{{\text{E}}_{\text{y}}^2}$$ Equation 3

In the above equation, the twist angle can be neglected due to the assumption that the strands adopt a symmetrical β-barrel structure in which the twist angle is held fixed.^{40, 69} For a simple βsheet structure consisting of two hydrogen bonded antiparallel strands, the twist angle should be considered. The necessary orientation relations can be derived by considering the known vibrational modes of a β-sheet in the extended conformation. In general, the dichroic ratio from s and p polarized IR absorption is given⁴⁰ by:

$$R^{\mathit{ATR}}=\frac{A_{\left|\right|}}{A_{\perp }}=\frac{E_x^2}{E_y^2}+\frac{\langle M_z^2\rangle }{\langle M_y^2\rangle }·\frac{E_z^2}{E_y^2}$$ Equation 4

The angled brackets indicate orientational averaging, and M_x, M_y, and M_z refer to the respective components of the dipole moment in the laboratory coordinate system with axes x, y, and z. These dipole moment components can be calculated based on the known axial orientations of the three IR-active antiparallel β-sheet vibrational modes: B₁, B₂, and B₃, which are known to orient along the molecular c, b, and a axes of the β-sheet, respectively.^{17, 70} A correction for the orientations of individual transition moments of the individual peptide units³⁷ was, therefore, found to be unnecessary in our analysis.

If one assumes that the entire dipole moment of the molecule lies along the c axis of its coordinate system initially, and is projected by an angle Θ into the sheet coordinate frame, then the expected dipole moment components for the β-sheet in the lab frame required by Equation 4 can be derived. As shown in Figure 2, the molecular coordinate system (a, b, c) for the peptide is defined so that the plane of the sheet corresponds to the bc plane; this coordinate system was chosen as to be consistent with previously published relations for SFG analysis.¹⁷

$$\begin{array}{c}{\mu }_{\mathit{lab},B_1}=R_z(\phi )R_y(\theta )R_z(\psi )\left[\begin{array}{c}0\\ 0\\ \mid \mu \mid \end{array}\right]\\ {\mu }_{\mathit{lab},B_2}=R_z(\phi )R_y(\theta )R_z(\psi )R_x(\mathrm{\Theta })\left[\begin{array}{c}0\\ 0\\ \mid \mu \mid \end{array}\right]\\ {\mu }_{\mathit{lab},B_3}=R_z(\phi )R_y(\theta )R_z(\psi )R_y(\mathrm{\Theta })\left[\begin{array}{c}0\\ 0\\ \mid \mu \mid \end{array}\right]\end{array}$$ Equation 5

where the rotation matrices about the intrinsic molecular axes for an arbitrary rotation angle α are of the form:

$$\begin{array}{c}{R}_x(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\alpha & sin\alpha \\ 0& -sin\alpha & cos\alpha \end{array}\right];R_y(\alpha )=\left[\begin{array}{ccc}\mathit{cos}\alpha & 0& -\mathit{sin}\alpha \\ 0& 1& 0\\ \mathit{sin}\alpha & 0& \mathit{cos}\alpha \end{array}\right]\\ R_z(\alpha )=\left[\begin{array}{ccc}\mathit{cos}\alpha & \mathit{sin}\alpha & 0\\ -\mathit{sin}\alpha & \mathit{cos}\alpha & 0\\ 0& 0& 1\end{array}\right]\end{array}$$ Equation 6

The transition moment orientation Θ =90° corresponds to the amide I band, and averaging is performed over the azimuthal angle φ to reflect that individual molecules are randomly oriented in the plane of the surface. Then, from Equation 4, Equation 5 and Equation 6, orientation relations for the B₁, B₂, and B₃ amide I modes may be derived:

$$\begin{array}{c}{R}^{\mathit{ATR}}(B_1)=\frac{E_x^2}{E_y^2}+2\langle {\mathit{cot}}^2\theta \rangle ·\frac{E_z^2}{E_y^2}\\ R^{\mathit{ATR}}(B_2)=\frac{E_x^2}{E_y^2}+\frac{-2\langle {\mathit{sin}}^2\psi \rangle \langle {\mathit{sin}}^2\theta \rangle }{\langle {\mathit{sin}}^2\psi \rangle \langle {\mathit{sin}}^2\theta \rangle -1}·\frac{E_z^2}{E_y^2}\\ R^{\mathit{ATR}}(B_3)=\frac{E_x^2}{E_y^2}+\frac{2\langle {\mathit{cos}}^2\psi \rangle \langle {\mathit{sin}}^2\theta \rangle }{\langle {\mathit{sin}}^2\psi \rangle \langle {\mathit{sin}}^2\theta \rangle -\langle {\mathit{sin}}^2\theta \rangle }·\frac{E_z^2}{E_y^2}\end{array}$$ Equation 7

Using these equations, it is possible to extract the full range of orientation information from the combination of SFG and ATR-FTIR measurements. Expressions for the electric field amplitudes $E_x^2,E_y^2$, and $E_z^2$ have been derived previously⁵, and depend on the indices of refraction for the substrate, interfacial layer (in this case, the PS film), and solvent. These indices are taken to be 4.00, 1.55, and 1.33, respectively.^{5, 17, 71–73} For the polymer interface, this leads to values for $E_x^2,E_y^2$, and $E_z^2$ of 1.97, 2.25, and 1.36, respectively.

Only signals from the strong B₂ mode peak ~1635 cm⁻¹ were observed. Hence the possible orientations of the β-sheet structure may be determined from the available experimental measurements by considering all orientations that provide a match for the following experimentally measured quantities:

$$\{\begin{array}{c}\frac{{\chi }_{\mathit{ssp}}^{(2)}}{{\chi }_{\mathit{spp}}^{(2)}}=\frac{L_{\mathit{yyz}}}{L_{\mathit{yzx}}}\frac{N_s\langle {\mathit{cos}}^3\theta \mathit{cos}\psi \mathit{sin}\psi -\mathit{cos}\theta \mathit{cos}\psi \mathit{sin}\psi \rangle {\beta }_{\mathit{acb}}}{-\frac{1}{2}{N}_s\langle {\mathit{cos}}^2\theta -{\mathit{sin}}^2\theta {\mathit{cos}}^2\psi \rangle {\beta }_{\mathit{acb}}}=1.04\\ R^{\mathit{ATR}}(B_2)=\frac{E_x^2}{E_y^2}+\frac{-2\langle {\mathit{sin}}^2\psi \rangle \langle {\mathit{sin}}^2\theta \rangle }{\langle {\mathit{sin}}^2\psi \rangle \langle {\mathit{sin}}^2\theta \rangle -1}·\frac{E_z^2}{E_y^2}=0.95\end{array}$$ Equation 8

If one assumes that all molecules of peptide on the surface adopt exactly the same orientation, then the angles θ and ψ can be solved for directly from the above as a system of nonlinear equations. However, this may result in multiple unique solutions, and the relationship between results is not always clear- particularly when large experimental error bars are involved. In order to better illustrate the effect of possible larger uncertainties in the experiments and data analysis (due to factors such as uncertainty in the Fresnel coefficients and interfacial electric field amplitudes), the scoring function and graphical presentation developed previously⁷⁴ (see supporting information) was applied to illustrate all matches within ±40% of the target criteria. (Figure 6)

Figure 6.

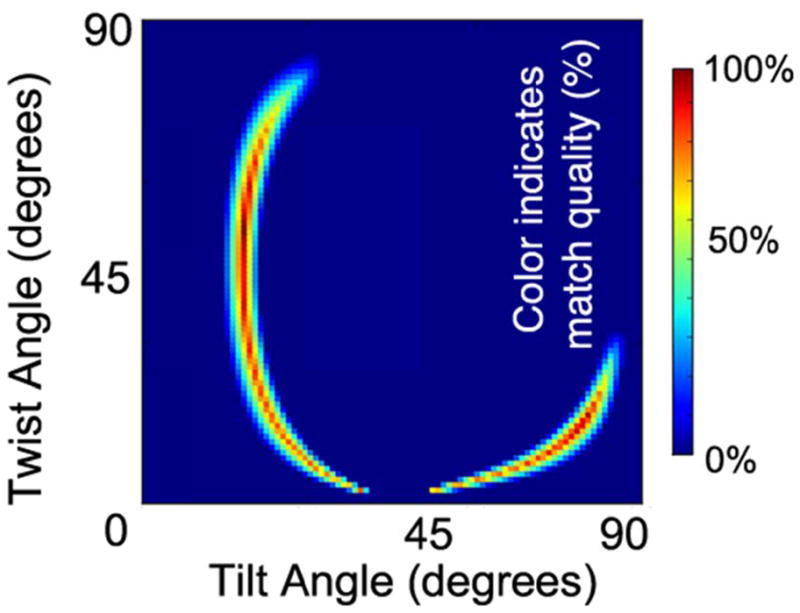
Final orientations of Tachyplesin I that best sa atisfy all three experimental constraints: a match for the SFG ssp/spp and ATR-FTIR dichroic ratios (±40%), and B₂ signal intensity greater than B₁ signal intensity. Within the allowed error bars, a color scheme is applied to indicate overall match quality based on closeness of the calculated and exper rimental values.

Upon combining the measurements from SFG and ATR-FTIR, it may be seen that two broad arcs of high-scoring matches for experimental measurements exist. One region of high-scoring matches occurs at low tilt angles, which would correspond to the peptide roughly standing up. However, such low tilt angles would provide extremely poor contact between the peptide and the surface, and could only be adopted if either the charged residues of the disordered tail or the charged arginine at the β-turn (residue 9) were unfavorably buried on the surface while hydrophobic contacts with the surface were kept minimal. In our simulations, we explored initial conditions where contact between the peptide and surface was initially poor. In these cases, the peptide either quickly collapsed down to lie flat on the surface, failed to adsorb (tachx235), or (in the case of tachx180) adsorbed, but only upon significant distortion of the peptide backbone as dramatic side chain reorganizations took place.

The second region of high scoring matches is more physically reasonable, as the highest scores are assigned to positions where the plane of the sheet lies nearly parallel to the surface (θ = 80°, ψ = 10°). Such a final position is consistent with at least some of the simulation windows considered. Although not all simulation windows converge to this position, it is possible that the lack of convergence to a final sheet orientation parallel to the surface in the timescales studied is due to the need for side chains to reorganize prior to the peptide lying flat on the surface. This is supported by the structural deformations observed in some windows, as well as the observation that the process of peptide adsorption could occur differently when disulfide bonds were preserved or removed. Thus, some conclusions may be hampered by limitations in simulation length.

Both simulations and experiments support the observation that the long axis of the sheet lies parallel to the surface in a narrow range of tilt angles (θ ≈ 90°). If SFG experiments are interpreted by assuming only a δ distribution in tilt and twist angles, then it would appear that the plane of the peptide also lies flat on the surface (ψ ≈ 10°). Given the orientation of the B₂ mode transition moment and the assumption that individual molecules are randomly oriented in the plane of the surface, such a twist angle might lead to very weak, or even undetectable, SFG signals, which would be at odds with the experimental observation of B₂ mode signals originating from the peptide in a β-sheet conformation. However, our MD simulation results do point to the feasibility of adopting a range of twist angles (such as the orientations shown in Figure 4), since driving factors for adsorption- such as surface area burial- appear to be similarly satisfied for windows with other small (45°) twist angles (Table 4). Due to the limited number of experimental measurements, a distribution of angles could not be directly characterized, but we believe that advances in computer simulation performance and new experimental techniques will make such characterization possible in the future.

Conclusions

New experimental techniques provide a powerful means to probe the orientation of peptides at interfaces, but often require key assumptions. In this paper, we explored several of those assumptions with regards to the adsorption behavior of the small β-sheet peptide tachyplesin I. The orientation and secondary structure change was characterized using a variety of metrics. General agreement was found between simulations and experiments with regards to the role of disulfide bonds in preserving the secondary structure, but simulations revealed a flexible interfacial structure that may affect data analysis methodologies which depend on the assumption of a linear and extended β-sheet conformation (or of any single rigid conformation). For the short β-sheet region in tachyplesin I, our results suggest that ignoring structural deformation is a reasonable approximation, but our simulations highlight the need to consider dynamic behavior as well as the well-known twisting of β-strands for future studies of larger β-sheet proteins.

Our findings from molecular dynamics were used to inform the interpretation of results from SFG and ATR-FTIR by deriving orientation relations for ATR-FTIR in a consistent rotation convention with SFG. The result was a more complete picture of molecular orientation and adsorption behavior. It was found that the long axis of the sheet will orient parallel to the plane of the surface in order to maximize favorable interactions, and that further rearrangements of the backbone will occur upon removal of the disulfide bonds. Our simulation results suggest that the peptide adopts a range of twist angles that would provide equally effective peptide-surface interactions, which would better explain the observed SFG signal intensities despite the lack of sufficient measurements to characterize a distribution of tilt angles directly from experiments. Lastly, time-dependent trends in adsorption seen in our simulation suggest the importance of side chain reorganization in determining the final orientation and adsorption timescale.

We believe that our simulation results, combined with the improved combination of ATR-FTIR and SFG orientation relations, thus provide a more complete picture of adsorbed orientation behavior, as well as representing an important step towards future vibrational spectroscopic studies of more complex β-sheet containing proteins.