Computational modeling of growth Systemic and pulmonary hypertension in the heart

Abstract

We introduce a novel constitutive model for growing soft biological tissue and study its performance in two characteristic cases of mechanically-induced wall thickening of the heart. We adopt the concept of an incompatible growth configuration introducing the multiplicative decomposition of the deformation gradient into an elastic and a growth part. The key feature of the model is the definition of the evolution equation for the growth tensor which we motivate by pressure-overload induced sarcomerogenesis. In response to the deposition of sarcomere units on the molecular level, the individual heart muscle cells increase in diameter, and the wall of the heart becomes progressively thicker. We present the underlying constitutive equations and their algorithmic implementation within an implicit nonlinear finite element framework. To demonstrate the features of the proposed approach, we study two classical growth phenomena in the heart: left and right ventricular wall thickening in response to systemic and pulmonary hypertension.

1 Introduction

Biological tissue is different from most engineering materials in that it is able to adapt to changes in its mechanical environment [50]. We can see this remodeling process in skeletal muscle, for example, as a growth in the muscle’s cross section in response to increased load during exercise. Similarly, cardiac muscle that experiences elevated stress due to abnormally high blood pressure in the ventricles, the lower chambers of the heart, undergoes transverse thickening, known as cardiac hypertrophy [16]. Even mild hypertension, if sufficiently prolonged, may induce hypertrophic ventricular growth. One out of four Americans suffers from hypertension of at least this degree [39]. On a microscopic scale, hypertrophic wall thickening can be attributed to a parallel addition of sarcomeres, the basic motor units of the muscle cell, associated with an increase in cellular volume and mass [48]. Even though muscular growth is initially an adaptive process that normalizes ventricular wall stress and ensures adequate supply of blood to our body, it may progress to heart failure, a maladaptive condition associated with high morbidity and mortality [4].

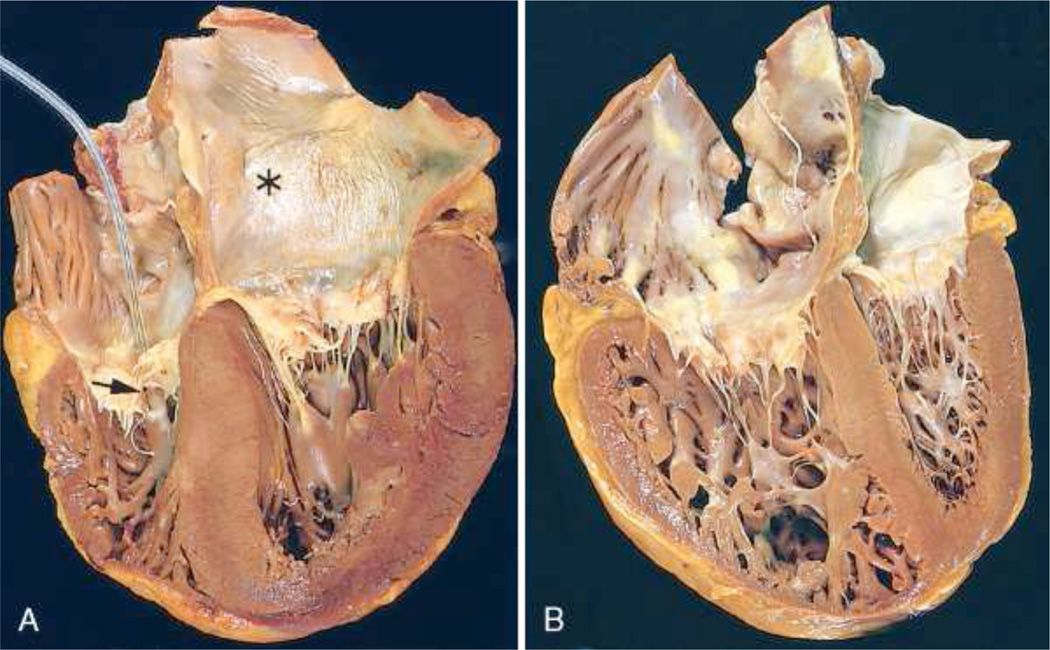
Numerous clinical conditions have been correlated with elevated left ventricular blood pressure. However, in most cases increased systemic resistance due to outflow obstruction is the cause [7]. Among other reasons, aortic stenosis, a partial occlusion of the outflow tract of the left ventricle, and a narrowing of the downstream blood vessels, the arteries, contribute to the increased resistance to blood flow. Subsequently, the left heart undergoes a series of changes initially compensating for the higher mechanical demands [28]. Under chronic hypertension, however, an increased left ventricular wall thickness may result in impaired perfusion of the cardiac tissue, increased stiffness and, as a consequence, a reduction in cardiac function [45], see Figure 1, left. In addition, secondary to left ventricular changes, enlargement of the left atrium, the upper chamber on the left side of the heart, may corrupt proper signal conduction and result in uncoordinated left atrial and ventricular contraction. If untreated, the maladaptive response of the left heart to hypertension may lead to congestive heart failure and consequently death [41].

Fig. 1.

Systemic and pulmonary hypertension in the heart. Systemic, or left-sided, hypertension is characterized through concentric thickening of the left ventricular wall causing a reduction in cavity volume, left. Pulmonary, or right-sided, hypertension is characterized through a significantly dilated right ventricle with a thickened free wall, right. The shape of the left ventricle has been distorted by the enlarged right ventricle. The left ventricle is shown on the right, the right ventricle is shown on the left, in these apical four-chamber views of the heart. Reprinted with permission [39].

The study of the right side of the heart is a relatively young field [20]. Although it has in principle the same function as the left side, that is to pump blood to the downstream tissue, its appearance is much different. Since the right heart has to overcome a significantly smaller pressure gradient when pumping blood to the lungs, its wall thickness is smaller than the thickness of the left side [21]. In addition, its geometry deviates from an ellipsoid and has been described as crescent shaped in cross section. These differences make the right side more compliant than the left ventricle and more prone to geometric alterations in response to hypertension [52]. Increased afterload of the right side of the heart, known as pulmonary hypertension, can have many origins. Often it is secondary, however, to disease in the left ventricle or to disorders of the lung [53]. In either case, similarly to the left side under systemic hypertrophy, extensive growth of the right ventricle may lead to heart failure, see Figure 1, right. Because of the interdependence of both ventricles, hypertrophy in the right side of the heart may also impair left ventricular function [20].

A vast amount of research has been conducted to deepen our understanding of causes, disease progression, disease treatment, and prevention of maladaptive cardiac growth due to elevated blood pressure. Despite these efforts, unfortunately, there still are a large number of patients suffering from the consequences of pathological remodeling of cardiac tissue. The development of computational models as analytical and predictive tools will provide an improved understanding, particularly from a mechanical point of view, and could be essential in reducing the prevalence of hypertensive cardiac growth.

The first model for volumetric growth in biological tissues was introduced about two decades ago [46]. Adopting ideas from finite strain plasticity [40], this model utilizes the concept of an incompatible growth configuration, introducing the multiplicative decomposition of the deformation gradient into an elastic and a growth part [10, 23, 50]. The last decade has seen tremendous efforts to refine this approach and establish continuum theories of finite growth with the ultimate goal to predict growth in different types of tissue [3, 8, 42, 44]. While there seems to be a general agreement on the multiplicative decomposition of the deformation gradient, growth theories are still lacking a rigorous approach to appropriately characterize the evolution of the growth tensor. This is partly due to the fact that there is obviously no universal growth law, since different types of tissue grow in different ways. Typical examples are growth of tumors [2], tendons [9], vascular tissue [1, 27, 37, 51], and the heart [16, 32].

The main idea of this manuscript is to closely tie the definition of the macroscopic growth tensor and the forces driving its temporal evolution to observations on the microstructural level [15]. The heart is an excellent model system for this approach since it consists primarily of cardiomyocytes, which are incapable of dividing or self-renewing [7]. Accordingly, the number of cells in the heart, approximately 6 billion at birth, remains relatively constant throughout an individual’s life time. The shape of these cells, however, may change and adapt to mechanical loading. It does so by the parallel and serial deposition of its basic functional building blocks, the sarcomere units, which themselves tend to be unaffected by growth maintaining a constant optimal operating length [39].

The advantage of studying growth of the heart, as compared to growth of other soft tissues, is that changes in cell size and sarcomere number are relatively easy to visualize in vitro [11] and therefore straightforward to manipulate and quantify [47, 55]. Moreover, it has been demonstrated experimentally that remodeling and cardiomyocyte slippage play a rather insignificant role during cardiac growth [11]. Accordingly, we attribute pathological changes in systemic and pulmonary hypertension exclusively to morphological changes of the cardiomyocytes themselves, neglecting the effects of extracellular matrix remodeling and fiber reorientation [24,36,38]. In hypertension, new sarcomeres are added in parallel to existing sarcomere units to form new myofibrils, the number of which may approximately triple, from about 50–100 to 200 per cardiomyocyte, in response to chronically elevated pressure levels. Accordingly, the individual cardiomyocytes increase in diameter, from approximately 15 to 40 µm [39], and the wall thickness can increase from 1 to 3 cm in the left ventricle [43], and from 0.5 to 1.5 cm in the right ventricle [52].

This manuscript is organized as follows. In Section 2 we briefly revisit the modeling of biological growth. In particular, we present a novel constitutive model for growth in anisotropic soft biological tissues, and illustrate its algorithmic implementation within an implicit nonlinear finite element setting. In Section 4, we demonstrate the features of the proposed growth model in systemic and pulmonary hypertension associated with left- and right-sided heart failure. Finally, we compare the results to pathological observations and discuss potential future directions in Section 5.

2 Continuum modeling of cardiac growth

In this section, we illustrate the governing equations of stress-induced cardiac growth. We briefly summarize the kinematic equations, the equilibrium equation, and the constitutive equations.

2.1 Kinematics of hypertensive growth

To characterize growth, we adopt the multiplicative decomposition of deformation gradient F into an elastic part F^e and a growth part F^g [46],

$$\begin{array}{ccc}\hfill \mathit{F}={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}}\hfill & \hfill \text{with}\hfill & \hfill \mathit{F}={\nabla }_{\mathit{X}}\mathit{\phi },\hfill \end{array}$$ (1)

a concept that was first proposed in the context of finite elasto-plasticity [40]. Herein, φ is the deformation map between the undeformed and the deformed configuration and ∇_X denotes its spatial gradient with respect to the undeformed coordinates X. Motivated by physiological observations during hypertrophic wall thickening, we introduce a single scalar-valued growth multiplier ϑ, that reflects the parallel deposition of sarcomeres associated with transversely isotropic cardiomyocyte growth on the molecular level [15]. The growth tensor F^g can thus be expressed as a simple rank-one update of the identity tensor.

$${\mathit{F}}^{\mathrm{g}}=\mathit{I}+[\vartheta -1]{\mathit{s}}_0\otimes {\mathit{s}}_0$$ (2)

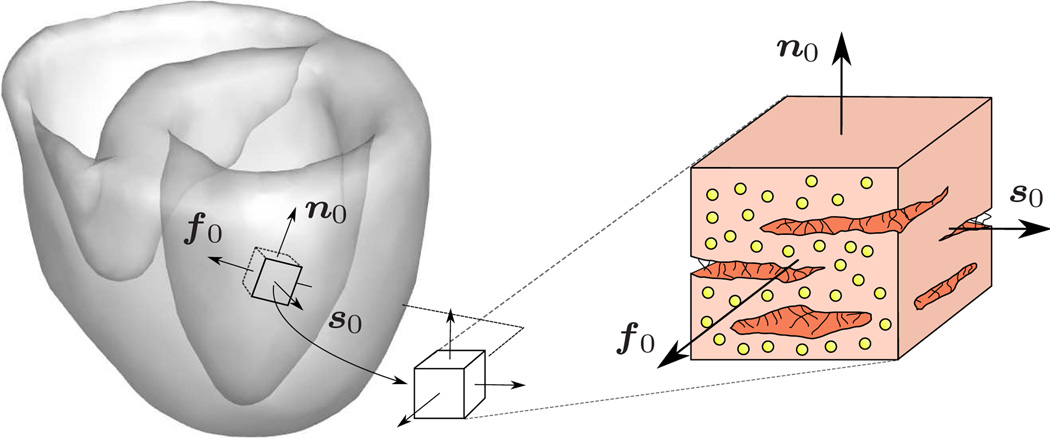
We adopt the concept of myocardial sheets [22] in which the individual muscle fibers are arranged in layers resulting in a locally orthotropic material characterization [14,25] as illustrated in Figure 2. With the common understanding that the sheet vector s₀ is pointing approximately in the radial direction, this form of cardiac growth is directly associated with ventricular wall thickening. The corresponding Jacobians J = J^e J^g follow accordingly with J = det(F), J^e = det(F^e) and J^g = det(F^g) = ϑ. With the definition of the growth tensor (2), we can immediately extract the elastic part of the deformation gradient F^e = F · F^{g − 1} which will be essential to characterize the elastically deformed fiber and sheet directions f^e = F^e · f₀ and s^e = F^e · s₀ as illustrated in Figure 2. We can then introduce the left Cauchy Green or Finger tensor b and its elastic counterpart b^e

$$\begin{array}{cc}\hfill \mathit{b}=\mathit{F}·{\mathit{G}}^{-1}·{\mathit{F}}^{\mathrm{t}}\hfill & \hfill {\mathit{b}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{e}}·{\mathit{G}}^{\mathrm{e}-1}·{\mathit{F}}^{\text{e t}}\hfill \end{array}$$ (3)

as the push forward of the inverse material metric G⁻¹ and the inverse intermediate metric G^e−1, respectively.

Fig. 2.

Characteristic orthotropic architecture of the myocardium made up of cardiac muscle fibers which are arranged in layers of sheets [22]. The orthogonal unit vectors f₀ and s₀ indicate the fiber and sheet directions in the undeformed configuration. The sheet plane unit normal n₀ is orthogonal to the both by its definition n₀ := [f₀ × s₀]/|f₀ × s₀|, [14, 25].

2.2 Equilibrium equation of hypertensive growth

In the absence of transient terms and external forces, the balance of linear momentum can be expressed in the following reduced format,

$$\text{div}(\mathit{\sigma })=\mathbf{0}$$ (4)

where div(σ) denotes the divergence of the total Cauchy stress σ with respect to the spatial position x. Experimental and clinical studies suggest that hypertrophic wall thickening is primarily a response to elevated systolic stresses [39]. While clinical approaches typically model the difference between systolic and diastolic stresses through increasing the elastic material parameters [29, 31], we will adopt a more mechanical approach and express the total Cauchy stress

$$\mathit{\sigma }={\mathit{\sigma }}^{\text{pas}}+{\mathit{\sigma }}^{\text{act}}$$ (5)

as the sum of passive and active contributions [5, 13, 18]. Both will be introduced constitutively in the sequel along with the constitutive definition of the growth multiplier ϑ.

2.3 Constitutive equations of hypertensive growth

To constitutively define the passive stress σ^pas, we introduce the following Helmholtz free energy function

$${\psi }^{\text{pas}}={\psi }_J+{\psi }_1+{\psi }_{\mathrm{f}}+{\psi }_{\mathrm{s}}+{\psi }_{\text{fs}}$$ (6)

motivated by a recently proposed approach for orthotropic cardiac tissue [14, 25]. It consists of two isotropic and three anisotropic contributions

$$\begin{array}{cc}{\psi }_J=\kappa [J^{\mathrm{e}}-\text{ln}(J^{\mathrm{e}})-1]\hfill & J^{\mathrm{e}}=\text{det}({\mathit{F}}^{\mathrm{e}})\hfill \\ {\psi }_1=\frac{a}{2b}\text{ exp}(b[I_1^{\mathrm{e}}-3])\hfill & I_1^{\mathrm{e}}=\mathit{g}:{\mathit{b}}^{\mathrm{e}}\hfill \\ {\psi }_{\mathrm{f}}=\frac{a_{\mathrm{f}}}{2b_{\mathrm{f}}}[\text{exp}(b_{\mathrm{f}}{[I_{\mathrm{f}}^{\mathrm{e}}-1]}^2)-1]\hfill & I_{\mathrm{f}}^{\mathrm{e}}=\mathit{g}:[{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}]\hfill \\ {\psi }_{\mathrm{s}}=\frac{a_{\mathrm{s}}}{2b_{\mathrm{s}}}[\text{exp}(b_{\mathrm{s}}{[I_{\mathrm{s}}^{\mathrm{e}}-1]}^2)-1]\hfill & I_{\mathrm{s}}^{\mathrm{e}}=\mathit{g}:[{\mathit{s}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}]\hfill \\ {\psi }_{\text{fs}}=\frac{a_{\text{fs}}}{2b_{\text{fs}}}[\text{exp}(b_{\text{fs}}{I}_{\text{fs}}^{\mathrm{e}2})-1]\hfill & I_{\text{fs}}^{\mathrm{e}}=\mathit{g}:{[{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}]}^{\text{sym}}\hfill \end{array}$$ (7)

parameterized in terms of five elastic invariants $J^{\mathrm{e}},I_1^{\mathrm{e}},I_{\mathrm{f}}^{\mathrm{e}},I_{\mathrm{s}}^{\mathrm{e}},\text{and }{I}_{\text{fs}}^{\mathrm{e}}$ , weighted by the bulk modulus κ and the four sets of parameters a and b. Using standard arguments of thermodynamics, the passive Kirchhoff stress τ^pas = J σ^pas then follows naturally as the derivative of the Helmholtz free energy ψ^pas with respect to the covariant spatial metric g,

$${\mathit{\tau }}^{\text{pas}}=2\frac{\partial {\psi }^{\text{pas}}}{\partial \mathit{g}}=\kappa [J^{\mathrm{e}}-1]{\mathit{g}}^{-1}+2{\psi }_1^{\prime }{\mathit{b}}^{\mathrm{e}}+2{\psi }_{\mathrm{f}}^{\prime }{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}+2{\psi }_{\mathrm{s}}^{\prime }{\mathit{s}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}+2{\psi }_{\text{fs}}^{\prime }{[{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}]}^{\text{sym}}$$ (8)

in terms of two isotropic and three anisotropic contributions with

$$\begin{array}{cc}{\psi }_1^{\prime }=\begin{array}{cc}a\hfill & \hfill \frac{1}{2}\end{array}\hfill & \text{exp }(b[I_1^{\mathrm{e}}-3])\hfill \\ {\psi }_{\mathrm{f}}^{\prime }=a_{\mathrm{f}}[I_{\mathrm{f}}^{\mathrm{e}}-1]\hfill & \text{exp }(b_{\mathrm{f}}{[I_{\mathrm{f}}^{\mathrm{e}}-1]}^2)\hfill \\ {\psi }_{\mathrm{s}}^{\prime }=a_{\mathrm{s}}[I_{\mathrm{s}}^{\mathrm{e}}-1]\hfill & \text{exp }(b_{\mathrm{s}}{[I_{\mathrm{s}}^{\mathrm{e}}-1]}^2)\hfill \\ {\psi }_{\text{fs}}^{\prime }=a_{\text{fs}}{I}_{\text{fs}}^{\mathrm{e}}\hfill & \text{exp }(b_{\text{fs}}{I}_{\text{fs}}^{\mathrm{e}2}).\hfill \end{array}$$ (9)

We assume that the active stress τ^act = J σ^act is acting exclusively along the fiber direction f^e,

$${\mathit{\tau }}^{\text{act}}=T^{\text{act}}(I_{\mathrm{f}}^{\mathrm{e}},c_{\text{Ca}}){\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}$$ (10)

and that its magnitude T^act is dependent on the intracellular calcium concentration c_Ca and on the current sarcomere length $l=\sqrt{I_{\mathrm{f}}^{\mathrm{e}}}L$ , where L is the sarcomere resting length in the underformed configuration [18,19]. In particular, we choose the following formulation,

$$T^{\text{act}}=T^{\text{max}}\frac{{c_{\text{Ca}}}^2}{{c_{\text{Ca}}}^2+{{\tilde{c}}_{\text{Ca}}}^2}\text{ with }{\tilde{c}}_{\text{Ca}}={\tilde{c}}_{\text{Ca}}(I_{\mathrm{f}}^{\mathrm{e}})$$ (11)

where T^max is the maximum isometric tension found at the maximum intracellular calcium concentration $c_{\text{Ca}}^{\text{max}}$ , and c̃_Ca is the length dependent calcium concentration. We slightly modify its original definition ${{\tilde{c}}_{\text{Ca}}}^2=1/[\text{exp}(\beta [l-l_0])-1]c_{\text{Ca}}^{\text{max }2}$ proposed in [18], to obtain a smooth dependence of the active stress on the current sarcomere length $l=\sqrt{I_{\mathrm{f}}^{\mathrm{e}}}L$

$${{\tilde{c}}_{\text{Ca}}}^2=[1/\text{exp}(-\text{exp}(-\xi [l-l_0]))-1]c_{\text{Ca}}^{\text{max}2}$$ (12)

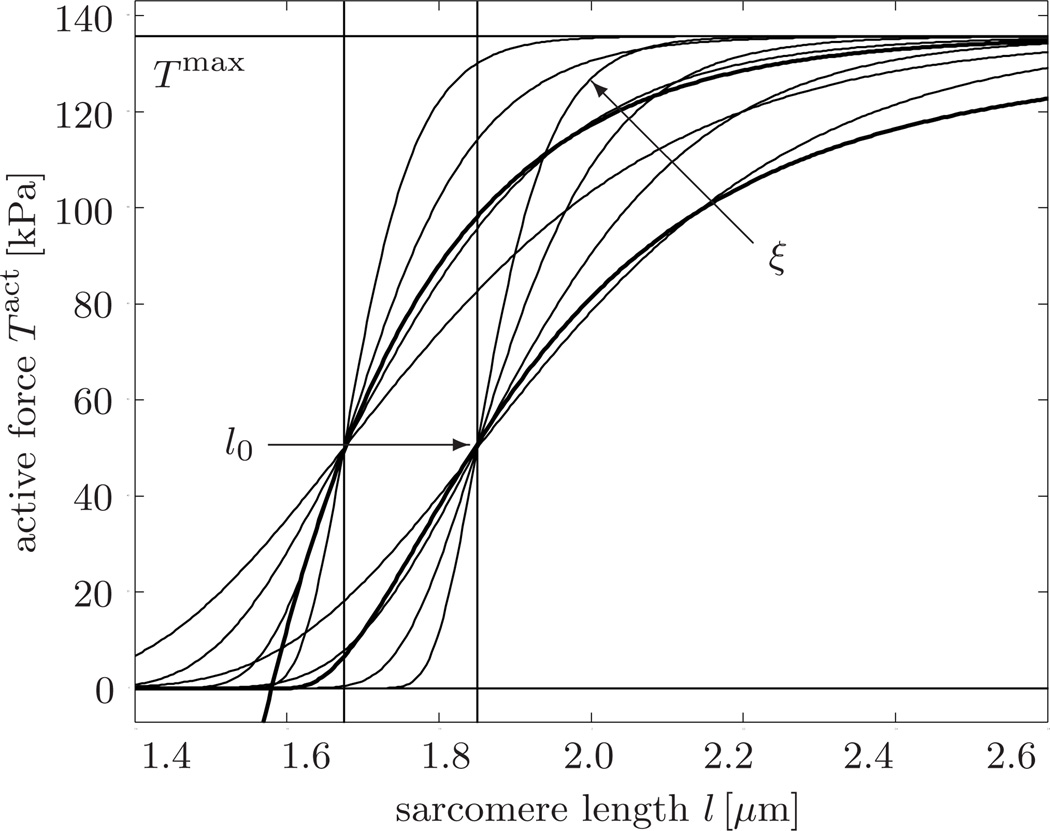
The parameters ξ and l₀ characterize the slope of the Starling curve and the optimal sarcomere operating length, respectively. Since we are not interested in calcium dynamics but rather in the state of maximum systolic stress, we assume optimal calcium conditions [19], $c_{\text{Ca}}^{\text{max}}=c_{\text{Ca}}$ , such that equation (11) reduces to the following simplified expression illustrated in Figure 3.

$$T^{\text{act}}=T^{\text{max}}\text{ exp}(-\text{exp}(-\xi [l-l_0]))$$ (13)

Fig. 3.

Active force vs. sarcomere length. According to Starling’s law, the active force increases with increased sarcomere length. The thin lines illustrate our smooth active force relation, T^act = T^max exp(−exp(−ξ[l − l₀])). Increasing the slope parameter ξ increases the slope of the active force curve. Increasing the optimal sarcomere operating length l₀ shifts the active force curve to the right. The thick lines in the background illustrate the original active force relation proposed in the literature [18, 19].

Motivated by pathological observations, we introduce a stress-driven evolution equation for concentric hypertrophic growth

$$\dot{\vartheta }=k(\vartheta )\varphi (\mathit{\tau })$$ (14)

in terms of the growth scaling function k(ϑ) and the growth criterion ϕ(τ) with

$$k=\frac{1}{{\tau }_{\vartheta }}{\left[\frac{{\vartheta }^{\text{max}}-\vartheta }{{\vartheta }^{\text{max}}-1}\right]}^{\gamma }\text{ and }\varphi =\text{tr}(\mathit{\tau })-p^{\text{crit}}.$$ (15)

Herein, τ_ϑ denotes the adaptation speed, ϑ^max is the area fraction of maximum parallel sarcomere deposition, and γ is the degree of sarcomere deposition nonlinearity [15, 42]. Following thermodynamical considerations, we choose the physiological overstress tr(τ) − p^crit, i.e., the difference between the trace of the Kirchhoff stress tr(τ) = τ : g and the baseline pressure level p^crit as the driving force for growth [8, 23].

Remark 1 (Growth and incompressibility) In the kinematic setting of finite growth, incompressibility could be taken into account by penalizing the total volume change. However, this approach does not seem justified for soft tissues that may undergo considerable volume changes during growth. In particular in the context of hypertrophic wall thickening it seems more appropriate to impose incompressibility [49] or quasi-incompressibility [23] on the elastic part of the deformation. Rather than requiring strict incompressibility as we have recently proposed [14], in this manuscript, we will impose quasi-incompressibility through a sufficiently large bulk modulus κ in the volumetric part of the free energy. Quasi-incompressibility might be justified for cardiac muscle which has been reported to undergo volume changes of up to 5–10% attributed to the vascular network that constitutes about 10–20% of the total muscle volume [54].

Remark 2 (Growth and open systems) In the present approach, we characterize the growth process through a single growing solid phase and essentially neglect the biochemical origin of the growing material. In a thermodynamic sense, this implies that we are modeling the growing tissue as an open system that is allowed to increase its mass [33–35]. This mass change gains a more illustrative biochemical interpretation in the context of mixture theories [9, 26].

3 Computational modeling of cardiac growth

In this section, we will illustrate the algorithmic realization of finite growth within an incremental iterative nonlinear finite element setting. In particular, we illustrate the linearizations required for the local and global Newton iterations, and summarize the algorithm in an illustrative flowchart.

3.1 Local Newton iteration - Iterative update of growth multiplier

Our goal is to determine the current growth multiplier ϑ for a given deformation state F at time t, and a given growth multiplier ϑ_n at the end of the previous time step t_n.

We introduce the following finite difference approximation of the first order material time derivative, ϑ̇ = [ϑ − ϑ_n] /Δt where Δt = t − t_n > 0 denotes the current time increment. In the spirit of implicit time stepping schemes, we now reformulate the evolution equation (14) with the help of this finite difference approximation, introducing the discrete residual 𝗥 in terms of the unknown growth multiplier ϑ.

$$𝗥=\vartheta -{\vartheta }_{\mathrm{n}}-\frac{1}{{\tau }_{\vartheta }}{\left[\frac{{\vartheta }^{\text{max}}-\vartheta }{{\vartheta }^{\text{max}}-1}\right]}^{\gamma }[\text{tr}(\mathit{\tau })-p^{\text{crit}}]\Delta t\doteq 0$$ (16)

Within each local Newton iteration, we can then express the iterative update of the growth multiplier ϑ ← ϑ −𝗥 /𝗞 in terms of the discrete residual 𝗥 and its linearization 𝗞.

$$𝗞=\frac{\mathrm{d}𝗥}{\mathrm{d}\vartheta }=1-[k\frac{\partial \varphi }{\partial \vartheta }+\varphi \frac{\partial k}{\partial \vartheta }]\Delta t$$ (17)

The discrete sensitivities in the above equation take the following explicit representations,

$$\frac{\partial \varphi }{\partial \vartheta }=\frac{\partial \mathit{\tau }}{\partial \vartheta }:\mathit{g}\text{ and }\frac{\partial k}{\partial \vartheta }=-\frac{\gamma }{[{\vartheta }^{\text{max}}-\vartheta ]}k.$$ (18)

3.2 Global Newton iteration - Consistent linearization of hypertensive growth

Upon convergence of ϑ, we can successively update the growth tensor F^g = I + [ϑ − 1] s₀ ⊗ s₀ from equation (2), the elastic tensor F^e = F · F^{g − 1} from equation (1), and the Kirchhoff stress τ = 2 ∂ψ/∂g from equation (5), to finally evaluate the global equilibrium equation (4). For its solution, we propose a global Newton iteration based on the consistent algorithmic linearization of the Kirchhoff stress τ with respect to the spatial metric g introducing the Eulerian constitutive moduli e.

$$\mathbf{e}=2\frac{\mathrm{d}\mathit{\tau }}{\mathrm{d}\mathit{g}}=2\frac{\partial \mathit{\tau }}{\partial \mathit{g}}{|}_{\vartheta }+2\frac{\partial \mathit{\tau }}{\partial \vartheta }{|}_{\mathit{g}}\otimes \frac{\partial \vartheta }{\partial \mathit{g}}={\mathbf{e}}^{\mathrm{e}}+{\mathbf{e}}^{\mathrm{g}}$$ (19)

The first term represents the classical elastic Eulerian moduli

$${\mathbf{e}}^{\mathrm{e}}=2\frac{\partial \mathit{\tau }}{\partial \mathit{g}}={\mathbf{e}}^{\text{pas}}+{\mathbf{e}}^{\text{act}}$$ (20)

which can be expressed as the sum of passive

$${\mathbf{e}}^{\text{pas}}=2\frac{\partial \mathit{\tau }}{\partial \mathit{g}}\stackrel{\text{pas}}{=}{J}^{\mathrm{e}}\kappa {\mathit{g}}^{\mathit{-}1}\otimes {\mathit{g}}^{-1}+2\kappa [J^{\mathrm{e}}-1]{\partial }_{\mathit{g}}{\mathit{g}}^{-1}+4{\psi }_1^{″}{\mathit{b}}^{\mathrm{e}}\otimes {\mathit{b}}^{\mathrm{e}}+4{\psi }_{\mathrm{f}}^{″}{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}+4{\psi }_{\mathrm{s}}^{″}{\mathit{s}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}+4{\psi }_{\text{fs}}^{″}{[{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}]}^{\text{sym}}\otimes {[{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}]}^{\text{sym}}$$ (21)

and active contributions.

$${\mathbf{e}}^{\text{act}}=2\frac{\partial \mathit{\tau }}{\partial \mathit{g}}\stackrel{\text{act}}{=}2T^{\text{act}\prime }{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}\otimes {\mathit{f}}^{\mathrm{e}}$$ (22)

The derivatives in equations (21) and (22) take the following explicit representations

$$\begin{array}{ccc}{\psi }_1^{″}=a\hfill & \hfill \frac{1}{2}b\hfill & \text{exp }(b[I_1^{\mathrm{e}}-3])\hfill \\ {\psi }_{\mathrm{f}}^{″}=a_{\mathrm{f}}\hfill & [1+2b_{\mathrm{f}}{[I_{\mathrm{f}}^{\mathrm{e}}-1]}^2]\hfill & \text{exp }(b_{\mathrm{f}}{[I_{\mathrm{f}}^{\mathrm{e}}-1]}^2)\hfill \\ {\psi }_{\mathrm{s}}^{″}=a_{\mathrm{s}}\hfill & [1+2b_{\mathrm{s}}{[I_{\mathrm{s}}^{\mathrm{e}}-1]}^2]\hfill & \text{exp }(b_{\mathrm{s}}{[I_{\mathrm{s}}^{\mathrm{e}}-1]}^2)\hfill \\ {\psi }_{\text{fs}}^{″}=a_{\text{fs}}\hfill & [1+2b_{\text{fs}}{I}_{\text{fs}}^{\mathrm{e}2}]\hfill & \text{exp }(b_{\text{fs}}{I}_{\text{fs}}^{\mathrm{e}2}).\hfill \end{array}$$ (23)

and, for the case of $c_{\text{Ca}}=c_{\text{Ca}}^{\text{max}}$ considered herein,

$$T^{\text{act}\prime }=\frac{1}{2}{T}^{\text{act}}\xi \text{ exp}(-\xi [l-l_0])L^2/l.$$ (24)

The second term in the overall Eulerian moduli (19) reflects the effects of hypertensive growth and is only active in the inelastic case.

$${\mathbf{e}}^{\mathrm{g}}=2\frac{\partial \mathit{\tau }}{\partial \vartheta }\otimes \frac{\partial \vartheta }{\partial \mathit{g}}$$ (25)

It consists of the linearization of the Kirchhoff stress τ with respect to the growth multiplier ϑ, a term which obviously depends on the particular choice of the constitutive equation.

$$\frac{\partial \mathit{\tau }}{\partial \vartheta }=\frac{1}{\vartheta }{J}^{\mathrm{e}}\kappa {\mathit{g}}^{-1}-\frac{4}{\vartheta }[{\psi }_1^{\prime }{I}_{\mathrm{s}}^{\mathrm{e}}{\mathit{b}}^{\mathrm{e}}+[{\psi }_{\mathrm{s}}^{\prime }{I}_{\mathrm{s}}^{\mathrm{e}}+{\psi }_{\mathrm{s}}+{\psi }_1]{\mathit{s}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}+[{\psi }_{\text{fs}}^{\prime }{I}_{\text{fs}}^{\mathrm{e}}+{\psi }_{\text{fs}}]{[{\mathit{f}}^{\mathrm{e}}\otimes {\mathit{s}}^{\mathrm{e}}]}^{\text{sym}}]$$ (26)

This term is multiplied with the consistent algorithmic linearization of the converged growth multiplier ϑ with respect to the spatial metric g.

$$\frac{\partial \vartheta }{\partial \mathit{g}}=\frac{k}{𝗞}\Delta t[\frac{1}{2}{\mathit{e}}^{\mathrm{e}}:\mathit{g}+\mathit{\tau }]$$ (27)

We would like to point out that only very specific stress-driven isotropic growth formulations actually yield a symmetric tangent operator, while this formulation obviously does not, see [16] for details.

3.3 Algorithmic treatment of hypertensive growth

Table 1 illustrates the algorithmic treatment of stress-driven transversely isotropic growth through parallel sarcomere deposition.

Table 1.

Algorithmic treatment of stress-driven transversely isotropic growth through parallel sarcomere deposition.

given F and ϑn
initialize ϑ ← ϑn
local Newton iteration
calculate growth tensor Fg = I + [ϑ − 1 ] s0 ⊗ s0	(2)
calculate elastic tensor Fe = F · Fg −1	(1)
calculate elastic Finger tensor be = Fe · Fe t	(3)
calculate Kirchhoff stress τ = τpas + τact	(5),(8),(10)
check growth criterion ϕ = tr(τ) − pcrit ≥ 0 ?	(15.1)
calculate growth function k(ϑ)	(15.2)
calculate residual 𝗥 = ϑ − ϑn − k ϕΔt	(16)
calculate tangent 𝗞 = ∂𝗥 / ∂ϑ	(17),(18)
update growth multiplier ϑ ← ϑ − 𝗥/𝗞
check convergence 𝗥 ≤ tol ?
calculate Eulerian moduli e	(19)–(27)

4 Examples

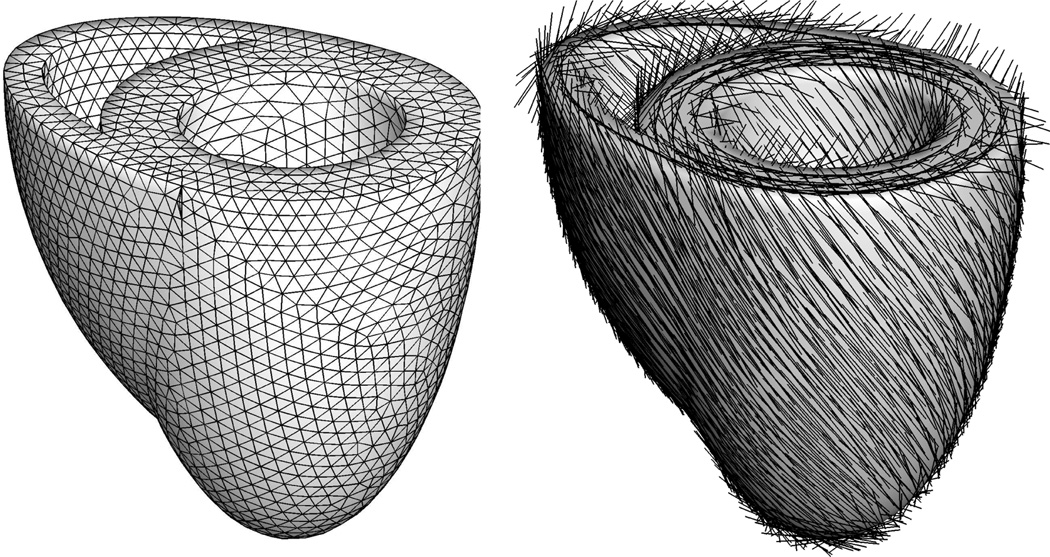
To explore the features of the proposed growth model, we study the effects of systemic and pulmonary hypertension in a generic biventricular heart geometry [14]. In this idealized prototype model, the left and right ventricles are represented through two truncated ellipsoids with heights of 70mm and 60mm and radii of 30mm and 51mm, respectively. They are connected such that the right ventricle blends smoothly into the left ventricle from apex to base, see Figure 5. The left ventricle which pumps oxygenated blood into the body operates at a higher pressure and typically has a larger wall thickness than the right ventricle which pumps deoxygenated blood into the lungs. We therefore assume an initial left ventricular wall thickness of 12mm while the right ventricular wall is assumed to be 6mm thick. The generic biventricular heart is discretized with 33,713 linear tetrahedral elements connected at 6,718 nodes. In the healthy heart, cardiomyocytes are arranged helically around the ventricles. We therefore assume the fiber direction f₀ to vary transmurally from an inclination of −70° in the epicardium, the outer layer, to +70° in the endocardium, the inner layer, measured with respect to the basal plane, see Figure 5. For the sake of simplicity, the myocardial sheet directions s₀ are assumed be oriented normal to the endocardium and epicardium. The left and right ventricular endocardium are subject to ventricular pressures which are increased linearly, then held constant, and finally decreased linearly back to zero, see Figures 6 and 9. As baseline values, we assume a left and right ventricular pressure of p_LV = 100mmHg and p_RV = 20mmHg, respectively. For the lack of better knowledge, we apply homogeneous Dirichlet boundary conditions to all nodes in the basal plane. In addition, to mimic the boundary conditions imposed by the surrounding tissue, we support all nodes of the epicardium by linear springs with a stiffness of k = 10⁻³ N/mm in the radial and tangential directions. The material parameters for the passive elastic response, a = 0.000496, b = 7.21, a_f = 0.0152, b_f = 20.42, a_s = 0.00328, b_s = 11.18, a_fs = 0.00066, and b_fs = 9.4662, have been identified using six cyclic simple shear experiments [6] as recently demonstrated [14,25]. The bulk modulus is chosen to κ = 2.87MPa. The material parameters characterizing the active contraction are the maximum isometric tension T^max = 0.1357MPa, the sarcomere resting length L = 1.85 µm, the intracellular calcium concentration c_Ca = 4.35 µmol/L, and the maximum intracellular calcium concentration $c_{\text{Ca}}^{\text{max}}=4.35\mu \text{mol}/\mathrm{L}$ , adopted from the literature [18, 19]. The slope parameter ξ = 10 µm⁻¹ and the optimal sarcomere operating length l₀ = 2.00 µm are fit to match the active force curve reported in the literature [19] according to the sensitivity studies reported in Figure 3. The additional growth parameters are the adaptation speed τ_ϑ = 1.0MPa s, the degree of growth nonlinearity γ = 3.0, the area fraction of maximum parallel sarcomere deposition ϑ^max = 4.0, and the growth stress p^crit = 0.08 MPa, which would take the interpretation of the yield stress in the theory of plasticity. The growth parameters are adopted from the recent literature [15, 16], and their sensitivities are illustrated in Figure 4. At this point, the choices of the time parameter τ_ϑ and the nonlinearity parameter γ are relatively generic since they only affect the speed of growth, but not the end result of the growth process itself. In the future, however, we will use these two parameters to calibrate our model against long-term chronic studies.

Fig. 5.

Generic biventricular heart model generated from two truncated ellipsoids, with heights of 70mm and 60mm, radii of 30mm and 51mm, and wall thicknesses of 12mm and 6mm, respectively [13, 14]. The generic heart is discretized with 33,713 linear tetrahedral elements connected at 6,718 nodes, left. Fiber orientations vary transmurally from −70° in the epicardium, the outer layer, to +70° in the endocardium, the inner layer, right.

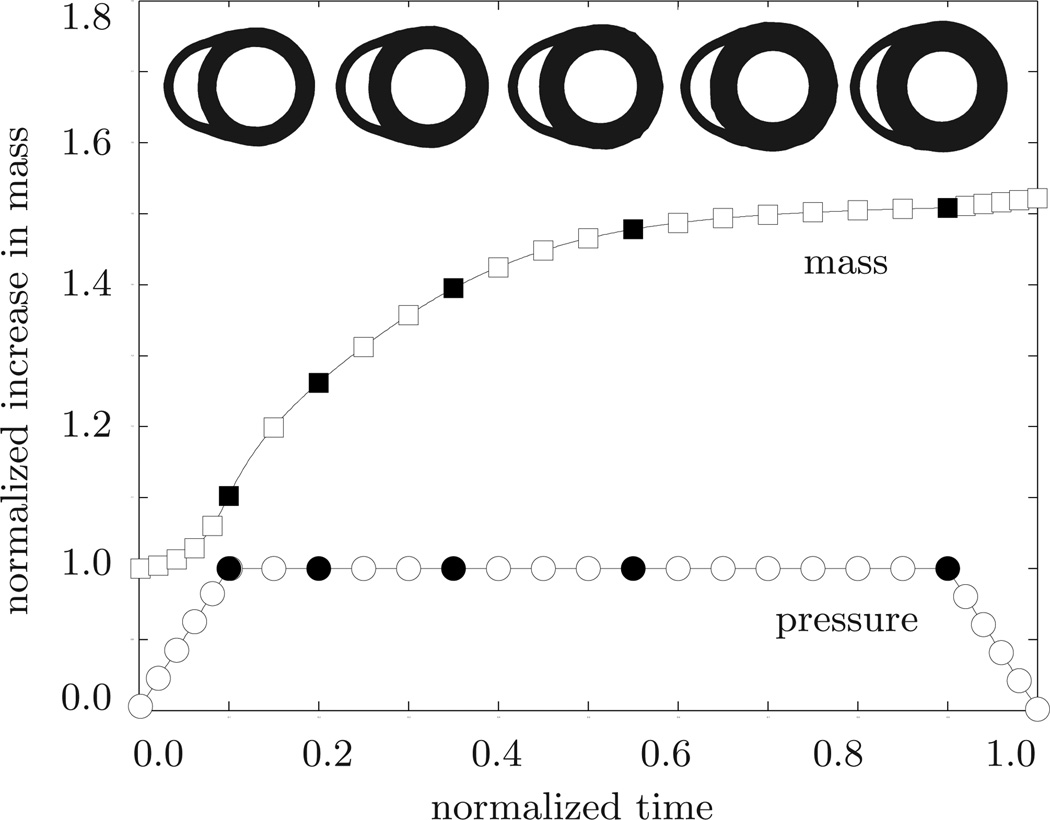
Fig. 6.

Systemic hypertension. Temporal evolution of normalized applied pressure and normalized mass. An elevated left ventricular pressure induces a progressive left ventricular wall thickening accompanied by an increase in cardiac mass. Convergence is obtained at a mass increase of approximately 52%. At this point, the left ventricular wall has grown thick enough to withstand the elevated pressure level. The five sketched cross sections correspond to the five black symbols in the pressure and mass curves.

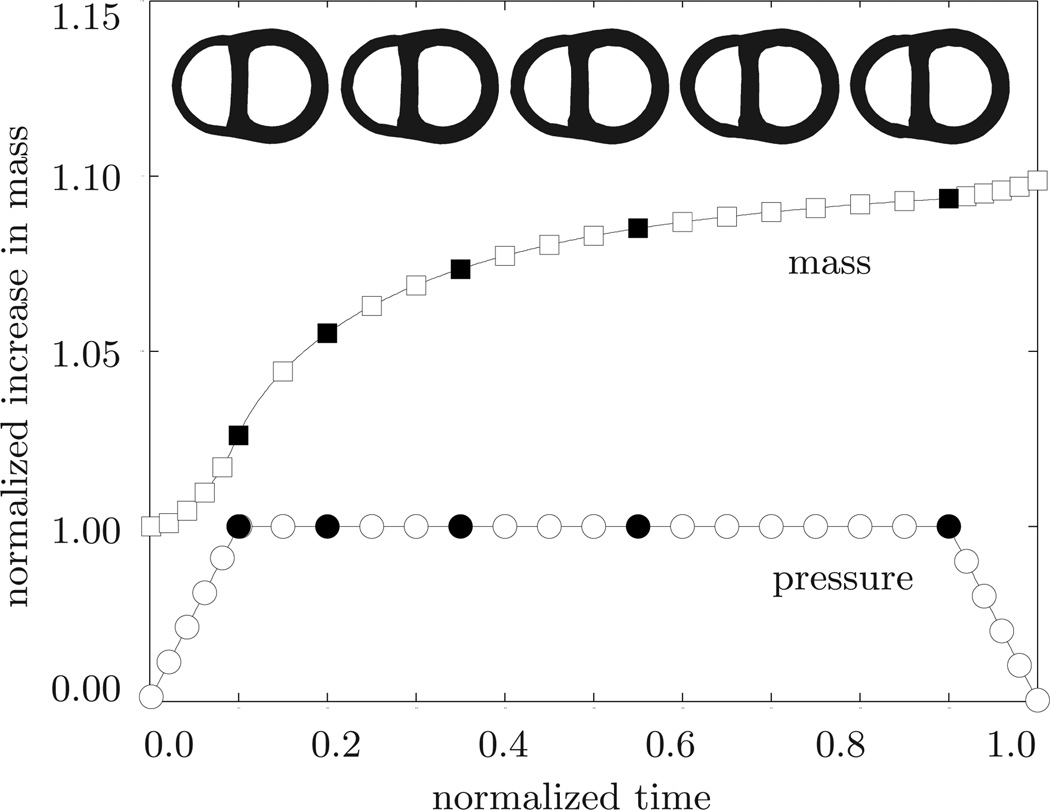
Fig. 9.

Pulmonary hypertension. Temporal evolution of normalized applied pressure and normalized mass. An elevated right ventricular pressure induces a progressive right ventricular wall thickening accompanied by an increase in cardiac mass. Convergence is obtained at a mass increase of approximately 10%. At this point, the right ventricular wall has grown thick enough to withstand the elevated pressure level. The five sketched cross sections correspond to the five black symbols in the pressure and mass curves.

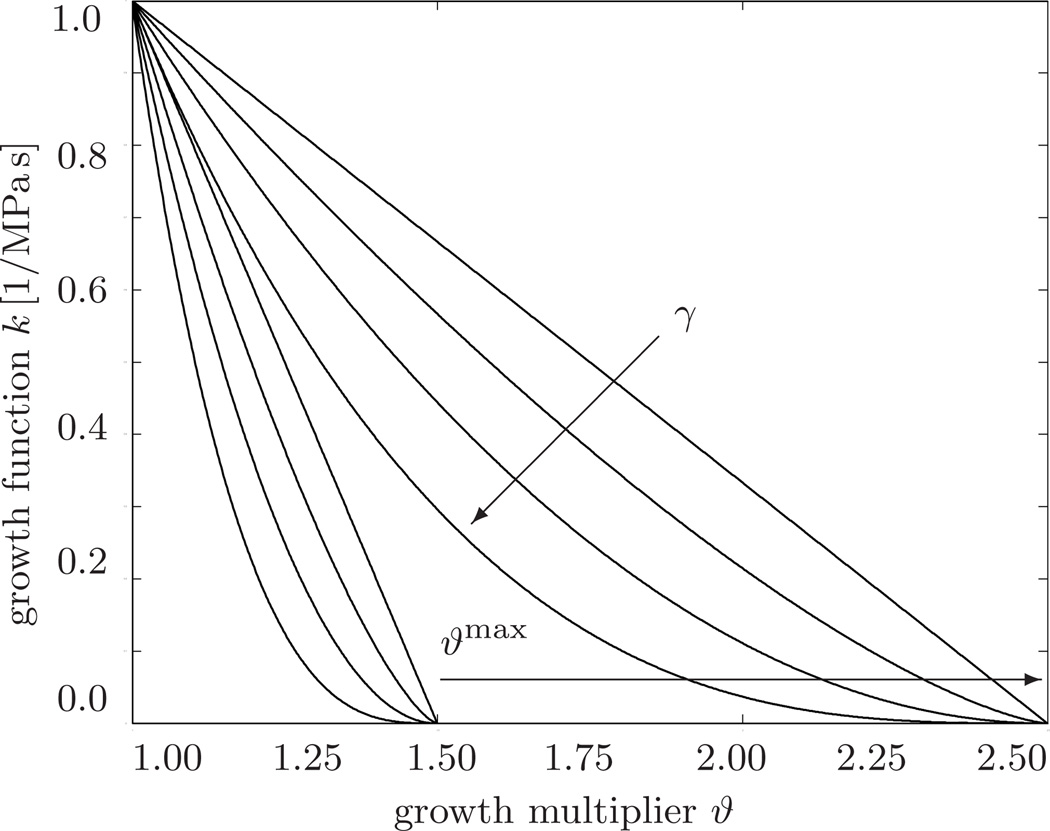
Fig. 4.

Growth function vs. growth multiplier. The growth function k = [[ϑ^max − ϑ]/[ϑ^max − 1]]^γ/τ_ϑ decreases gradually as the growth multiplier ϑ reaches the maximum parallel sarcomere deposition ϑ^max. Increasing the degree of growth nonlinearity changes the rate of parallel sarcomere deposition. Increasing the maximum parallel sarcomere deposition ϑ^max increases the amount of potential growth.

4.1 Cardiac hypertrophy in systemic hypertension

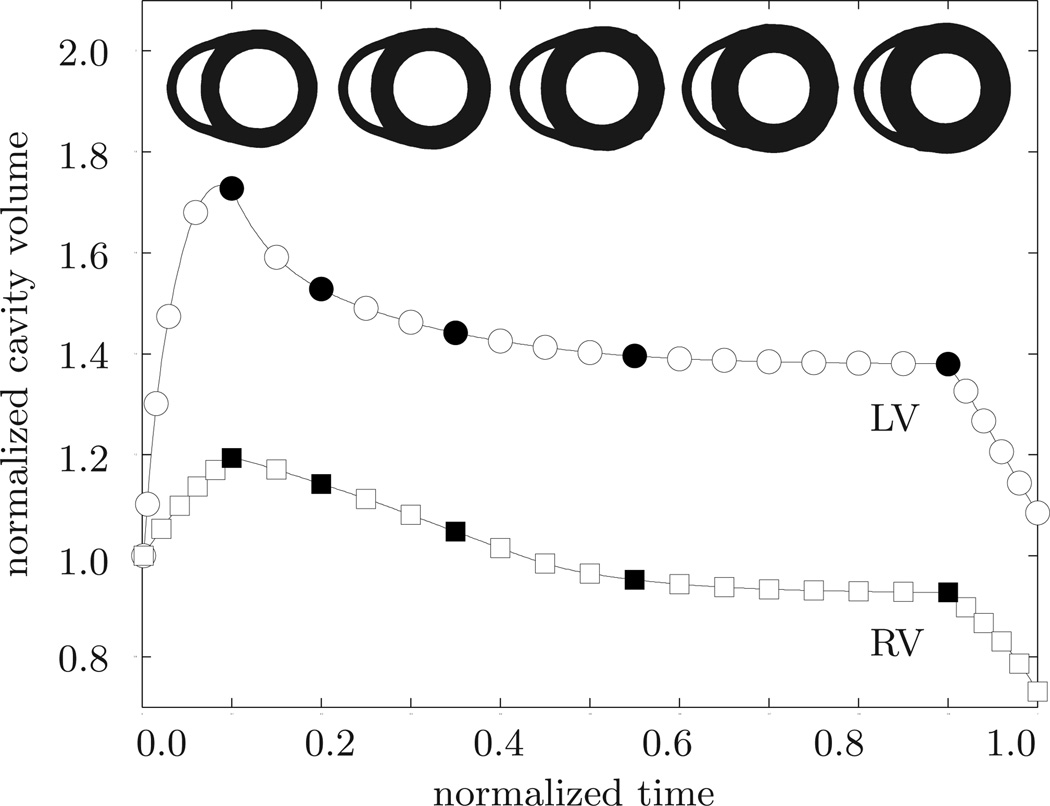
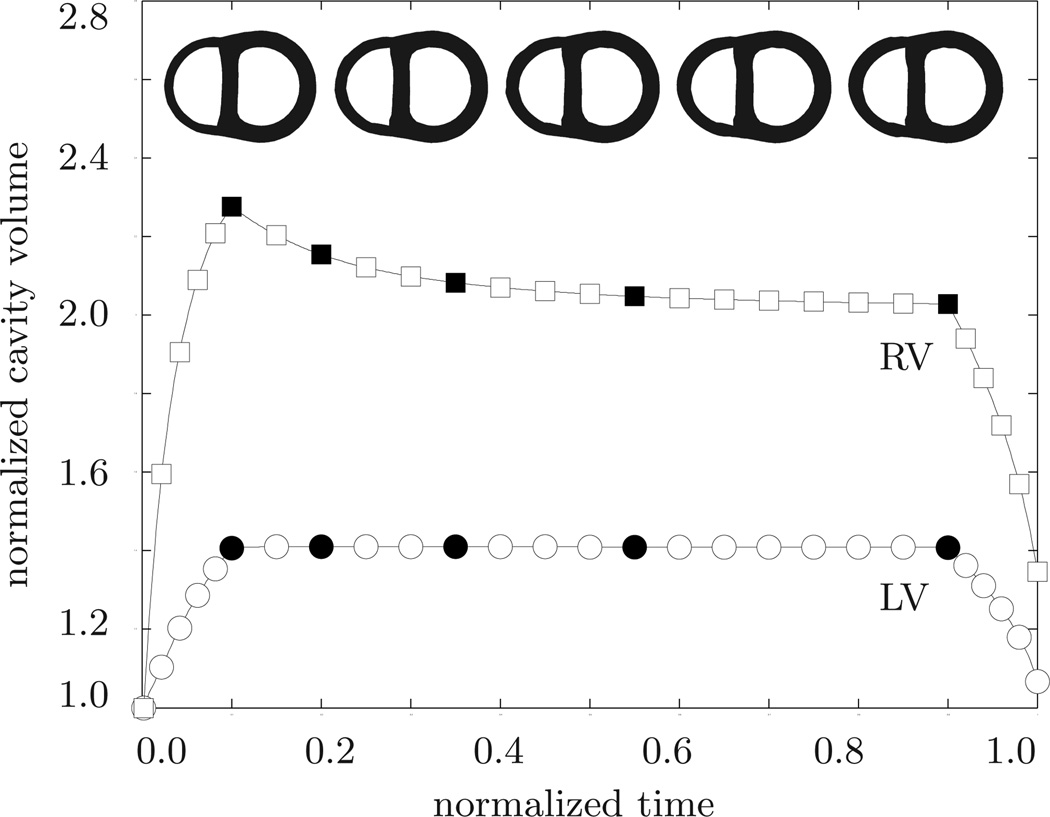
Our first example illustrates the performance of the growth algorithm in the context of systemic hypertension. To mimic the effect of an increased systemic resistance, we increase the left ventricular pressure while the right ventricular pressure remains at its baseline value, i.e., p_LV > 100 mmHg and p_RV = 20 mmHg, respectively. The linear pressure increase towards these values, its constant plateau, and its linear decrease are documented in Figure 6. In addition, Figure 6 displays the normalized increase in cardiac mass. In response to pressure overload, the left ventricular wall thickens and the mass of the heart increases by approximately 52%. This increase in mass agrees favorably with the mass increase reported in the literature from an initial value of 300–350 g to more than 500 g in response to severe systemic hypertension [39]. The mass increase decays over time until convergence is obtained. At that point, the ventricular wall has grown strong enough to pump against the elevated blood pressure. Figure 7 illustrates the temporal evolution of the normalized left and right cavity volume. Both increase initially as the pressure load is increased. Then, at constant pressure, the left ventricular wall begins to thicken in response to pressure overload. Accordingly, the left ventricular cavity volume decreases. The marked concentric thickening of the left ventricular wall associated with a significant reduction in lumen size agrees well with the pathophysiology of systemic hypertension [39]. As the wall thickens, it pushes into the right ventricle and induces a shrinkage of the right ventricular cavity volume.

Fig. 7.

Systemic hypertension. Temporal evolution of normalized left and right cavity volume. Accutely, the left ventricular cavity volume increases in response to left ventricular pressure overload. Chronically, due to progressive left ventricular wall thickening in response to pressure overload, the left ventricular cavity volume decreases progressively. At the same time, the left ventricle pushes into the right ventricle and its cavity volume decreases accordingly. The five sketched cross sections correspond to the five black symbols in the normalized cavity volume curves.

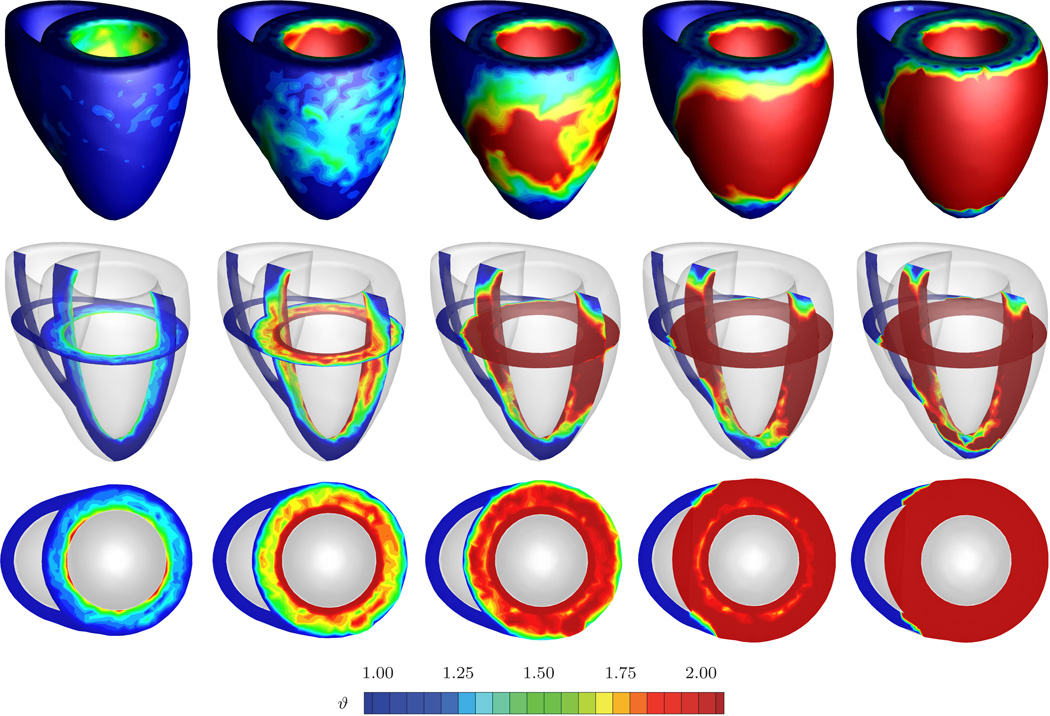
Figure 8 displays the spatio-temporal evolution of the growth multiplier projected onto the adaptively grown heart. The five snapshots correspond to the five black symbols in Figures 6 and 7. Overall, systemic hypertension manifests itself in left ventricular muscle thickening in an attempt to handle the higher left ventricular pressure. As such, left ventricular wall thickening is conceptually similar to wall thickening in arteries driven by hypertension [37]. However, the complex geometry of the heart, in combination with its anisotropic microstructure, induces a heterogeneous stress profile which, in turn, triggers a heterogeneous progression of growth. The growth multiplier increases gradually from ϑ = 1.00 to ϑ = 2.00 as the individual cardiomyocytes of the left ventricle grow concentrically due to parallel sarcomere deposition. This is in quantitative agreement with a reported doubling of the cardiomyocyte diameter from approximately from 15 µm up to 40 µm [39, 45]. The growth process is initiated in the endocardium and progresses outward towards the epicardium until the entire left ventricular wall has grown from an initial value of 1.2 cm to a converged value of 2.4 cm. These values are in excellent quantitative agreement with the reported values of hypertrophic left ventricular wall thicknesses between 2.0 and 3.0 cm [39, 43]. The right ventricle and the apex, however, are unaffected by the growth process and maintain their original thicknesses. In summary, the simulation illustrated in Figure 8 is in excellent qualitative and quantitative agreement with the pathophysiological characteristics of systemic hypertension: progressive left ventricular wall thickening, increase in cardiac mass, and decrease in left ventricular cavity volume. Under chronic conditions, these geometric changes might eventually impair diastolic filling, reduce cardiac output, and decrease the overall blood supply to the body.

Fig. 8.

Systemic hypertension. Spatio-temporal evolution of grown configuration and growth multiplier. On the macroscopic scale, systemic hypertension manifests itself in a progressive transmural left ventricular wall thickening to enable the left ventricule to pump against higher pressure levels. The right ventricle remains virtually unaffected. On the microscopic scale, left ventricular cardiomyocytes grow concentrically as the growth multiplier ϑ increases gradually from 1.00 to 2.00, while right ventricular cardiomyocytes maintain their normal shape. The five snapshots correspond to the five black symbols in Figures 6 and 7.

4.2 Cardiac hypertrophy in pulmonary hypertension

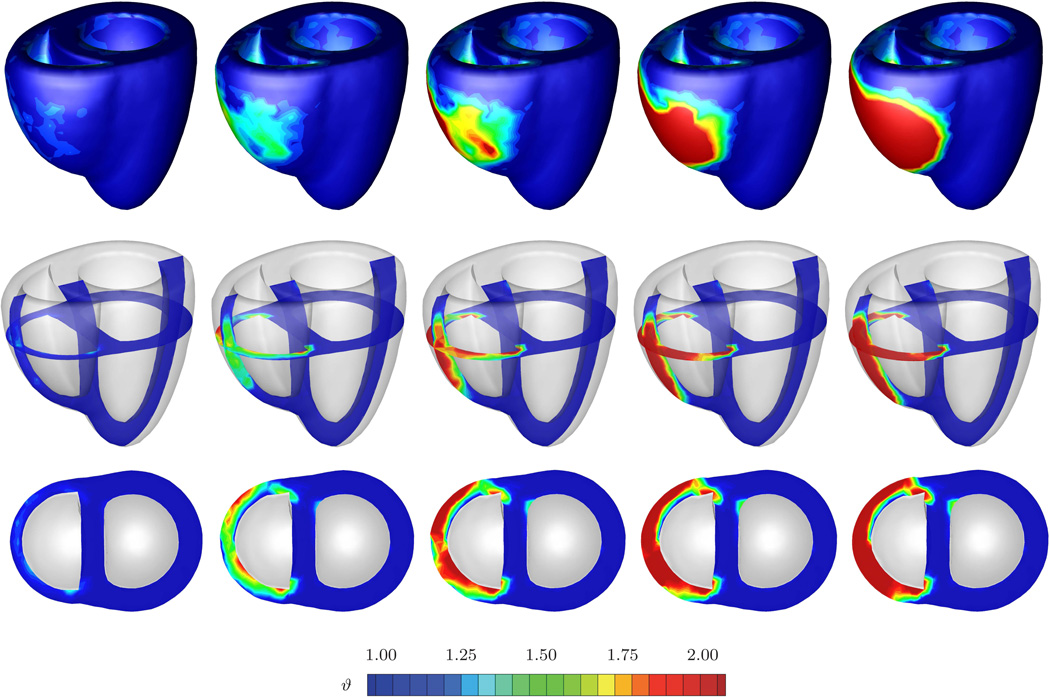
The second example illustrates the performance of the growth algorithm in pulmonary hypertension. Increased pulmonary resistance is modeled by increasing the right ventricular pressure while the left ventricular pressure remains at its baseline value, i.e., p_LV = 100 mmHg and p_RV > 20 mmHg, respectively. In addition to the temporal evolution of the prescribed pressure loading, Figure 9 shows the normalized increase in cardiac mass. In response to pressure overload, the cardiac mass increases as the right ventricular wall thickens. At a converged mass increase of approximately 10%, the right ventricular wall has grown thick enough to withstand the elevated pressure level. For this model, it seems that the overall mass increase in response to pulmonary hypertension is smaller than the mass increase in response to systemic hypertension. Figure 10 shows the temporal evolution of both cavity volumes. In contrast to the previous example, the left ventricular cavity volume now remains constant once the full pressure level is applied, while the right ventricular cavity volume decreases initially and then converges towards a plateau value. Similar to the previous example, pressure overload induced wall thickening is responsible for the reduction in right ventricular cavity volume. Finally, Figure 11 documents the spatio-temporal evolution of the growth multiplier in pulmonary hypertension. Again, the depicted snapshots correspond to the five black symbols in Figures 9 and 10. Acute pulmonary hypertension is characterized through a marked dilation of the right ventricle, initially without hypertrophy, see Figure 11, left column. In agreement with pathological observations, in the cross-sectional view, Figure 11, bottom row, the normal crescent shape of the right ventricle is transformed to a dilated ovoid [52]. The dilation of the right ventricle shifts the interventricular septum toward the left ventricle, squeezing the left ventricle into its characteristic D-shaped form [20]. As a chronic consequence of pulmonary hypertension the right ventricular wall begins to thicken. Similar to the previous example, the progression of growth is heterogeneous across the ventricle driven by a heterogeneous stress profile caused by microstructural anisotropy. In an attempt to maintain right ventricular wall stresses at a physiological level, the growth multiplier increases gradually from ϑ = 1.00 to ϑ = 2.00 as the individual cardiomyocytes of the right ventricle grow concentrically due to parallel sarcomere deposition. Convergence is obtained at a wall thickness of 1.2 cm, which agrees favorably with right ventricular wall thicknesses of more than 1.0 cm reported in the literature [39]. Although the left ventricle undergoes changes in shape which might significantly impair its distensibility, preload, and elastance, its wall thickness remains virtually unaffected by the growth process. In summary, the simulation illustrated in Figure 11 is in excellent agreement with the pathophysiological observations in pulmonary hypertension, both acutely and chronically: dilation of the right ventricle associated with cross-sectional shape changes from crescent shaped to oval, flattening of the interventricular septum, lateral compression of the left ventricle associated with cross-sectional shape changes from circular to D-shaped, progressive right ventricular wall thickening, and increase in cardiac mass. Under chronic conditions, these geometric changes may induce abnormal septal function, and impair left ventricular performance through ventricular interdependence.

Fig. 10.

Pulmonary hypertension. Temporal evolution of normalized right and left cavity volume. Acutely, the right ventricular cavity volume increases drastically in response to pressure overload. Chronically, the right cavity volume decreases slightly due to progressive right ventricular wall thickening in response to right ventricular pressure overload, while the left ventricular cavity volume remains virtually unaffected. The five sketched cross sections correspond to the five black symbols in the normalized cavity volume curves.

Fig. 11.

Pulmonary hypertension. Spatio-temporal evolution of grown configuration and growth multiplier. On the macroscopic scale, acute pulmonary hypertension manifests itself in a significant enlargement of the right ventricle associated with a flattening of the interventricular septum and a compressed D-shaped left ventricle, left column. Chronic pulmonary hypertension initiates a progressive transmural right ventricular wall thickening, from left to right, to enable the right ventricle to pump against higher pressure levels. On the microscopic scale, right ventricular cardiomyocytes grow concentrically as the growth multiplier ϑ increases gradually from 1.00 to 2.00, while left ventricular cardiomyocytes maintain their normal shape. The five snapshots correspond to the five black symbols in Figures 9 and 10.

5 Discussion

Similar to many other organs, the heart is known to adapt to changes in mechanical loading. When exposed to chronically elevated pressure levels, it is capable of increasing its wall thickness in an attempt to maintain wall stresses at their physiological levels. Hypertrophic wall thickening is a pathological adaptation of the heart muscle that is usually progressive and irreversible. Although the mechanical origins of wall thickening are similar under systemic and pulmonary hypertension, their pathophysiologies may be significantly different. Systemic hypertension primarily increases the thickness of the left ventricular wall with potentially unfavorable consequences of insufficient blood supply and impaired filling due to an increased wall stiffness. Pulmonary hypertension increases the thickness of the right ventricular wall, but in addition, it induces significant changes in cardiac geometry by pushing the septal wall into the left ventricle which might severely impair left ventricular performance and overall cardiac function. Neither systemic nor pulmonary hypertension are local conditions that affect only one side of the heart and their overall pathophysiology is typically characterized through ventricular interdependence.

In this manuscript, we have presented a methodology to explain and predict acute and chronic changes of cardiac form and function in response to hypertension using the field theories of continuum mechanics. We have adopted the concept of finite growth based on the introduction of an incompatible growth configuration introducing the multiplicative decomposition of the deformation gradient into an elastic and a growth part. For the growth part, we have proposed a micromechanically motivated definition, characterizing growth through a single scalar growth multiplier. For its evolution, we have suggested a stress-driven evolution equation governed by four material parameters. Since this evolution equation is motivated by observations on the molecular and cellular levels, its parameters have a clear biochemical interpretation. In particular, we model growth as the parallel addition of sarcomeres inside a cardiomyocyte, which thereby increases its cross sectional area. The scalar growth multiplier of our model is therefore directly correlated with the number of sarcomere units within each cell, and, accordingly, with the cross sectional area of the cells themselves. Through locally varying fiber and sheet angles, cellular growth can have a different impact at different locations in the heart. We have combined the underlying approach with a recently proposed locally orthotropic model for cardiac muscle tissue and embedded the overall constitutive formulation in a geometrically nonlinear finite element setting with the growth multiplier treated as an internal variable on the integration point level. For its advancement in time, we have proposed an implicit Euler backward time integration scheme. To integrate the solution of the governing equations in an incremental iterative Newton-Raphson scheme, we have performed the consistent linearization of the the underlying equations in their Eulerian format. We have demonstrated the performance of the proposed growth model in systemic and pulmonary hypertension using a generic biventricular heart geometry. The simulation has shown an excellent agreement with the pathophysiologies of acute and chronic left and right ventricular pressure overload capturing the characteristic changes in cardiac form and function.

The proposed model is, of course, a significant simplification of the complex pathways of systemic and pulmonary hypertension. It is based on the key assumption that molecular, cellular, and tissue level growth are affine. Since cardiomyocytes comprise more than three-fourths of the cardiac tissue volume, we believe that this is a reasonable first approximation, but plan to explore the incorporation of different mechanisms for growth such as cardiomyocyte disarray in the near future. In the present model, growth is assumed to be driven by the trace of the overall stress tensor, i.e., by the pressure generated by both passive and active stresses. We are currently investigating different driving forces for hypertrophic growth such as the overall fiber stress or the active fiber stress which might be physiologically more realistic candidates to govern the growth process. In addition, it would be interesting to correlate the active stress to the electrical excitation [12, 17, 30] to study how pathological growth might impair the conduction system of the heart. Finally, one of the most exciting challenges is, of course, the calibration of the growth parameters in patient specific geometries. Along these lines, global metrics of cardiac function such as end diastolic and end systolic left ventricular volumes, stroke volume, and ejection fraction could be extracted from the simulation and compared to clinically measured patient data to calibrate and validate the model. We believe that, ultimately, this model has the potential to predict individual pathophysiologies in an attempt to design and optimize personalized treatment strategies.