Insights into the Phosphoryl Transfer Mechanism of Cyclin-dependent Protein Kinases from Ab Initio QM/MM Free-energy Studies

Abstract

Phosphorylation reactions catalyzed by kinases and phosphatases play an indispensible role in cellular signaling, and their malfunctioning is implicated in many diseases. A better understanding of the catalytic mechanism will help design novel and effective mechanism-based inhibitors of these enzymes. In this work, ab initio quantum mechanical/molecular mechanical studies are reported for the phosphoryl transfer reaction catalyzed by a cyclin-dependent kinase, CDK2. Our results suggest that an active-site Asp residue, rather than ATP as previously proposed, serves as the general base to activate the Ser nucleophile. The corresponding transition state features a dissociative, metaphosphate-like structure, stabilized by the Mg²⁺ ion and several hydrogen bonds. The calculated free-energy barrier is consistent with experimental values. Implications of our results in this and other protein kinases are discussed.

I. Introduction

Cellular signaling is largely controlled by post-translational modification of protein residues, such as phosphorylation catalyzed by protein kinases and dephosphorylation by protein phosphatases.¹ Mutations of these enzymes have been implicated in many disease states, including cancer.² As a result, there is strong interest in finding effective inhibitors for these key enzymes.^3–5 Significant effort has been devoted to structural and mechanistic studies.^6–7

There are more than five hundred protein kinases encoded in the human genome, representing one of the largest protein families.⁸ Despite sequence and structural diversities, many share nearly conserved catalytic domains.⁹ We are concerned here with an important class of protein kinases, namely cyclin-dependent kinases (CDKs), which regulate the cell cycle in eukaryotes by a complex signal transduction network.^10–11 Of the 11 known human CDKs, CDK1 (also known as CDC2) is the most essential to the proper functioning of the cell cycle and is also the evolutionary analog to the primitive CDC28 first studied in yeast.¹¹ Mice knockout studies have shown that a loss of a single CDK can lead to lethality, such as with CDK5, or a host of developmental defects, such as CDK2, CDK4, CDK6, and CDK11.¹² The activity and specificity of these CDKs depend on the binding of cyclin subunits, including cyclin classes A, B, D, and E that are differentially expressed over the course of the cell cycle.¹³ The precise regulation of the cell cycle is nominally controlled by the rise and fall of different cyclin levels and the activity of their CDK complexes, but many additional positive and negative feedbacks exist as well, including natural inhibitor families INK4 and Cip/Kip, as well as genetic and metabolic checkpoints.¹⁴

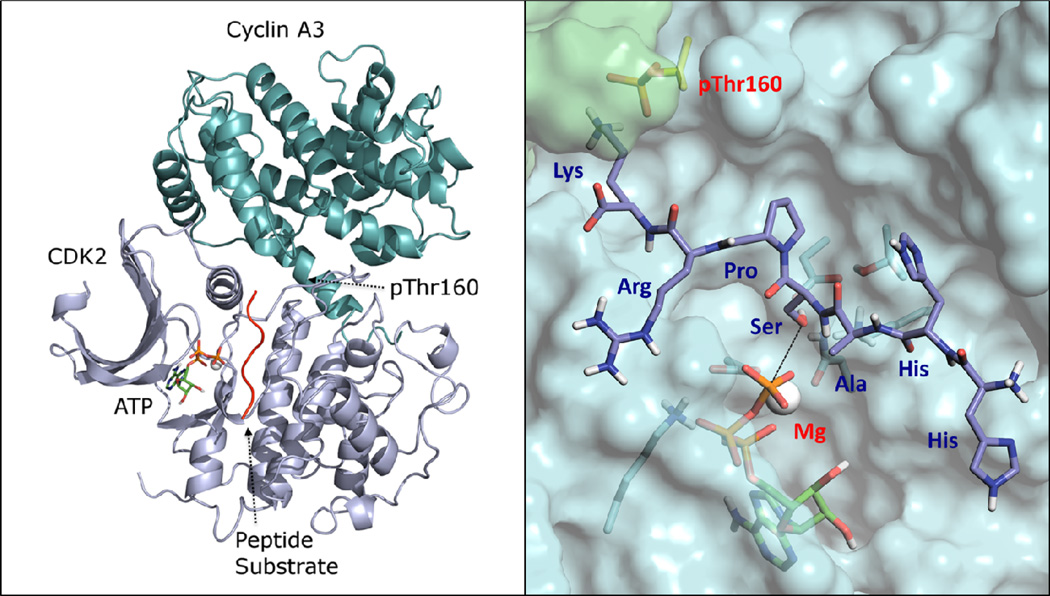
In this work, we focus on the catalytic mechanism of CDK2, which is perhaps the most extensively studied interphase CDK. With over 200 published X-ray structures in the Protein Data Bank (PDB) since the pioneering work of De Bondt et al.,¹⁵ it has served as a basis for much CDK research. CDK2 is generally classified as a serine/threonine protein kinase (SPK), and often more specifically as a proline-directed kinase with regards to substrate recognition, with the phosphorylation site (P) adjacent to a proline residue (P+1) in the direction of the C-terminus. Many substrates have been identified for CDK2, including pRb, p107, p53, and others that satisfy the consensus sequence from the P to P+3 position of (S/T)-P-X-(R/K), where X is any residue.¹⁴ For full functioning, CDK2 must bind with its cyclin partners A or E, a molecule of ATP, and at least one Mg(II) ion. In addition, it must have a conserved threonine residue (Thr160) on the activation loop phosphorylated by a separate enzyme called CDK Activating Kinase (CAK).¹⁶ The overall structure of a CDK2-Cyclin-ATP-Mg-substrate complex¹⁷ is shown in Figure 1.

Figure 1.

Overall protein fold of the activated CDK complex with cyclin A3, Mg-ATP, and the peptide substrate¹⁷ on the left panel. A close up picture of substrate binding is shown in the right panel.

The chemical step catalyzed by CDK2 is the transfer of a phosphoryl group from the γ position of ATP to the hydroxyl group of a Ser or Thr residue of the substrate. For such phosphoryl transfer reactions, three limiting-case mechanisms are possible.^18–19 The dissociative (D_N + A_N) mechanism envisions an initial dissociation of a free metaphosphate followed by addition. The associative (A_N + D_N) mechanism, on the other hand, features a pentacovalent phosphorane intermediate, flanked by two transition states. Finally, the concerted (A_ND_N) mechanism is characterized by a single transition state as a middle point for the cleavage and formation of P-O bonds. Within the concerted mechanism, the transition state could be either associative, featuring a pentacovalent phosphorane-like species, or dissociative, featuring a metaphosphate-like species. For uncatalyzed phosphoryl transfer reactions involving phosphate monoester dianions, such as ATP, it is widely believed that the preferred pathway involves a concerted mechanism with a dissociative transition state.²⁰ (For an interesting and alternative perspective, see Ref. 21.) For the corresponding enzymatic reactions, on the other hand, the mechanism is not well established. There is thus a strong desire to uncover whether enzymatic reactions use the same mechanism as uncatalyzed reactions and how they are catalyzed.

The active site of the activated CDK2-substrate complex¹⁷ shown in Figure 1 consists of a shallow grove for substrate binding, an ATP hydrophobic binding pocket that aligns the γ -phosphate with the help of with a single magnesium ion, and a triad of residues: Asp127, Lys129, and Thr165 which bracket the substrate serine oxygen on three sides, forming a hydrogen bond network and helping align the serine with the phosphate group to be transferred. The Mg(II) ion binds with conserved Asn132 and Asp145 residues, which help align and polarize the γ-phosphate. Very recently, a new X-ray structure of a CDK2/Cyclin complex with a transition-state mimic (MgF₃⁻) has been reported.²² Interestingly, two Mg(II) ions have been found in the active site, although the second Mg(II) is thought to bind in a transient fashion during turnover.

Despite its importance, kinetic studies of CDK2 catalysis are surprisingly sparse, especially when compared with the other kinase prototype PKA (protein kinase A or cAMP-dependent protein kinase). The first kinetic study by Hogopian et al. indicated that the phosphorylation step is fast (k₃ = 22 s⁻¹), but overall rate is limited by product release (k₄ = 11 s⁻¹).²³ The former rate constant was later revised to 35 s⁻¹.²⁴ Another kinetic investigation found the reaction has a random anticooperative mechanism, but did not report the rate constant for the chemical step.²⁵ Subsequently, there have also been kinetic studies focusing on the effect of Cyclin partners E1 and A2,²⁶ a comparative study of CDK1/CDK2 partnered with Cyclin A1 and A2,²⁷ and more recently on the effect of a mutation in the PSTAIRE helix on cyclin binding.²⁸ In addition, mechanistic studies have been reported for CDK5,^29–30 which shares ~60% sequence similarities with CDK2 and is likely to have the same catalytic mechanism. To our best knowledge, no systematic mutagenesis studies of active-site residues of any CDKs have so far been reported.

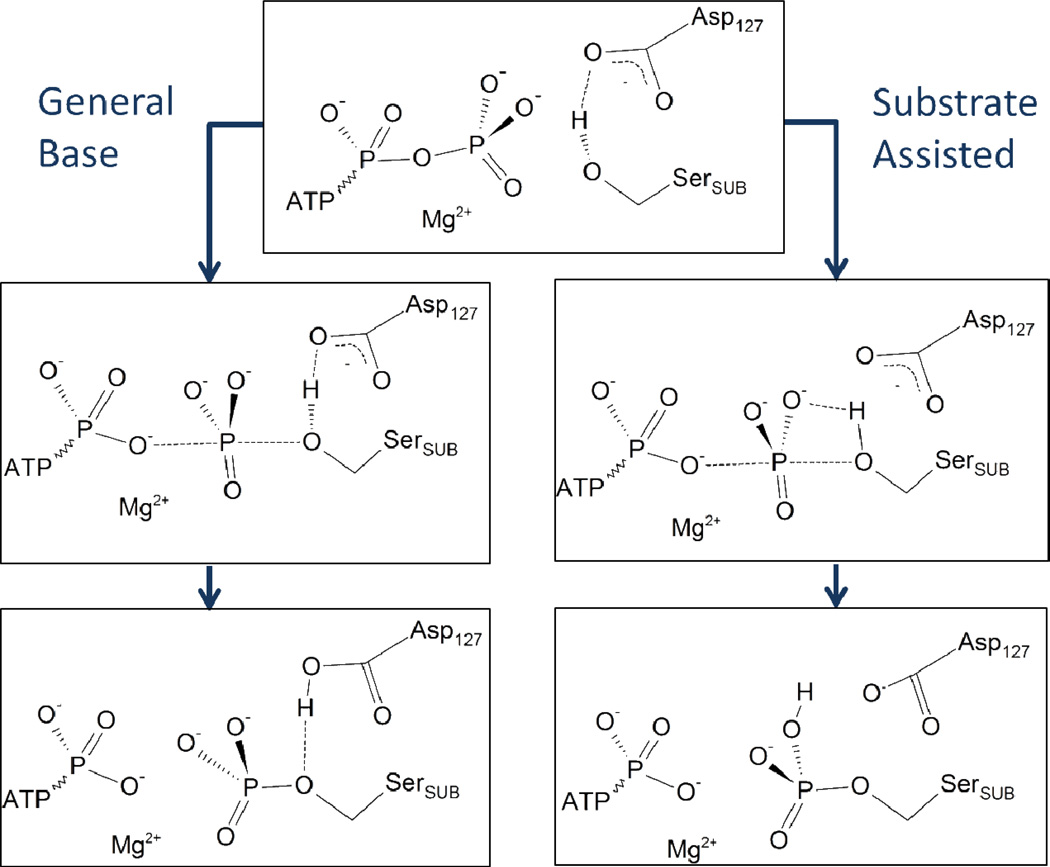
While these kinetic studies reported K_M and k_cat values, the molecular details of the catalysis are still unclear. For example, is the mechanism dissociative, associative, or concerted? What is the character of the transition state? What is the identity of the general base needed to activate the serine nucleophile? What is the role played by the Mg(II) cofactor and several active-site residues such as Lys33 and Lys129? To answer these questions, several theoretical models have been developed. An earlier density functional theory (DFT) study with a truncated active-site model,³¹ and a subsequent QM/MM model³² both suggested a ATP-assisted mechanism, in which the nucleophilic serine is deprotonated by the γ-phosphate of ATP, while the nearby Asp127 residue helps to align the substrate oxygen but not participating in proton transfer. In addition, the transition state was found to have a distinct associative character. However, this proposal is at odds with the mechanism proposed for other protein kinases, most notably the extensively characterized PKA,^33–37 where the general base has been identified as a conserved active-site Asp. In CDK2, this conserved Asp residue is Asp127, and its potential role as the general base has also been proposed before.¹⁷ In addition, the associative transition state obtained by these theoretical models is inconsistent with recent X-ray structures of CDK2/cyclin bound with transition-state analogs (nitrate and MgF₃⁻), which suggest a dissociative transition state.^22,38 The Asp127 residue was not included in the QM region in the QM/MM simulations of De Vivo et al.,³² thus precluding its capacity to serve as the general base, though the authors did not fully rule out this possibility. In this publication, we reexamine the two mechanistic proposals shown in Scheme 1, using an ab initio QM/MM method, and also calculate the free-energy for our proposed reaction scheme to take into account the fluctuation in the context of the protein environment. Our results clearly support a concerted mechanism in which Asp127 serves as the general base. Furthermore, a single dissociative, metaphosphate-like, transition state was identified. The roles played by various frontline residues and the Mg(II) cofactor are also discussed. This work is organized as follows: Section II discusses methods and details of models for determining the reaction pathways. Section III presents the free-energy profile and geometric/charge data. Section IV discusses the comparison of these results with previous theoretical and experimental data and implications in the general mechanism of protein kinases. The final section (V) concludes.

Scheme 1.

Two mechanism proposals for the phosphoryl transfer reaction catalyzed by CDK2

II. Method

Due to the large size of the enzymatic system, it is impractical to use conventional quantum chemistry methods to study the catalyzed reaction. Here, we treat the system within the QM/MM framework,^39–40 which divides the system into two parts. The QM region is treated here with DFT, while the MM region by force fields. Such an approach has been widely and successfully used in studying enzymatic reactions.^41–44

The starting geometry for CDK2 was largely based on the crystal structure 1QMZ,¹⁷ which was also used in the earlier QM/MM study of De Vivo et al.³² This composite structure contains CDK2 with phosphorylated Thr160, bound with Cyclin A3, ATP, a single Mg(II) cofactor, and a peptide substrate. The peptide substrate has the resolved sequence HHASPRK containing the (S/T)-P-X-(R/K) motif required for substrate recognition. Residues Arg297 and Leu298 on the N-terminus of CDK2 and residue Glu174 on the C-terminus of Cyclin A3 were restored using PyMOL (www.pymol.org) and allowed to relax with a short minimization. After careful consideration of hydrogen bond networks, histidine residues were assigned as HID120 and HID122 in CDK2, HID361 and HID424 in Cyclin A3, and all other histidines were assigned as HIE.

The AMBER 10 simulation package⁴⁵ was used for initial setup, addition of hydrogens, solvation, neutralization, initial minimization of the structure, and molecular dynamics (MD). Force field parameters included the AMBER99SB force field for the proteins,^46–47 ATP parameters developed by Meagher et al.,⁴⁸ and pThr parameters developed by Homeyer et al.⁴⁹ The system was then solvated with a rectangular box of TIP3P waters⁵⁰ with dimensions of 88 × 95 × 106 ų, allowing for a 10 Å buffer on all sides between protein atoms and the periodic boundary. Two Na⁺ ions were added to neutralize the box and gave a total system size of 74,938 atoms. Periodic boundary conditions were imposed with the long-range electrostatic interactions treated with the particle mesh Ewald (PME) method.^51–52 Van der Waals interactions were calculated with an 8 Å cutoff. In MD simulations, hydrogens were restrained by the SHAKE algorithm,⁵³ and the time step was 1 fs.

After hydrogen atoms were allowed to relax with all heavy atoms fixed, a constrained minimization procedure was employed using harmonic restraining potentials with force constants ranging from 50 kcal·mol⁻¹·Å⁻² to 5 kcal·mol⁻¹·Å⁻² on the protein and substrate. The structure was slowly relaxed by alternating MD and minimization as the constraint was scaled down, ending with a 2000 step unconstrained minimization. To equilibrate the refined structure, a 10 kcal·mol⁻¹·Å⁻² constraint remained on the active-site region (Lys33, Asp127, Lys129, Asn132, Asp145, Thr165, ATP, Mg, and substrate) as the system was heated to 300 K over 100 ps. Dynamics was then continued for 100 ps at this constraint, and a further 200 ps where the active site constraint was reduced to 5 kcal·mol⁻¹·Å⁻². The final snapshot became the basis for the subsequent QM/MM studies.

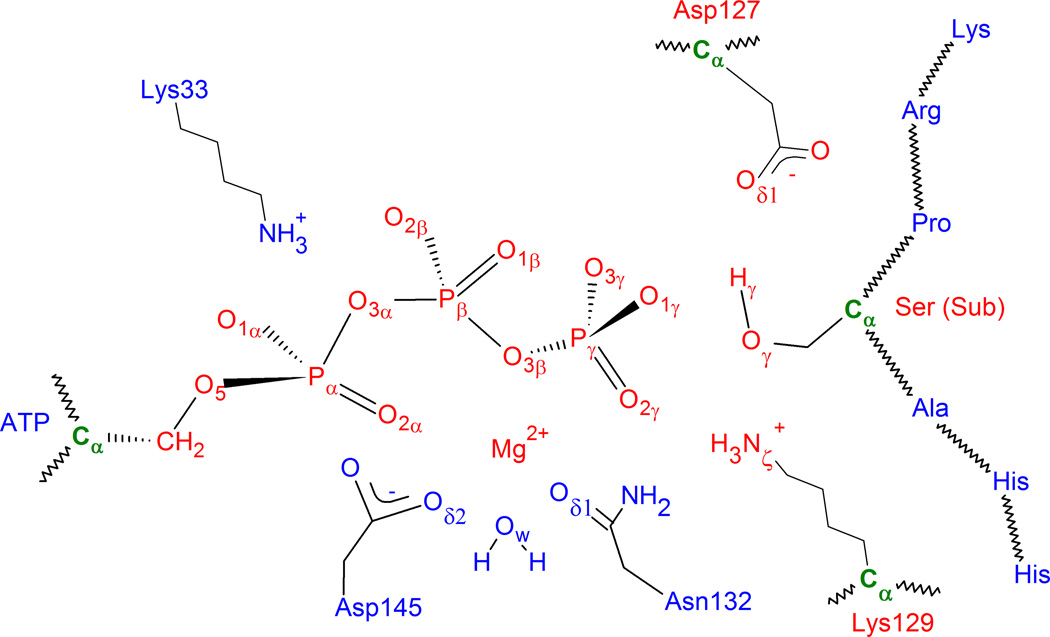
In our investigation of the phosphorylation step, we used the pseudo-bond ab initio QM/MM approach,^54–57 which has been used to successfully investigate several enzymes,^58–66 including a protein kinase (PKA).³⁵ The QM/MM model was based on the last snapshot of the classical MD simulation by including all atoms within a 27 Å radius centered on the P_γ atom of ATP, resulting in 13,533 atoms. Atoms greater than 20 Å away from P_γ of ATP were held fixed in order to reduce computational costs. As shown in Figure 2, the QM subsystem, which consists of the Mg ion, the triphosphate portion of ATP, and the side chains of Asp127, Lys129, and the substrate serine, has 48 atoms; and they are treated at the B3LYP/6–31G(d) level of theory. An ab initio treatment of the QM system is important because of the involvement of the d orbitals in P.^67–68 On the other hand, the MM subsystem was modeled with the same force fields described above for the initial minimization/MD. All calculations were done using a modified version of the QChem⁶⁹ and TINKER⁷⁰ program. Cutoff radii were 12 Å for van der Waals interactions and 18 Å for electrostatic interactions between MM atoms, and no cutoff was imposed for electrostatic interactions between QM and MM atoms.

Figure 2.

Model showing several key active-site residues and QM subsystem (in red) with boundary atoms in green.

It should perhaps be pointed out that the model developed here is by no means perfect, due to limitations of computational resources. One area of possible errors is the treatment of the Mg(II) coordination sphere. While Mg(II) and some ligands are in the QM region, others are in the MM region, which might cause overpolarization of the substrates. Fortunately, we expect the errors to be reasonably small as the ligand-metal interactions are dominated by electrostatic interactions.

The QM/MM model was then minimized and reaction paths were explored using the reaction coordinate driving (RCD) method.⁵⁵ Several reaction coordinates have been used to explore the reaction mechanism, as discussed in Section III. Along each reaction path, the ESP charges of all quantum atoms were calculated. To calculate the potential of mean force (PMF), we have used the following reaction coordinate, RC_I = d(O_3β-P_γ) - d(O_γ-P_γ) - d(O_δ1-H_γ). (The definition of atomic labels can be found in Figure 2.) To sample high energy regions, the umbrella sampling method⁷¹ was used. Specifically, the reaction path was partitioned into 22 windows, each with a harmonic bias potential with a force constant between 40 and 120 kcal·mol⁻¹·Å⁻² adjusted iteratively depending on the resulting sampling histogram. The MD trajectories were propagated using the Beeman algorithm⁷² at a time step of 1 fs, with the Berendsen thermostat⁷³ to maintain the system at 300 K. During the MD simulations, the MM subsystem was first allowed to move for 500 ps with the QM subsystem fixed. This is followed by MD for the entire system for 30 ps using the QM/MM potential. The resulting probability distributions were then converted to the PMF by use of the weighted histogram analysis method (WHAM).⁷⁴

In addition to the PMF calculations, we have also carried out perturbation calculations to evaluate the influence of surrounding residues on the reactant complex and transition state.⁷⁵ To this end, electrostatic (ES) and van der Waals (vdW) contributions of individual MM residues on the QM subsystem were calculated at the two critical points. The individual residue contribution was calculated as: $\Delta E_i=E{(\mathit{\text{vdW}}+\mathit{\text{ES}})}_i^{\mathit{\text{TS}}}-E{(\mathit{\text{vdW}}+\mathit{\text{ES}})}_i^{\mathit{\text{RC}}}$, in which the superscripts TS and RC denote the reactant complex and transition state, respectively. A negative value indicates that the interaction of that particular residue is favorable for catalysis, while a positive value is unfavorable.

III. Results

As shown in Table I, the serine nucleophile and the transferring phosphoryl group are well aligned in the reactant complex (RC), with an O_γ-P_γ distance of 3.39 Å. This can be compared with the X-ray structure, in which the corresponding distance is 3.68 Å.¹⁷ The O_γ-O_3β distance of 5.09 Å is larger than 4.9 Å, which was suggested by Mildvan to be the onset for the dissociative concerted mechanism.⁷⁶ This in-line attack configuration is held in place by a number of interactions. For example, the serine nucleophile has its hydroxyl group donating a hydrogen bond to the carboxylate of Asp127 (d(H_γ-O_δ1)=1.63 Å, d(O_γ-O_δ1)=2.63 Å) and accepts a hydrogen bond from Lys129 (d(H_ζ3-O_γ)=1.72 Å, d(N_ζ-O_γ)=2.64 Å). These distances between hydrogen bonded heavy atoms are also consistent with those in the X-ray structure (2.69 Å and 2.55 Å).¹⁷ In addition, both Lys129 and Asp127 are hydrogen bonded with Thr165, forming a relatively strong hydrogen bond network.

Table I.

Key interatomic distances for the phosphorylation reaction at three stationary points along the reaction path in Model I.

Inter-atomic distance (Å)			Expt.19	RC	TS	PC
Pγ	-	Ser-Oγ	3.68	3.39	2.46	1.74
Pγ	-	O3β	1.60	1.81	2.54	3.24
Ser-Oγ	-	Ser-Hγ	-	1.01	1.04	1.83
Ser-Hγ	-	Asp127-Oδ1	-	1.63	1.58	1.00
Ser-Hγ	-	O2γ	-	3.11	2.73	2.80
Mg	-	O2γ	2.25	2.00	2.08	2.08
Mg	-	O3β	2.12	2.20	2.05	2.01
Mg	-	O2α	2.07	2.04	2.04	2.12
Mg	-	OWAT	2.14	2.10	2.13	2.19
Mg	-	Asn132-Oδ1	2.00	1.94	1.99	2.02
Mg	-	Asp145-Oδ2	1.91	1.87	1.87	1.88
Lys33-Nζ	-	O1α	3.00	2.90	2.91	2.90
Lys33-Nζ	-	O3α	3.19	2.87	2.84	2.84
Lys33-Nζ	-	Asp145-Oδ1	3.85	2.81	2.82	2.82
Lys129-Nζ	-	O2γ	3.58	4.17	4.00	3.94
Lys129-Nζ	-	Ser-Oγ	2.55	2.64	2.72	2.80
Lys129-Nζ	-	Thr165-Oγ1	2.69	2.85	2.86	2.89
Asp127-Oδ2	-	Thr165-Oγ1	2.90	2.74	2.70	2.81
Asn132-Nδ2	-	O2γ	3.66	3.40	3.17	2.91

On the other hand, the ATP is stabilized by a number of electrostatic interactions with surrounding moieties. For instance, the Mg(II) ion coordinates with O_2γ, O_3β, O_2α of ATP, in addition to the side chains of Asp145, Asn132, and a water, in an octahedral coordination sphere. Furthermore, ATP is hydrogen bonded to Lys33, as evidenced by the H_ζ3-O_1α distance of 1.88 Å. In addition, a number of solvent water molecules are found to hydrogen bond with non-bridging oxygens of the triphosphate group. These interactions help in aligning the reactant for the in-line near attack configuration. Finally, the phosphorylated Thr160 of CDK2 forms a strong interaction with a crown of CDK2 arginine residues Arg50, Arg126, Arg150, and the Lysine residue of the peptide substrate. Two of these arginine residues, Arg50 and Arg150, form hydrogen bonds with the backbone of Cyclin A3. The distances in our model are largely consistent with those reported in the X-ray structure,¹⁷ as shown in Table I.

The only sizable difference between our model of the Michaelis complex and the X-ray structure is the distance between N_ζ(Lys33) and O_δ1(Asp145). The model distance is 2.81 Å, significantly shorter than that in the X-ray structure (3.85 Å).¹⁷ It is not clear about the origin of the discrepancy, but we hypothesize that it might have something to do with the possibility of a disordered second Mg(II) ion, which would neutralize some of the positive charge in the sidechain of Asp145, thus weakening the hydrogen bond with Lys33. Indeed, the Mg(II) concentration used in soaking the crystal was quite high, and a recent kinetic study of CDK5 has clearly demonstrated the necessity of a second Mg(II) in activating the catalysis.³⁰ This second Mg(II) ion is now confirmed by a recent X-ray structure of CDK2/Cyclin with a transition-state analog (MgF₃⁻), but it was suggested that the binding of the second Mg(II) is transient.²²

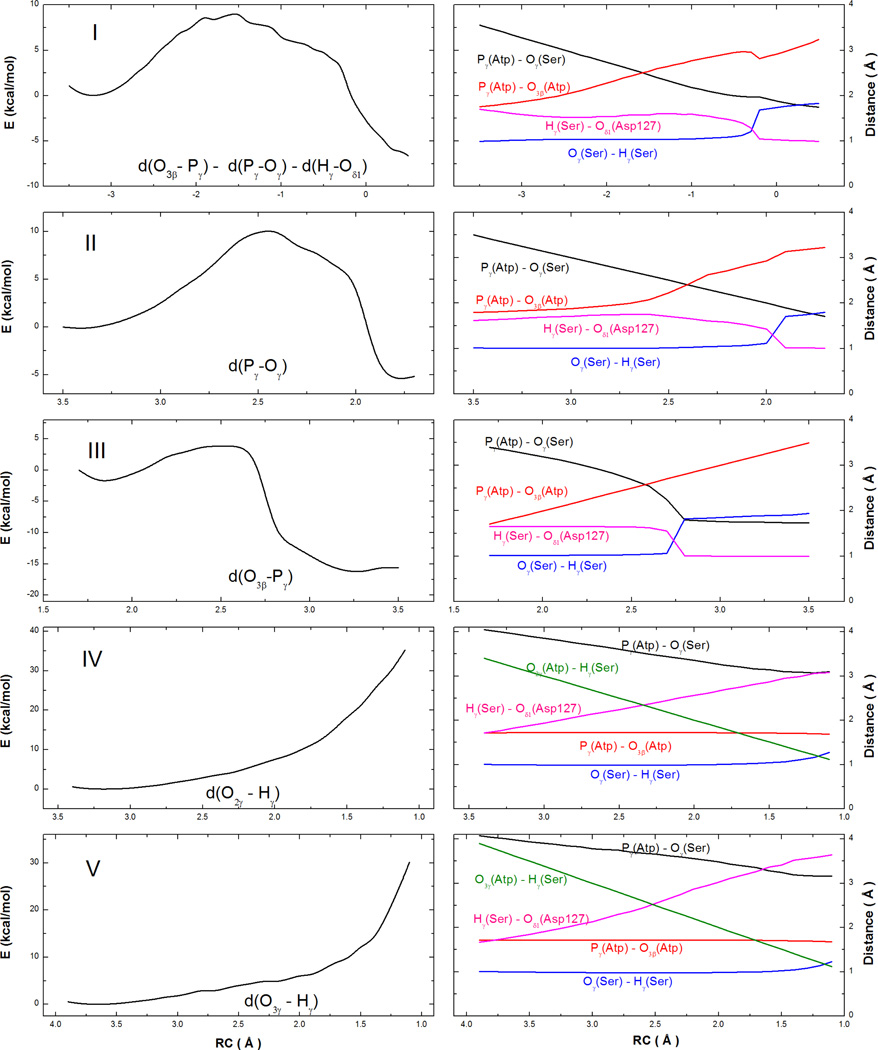
To explore the reaction mechanism, several reaction coordinates have been tested. The general base pathway was tested using the combined coordinate, RC_I = d(O_3β-P_γ) - d(O_γ-P_γ) - d(O_δ1-H_γ). Models II and III used the P-O bond distances to probe the associative and dissociative mechanisms: RC_II = d(O_3β-P_γ) and RC_III = d(O_γ-P_γ). Model IV and V tests the substrate-assisted mechanism by using the following reaction coordinates: RC_IV = d(O_2γ-H_γ) and RC_V = d(O_3γ-H_γ), which pushes the Ser hydrogen (H_γ) to either the Mg-coordinated phosphate O_2γ or the non-Mg-coordinated O_3γ. The minimal energy paths calculated using these reaction coordinates and key distances are displayed in Fig. 3.

Figure 3.

Reaction paths for five models (I–V) with different reaction coordinates are displayed in the left panels. Variations of several key interatomic distances with the reaction coordinate are given in the right panels.

It is clear from Fig. 3 that energy increases monotonically if the proton is forced to transfer to a phosphate oxygen in Models IV and V. The non-productive reaction paths thus discount the substrate-mediated mechanism. The associative and dissociative mechanisms can also be ruled out as the P-O bond lengths change in tandem in Models I, II, and III, strongly suggesting a concerted mechanism. Neither a free metaphosphate nor a pentacovalent phosphorane intermediate was found. Instead, only one transition state exists. As the system approaches the transition state in Model I, the P_γ-O_γ distance is reduced from 3.39 to 2.46 Å, while the P_γ-O_3β distance increases from 1.81 to 2.54 Å. The O_γ-O_3β distance of 4.9 Å at the transition state is consistent with that (5.5 – 5.7 Å) found in the X-ray structure of CDK2 complex with a transition-state analogue (nitrate).³⁸ Furthermore, the two P-O distances are also in good agreement with the more recent transition-state structure, with the corresponding distances of 2.8 and 2.5 Å.²² Interestingly, the proton transfer lags behind the phosphoryl transfer.

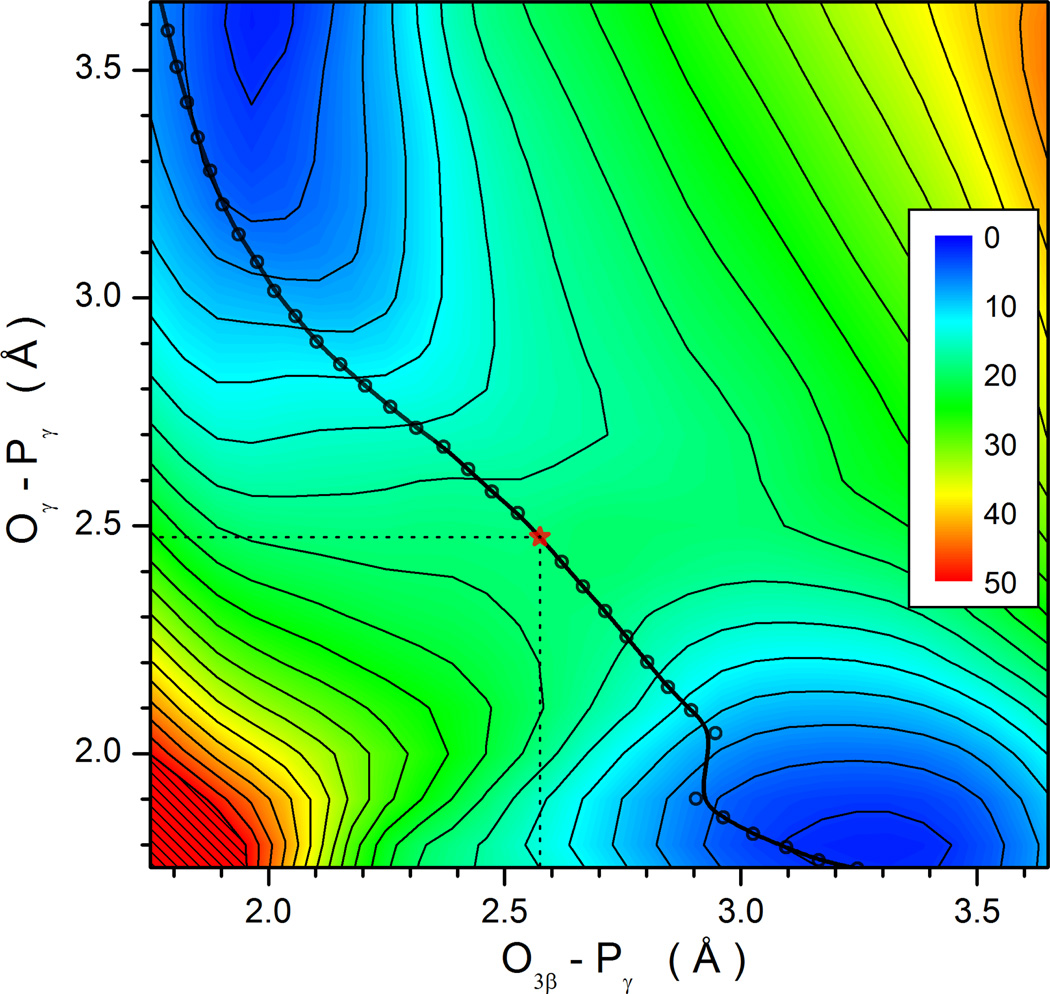
To further demonstrate the concerted nature of the reaction path, we have mapped out using RC_II and RC_III a two-dimensional minimal energy surface, as shown in Fig. 4. The reaction path proceeds essentially as a diagonal cut of the map from one minimum to another. The dissociative character of the transition state can also be estimated using Pauling’s formula: D(n) = D(1) − 0.6logn, as suggested by Mildvan.⁷⁶ Here, D(1) = 1.73 Å for the P-O bond, and D(n) is defined as the average of the two P-O distances (2.5 Å) at the transition state. The fractional bond number (n) is thus 0.05, which gives a dissociative character of 95%. It is clear from the figure that the dissociative character of the concerted transition state is predetermined by the large O-O distance in the Michaelis complex.

Figure 4.

Two-dimensional minimal energy surface in RC_II and RC_III defined in text. The minimal energy path and the transition state are shown.

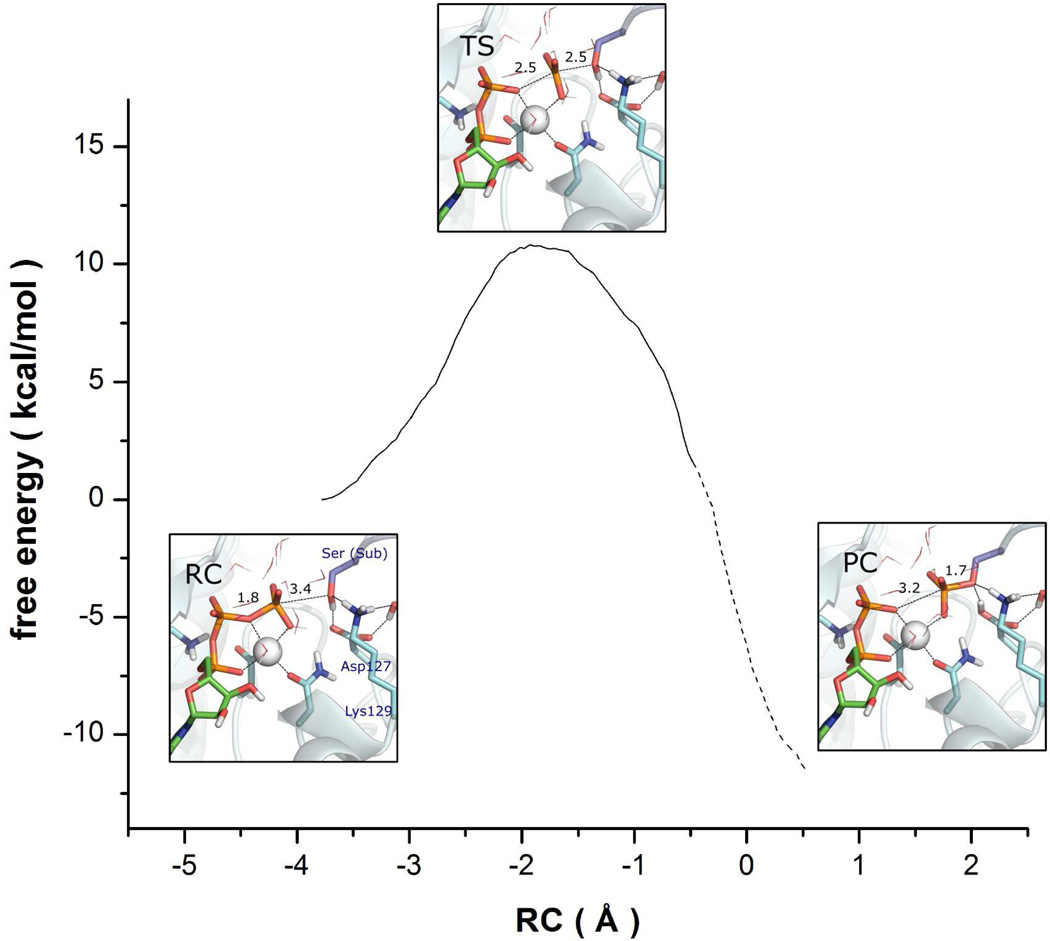
Based on the aforementioned reaction path calculations and our test calculations of various combined coordinates, RC_I was selected as our choice for analysis and construction of the PMF. The sole transition state (TS) in this model features a trigonal planar metaphosphate-like phosphoryl group between the leaving group (O_3β) and nucleophile (O_γ) with large P-O distances. Interestingly, the proton transfer from the nucleophilic Ser OH group to the Asp127 is delayed: the O_γ-H_γ distances increases from 1.01 Å at RC to 1.04 Å at TS, and finally to 1.83 Å at the product complex (PC). On the other hand, the H_γ-O_δ1 distances varies from 1.63 Å at RC, to 1.58 Å at TS, and finally to 1.00 Å at PC. The late proton transfer at the TS, which was also observed in earlier QM/MM studies of PKA,^33,35,37 supports the dissociative character of the transition state, as the P_γ-O_γ bond formation, which is facilitated by proton transfer to Asp127, has not progressed significantly at the transition state.

Charges on several key atoms are listed in Table II. The most important change occurs for O_3β, which is converted from a bridging oxygen to a non-bridging one in the course of the reaction. As a result, its charge changes from −0.67 at RC to −0.92 at TS, and finally to −0.99 at PC. The increased charge leads to a stronger coordination with the Mg(II) ion, as evidenced by the corresponding distance changing from 2.20 Å at RC, to 2.05 Å at TS, and finally to 2.01 Å at PC. In the mean time, the bonds between Mg(II) and O_2γ weakens somewhat, indicated by slight elongation of the corresponding bond distance in Table I. These changes are presumably in response to the strengthened Mg-O_3β bond. On the other hand, the bonding of Mg(II) with Asp145 and Asn132 changes little during the course of the reaction.

Table II.

Key atomic charges at three stationary points along the reaction path of Model I.

Atom	RC	TS	PC
Pγ	1.18	1.17	1.30
O1γ	−0.80	−0.73	−0.86
O2γ	−0.98	−0.88	−0.98
O3γ	−0.83	−0.74	−0.92
Pβ	1.17	1.26	1.31
O1β	−0.86	−0.92	−0.95
O2β	−0.82	−0.88	−0.90
O3β	−0.67	−0.92	−0.99
Pα	1.22	1.24	1.23
O1α	−0.82	−0.84	−0.86
O2α	−0.76	−0.78	−0.78
O3α	−0.52	−0.56	−0.57
Mg	1.68	1.69	1.69
Ser-Oγ	0.03	−0.13	−0.14
Ser-Hγ	0.36	0.44	0.37
Asp127-Oδ1	−0.85	−0.86	−0.63
Lys129-Nζ	−0.59	−0.79	−0.86

As shown in Figure 5, the three non-bridging oxygens of the transferring phosphoryl group are stabilized during the transition state. Specifically, O_1γ forms hydrogen bonds with 4 solvent waters, O_2γ bonds primarily with Mg(II), and O_3γ forms hydrogen bonds with 3 solvent waters. As a result, the total charge of the phosphoryl group progresses from −1.42 (RC), to −1.18 (TS), and then back to −1.47 (PC). The Mg(II) ion clearly helps stabilize the transition state, as shown by the charge on its associated phosphate oxygen, O_2γ, which changes from −0.98 (RC), to −0.88 (TS), to −0.98 (PC). This charge stabilization is nearly equivalent to that of O_1γ, which is complexed by four waters. It is interesting to note that there is no proton transfer between the ammonium group of Lys129 and other moieties during the reaction, despite the fact that the side chain is included in the QM region. It appears that the role of Lys129 is a structural one, mainly responsible for positioning the reactants in the near-attack configuration. Similar observations have been made for PKA.³⁵

Figure 5.

Calculated free-energy profile for the phosphoryl transfer reaction catalyzed by CDK2 using RC_I as the reaction coordinate. The dashed line indicates the region where the PMF convergence is less satisfactory. The configurations of the RC, TS, and PC complexes obtained in the reaction coordinate calculations are also shown with the hydrogen bonds and Mg coordination bonds indicated in dashed lines.

The product complex (PC) features a phosphorylated serine residue in the substrate, with O_γ hydrogen bonded with the protonated Asp127. The phosphoryl group in the phosphorylated serine residue bonds with Mg(II) ion, and forms hydrogen bonds with Asn132 and six waters. On the other hand, the ADP have two non-bridging oxygens (O_2α and O_3β) chelating the Mg(II) ion, and form hydrogen bonds with Lys33, and a number of water molecules.

As shown in Figure 5, the calculated free-energy profile (PMF) gives a barrier height of 10.8 kcal/mol. To test convergence, the difference in the barrier height between 10 ps and 30 ps sampling was found to be less than 1.0 kcal/mol, although the PC region (indicated in dashed line) is less converged. This barrier height is significantly lower than that found using the associative pathway, 23.7 ± 4.5 kcal/mol, as reported by De Vivo et al.³²

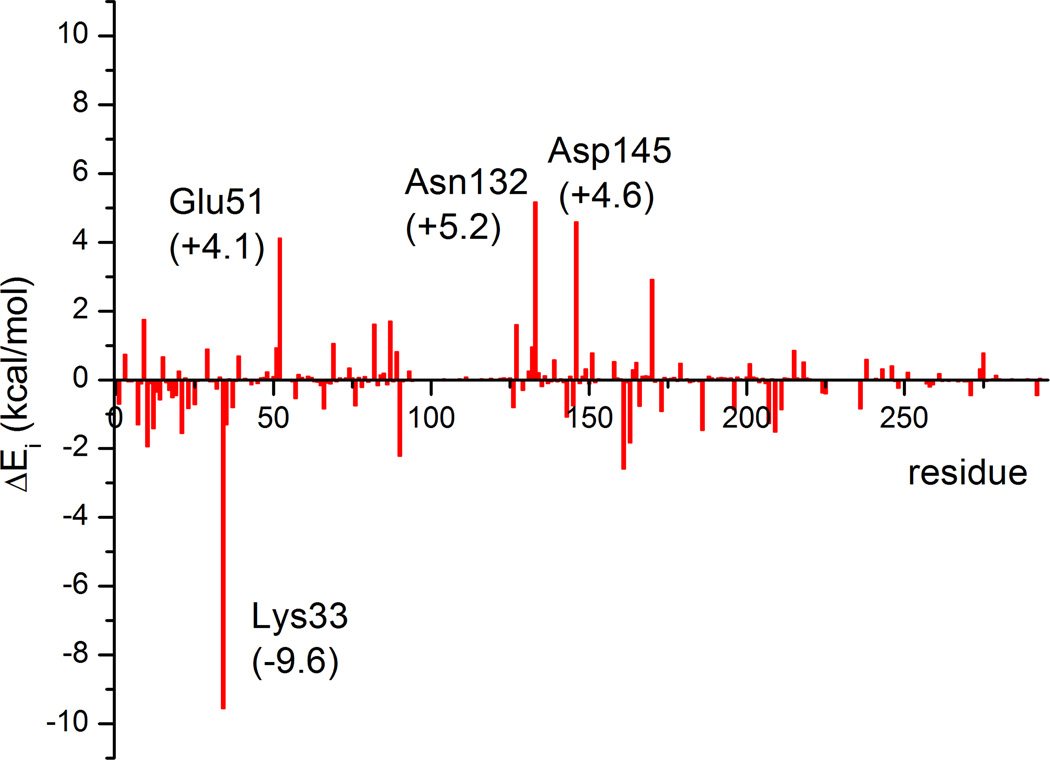
To further understand the roles played by other non-frontier residues in the catalysis, a perturbation analysis has been performed along the reaction path. As shown in Figure 6, Lys33 has the largest effect. Since it helps to stabilize ATP by forming a hydrogen bond with O_1α, it is not difficult to understand that it preferentially stabilizes TS, where the charges of the ATP oxygen atoms increase relative to RC. It is known that its counterpart in PKA (Lys72) plays the same role, as demonstrated by mutagenesis⁷⁷ and computational studies.³⁵ On the other hand, the Asn132 and Asp145 residues have positive values, which stem presumably from their coordination with the Mg(II) cofactor, as seen in PKA.³⁵ It should however be note that the magnitudes indicated in Figure 6 can only be considered qualitative, because significant enzyme reorganization might occur for mutants.

Figure 6.

Results of the charge perturbation analysis of the non-frontline residues in CDK2. A negative or positive value indicates that the charge of the residue increases or decreases the barrier, respectively.

IV. Discussion

The results of our ab initio QM/MM free-energy simulations suggest that the CDK2 catalysis proceeds with a concerted phosphoryl transfer mechanism with Asp127 serving as the general base. The dissociative transition state observed in our calculation is consistent with two X-ray structures of activated CDK2/Cyclin A transition-state anaglogs.^22,38 For example, one X-ray structure indicates that the nitrate moiety binds between ADP and the phosphorylizable serine, but lacks stabilization from positively charged residues, consistent with observation that nitrate is not an effective inhibitor of CDK2.³⁸ On the other hand, these authors found that orthovanadate, a mimic for an associative transition state, did not bind the CDK2 complex and did not inhibit the catalysis. These observations led them to conclude that the phosphorylation reaction catalyzed by CDK2 follows a mostly concerted mechanism with a dissociative transition state, which is also the conclusion derived from our QM/MM calculations reported here. In the more recent X-ray structure,²² a transition-state analog, MgF₃⁻, was found between ADP and the Ser nucleophile, with distances of 2.8 and 2.5 Å. This is again consistent with a dissociative transition state.

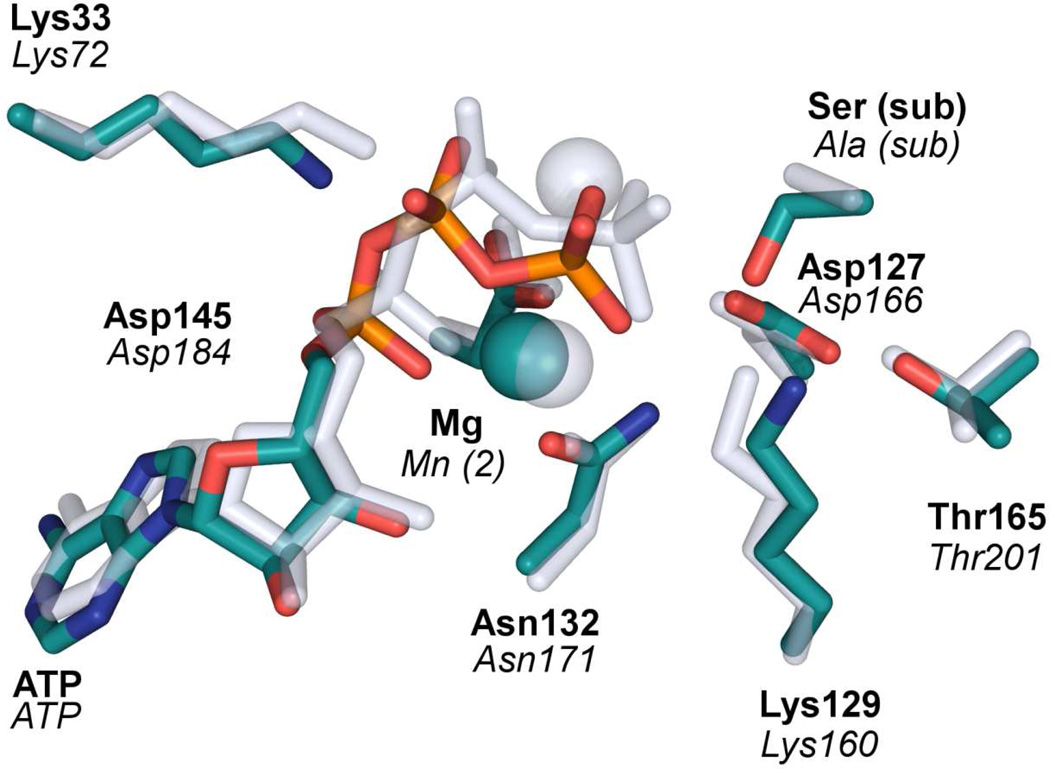
As mentioned earlier, most protein kinases share the same catalytic domain with highly conserved active-site residues despite sequence and structure diversities. In addition, the active-site residues in the activated form of protein kinases are arranged in a similar fashion, suggestive of a common catalytic mechanism.⁶ In Fig. 8, the active site of CDK2 is overlaid with that of PKA⁷⁸ to illustrate the striking similarities in the catalytic scaffold of the two kinases. In the more extensively studied PKA, there was also a controversy on the role of the Asp residue (Asp166) that is hydrogen bonded with the serine nucleophile.⁷⁹ Despite mutagenesis data that its replacement by Ala reduced k_cat by approximately three orders of magnitude,⁷⁷ some experimental data have cast doubt on its role as the general base.⁸⁰ Theoretically, it was suggested based on a semi-empirical model that Asp plays a structural, rather than catalytic, role in the PKA catalysis.^81–82 However, it was latter argued by several authors using more accurate ab initio models that Asp indeed serves as the general base.^33,35,37 Our results reported here also support a general base mechanism for Asp127 for CDK2, consistent with the proposed mechanism for PKA,^33,35,37 and other protein kinases.⁸³

The calculated barrier height for the phosphorylation step (10.8 kcal/mol) is somewhat lower than that derived from the kinetic data (15.3 kcal/mol from k₃=35 s⁻¹).²⁴ (k_cat for CDK2 is much smaller due to the fact that the reaction, like that catalyzed by PKA, is limited by product release.^23–24) However, the substrate used in the kinetic studies of Hagopian et al. has the PKTPKKAKKL sequence,^23–24 which differs significantly from the one used in our study (HHASPRK), including the identity of the nucleophile (T vs. S). Although there has been no kinetic data on the differences between serine and threonine, a recent theoretical study suggested that the former has a lower barrier for the phosphoryl transfer reaction by approximately 3 kcal/mol.⁸³ This difference would bring the theoretical and experimental data to a much better agreement. On the other hand, the work of De Vivo et al. reported a barrier of ~24 kcal/mol,³² which is in less favorable agreement with the experimental data.

The role of Asp127 as the general base is also supported by a recent study of proton inventory of the CDK5/p35 enzyme, which suggests a general base with a pK_a of 6.1.³⁰ In the same study, a solvent kinetic isotope effect (SKIE) of 2.0 was observed for k_cat at high Mg²⁺ concentrations, which has been interpreted as the evidence that a single proton transfer is coupled with the transition state. Interestingly, at low Mg²⁺ concentrations, which are probably more relevant to our model, no SKIE was observed. However, this could be due to the fact that the product release is slower than the chemical step.^23–24 In any event, it should be pointed out that our calculations did not consider the potential involvement of a second Mg(II) ion in the active site of CDK2, for which a binding pocket exists. The involvement of the second Mg(II) ion is known for many other protein kinases, such as PKA (see Figure 8).⁷⁹ Interestingly, a recent X-ray structure of CDK2/Cyclin A complexed with a transition-state analog (MgF₃⁻) did found two Mg(II) ions in the active site, but the second Mg(II) is believed to be transitory during turnover.²² MD studies by the same authors have indicated that the binding of the second Mg(II) cofactor seems to rigidify the complex, which might in turn helps the catalysis. In addition, the kinetic study of CDK5 showed that k_cat increases significantly with the Mg(II) concentration, suggesting a role of the second Mg(II) ion in the catalysis.³⁰

It appears that both experimental and theoretical evidence exists in support of the role of Asp127 as the general base in CDK2 catalysis. The different conclusion reached by De Vivo et al.,³² that Asp127 plays a structural role and the activation of the serine nucleophile is due to proton transfer to ATP, may be explained by the exclusion of Asp127 from the QM region, which precludes its catalytic role. The earlier DFT cluster model of the same group³¹ did not consider the enzyme/solvent environment. The different conclusions reached by the two QM/MM studies underscore the importance of model building.

The mechanistic proposal suggested by De Vivo et al.³² can be considered as a reincarnation of an earlier proposal for non-enzymatic phosphorylation reactions involving phosphate monoester dianions in solution, in which the transferring phosphoryl group is supposed to serve as the general base to deprotonate the nucleophile.⁸⁴ However, this substrate-assisted mechanism was later found to be inconsistent with experimental data.²⁰ This point is interesting in that our results, along with an increasing body of evidence,^33–37,83 seem to suggest that protein kinases employ the same mechanism as non-enzymatic phosphoryl transfer reactions for phosphate monoester dianions. The important determinants of this catalytic machinery include an active site that aligns the reactants for in-line attack, one or more Mg(II) ions that help to bind the ATP and to stabilize transition state, and an elaborate hydrogen bond network that stabilizes the charges in the transition state. In addition, there is increasing evidence from ab initio QM/MM studies that several other enzyme-catalyzed phosphoryl transfer reactions involving phosphate monoesters also favors the dissociative transition state.^85–87

V. Conclusions

We report here extensive ab initio QM/MM studies of the phosphoryl transfer mechanism in the CDK2 catalyzed phosphorylation of a peptide serine residue. In contrast to an earlier QM/MM study which assigned ATP as the general base,³² our results suggest a catalytic role for the conserved Asp127, which activates the serine nucleophile via proton transfer. Our model has also found that that the catalyzed phosphoryl transfer reaction has a concerted mechanism, featuring a single dissociative metaphosphate-like transition state. The role of the Mg(II) ion is primarily to provide stability of the charges developed along the reaction path. This is helped by several hydrogen bonds provided by some conserved residues in the active site. The catalytic mechanism suggested by our QM/MM calculations is consistent with that determined for a more extensively studied protein kinase, namely PKA. This and other mechanistic studies of protein kinases thus suggest a common catalytic mechanism featuring a dissociative phosphoryl transfer mechanism assisted by a conserved Asp general base.

Figure 7.

Comparison of the active-site arrangement of CDK2 (green)¹⁷ and PKA (gray).⁷⁸ Note that the nucleophilic Ser in the PKA structure was mutated to Ala, and the two Mg(II) ions were replaced by Mn(II) ions.