Determination of Conformational Equilibria in Proteins Using Residual Dipolar Couplings

Abstract

In order to carry out their functions, proteins often undergo significant conformational fluctuations that enable them to interact with their partners. The accurate characterization of these motions is key in order to understand the mechanisms by which macromolecular recognition events take place. Nuclear magnetic resonance spectroscopy offers a variety of powerful methods to achieve this result. We discuss a method of using residual dipolar couplings as replica-averaged restraints in molecular dynamics simulations to determine large amplitude motions of proteins, including those involved in the conformational equilibria that are established through interconversions between different states. By applying this method to ribonuclease A, we show that it enables one to characterize the ample fluctuations in interdomain orientations expected to play an important functional role.

Introduction

The accurate determination of the conformational transitions associated with the interactions between proteins and their partners is a key challenge to understand the mechanism of action of these macromolecules.¹⁻⁴ A view that is rapidly gaining momentum is that proteins can recognize and bind their partners because in their free states they often already transiently populate the conformations that they adopt in the bound states.^2,3,5,6 A major role in the establishment of this idea has been played by nuclear magnetic resonance (NMR) spectroscopy, which is a technique that can provide detailed information about the dynamics of proteins.^2,7−11 Residual dipolar couplings (RDCs), which report on the orientation of interatomic bonds with respect to an external magnetic field,^12,13 are most useful in this context. A number of procedures to employ RDCs for the characterization of the structure and dynamics of proteins and nucleic acids have been proposed, including analytical deconvolution,¹⁴⁻¹⁶ the Gaussian axial fluctuations method,^10,17 restrained molecular dynamics simulations in which the alignment tensor is either fitted to the experimental RDCs¹⁸⁻²² or calculated directly from the structure,^23,24 and direct comparison with molecular dynamics simulations.^10,25−29

We discuss here an approach in which RDCs are used to determine ensembles of structures representing conformational equilibria of proteins undergoing large-amplitude motions. In this approach, RDCs are employed as replica-averaged restraints in molecular dynamics simulations to bias the trajectory of the protein molecules toward the state observed experimentally. In order to reproduce the time and ensemble averaging that is implicit in NMR measurements, several molecules (the replicas) are simulated simultaneously, and NMR parameters are back-calculated as average values over them. To implement the restraints, RDCs are calculated from the shape and charge of each individual replica in the set used in the simulations,^25,30−34 and the resulting average values are then required to match the measured RDCs. Since in heterogeneous states of proteins and nucleic acids the alignment tensors, as well as the corresponding RDCs of the individual conformations populated during the dynamics, can differ very significantly,^29,30,35,36 this approach, which does not require the assumption that the fluctuations of the alignment tensor remain relatively small and that they are uncorrelated with the fluctuations of the structure,^29,35,36 is expected to be particularly suitable for enabling the description of the conformational interconversions associated with the function of these macromolecules.

In this work we present a validation of this method by considering the test of the “reference ensemble”.^22,37,38 In this test a reference ensemble is generated at first by using molecular dynamics simulations with a given force field. A set of RDC values is then back-calculated from the structures of this ensemble. These RDC values, which are not measured experimentally but derived computationally from known structures, are then used as restraints in new molecular dynamics simulations with another force field. In the absence of the RDC restraints, this second force field gives rise to an ensemble of conformations different from the reference ensemble. The presence of the RDC restraints, however, induces the second force field to sample an ensemble of conformations closely reproducing the starting reference ensemble, provided that the restraints are implemented correctly. Since in this procedure one knows exactly the ensemble of structures that give rise to the RDC values used as restraints, it is possible to assess very accurately whether the restraints are effectively implemented to bias the conformational sampling toward the reference ensemble. We show that by applying this method, it is possible to characterize motions of large amplitude in ribonuclease A (RNase A). RNase A is a V-shaped protein whose concerted motions of the two antiparallel β-sheet regions (V1 and V2) are closely connected to its function, which involves substrate binding and release.³⁹⁻⁴¹ These low-frequency “breathing” motions, which have been extensively studied experimentally,⁴¹⁻⁴³ make RNase A a paradigmatic system to study the relationship between conformational fluctuations and function.

Results

Test of the Reference Ensemble

In order to carry out a rigorous test of the method for carrying out molecular dynamics simulations with replica-averaged RDC restraints that we discuss in this work, we applied the test of the reference ensemble.^22,37,38 For this method, a ‘reference ensemble’ of conformations was generated by unrestrained molecular dynamics simulations (see Reference Ensemble Calculations in the Materials and Methods Section). RDCs were calculated from the structures of this reference ensemble (see Structure-Based Calculation of the Alignment Tensors in the Materials and Methods Section) and employed as structural restraints (see Restrained Ensemble Calculations in the Materials and Methods Section) to generate a ‘restrained ensemble’, which was then shown to closely reproduce the conformational properties of the original reference ensemble. The advantage of using this reference ensemble test is that it allows for a stringent validation analysis in which the atomic coordinates of the conformations in the reference ensemble are known exactly, and therefore, the accuracy of the conformations in the restrained ensemble can be assessed with great confidence.^22,37,38

Generation of the Reference Ensemble

The reference ensemble was generated by a 100 ns unrestrained trajectory of RNase A by using the Gromos96 force field; for comparison an ‘unrestrained ensemble’ was generated from a 100 ns trajectory by using the Amber99SB force field (see Reference Ensemble Calculations in the Materials and Methods Section). The two force fields generated two different types of breathing motions in the native state of RNase A, with Amber99SB oscillating around a moderately open state and Gromos96 populating both open and closed conformations (Figure S1, Supporting Information). The differences between the reference and unrestrained ensembles arise in part from the fact that the Gromos96 force fields implements a united-atom representation, which speeds up the sampling of the conformational space.

Structure-Based Alignment Approach in Molecular Dynamics Simulations

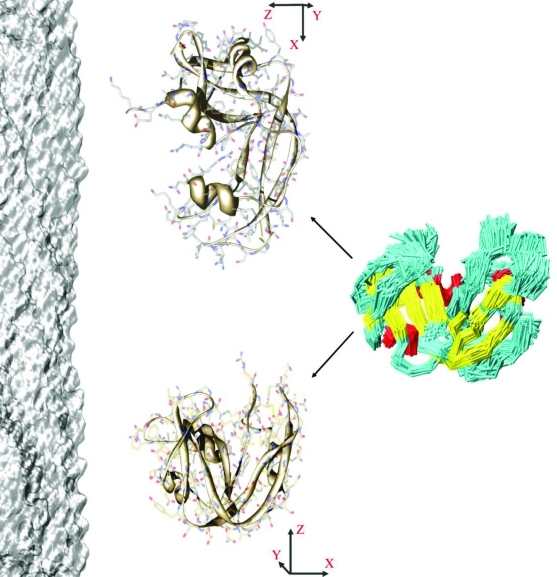
To enforce the RDCs as structural restraints in molecular dynamics simulations, we implemented our own version of the PALES method^30,34 for both steric and electrostatic alignment media in the GROMACS package (see Structure-Based Calculation of the Alignment Tensors in the Materials and Methods Section). The employment of structure-based calculations of the alignment tensor during the sampling is crucial to obtain an accurate determination of conformationally heterogeneous states of proteins, as the alignment that these molecules can adopt can vary significantly during the dynamics (Figure 1), and it is therefore often not possible to make the approximation that all the structures in the ensemble have the same alignment tensor.^29,35,36

Figure 1.

The alignment tensor is highly sensitive to the conformation of the protein. The preferential orientations of a protein with respect an alignment medium, especially in electrostatic cases, can vary significantly within the conformational ensemble of the protein. Such dependence is illustrated here by considering two conformations within the RNase A reference ensemble that have very different alignment tensors in the presence of Pf1 (shown in surface representation on the left).

Replica-Averaged RDC Restraints

The approach that we followed in this study includes an averaging of the RDCs over multiple replicas of the protein molecule, which allows experimental restraints to be imposed as an ensemble property.^18,19,22,44 This approach is particularly efficient in sampling protein ensembles representing conformationally heterogeneous states because the replica averaging allows populating simultaneously different conformational basins that are present in solution and that contribute to the experimental observables.^19,44,45 In this paper, by analyzing the effects of using different numbers of alignment media and different numbers of replicas (Figures S2 and S3, Supporting Information), we defined an optimal protocol based on replica-averaged RDC restraints with 16 replicas and RDCs data for two bond vectors from three alignment media. The employment of in silico experiments allows also for accurately assessing the effects of the errors on the RDC data in the performance of the structure-based alignment prediction (Figure S4, Supporting Information).

RDC-Based Determination of Large-Scale Motions of RNase A

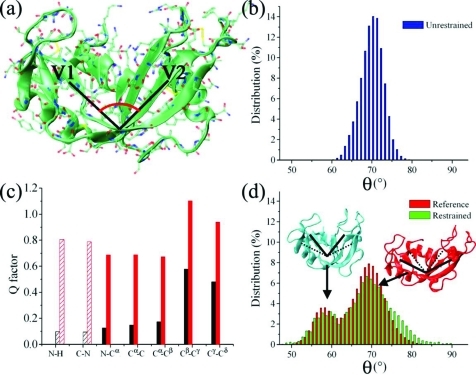
The main result of this work is the demonstration that it is possible to use information derived from RDCs to characterize with high-accuracy distinct states in conformational equilibrium. To illustrate our approach, we considered the open and the closed forms of RNase A. In order to follow the conformational changes involved in the breathing motions of RNase A, we used the angle (‘pincer angle’) between the centers of mass of V1 and V2 and their hinge region (Figure 2a), which discerns between the open and closed conformations. We show that, while only the open state is present in the unrestrained Amber99SB simulations (Figure 2b), the use of RDC restraints drives a series of conformational interconversions between the open and closed states, which generates an ensemble with essentially correct Boltzmann weights despite the presence of an underlying force field that has a different behavior when considered on its own (Figure 2d). We further validate these results by reporting the Q factors (see Materials and Methods) for the unrestrained and restrained ensembles compared to the reference ensembles. In addition to the bonds vectors employed for generating the restrained ensemble, which expectedly exhibited a better agreement in the case of the restrained ensemble, all other bond vectors analyzed showed improved Q factors for the restrained ensemble (Figure 2c).

Figure 2.

Determination of large-amplitude structural fluctuations from RDCs. (a) Representation of the structure of RNase A (Protein Data Bank code 7RSA [32]); the pincer angle, which accounts for the large motions between the antiparallel β-sheets V1 (residues 61–63, 71–75, 105–111, and 116–12) and V2 (residues 42–46, 82–87, and 96–101), is indicated schematically. The value of the pincer angle is calculated from the three centers of mass of the Cα-atoms of three protein regions: region 1 (V2) spanning residues 42 and 43, region 2 (hinge) spanning residues 48, 49, and 80, and region 3 (V1) spanning residues 72 and 73. (b) Pincer angle distribution in 100 ns unrestrained Amber99SB simulations. (c) Agreement (Q factor) between RDCs of the reference and restrained ensembles (black) and the reference and unrestrained ensembles (red); dashed lines indicate bond vectors employed as restraints. (d) Pincer angle distribution in the reference (red) and restrained (green) ensembles calculated with three alignment media and 16 replicas (Figure S6, Supporting Information); the bimodal distribution includes both closed (blue) and open (red) conformations. Thirty structures per replica are recorded in the final part of each cycle (sampled at 300 K) of the restrained ensemble with a total of 9600 conformations.

Structural Accuracy of the RDC-Driven Sampling

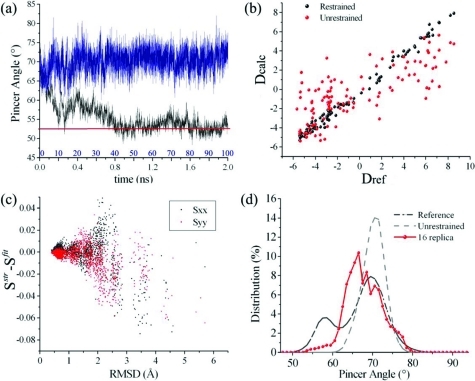
In order to investigate more in detail how structure-based calculations of the alignment tensor can be used to drive conformational transitions, we calculated the RDCs corresponding to a selected closed conformation from the reference ensemble and used them to restrain one-replica molecular dynamics simulations that started from the open state and ended up in the closed state (Figure 2a). These simulations show that by imposing the RDC restrains on an open conformation it is possible in 1 ns to drive the conformational sampling toward the pincer angle corresponding to the closed conformation (Figure 2a), with a very significant reduction of the root-mean-square deviation (rmsd) from the closed conformation itself (from ∼5.3 to ∼0.5 Å) (Figures S5 and 6S, Supporting Information). For comparison, by using an alternative approach in which the conformations that better reproduce the experimental data are selected from an unrestrained sampling, we could only obtain a relatively poor agreement with RDCs (Q = 0.43, Figure 3b) compared to the restrained simulations (Q = 0.16). We found the conformations selected from the unrestrained ensemble to be all quite far from the target structure in terms of pincer angle values (Figure 3a, red line), thereby resulting in an inaccurate conformational ensemble.

Figure 3.

Structural accuracy of the RDC-driven sampling. (a) Time series of the pincer angle in the 100 ns unrestrained (Amber99SB) simulations (blue line) and 2 ns restrained (Amber99SB) simulations (black line), enforcing RDCs calculated from a closed structure of RNase A; the restraint force is gradually enforced during the first 1 ns. The red line indicates the angle value of the target structure. (b) Comparison between the RDCs of the target closed structure (D^ref), of the structures obtained in the last 1 ns of the restrained simulations (D^calc, black dots), and of the structures selected from the unrestrained simulations (D^calc, red dots). (c) Principal elements of the alignment tensors as a function of the rmsd between conformations extracted from the restrained simulation and the target structure from which the RDCs have been calculated; the plot shows the differences between fitted (S^fit) and structure-based alignment (S^str) tensors. (d) Comparison of the distribution of the pincer angle in the restrained ensemble obtained using only one steric alignment medium and 16 replicas (red) with the distributions from the reference (black dot-dashed) and unrestrained (gray dashed) ensembles.

Discussion

Our knowledge of the three-dimensional states that biological macromolecules adopt in solution has enormously improved in recent years.^8,9,46−49 It has also been established that even in their native states, proteins constantly undergo structural fluctuations with time scales ranging from picoseconds to seconds and beyond, which are biologically relevant and influence a wide variety of processes, including enzymatic catalysis, ligand binding, and the formation of biomolecular complexes.^2,7−11,44 States of this type pose a formidable challenge for structure determination, because, in many cases, they are inherently flexible and conformationally highly heterogeneous.

We have described a computational procedure for using NMR measurements of residual dipolar couplings as replica-averaged restraints in molecular dynamics simulations to determine large amplitude motions of proteins, including those involved in the conformational equilibria often associated to their functions. When proteins undergo significant motions, as in the case of RNase A considered here, the method that we have described is highly effective in exploiting the structural and dynamical information provided by RDCs to determine accurately conformational ensembles and the associated Boltzmann weights (Figure 2d). For comparison, related methods for determining the alignment tensor by a fit to experimental RDCs¹⁸⁻²² can be expected to be accurate primarily when the conformational heterogeneity of the solution state is limited; this is because the experimental RDCs, which are averaged over the molecules in solution, can be significantly different from the specific RDCs of individual conformations in the corresponding ensemble, and their alignment tensors can be very different from each other and depart substantially from the average alignment tensor (Figures 1 and 3c). It should also be noted that, when the conformational fluctuations are of large amplitude, the structural interpretation of RDCs that is adopted here may raise concerns, especially when the time scale of alignment is faster than that of interconversion between different conformers.(23) Since, however, RDCs are measured under equilibrium conditions, the specific features of the dynamics of the alignment process should not affect their values. Another concern derives from the possibility of perturbing the conformational properties through the process of measurement itself. Also in this case, however, as long as the interaction between proteins and alignment media is weak so that only the orientation of the proteins with respect to an external reference frame, but not their internal conformational space, is altered significantly by the presence of the alignment media. We suggest that for these reasons the structure-based calculation of the alignment tensors implemented here to enforce the replica-averaged RDC restraints can provide an accurate representation of conformational equilibria.

In conclusion, we have described a method of using RDCs as replica-averaged restraints in molecular dynamics simulations to provide a quantitative description of the free energy landscapes associated with large-scale motions of proteins.

Material and Methods

Reference Ensemble Calculations

Unrestrained molecular dynamics simulations were performed with the Gromacs package.(50) Two independent molecular dynamics simulations have been carried out. In the first simulation we generated the ‘unrestrained ensemble’, employing the all-atom Amber99SB force field^51,52 and the TIP3P explicit water model,(53) and in the second simulation we generated the ‘reference ensemble’, employing the Gromos96 force field(54) and the SPCE water model.(55) The starting coordinates were derived from the crystal structure of the RNase A (Protein Data Bank code 7RSA).(56) All simulations were carried out in the NPT ensemble with periodic boundary conditions at a constant temperature of 300 K and pressure of 1 atm. A dodecahedron box was employed for accommodating the protein, water molecules, and ions. Bonds were constrained by the LINCS(57) algorithm. The particle-mesh Ewald (PME) method(58) was used to account for the electrostatic contribution to nonbonded interactions (grid spacing of 0.12 nm). To model a system at pH of 7, the protonation states of pH-sensitive residues were set as follows: Arg and Lys residues were positively charged, Asp and Glu residues were negatively charged, and His residues were neutral. The protonation state of His residues was derived by comparing high-resolution X-ray structures performed at different pH values;(59) His12 and His48 were protonated at Nδ, and His105 and His119 were protonated at Nε. The net charge of the protein was neutralized by the addition of Cl^– ions. Simulations were continued for 100 ns. The Gromos96 trajectory was selected to provide the reference ensemble, whereas the Amber99SB trajectory was analyzed as an unrestrained ensemble to be compared with the restrained ensemble, which employed the same molecular dynamics settings with the addition of the RDC restraints (see Restrained Ensemble Calculations Section).

Restrained Ensemble Calculations

Molecular dynamics simulations with replica-averaged RDC restraints were implemented in the Gromacs package, by adopting a structure-based calculation of the alignment tensor (see Fitting Procedure for the Calculation of the Alignment Tensors Section). In this approach, restraints are imposed by adding a pseudoenergy term (E_RDC) to a standard molecular mechanics force field (E_MM):

The resulting force field (E_TOT) was used in the molecular dynamics simulations. The E_MM that we employed was the Amber99SB (settings as in the unrestrained simulation section), and the pseudoenergy term is given by^18−20,22

An initial equilibration simulation at 300 K was run, during which the agreement between calculated and experimental data, represented by their mean square deviation, eq 2, was allowed to converge. This result was achieved by gently raising the restraint force constant α. Subsequently, a series of 20 cycles of simulated annealing between 300 and 500 K was carried out to sample effectively the conformational space. Each cycle was carried out for a total of 250 ps (125 000 molecular dynamics steps) by using an integration step of 2 fs. The restraints were imposed as averages over M replicas of the protein molecule; we employed simulations with M = 2, 4, 8, and 16. For each replica, the alignment tensors are independently computed using a structure-based method (see Structure-Based Calculation of the Alignment Tensors Section) and used in eq 2.

We are planning to include the implementation of the RDC restraints presented in this work in the standard Gromacs distribution.

Fitting Procedure for the Calculation of the Alignment Tensors

When we did not carried out structure-based calculations of the alignment tensor, the PALES code was used to perform calculations of the alignment tensor by fitting the RDCs to the structures.^30,34

Structure-Based Calculation of the Alignment Tensors

In order to calculate the RDCs corresponding to a given structure, we implemented our own version of the PALES code^30,34 into the Gromacs package. We used three alignment media (Table 1): two steric (DMPC/DHPC and Pf1 at high ionic strength, Pf1-s) and an electrostatic (Pf1-e).

Table 1. Comparison of the Three Alignment Media Used in This Work^a.

	NSPE	correlation	SD (Hz)	Q-factor
Pf1-e vs Pf1-s	–0.32	0.45	11.2	1.375
Pf1-e vs DHCP/DMCP	0.3	0.31	15.67	1.219
Pf1-s vs DHCP/DMCP	–0.54	0.86	8.62	0.533

^aThree alignment media: two steric (DMPC/DHPC and Pf1 at high ionic strength, Pf1-s) and an electrostatic (Pf1 at low ionic strength, Pf1-e).

Definition of Q-Factors for RDCs

The quality factor for a given RDC (Q-factor) is defined as(60)

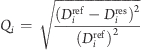where D_i^ref is the RDC of a bond i in the reference ensemble and D_i is the corresponding RDC in the restrained ensemble.

Comparison of the Alignment Tensors

The independence of the RDC sets was tested by four similarity indexes (Table 1). In addition to standard analyses (i.e., correlation, standard deviation, Q-factor), we introduced the normalized scalar product of alignment tensors eigenvectors (NSPE):

where d⃗_a(i) and d⃗_a(i) represent the three eigenvectors of the alignment tensors of the media a and b, respectively. The NSPE index ranges from −1, for completely opposite alignment tensors, to 1 for totally overlapping tensors.

RDCs Calculation from the Reference Ensemble

For a given protein structure, the RDC calculated on the bond vector between atoms P and Q is given by

where A is the alignment tensor, r is the bond vector module, ℏ is the Planck constant, m₀ is the dielectric permittivity, and γ is the gyromagnetic radius. This formula requires the determination of the orientation of the protein in the alignment medium, which was done using a structure-based method (see Structure-Based Calculation of the Alignment Tensors Section). Although we have used a reference ensemble approach, and thus in principle we are able to define reference RDCs for all bond vectors in the protein, we have used only NH and CN bond vectors, which are the most commonly measured RDCs. To ensure a realistic case, we randomly removed 17% of the RDCs from the loop or terminal regions of the protein, including glycine residues, which usually give rise to signal broadening, and proline residues, which do not have an NH group. In total we employed 610 RDC values. In addition, a random perturbation of 0.15 Hz was applied on the final calculated values of the reference RDCs in order to account for experimental errors.

RDCs Calculation in the Restrained Simulations

The restrained simulations were carried out by using multiple replicas, a procedure that requires an averaging of the RDCs over the M replicas:

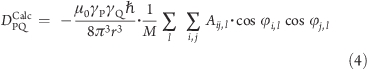where l runs over the M replicas.

Supporting Information Available

Figures S1–S6. This material is available free of charge via the Internet at http://pubs.acs.org.