Abstract
The mechanical properties of cells play an essential role in numerous physiological processes. Organized networks of semiflexible actin filaments determine cell stiffness and transmit force during mechanotransduction, cytokinesis, cell motility and other cellular shape changes1–3. Although numerous actin-binding proteins have been identified that organize networks, the mechanical properties of actin networks with physiological architectures and concentrations have been difficult to measure quantitatively. Studies of mechanical properties in vitro have found that crosslinked networks of actin filaments formed in solution exhibit stress stiffening arising from the entropic elasticity of individual filaments or crosslinkers resisting extension4–8. Here we report reversible stress-softening behaviour in actin networks reconstituted in vitro that suggests a critical role for filaments resisting compression. Using a modified atomic force microscope to probe dendritic actin networks (like those formed in the lamellipodia of motile cells), we observe stress stiffening followed by a regime of reversible stress softening at higher loads. This softening behaviour can be explained by elastic buckling of individual filaments under compression that avoids catastrophic fracture of the network. The observation of both stress stiffening and softening suggests a complex interplay between entropic and enthalpic elasticity in determining the mechanical properties of actin networks.
Monomers of actin assemble into polar filaments that are organized by various actin-binding proteins into branched, bundled and/or crosslinked networks essential for basic cellular functions1. In crawling cells, growth of actin filament networks characterized by a dendritic architecture—highly branched structures with short filaments (~0.1–1 µm) oriented in the direction of migration—generates force at the cell periphery for membrane protrusions1,9,10.
Actin filaments, as well as other biological and synthetic polymers, are categorized by the relationship between their persistence length Lp and contour length Lc. The persistence length is defined as the average length over which the filament orientation changes due to thermal fluctuations, and the contour length is the length of the completely extended filament. For flexible polymers (Lc ≫ Lp) the resistance to extension and compression is determined by the conformational entropy of the chain and is described as entropic elasticity. Flexible polymers exhibit stress stiffening near full extension because there is ultimately only one fully extended conformation, assuming inextensibility11. For stiff polymers (Lc ≪ Lp) resistance to extension, bending and compression is due to straining of molecular links from equilibrium, which is quantified by the bending modulus κ and described as enthalpic elasticity. Under compressional forces, stiff polymers buckle at the Euler buckling force12 , whereas there is no equivalent buckling instability for flexible polymers because random thermal forces exceed the Euler buckling force. Actin filaments are considered to be semiflexible polymers because their persistence length (~10–17 µm)8,13 is comparable to their physiological contour length (~0.1–10 µm)10. At physiological temperatures, individual filaments are expected to exhibit a combination of both entropic and enthalpic elasticity that is sensitive to the ratio of Lc to Lp and stiffen at strains much lower than in flexible polymers6,14.
The mechanical properties of actin networks have been studied extensively using rheology of random networks formed by mixing purified actin and various actin-binding proteins in solution2,4–6. Recent studies have demonstrated stress stiffening of crosslinked actin networks in vitro under shear and explained this behaviour as arising from the inherent stress stiffening of individual filaments or flexible crosslinkers between filaments under extension, suggesting that the elasticity of these networks is entropic5–7. Filaments resisting compression have not been found to be important6. However, as filament length decreases from lengths seen in these in vitro assays (~2–70 µm) to physiological values, filaments are expected to support more significant bending and compressional forces14. Indeed, the increasing importance of enthalpic elasticity has been predicted for high concentrations of actin and crosslinkers when the distance between crosslinks becomes small5,15. Here we report that dendritic actin networks reconstituted in vitro exhibit a regime of reversible stress softening. This stress softening can be explained by the elastic buckling of individual filaments, providing evidence for an elastic response of dendritic actin networks that is enthalpic under large compressional forces and is dominated by the resistance of individual filaments to compression.
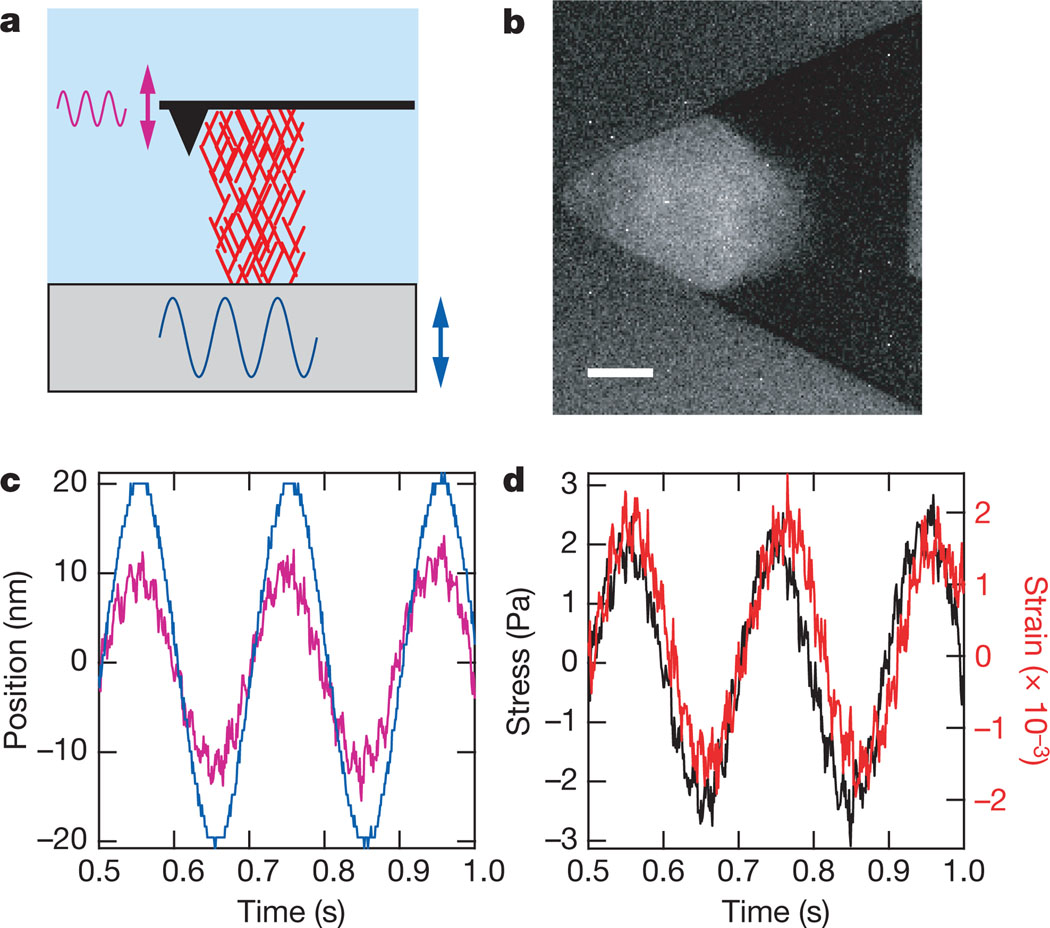
We studied the mechanical properties of growing dendritic actin networks in vitro using a recently developed dual-cantilever atomic force microscope (AFM) that uses a second cantilever to improve instrument stability (see Supplementary Information A, B)16. Dendritic networks, like those formed during cell motility, must be assembled hierarchically from a nucleating surface and cannot be formed randomly in equilibrium solutions of component proteins. In our assay, the nucleation promotion factor ActA, from the bacterial pathogen Listeria monocytogenes, was nonspecifically adhered to the end of an AFM cantilever before immersion in cytoplasmic extract from Xenopus laevis eggs. Upon immersion, ActA activates the Arp2/3 complex, which nucleates growing filaments as 70° branches off of existing filaments, catalysing the formation of a growing dendritic actin network between the cantilever and a nearby glass surface (Fig. 1a,b)1,10,17. Surfaces coated with ActA and other nucleation promotion factors have been shown to grow dendritic actin networks in cytoplasmic extract17,18. The AFM cantilever behaves like a hookean spring for small deflections (for which F = kΔx), allowing measurement and application of compressional forces to the growing network.
Figure 1. AFM-based microrheology of growing dendritic actin networks.
a, Cartoon illustrating the measurement geometry in which the surface is driven sinusoidally (blue sinusoid and double-headed arrow), and the force transmitted through the network (red mesh) is transduced by the cantilever (pink sinusoid and double-headed arrow). b, Fluorescence micrograph of the actin network, which is used to calculate the network area A. Scale bar is 10 µm. c, Graph showing surface drive and cantilever response signal as a function of time for a 5 Hz measurement (colours are as in a). Note the cantilever response is damped with respect to the drive signal indicating compression of the network. This technique has the effect of applying a sinusoidal stress on the network where hydrodynamic coupling was found to be negligible (see Supplementary Information B). d, Stress and strain graph calculated from measurement in c showing stress (black) and strain (red) as a function of time (see Methods).
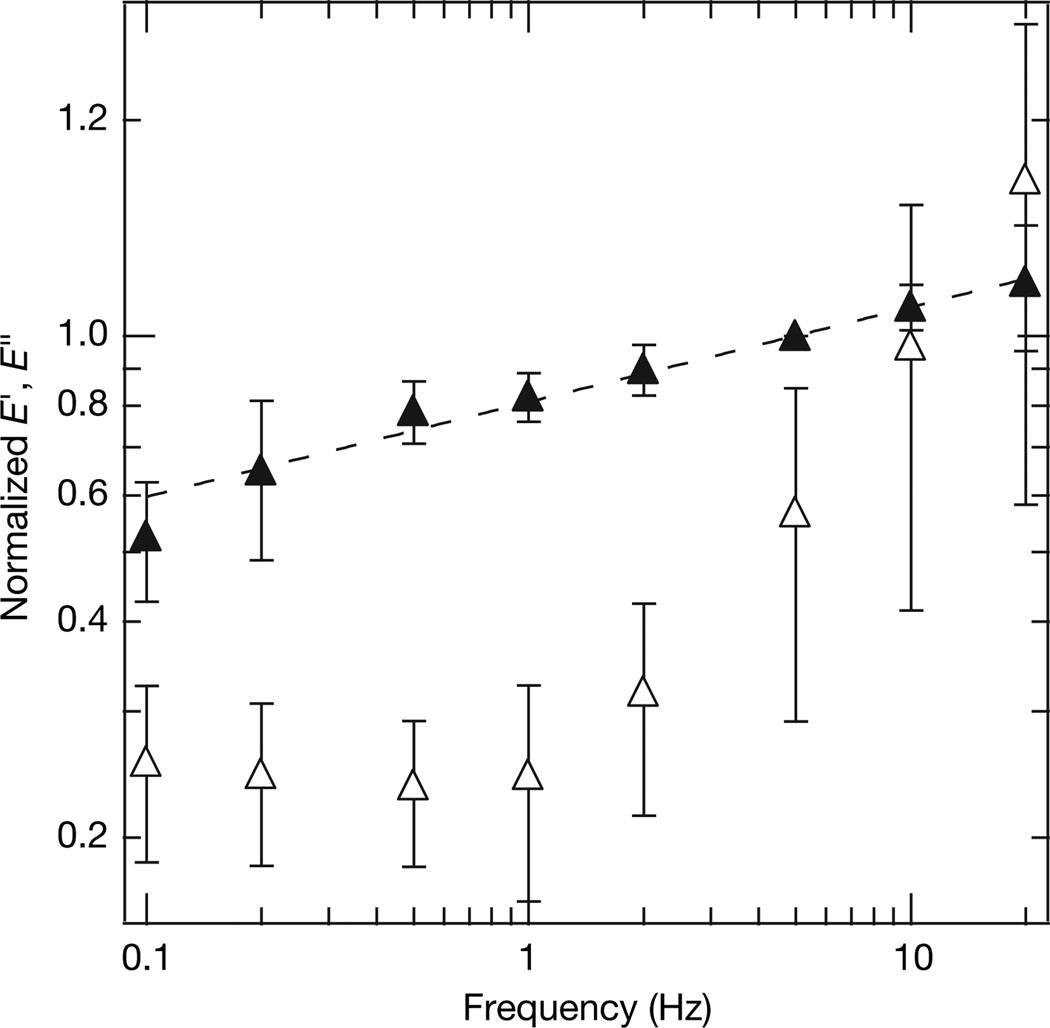
Using AFM-based microrheology19,20 (Fig. 1c, d, Methods), we measured frequency-dependent elastic (storage) and viscous (loss) moduli. After normalization at a reference frequency (see Supplementary Information C), we find that the frequency dependence of the elastic modulus E′ is consistent with power-law rheology, E′∝fx, with x = 0.13 (Fig. 2). This falls within the range of exponents measured from cells (x = 0.12–0.25)20–22. The average linear elasticity of the dendritic actin networks, 985 ± 655 Pa (mean ± s.d.) at 5 Hz, is similar to the elastic modulus measured on various cell types19–22 and in a previous reconstitution of actin-based motility23. Dendritic actin network elasticity is significantly higher than the elasticity of actin networks reconstituted in solution containing the Arp2/3 complex (~1 Pa), though differences in concentration and components could account for this disparity24,25. The average elasticity of the actin networks studied here was found to be independent of prestressing by myosin II motors (see Supplementary Information D).
Figure 2. Frequency dependence of elastic (filled triangles, E′) and viscous (open triangles, E″) moduli.
The traces were constructed by averaging normalized data from 11 separate experiments and 21 different frequency sweeps. Each measurement of the elastic and viscous moduli was normalized by the average elastic modulus at 5 Hz taken before and after the measurement (see Supplementary Information C). The best-fit power-law exponent for E′(f) was determined to be x = 0.13 (dotted line), and the average elastic modulus at 5 Hz was 985 ± 655 Pa (mean ± s.d.), which are consistent with previous studies on cells. In addition to the power-law behaviour, the viscous modulus has a similar shape to those seen previously. Error bars on both curves are normalized s.d.
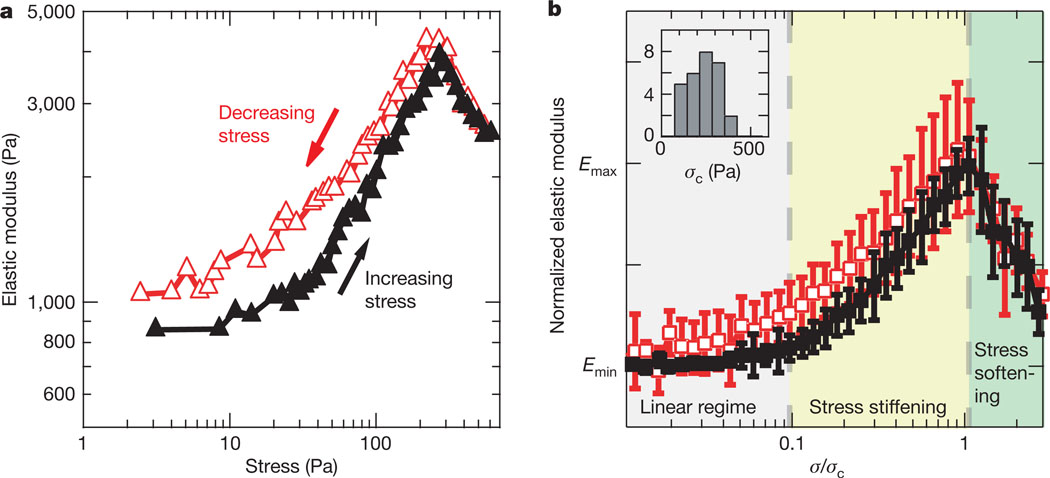
To understand further the mechanical properties of growing dendritic actin networks, we probed the stress dependence of the elastic modulus5,7 (see Methods). A typical experiment is shown in Fig. 3a (black trace) where stress was increased on the network incrementally, and the elasticity at each value of applied stress was measured. For stresses up to ~15 Pa the elasticity remained constant, indicating a linear elastic regime. Then the elasticity increased with stress in a stress-stiffening regime, as has been seen previously4–6, for stresses up to a critical stress, σc ≈ 270 Pa. Above the critical stress, we found that the elasticity of the network gradually decreased with stress in a stress-softening regime.
Figure 3. Dendritic actin networks exhibit stress stiffening and reversible stress softening.
a, In a typical nonlinear elasticity measurement, the stress on the network is first increased incrementally (black trace) to and then decreased incrementally from a maximum stress (red trace) of ~600 Pa, with the elasticity measured at each stress at 5 Hz. The elasticity remains constant for stresses up to ~15 Pa and then increases in a stress-stiffening regime. For stresses above the critical stress σc of ~270 Pa, the elasticity decreases in a stress-softening regime that is reversible, as indicated by the overlay of the black and red traces. b, Averaged and normalized trace of the nonlinear elasticity of actin networks (see Supplementary Information A). Each individual measurement was normalized by the difference between the elasticity before the measurement Emin and the maximum elasticity for increasing stresses Emax and σc. The results of 28 different measurements from 12 separate experiments were averaged together (mean ± s.d. shown) and found to exhibit three distinct regimes of elasticity: linear, stress stiffening and stress softening. The stress softening is shown to be reversible. Note that the elasticity in b is shown on a linear scale while the elasticity in a is shown on a log scale. The inset shows a histogram of σc for which the mean value was 233 Pa.
Stress softening has been previously explained by network rupture or crosslinker rearrangement. In rigidly crosslinked actin networks, stress softening has been attributed to the fracture of extended filaments or crosslinking/branch points at σc, after which elasticity drastically decreased4–6. Alternatively, softening was proposed to occur as a result of the unbinding of flexible crosslinkers above σc, which either remain unbound or re-bind to form crosslinks at different positions7. For either of these explanations, stress softening would reflect permanent alterations in the network that would lead to irreversibility in the elasticity of the network. That is, higher elasticities could not be recovered by reducing network loading from stresses above σc (refs 4–7). However, in dendritic actin networks, the stress-softening behaviour was reversible: the elasticity measured as the stress was reduced to σc matched the elasticity seen for increasing stress (Fig. 3a, red trace). This was seen in all experiments (Fig. 3b), so stress softening in the dendritic actin network must arise from a reversible mechanism.
A plausible explanation for reversible stress softening is through elastic buckling of individual filaments under compression. A population of filaments in the dendritic network, based on their length and orientation, will begin to buckle at a threshold stress. Upon buckling, these filaments are infinitely compliant while still supporting Fb (ref. 12). As a result, the number of load-bearing elements decreases for higher stresses, resulting in a decrease in the effective stiffness of the network. As the stress is increased, more filaments buckle, reducing the elasticity of the network further. Because filaments are assembled into an interconnected dendritic network, buckled filaments do not collapse completely, and they can unbuckle when the force is reduced, making the process of buckling reversible with load. Stress softening has been predicted from simulations of athermal crosslinked actin networks to occur as a result of filament buckling and also in an elastic element model of the cytoskeleton26,27, although such models do not predict stress stiffening before softening. Interestingly, reversible elastic buckling of component elements is observed under high compressional forces in some types of foams28. Electron micrographs have shown the actin cytoskeleton ultrastructure to exhibit similarities with open lattice foams, so that this buckling behaviour might be expected3.
Buckling of individual filaments can occur at forces consistent with the observed stress softening, based on a simple calculation. Using published electron micrographs of dendritic actin networks reconstituted in vitro in a similar biochemical system, we estimate filament lengths Lc to be 0.1–1 µm(ref. 17). We calculate an expected buckling force Fb of 0.5–50 pN per filament using these lengths and assuming Euler buckling, although the behaviour in a constrained environment can lead to higher buckling forces29. In our experiments, the average force per filament at σc (233 Pa, the mean value from the inset of Fig. 3b), using an average filament spacing of 50–100 nm (ref. 17), is calculated to be 0.45–2 pN, which lies within the lower range of predicted buckling forces. We note that the buckling instability is smoothed entropically for a semiflexible polymer at finite temperature, so that individual polymers will undergo stress softening as the compressional force approaches the Euler buckling force. The overlap in the lower range of predicted buckling forces with the range of calculated applied force per filament at σc supports the idea that buckling explains stress softening, because σc represents the threshold stress at which filament buckling dominates nonlinear elasticity. As the stress is increased, up to 3σc in our experiments, shorter filaments buckle, and the elasticity decreases further.
Our measurements of nonlinear elasticity in dendritic actin networks are consistent with a model in which a combination of compression, bending and extension gives rise to network mechanical properties (Fig. 4). As stress is initially applied to the network, the elasticity increases as a result of entropic resistance to filament and flexible crosslinker extension normal to the direction of compression, in addition to possible effects from nonlinear compliance of the Arp2/3 complex (Fig. 4a, b). As stress on the network is further increased, filaments oriented in the direction of compression begin to buckle, reducing the elasticity of the network at higher stresses (Fig. 4c, d). Buckling occurs only after filaments have already been supporting a load, so the enthalpic resistance of filaments to compression is likely to play a significant role in the linear and stress-stiffening regimes.
Figure 4. Stress stiffening and stress softening can arise in dendritic networks owing to filaments resisting extension and buckling of filaments resisting compression.
a, b, When the stress on the network (σ, indicated by black arrows) is increased from σ = 0, a population of filaments or crosslinkers is stretched (as indicated by green arrows) as the material expands laterally, and the resistance to extension of filaments increases owing to entropic elasticity, leading to a stress-stiffening regime. c, However, as the stress is increased above σc, some filaments resisting compression buckle when the compressional force (green arrows) exceeds the Euler buckling force. Buckled filaments exhibit infinite compliance, so they no longer contribute to the elasticity, but they do not collapse because they have connections with the network and thus still support the buckling force. d, As the stress is further increased, more filaments buckle and the elasticity of the network is decreased further, leading to the stress-softening regime. In principle, this process is completely reversible because buckled filaments will unbuckle once the stress is reduced.
The difference in the elasticity of dendritic networks grown from surfaces and crosslinked networks formed in solution can be explained in part by the actin concentration in the network. The modulus of elasticity is expected to scale as (ref. 8) for isotropically crosslinked actin networks, where CA is the concentration of actin in the network and the crosslinks are assumed to be rigid. The concentration of actin in dendritic networks has been estimated to be ~1 mM (ref. 30), whereas the concentration of networks studied in vitro was of the order of ~10 µM (refs 24, 25), suggesting that the magnitude of elasticities for dendritic networks should be significantly higher. Component concentration alone is sufficient to describe network properties in flexible polymer networks (Lc ≫ Lp), where Lp is much less than the distance between crosslinks, because initial orientation and lengths of the filaments do not matter. However, for semiflexible polymer networks, filament length can be important when Lp is greater than the distance between crosslinks15. Additionally, the particular orientation of a filament in the network determines whether the filament deforms by compression, bending or extension. Our finding of an elastic response in which filaments resisting extension and compression are both significant, suggests that architecture—filament length and orientation—influences the elastic behaviour of actin networks.
The reversible elastic behaviour and large elastic modulus of dendritic actin networks indicate that these networks have an architecture that is geared towards bearing high compressive loads. Because the leading edge of crawling cells is normally under compression during motility, we expect these measurements to be relevant to the mechanics of lamellipodial protrusions. Dynamic remodelling of dendritic actin network architecture may provide a mechanism for altering network elasticity in response to changing external loads.
METHODS
AFM-based microrheology
In AFM based microrheology, the deformation of the material is measured in response to a small sinusoidal stress at a given frequency, f (refs 19, 20). The elastic modulus E′ and the viscous modulus E″ are then calculated as E′(f) + iE″ (f) = σ̃(f)/ε̃(f), where σ̃ and ε̃ are the Fourier transforms of the stress σ and the strain ε, respectively (Fig. 1d). This method is necessary for growing actin networks because only the response at the drive frequency is analysed, thereby decoupling mechanical property measurements from network growth. Changes in network length due to growth over measurement timescales (~5 min) would obscure the true strain values needed for traditional stress–strain measurements.
After the network length reached ~6 µm while growing under a small constant force, the force clamp (see Supplementary Information A) was released and the bottom surface was sinusoidally oscillated with an amplitude of 20 nm at 0.1, 0.2, 0.5, 1, 2, 5, 10 and 20 Hz using the piezoelectric positioner. This applies a sinusoidal stress to the network where hydrodynamic coupling was found to be negligible (see Supplementary Information B). At each frequency, the surface was oscillated ten times and the cantilever deflection data was used to calculate both the σ and ε (shown in Fig. 1) on the network.
Stress-dependent elasticity measurements
We adapted a technique to quantify the stress dependence of elasticity used by Gardel et al. on crosslinked random actin networks to our AFM-based system5,7. Because the relaxation processes are very slow (x ≈ 0.13), the elasticity at a given stress changes very slowly, and this technique provides a well-defined stress–elasticity relation. In this technique, the bottom surface was incrementally stepped into (or away from) the network, and a rheology test at 5 Hz was performed to obtain the elastic modulus as a function of stress on the network. At the beginning of a nonlinear elasticity measurement, the stress on the network was reduced to nearly zero, and a 5 Hz rheology test was conducted. We incrementally increased the force on the network, and obtained the elastic modulus at each incremental stress. The stress on the network was increased until ~600 Pa, after which we incrementally decreased the stress on the network by moving the bottom surface away from the cantilever, continuing to conduct 5 Hz rheology tests after each step. Subsequent tests on the same network were started at a stress of zero.
Data analysis
In each measurement, the cantilever voltage signals were converted to deflection in Igor Pro 5 (Wavemetrics, Inc) using a voltage-deflection calibration constant that was determined at the beginning of each experiment. The length of the actin network was calculated as the distance between the two cantilevers plus an additional 3 µm due to the size of the tip. The force was determined by multiplying cantilever deflection by the stiffness (100 pN nm−1). The network area was determined by thresholding the image at a greyscale value midway between the highest and lowest value along the cantilever in the ImageJ program (NIH). There is a 0.1% error in this measurement due to the diffraction-limited resolution of the fluorescence imaging.
To obtain the elastic and viscous moduli, the best-fit line was initially subtracted from the measurement cantilever deflection to eliminate the effect of slow timescale growth. We approximate the geometry of the system as a network sandwiched between two parallel plates so that σ = F/A and ε = ΔL/L, where F is the force exerted on the network by the cantilever, A is the cross-sectional area of the network and L is the length of the network. The parallel plate approximation ignores the effect of the pyramidal geometry of the tip because the tip typically represents less than 2.5% of the network area.
Additional methods are described in Supplementary Information A.
Supplementary Material
Acknowledgements
We thank J. W. Shaevitz, M. J. Rosenbluth, S. Pronk, P. L. Geissler and J. Alcaraz for discussions and reading of the manuscript as well as the entire Fletcher laboratory for support. We are also grateful to R. L. Jeng and M. J. Footer for assistance in protein preparation. This work was supported by an ASEE NDSEG Fellowship to O.C., an ARCS Fellowship to S.H.P., and an NSF Career Award and NIH grants to D.A.F.
Footnotes
Supplementary Information is linked to the online version of the paper at www.nature.com/nature.
Author Information Reprints and permissions information is available at www.nature.com/reprints. The authors declare no competing financial interests.
References
- 1.Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 2.Janmey PA, Weitz DA. Dealing with mechanics: mechanisms of force transduction in cells. Trends Biochem. Sci. 2004;29:364–370. doi: 10.1016/j.tibs.2004.05.003. [DOI] [PubMed] [Google Scholar]
- 3.Satcher RL, Dewey CF. Theoretical estimates of mechanical properties of the endothelial cell cytoskeleton. Biophys. J. 1996;71:109–118. doi: 10.1016/S0006-3495(96)79206-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Xu JY, Tseng Y, Wirtz D. Strain hardening of actin filament networks—Regulation by the dynamic cross-linking protein α-actinin. J. Biol. Chem. 2000;275:35886–35892. doi: 10.1074/jbc.M002377200. [DOI] [PubMed] [Google Scholar]
- 5.Gardel ML, et al. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 6.Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 7.Gardel ML, et al. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl Acad. Sci. USA. 2006;103:1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mackintosh FC, Kas J, Janmey PA. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 9.Mullins RD, Heuser JA, Pollard TD. The interaction of Arp2/3 complex with actin: Nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc. Natl Acad. Sci. USA. 1998;95:6181–6186. doi: 10.1073/pnas.95.11.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Svitkina TM, Borisy GG. Arp2/3 complex and actin depolymerizing factor cofilin in dendritic organization and treadmilling of actin filament array in lamellipodia. J. Cell Biol. 1999;145:1009–1026. doi: 10.1083/jcb.145.5.1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bustamante C, Marko JF, Siggia ED, Smith S. Entropic elasticity of λ-phage DNA. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 12.Landau LD, Lifshitz EM. Theory of Elasticity. Oxford: Butterworth-Heinemann; 1986. [Google Scholar]
- 13.Gittes F, Mickey B, Nettleton J, Howard J. Flexural rigidity of microtubules and actin-filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kroy K, Frey E. Force-extension relation and plateau modulus for wormlike chains. Phys. Rev. Lett. 1996;77:306–309. doi: 10.1103/PhysRevLett.77.306. [DOI] [PubMed] [Google Scholar]
- 15.Head DA, Levine AJ, MacKintosh EC. Deformation of cross-linked semiflexible polymer networks. Phys. Rev. Lett. 2003;91 doi: 10.1103/PhysRevLett.91.108102. 108102. [DOI] [PubMed] [Google Scholar]
- 16.Parekh SH, Chaudhuri O, Theriot JA, Fletcher DA. Loading history determines the velocity of actin-network growth. Nature Cell Biol. 2005;7:1119–1123. doi: 10.1038/ncb1336. [DOI] [PubMed] [Google Scholar]
- 17.Cameron LA, Svitkina TM, Vignjevic D, Theriot JA, Borisy GG. Dendritic organization of actin comet tails. Curr. Biol. 2001;11:130–135. doi: 10.1016/s0960-9822(01)00022-7. [DOI] [PubMed] [Google Scholar]
- 18.Cameron LA, Footer MJ, van Oudenaarden A, Theriot JA. Motility of ActA protein-coated microspheres driven by actin polymerization. Proc. Natl Acad. Sci. USA. 1999;96:4908–4913. doi: 10.1073/pnas.96.9.4908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mahaffy RE, Shih CK, MacKintosh FC, Kas J. Scanning probe-based frequency-dependent microrheology of polymer gels and biological cells. Phys. Rev. Lett. 2000;85:880–883. doi: 10.1103/PhysRevLett.85.880. [DOI] [PubMed] [Google Scholar]
- 20.Alcaraz J, et al. Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophys. J. 2003;84:2071–2079. doi: 10.1016/S0006-3495(03)75014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stamenovic D, Suki B, Fabry B, Wang N, Fredberg JJ. Rheology of airway smooth muscle cells is associated with cytoskeletal contractile stress. J. Appl. Physiol. 2004;96:1600–1605. doi: 10.1152/japplphysiol.00595.2003. [DOI] [PubMed] [Google Scholar]
- 22.Fabry B, et al. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87 doi: 10.1103/PhysRevLett.87.148102. 148102. [DOI] [PubMed] [Google Scholar]
- 23.Marcy Y, Prost J, Carlier MF, Sykes C. Forces generated during actin-based propulsion: A direct measurement by micromanipulation. Proc. Natl Acad. Sci. USA. 2004;101:5992–5997. doi: 10.1073/pnas.0307704101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tseng Y, Wirtz D. Dendritic branching and homogenization of actin networks mediated by Arp2/3 complex. Phys. Rev. Lett. 2004;93 doi: 10.1103/PhysRevLett.93.258104. 258104. [DOI] [PubMed] [Google Scholar]
- 25.Nakamura F, Osborn E, Janmey PA, Stossel TP. Comparison of filamin A-induced cross-linking and Arp2/3 complex-mediated branching on the mechanics of actin filaments. J. Biol. Chem. 2002;277:9148–9154. doi: 10.1074/jbc.M111297200. [DOI] [PubMed] [Google Scholar]
- 26.Onck PR, Koeman T, van Dillen T, van der Giessen E. Alternative explanation of stiffening in cross-linked semiflexible networks. Phys. Rev. Lett. 2005;95 doi: 10.1103/PhysRevLett.95.178102. 178102. [DOI] [PubMed] [Google Scholar]
- 27.Coughlin MF, Stamenovic D. A tensegrity model of the cytoskeleton in spread and round cells. J. Biomech. Eng. Trans. Asme. 1998;120:770–777. doi: 10.1115/1.2834892. [DOI] [PubMed] [Google Scholar]
- 28.Gibson LJ, Ashby MF. Cellular Solids: Structure and Properties. Cambridge: Pergamon Press; 1988. [Google Scholar]
- 29.Brangwynne CP, et al. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pollard TD, Blanchoin L, Mullins RD. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu. Rev. Biophys. Biomol. Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.