Mechanistic Insight into the H₂O/D₂O Isotope Effect in the Proton Transport of the Influenza Virus M2 Protein

Abstract

The M2 proton channel is essential for the replication of the flu virus and is a known drug target. The functional mechanism of channel activation and conductance is key to both the basic biology of viral replication and the design of drugs that can withstand mutations. A quantitative model was previously developed for calculating the rate of proton transport through the M2 channel. The permeant proton was assumed to diffuse to the pore, obligatorily bind to the His37 tetrad, and then dissociate and be released to either side of the tetrad. Here we use the model to calculate the effect of a change in solvent from H₂O to D₂O on the rate of proton transport. The solvent substitution affects two parameters in the model: the proton diffusion constant and the pK_a for proton binding to the His37 tetrad. When the known effects on these two parameters are included, the deuterium isotope effect calculated from the model is in quantitatively agreement with experimental results. This strict test of the theoretical model provides strong support for the hypothesis that the permeant proton obligatorily binds to and then unbinds from the His37 tetrad. This putatively essential role of the His37 tetrad in the functional mechanism of the M2 channel makes it a promising target site for designing mutation-tolerant drugs.

The influenza virus relies on the proton conductance activity of the M2 protein for replication. This proton channel is the target of antiviral drugs amantadine and rimantadine. However, an M2 Ser31 to Asn mutation has conferred drug resistance to viruses in recent flu seasons (Nelson et al. 2009) and in the 2009 H1N1 pandemic (Gubareva et al. 2009). To understand the basic biology of virus replication and to help design drugs that can withstand mutations, many studies have focused on the functional mechanism of this tetrametic proton channel (Chizhmakov et al. 1996; Pinto et al. 1997; Sansom et al. 1997; Mould et al. 2000; Lin and Schroeder 2001; Chizhmakov 2003; Lear 2003; Venkataraman et al. 2005; Hu et al. 2006; Chen et al. 2007; Khurana et al. 2009; Yi et al. 2009; Zhou 2010; Acharya et al. 2010; Leiding et al. 2010; Hu et al. 2010; Sharma et al. 2010; Polishchuk et al. 2010; Pielak and Chou 2010; Zhou 2011; Peterson et al. 2011). The channel is activated by acidification of the viral exterior (Chizhmakov et al. 1996; Mould et al. 2000; Venkataraman et al. 2005; Leiding et al. 2010; Pielak and Chou 2010). It is generally accepted that the pH sensor is the His37 tetrad lining the channel pore (Fig. 1A) (Venkataraman et al. 2005); specifically, binding of the third proton, with a pK_a ~ 6, leads to channel activation (Hu et al. 2006). However, the mechanism of acid activation has been debated. Proposed models broadly belong to two types: those based on the idea that protonation of the His37 tetrad opens the pore to allow for the permeation of protons (Sansom et al. 1997; Chen et al. 2007), and those based on the idea that the permeant protons obligatorily bind to the His37 tetrad and are then relayed to the other side of the tetrad (Pinto et al. 1997).

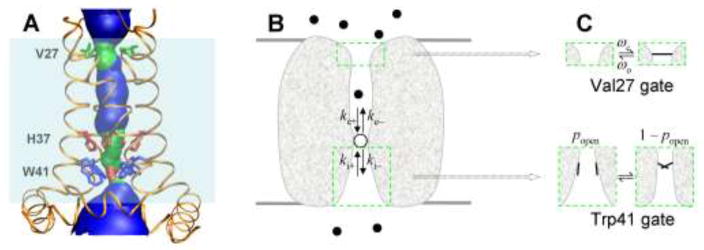
Fig. 1.

Structure and mechanistic model of the M2 proton channel. A Pore structure in the closed state (Sharma et al. 2010). Three key residues, Val27, His37, and Trp41, are indicated. Light shading indicates the lipid bilayer. B The model for calculating the rate of ion transport. Note that k_e+ and k_i+ are effective rate constants, involving the whole process of a proton starting in the exterior or interior bulk solution, diffusing into the dynamic channel and to the internal site, and finally binding to it. The green boxes indicate the Val27 and Trp41 gates. C Details of the Val27 and Trp41 gates.

The His37-relay type of model appears to be favored by observations such as the low rate of proton transport, ~100 protons per second per channel (Mould et al. 2000; Lin and Schroeder 2001; Leiding et al. 2010; Sharma et al. 2010; Pielak and Chou 2010; Peterson et al. 2011). In a number of studies (Lear 2003; Yi et al. 2009; Leiding et al. 2010; Polishchuk et al. 2010; Pielak and Chou 2010), the rate of proton transport has been calculated by modeling the obligatory binding to the His37 tetrad as rate processes. The rate constants in these calculations were treated as adjustable parameters.

We have developed a theoretical model (Zhou 2010) in which the rate constants are further calculated by treating the diffusional motion of the permeant ion and the gating motions of the channel protein (Fig. 1B, C). Let the diffusion-influenced rate constants for proton binding to the internal site from the viral exterior and interior be k_e+ and k_i+, respectively, and the rate constants for releasing a bound proton to the viral exterior and interior be k_e− and k_i−, respectively. The rate of proton transport per channel is

$$I=\frac{k_{\text{e}+}{k}_{\text{i}-}{[\text{H}]}_{\text{e}}-k_{\text{i}+}{k}_{\text{e}-}{[\text{H}]}_{\text{i}}}{k_{\text{e}-}+k_{\text{i}-}+k_{\text{e}+}{[\text{H}]}_{\text{e}}+k_{\text{i}+}{[\text{H}]}_{\text{i}}}$$ (1)

where [H]_e = 10^−pHe and [H]_i = 10^−pHi denote the proton concentrations in the viral exterior and interior, respectively. The theoretical basis of Eq. 1 has been rigorously established (Zhou and Szabo 2012). The ratios k_e−/k_e+ and k_i−/k_i+ are equilibrium constants fully determined by the pK_a for the binding of the third, i.e., permeant proton to the His37 tetrad. The individual rate constants are, however, influenced by several factors, e.g., for k_e+, diffusion to the channel, passage through the Val27 sphincter, diffusion through the central cavity, and binding to the His37 tetrad. For k_i−, these factors include release from the His37 tetrad, release from the water-filled cavity between the His37 tetrad and the Trp41 tetrad, passage by the Trp41 gate, and diffusion away from the channel. Of particular interest here, with k_e+ and k_i+ calculated from the specific geometry of the M2 channel and the detailed dynamics of the Trp41 primary gate and Val27 secondary gate (and k_e− and k_i− further determined from the His37 pK_a), the model reproduced well the experimental results for the dependencies of the M2 proton transport rate on voltage and pH (Zhou 2011).

H₂O/D₂O isotope effects have played important roles in testing mechanistic hypotheses on proton channels (Akeson and Deamer 1991; DeCoursey and Cherny 1997; Chernyshev et al. 2003). Mould et al. (2000) have measured the change in rate of proton transport by M2 channels when the solvent was changed from H₂O to D₂O. The purpose of the present study is to use the measured deuterium isotope effect to interrogate our theoretical model.

A change in solvent from H₂O to D₂O affects two parameters in our model. The first is the ion diffusion constant, D, which has a value of 10³ Ų/ns for proton (Roberts and Northey 1974) and a value 1.4-fold lower for deuteron (Lewis and Doody 1935; Roberts and Northey 1974). In addition, deuteron has higher affinity for titratable groups than proton, resulting in an upward shift in pK_a by ~0.4 pH units (Schowen 1977; Bundi and Wüthrich 1979; DeCoursey and Cherny 1997). We thus assume His37 pK_a value of 6 for third protonation (Hu et al. 2006) and 6.4 for third deuteronation.

In Fig. 2 we compare the calculated proton and deuteron current-voltage relations at both pL_e = 6.2 and pL_e = 6.4 (L = H or D; see figure legend) with the experimental results of Mould et al. (2000). Because our model predicts the rates of ion transport for a single channel whereas Mould et al. measured the total currents through many M2 channels in the membrane of a cell, we scaled up our calculation results by a factor of 10¹¹, which would be our estimate of the number of M2 channels per cell. Over the entire voltage range, our calculations accurately reproduce the experimental currents in both H₂O and D₂O and at both pL_e values.

Fig. 2.

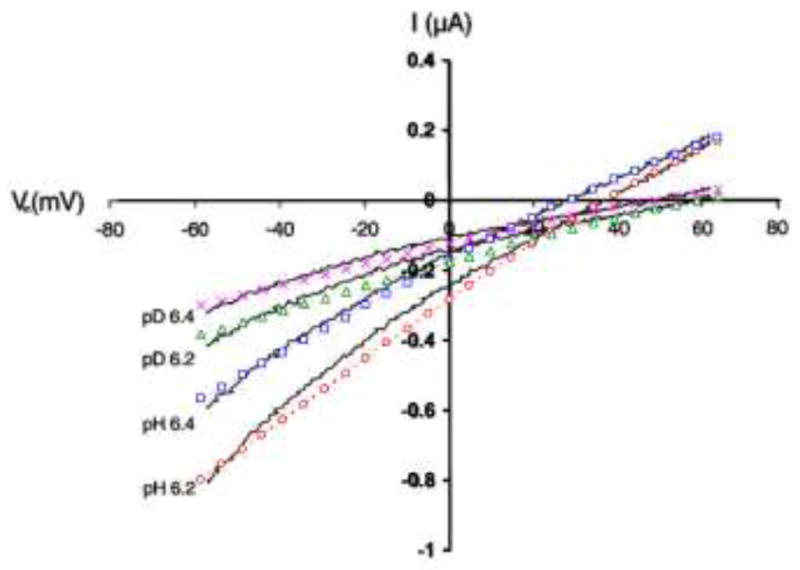
Comparison of calculated (symbols) and experimental (curves) current-voltage relations for M2 in H₂O and in D₂O. The experimental results are taken from Mould et al. (2000). pL (L = H or D) indicates proton or deuteron concentration in the viral exterior. In the experiments of Mould et al., pL_e was very precisely controlled, but there appeared to be some uncertainty on pL_i. We chose to deduce the pL_i values in the experiments by equating the experimental reversal potential to the proton or deuteron equilibrium potential calculated from pL_i – pL_e by the Nernst equation. The channel geometry and gating parameters were fixed in our previous study (Zhou 2011). In particular, the transition rates between open and closed Val27 gate were 0.1 ns⁻¹ for ω_o and 1 ns⁻¹ for ω_c, and the population fraction of the open Trp41 conformation was p_open = 5% at the pL_e studied here (i.e., ~ 6).

At transmembrane voltage V_m = −60 mV and either pL_e value, the calculated and measured currents in D₂O are both ~2-fold lower than their counterparts in H₂O. The decrease in D and the increase in the pK_a each account for roughly half of the difference between the currents in H₂O and D₂O. Therefore, neither the decrease in D nor the increase in pK_a alone can explain the observed isotope effect. The rate of ion transport, as given by Eq. 1, is determined by the binding and unbinding rate constants k_e± and k_i±. These rate constants are all proportional to D. The deuterium isotope effect on D thus results in a 1.4-fold decrease in both the binding and unbinding rate constants. In addition, the unbinding rate constants are affected by the pK_a of the internal binding site. A 0.4-unit increase in the pK_a corresponds to a 2.5-fold decrease in k_e− and k_i−. Compounding the effects on D and on pK_a, the change in solvent from H₂O to D₂O results in an overall decrease of 3.5-fold in the unbinding rate constants. Relative to H₂O, D₂O first slows down the diffusion of the permeant ion into the pore and hence the diffusion-controlled binding to the His37 tetrad, and then slows down its dissociation from the binding site and subsequent release into the bulk solution. The 1.4-fold decrease in k_e+ and k_i+ and 3.5-fold decrease in k_e− and k_i− together (Eq. 1) result in the net 2-fold isotope effect on the transport rate.

Importantly, our estimate of the number of M2 channels per cell, 10¹¹, is in reasonable agreement with the M2 expression level of Mould et al. They reported that 3 ng of M2 proteins was expressed per cell. That amount translates into 0.4 × 10¹¹ channels per cell (Lin and Schroeder 2001).

Our quantitative explanation of the deuterium isotope effect provides an important validation of the mechanistic assumptions underlying the model for calculating the ion transport rate. In particular, the isotope effect seems to directly support the hypothesis that the permeant proton obligatorily binds to and then unbinds from the His37 tetrad.

It is of interest to compare the deuterium isotope effect on the M2 proton transport rate with those observed on other proton channels. For gramicidin A, Akeson and Deamer (1991) and Chernyshev et al. (2003) observed ratios of proton currents and deuteron currents between 1.2 and 1.35, which could be explained by a decrease in D alone. In contrast, for the voltage-gated proton channel in rat alveolar epithelial cells, the deuteron conductance was ~2-fold lower than the proton conductance (DeCoursey and Cherny 1997), similar to the isotope effect observed on the M2 conductance and thus suggesting a similar explanation. Deuterium isotope effects on the channel opening and closing rates were also found: an H₂O to D₂O solvent substitution resulted in ~3-fold decrease in the opening rate and ≤1.5-fold decrease in the closing rate (DeCoursey and Cherny 1997). These results could be explained if proton unbinding from an internal site is rate-limiting for channel opening and proton binding is rate-limiting for channel closing.

In conclusion, the change in solvent from H₂O to D₂O affects two parameters in our theoretical model for calculating the ion transport rate: the proton diffusion constant and the pK_a for the binding of the permeant proton to the His37 tetrad. When the known effects on these two parameters are included, the deuterium isotope effect calculated from the model is in quantitatively agreement with experimental results on the M2 proton conductance. This strict test of the model provides strong support for the hypothesis that the permeant proton obligatorily binds to and then unbinds from the His37 tetrad. Given the putative essential role of the His37 tetrad in the functional mechanism of the M2 channel, drugs that target this site will likely have good chances of surviving mutations.