Robust Design of Biological Circuits: Evolutionary Systems Biology Approach

Abstract

Artificial gene circuits have been proposed to be embedded into microbial cells that function as switches, timers, oscillators, and the Boolean logic gates. Building more complex systems from these basic gene circuit components is one key advance for biologic circuit design and synthetic biology. However, the behavior of bioengineered gene circuits remains unstable and uncertain. In this study, a nonlinear stochastic system is proposed to model the biological systems with intrinsic parameter fluctuations and environmental molecular noise from the cellular context in the host cell. Based on evolutionary systems biology algorithm, the design parameters of target gene circuits can evolve to specific values in order to robustly track a desired biologic function in spite of intrinsic and environmental noise. The fitness function is selected to be inversely proportional to the tracking error so that the evolutionary biological circuit can achieve the optimal tracking mimicking the evolutionary process of a gene circuit. Finally, several design examples are given in silico with the Monte Carlo simulation to illustrate the design procedure and to confirm the robust performance of the proposed design method. The result shows that the designed gene circuits can robustly track desired behaviors with minimal errors even with nontrivial intrinsic and external noise.

1. Introduction

The cell is the functional unit of all living things either unicellular or multicellular [1]. A cell can sense many different signals from the internal or external and respond to the constantly changing environment via appropriate cellular processes. Also, cells can interact to each other by cell-cell communication and achieve specific physiological functions essential for life cooperatively [1]. However, there are many fundamental questions: how cellular phenomena arise from the interactions among genes and proteins, what features make the cell operate reliably in diverse conditions, and how cells are responsible for the reliable operation. To gain insight into the questions, one could construct and analyze the underlying mechanisms that constitute the web of interactions. This idea is useful to separate a complicated network into many simpler ones that resemble the modules of gene regulation. These modules, which act as simple switches or oscillators, can work on independently and may be combined eventually into a functional entity. While the concept of synthetic gene networks is still in its infancy, the long-term goal of this work is to design and manufacture the biological systems with predictable functions [2, 3].

In recent years, the use of existing genetic engineering technologies together with concepts in circuit design has developed a new strategy to design gene networks [3–6]. In this approach, the web of interactions among gene and protein is then synonymous with genetic circuit which contains standard and well-characterized components such as promoters, ribosome binding sites, and regulatory sequences. These biological parts can be combined into devices with different configurations, which can be further integrated into a functional whole [3, 7]. In order to build genetic circuits with the specified purpose, one may need the design process that involves describing the specification with respect to the desired goal, converting the technical details into block diagrams at the abstract stage, evaluating the feasibility via mathematical model and computational simulation, and repeating the earlier stage until the parts in the combination and configuration could exhibit suitable performance. For example, Terzer et al. [8] present the construction of a genetic half adder that comprises two main biological gates, that is, AND gate and XOR gate. Two biological stimuli, light signal and chemical signal, are sensed by respective device. This composition allows the half adder to be in one of three possible states, RFP synthesis, GFP synthesis, or the absence of both reporter proteins. In the case when one of two stimuli signals is present, the XOR gate is activated and produces RFP protein. When two stimuli signals are present, the AND is activated and leads to the synthesis of GFP protein. For lack of both stimuli signals, the state is maintained and none of reporter protein is synthesized. This study includes mathematical and computational analysis in determining the combination of parts among different configurations to obtain the desired function. A similar design process has been used in other applications such as switch [9–11], oscillator [12], timer [13], counter [14], gene regulation [15], and pattern formation [16].

Although synthetic biologists have accomplished a great deal in a short time, major obstacles remain to be overcome before the practical application of the technology can be realized. One important problem is that the behavior of bioengineered systems remains noisy and uncertain. Synthetic gene circuits also tend to mutate rapidly and become nonfunctional [17–20]. Generally, the variability in biological circuits might be classified into two main categories: intrinsic fluctuations, which are associated with fluctuations in transcription and translation, random changes in DNA sequence and variations in molecular concentrations, and extrinsic disturbances, which correspond to interactions with extra cellular environment [2]. If the intrinsic fluctuations and extrinsic disturbances are all considered in mathematical model and computational simulation to mimic the realistic environment in the host cell, the biological circuits will be more robust towards the desired goal under these uncertainty conditions. Therefore, in this work, a nonlinear stochastic system with state-dependent noise is introduced to model the biological systems in vivo with intrinsic perturbations and extrinsic noise in the cellular context. In fact, a number of studies recently have developed methodologies for nonlinear stochastic systems to assist the evaluation of parts in combinations and configurations. Sensitivity analysis [21] is a common way used in genetic circuit design to understand the effect of elements on overall system performance. As compared with the views available to the conventional design strategies for assembling devices by intuition alone, the sensitivity information may offer a possible guideline concerning the selection of the optimal configurations to satisfy the design consideration. Such analysis tool can help the choice of an appropriate element combination for biological circuit that functions well in noisy and uncertain environment. Recently, some robust synthetic gene network design methods have been proposed to select certain kinetic parameters of a gene circuit so that the effect of random parameter fluctuations and environmental noise can be efficiently attenuated by game theory [22] or the synthetic gene circuit can track a desired reference to satisfy design specifications [23].

As yet, however, applying the analysis of nonlinear stochastic system to evaluate the flexibility in combination of biological components is not straightforward in general. In light of natural selection on traits best-suited for environmental change being an important mechanism in evolution [24], the question arises whether a similar strategy can be adapted for genetic circuits design. Inspired by biological evolution such as mutation, recombination, and selection, the evolutionary algorithm is a population-based methodology to solve optimization problems [25]. Recently, evolutionary systems biology focuses on links between evolution and function, that is, evolutionary interplay between the genotype and phenotype, to develop methods to reconstruct and compare transcriptional regulatory network [26–29]. Here, an evolutionary systems biology algorithm is employed in tuning the kinetic parameters with respect to component characteristics to maximize the fitness under the parameter variations and molecular noise in the cellular context. In order to mimic the naturally occurring biological systems in the evolutionary process, the fitness function is selected to be inverse proportion to the tracking error so that evolutionary kinetic parameters of biological circuit can achieve the optimal tracking via the maximization of fitness with all speed to mimic the evolution process of a gene circuit. If the adaptations of kinetic parameters of biological circuit are reflected by the proposed evolutionary systems biology algorithm to achieve the optimal fitness, the evolutionary gene circuit will track the desired biologic function in spite of intrinsic parameter fluctuations and extrinsic noise and will behave more robustly inside a living cell.

In this study, the intrinsic parameter fluctuations and external noise are modeled in the stochastic dynamic systems of biologic circuits to mimic the stochastic behaviors of biological system in the host cells. Then, based on the evolutionary systems biology algorithm, the kinetic parameters of biologic circuits can be self-adaptively tuned to optimally track the desired biologic function to achieve the optimal fitness to mimic the natural selection of naturally occurring gene circuits in evolution. Because the optimal tracking of evolutionary gene circuit to a desired logical function is achieved under intrinsic parameter fluctuations and external noise, the designed gene circuit will be more robust when embedded in the host cells with the similar stochastic environments. The remainder of this article is organized as follows. In the next section, we provide a brief description of the biologic model under intrinsic parameter fluctuation and extrinsic noise. Then an evolutionary systems biology design algorithm and several design examples with computer simulation will be presented. Finally, a conclusion is given to summarize the results in the last section.

2. Stochastic Model for Biological System In Vivo under Intrinsic Parameter Fluctuations and Extrinsic Noise

The dynamic behaviors of biological circuits have been modeled by nonlinear differential equations. These nonlinear differential equations contain four types of dynamics to describe constitutive transcription, enzymatic transformation, regulated transcription, and translation [30]. A simple biological module as shown in Figure 1 is given to illustrate the nonlinear dynamic equation of these biochemical processes [8]. Suppose this module generates an output signal only when it gets biochemical signals from both of its inputs. Based on the requirement, the substrate S is designed to bind an enzyme E essential for the reaction, which can be triggered by the input signals, say u₁ and u₂, cooperatively. In the process, the two proteins can combine together to form a complex C which then breaks down into the production P releasing E, that is, the conversion of substrate S into production P is catalyzed by an enzyme E. Here the presence of production P alone leads to the synthesis of the output signal, the reporter protein GFP. The following is a more detailed system description about dynamic interaction equations for biological module in synthetic gene circuit.

Figure 1.

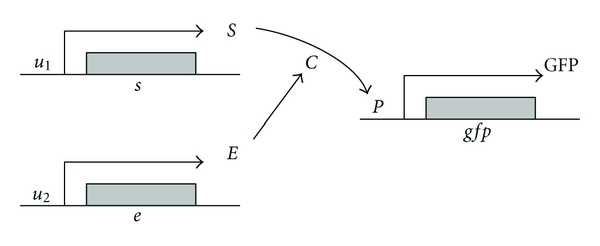
An example of a biological module. The substrate S is designed to bind an enzyme E essential for the reaction, which can be triggered by the input signals, say u₁ and u₂, cooperatively. In the biologic process, the two proteins can combine together to form a complex C which then breaks down into the production P with E being released. The presence of production P alone leads to the synthesis of the output signal, the reporter protein GFP.

2.1. Constitutive Transcription

The constitutive transcription is the process of creating message RNA from the stimulation of biochemical signal. In this case, transcription of gene s occurs only when the input signal u₁ is present. This is similar to gene e if only the input signal u₂ appears. Both of these reactions result in the accumulation of mRNA molecular with respect to each gene, which can be balanced by the degradation process. Thus the dynamics of mRNA governed by the production and degradation as the equations below:

$$\begin{array}{c}\frac{d{x}_{mS}}{dt}=k_1{u}_1-{\lambda }_1{x}_{mS},\\ \frac{d{x}_{mE}}{dt}=k_2{u}_2-{\lambda }_2{x}_{mE},\end{array}$$ (1)

where x_mS is the concentration of mRNA transcribed from u₁ and x_mE is the concentration of mRNA transcribed from u₂. The input signals, say u₁ and u₂, represent the number of RNA polymerases per unit of time to transcribe the gene s and gene e, respectively. The parameters k₁ and k₂ stand for the reaction rate constant; the parameters λ₁ and λ₂ are the degradation constant for mRNA.

2.2. Enzymatic Transformation

Followed by the constitutive transcription of gene s and gene e, the mRNA molecules can be further translated into substrate S and enzyme E. The process of enzymatic transformation is for the reaction catalyzed by an enzyme, which helps convert substrates into productions. Here we suppose that the substrate S  combined with E can form the complex C which then dissociates into enzyme E and production P. The reverse reaction for complex C synthesis is also considered here. Thus the change in concentration of substrate S, enzyme E, complex C, and production P with respect to time is given by

$$\begin{array}{cc}\hfill \frac{d{x}_S}{dt}& =k_3{x}_{mS}-k_5{x}_S{x}_E+k_6{x}_C-{\lambda }_3{x}_S,\hfill \\ \hfill \frac{d{x}_E}{dt}& =k_4{x}_{mE}-k_5{x}_S{x}_E+\left(k_6+k_7\right)x_C-{\lambda }_4{x}_E,\hfill \\ \hfill \frac{d{x}_C}{dt}& =k_5{x}_S{x}_E-\left(k_6+k_7\right)x_C-{\lambda }_5{x}_C,\hfill \\ \hfill \frac{d{x}_P}{dt}& =k_7{x}_C-{\lambda }_6{x}_P,\hfill \end{array}$$ (2)

where x_S, x_E, x_C, and x_P denote the concentration of substrate S, enzyme E, complex C, and production P, respectively. The parameters k₃ and k₄ stand for the kinetic constants of translation for substrate S and enzyme E, respectively. The parameter k₅ is the forward reaction rate constant for complex C, and k₆ is the backward one. The production formation rate constant is k₇. The parameters λ₃, λ₄, λ₅ and λ₆ are the degradation constants for substrate S, enzyme E, complex C and production P, respectively.

2.3. Regulated Transcription

The process related to the transcriptional regulation is to create message RNA resulted from the control of transcription factor. Transcription factor can bind to a specific DNA site to increase the rate of transcription when an activator, or to reduce the rate when a repressor. In this example, the production P is made to activate the green fluorescent protein gene, rendering the accumulation of mRNA molecules. It means that the transcription of the green fluorescent protein gene is regulated by an activator, that is, the production P. Then the mRNA dynamics for the GFP gene is described as the equation below:

$$\begin{array}{cc}\hfill \frac{d{x}_{m\text{GFP}}}{dt}& =P_{m\text{GFP}}+\frac{k_8{\left(x_P/K\right)}^n}{1+{\left(x_P/K\right)}^n}-{\lambda }_7{x}_{m\text{GFP}},\hfill \end{array}$$ (3)

where x_mGFP denotes the concentration of mRNA for green fluorescent protein gene. The parameters k₈ and λ₇ are the kinetic constant of transcription and degradation constant, respectively. P_mGFP represents the constant of background level. Cooperativeity is denoted by the Hill coefficient n and K is the Hill constant.

2.4. Translation

Translation corresponds to the process for coding protein from message RNA. Here the mRNA codon with respect to green fluorescent protein gene is translated into the output signal, the reporter protein GFP. It leads to the accumulation of reporter protein, which can be balanced by the degradation process. Then the dynamical evolution of the output signal is affected by synthesis and degradation. Consequently, the term of the GFP rate equation will be as follows:

$$\begin{array}{cc}\hfill \frac{d{x}_{\text{GFP}}}{dt}& =k_9{x}_{m\text{GFP}}-{\lambda }_8{x}_{\text{GFP}},\hfill \end{array}$$ (4)

where x_GFP represents the concentration of the reporter protein. The parameters k₉ and λ₈ are the kinetic constant of translation and degradation constant for GFP, respectively.

From the nonlinear differential equations as mentioned above, it can be known that the dynamics of a biological module depends on some factors, such as the kinetic constants, degradation constant, and background level. However, these factors or parameters are uncertain inherently and the biological circuit also suffers from environmental noise in the context of host cell. In this situation, the dynamic model of biological circuit in vivo should be modified as follows:

$$\begin{array}{cc}\hfill \frac{d{x}_{mS}}{dt}& =\left(k_1+\mathrm{\Delta }{k}_1{n}_1\right)u_1-\left({\lambda }_1+\mathrm{\Delta }{\lambda }_1{n}_4\right)x_{mS}+v_1,\hfill \\ \hfill \frac{d{x}_{mE}}{dt}& =\left(k_2+\mathrm{\Delta }{k}_2{n}_1\right)u_2-\left({\lambda }_2+\mathrm{\Delta }{\lambda }_2{n}_4\right)x_{mE}+v_2,\hfill \\ \hfill \frac{d{x}_S}{dt}& =\left(k_3+\mathrm{\Delta }{k}_3{n}_2\right)x_{mS}-\left(k_5+\mathrm{\Delta }{k}_5{n}_3\right)x_S{x}_E\hfill \\ \hfill & \hspace{1em}+\left(k_6+\mathrm{\Delta }{k}_6{n}_3\right)x_C-\left({\lambda }_3+\mathrm{\Delta }{\lambda }_3{n}_4\right)x_S+v_3,\hfill \\ \hfill \frac{d{x}_E}{dt}& =\left(k_4+\mathrm{\Delta }{k}_4{n}_2\right)x_{mE}-\left(k_5+\mathrm{\Delta }{k}_5{n}_3\right)x_S{x}_E\hfill \\ \hfill & \hspace{1em}+\left(k_6+\mathrm{\Delta }{k}_6{n}_3+k_7+\mathrm{\Delta }{k}_7{n}_3\right)x_C\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_4+\mathrm{\Delta }{\lambda }_4{n}_4\right)x_E+v_4,\hfill \\ \hfill \frac{d{x}_C}{dt}& =(k_5+\mathrm{\Delta }{k}_5{n}_3)x_S{x}_E-(k_6+\mathrm{\Delta }{k}_6{n}_3+k_7+\mathrm{\Delta }{k}_7{n}_3)x_C\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_5+\mathrm{\Delta }{\lambda }_5{n}_4\right)x_C+v_5,\hfill \\ \hfill \frac{d{x}_P}{dt}& =\left(k_7+\mathrm{\Delta }{k}_7{n}_3\right)x_C-\left({\lambda }_6+\mathrm{\Delta }{\lambda }_6{n}_4\right)x_P+v_6,\hfill \\ \hfill \frac{d{x}_{m\text{GFP}}}{dt}& =P_{m\text{GFP}}+\frac{\left(k_8+\mathrm{\Delta }{k}_8{n}_1\right)\mathrm{\hspace{0.17em}\hspace{0.17em}}{\left(x_P/K\right)}^n}{1+{\left(x_P/K\right)}^n}\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_7+\mathrm{\Delta }{\lambda }_7{n}_4\right)x_{m\text{GFP}}+v_7,\hfill \\ \hfill \frac{d{x}_{\text{GFP}}}{dt}& =\left(k_9+\mathrm{\Delta }{k}_9{n}_2\right)x_{m\text{GFP}}-\left({\lambda }_8+\mathrm{\Delta }{\lambda }_8{n}_4\right)x_{\text{GFP}}+v_8,\hfill \end{array}$$ (5)

where Δk_i, Δλ_i denote the amplitudes of parameter fluctuations around kinetic constants and degradation constants due to genetic variations, respectively. n₁, n₂, n₃, and n₄ are random white noise with zero mean and unit variance, which denote the independent random fluctuation sources in transcription, translation, reaction, and degradation process, respectively. The variances of kinetic parameter perturbations are given as var(Δk_in_j) = (Δk_i)², var(Δλ_in_j) = (Δλ_i)²; that is, Δk_i and Δλ_i represent the standard deviations of the corresponding stochastic parameter fluctuations. v_i denotes the corresponding external stochastic noise with variance σ_i². Note that the perturbation of background level P_mGFP is merged into v₇. Then depending on the stochastic system in (5), a more general stochastic model for any synthetic biological gene circuit with intrinsic parameter fluctuations and extrinsic noise in vivo can be represented as a set of nonlinear stochastic differential equation with state-dependent noise in the form

$$\begin{array}{c}\dot{x}=f\left(x,k,u\right)+{\displaystyle \sum }_{i=1}^m{h}_i\left(x,\mathrm{\Delta }k,\mathrm{\Delta }\lambda \right)n_i+v,\\ y=cx,\end{array}$$ (6)

where f is a nonlinear nominal interaction vector function concerning the state vector x = [x₁,…, x_n]^T for concentrations of n reactant species, kinetic constants k, and input signals u. n_i are the independent intracellular random fluctuation sources. h_i are fluctuation functions due to random fluctuation source n_i. v = [v₁,…, v_n]^T represents the vector of external disturbances. y stands for the output vector. In Figure 1, y = x_GFP and c = [0,0, 0,0, 0,0, 0,1].

In real biological system, the gene circuit in (6) could evolve adaptively with kinetic parameters in k by natural selection through mutation and genetic variation so that y(t) can robustly achieve some desired behavior in spite of intracellular molecular noise and external disturbance. In this study, we will mimic the evolutionary biological system to adapt the kinetic parameters of synthetic gene network in (6) through an evolutionary systems biology algorithm under a fitness function so that the synthetic gene circuit can achieve a desired behavior in spite of intracellular noise and external disturbance specified beforehand to be tolerated in vivo.

3. Robust Design of Biological Circuit via Evolutionary Systems Biology Algorithm

Once a model describing the biological circuit system of interest has been constructed, the next step for synthetic biologists is to select adequate parameters k_i, i = 1,…, l, to achieve some design specifications. For example, in the design of biological logic circuit [8], transcriptional rate constants k₁, k₂, and k₈ in (5), which depend on the affinity of binding site in the promoter region of the corresponding target gene, should be selected to achieve the robust synthetic biological circuit design to optimally track a desired logic function under intrinsic parameter fluctuations and extrinsic noise in vivo. Based on the analysis above, the design specifications of robust synthetic biologic circuits for tracking a desired logic circuit are given as follows.

1. Choose a desired logic circuit to be tracked by the synthetic biologic circuit.

2. Give the standard deviations Δk_i, Δλ_i in (6) to represent the stochastic parameter fluctuation to be tolerated and the variances σ_i² to represent the external stochastic disturbances v_i to be attenuated by the synthetic biologic circuit in host cells.

3. Give the feasible ranges of design parameters k_i according to the real design condition in vivo:

$$\mathrm{\hspace{0.17em}\hspace{0.17em}}{k}_i\in \left[k_i^L,k_i^U\right],\hspace{1em}i=\mathrm{1,2},3,\dots ,l.$$ (7)

Given the above design specifications, our design objective is to tune the design parameters k_i ∈ [k_i^L, k_i^U], i = 1,2, 3,…, l, to achieve the optimal tracking under intrinsic parametric fluctuations and extrinsic noise as shown in Figure 2. Suppose the tracking error is defined as

Figure 2.

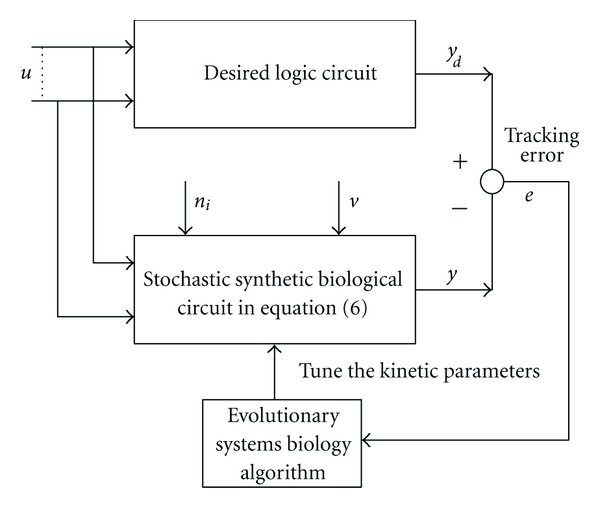
The block diagram of the proposed optimal tracking scheme for synthetic biological circuit design via an evolutionary systems biology algorithm.

$$\begin{array}{cc}\hfill e& =y_d-y,\hfill \end{array}$$ (8)

where y_d denotes the output of the desired logic circuit. Then, our design purpose is to tune design parameter k_i by evolutionary systems biology algorithm so that the dynamic gene circuit in (6) can achieve the following optimal tracking:

$$\underset{k_i,i=1,\dots ,l}{\min }E\underset{0}{\overset{T_p}{{\displaystyle \int }}}{e}^T\hspace{0.17em}edt,$$ (9)

where E denotes the expectation, T_p denotes the present time, and e^T denotes the transpose of e. If the above mean square tracking error can be minimized under the design specifications (i)–(iii), the robust synthetic gene circuit design can be achieved under the stochastic parameter fluctuation and external noise in vivo so that the stochastic biologic circuit can track a desired logic circuit more reliably in the host cells.

In general, it is not easy to solve the constrained optimal tracking design problem in (9) for nonlinear stochastic gene network in (6) by the conventional optimal method directly. Here, to mimic the parametric tuning of biological circuit to achieve a desired function via natural selection in evolution, an artificial evolutionary systems biology algorithm is employed to tune the design parameter k_i to achieve the optimal tracking in (9) but with a faster speed than natural selection. Evolutionary algorithms [25, 31] are a result of an effort to model adaptation phenomena in natural and artificial systems. These evolutionary algorithms will be modified to tune the kinetic parameters of nonlinear stochastic synthetic gene network in (6), that is, the so-called evolutionary systems biology algorithm, to fast evolve to a desired output behavior via a fitness function. In the nonlinear stochastic system of biological circuit in (6), the state vector x is considered as phenotype and the kinetic parameter vector k = (k₁,…, k_l) is considered as genotype. In the evolutionary systems biology algorithm, the kinetic parameter vector k is called chromosome. Let us denote the mean square error in (9) as

$$\begin{array}{cc}\hfill J\left(k\right)& =E\underset{0}{\overset{T_p}{{\displaystyle \int }}}{e}^T\hspace{0.17em}edt,\hfill \end{array}$$ (10)

where the chromosome k_i ∈ [k_i^L, k_i^U], for i = 1,…, l, the feasible parameter space or feasible genotype space. Define the fitness function F(k) as

$$\begin{array}{cc}\hfill F\left(k\right)& =\frac{1}{J\left(k\right)},\hfill \end{array}$$ (11)

that is, a small mean square error means a large fitness and vice versa. If we adapt a parameter vector (chromosome) k_i ∈ [k_i^L, k_i^U] by evolutionary systems biology algorithm to minimize J(k) in (10) or (11), then we achieve the maximization of fitness function in (11) for synthetic gene circuit (6) to meet the natural selection in evolution. Therefore, the robust biological circuit design in (6) with a desired output behavior y(t) is equivalent to solving the following fitness maximization problem by the evolutionary systems biology method:

$$\begin{array}{cc}\hfill F\left(k^{\ast }\right)& =\underset{k}{\max }\hspace{0.17em}F\left(k\right).\hfill \end{array}$$ (12)

The evolutionary systems biology algorithm is employed to solve the above fitness maximization problem via the genetic operators such as selection, crossover, and mutation to mimic the nature selection in the evolutionary process to tune the kinetic parameter vector k of synthetic gene circuit to solve the optimization problem in (12) to achieve robust optimal tracking of the desired behavior. A simple evolutionary systems biology algorithm is proposed as follows [25, 31].

3.1. Initialization

Initialize a population of candidate solutions to the problem, that is, randomly generate a population of candidate chromosomes. In the real coding representation, each chromosome with the same length as the vector of decision variables is encoded as a vector of floating-point numbers. The vector k = (k₁,…, k_l) is as a chromosome to represent a solution of optimization problem for the desired behavior tracking of nonlinear synthetic gene circuit. Initialization procedure produces M chromosomes k¹,…, kⁱ,…, k^M, where M denotes the population size.

3.2. Fitness

Fitness is a measure to evaluate the suitability of chromosome. By the principle of survival of the fittest, a chromosome with higher fitness value has a higher probability of contributing one or more offspring in the next generation. By employing evolutionary algorithms to our fitness optimization problem, we must relate the M chromosomes with their fitness functions F(k¹),…, F(k^M). In our synthetic gene circuit design problem, an optimal tracking circuit design is to select a maximum fitness function F(k*) among these fitness functions F(k¹),…, F(kⁱ)…, F(k^M).

3.3. Reproduction

Reproduction is a basic operator of evolutionary algorithms to generate more offspring to increase the possibility to search for the optimal fitness. It is operated on the basis of the survival of the fitness. In each generation, the chromosomes of the current population are reproduced or copied in the next generation according to their reproduction probability p_ri, which are defined as

$$\begin{array}{cc}\hfill p_{r_i}& =\frac{F\left(k^i\right)}{{\sum }_{i=1}^{M}F\left(k^i\right)},\hspace{1em}i=1,\dots ,M,\hfill \end{array}$$ (13)

where M is the population size. It is shown that the higher fitness value, the higher reproduction probability. Once the chromosomes are reproduced or copied in the next generation, the other chromosomes stay in a mating pool as shown in Figure 3 and await the action of the other two genetic operators.

Figure 3.

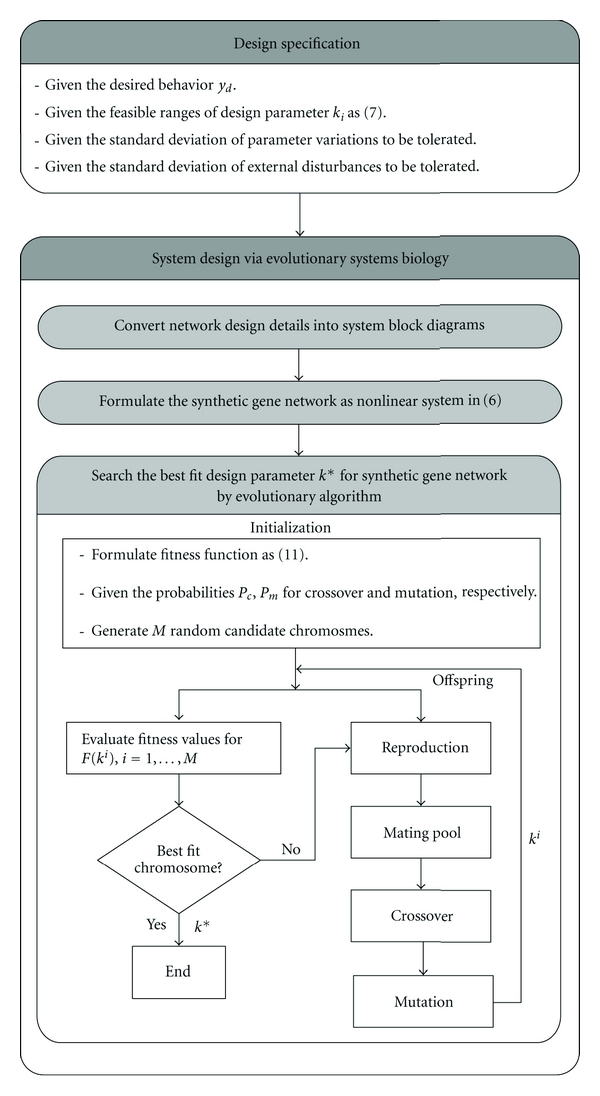
The flowchart of evolutionary systems biology algorithm for solving the best fit k* from the maximization problem of fitness function in (12).

3.4. Crossover

Reproduction directs the search of evolutionary algorithms toward the best individuals. Crossover performs to exchange the information of any chromosomes via probabilistic decision in the mating pool and provides a mechanism to mix and match the desirable qualities through a random process. For two chromosomes kⁱ and k^j randomly selected according to the crossover probability p_c, the resulting offspring k′ is

$$\begin{array}{cc}\hfill k^{\prime }& =r\left(k^i+k^j\right),\hfill \end{array}$$ (14)

where r ∈ (0,1).

3.5. Mutation

Reproduction and crossover provide the most search power for evolutionary algorithms. However, the mating pool tends to become more and more homogeneous as one better solution begins to dominate after several generations and leads to premature convergence. In the situation, the third operator, mutation, is introduced into the evolutionary algorithm with appropriate probability p_m. For a given chromosome k = (k₁, k₂,…, k_n,…, k_l), if the element k_n is randomly selected for mutation, the resulting offspring is k′ = (k₁, k₂,…, k_n′,…, k_l). The new gene k_n′ is

$$\begin{array}{cc}\hfill k_n^{\prime }& =k_n+{\sigma }_n{m}_n,\hfill \end{array}$$ (15)

where σ_n is standard derivation and m_n is a random variable with standard normal distribution function. Mutation is an insurance strategy to ensure that all points in the search space can be ultimately reached. Note that mutation should be used sparingly because it is inherently a random search operator. The evolutionary algorithm could become more similar to random search if the mutation probability is high.

Since the proposed evolutionary systems biology design method not only achieves the best fitness for optimal desired behavior tracking but also robustly tolerates random kinetic parameter fluctuation and external disturbance simultaneously, it will play an important role for synthetic gene network from the evolutionary systems biology perspective. The evolutionary systems biology approach of how to select a parameter vector (or chromosome) k to solve the fitness maximization problem in (12) for the optimal behavior tracking is summarized as follows.

Step 1 —

Give the design specifications (i)–(iii).

Step 2 —

Model the synthetic gene network as the nonlinear stochastic system in (6).

Step 3 —

Specify the probabilities p_c and p_m for crossover and mutation, respectively, and the population size M.

Step 4 —

Generate randomly a population of candidate chromosomes.

Step 5 —

Evaluate the fitness F(kⁱ) for each candidate solution (chromosome) kⁱ in the population to find the best fit k* to achieve the best fitness F(k*).

Step 6 —

If the search goal is achieved, or an allowable generation is attained, then stop. Otherwise, continue.

Step 7 —

Replace the current population with a new population by applying selection, crossover, and mutation operations on the current population. Go to Step 5.

Remark 3.1 —

(1) In addition, in the evolutionary systems biology algorithm, the elitist strategy can be incorporated to enhance the convergence of evolutionary systems biology algorithm. This strategy copies the best chromosomes from the old population into the next population to prevent losing the best solutions in the succeeding iterations. It has been shown that the elitist strategy can improve the performance of evolutionary systems biology algorithm.

(2) The proposed evolutionary systems biology algorithms is a powerful search algorithm for parameter selection in the synthetic gene network design procedure based on natural genetics and are inherently parallel, because they simultaneously evaluate many points in the parameter space (genotype space) for the best fitness F(k*) to achieve the robust synthetic gene network deign with a desired behavior in vivo.

4. Design Example In Silico

After the development of design procedure for the robust gene circuits in the above section, two examples will be given in silico to illustrate the design procedure and to confirm the performance of synthetic gene circuit by the proposed evolutionary systems biology design method.

4.1. Robust Biological AND Gate Design

Consider the biological AND gate as shown in Figure 4 [8]. The biological AND gate generates an output signal only when it gets biochemical signals from both of its inputs. In the process, the input signal u₁ leads to the transcription of T7 polymerase gene, containing an early stop codon in the coding sequences that block translation. The input signal u₂ leads to the synthesis of a suppressor tRNA, which prevents the premature termination and enables the translation of polymerase. When both of these inputs are present, the functional T7 RNA polymerase leads to the synthesis of the output signal, the reporter protein GFP. The following is a description about dynamic differential equations of biological AND gate in Figure 4 [8]:

$$\begin{array}{cc}\hfill \frac{d{x}_{m\text{T}7\text{Pol}}}{dt}& =k_1{u}_1-{\lambda }_1{x}_{m\text{T}7\text{Pol}},\hfill \\ \hfill \frac{d{x}_{m\text{tRNA}}}{dt}& =k_2{u}_2-{\lambda }_2{x}_{m\text{tRNA}},\hfill \\ \hfill \frac{d{x}_{{\text{T}7\text{Pol}}^{\ast }}}{dt}& =k_3{x}_{m\text{T}7\text{Pol}}-{\lambda }_3{x}_{{\text{T}7\text{Pol}}^{\ast }},\hfill \\ \hfill \frac{d{x}_{\text{tRNA}}}{dt}& =k_4{x}_{m\text{tRNA}}-{\lambda }_4{x}_{\text{tRNA}},\hfill \\ \hfill \frac{d{x}_{\text{T}7\text{Pol}}}{dt}& =k_5{x}_{m\text{T}7\text{Pol}}{x}_{\text{tRNA}}-{\lambda }_5{x}_{\text{T}7\text{Pol}},\hfill \\ \hfill \frac{d{x}_{m\text{GFP}}}{dt}& =P_{m\text{GFP}}+\frac{k_6{\left(x_{\text{T}7\text{Pol}}/K\right)}^n}{1+{\left(x_{\text{T}7\text{Pol}}/K\right)}^n}-{\lambda }_6{x}_{m\text{GFP}},\hfill \\ \hfill \frac{d{x}_{\text{GFP}}}{dt}& =k_7{x}_{m\text{GFP}}-{\lambda }_7{x}_{\text{GFP}},\hfill \end{array}$$ (16)

where x_mT7Pol, x_mtRNA, and x_mGFP are the concentrations of mRNA transcribed from genes T7Pol, tRNA, and gfp, respectively; concentrations of the corresponding proteins are represented by x_T7Pol*, x_tRNA, and x_GFP, respectively. k₁, k₂, and k₆ are the transcription rate. λ₁, λ₂, and λ₆ are the respective degradation rate of mRNA for T7Pol, tRNA, and gfp. Parameters k₃, k₄, and k₇ are the translation rates of the proteins from the mRNAs, and λ₃, λ₄, and λ₇ represent the degradation rate of protein nonfunctional T7 RNA polymerase, tRNA and GFP, respectively. x_T7Pol is the concentration of functional T7 RNA polymerase. k₅ is the reaction rate constant and λ₅ stands for the corresponding degradation constant. n is the Hill coefficient and K is the Hill constant. P_mGFP is the basal level.

Figure 4.

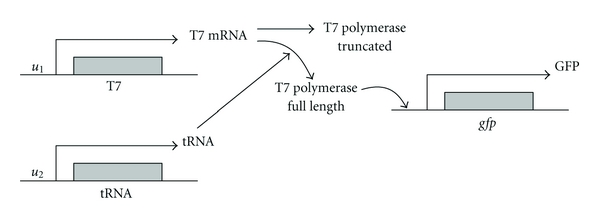
Synthetic gene AND gate. The input signal u₁ leads to the transcription of T7 polymerase gene, containing an early stop codon in the coding sequences that block translation. The input signal u₂ leads to the synthesis of a suppressor tRNA, which prevents the premature termination and enables the translation of polymerase. When both of these inputs are present, the functional T7 RNA polymerase leads to the synthesis of the output signal, the reporter protein GFP.

From the nonlinear differential equations as mentioned above, it can be seen that the dynamics of the biological AND gate depends on some biochemical factors, such as the kinetic constant, degradation constant, and basal level. However, these factors or parameters are uncertain inherently and the biological circuit also suffers from environmental noise. In this situation, the dynamic model of synthetic biological circuit in vivo should be modified as follows:

$$\begin{array}{cc}\hfill \frac{d{x}_{m\text{T}7\text{Po}}}{dt}& =\left(k_1+\mathrm{\Delta }{k}_1{n}_1\right)u_1-\left({\lambda }_1+\mathrm{\Delta }{\lambda }_1{n}_4\right)x_{m\text{T}7\text{Pol}}+v_1,\hfill \\ \hfill \frac{d{x}_{m\text{tRNA}}}{dt}& =\left(k_2+\mathrm{\Delta }{k}_2{n}_1\right)u_2-\left({\lambda }_2+\mathrm{\Delta }{\lambda }_2{n}_4\right)x_{m\text{tRNA}}+v_2,\hfill \\ \hfill \frac{d{x}_{{\text{T}7\text{Pol}}^{\ast }}}{dt}& =\left(k_3+\mathrm{\Delta }{k}_3{n}_2\right)x_{m\text{T}7\text{Pol}}\hfill \\ \hfill & -\left({\lambda }_3+\mathrm{\Delta }{\lambda }_3{n}_4\right)x_{{\text{T}7\text{Pol}}^{\ast }}+v_3,\hfill \\ \hfill \frac{d{x}_{\text{tRNA}}}{dt}& =\left(k_4+\mathrm{\Delta }{k}_4{n}_2\right)x_{m\text{tRNA}}-\left({\lambda }_4+\mathrm{\Delta }{\lambda }_4{n}_4\right)x_{\text{tRNA}}+v_4,\hfill \\ \hfill \frac{d{x}_{\text{T}7\text{Pol}}}{dt}& =\left(k_5+\mathrm{\Delta }{k}_5{n}_3\right)x_{m\text{T}7\text{Pol}}{x}_{\text{tRNA}}\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_5+\mathrm{\Delta }{\lambda }_5{n}_4\right)x_{\text{T}7\text{Pol}}+v_5,\hfill \\ \hfill \frac{d{x}_{m\text{GFP}}}{dt}& =P_{m\text{GFP}}+\frac{\left(k_6+\mathrm{\Delta }{k}_6{n}_1\right){\left(x_{\text{T}7\text{Pol}}/K\right)}^n}{1+{\left(x_{\text{T}7\text{Pol}}/K\right)}^n}\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_6+\mathrm{\Delta }{\lambda }_6{n}_4\right)x_{m\text{GFP}}+v_6,\hfill \\ \hfill \frac{d{x}_{\text{GFP}}}{dt}& =\left(k_7+\mathrm{\Delta }{k}_7{n}_2\right)x_{m\text{GFP}}-\left({\lambda }_7+\mathrm{\Delta }{\lambda }_7{n}_4\right)x_{\text{GFP}}+v_7,\hfill \end{array}$$ (17)

where Δk_i, Δλ_i denote the amplitudes of parameter fluctuations for kinetic constants and degradation constant, respectively. n_j are random white noise with zero mean and unit variance, which denote the independent random fluctuation sources in transcription, translation, reaction, and degradation process, respectively. The variances of parameter perturbations are given as var(Δk_in_j) = (Δk_i)², var(Δλ_in_j) = (Δλ_i)², that is, Δk_i and Δλ_i represent the standard deviations of the corresponding stochastic parameter fluctuations to be tolerated by the synthetic gene circuit in vivo. v_i denotes the corresponding external noise with variance σ_i². Note that the perturbation of basal level P_mGFP is merged into v₆.

The design specifications and parameters are given as follows. The desired transient behaviors of biological AND gate are as shown in Figure 5. The standard deviations of uncertain fluctuations of kinetic parameters and decay rates to be robustly tolerated are specified as Δk₁ = 0.2, Δk₂ = 0.2, Δk₃ = 0.02, Δk₄ = 0.02, Δk₅ = 0.000005, Δk₆ = 0.2, Δk₇ = 0.02, Δλ₁ = 0.04, Δλ₂ = 0.04, Δλ₃ = 0.05, Δλ₄ = 0.05, Δλ₅ = 0.05, Δλ₆ = 0.04, and Δλ₇ = 0.05. The variance of external disturbance v_i is σ_i² = (0.1)². The feasible ranges of kinetic parameters to be designed are specified in the range from 0 to 1. The other parameters are set as λ₁ = λ₂ = λ₆ = 0.0231, λ₃ = λ₅ = λ₇ = 0.0023, λ₄ = 0.0002, K = 400, and n = 1 [8].

Figure 5.

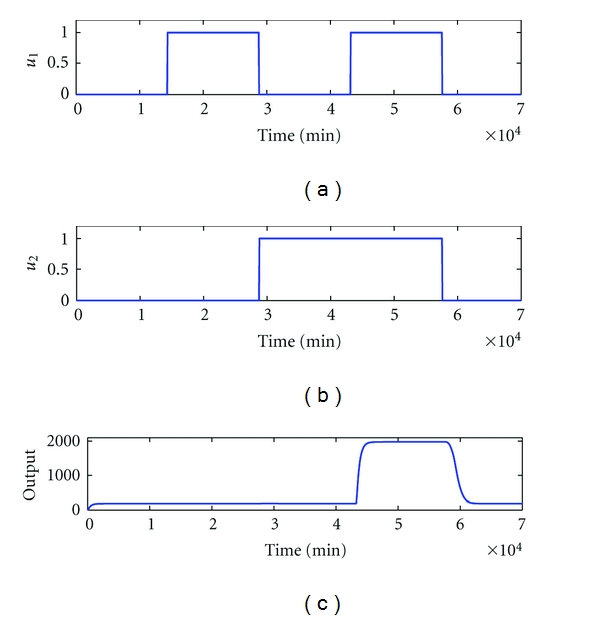
Desired transient behaviors of biological AND gate. The biological AND gate generates an output signal only when it gets biochemical signals from both of its inputs.

Given the above design specifications, our design objective is to adapt the design parameters by the proposed evolutionary systems biology method to achieve the optimal tracking under intrinsic parametric fluctuations and extrinsic noise. In this example, the parameters of evolutionary algorithm are chosen as M = 100, p_c = 0.9, and p_m = 0.2. The software MATLAB is used to perform the simulation. After 100 generations, the best fit design parameters k₁* = 0.6042, k₂* = 0.8410, k₃* = 0.9272, k₄* = 0.2063, k₅* = 0.00001, k₆* = 0.8640, and k₇* = 0.1235 are obtained by the proposed evolutionary systems biology method with the best fitness F(k*) = 1.09 × 10⁻⁴. By Monte Carlo simulation with 50 rounds, the output of the synthetic gene network with the design parameters under intrinsic parametric fluctuations and extrinsic noise is shown in Figure 6(a). It can be seen that the synthetic gene network has robust regulation ability to achieve the desired transient behaviors in spite of uncertain initial state, kinetic parameter fluctuations, and disturbances on the host cell. On the contrary, as shown in Figure 6(b), if the design parameters are selected aside the optimal design parameter k*, for example, with k₁ = 0.9, k₂ = 0.6, k₃ = 0.95, k₄ = 0.25, k₅ = 0.00002, k₆ = 0.6, and k₇ = 0.15 and the fitness F(k) = 3.54 × 10⁻⁵, the expression of the synthetic gene network is with more fluctuation and cannot achieve the desired transient behaviors. Obviously, the robust synthetic gene network by the proposed evolutionary systems biology method has a good robust stability to overcome the uncertain initial conditions and an enough filtering ability to attenuate the disturbances on the host cell and eventually approach the desired transient behaviors.

Figure 6.

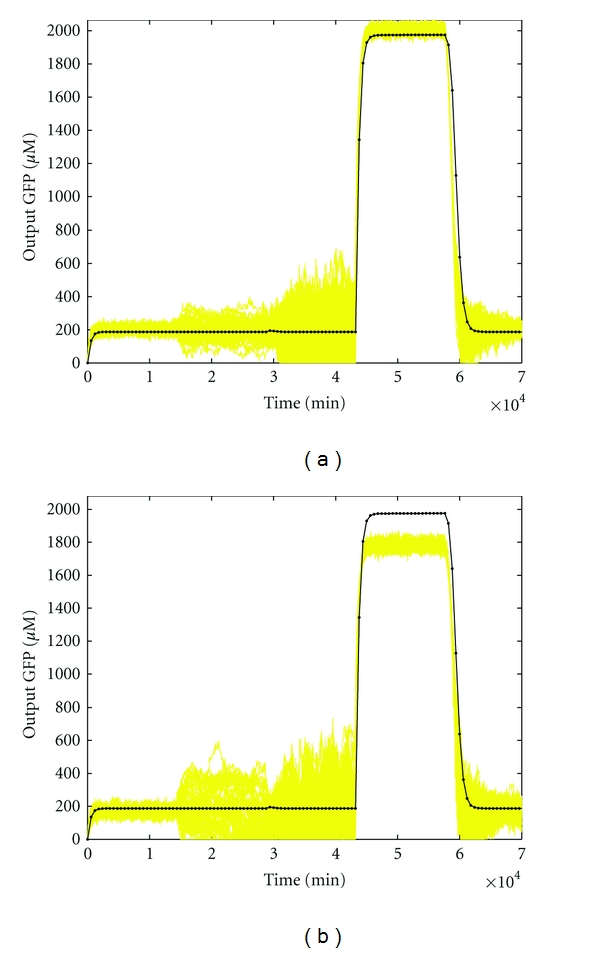
Simulation result of biological AND gate. (a) In order to confirm the robustness and filtering ability of the synthetic gene network, the parameters are specified as follows. The standard deviations of uncertain kinetic parameters and decay rates to be robustly tolerated are specified as Δk₁ = 0.2, Δk₂ = 0.2, Δk₃ = 0.02, Δk₄ = 0.02, Δk₅ = 0.000005, Δk₆ = 0.2, Δk₇ = 0.02, Δλ₁ = 0.04, Δλ₂ = 0.04, Δλ₃ = 0.05, Δλ₄ = 0.05, Δλ₅ = 0.05, Δλ₆ = 0.04, and Δλ₇ = 0.05. The variance of external disturbance v_i is σ_i² = (0.1)². The Monte Carlo simulations are performed by 50 rounds. The mean error is $\bar{e}=(1/50){\sum }_{i=1}^{50}{e}_i=121.95$ with a standard deviation of 9.93, where e_i is the root mean squared error of the ith Monte Carlo simulation. (b) In contrast to the above design case, the design parameters are specified aside the optimal design parameter k*, with k₁ = 0.9, k₂ = 0.6, k₃ = 0.95, k₄ = 0.25, k₅ = 0.00002, k₆ = 0.6, and k₇ = 0.15. In this design case, the mean error is $\bar{e}=165.90$ with standard deviation of 18.67.

4.2. Robust Repressilator Design

Consider the biological repressilator (biological oscillator) as shown in Figure 7. The repressilator is a network of three genes, whose products inhibit the transcription of each other in a cyclical manner [32]. The gene lacI (from E. Coli.) expresses protein LacI, which inhibits transcription of the gene tetR. The product of TetR inhibits the transcription of gene cI (from λ phage), and the protein product CI in turn inhibits expression of lacI, completing the cycle. From the scheme of coupled repressilator in Figure 7, the mRNA dynamics is governed by repressible transcription for three genes [32]:

Figure 7.

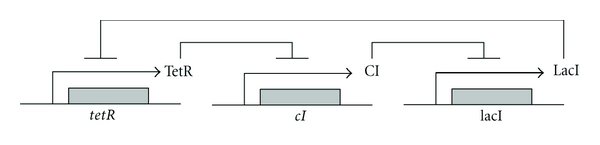
Synthetic transcriptional cascade loop for repressilator. TetR represses lacI, LacI represses cI, and CI represses tetR.

$$\begin{array}{cc}\hfill \frac{d{x}_a\left(t\right)}{dt}& =k_1\frac{1}{\mu +x_C^n\left(t\right)}-{\lambda }_1{x}_a\left(t\right),\hfill \\ \hfill \frac{d{x}_b\left(t\right)}{dt}& =k_2\frac{1}{\mu +x_A^n\left(t\right)}-{\lambda }_2{x}_b\left(t\right),\hfill \\ \hfill \frac{d{x}_c\left(t\right)}{dt}& =k_3\frac{1}{\mu +x_B^n\left(t\right)}-{\lambda }_3{x}_c\left(t\right),\hfill \end{array}$$ (18)

where x_a, x_b, and x_c are the concentrations of mRNA transcribed from genes tetR, cI, and lacI, respectively; concentrations of the corresponding proteins are represented by x_A, x_B and x_C, respectively. k₁, k₂, and k₃ are the transcription rate in the absence of repressor and μ is the repression coefficient. λ₁, λ₂, and λ₃ are the respective degradation rate of mRNA for tetR, cI, and lacI, respectively, and n is the Hill coefficient. Followed by the transcription, the dynamics of proteins TetR, CI and LacI is given, respectively, as [32]

$$\begin{array}{cc}\hfill \frac{d{x}_A\left(t\right)}{dt}& =k_4{x}_a\left(t\right)-{\lambda }_4{x}_A\left(t\right),\hfill \\ \hfill \frac{d{x}_B\left(t\right)}{dt}& =k_5{x}_b\left(t\right)-{\lambda }_5{x}_B\left(t\right),\hfill \\ \hfill \frac{d{x}_C\left(t\right)}{dt}& =k_6{x}_c\left(t\right)-{\lambda }_6{x}_C\left(t\right),\hfill \end{array}$$ (19)

where parameters k₄, k₅, and k₆ are the translation rates of the proteins from the mRNAs, and λ₄, λ₅, and λ₆ represent the dimensionless degradation rate of protein TetR, CI, and LacI, respectively.

From the nonlinear differential equations as mentioned above, it can be seen that the dynamics of the biological repressilator depends on some biochemical factors, such as the kinetic constant, degradation constant, and basal level. However, these factors or parameters are uncertain inherently and the biological circuit also suffers from environmental noise. In this situation, the dynamic model of synthetic biological circuit in vivo should be modified as follows:

$$\begin{array}{cc}\hfill \frac{d{x}_a\left(t\right)}{dt}& =\left(k_1+\mathrm{\Delta }{k}_1{n}_1\left(t\right)\right)\frac{1}{\mu +x_C^n\left(t\right)}\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_1+\mathrm{\Delta }{\lambda }_1{n}_3\left(t\right)\right)x_a\left(t\right)+v_1,\hfill \\ \hfill \frac{d{x}_b\left(t\right)}{dt}& =\left(k_2+\mathrm{\Delta }{k}_2{n}_1\left(t\right)\right)\frac{1}{\mu +x_A^n\left(t\right)}\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_2+\mathrm{\Delta }{\lambda }_2{n}_3\left(t\right)\right)x_b\left(t\right)+v_2,\hfill \\ \hfill \frac{d{x}_c\left(t\right)}{dt}& =\left(k_3+\mathrm{\Delta }{k}_3{n}_1\left(t\right)\right)\frac{1}{\mu +x_B^n\left(t\right)}\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_3+\mathrm{\Delta }{\lambda }_3{n}_3\left(t\right)\right)x_c\left(t\right)+v_3,\hfill \\ \hfill \frac{d{x}_A\left(t\right)}{dt}& =\left(k_4+\mathrm{\Delta }{k}_4{n}_2\left(t\right)\right)x_a\left(t\right)-\left({\lambda }_4+\mathrm{\Delta }{\lambda }_4{n}_3\left(t\right)\right)x_A\left(t\right)+v_4,\hfill \\ \hfill \frac{d{x}_B\left(t\right)}{dt}& =\left(k_5+\mathrm{\Delta }{k}_5{n}_2\left(t\right)\right)x_b\left(t\right)-\left({\lambda }_5+\mathrm{\Delta }{\lambda }_5{n}_3\left(t\right)\right)x_B\left(t\right)+v_5,\hfill \\ \hfill \frac{d{x}_C\left(t\right)}{dt}& =\left(k_6+\mathrm{\Delta }{\lambda }_6{n}_2\left(t\right)\right)x_c\left(t\right)\hfill \\ \hfill & \hspace{1em}-\left({\lambda }_6+\mathrm{\Delta }{\lambda }_6{n}_3\left(t\right)\right)x_C\left(t\right)+v_6,\hfill \\ \end{array}$$ (20)

where Δk_i, Δλ_i denote the amplitudes of parameter fluctuation for kinetic constant and degradation constant, respectively. n₁, n₂, and n₃ are random white noise with zero mean and unit variance, which denote the independent random fluctuation sources in transcription, translation, and degradation process, respectively. The variances of parameter perturbations are given as var(Δk_in_j) = (Δk_i)², var(Δλ_in_j) = (Δλ_i)², that is, Δk_i and Δλ_i represent the standard deviations of the corresponding stochastic parameter fluctuations to be tolerated by the synthetic gene circuit in vivo. v_i denotes the corresponding external stochastic noise with variance σ_i².

The design specifications and parameters are given as follows. The desired transient behaviors of biological repressilator are as shown in Figure 8. The standard deviations of random fluctuations of kinetic parameters and decay rates to be robustly tolerated are specified as Δk₁ = 0.2, Δk₂ = 0.2, Δk₃ = 0.2, Δk₄ = 0.02, Δk₅ = 0.02, Δk₆ = 0.02, Δλ₁ = 0.04, Δλ₂ = 0.04, Δλ₃ = 0.04, Δλ₄ = 0.05, Δλ₅ = 0.05, and Δλ₆ = 0.05. The variance of external disturbance v_i is σ_i² = (0.03)². The feasible ranges of kinetic parameters to be designed are specified in a range from 0 to 2. The other parameters are set as λ₁ = 0.4, λ₂ = 0.4, λ₃ = 0.4, λ₄ = 0.5, λ₅ = 0.5, λ₆ = 0.5, μ = 1.3, and n = 4.

Figure 8.

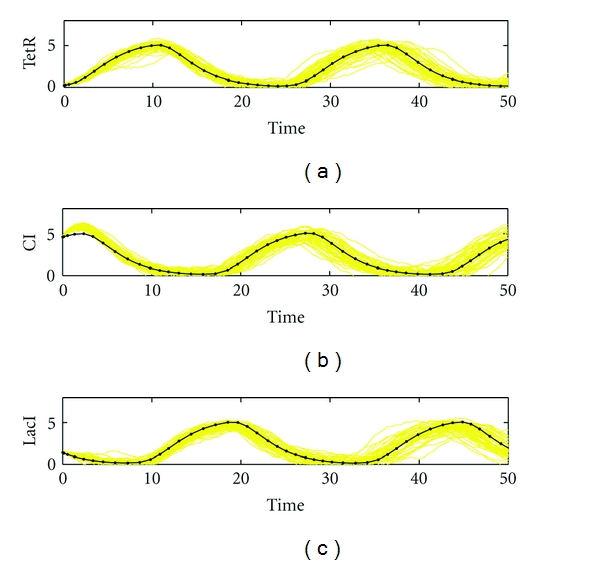
Monte Carlo simulation of biological repressilator by the proposed evolutionary systems biology method. (a) TetR; (b) CI; (c) LacI. The parameters are specified as follows. The standard deviations of uncertain kinetic parameters and decay rates to be robustly tolerated are specified as Δk₁ = 0.2, Δk₂ = 0.2, Δk₃ = 0.2, Δk₄ = 0.02, Δk₅ = 0.02, Δk₆ = 0.02, Δλ₁ = 0.04, Δλ₂ = 0.04, Δλ₃ = 0.04, Δλ₄ = 0.05, Δλ₅ = 0.05, and Δλ₆ = 0.05. The variance of external disturbance v_i is σ_i² = (0.03)². The Monte Carlo simulations are performed by 50 rounds. The mean errors $\bar{\text{e}}$ are 0.85, 0.90, and 0.90 with standard deviations of 0.38, 0.38, and 0.37 for TetR, CI, and LacI, respectively.

Given the above design specifications, our design objective is to adapt the design parameters by the proposed evolutionary systems biology method to achieve the optimal tracking under intrinsic parametric fluctuations and extrinsic noise. In this example, the parameters of evolutionary algorithm are chosen as M = 100, p_c = 0.9, and p_m = 0.2. The software MATLAB is used to perform the simulation. After 100 generations, the best fit design parameters k₁* = 1.7799, k₂* = 1.3432, k₃* = 1.4602, k₄* = 0.8298, k₅* = 1.0683, and k₆* = 0.9337 are obtained by the proposed evolutionary systems biology method with the best fitness F(k*) = 2.03. By Monte Carlo simulation with 50 rounds, the output of the system with the best fit design parameters under intrinsic parametric fluctuations and extrinsic noise is shown in Figure 8. It can be seen that the synthetic gene network has robust tracking ability to achieve the desired transient behaviors in spite of uncertain initial state and disturbances on the host cell. On the contrary, as shown in Figure 9, if the design parameters are selected aside the best fit parameter k*, for example, with k₁ = 1.5, k₂ = 1.9, k₃ = 1.2, k₄ = 0.79, k₅ = 1.1, and k₆ = 0.96 and the fitness F(k) = 0.29, the expression of the synthetic gene network is with more fluctuation and cannot achieve the desired transient behaviors. Obviously, the robust synthetic gene network by the proposed evolutionary systems biology design method has a good tracking ability to achieve the desired behavior, robust stability to overcome the uncertain initial conditions, and kinetic parameters fluctuations and an enough filtering ability to attenuate the disturbances on the host cell and eventually approach the desired transient behaviors. If the parameters of decay rate λ₁,…, λ₆ are also considered to be designed by the proposed method, then the robust tracking performance can be improved significantly because of more design freedom to choose. However, this will make the design procedure more complicated.

Figure 9.

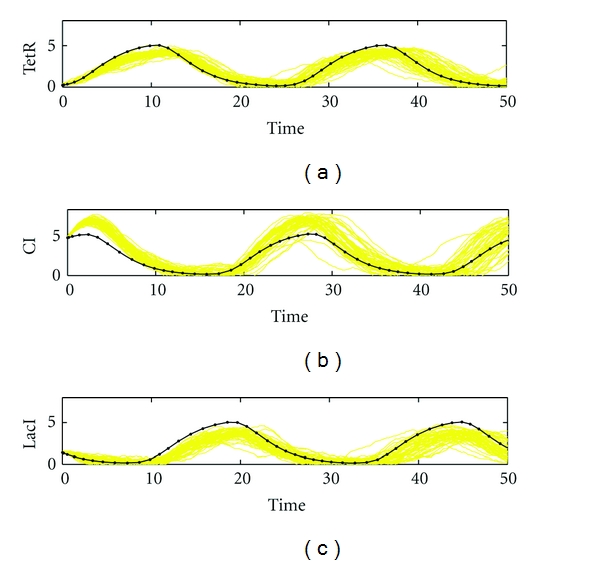
Simulation of biological repressilator: (a) TetR; (b) CI; (c) LacI. In contrast to the above design case, the design parameters are specified aside the best fit parameter k*, for example, with k₁ = 1.5, k₂ = 1.9, k₃ = 1.2, k₄ = 0.79, k₅ = 1.1, and k₆ = 0.96. In this design case, the mean errors $\bar{e}$ are 0.91, 1.36, and 1.18 with standard deviations of 0.29, 0.35, and 0.27 for TetR, CI, and LacI, respectively.

5. Discussion

One of main challenges for synthetic biology is that the engineered biological circuits are influenced by the effects of unavoidable intracellular fluctuations and environmental disturbances [17, 18, 20, 33–36]. The noise and uncertainties currently hinder us from engineering synthetic gene circuits with reliable functions. In this study, we propose an evolutionary systems biology methodology to select an adequate parameter set for nonlinear stochastic gene circuit systems. The proposed algorithm can evaluate biological parts in different combinations and configurations for their tracking ability. Therefore, our approach may offer a possible design guideline concerning the selection of the optimal configuration of a robust synthetic gene network with desired behavior. Each circuit is represented by a set of transcription rate vector k, which in turn uses a combination of corresponding promoters and ribosome binding site (RBS) from preconstructed libraries [3, 7] to satisfy the design considerations under noisy and uncertain environment in vivo.

In the light of natural selection on traits best suited for environmental change being an important mechanism in evolution [24], the similar evolutionary strategy seems more suitable to gene circuit design if we can speed up the evolutionary process through fast parallel evolutionary computations. Inspired by biological evolution such as reproduction, mutation, recombination, and selection, the evolutionary algorithm is an efficient method to solve optimization problems [25]. An evolutionary systems biology algorithm is employed here to solve the best fitness function to gradually improve the desired behavior tracking ability of a synthetic gene circuit design one generation by one generation to mimic the natural selection in the evolutionary process. Unlike the necessity of some complicated computations in the conventional design strategies, only some simple operators (e.g., selection, crossover, and mutation) and some simple calculations are required for selecting optimal design parameters iteratively by the proposed evolutionary systems biology design method, but with synthetic gene circuit robust enough against intrinsic parameter fluctuation and external disturbance. This attractive property makes the proposed design method being easily implemented in the practical applications. Since the proposed evolutionary systems biology method has included design specifications such as the tolerable variances of intrinsic stochastic parameter variations and external disturbances, the feasible ranges of design kinetic parameters and decay rates, and the desired steady state or transient behaviors of output y(t), the synthetic gene circuit can be guaranteed to achieve all possible design purposes by only solving a constrained optimization problem in (9) by maximizing a corresponding fitness function F(k) in (12) through evolutionary algorithm. Though the proposed evolutionary gene circuit designs may not produce the best tracking performance within the finite generations of evolutionary algorithm, they are near optimal gene circuit designs to achieve the desired behavior. Therefore, the proposed design method has potential applications to the synthetic gene circuit design for biotechnological purposes in the near future.

Given the above evolution framework, we are given the foundation to build robust biological parts. To achieve this goal, there are many more interesting problems to be solved. For gene circuits, it may not be feasible to implement the optimal set of transcription rate vector k, where limited choices are available. It could be necessary to turn the above proposed algorithm into searching a set of biological parts from libraries of genetic devices, but the algorithm should remain flexible at choosing biological parts. The other design problem comes from the assumed noise level: an accurate estimation may not readily be available for fluctuations of all parameters in biochemical processes. Of course, we may start from basic operation principals and models to calculate the fluctuation level. For example, noise in gene regulation can be modeled from transcription control, alternative splicing, translation, and diffusion to biological modification reactions of transcription factors. Such stochastic process noise can affect significantly the dynamics of biological systems. Knowledge (and multitude in experimental analysis and design) in this regard in fact may help determine the flexibility of biological parts in combinations and configurations. However, absolute accuracy is not required in the above design process, since we can always include design margins into the rate parameters by considering tracking problems outside (near) the boundary of the noise ranges. Also, we cannot always control external environment fluctuations. A different set of gene circuits may be enabled through sensing environmental transcription factors, that are designed to handle wide variety of outside changes. Lastly but not the least, we have to consider the complexity of interacting with other gene operations, that may directly impact the designed circuit and cannot be modeled as pure noise. It is certainly possible to extend the proposed algorithm by considering relational biochemical reactions. Still, at certain level, we would like to abstract more information in the design process for the method to handle larger scale biological systems.

6. Conclusion

Robust design to overcome intrinsic and external molecular noise in vivo to achieve a desired behavior becomes an important topic in synthetic gene networks. The contribution of the paper includes the following. (1) A stochastic synthetic biologic circuit with the intrinsic parameter fluctuations and external noise is modeled as an evolutionary nonlinear stochastic system with the state-dependent noise and external disturbance to mimic the stochastic behavior of synthetic biological circuit in host cells. (2) Based on nonlinear stochastic system and design specifications, the design problem of robust synthetic biological circuit with desired behavior is transformed to an equivalent optimal tracking problem and then a fitness optimization problem in evolution. (3) An evolution systems biology algorithm is proposed to tune the design kinetic parameters (chromosomes) of synthetic gene network to achieve the fitness optimization to some desired behaviors to mimic the evolutionary process of biological genetic circuit to fit the change of environment via nature selection. Finally, several simulation results have also confirmed the robust desired behavior tracking performance of synthetic biologic circuits by the proposed evolutionary systems biology design method.