A Generative Approach for Image-Based Modeling of Tumor Growth

Abstract

Extensive imaging is routinely used in brain tumor patients to monitor the state of the disease and to evaluate therapeutic options. A large number of multi-modal and multi-temporal image volumes is acquired in standard clinical cases, requiring new approaches for comprehensive integration of information from different image sources and different time points. In this work we propose a joint generative model of tumor growth and of image observation that naturally handles multimodal and longitudinal data. We use the model for analyzing imaging data in patients with glioma. The tumor growth model is based on a reaction-diffusion framework. Model personalization relies only on a forward model for the growth process and on image likelihood. We take advantage of an adaptive sparse grid approximation for efficient inference via Markov Chain Monte Carlo sampling. The approach can be used for integrating information from different multi-modal imaging protocols and can easily be adapted to other tumor growth models.

1 Introduction

Processes related to tumor growth can be modeled at different scales ranging from signaling at sub-cellular level, via multi-cellular processes determining metabolic properties of the tumor, to the gross bio-mechanical behavior of tumor-affected tissue at a macroscopic scale. Tumor models in medical image analysis rely almost exclusively on information from morphologic images and consequently focus on the macroscopic phenomena of tumor evolution. An important class of macroscopic tumor models is based on the reaction-diffusion equations [5,24,6,1,14,23,13,16,10]. In this paper, we propose an efficient Bayesian framework for image-based inference in this type of tumor growth models.

Tumor models are used to describe effects a lesion has on surrounding healthy tissue. Modeling this effect helps to improve inter-subject image and atlas registration [10,17,25,26,2] and to improve tissue segmentation in the presence of the lesion [12,8]. As the tumor location it is not consistent across patients, tumor shape is often employed for constructing spatial priors. For example, a large number of simulated tumors can be used to learn characteristic tumor-induced deformations [21,2]. For data of individual patients growth models also help to estimate deformation fields and tissue perturbations [10,26]. Most of these methods take a static approach to modeling tumors for removing the tumor-induced effects from the analysis of the subject’s brain itself.

Other biophysical tumor models describe explicitly the evolution of the lesion. (For a short review see [20].) For glioma most such models follow a reaction-diffusion framework [5]. They assume an infiltrative growth of the tumor cells, may consider differences in cell diffusion in white and gray matter [24], and model locally anisotropic migration patterns by integrating information from diffusion tensor images (DTI) [6]. Some models also include the mechanical effect of the lesion on surrounding structures by modeling the interaction between the tumor mass and the invaded tissue [6,14], or couple the growth dynamics with phenomenological image models for Gadolinium uptake and changes in DTI [23]. The primary application for these image-based dynamical tumor models is in simulating tumor growth, either to analyze macroscopic patterns of disease progression [1], or to generate realistically appearing tumor images to be used for validation of tumor segmentation methods [23].

Many dynamical tumor models could serve as a framework for integrating complex information from different image modalities and longitudinal data sets. But unlike the static whole brain models, the image-based personalization remains challenging for most forward simulators. As a consequence, some studies only provide qualitative measures for analyzing lesions and their progression [7], employ strict assumptions on the relationship between the tumor cell density and image observation [24], or focus on a theoretical treatment of the inverse problem under the assumption of having appropriate observables available at a later stage [14]. The PDE-constrained optimization approach in [14] relates the tumor growth model to landmark-based registration using a reaction-diffusion-advection model. This approach is similar to the whole brain modeling [10,26,21], but depends critically on the tumor-tissue interaction model. Alternatively, a traveling wave approximation of the reaction-diffusion model can be used to estimate model parameters from the temporal evolution of the tumor front [16]. Unfortunately, this approach only provides the speed of growth. Furthermore, all of the previous methods focus on point-estimates of the process. This presents significant challenges in presence of noisy observations and uncertainty in evolution models.

In this paper, we develop a novel approach for personalizing tumor models, for integrating multi-modal data, and for quantifying uncertainty. We formulate a generative model that includes a biophysical tumor growth model and statistical observation models for different image modalities. We devise an efficient inference scheme based on the forward model and applicable in high-dimensional observation settings. We demonstrate the resulting method in experiments with both synthetic and clinical patient data. We envision that a joint tumor and image modeling will close the gap between functional image interpretation and disease modeling, and will provide new directions for therapy optimization.

2 Tumor Growth Model

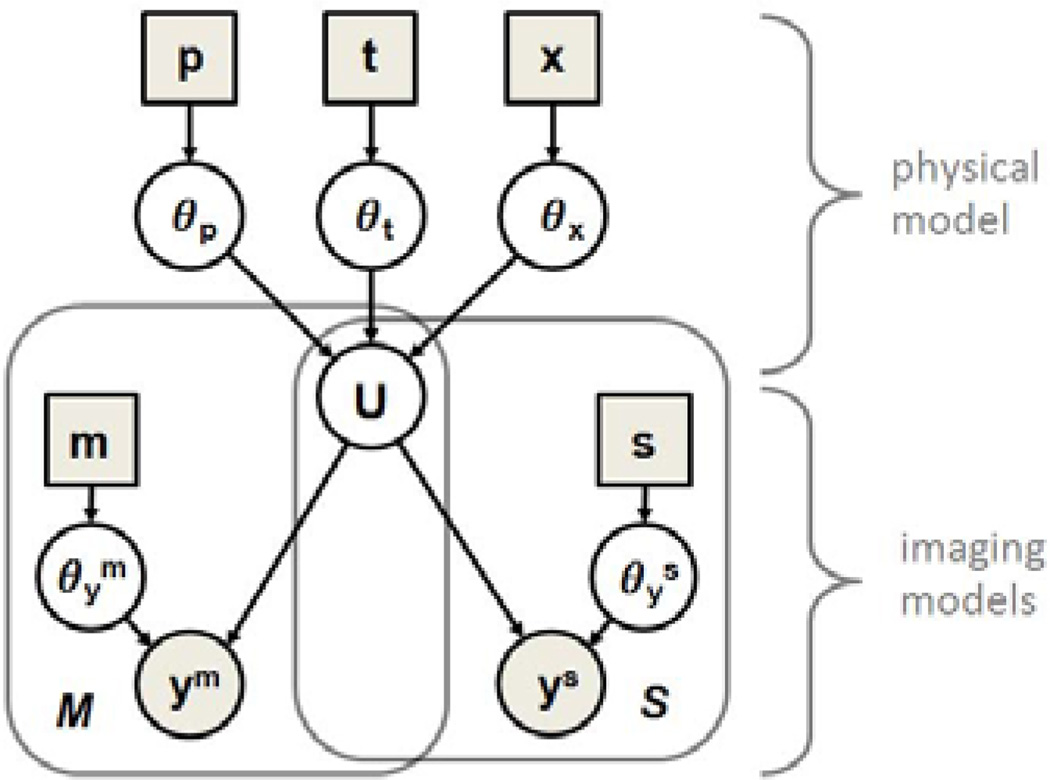
Our approach includes a physical process model that describes the progression of the disease through the evolution of the tumor cell concentration u and a probabilistic imaging model that captures the relationship between the latent state u and the image observations y. Figure 1 presents the full graphical model described in this section.

Fig. 1.

Joint process and observation model. The physical model defines the state variable u as a function of model parameters θ_p and initial conditions θ_x and θ_t. The imaging models relate u to the image observations y^m and y^s, representing functional maps and tumor segmentations, respectively. Variables are represented by circles, parameters are shown as squares. We estimate the model parameters θ_p to characterize the state of disease visible from images y.

2.1 Physical Process Model

We let u = (u₁,…, u_I)^T be the latent state variables where u_i ∈ [0, 1] is the tumor cell concentration in voxel i (1 ≤ i ≤ I). We model the temporal evolution of the tumor as an inhomogeneous anisotropic diffusion governed by the Fisher-Kolmogorov equation [5]:

$$\frac{\partial \mathbf{u}}{\partial t}={\nabla }_x(\mathbf{D}{\nabla }_x\mathbf{u})+\rho ·\mathbf{u}(1-\mathbf{u}),$$ (1)

where ∇_x represents the spatial derivative operator. The equation describes the growth of a glioma as an infiltrative process with diffusivity tensor D and self-limiting growth with proliferation rate ρ. We further assume that D = D · D̂, where D̂ is an patient-specific diffusion tensor, observed via DTI, and D is a global diffusivity parameter [6]. We apply Neumann border conditions, and assume that tumor cells migrate in the white and gray matter only, with higher diffusivity in the white matter (D_w ≫ D_g). To personalize the model, we construct estimates of the model parameters θ_p = {D, ρ} individually for every patient.

By integrating Eq. (1) over time – starting from the initial state u(t = 0) when the first image of the tumor was acquired – we obtain a 4D functional model U(x, y, z, t) that describes the evolution u(t) at any time point t. We choose a parametric representation for the initial state by placing a seed u^init in a voxel located at θ_x = {x, y, z} and by growing the tumor for the time interval θ_t. We form the deterministic tumor evolution model:

$$p(\mathbf{u}(t)|{\theta }_x,{\theta }_t,{\theta }_p)=\delta (U(x,y,z,t;{\theta }_x,{\theta }_t,{\theta }_p)-\mathbf{u}(x,y,z,t)),$$ (2)

where δ is Dirac’s delta indicating that u is an exact solution of the functional U(x, y, z, t). We choose to use a deterministic model without a stochastic component in Eq. (1) or noise term in Eq. (2) as it represents a stronger constraint on the growth process. We incorporate non-deterministic behavior into our framework via a probabilistic model of the imaging process, as described below.

2.2 Imaging Models

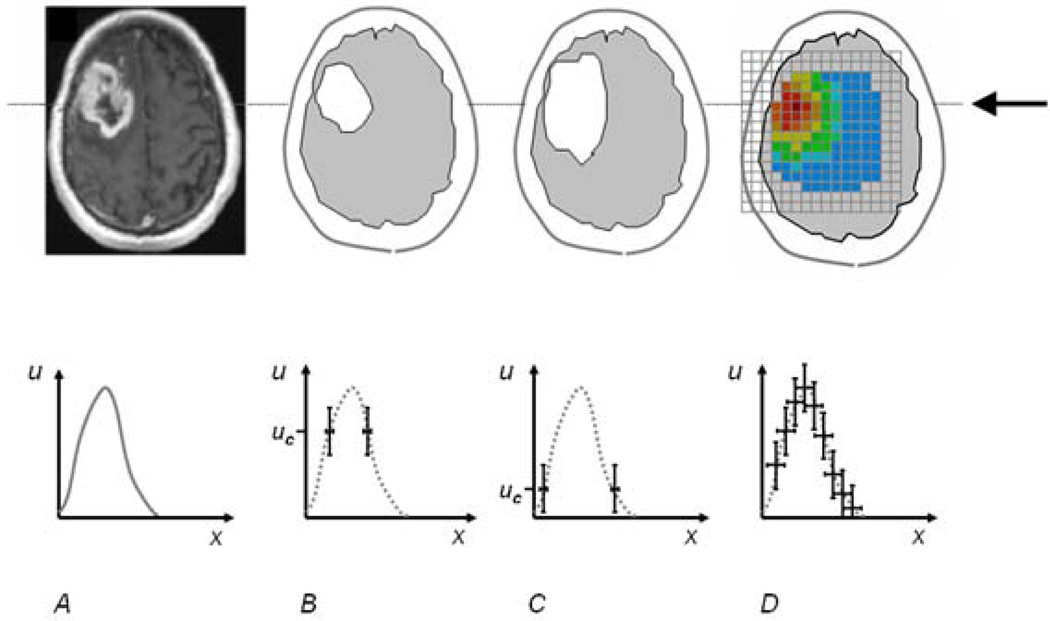
Observations y = (y₁,…, y_I)^T are acquired at each voxel i at specific times t, representing partial observations of the process. We evaluate every image volume y(t) with the corresponding state vector u(t). For notational simplicity we drop the time index in the imaging models below. As illustrated in Fig. 2, we assume that there are two different types of observations that can be related to u: continuous functional maps and binary tumor segmentations which are the most common observation.

Fig. 2.

Example relationships between image information y (top) and tumor cell density u (bottom). A: actual T₁gad image and the schematic tumor cell distributions along the line indicated by the arrow in the top row. B, C: exemplary modalities where only the visible tumor segmentation y^s can be correlated with specific values u_c of the state variable u. D: exemplary modality where all entries of the functional map y^m can be correlated with the latent state variable u.

Functional maps

Functional maps y^m contain continuous values $y_i^m\in ℝ$. They represent imaging modalities with functional parameters that can be directly correlated with the latent physiological variable u using a (possibly nonlinear) forward observational operator F. Formally,

$$p({\mathbf{y}}^m|\mathbf{u},{\theta }_y^m)={\displaystyle \prod _i}p(y_i^m|\mathbf{u},{\theta }_y^m)={\displaystyle \prod _i}𝒩(y_i^m;{\mu }_i,{\sigma }_m^2),$$ (3)

where 𝒩(·; μ, σ²) denotes a normal distribution with mean μ and variance σ². Eq. 3 represents a noisy observation of

$${\mu }_i=F{(b^c·\mathbf{u})}_i.$$ (4)

We let ${\theta }_y^m=\{b^c,{\sigma }_m^2\}$ be the parameters of this model, where b^c is the coefficient in a linear model relating u and y^m in a first order approximation, relevant for example for magnetic resonance spectroscopic images (MRSI). A function F(·) could be, for example, a known nonlinear smoothing and subsampling operator, modeling the point spread function of the imaging process and different spatial resolution of y^m and u. Examples for y^m include metabolic maps from MRSI [9], or apparent diffusion coefficient maps from DTI.

Binary segmentations

Tumor segmentations contain discrete labels y^s, $y_i^s\in \{0,1\}$. Since tumor outlines are commonly associated with constant tumor infiltration, we model observation y^s for a given tumor cell concentration u as a Bernoulli random variable:

$$p({\mathbf{y}}^s|\mathbf{u},{\theta }_y^s)={\displaystyle \prod _i}p(y_i^s|\mathbf{u},{\theta }_y^s)={\displaystyle \prod _i}{\alpha }_i^{y_i^s}·{(1-{\alpha }_i)}^{1-y_i^s},$$ (5)

where α_i is the probability of observing characteristic tumor-induced changes:

$${\alpha }_i=.5+.5·\text{sign}(u_i-u^c)(1-e^{-\frac{{(u_i-u^c)}^2}{{\sigma }_s^2}}),$$ (6)

which is a double logistic sigmoid function with parameters ${\theta }_y^s=\{u^c,{\sigma }_s^2\}$. We essentially assume that the tumor cell infiltration is invisible below the threshold u^c but modifies the image signal in a predictable way after surpassing u^c [24]. Parameter ${\sigma }_s^2$ transforms the hard threshold into a smoother decision, also reflecting the uncertainty in the threshold u^c.

2.3 Joint Model

Combining the deterministic tumor growth model in Eq. (2) with the image observation models in Eqs. (3)–(5) and letting Y = [y₁,… y_k] denote the collection of all k image observations acquired at N time points t_n, we obtain

$$\begin{array}{cc}p(\mathbf{Y}|{\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y)\hfill & ={\displaystyle \prod _{t_n}}p(\mathbf{y}(t_n)|{\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y)\hfill \\ \hfill & ={\displaystyle \prod _{t_n}}{\displaystyle {\int }_{\mathbf{u}(t_n)}}p(\mathbf{y}(t_n)|\mathbf{u}(t_n),{\theta }_y)p(\mathbf{u}(t_n)|{\theta }_x,{\theta }_t,{\theta }_p)\mathrm{d}\mathbf{u}(t_n)\hfill \\ \hfill & ={\displaystyle \prod _{t_n}}{\displaystyle {\int }_{\mathbf{u}(t_n)}}{\displaystyle \prod _k}p({\mathbf{y}}_k(t_n)|\mathbf{u}(t_n),{\theta }_y)p(\mathbf{u}(t_n)|{\theta }_x,{\theta }_t,{\theta }_p)\mathrm{d}\mathbf{u}(t_n),\hfill \end{array}$$ (7)

assuming that all observations are conditionally independent given the latent state u. We adapt a factored prior p(θ_x, θ_t, θ_p, θ_y) = p(θ_x)p(θ_t)p(θ_p)p(θ_y) and choose uniform distributions for all parameters. Similar to [1], we choose the range for the evolution parameters θ_p as illustrated in Fig. 3. We use experimental evidence [24,9] to set the range of the imaging parameters θ_y and use the life expectancy of a healthy person to set the range for the temporal parameter θ_t. We assume that the tumor started growing from a location within the hyperintense areas in T₂ MRI at t = 0 to set a prior on the spatial parameter θ_x. We obtain the joint posterior distribution of the parameters using Bayes’ rule:

$$p({\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y|\mathbf{Y})\propto p(\mathbf{Y}|{\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y)p({\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y),$$ (8)

from which we compute the posterior distribution of θ_p via marginalization

$$p({\theta }_p|\mathbf{Y})={\displaystyle {\int }_{{\theta }_x}}{\displaystyle {\int }_{{\theta }_t}}{\displaystyle {\int }_{{\theta }_y}}p({\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y|\mathbf{Y})\mathrm{d}{\theta }_x\mathrm{d}{\theta }_t\mathrm{d}{\theta }_y.$$ (9)

p(θ_p|Y) = p(D, ρ|Y) is the desired quantity of diagnostic interest in our application.

Fig. 3.

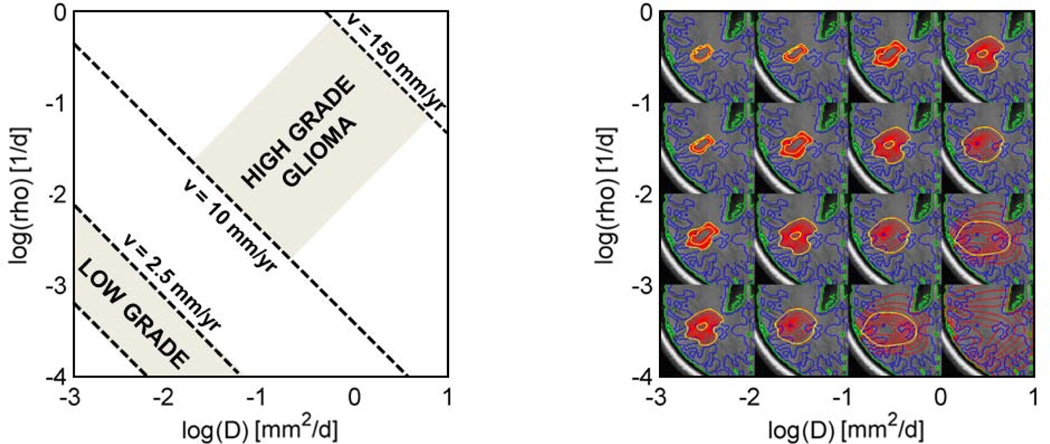
Parameter space of the tumor model with tumor cell diffusivity D and proliferation rate ρ. Left: Parameterization for high- and low-grade glioma [1,22]. The speed of growth υ can be obtained from times series of images [16]. It provides complementary information to tumor shape. Right: Shapes of equally large tumors for different parameterizations. Isolines of u = .05 and u = .6 are shown in yellow. We use the information from both time series and tumor shape jointly to characterize infiltrative and proliferative behavior of the tumor.

3 Inference

The posterior distribution of θ_p = {ρ, D} allows us to summarize a large set of image observations y through diffusivity D and cell doubling rate ρ (Fig. 3). We aim at visualizing p(θ_p|Y) by drawing samples from it using an efficient Markov Chain Monte Carlo (MCMC) sampling strategy. MCMC constructs a random walk through the parameter space which converges towards the solution. The method avoids intractable integrals in Eq. (7). Unfortunately, the repeated evaluation of Eq. (9) for this walk requires the costly forward integration of the physical model in Eq. (1) for any sample from θ_p. To overcome this challenge, we separate the integration over the model parameters in Eq. (9): we integrate over parameters θ_t and θ_y which can be calculated sequentially at any step when propagating the forward model, and rely on MCMC only to sample from θ_x and θ_p.

Sequential integration of θ_t and θ_y

Given the parameters of the tumor growth model θ_p and a starting point θ_x, we propagate the physical model in Eq. (1) based the deterministic model U in Eq. (2). During the forward integration of Eq. (1), the integral

$$p({\theta }_p,{\theta }_x|\mathbf{Y})={\displaystyle {\int }_{{\theta }_y}}{\displaystyle {\int }_{{\theta }_t}}p({\theta }_x,{\theta }_t,{\theta }_p,{\theta }_y|\mathbf{Y})\mathrm{d}{\theta }_t\mathrm{d}{\theta }_y$$ (10)

can be calculated efficiently in a single sweep, by evaluating the image likelihood p(y|u, θ_y) at any step forward in time, and subsequently integrating over all steps. This procedure represents an integration over θ_t on a regularly spaced grid. Similarly, we integrate over the parameters ${\theta }_y^m\text{ and }{\theta }_y^s$ on a regularly spaced grid. This step can be performed very quickly once u(t_n) has been calculated for the different observations y(t_n). This procedure approximates Eq. (10) by a sum:

$$p({\theta }_p,{\theta }_x|\mathbf{Y})\approx {\displaystyle \sum _{{\theta }_t^{(g)}}}{\displaystyle \sum _{{\theta }_y^{(g)}}}p({\theta }_x,{\theta }_t^{(g)},{\theta }_p,{\theta }_y^{(g)}|\mathbf{Y}).$$ (11)

Efficient sampling of θ_x and θ_p

Even with the proposed sequential integration scheme, evaluating p(θ_p, θ_x|Y) repeatedly for different values {θ_p, θ_x} during MCMC sampling remains prohibitively time consuming. We therefore rely on a representation of p(θ_p, θ_x|Y) that can be sampled more efficiently. In particular, we approximate p(θ_p, θ_x|Y) through p̃(θ_p, θ_x|Y) using a so-called sparse grid basis [3,15] in the first step. This approximation allows us to sample the space of p(θ_p, θ_x|Y) in a structured way, with less redundant computations, and systematically increasing the accuracy of the approximation with every sample. More specifically, we interpolate between G pre-computed sampling points:

$$\tilde{p}({\theta }_p,{\theta }_x|\mathbf{Y})={\displaystyle \sum _{g=1}^G}p({\theta }_p^{(g)},{\theta }_x^{(g)}|\mathbf{Y})·{\Phi }_s({\theta }_p,{\theta }_x),$$ (12)

relying on a hierarchical linear basis function Φ_G that spans the space of θ_p and θ_x. This approximation is constructed from a small number of evaluations of p(θ_p, θ_x|Y), sampled at specific grid locations $\{{\theta }_p^{(g)},{\theta }_x^{(g)}\}$ within the range of p(θ_x) and p(θ_p). The interpolated posterior distribution can be evaluated at little computational cost. In the second step, we use the pre-computed approximation p̃(θ_p, θ_x|Y) when evaluating a large number of samples from p(θ_p, θ_x|Y) via MCMC. Efficiently sampling from p̃(θ_p, θ_x|Y) also allows us to tune the sampling algorithm more easily in the presence of local minima. In the final step, we construct

$$\tilde{p}({\theta }_p|\mathbf{Y})={\displaystyle {\int }_{{\theta }_x}}\tilde{p}({\theta }_p,{\theta }_x|\mathbf{Y})d{\theta }_x$$ (13)

by aggregating values of θ_p from our samples θ_x, θ_p. In order to minimize the number of necessary samples from p(θ_p, θ_x|Y), i.e., the number of forward integrations of the physical model, we choose the sparse grid collocation from [18,27], but with a depth first search strategy for local refinement. To sample efficiently from Eq. (12) we use the Delayed Rejection Adaptive Metropolis (DRAM) variant of the Metropolis-Hastings MCMC sampler [11].

4 Experiments

We evaluate our method on a series of images acquired for monitoring patients with low-grade glioma. The low-grade glioma is typically only visible as hyperintense lesion in T₂/FLAIR images. Patients are monitored for the occurrence of T₁gad enhancements indicating the transition to high-grade disease and to be treated immediately. However, clinical evidence suggests that the dynamics of the tumor growth can predict this transition at a much earlier stage [22,4] (Fig. 3, left). We hypothesize that model parameters θ_p may provide more accurate information about the state of disease. Here we evaluate our approach under this clinical objective on synthetic ground truth and real clinical data. We also compare standard MCMC sampling with the proposed adaptive sparse grid MCMC sampling.

Implementation

We implement the tumor growth model in Eq. (1) by employing the preconditioned conjugate gradient descent to solve the state equations [19]. We sequentially evaluate Eq. (10) while integrating Eq. (1). In every forward step we evaluate the image likelihood, integrating on a grid over u_c(T₂) = .01 ….2 and u_c(T₁gad) = .6 ….8 with ${\sigma }_2^s=.05\dots 100$ and for metabolic maps for b^c(Choline) = 1 … 8 and b^c(NAA) = −8 … 1 with ${\sigma }_m^2=.5\dots 2$. We impose general physiological constraints such as a maximum time of growth of 50 years and a maximal sustainable tumor volume of 150 cm³.

We perform integration by sampling in a five dimensional space with {D, ρ} = θ_p and {x, y, z} = θ_x and always initialize the sampling in the center of the valid parameter space. We evaluate the samples via MCMC both with and without sparse grid representation. In the first case (direct MCMC) we perform a random walk with 2000 samples. We use the last 1500 samples for evaluating the statistic of the parameters. Similar to [11], we use 100 samples to adapt the proposal distribution, and propagate up to two steps into suboptimal directions of the sampling space. We obtain rejection rates of 40%–60% with approximately 3000–5000 integrations of Eq. (10). In the second case (sparse grid MCMC) we evaluate Eq. (10) about the same number of times, i.e., for 3000 basis vectors, but at positions in the parameter space defined by an adaptive sparse grid with “maximum norm” basis [15]. We then perform MCMC sampling under the same settings as for the direct MCMC, but use the approximated posterior, interpolated from the sparse grid basis, as the function to be evaluated for each sample. The direct sampling takes about 6–12 hours for each test case on a standard personal computer. The sparse grid sampling takes a similar amount of computing, but can be easily parallelized, resulting in an algorithm that is 8–10 times faster. Subsequent MCMC sampling using the sparse grid interpolation is accomplished within minutes.

Data

In the first experiment, we model a synthetic low-grade glioma. We use DTI and tissue segmentations from a healthy segment of a patient data set to evolve a synthetic tumor with D = 10⁻² and ρ = 10^−2.3 for θ_t = 2000 days, starting from a tumor seed point u^init with 10% infiltration in a 1 mm³ volume. We assume D = D_w = 10³D_g [1,16]. We model a second observation by propagating the model for another 180 days. For both observations we model the segmentations from T₂/FLAIR images using a threshold of u_c(T₂) = .095. We set u_c(T₁gad) = .695. This is higher than the maximum value of u at both time points and our synthetic T₁gad images do not show contrast agent-enhanced regions. We model metabolic maps from MRSI by smoothing u with a 1 cm wide Gaussian kernel and subsampling the volume on a grid with 1 cm voxels and model two metabolite maps with coefficients b^c(Cho) = 1.8 and b^c(NAA) = −4.6. In the second experiment, we model a developing high-grade tumor. We use the same setting as above, but with D = 10^−0.2 and ρ = 10^−1.3. The tumor is evolved for 250 days for the first observation, and another 90 days for the second. Figure 4 (left) shows the second time point. All observations are modeled as above; T₁gad images do not show enhancements in this experiment either, and the tumor still appears as a low-grade glioma.

Fig. 4.

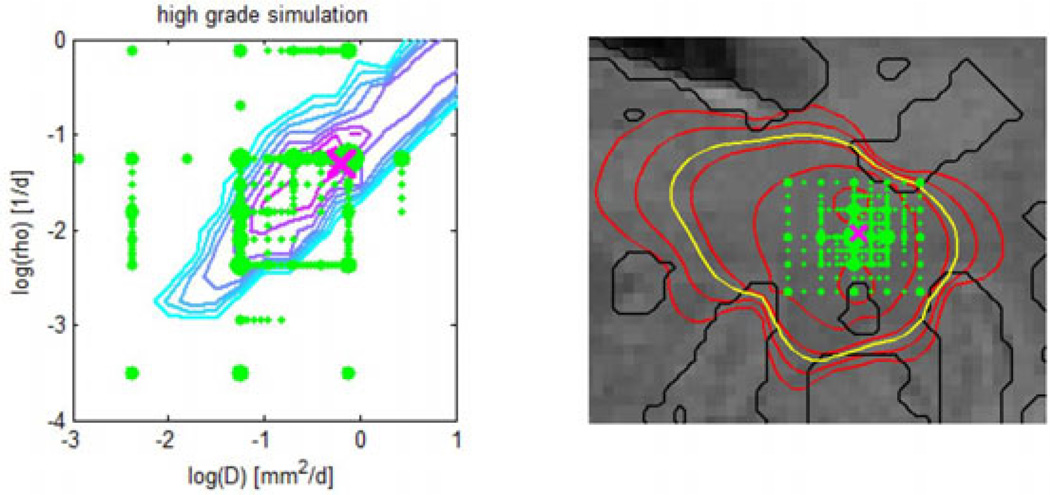
Adaptive sampling of the parameter space for the synthetic high-grade data set. Left: Sampling points (green) for the model parameters θ_p = {D, ρ}. The contour map shows the posterior distribution p(θ_p|Y) evaluated on a regular grid (cyan–low, pink–high). Right: Sampling points (green) for the {x, y} coordinates of the tumor seed θ_x. The Fig. also shows isolines of tumor cell density (red), the predicted extensions of the T₂ hyper-intense area (yellow) and tissue boundaries (black). In both figures the size of the green sampling points indicates how often the indicated parameter was evaluated under different combinations. The ground truth is indicated by the pink cross. Most adaptively chosen sampling points are close to the ground truth.

In addition to the two test cases with ground truth for D and ρ, we evaluate our model on two clinical data sets. The first data set comprises six sets of images acquired approximately every 3 months over 1.5 years. The second data set comprises four sets of images, acquired every 3–6 months in a similar time span. Available are in both cases DTI, T₂/FLAIR and T₁gad images. T₂/FLAIR images show a visible progression of the tumor front, while T₁gad is free of Gadolinium enhancements. The lesion is segmented manually in three 2D slices intersecting with the tumor center in the first case; it is manually segmented in all slices for the second case. To ensure the diffusion tensor to be free of tumor-induced effects, we use the mirrored DTI of the contra-lateral, disease-free hemisphere to evolve the tumor. The second data set was provided by the authors of [16], who reported the speed of tumor growth in the white matter of ${\upsilon }_w=2\sqrt{D_w\rho }=2\sqrt{.2·.008}$ mm/d for this patient.

Results

Fig. 4 shows the adaptive sparse grid for the parameters of the growth model θ_p (left) and the tumor seed point θ_x (right). Green dots represent sampling points used to construct the approximation of the posterior in Eq. (12). The right image shows the central slice of the synthetic high grade data set. Indicated by dots are {x, y} positions of the location parameters θ_x. Dot size indicates the number of model evaluations with varying {z,D, ρ} for the given {x, y}. We find most of the adaptively chosen locations to be close to the real location of the tumor (pink cross). This also holds true for the parameter space spanned by diffusivity D and proliferation ρ in the left image. Here the location close to the actual parameter (pink cross) is the one evaluated for the highest number of different seed points. The contour map shows the likelihood evaluated on a regular grid with the true seed point θ_x and is in good agreement with the adaptively sampled locations on the sparse grid. The most likely region is a diagonal line in D-ρ space, similar to areas of constant shape in Fig. 3 (right) and orthogonal to regions of constant speed of growth in Fig. 3 (left). This indicates that information about the shape of the tumor is effectively used to infer model parameters in our proposed approach.

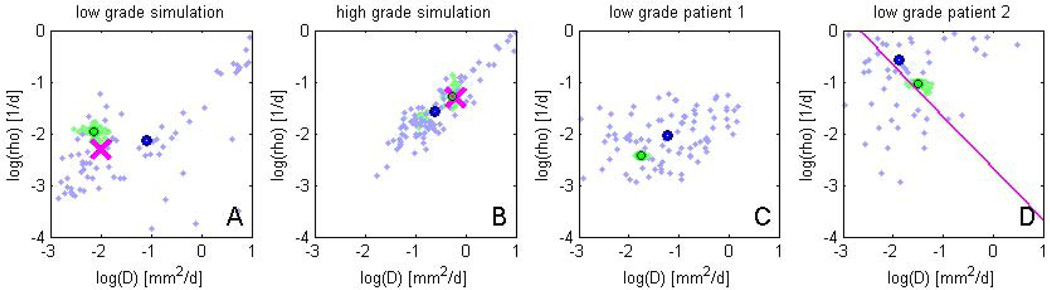
Fig. 5 reports estimates of the model parameters D and ρ for all four test cases and both the direct sampling (blue) and the sparse grid sampling (green). For the first two data sets (A, B), the sparse grid sampling is in good agreement with the ground truth (pink cross). The mean value of the direct sampling (blue/black circle) is relatively close to ground truth and the mean of the sparse grid sampling (green/black circle). We find the sparse grid results to be much more compact with noticeably less variation. This observation is also true for the patient data (C, D). We used the current number of 3000 samples for sparse grid MCMC only to allow for a direct comparison of both approaches. Already an interpolation with a few hundred samples led to results similar to those in Fig. 3, demonstrating the benefits of the sparse sampling approach for estimating parameters of the tumor model.

Fig. 5.

MCMC sampling results in the space spanned by model parameters D and ρ, for the four experiments. Green samples are obtained from the sparse grid interpolation Eq. (12), blue-purple samples come from the direct sampling in Eq. (10). Black circles indicate means of the two distributions. Ground truth for A and B are indicated by the pink cross. In D the previously estimated speed of growth [16] is shown by the pink line. The sparse grid sampling approximation performs better than the direct MCMC (A–B). Estimates correlate well with results from [16], but provide a more accurate characterization of the state of disease (D).

Results in Fig. 5 can also be interpreted in terms of the diagnostic task. In subfigure C, results suggest a “classical” low-grade tumor, well in agreement with the expected parameters for low-grade patients (Fig. 3, left). In subfigure D, we observe a more infiltrative and rapidly growing tumor. This is in good agreement with the clinical observation of the tumor expanding several centimeters per year and showing a star-shaped pattern, often associated with poor prognosis. The data in D had already been evaluated in [16] and the authors had estimated the speed of the tumor front shown as the red pink diagonal line in D. We observe a good agreement of our results with this earlier estimate, but obtain the additional information that the expansion of the tumor is not due to a fast infiltration, but a rapid doubling of tumor cells with a direr prognosis for this particular patient.

5 Conclusions

The proposed tumor modeling approach links the physical process model with the statistical image observation model and enables efficient estimation of model parameters in a Bayesian framework, potentially also to be used with model components at different scales and with different sources of information. Preliminary results are promising. The approach can readily be adapted to incorporate information from other functional imaging modalities, and to model mass effect and tissue translations, or tissue alterations resulting from therapy.