OSCILLATION MECHANICS OF THE RESPIRATORY SYSTEM: APPLICATIONS TO LUNG DISEASE

Abstract

Since its introduction in the 1950s, the forced oscillation technique (FOT) and the measurement of respiratory impedance have evolved into powerful tools for the assessment of various mechanical phenomena in the mammalian lung during health and disease. In this review, we highlight the most recent developments in instrumentation, signal processing, and modeling relevant to FOT measurements. We demonstrate how FOT provides unparalleled information on the mechanical status of the respiratory system compared to more widely-used pulmonary function tests. The concept of mechanical impedance is reviewed, as well as the various measurement techniques used to acquire such data. Emphasis is placed on the analysis of lower, physiologic frequency ranges (typically less than 10 Hz) that are most sensitive to normal physical processes as well as pathologic structural alterations. Various inverse modeling approaches used to interpret alterations in impedance are also discussed, specifically in the context of three common respiratory diseases: asthma, chronic obstructive pulmonary disease, and acute lung injury. Finally, we speculate on the potential role for FOT in the clinical arena.

INTRODUCTION

The primary function of the respiratory system is gas exchange, which relies on the movement of air to and from the alveoli, a physiologic process known as ventilation. Ventilation requires driving pressures to overcome the resistive, elastic, and (under special circumstances) inertial components of the lungs and chest wall. The magnitudes of these components are often used as indices of energy dissipation and storage associated with the process of ventilation and work of breathing. The resistance and elastance of the respiratory system exhibit dependence on breathing frequency across all mammalian species due to several mechanical processes, such as tissue viscoelasticity ¹, parallel and serial time constant heterogeneity ^2,3, and collateral ventilation ^4,5. Since its introduction in the 1950s, the forced oscillation technique (FOT) has evolved into a useful method for determination of these processes’ relative roles in ventilation during health and disease, as well as their unique and distinct contributions to the lung’s mechanical behavior. With FOT, time-varying flows of one or more frequencies are forced into the lungs at the airway opening. The complex ratio of the resulting pressure to the delivered flow is defined as the mechanical input impedance, Z. Experimental studies in both humans and animals, as well as simulation studies with morphometric models, indicate that the frequency-dependent features of Z permit inferences on the distribution of obstruction in the airways ^6,7 and in some situations, allow the partitioning of airway and parenchymal mechanical properties ^8-10. Such information may provide the clinician with much needed insight into the pathophysiological mechanisms contributing to compromised lung function and the effectiveness of medical and/or surgical interventions.

Many diseases of the respiratory system manifest themselves as mechanical derangements, which are usually assessed using various standard tests of pulmonary function ¹¹. Nonetheless data from such tests (i.e., plethysmography and maximal effort spirometry) are very nonspecific for identifying pathologic structural alterations in the lungs. In contrast, impedance data, especially when interpreted with models unique to specific physiologic mechanisms and/or pathologic alterations, do provide very unique insight into structure-function relationships ^12-15. Moreover, FOT approaches require minimal subject cooperation, a considerable advantage when dealing with pediatric or critically-ill patients. Despite the diagnostic potential of FOT, there has been relatively little effort to incorporate its use into routine clinical practice ¹⁶. This may reflect the technical difficulty in its measurement, as well as its obscure physiological interpretation in the presence of highly nonlinear and pathologic processes such as dynamic airway compression ^17-19, intratidal derecruitment ²⁰, and parenchymal overdistention ²¹. Moreover, clinically practical and efficient methods to measure impedance in patients have remained elusive until recently ^18,22-25.

This review will emphasize the authors’ own experience with FOT, as well as most recent developments in relevant instrumentation, signal processing, and modeling. Similar to earlier reviews on the topic ^26-30, this paper will illustrate how FOT provides unparalleled information on the mechanical status of the respiratory system compared to more widely used measures of pulmonary function. We will review the concept of mechanical impedance and the various measurement techniques used to acquire such data. Emphasis will be placed on the analysis of lower, physiologic frequency ranges (typically less than 10 Hz) that are particularly sensitive to normal physical processes as well as pathologic structural alterations. We will also discuss various inverse modeling approaches used to interpret alterations in impedance, specifically in the context of three common respiratory diseases: asthma, chronic obstructive pulmonary disease (COPD), and acute lung injury (ALI). Finally, we will speculate on future developments for FOT and its use in the clinical arena.

CONCEPT OF MECHANICAL IMPEDANCE

FOT was first introduced in the 1950s by Dubois et al. to measure the mechanical impedance of the respiratory system ³¹. The concept of mechanical impedance, similar to electrical impedance in AC circuit analysis, is grounded in the theory of linear systems ^32,33, in which a black-box representation of the respiratory system embodies a precise quantitative relationship between specific pressures and flows measured during oscillatory motion. Presumably, this relationship arises from the resistive, inertial, and elastic contributions of the lungs and / or chest wall. Impedance (Z) is defined as the complex ratio of pressure (P) to flow (V̇) as a function of oscillation frequency (ω):

(1) $$Z\left(\omega \right)=\frac{P\left(\omega \right)}{\stackrel{.}{V}\left(\omega \right)}$$

In polar notation, Z is expressed with a magnitude, to account for relative differences in the amplitudes between the sinusoidal pressures and flows, as well as a phase angle, to account for time shifts (i.e., leads or lags) between them ³⁴. More commonly, Z is expressed in Cartesian coordinates in the complex plane, with resistive (R) and reactive (X) components, allowing for separation of those processes associated with energy dissipation and energy storage, respectively:

$$Z\left(\omega \right)=R\left(\omega \right)+jX\left(\omega \right)$$ (2)

where j is the unit imaginary number, defined as $\sqrt{-1}$. For the respiratory system, resistance arises from the viscous flow of gas through the airways ³⁵, as well as energy losses associated with the deformation of the parenchyma ³⁶ and chest wall ³⁷. For frequencies below 10 Hz, reactance is comprised of an inertial component (I) due to acceleration of gas in the central airways, as well as an elastic component (E) due to the recoil of the parenchyma and chest wall:

$$X\left(\omega \right)=\omega I-\frac{E}{\omega }$$ (3)

Equation 3 demonstrates that a specific frequency exists, termed the resonant frequency (ω_o), for which the reactance will be zero and impedance will be due solely to resistive losses. Rearranging Equation 3 and solving for X(ω) = 0, we obtain

$${\omega }_o=\sqrt{\frac{E}{I}}$$ (4)

At ω_o, the magnitude of impedance will be at a minimum. Over low frequencies (i.e., ω << ω_o), inertia will have a negligible contribution to impedance, and the reactance will be determined largely by the recoil of the parenchymal or respiratory tissues. In this situation, it is common practice to express reactance as elastance as a function of frequency ^38-40:

$$E\left(\omega \right)=-\omega X\left(\omega \right)$$ (5)

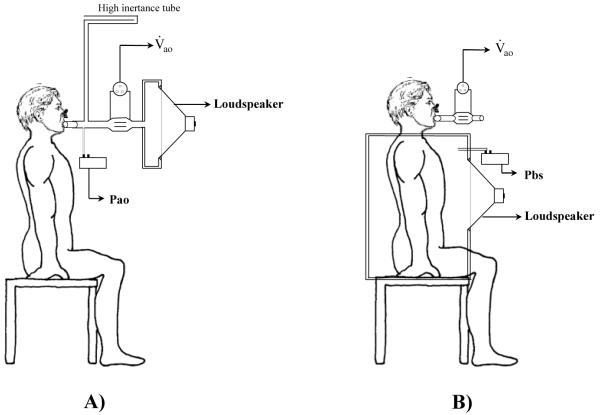
Generally, mechanical impedance is measured in one of two ways. First, pressure oscillations may be generated around the body surface (P_bs) while measuring the resulting flow at the airway opening (V̇_ao). Here the subjects’ torso, or entire body, is encased in an airtight chamber (Figure 1-B). The ratio between P_bs and V̇_ao is termed transfer impedance (Z_tr) ³¹. Alternatively, oscillatory flows may be presented to the airway opening while simultaneously measuring the resulting airway opening pressure (P_ao) relative to atmosphere. The ratio between P_ao and V̇_ao, when the chest wall is intact, is the input impedance of the total respiratory system (Z_rs). If P_ao is measured relative to the pressure at the pleural surface (P_pl, often approximated using an esophageal balloon in the living subject), the ratio (P_ao − P_pl)/V̇ is the input impedance of the lungs alone (Z_L). Given that P_ao and V̇_ao are usually the most easily accessible and transduced variables in the clinical setting, this review will concentrate on the more intuitive input impedance only.

Figure 1.

Two methods for measuring impedance with forced oscillations. (A) Input impedance (Z_in) technique, in which oscillatory V̇_ao is applied at the mouth or trachea while measuring airway opening pressure (P_ao). (B) Transfer impedance (Z_tr) technique, in which pressure oscillations are applied at the body surface (P_bs) while flow at the airway opening (V̇_ao) is measured.

Mechanical impedance reflects very different physical processes depending on the frequency range studied or the presence of lung disease. Traditionally, input impedance data was acquired in the range of 4 to 32 Hz, as this allowed the human subject to breath spontaneously through a high inertance tube to-and-from ambient during the measurement, with minimal band-overlap between the spectral energy of the natural breathing waveforms and the imposed oscillations ^27,29. After high pass filtering the measured flow and pressures signals, impedance could be computed using various Fourier Transform methods ^34,41,42. While simple to acquire, impedance data acquired within this bandwidth is the least informative in terms of physiology ⁴³. Over this frequency range, the real part of impedance is generally constant with frequency, while the imaginary part increases monotonically with frequency, behaviors consistent with simple, constant resistive-inertial-compliant properties of the respiratory system ^29,31.

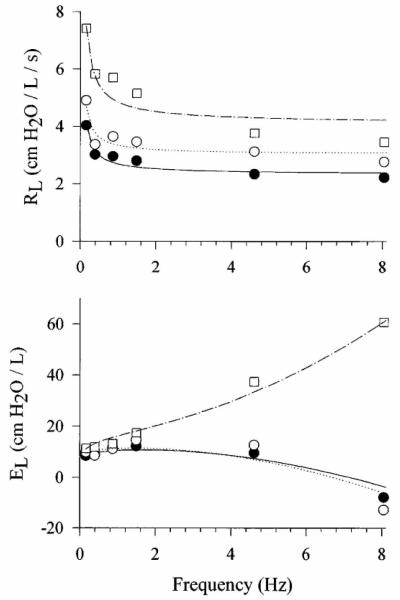
By contrast, input impedance measured over the 0.1 to 10 Hz bandwidth reflects far more interesting phenomena. For example, parallel time constant heterogeneity ², airway wall distensibility ³, parenchymal viscoelasticity ^44-46, expiratory flow-limitation ⁴⁷ and collateral ventilation ⁴ have their greatest influence on input impedance over this lower frequency range. A typical impedance spectrum from 0.156 to 8.1 Hz, expressed as lung resistance (R_L) and elastance (E_L), is shown for a healthy awake human subject in Figure 2. Both R_L and E_L are strongly dependent on oscillation frequency, primarily due to viscoelasticity of the parenchymal tissues⁴⁸. Specifically, R_L shows a frequency-dependent drop from 0.156 to 1.0 Hz, and attains a plateau by 2-4 Hz. The E_L increases slightly with frequency between 0.156 to 1.0 Hz, then decreases at higher frequencies and becomes negative due to the inertia of gas in the central airways. Figure 3 shows R_L and E_L spectra for a healthy subject at baseline and following small and large doses of inhaled methacholine, a cholinergic agonist that causes bronchoconstriction. With mild bronchoconstriction, R_L slightly increases compared to baseline at all frequencies, while E_L changes minimally. For the more moderate level of bronchoconstriction, R_L becomes highly elevated at all frequencies relative to baseline. While E_L is increased slightly for frequencies below 1 Hz, it demonstrates a strong positive frequency-dependence above 1 Hz. The physiologic mechanisms contributing to such observed behavior in R_L and E_L will be discussed below in the context of inverse modeling.

Figure 2.

Lung resistance (R_L) and elastance (E_L) versus frequency in a representative healthy human subject under baseline conditions. Shown are the actual measured data (symbols) along with corresponding model fit (lines) using Equation 9. Modified from Reference ³⁸, with permission.

Figure 3.

Lung resistance (R_L) and elastance (E_L) versus frequency in a representative human subject at baseline (●) and following inhalation of methacholine aerosol at concentrations of 0.025 mg/ml (○) and 20.0 mg/ml (□). Also shown are corresponding model fits using Equation 9 (lines). Modified from Reference ³⁸, with permission.

MEASUREMENT TECHNIQUES

Instrumentation

A key requirement for any study of oscillatory mechanics of the respiratory system is a device capable of generating high-fidelity pressure or flow excitations to which the lungs and/or chest wall will be exposed. For frequencies within the commonly used 4-32 Hz bandwidth, this can usually be accomplished with a loudspeaker system with appropriate dynamic response^34,49, which may be placed in parallel with a mechanical ventilator or other respiratory assist devices^50-53. Lower excitation frequencies, especially those surrounding physiologic breathing rates, require relatively load-independent generators with sufficient dynamic responses that encompass such bandwidths. Measurements at these lower frequencies have traditionally been obtained with reciprocating piston-pumps actuated by servo-controlled linear motors ^31,54,55. More recently, low frequency pressure waveforms have been generated with considerable fidelity using a proportional solenoid valve incorporated into a closed-loop system, as this allows for fine control of both mean and oscillatory components of airway pressure^12,40,56. However in awake subjects, such low frequency measurements require considerable training and cooperation to allow complete relaxation of the diaphragm and chest wall muscles^38,39,57, which may be impractical for patients with lung disease²². Many of these forced oscillation systems can easily be incorporated into existing ventilator platforms in the operating room or intensive care unit, to allow for bedside assessment of respiratory mechanics with minimal disruption of ventilatory support^51,52.

Recent advances in digital microelectronics have lead to the availability of powerful microprocessors at very low cost, allowing for simple, robust, and portable designs for FOT devices. Rigau et al. have shown that FOT was potentially applicable to home monitoring ^58,59. A recent study by Dellaca et al. demonstrated the feasibility of using an inexpensive FOT system for real-time data acquisition, processing, and internet streaming ²⁴. These preliminary studies support the idea that FOT could potentially be used for daily home assessment of obstructive lung diseases and the management of their exacerbations.

Another necessary requirement for FOT is the accurate measurement of oscillatory signals during the excitation, which must be electrically transduced to allow for necessary filtering, display, digitization, and storage. This requires knowledge of a particular transducer’s linearity, measurement range, frequency response^60,61. Fundamental to any study of oscillatory mechanics of the respiratory system is the measurement of pressure, which may be obtained at the airway opening³⁸, around the body surface³¹, within the esophagus⁶², or even within the airways or alveoli^63-65. Any of these pressures may be transduced relative to atmosphere by differential sensors with one of the two inputs left open to ambient. Traditionally, variable reluctance transducers have been used for FOT measurements, as they have both high sensitivity and adequate frequency response^66,67. These transducers behave similarly to an AC transformer, in which a pressure-sensing diaphragm made of magnetically permeable material is mounted between two induction coils. The primary coil is exciting by an AC current of several kHz, which induces a voltage in the secondary coil. When diaphragm moves in response to a differential pressure, the deformation affects the efficiency of induction in the secondary coil. This results in an alteration in the magnetic flux linkage between the coils, which can be detected by appropriate electronic circuits. More recently, improvements in semiconductor production have lead to the development of reliable, accurate, and inexpensive piezoresistive transducers, in which the electrical resistance of the sensing diaphragm changes in response to an applied force. These small devices also have reduced internal gas volume and diaphragm compliance, resulting in an even better frequency response compared to variable reluctance transducers.

Oscillatory flow measurements are commonly made with pneumotachographs, which maybe of the mesh screen or capillary tube type (Fleisch) variety⁶⁸. These devices produce a pressure drop that is ideally linearly related to flow according to Poiseuille’s Law⁶⁹. The effective mechanical resistance offered by the pneumotachograph, and hence its corresponding pressure drop, will be dependent not only on the geometry of its connecting conduits, but also on the viscosity of the particular species of gas being measured⁷⁰. Several calibrations may therefore be required if flow measurements are to be made under varying oxygen levels or different concentrations of inhaled anesthetics ⁷¹. Moreover, all pneumotachographs have unique dynamic responses that will systematically distort the measured magnitude and phase of any oscillatory flow, depending on frequency ⁷². This may require additional dynamic compensation, especially for frequencies above 20 Hz ^73-75. In addition, since the measured flow is based on a differential pressure drop, pneumotachographs may require correction for transducer asymmetry and finite common-mode rejection ratio⁷⁶. Finally for prolonged measurements, the pneumotachograph should contain a heating element to minimize the error associated with condensation⁷⁰, although this will not prevent it from becoming clogged with respiratory secretions. Alternatively, hot wire anemometers can also measure oscillatory flows over a much broader bandwidth^77,78. In contrast to pneumotachography, which relies on the measurement of a pressure drop across a fluid resistive element, hot wire anemometry relies on changes in the electrical resistance of a current-carrying filament⁷⁹. As gas flows past the wire, its temperature decreases, resulting in a corresponding change in its electrical conductivity which can be measured with a standard Wheatstone bridge circuit⁸⁰.

Signal Processing

To calculate impedance spectra from oscillatory flow and pressure waveforms, several signal processing techniques can be used. The simplest and most direct is to excite the respiratory system at one discrete frequency while the subject remains apneic, and then determine the value of impedance from the corresponding pressure and flow using Equation 1 at this frequency. By continually forcing the respiratory system with different discrete frequencies, values of the impedance can be obtained over a particular frequency range^81-83. Obviously this method becomes quite time consuming, depending on the desired frequency resolution and range, and is impractical for serial impedance measurements to assess the temporal dynamics of a pharmacologic agonist⁸⁴. A more efficient method involves exciting the system with broadband waveforms which simultaneously contain all frequencies of interest. This can be done using multiple sinusoids⁸⁵ or small-amplitude random noise ³⁴. The input flow and output pressure signals can then be spectrally decomposed into their individual frequency components using standard Fourier analysis^41,86,87, from which the value of the impedance can be determined at each particular frequency. When multi-frequency forcing signals are used, the spectra are most reliably estimated as:

$$Z\left(\omega \right)=\frac{G_{P\stackrel{.}{V}}\left(\omega \right)}{G_{\stackrel{.}{V}\stackrel{.}{V}}\left(\omega \right)}$$ (6)

where G_PV̇ is the cross-power spectrum between pressure and flow, and G_V̇V̇ is the auto-power spectrum of flow. The estimates of G_PV̇ and G_V̇V̇ are obtained by averaging the periodograms computed from several data segments, with each segment containing one or more forcing periods⁴¹. The advantage of this periodogram approach is that it readily yields the so-called coherence function (γ²) between flow and pressure at each frequency:

$${\gamma }^2\left(\omega \right)=\frac{\mid G_{P\stackrel{.}{V}}^2\left(\omega \right)\mid }{G_{\stackrel{.}{V}\stackrel{.}{V}}\left(\omega \right)G_{PP}\left(\omega \right)}$$ (7)

The coherence can be used as an index of causality between the input flow and output pressure of the respiratory system⁸⁸, and ranges in value between 0 and 1. For the purposes of assessing the quality of impedance data, values less than 0.95 are usually discarded^38,39. Nonlinearities in the respiratory system may result in a distorted estimate of Z or γ^{2 88,89}, although such distortions can be minimized by excitation with frequencies that are non-integer multiples of the fundamental frequency⁹⁰ or that are mutually prime^38,91,92.

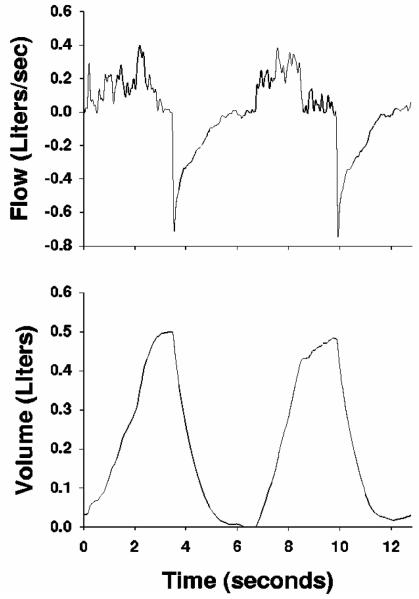
For low frequencies surrounding typical breathing rates, small amplitude forcings, which require the awake subject to remain apneic⁵⁷, may be impractical for patients with significant lung disease. Moreover their use in intubated patients usually requires discontinuation of artificial ventilatory support⁵¹, although attempts have been made to extract impedance data at multiple frequencies using standard volume-cycled waveforms^87,93-95. These attempts have been largely unsuccessful due to the limited spectral energy in such waveforms above the fundamental frequency, yielding poor signal-to-noise ratio at the higher harmonics. To overcome these limitations, Lutchen et al. proposed the use of an Optimal Ventilator Waveform (OVW) as a more practical and efficient method for measuring low frequency input impedance in humans ⁹². The OVW is a broad-band oscillatory flow input designed to estimate the frequency response of the lungs during tidal-like excursions (Figure 4-A). The signal-to-noise ratio of this waveform is enhanced for frequencies above the fundamental frequency, and its spectral energy is concentrated only at specific frequencies to minimize harmonic distortions in the resulting pressure⁹¹. In a subsequent study, Kaczka et al. designed a variation of this original OVW to make it more amenable for awake humans³⁸. Here the magnitude spectrum of the waveform is adjusted such that the primary frequency of ventilation was more comfortable for the subject, but modulated by smaller amplitude energy at lower frequencies (Figure 4-B). While the OVW is useful for patients with mild-to-moderate obstruction who can be trained to relax their chest wall muscles^38,39, it is not appropriate to use in severely obstructed patients²². Moreover since the OVW is delivered via a closed system, a bias flow of fresh gas must be delivered into the breathing circuit to ensure sufficient gas exchange³⁸.

Figure 4.

Flow and volume tracings for two types of Optimal Ventilator Waveforms (OVWs) with 12.8-second periods. (A) OVW in which peak spectra energy occurs at 0.156250 Hz, with two distinct physiologic breaths per period. (B) OVW in which peak spectra energy occurs at 0.390625 Hz, with five distinct physiologic breaths per period and lower frequency modulation at 0.156250 Hz. Modified from Reference ³⁸, with permission.

One drawback of using the above Fourier analysis method to estimate respiratory impedance is the assumption of system stationarity during the measurement period. However when a discrete sinusoidal forcing is used with a frequency sufficiently faster than breathing rates (i.e., 5-10 Hz), it is possible to compute impedance with a high temporal resolution and track within-breath variations of respiratory mechanical properties. In this case the impedance can be obtained from algorithms based on cross-correlation^96,97, Fast Fourier Transforms^53,98, or various recursive and nonrecursive least square techniques^47,87,99-102. Within-breath analysis of impedance is potentially valuable for a wide range of clinical applications, such as detection of obstructive sleep apnea and expiratory flow-limitation ^25,47,103, the evaluation of lung mechanics during positive pressure ventilation ¹⁰⁴, and examining the effects of deep inspirations on airway constriction ^101,105,106.

INVERSE MODELING OF IMPEDANCE

One way to characterize the relationship between pressure and flow of the respiratory system is to develop an electromechanical analogue that is structurally sensible and can simulate actual impedance data. Ideally, the parameters of such a model should be related to the basic physiologic properties of the respiratory system. Input impedance within the commonly used 4-32 Hz bandwidth can be reasonably predicted (Ẑ) with simple linear resistance (R), inertance (I), and elastance (E) elements in series, all of which are assumed to be constant with frequency ³¹:

$$\widehat{Z}\left(\omega \right)=R+j\omega I+\frac{E}{j\omega }$$ (8)

Nonetheless, such a model is far too simple to characterize dynamic mechanical behavior for most pathologies of the respiratory system, especially for frequencies below 4 Hz where natural breathing occurs. As already noted, dependence of R and E on breathing frequency has been observed across all mammalian species in both health and disease, and many different but physically plausible mechanisms can account for such dependencies. Thus more complicated models must be used to mimic many of these phenomena³³.

When pressures across the airways and within the parenchyma are sampled using alveolar capsules in healthy mammalian lungs⁶⁴, it is observed that parenchymal tissue resistance decreases near-hyperbolically with increasing frequency, while airway resistance remains fairly constant^107-109. Such behavior is consistent with the parenchyma being a viscoelastic material ⁴⁸. Given these distinct frequency responses of the airways and tissues, Hantos et al.¹¹⁰ described Z_L with a frequency-domain variant of Hildebrandt’s stress-relaxation model¹¹¹, consisting of a homogeneous airways compartment containing an airway resistance (R_aw) and inertance (I_aw) elements leading to a viscoelastic, constant-phase tissue compartment (Figure 5-A). This tissue compartment has two parameters: tissue damping (G) and tissue elastance (H). For this model, the predicted lung impedance (Ẑ_L) as a function of angular frequency (ω) is given by:

$${\widehat{Z}}_L\left(\omega \right)=R_{aw}+j\omega I_{aw}+\frac{G-jH}{{\omega }^{\alpha }}$$ (9)

where

$$\alpha =\frac{2}{\pi }{\tan }^{-1}\left(\frac{H}{G}\right)$$ (10)

This model has four independent parameters (R_aw, I_aw, G, and H) which may be estimated using various nonlinear gradient search algorithms^107,112,113 or recursive multiple linear regression³³. Moreover it is compatible with ‘structural-damping’, which assumes that the ratio of dissipative and elastic processes in the lung parenchyma, referred to as hysteresivity³⁶, is constant with frequency and given by η = G/H. Also consistent with alveolar capsule data^10,109, the model predicts that parenchymal tissue resistance (R_ti) decreases quasi-hyperbolically with frequency:

$$R_{ti}\left(\omega \right)=\frac{G}{{\omega }^{\alpha }}$$ (11)

A limitation of this model, however, is the assumption that impedance can be sufficiently described by serial compartments representing homogenous airways and tissues. Such an assumption is not always valid, especially under pathologic conditions for which heterogeneity results in additional frequency-dependence in impedance that is not due to viscoelasticity alone^9,40,114,115. For example the subject of Figure 3 experiences widespread peripheral airway constriction following a large dose of inhaled methacholine, which results in the shunting of oscillatory flows into the central airway walls^116,117. Above 1 Hz, the measured E_L for this subject increases with frequency, as its value approaches the elasticity of the central airway walls³. In this case, the model of Equation 9 can be modified by dividing the homogeneous airway compartment into two equal halves by an additional shunt airway compliance parameter to account for non-rigid airway walls (Figure 5-C). Such a model may be more appropriate to describe lung mechanics in patients with severe asthma³⁹ or COPD²², as it mimics this ‘airway shunting’ behavior and more accurately partitions the mechanical behavior of the airways and lung tissues³⁸.

Figure 5.

Various models used to describe oscillatory mechanics of the lungs. (A) Model consisting of homogeneous airways with resistive (R_aw) and inertial (I_aw) components in series, with ‘constant-phase’ viscoelastic tissues containing parameters for tissue damping (G) and tissue elastance (H). (B) Inhomogeneous airways model with two separate parallel pathways, each containing distinct airway resistive parameters (R_aw1 and R_aw2) but identical I_aw parameters and identical tissue compartments (C) Model containing an airway compliance parameter (C_aw) to account for the shunting of oscillatory flow into non-rigid airway walls. j, unit imaginary number; ω, angular frequency; P_pl, pleural pressure. Modified from Reference ³⁸, with permission.

To compensate for parallel time-constant inhomogeneities, the homogeneous airways model can also be modified to contain two separate R_aw pathways, both leading to identical constant phase tissues (Figure 5-B). The resulting inhomogeneous airways model is structurally analogous to a similar two-compartment model first described by Otis et al. ², which compartmentalizes the lungs into ‘healthy’ and ‘diseased’ portions. However a more accurate description of lung mechanical behavior for many different pathologies may be obtained by distributing parallel heterogeneity across an arbitrary number of parallel pathways^{12,40,118-120}. Such models allow for stochastic variability in R_aw or H, depending on whether one seeks to ascribe the variation to airway or tissue heterogeneity, respectively. For example to characterize heterogeneous airway obstruction, we may assume that the distribution of parallel airway resistances can be approximated with a predefined probability density function, P(R_aw), with lower and upper bounds R_aw,min and R_aw,max, respectively. The impedance predicted by such a model is given by:

$${\widehat{Z}}_L\left(\omega \right)={\left[\underset{R_{aw,min}}{\overset{R_{aw,max}}{\int }}\frac{P\left(R_{aw}\right)}{R_{aw}+j\omega I_{aw}+\frac{G-jH}{{\omega }^{\alpha }}}d{R}_{aw}\right]}^{-1}$$ (12)

In contrast to the model described by Equation 9 with four independent parameters, this model requires the estimation of five parameters (R_aw,min, R_aw,max, I_aw, G, and H). For pathologies associated with heterogeneity in parenchymal mechanics, such as emphysema or acute lung injury, we may assume a similar topology that allows for variations in tissue elastance between H_min and H_max:

$${\widehat{Z}}_L\left(\omega \right)={\left[\underset{H_{min}}{\overset{H_{max}}{\int }}\frac{P\left(H\right)}{R_{aw}+j\omega I_{aw}+\frac{G-jH}{{\omega }^{\alpha }}}dH\right]}^{-1}$$ (13)

Both of the models described by Equations 12 and 13 yield an ‘effective’ airway resistance or tissue elastance from the mean of the distribution function P. An estimate of the ‘heterogeneity’ of the airways or tissues can be obtained from the standard deviation of P^40,118.

While the models described by Equations 9, 12, and 13 do not provide any specific information on anatomy or structure, they do have the ability to characterize global dynamic lung function with a minimal number of physical parameters^114,118. Of course, the validation of any candidate model of lung mechanics requires reliable information on the structural alterations associated with a particular disease for comparison with model predications^12,33,114. Recent studies combining various functional imaging modalities with impedance measurements have yielded tremendous insight into how specific alterations in structure impact mechanical function^{12,13,121-123}.

There are limitations with inverse modeling, as one cannot expect to extract all of the mechanisms contributing to the frequency-dependent features in Z, especially when the number of data points fitted is slightly larger than the number of model parameters¹¹⁴. While increasing the complexity of the model to account for additional mechanisms may significantly improve the fit to the data, the resulting parameters may become statistically unreliable^124,125. Moreover, obtaining a model with the best statistical fit to the data does not imply that all of the physiological mechanisms contributing to the frequency dependence of Z have been account for. Indeed depending on pathology, many different mechanisms may simultaneously contribute to the respiratory system’s mechanical behavior over similar frequency ranges. Nonetheless, inverse modeling is useful in distinguishing which mechanisms dominate the impedance data for a specific physiologic state or disease¹².

ASTHMA

Asthma is a disease characterized by a hyperresponsiveness to a variety of stimuli (e.g., allergens, cold air, exercise, aspirin), resulting in variable airflow obstruction and increased airway resistance. In allergic asthma (the most common form), the airways exhibit hypertrophy of surrounding smooth muscle and mucous glands, along with extensive infiltration by eosinophils. Here, inhaled allergens bind to IgE antibodies on the surface of mast cells within the bronchial mucosa. This antigen-antibody reaction causes mast cells to degranulate and release a variety of inflammatory mediators, such as histamine, neutrophil and eosinophil chemotactic factors, bradykinin, and others. It is these mediators that result in smooth muscle contraction and mucus production, as well as increased vascular permeability and edema. The release of mediators from eosinophils (leukotriene B₄ and PAF) result in damage to the bronchial epithelium, causing further bronchoconstriction and mucus secretion via reflex vagal discharge. If these inflammatory processes are left untreated, airway wall remodeling and adventitial thickening can develop, which may attenuate the dynamic tethering forces that airway smooth muscle is normally subjected to during tidal breathing. This decreases the load against which the muscle must shorten, thus further predisposing it to constriction ¹²⁶. During asthmatic exacerbations, airway resistance can become highly elevated due to contraction and hypertrophy of airway smooth muscle, mucus plugging, and edema. This elevation in airway resistance can often, though not always, be reversed by inhalation of a β-agonist such as albuterol, which relaxes airway smooth muscle^127,128.

While asthma has traditionally been considered an airway disease, plethysmographic measurements in asthmatics raised the possibility that parenchymal tissue resistance, R_ti, may also have a significant role in its pathophysiology^129-131. For example, alveolar capsule studies in different species have reported greater increases in R_ti during histamine or methacholine induced-bronchoconstriction compared to that of R_aw ^132-135. Such alterations in R_ti may be the result of airway-tissue interdependence¹³⁶ or a contractile response of the parenchymal tissue itself^137,138. However, the exact mechanism for increases in R_ti remains a matter of controversy. For example, previous studies have demonstrated that airway heterogeneity can result in an artifactually high R_ti, whether measured directly with alveolar capsules or based on inverse modeling of Z_L ^8,9,84,110. Nonetheless, information on R_ti may be clinically important to separate those asthmatics whose disease involves primarily airway smooth muscle constriction from those with a more inflammatory component which may alter or damage the lung tissues.

To answer these questions, Kaczka et al. used the OVW to measure low-frequency Z_L in 21 asthmatic human subjects during spontaneous bronchoconstriction and following albuterol inhalation³⁹. To determine the relative contributions of R_aw and R_ti to R_L in these subjects, the resulting Z_L spectra were analyzed in terms of the various model forms of Figure 5. These authors demonstrated that asthmatics can be classified into two distinct groups based on their Z_L spectra (Figure 6). Eleven subjects were classified as Type A asthmatics, displaying slightly elevated R_L for all frequencies at baseline, but normal E_L. After albuterol inhalation, their R_L decreased while E_L remained unchanged. Their Z_L data were best described by the homogeneous airways constant-phase model of Figure 5-A pre- and post-albuterol. The other 10 subjects were classified as Type B asthmatics. They demonstrated highly elevated R_L at baseline and pronounced posititve-frequency-dependence in E_L for frequencies above 2 Hz. The baseline Z_L data for these subjects were best described by the airway shunt model of Figure 5-C, consistent with pronounced peripheral airway constriction and shunting of oscillatory flow into the central airway walls. However post-albuterol, the Z_L data of the Type B asthmatics were best described by the homogeneous airways model. Spirometric data were consistent with higher levels of bronchoconstriction in Type B subjects. The inverse model parameters from both groups demonstrated significant reductions in R_aw and G following albuterol, although only the Type B asthmatics demonstrated significant reductions in H. More importantly, the percent contributions of R_aw and R_ti to R_L were similar for both groups, with R_aw contributing about 70% of R_L near physiologic breathing frequencies, and did not change following albuterol inhalation. Thus, the contribution of R_ti to R_L appears to be independent of the degree of smooth muscle constriction. Moreover, this assessment of impedance in human subjects demonstrates the importance of peripheral airway constriction in the pathophysiology of mild-to-moderate asthma. This has also been confirmed more recently by combining various functional lung imaging techniques (i.e., PET, hyperpolarized MRI) with impedance measurements in asthmatics during bronchoprovocation^121-123.

Figure 6.

Examples of lung resistance (R_L) and elastance (E_L) versus frequency for two representative patients with asthma before (○) and following (●) albuterol inhalation. Also shown are corresponding fits using the homogenous airways model of Equation 9 (solid line) as well as the airway shunt model of Figure 5-C (dashed line). Modified from Reference ³⁹, with permission.

CHRONIC OBSTRUCTIVE PULMONARY DISEASE

Chronic obstructive pulmonary disease (COPD) is associated with irreversible airway obstruction (bronchitis) as well as parenchymal tissue destruction (emphysema). Pulmonary function deteriorates in a slow and progressive manner. Chronic obstructive pulmonary disease (COPD) refers to either chronic bronchitis, emphysema, or a combination of the two¹³⁹. Chronic bronchitis is defined as the presence of a chronic productive cough without a discernible cause for more than half the time over a period of two years. Emphysema is an anatomic diagnosis, characterized by a pathological enlargement of air spaces distal to terminal bronchioles and progressive destruction of the alveolar walls. A common factor in the development of emphysema is the reduction in activity of elastase inhibitors, resulting in destruction and disorganization of elastin fibers in the lung. Thus, emphysematous lungs have an increased compliance and a reduced elastic recoil pressure. The destruction of lung parenchyma may cause a loss of radial traction on the airways. This loss of airway tethering, combined with the loss of elastic recoil pressure, enhances the dynamic compression of the airways during expiration, resulting in expiratory flow-limitation (EFL) that can severely compromise tidal breathing. EFL is a central feature of the pathophysiology of COPD. Moreover, it is a highly nonlinear phenomenon in which airflow is no longer dependent on the pressure drop across the airways. Its presence during tidal breathing or forced oscillations will obscure the physiologic meaning of linear, time-invariant descriptions of lung mechanics, such as impedance. For example, the effect of bronchodilators in COPD as assessed with impedance is greatly underestimated if EFL is present ¹⁹.

Most techniques used to quantify functional impairment in patients with COPD rely on spirometry, although this can be very nonspecific in distinguishing fixed, bronchitic airway obstruction from premature expiratory airway collapse arising from decreased parenchymal tethering. Nonetheless, the effects of EFL on Z_rs can also be used to provide a sensitive and specific method to detect its presence. In 1993, Peslin et al. reported that during mechanical ventilation, some COPD patients develop large negative swings in respiratory system reactance (X_rs) measured by FOT¹⁰⁴. Similar results could also be obtained using a simplified mechanical model of the respiratory system which included a flow-limiting resistance¹⁴⁰, as well as in mechanically ventilated rabbits after intravenous methacholine infusion¹⁰³. The reasons for this behavior in reactance has been interpreted as follows: when EFL is present, the linear velocity of gas passing through regions of dynamic airway compression (i.e., choke points) equals the local speed of pressure wave propagation (Figure 7)¹⁴¹. Under normal conditions, reactance reflects the elastic and inertial properties of the entire respiratory system. However when EFL is present, the oscillatory signal cannot pass through these choke points and reach the alveoli. Thus flow becomes independent of the driving pressure, with the choke points prevent the propagation of oscillations to the lung periphery. During EFL, impedance will reflect the mechanical properties of airways proximal to the choke points, which are much stiffer that the periphery. This results in a marked reduction of the respiratory compliance, as well as reactance, when measured by FOT (Figure 7).

Figure 7.

Volume, resistance (R_rs), and reactance (X_rs) tracings in a representative human subject exhibiting expiratory flow-limitaiton. ΔX_rs denotes the difference in reactance values measured at the beginning and end of an expiration. EFL: expiratory flow-limitation. Modified from Reference ⁴⁷, with permission.

A result of this is that FOT can reliably detect EFL by intrabreath variations in X_rs at 5 Hz with 100% specificity and sensitivity compared to the gold standard method using analysis of flow and transpulmonary pressure signals^47,142. Moreover, the measurement of impedance has the advantage of being suitable for the continuous and automatic monitoring of EFL¹⁴³. It has also been shown to be reliable during continuous positive airway pressure delivered by nasal mask²⁵, opening new perspectives for the automatic adjustment of positive end-expiratory pressure (PEEP) during non-invasive mechanical ventilation.

By contrast, Kaczka et al. restricted their analyses of oscillatory pressure-flow relationships in COPD patients to inspiratory periods only, during which EFL nonlinearities were absent. For this, they introduced the concept of “inspiratory impedance” ($Z_L^{insp}$), a linear and theoretically valid description of lung mechanics that avoids the confounding influence of EFL¹⁸. To measure $Z_L^{insp}$, they proposed use of a modified OVW, referred to as the Enhanced Ventilator Waveform (EVW). The EVW excites the respiratory system with an inspiratory flow pattern consisting of multiple sinusoids while permitting a patient-driven exhalation to the atmosphere or against externally applied PEEP (Figure 8). The EVW’s ability to measure $Z_L^{insp}$ while simultaneously maintaining adequate ventilation makes it an ideal tool for assessing inspiratory mechanics in ventilated or flow-limited patients²³. Kaczka et al. also developed a weighted least squares technique for computing $Z_L^{insp}$ from EVW pressure and flow inspirations, and validated it using simulated data as well as data from anesthetized-paralyzed patients¹⁸.

Figure 8.

Flow and volume tracings for Enhanced Ventilator Waveform (EVW), consisting of an inspiratory pattern of multiple sinusoids delivered with a tidal volume of fresh gas, as well a patient-driven exhalation to the atmosphere or against PEEP. Modified from Reference ¹⁸, with permission.

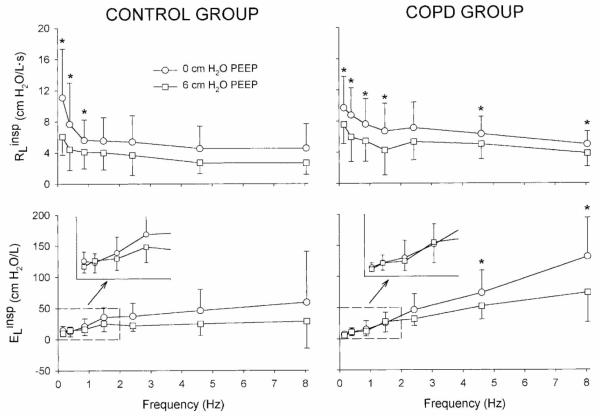
Figure 9 shows a summary of $Z_L^{insp}$ data, expressed as inspiratory lung resistance ($R_L^{insp}$) and elastance ($E_L^{insp}$), for two groups of surgical patients under general anesthesia: a control group of six patients with relatively normal lung function undergoing various thorascopic procedures, as well as group of eight patients with severe COPD undergoing lung volume reduction surgery. Measurements were made at PEEPs of 0 and 6 cm H₂O, immediately after induction of anesthesia but prior to any surgical manipulation. For the control group, PEEP significantly reduced $R_L^{insp}$ only at the very lowest frequencies. However for the COPD patients, $R_L^{insp}$ was reduced at nearly all frequencies with application of PEEP. In addition, PEEP significantly reduced the $E_L^{insp}$ at the highest frequencies for the COPD group, but not in the control group. These data then demonstrate how PEEP is beneficial in ventilated COPD patients, specifically by reducing peripheral airway resistance as indicated by the corresponding decrease in $E_L^{insp}$ at the higher frequencies. This is similar to the reduction in peripheral airway constriction in asthmatics following albuterol inhalation (Figure 6).

Figure 9.

Comparison of preoperative inspiratory lung resistance and elastance spectra measured with the Enhanced Ventilator Waveform (Figure 8) at positive end-expiratory pressures of 0 and 6 cmH₂O for control (left) and COPD (right) patients. *Significant difference between PEEP levels (P < 0.05) via paired t-test. Modified from Reference ²², with permission.

ACUTE LUNG INJURY AND ACUTE RESPIRATORY DISTRESS SYNDROME

Acute lung injury (ALI) and the acute respiratory distress syndrome (ARDS) are complex pathologic processes associated with extremely heterogeneous interactions of mechanical and biochemical processes. Both are characterized by widespread airway closure and atalectasis (derecruitment), alveolar flooding, increased lung resistance, and reduced lung compliance ¹⁴⁴. Endotracheal intubation and positive pressure ventilation is the current mainstay of treatment. Nonetheless, the mortality of ALI / ARDS is reported to be 30-40%, resulting from overwhelming sepsis and multiorgan failure ¹⁴⁵. Moreover artificial ventilation, especially in the presence of heterogeneous regional lung mechanics, can actually worsen the existing injury through two distinct mechanisms. The first is through the overdistention of lung units from high tidal volumes which are maldistributed (otherwise known as volutrauma), as well as the shear stresses associated with cyclic and repetitive opening and closing of individual lung units (or atelectrauma). Both mechanisms can result in the release of inflammatory cytokines (biotrauma) that may worsen the injury. Consequently recent emphasis has been on the development of more optimal ventilator protocols, specifically by adjusting PEEP to maximize the recruited lung ^15,146, and tidal volumes or inspiratory pressures to minimize overdistention ¹⁴⁷. Thus the ability to quantify heterogeneous mechanical derangements during ventilation may provide insight into the ongoing processes of derecruitment, alveolar flooding, and parenchymal overdistention. Such information may therefore be of use for optimizing parameters such as PEEP, tidal volume, or frequency

Recent studies in mammalian models of ALI have demonstrated that the frequency-dependent features of impedance can be very sensitive indicators of mechanical heterogeneity in the lungs^12,23,40,148. Moreover, these studies emphasized the importance of monitoring dynamic elastic properties of the lungs or total respiratory system to assess recruitment and overdistention during ventilation. For example, Kaczka et al. measured Z_rs in dogs from 0.078 to 8.1 Hz using broadband oscillations over mean airway pressures from 5 to 20 cm H₂O both at baseline and following oleic acid injury⁴⁰. To assess dynamic elastance and apparent tissue heterogeneity, their Z_rs spectra were fitted with the distributed tissue model of Equation 13. They found that both the effective dynamic elastance as well as the heterogeneity of tissue mechanics increased following ALI, consistent with derecruitment. However, both of these variables approached pre-injury levels as mean airway pressure increased, consistent with the recruitment of lung units.

By contrast, Dellaca et al. demonstrated how within-breath measurements of X_rs at 5 Hz could be used to monitor recruitment/derecruitment during ventilation in two different porcine models of lung collapse: unilateral absorption atelectasis and bronchoalveolar lavage¹⁴⁹. They found that changes in the oscillatory compliance at 5 Hz (the reciprocal of dynamic elastance, defined as −1/(2π×5×X_rs)), closely followed the amount of non-aerated tissue volume as measured by Hounsfield density in whole lung computed tomography (CT) scans (Figure 10). They also found a very strong linear relationship between percent derecruitment as determined by CT and oscillatory compliance (Figure 11). Given that single-frequency FOT measurements at 5 Hz allows for a very simple and robust assessment of recruitment in commercially-available mechanical ventilators, this technology would potentially be useful for tailoring the ventilatory settings in patients with ALI/ARDS.

Figure 10.

Upper panel: Computed tomographic scans of a representative animal at baseline, during left lung atelectasis induced by 10 min of single-lung ventilation at 100% oxygen, after a recruitment maneuver (RM), after bronchoalveolar lavage, and following RM after bronchoalveolar lavage. Lower panel: corresponding non-aerated tissue volume (V_tissNA%, closed symbols, solid line) and oscillatory compliance measured at 5 Hz (C_X5, open symbols, dotted line). Modified from Reference ¹⁴⁹, with permission.

Figure 11.

Correlation between oscillatory compliance measured at 5 Hz (C_X5) and non-aerated tissue volume (V_tissNA%) for six pigs baseline (open circles), during left lung atelectasis (closed triangles), after RM (open triangle), after bronchoalveolar lavage (closed squares), and following RM after bronchoalveolar lavage (open squares). Modified from Reference ¹⁴⁹, with permission.

CONCLUSIONS

The unique, frequency-dependent features of the mechanical impedance spectrum for the mammalian respiratory system are exquisitely sensitive to detecting and monitoring the progression of lung disease. In this paper, we have reviewed various experimental and theoretical techniques to acquire impedance data in clinical and research settings. We have discussed how such techniques may provide unique insight into pathophysiology and structure-function relationships in asthma, COPD, and acute lung injury. The interpretation of impedance with inverse models provides even more useful information on functional derangements in the airways and parenchyma, such as bronchoconstriction, expiratory flow-limitation, derecruitment, and overdistention, as well as the efficacy of various treatment protocols. This makes the forced oscillation technique an ideal diagnostic tool, both to complement more standard tests of pulmonary function, as well as the assessment of lung mechanics in intubated and artificially ventilated patients. Moreover there exist several physiologic and clinical questions in respiratory medicine for which a robust, noninvasive assessment of mechanical function will be required, and we anticipate that forced oscillations will be the ideal technique to address them in the future.

For example in asthma and COPD, short-term and diurnal variations in airway tone may be sensitive markers of airway instability and impending exacerbations due to the inherent complexities of airway structure and connective tissue matrices¹⁵⁰. Thus reliable measurements of impedance during quiescent breathing, especially using a portable home FOT device with telemedicine capabilities^24,58,59, may be useful for monitoring the dynamics of airway obstruction and its evolution over periods of weeks or months. Such data could provide far more insight into the management and control of obstructive lung diseases when compared to traditional, intermittent clinical assessment¹⁵¹.

For patients suffering from ALI / ARDS, current ventilator management strategies aim to maintain inspiratory and expiratory airway pressures within appropriate ranges for sufficient oxygenation and ventilation, while simultaneously minimizing furthering ventilator associated injury due to parenchymal overdistention and repetitive end-expiratory recruitment / derecruitment. While weight-based reduction in tidal volume has been shown to reduce the mortality of ALI and is now largely considered standard-of-care¹⁴⁷, the optimal PEEP to apply to an injured lung is still a matter of considerable controversy^146,152,153. Since ventilator associated injury is due primarily to the maldistribution of ventilation arising from variations in regional parenchymal mechanics, the ability to quantify lung tissue heterogeneity^13,40, derecruitment¹⁴⁹, and overdistention using FOT may have potential for further optimizing ventilatory parameters such as PEEP, tidal volume, or frequency for individual patients. However, clinical trials will be necessary to determine whether such ‘impedance-optimized’ approaches to ventilator management in ALI will result in improved outcomes.

Nonetheless for FOT to find its way into routine use in any clinical arena, future studies combining functional imaging, multi-scale modeling, and oscillatory mechanics will be necessary to determine how specific structural alterations in the lung will affect respiratory impedance assessed with forced oscillations. Such information will be indispensible for the rational development of novel medical and surgical therapies for the treatment of lung disease.