Effects of dynein on microtubule mechanics and centrosome positioning

When microtubules are severed by laser ablation, newly created minus ends increase in curvature, but they straighten when dynein is inhibited. It is found that cytoplasmic dynein generates tension and friction along microtubule lengths and that these forces govern the dynamics of centrosome centering.

Abstract

To determine forces on intracellular microtubules, we measured shape changes of individual microtubules following laser severing in bovine capillary endothelial cells. Surprisingly, regions near newly created minus ends increased in curvature following severing, whereas regions near new microtubule plus ends depolymerized without any observable change in shape. With dynein inhibited, regions near severed minus ends straightened rapidly following severing. These observations suggest that dynein exerts a pulling force on the microtubule that buckles the newly created minus end. Moreover, the lack of any observable straightening suggests that dynein prevents lateral motion of microtubules. To explain these results, we developed a model for intracellular microtubule mechanics that predicts the enhanced buckling at the minus end of a severed microtubule. Our results show that microtubule shapes reflect a dynamic force balance in which dynein motor and friction forces dominate elastic forces arising from bending moments. A centrosomal array of microtubules subjected to dynein pulling forces and resisted by dynein friction is predicted to center on the experimentally observed time scale, with or without the pushing forces derived from microtubule buckling at the cell periphery.

INTRODUCTION

Many essential eukaryotic cell functions, including migration and mitosis, involve force generation by microtubules. Although microtubules have a large bending stiffness, with a thermal persistence length of the order of several millimeters, they are nearly always bent or buckled in cells, which implies that they are being subjected to substantial lateral forces along their lengths (Waterman-Storer and Salmon, 1997; Salmon et al., 2002) or compressive forces at their tips (Brangwynne et al., 2006). Compressive forces have been proposed as the means by which the centrosome and spindle bodies are centered (Inoue and Salmon, 1995; Tran et al., 2001; Howard, 2006). In this mechanism, microtubules spanning the shorter distance between the centrosome and the cell boundary exert a larger force because the critical buckling force is a strong function of length, L (∝L⁻²). Consistent with this view, in vitro experiments (Holy et al., 1997) showed that microtubule-organizing centers could be centered by elongating microtubules pushing on the boundaries of a microfabricated chamber. On the other hand, there is increasing evidence that molecular motors play a key role in microtubule-based force generation. Tensile forces generated by cytoplasmic dynein—a molecular motor that walks toward microtubule minus ends while bound to the cortex—have been proposed as the driver for centrosome centering (Dujardin and Vallee, 2002; Burakov et al., 2003; Zhu et al., 2010). A similar dynein-driven mechanism has been proposed for spindle-body positioning in yeast cells (Vogel et al., 2009). Dynein has also been implicated in the buckling of microtubules by pushing segments toward the plus end (Bicek et al., 2009).

The apparently contradictory results of previous studies leave basic questions regarding in vivo microtubule mechanics unresolved. What is the contribution of dynein to the force balance on individual microtubules? Do microtubules exert tensile or compressive forces on the centrosome? How does a radial array of microtubules cause centrosome centering? To investigate these questions, we first performed experiments in which individual microtubules in bovine capillary endothelial (BCE) cells were severed by laser ablation. The goal was to remove a key element in the overall force balance, which is believed to be a combination of elastic forces from microtubule bending and elastic deformation of the surrounding cytomatrix (Ingber, 2003; Brangwynne et al., 2006). Surprisingly, our experiments showed that microtubules do not straighten after severing, which suggests a large frictional resistance to lateral motion. Instead, segments near a newly created minus end usually increase in curvature following severing, as if the end of the segment was under a compressive load. By contrast, in dynein-inhibited cells microtubule segments near the cut always straightened and did so much more rapidly than in normal cells. To explain these observations, we propose a model for dynein force generation that accounts for stochastic binding and unbinding of dynein motors from the microtubules. An ensemble of these motors develops a steady force in the direction of the tangent to the microtubule and a frictional resistance transverse to the microtubule. Numerical simulations of individual microtubules show that the model can explain the concentration of microtubule buckles near the cell periphery (Brangwynne et al., 2006). Simulations of centrosome centering by a radial array of microtubules are consistent with tensile forces on the centrosome; in the absence of motor forces the centrosome remains off center, which is consistent with observations in dynein-inhibited cells (Palazzo et al., 2001; Burakov et al., 2003; Gomes et al., 2005; Zhu et al., 2010).

RESULTS

Dynamics of severed microtubules

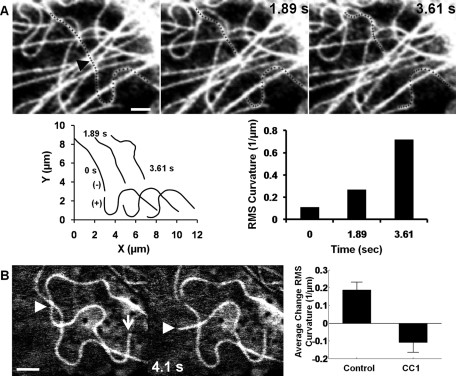
A large fraction of the microtubules in living cells are bent, with stored elastic energy apparently arising either from cytoplasmic motion (Brangwynne et al., 2007b) or from microtubules buckling under continual polymerization against the cell periphery (Brangwynne et al., 2006; Howard, 2006). It has been suggested that the bending stresses in the microtubule are balanced by compressive forces propagating from the microtubule tip, reinforced by lateral forces arising from elastic deformation of the surrounding cytomatrix (Brangwynne et al., 2006). We directly tested this assumption by severing bent microtubules in BCE cells to remove the longitudinal force at a point along the microtubule length. The two freed ends near the cut behaved differently after severing. Freed plus ends rapidly depolymerized along the original contour of the microtubule (the plus and minus ends were identified as explained in Materials and Methods). On the other hand, the more slowly depolymerizing segments near freed minus ends consistently increased in curvature after severing (Figure 1A, Supplemental Figure S1, and Movie S1), although the increase varied from microtubule to microtubule (Supplemental Figure S2). We found no correlation between the initial curvature of the microtubule and the extent to which curvature increased on severing (Supplemental Figure S2A), nor was there any correlation between the increase in curvature after severing and the distance of the cut from the cell periphery (Supplemental Figure S2B).

FIGURE 1:

Minus-end microtubules increase in bending after laser severing. Representative images highlighting changes in shape after severing a single microtubule in living cells. (A) Increased bending of minus-ended microtubules after severing near the nucleus (see also Supplemental Movie S1). The black arrowhead indicates the position of the cut, and the severed microtubule is highlighted by small crosses. Microtubule shapes in the images were measured in Matlab (see plots of severed microtubule shapes; the newly created plus and minus ends are indicated) and the root-mean-square (RMS) curvature was calculated. The minus-end microtubule (recognized as minus ended from the lack of significant depolymerization compared with the newly exposed plus end) showed a sevenfold increase in mean curvature over the visible segment length. However, the plus-end segment depolymerized but showed no measurable change in curvature. These observations are consistent with the hypothesis of minus end–directed motors pulling on the microtubule. Supplemental Figure S2 illustrates the increased buckling of a microtubule severed near the cell periphery. (B) Straightening of a bent microtubule in a dynein-inhibited cell (see also Supplemental Movie S2). The white arrow indicates the plus end of the microtubule, and the arrowhead tracks the severed end. The microtubule straightens significantly on time scales of a few seconds, supporting the hypothesis that there is an additional frictional force contributed by dynein. The plot compares the change in RMS curvature near severed minus ends in control and dynein-inhibited cells. Data are from at least 10 cells for each condition; the statistical significance is at p < 0.01. Error bars indicate standard error of the mean (SEM). The pooled data strongly support the hypothesis that dynein promotes bending of microtubules in living cells and that in the absence of dynein, microtubules straighten upon severing. Scale bars, 2 μm.

Previous work implicated dynein in anterograde transport of microtubule buckles (Bicek et al., 2009). We therefore investigated the role of cytoplasmic dynein in the bending and pinning of severed microtubules. Cells were transfected with a plasmid encoding DsRed-CC1, which competitively binds to dynein (Quintyne et al., 1999). Dynein inhibition was confirmed by dispersion of the Golgi complex (Burkhardt et al., 1997), as shown in Supplemental Figure S3; microtubules remained anchored to the centrosome (Supplemental Figure S4), consistent with previous reports (Palazzo et al., 2001). In dynein-inhibited cells, segments near a free minus end did not show any increase in curvature following severing; instead, the microtubules straightened rapidly, on time scales of the order of a few seconds (Figure 1B and Supplemental Movie S2). An increase in curvature in normal cells and a decrease in curvature in dynein-inhibited cells were consistently observed for severed minus-end microtubules (Figure 1B, bar graph).

The dynein-dependent increase in curvature of severed minus ends suggests that motor forces, directed toward the plus end, pull along the length of the microtubule. Because the increase in curvature after severing was consistently observed (Supplemental Figure S2A) and found to be independent of the distance from the periphery (Supplemental Figure S2B), we surmise that microtubules are under tension along most of their length (although tips near the cell periphery are likely to be under compression due to polymerization forces; Brangwynne et al., 2006). How might dynein generate pulling forces along a microtubule? We hypothesize that dynein molecules linking the cytomatrix to the microtubules along their lengths pull on microtubules as they walk toward the minus end.

The experimental observations also show that dynein contributes a significant frictional resistance to the motion of microtubules, because in normal cells we see no evidence of straightening, whereas in dynein-inhibited cells microtubules straighten on times scales of a few seconds (Supplemental Text, Microtubule mechanics). This observation could be explained by the transient nature of the cytomatrix–dynein–microtubule linkage leading to protein friction opposing microtubule motion.

Model for dynein-generated microtubule forces

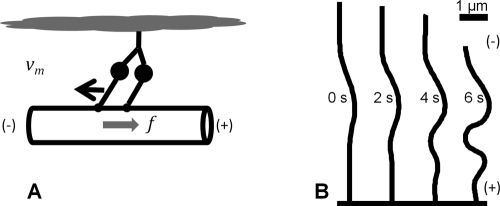
We next formulated a model for dynein force generation that considers the average behavior of an ensemble of motors transiently linking microtubules to the cytomatrix. Once a cytomatrix-linked motor binds to the microtubule, it exerts a force along the local tangent to the microtubule as it walks toward the minus end (see schematic in Figure 2A); the motor also exerts a force in response to motion of the attachment point. By assuming that dynein–cytomatrix linkages dissociate with first-order kinetics, we can write the ensemble-averaged force density (force per unit length) along the microtubule as (Supplemental Text, Model for dynein forces)

FIGURE 2:

Simulations predict dynein-induced buckling of microtubules. (A) Cartoon of a dynein motor indicating how the minus-directed motor bound to the cytomatrix exerts a force toward the microtubule plus end. (B) Simulations of an elastic filament based on the force balance in Eqs. 1 and 2 predict dynein-induced buckling near the minus end of a severed microtubule. The time scale can be compared with the experimental data in Figure 1A.

where ρ = 2 μm⁻¹ is the density of dynein–cytomatrix linkages (number of linkages per unit length), f₀ is the average force per linkage on a stationary microtubule (∼8 pN), and v₀ is the speed of the force-free motor (0.8 μm s⁻¹; Table 1). On average, a motor linked to the cytomatrix drives the microtubule in the direction of the local tangent, t, to compensate for the displacement of the motor toward the minus end. Motion in the transverse direction is limited by the frictional resistance 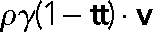, where the motor friction 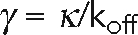is the quotient of the stiffness of the dynein linkage, κ, and the dynein dissociation rate, k_off.

TABLE 1:

Model parameters.

Symbol	Parameter	Range	Source	Value used
fmax	Maximum dynein force	5–8 pN	Gennerich et al. (2007)	8 pN
v0	Dynein speed (no force)	0.8 μm s−1	Toba et al. (2006)	0.8 μm s−1
κ	Dynein spring constant	0.1–1 pN nm−1	Howard (2001), Lindemann and Hunt (2003)	1 pN nm−1
koff	Dynein-nucleus off-rate	No value	Filament buckling	1 s−1
ρ	Dynein density (number/length)	No value	Filament buckling	2 μm−1
N	Number of microtubules	200–500	Gliksman et al. (1993)	100
vpol	Microtubule polymerization speed	0.1-0.2 μm s−1	Gliksman et al. (1993), Shelden and Wadsworth (1993)	0.1 μm s−1
vdepol	Depolymerization speed	0.2–0.3 μm s−1	Gliksman et al. (1993), Shelden and Wadsworth (1993)	0.3 μm s−1
kcat	Catastrophe rate constant	0.01–0.06 s−1	Gliksman et al. (1993), Shelden and Wadsworth (1993)	0.05 s−1
krec	Recovery rate constant	0.04–0.2 s−1	Gliksman et al. (1993), Shelden and Wadsworth (1993)	0.2 s−1
ξ	Effective friction		Filament relaxation	10 Pa s

The dynein friction coefficient was chosen by matching the times scales for individual microtubule motion found in simulations (see next section) with experimental data (e.g., Figure 1A and Supplemental Figure S5). (Further details of the determination of the motor friction are given in the Supplemental Text, Simulations of microtubule buckling.) The value of γ that best matches the experimental time scales (γ = 10³ pN μm⁻¹ s) can be obtained by taking the stiffness of the dynein linkage in the range κ ≈ 0.1–1 pN nm⁻¹ (Howard, 2001) and the dissociation rate k_off ≈ 0.1–1 s⁻¹. Our estimate of the dynein dissociation rate is consistent with observations of long-lived binding between dynein and microtubules (Gennerich et al., 2007) and with measurements of dynein exchange rates by photobleaching (Yamada et al., 2010). The time scales for microtubule motion are insensitive to the choice of dynein density, since individual motors contribute equally to the force and the friction.

Simulations of microtubule buckling dynamics

We next investigated whether dynein-mediated forces can explain the buckling of severed microtubules. By approximating the microtubule as an elastic slender body, we can write the force and torque balances on the microtubule as (Landau and Lifshitz, 1986)

where F(s) and M(s) are the force and bending moment, respectively, at contour position s. The motor force is given by Eq. 1 and the bending moment by 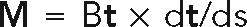, where B is the flexural rigidity. By representing the microtubule as discrete segments (Supplemental Text, Simulation methods) and solving for the velocity at each point along the contour length, we can track the motion of a motor-driven microtubule of a constant length. Our model for dynein force generation envisages a number of motors distributed uniformly along the microtubule. For clarity and simplicity we replaced a number of individual motors with a uniform (tangential) force and friction along the microtubule, which follows from a time (or ensemble) average over the positions of the individual motors.

Simulations based on this model explain how dynein can increase the curvature of a newly created minus end. As illustrated in the example in Figure 2B, following severing, small initial bends in the microtubule are predicted to be amplified due to the pulling forces generated by the dynein motors along the microtubule length. In addition, this buckling of the newly created minus-ended segment is predicted to occur on time scales comparable to the experimental observations (Figure 1A and Supplemental Figure S1).

Centrosome centering by motor-driven microtubules

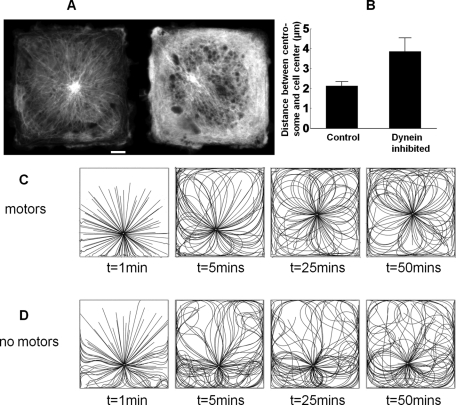
The experimental and theoretical evidence presented here is consistent with the hypothesis that microtubules in living cells are pulled by dynein motors distributed along their length (Bicek et al., 2009; Manneville et al., 2010; Zhu et al., 2010). We experimentally determined whether dynein-dependent forces are essential for centering the centrosome in endothelial cells. To do this, cells were patterned into square shapes using microcontact printing, and the position of the centrosome was determined by imaging cells expressing enhanced green fluorescent protein (EGFP)–α-tubulin. The centrosome was observed to be at or close to the center in normal cells, whereas it was substantially off-center in dynein-inhibited cells (Figure 3A). Data from 22 different cells consistently show that the centrosome is off center in dynein-inhibited cells (Figure 3B). These results support the hypothesis that dynein is necessary for centrosome centering and are therefore consistent with a pulling mechanism (Burakov et al., 2003; Bicek et al., 2009; Manneville et al., 2010; Zhu et al., 2010).

FIGURE 3:

Dynein forces are sufficient to center the centrosome. (A) Representative images showing the centrosome in square endothelial cells expressing EGFP–α-tubulin; control cell (left) and dynein-inhibited cell transfected with DsRed-CC1 (right). Scale bar, 5 μm. (B) Mean centrosome position in 42 control cells and 22 dynein-inhibited cells; the statistical significance is p < 0.01. Error bars indicate SEM. The centrosome is consistently observed to be at or close to the center of the square in control cells, whereas it is substantially off-center in dynein-inhibited cells. Simulations of centrosome centering in square cells with (C) and without (D) dynein motor activity (see also Supplemental Movies S3 and S4). The motor-driven microtubules (C) show considerable buckling near the cell periphery (clearly visible at t = 1 min), whereas without motor activity (D) the buckling is of Euler type. Only the motor-driven microtubules are observed to center an initially off-center centrosome.

Simulations of centrosome centering allowed us to compare the dynamics of an array of microtubules with and without dynein forces. Microtubules were randomly nucleated at the microtubule-organizing center (MTOC) and allowed to grow and disassemble by dynamic instability. We account for growth and shrinkage under dynamic instability (Mitchison and Kirschner, 1984) by using the experimentally measured parameters for the polymerization velocity, v_pol = 0.1 μm s⁻¹, and depolymerization velocity, v_depol = 0.3 μm s⁻¹, as well as the rates for switching to catastrophe, k_cat = 0.05 s⁻¹, and rescue, k_rec = 0.2 s⁻¹ (Gliksman et al., 1993; Shelden and Wadsworth, 1993). (More details of the simulation methods are available in the Supplemental Text, Simulation methods.)

One important experimental observation is that although microtubules in living cells are frequently observed to pin and buckle at the cell periphery, they sometimes continue to grow by sliding along the cell boundary (see Supplemental Figure S6). We incorporated both possibilities into a stochastic model of contact between the tip of a microtubule and the cell boundary, which was able to capture the main features of the pinning and sliding (Supplemental Text, Simulation methods).

Figure 3C shows configurations of motor-driven microtubules in a 40-μm square cell. Some of the microtubules near the periphery buckle into small wavelength (Figure 3C, t = 1 min), consistent with experimental observations (Brangwynne et al., 2006). The short-wavelength buckles might not be immediately obvious in Figure 3C because the eye is naturally drawn to the longer wavelengths in the body of the cell. Nevertheless an examination of the border regions, particularly near the corners, shows that the motor-driven microtubules have short-wavelength buckles (2–3 μm; Figure 3C), whereas without motors there are only long-wavelength buckles (>10 μm; Figure 3D).

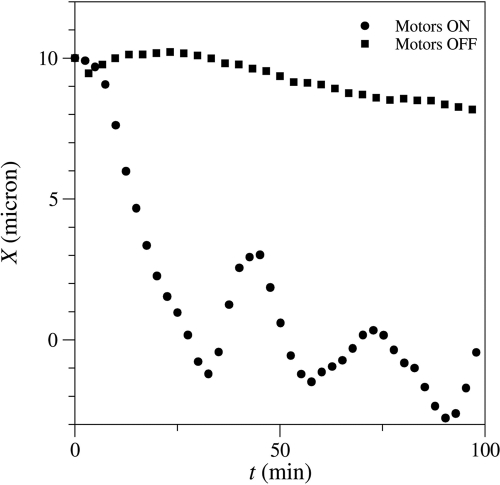
Motor-driven microtubules are predicted to drive an off-center centrosome toward the center (Supplemental Movie S3) with a time constant of the order of 10 min (Figure 4), similar to the time constant measured in living cells (Supplemental Text, Simulations of centrosome centering). Simulations also show that in the absence of motors (Figure 3D and Supplemental Movie S4) the centrosome remains essentially fixed in place for at least 100 min (the duration of the simulation). This is consistent with experimental observations in dynein-inhibited cells (Figure 3B), where the centrosome remains off center.

FIGURE 4:

Simulations of centrosome centering. The circles show simulated displacements of the centrosome, X(t), which centers on a time scale of the order of 10 min and thereafter oscillates about the central position. The squares show the same initial condition but with the motor forces and friction turned off. Here the microtubules experience a much reduced (100-fold) drag force from the cellular cytoplasm (as inferred from the laser severing experiments in dynein-inhibited cells), but the polymerization forces are unable to push the centrosome toward the center on experimentally relevant time scales.

To determine which forces are most important for centrosome centering, we formulated a simplified model assuming that the microtubules are rigid (Supplemental Text, Centrosome relaxation time). The predicted time scale for centering (∼24 min) remains comparable to experimental observations. Because the model only includes dynein tension and friction, the time scale is predicted to be independent of the number of microtubules and the density of active dynein motors along the microtubules. Therefore, a balance of tensile and frictional forces from the dynein motors is sufficient to explain centrosome centering on time scales comparable to experimental observations.

Pushing forces have been observed to cause centering in vitro (Holy et al., 1997) but not under physiological conditions. In particular, the viscosity of the buffer solution in these experiments was much smaller than the effective viscosity of the cellular fluid, as inferred from the cutting experiments described earlier (Figure 1). In addition, the fabricated cells were smaller (12 μm) than the endothelial cells used in our in vivo experiments (∼40 μm). To see whether we could resolve these apparent contradictions, we simulated the conditions described in Holy et al. (1997): a square cell of length (12 μm), a low-viscosity background fluid (water), and microtubules that were allowed to slip along the cell surface to mimic the smoothness of the glass walls. In addition, we adjusted the polymerization kinetics to allow for different steady-state lengths of microtubules. Our simulations showed the same behavior as the experiments; with short microtubules, an initially off-center centrosome moved toward the cell center (Supplemental Movie S5). In the small chamber, shorter microtubules generate a larger buckling force than the longer microtubules in the living cells (roughly 10-fold, since buckling forces scale with L⁻²). This, combined with the lower viscous drag of the fluid, is sufficient for the centrosome to center. However, if the polymerization kinetics is adjusted to create longer microtubules, then the centrosome drifts off center (Supplemental Movie S6), as observed experimentally (Holy et al., 1997). Thus our simulations explain a number of apparently contradictory experimental observations in terms of the relative magnitudes of compressive, tensile, and frictional forces. An MTOC can be centered by pushing forces under conditions in which microtubules are short and the viscosity of the fluid is similar to that of water but not in animal cells where the microtubules are longer and the friction is orders of magnitude larger. However, tensile motor forces can center the centrosome in capillary endothelial cells on the experimentally observed timescale. (Further details can be found in the Supplemental Text, Simulation of centrosome centering.)

DISCUSSION

The results of our investigation give new insight into the role of dynein in the force balance on microtubules. If individual microtubules were under compressive stress along their length, severing would result in a straightening of the microtubule, but we observed that the curvature generally increased near a newly created minus end. Conversely, when dynein activity was inhibited, microtubules straightened after severing. Severed plus-end segments in normal cells are observed to depolymerize along the original contour. Simulations suggest that microtubules pinned at their minus end do eventually straighten, but the time scale for the motors to push buckles toward the free plus end (∼10 s) is significantly longer than the depolymerization time. These observations are consistent with dynein motor forces pulling the microtubule segments toward the cell periphery. The fact that severed microtubules in normal cells are never observed to straighten indicates that dynein contributes a large frictional resistance to lateral motion in addition to its directional force; this is confirmed by the rapid straightening of severed microtubules in dynein-inhibited cells.

We developed a model for dynein force generation to explain the directional and frictional forces suggested by the experimental observations summarized in the previous paragraph. In this model, frictional forces arise from the binding and dissociation of dynein motors linking microtubules to the cytomatrix, whereas the tangential forces come from the motor activity of cytomatrix-bound dynein. The model makes several qualitative and quantitative predictions about the nature of the force balance on the microtubule. If a microtubule is pinned at its minus end at the centrosome, pulling forces from the dynein motors lead to a tensile stress along its length, with the maximum tension at the minus end (centrosome). If the microtubule has not reached the cell periphery, the stress at the free plus end must vanish. However, when its tip impinges on the cell periphery, a compressive force develops to accommodate the excess length of the polymerizing microtubule. The microtubule is then in a state of compression near the tip but in tension near the centrosome; the balance of forces is taken up by cytoskeletal-bound dynein. The model predicts that the dynein pulling force balances the tip compressive force at a distance d = F_p/ρf₀ (neglecting bending forces relative to dynein forces) from the tip, where F_p is the compressive force at the tip, and ρf₀ ≈ 16 pN/μm is the dynein force per unit length. The polymerization force is unknown in vivo, but in vitro it has been estimated to be ∼10 pN (Dogterom et al., 2005), for which d = 0.6 μm using our estimate of ρf₀. Even for larger polymerization forces of tens of piconewtons, the compressive force can be balanced by only a few motors near the microtubule tip, and the transition from tension to compression is predicted to occur within just a few microns. Therefore a key prediction of the model is that most of the microtubule is under tension despite large compressive forces at the tip. This would explain the experimentally observed increase in curvature of the minus end upon severing, indicating tension independent of distance from the periphery.

The model also helps to explain what happens upon severing. Once the tension is released at the cut point, the small longitudinal extension quickly relaxes, and the force generated from dynein motors along the segment near the newly created minus end quickly becomes compressive. This compressive force causes this segment to increase in curvature (i.e., buckle). The model predicts an increase in curvature for minus-ended segments even when the plus end is not impinging on the cell boundary. This is due to the large translational resistance from protein friction, which effectively immobilizes the microtubule segments far from the cut point.

Simulations predict that dynein motors pulling on a radial array of microtubules can center the centrosome in vivo, consistent with our observation that the centrosome is off-center in dynein-inhibited cells. Moreover, the time scale for centrosome centering, calculated with the same motor parameters as in the buckling simulations, is consistent with experimental measurements. Our model predicts that the centering time is insensitive to microtubule number and dynein density. Our simulations also explain why centering by microtubule pushing can occur in vitro without dynein (Holy et al., 1997) but only under conditions (low friction and short microtubules) in which buckling does not occur. Fission yeast, for example, appears to present conditions that favor pulling during meiotic prophase but pushing during interphase, by varying the cortical localization of dynein (Dogterom and Yurke, 1998; Dogterom et al., 2005; Manneville and Etienne-Manneville, 2006; Foethke et al., 2009; Pinot et al., 2009; Tolic-Norrelykke, 2010). However, under conditions found in animal cells, with longer microtubules and much higher frictional resistance, both simulations and experiments suggest that compressive buckling forces are insufficient to center the centrosome. Thus our model for dynein motor forces quantitatively ties the mechanics and dynamics of individual microtubules to the centering mechanism of the centrosome.

Although our results show that dynein is the dominant contributor to the lateral friction and that dynein forces are sufficient to buckle freed minus ends, we do not exclude the possibility of other motors playing a role in microtubule force generation. For example, it is possible that plus end–directed kinesin motors are simultaneously pulling in a direction opposite to the dynein forces. If this force is significant relative to dynein pulling, then the density of dynein linkages would be larger than our current estimate, but the qualitative predictions of the model would be unchanged.

Our findings have several important implications for the role of microtubules in cell mechanics. A microtubule in a living cell cannot be described by a static force balance because of the significant contribution of frictional forces from moving segments. The tangential and frictional forces generated by dynein motors dominate the elastic stresses from microtubule bending and cytomatrix deformation. Although numerical results indicate that a typical microtubule is under tension along most of its length, we do not rule out a compressive force at a microtubule tip impinging on the cell periphery. Dynein motors may in fact confine the compressive stresses to the region near the tip, consistent with a picture in which microtubule compressive forces at the periphery are transmitted to the actin cytoskeleton (Ingber, 2003), but through transient dynein–cytomatrix linkages rather than by elastic deformation (Brangwynne et al., 2006). Our model for dynein force generation provides a unifying explanation for the shapes of individual microtubules in the cell and how these shapes are consistent with tension-driven centering of the centrosome by a radial array of microtubules.

MATERIALS AND METHODS

Cell culture, plasmids, and transfection

BCE cells were cultured in DMEM (Mediatech, Manassas, VA) with 10% donor bovine serum (Life Technologies, Invitrogen, Carlsbad, CA), 1% 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (Mediatech), 1% GPS (l-glutamine–penicillin–streptomycin solution; Sigma-Aldrich, St. Louis, MO), and Fibroblast Growth Factor-Basic (2 ng/ml, Sigma-Aldrich). For microscopy, cells were cultured on glass-bottomed dishes (MatTek Corporation, Ashland, MA). These are stationary interphase cells. They are nonconfluent and unsynchronized. Adenoviral EGFP–α-tubulin was provided by Donald Ingber. DsRed-CC1 plasmid was provided by Trina Schroer. Yellow fluorescent protein–γ-tubulin was prepared from the MBA-91 AfCS Set of Subcellular Localization Markers (American Type Culture Collection, Manassas, VA). Transient transfection of plasmids into BCEs was done with Effectene Transfection Reagent (Qiagen, Valencia, Ca).

Time-lapse imaging and analysis

Time-lapse imaging was performed on a Nikon (Melville, NY) TE2000 inverted fluorescence microscope with a 60×/1.49 numerical aperture (NA) objective and charge-coupled device camera (CoolSNAP, HQ²; Photometrics, Tucson, AZ). During microscopy, cells were maintained at 37°C in a temperature-, CO₂-, and humidity-controlled environmental chamber. Images of the centrosome were taken every 2 min and imported into Matlab (MathWorks, Natick, MA). The positions of the centrosome were calculated to subpixel resolution using previously published image correlation methods (Russell et al., 2009). The autocorrelation function (Supplemental Figure S5) was calculated from the x- and y-position fluctuations in seven cells tracked for 1–2 h.

Laser ablation

An inverted (Axiovert 200M; Zeiss, Thornwood, NY) laser scanning confocal microscope (LSM 510 NLO) was used in laser ablation experiments with a 63×, 1.4-NA Plan Apochromatic oil immersion lens (Zeiss). A Ti:sapphire laser (Chameleon XR; Coherent, Santa Clara, CA) was used to sever the microtubules as described previously (Kumar et al., 2006; Lele et al., 2006; Russell et al., 2009). The Ti:sapphire laser was focused through the objective and scanned over a thin, ∼0.14-μm rectangle orthogonally crossing the width of the microtubule for one iteration. A wavelength of 790 nm was used with a laser-head power of 2 W, pulse duration of 140 fs, and repetition rate of 90 MHz. After ablation, confocal scans were collected using Zeiss LSM 510 4.2 software at 2–5 s per frame. The root-mean-square curvature was estimated from microtubule traces by fitting a one-dimensional Gaussian approximately orthogonally across the microtubule (Bicek et al., 2007, 2009; Brangwynne et al., 2007a). Coordinates were smoothed to eliminate short-wavelength measurement error and preserve long-wavelength microtubule buckles.

Severing produced two microtubule ends with a nearly threefold difference in their rates of depolymerization (Supplemental Figure S7). From experiments in which the plus end was clearly visible, we found that the newly created minus end always depolymerized much more slowly than the newly created plus end, consistent with previous studies (Tao et al., 1988; Colombelli et al., 2005; Wakida et al., 2007). The large difference in depolymerization rates allowed us to clearly identify the severed ends as plus and minus ends.

Cell shape patterning

Cell shape patterning was done by using the microcontact printing technique described in Fink et al. (2007). Molds for the stamps were produced with the UV lithography technique by illuminating a positive photoresist through a chrome photomask on which micropatterns were designed (Photo Sciences, Torrance, CA). Polydimethylsiloxane (PDMS; Sylgard 184 Kit, Dow Corning, Midland, MI) was cast on the resist mold and cured. For micropatterning, the PDMS stamp was treated with 50 μg/ml human fibronectin solution (BioCoat, BD Biosciences, San Diego, CA). The stamp was then dried and placed onto the substrate onto which the cells were plated. After 5 min, the stamp was removed, and the remaining area was blocked with poly(l-lysine)-g-polyethylene glycol (SuSoS, Dübendorf, Switzerland), preventing protein adsorption and cell attachment. After treatment the surface was washed and cells were plated.

Abbreviations used:

BCE

bovine capillary endothelial

CC1

coiled-coil region 1

MTOC

microtubule organizing center

RMS

root-mean-square

SEM

standard error of the mean