A Joint Model for Prognostic Effect of Biomarker Variability on Outcomes: long-term intraocular pressure (IOP) fluctuation on the risk of developing primary open-angle glaucoma (POAG)

Abstract

Primary open-angle glaucoma (POAG) is among the leading causes of blindness in the United States and worldwide. While numerous prospective clinical trials have convincingly shown that elevated intraocular pressure (IOP) is a leading risk factor for the development of POAG, an increasingly debated issue in recent years is the effect of IOP fluctuation on the risk of developing POAG. In many applications, this question is addressed via a “naïve” two-step approach where some sample-based estimates (e.g., standard deviation) are first obtained as surrogates for the “true” within-subject variability and then included in Cox regression models as covariates. However, estimates from two-step approach are more likely to suffer from the measurement error inherent in sample-based summary statistics. In this paper we propose a joint model to assess the question whether individuals with different levels of IOP variability have different susceptibility to POAG. In our joint model, the trajectory of IOP is described by a linear mixed model that incorporates patient-specific variance, the time to POAG is fit using a semi-parametric or parametric distribution, and the two models are linked via patient-specific random effects. Parameters in the joint model are estimated under Bayesian framework using Markov chain Monte Carlo (MCMC) methods with Gibbs sampling. The method is applied to data from the Ocular Hypertension Treatment Study (OHTS) and the European Glaucoma Prevention Study (EGPS), two large-scale multi-center randomized trials on the prevention of POAG.

1. Introduction

In many clinical trials and epidemiologic studies, investigators are interested in whether the variability of a biomarker is independently predictive of clinical outcomes. In the Honolulu Heart Program, for example, Iribarren et al (1995) reported that the subjects whose weight fluctuated most had a significantly higher risk of death from cardiovascular causes, non-cardiovascular and non-cancerous causes, as well as all causes. Grove et al (1997) and Rothwell et al (2010) found that the variability of systolic blood pressure is an independent risk factor for cardiovascular disease. In many of these studies regarding biomarker variability, the analysis is performed via a two-step approach where some sample-based descriptive statistics (e.g., standard deviation) of the longitudinal data are first calculated for each individual and then, as covariates assuming freedom from measurement error, used in the regression models to correlate with clinical outcomes. One limitation of this simplified approach is that it does not use longitudinal information efficiently. To deal with this concern, Hathaway and D’Agostino (1993) proposed an appealing approach that decomposes longitudinal data into 4 summary statistics including one component reflecting biomarker variability. Unfortunately this method requires two rather strong assumptions (namely, no missing observations and no intermediate endpoint events during the collection of longitudinal data) and this precludes its practical use in most longitudinal studies.

Another serious drawback of the two-step approach is that it ignores the measurement error inherent in sample-based summary statistics. Most clinical trials only have a handful of follow-up visits and thus the individual-level summary statistics are very unstable. In a regression analysis, it is well known that the measurement error in covariates can bias parameter estimates downward to null values and thus may mislead one into believing that a good predictive biomarker is poorly related to the outcome (Hughes, 1993; Prentice, 1982). To address this problem, Lyles et al (1999) proposed a model-based approach to estimate the “true” within-subject variability. In a study on subjects with human immunodeficiency virus (HIV) infection, Lyles et al used a full maximum likelihood method to estimate the variability of CD4 cell counts prior to infection and to assess its relationship with the CD4 level at time of infection. Specifically, CD4 measurements prior to infection were described using a linear mixed model that accounts for both random intercept and subject-specific variance,

$$\begin{array}{c}CD{4}_{ij}={\beta }_0+I_i+e_{ij},\\ \text{with}{\text{I}}_i\sim N(0,{\sigma }_{\text{I}}^2),e_{ij}\sim N(0,{\text{V}}_{\text{i}}),\text{and}log({\text{V}}_i)\sim N({\mu }_v,{\sigma }_{\text{v}}^2),\end{array}$$

where β₀ + I_i defines the “true” CD4 level for the ith individual as in the conventional linear mixed model (Laird and Ware, 1982), and V_i represents the “true” within-subject variability which follows a log-normal distribution with mean μ_v and variance ${\sigma }_{\text{v}}^2$. When the parameter ${\sigma }_v^2$ becomes 0, the above model reduces to a linear mixed model with homogenous variance.

In this paper, we extend the work of Lyles et al (1999) to the censored data setting. Our research is motivated by the Ocular Hypertension Treatment Study (OHTS), a multi-center randomized trial to evaluate the safety and efficacy of topical ocular hypotensive medication to prevent the development of primary open-angle glaucoma (POAG) (Gordon et al, 2002, 2007). POAG is among the leading causes of blindness in the United States and worldwide and, as of today, intraocular pressure (IOP) is the only factor that can be modified by the current treatment. While numerous randomized clinical trials have convincingly shown that elevated IOP is the leading risk factor and that IOP reduction can significantly reduce the incidence of POAG, an increasingly debated topic is the effect of IOP fluctuation, either diurnally (short-term) or visit to visit (long-term), on the risk of developing POAG (Singh and Shrivastava, 2009; Sultan et al, 2009). The aim of this paper is to seek an answer to this question via a joint analysis of follow-up IOP and time to POAG. We also use the data from another large-scale randomized clinical trial, the European Glaucoma Prevention Study (EGPS) (Miglior et al, 2007a, 2007b), as an independent external validation.

The task of using a series of IOP measurements for prediction is definitely more complicated than using simple summary statistics. However, since the parameters describing longitudinal process and time-to-event process are estimated simultaneously in a joint modeling setting, we expect a more accurate estimation of this relationship. Our joint model is factorized as two sub-models, a marginal longitudinal model for follow-up IOP and a conditional (given the longitudinal data) survival model for the risk of developing POAG. Specifically, the IOP trajectory is described by a linear mixed model similar to Lyles et al (1999), the time to POAG is fit using a piecewise exponential or Weibull distribution, and the two sub-models are linked via shared covariates and patient-specific random effects. The parameters in the proposed joint model will be estimated under Bayesian framework using Markov chain Monte Carlo (MCMC) methods with Gibbs sampling. This paper is organized as follows. In Section 2, we outline the data from OHTS and EGPS, two randomized clinical trials that facilitate our research. Section 3 describes model construction, parameter estimation and model selection for the proposed method. In Section 4 we analyze the OHTS and EGPS data and in Section 5 we conclude with a discussion.

2. Two real-world studies: OHTS and EGPS

2.1 Ocular Hypertension Treatment Study (OHTS)

OHTS was a multi-center randomized trial to evaluate the safety and efficacy of topical ocular hypotensive medication in preventing the onset of POAG. From 1994 to 1996, 1636 participants with ocular hypertension and no evidence of glaucomatous damage were randomized to either observation or treatment with ocular hypotensive medication. The primary outcome was the time to the development of POAG. Follow-up visits which included assessment of IOP and POAG status were scheduled every 6 months and the median follow-up time was 78 months. At the end of study, 104 (12.7%) out of 819 participants in the observational group developed POAG while the incidence rate was 5.4% (44 of 817) among those in the treatment group. Baseline factors that were predictive of POAG included older age, higher IOP, larger cup to disc ratio, greater pattern standard deviation, and thinner central corneal measurements (Gordon et al, 2002).

2.2 European Glaucoma Prevention Study (EGPS)

The EGPS was a double-masked, placebo controlled clinical trial conducted in 4 European countries with 1077 participants randomized to either an active treatment (dorzolamide) or placebo. IOP and POAG status were assessed every 6 months and the median follow-up in EGPS was 55 months. At the completion of the study, the cumulative probability of developing POAG was 13.4% in the dorzolamide group and 14.1% in the placebo group. Though the rate of progression to POAG was not statistically different between dorzolamide and placebo, EGPS identified similar baseline risk factors as in OHTS (Miglior et al, 2007a). EGPS and OHTS also shared some key similarities in the study protocols and a meta-analysis was performed using the pooled data from the OHTS observation and the EGPS placebo (Gordon et al, 2007). A new predictive model, Glaucoma 5-year Risk Calculator, was developed and well accepted by the ophthalmology community.

The purpose of this paper is to assess the effect of long-term IOP fluctuation on the time to POAG. Because treatment to lower IOP is usually initiated or intensified following POAG diagnosis and thus increases IOP variability, our study only includes IOP values prior to POAG onset. The primary endpoint is time from randomization to the onset of POAG, and those subjects without POAG are censored at the date of study closeout. Besides the post-randomization data, 6 baseline demographic and clinical characteristics are also included in this paper: the treatment indicator (TRT, 1 for active treatment and 0 otherwise), age (AGE, decade), central corneal thickness (CCT, μm), baseline IOP (IOP0, mmHg), pattern standard deviation (PSD, dB), and vertical cup/disc ratio (VCD). All the baseline factors except CCT were recorded at randomization. The CCT measurements (which turned out to be one of the most important predictors for POAG) were not included in the original protocols of both studies. However, because CCT is a life-long stable measurement, in all the analyses CCT was treated as a baseline factor though it was collected after randomization (Gordon et al, 2002, 2007; Miglior et al, 2007a, 2007b). Values for the eye-specific variables (CCT, IOP, PSD and VCD) for each participant are the average of two eyes (with the exception of the EGPS participants with only one eye eligible for the study).

In this paper, we exclude 34 participants from EGPS with Pigment Dispersion and Exfoliation Syndromes (an exclusion criterion in OHTS). We also exclude those participants without any follow-up data (18 in OHTS and 47 in EGPS), those without CCT measurements (185 in OHTS and 171 in EGPS), those with 2 or less follow-up visits (9 in OHTS and 13 in EGPS), and those with missing values in any other baseline factors (6 in EGPS). Therefore, these participants with complete baseline data and at least 3 follow-up visits constitute our study cohort (1424 from OHTS and 806 from EGPS). Table 1 presents the summary statistics of baseline covariates and follow-up IOP for our study cohort. Note that,

Table 1.

Summary statistics of baseline predictors and follow-up IOP for OHTS and EGPS, where categorical data are summarized as counts and frequencies (%), and continuous data are summarized in means and standard deviations (SD).

Variables	OHTS (N=1424)	EGPS (N=806)
Baseline predictors
TRT (N, %)
Medication	713 (50.1%)	408 (50.6%)
Observation/Placebo	711 (49.9%)	398 (49.4%)
AGE (decades)	5.55 (0.95)	5.72 (0.98)
CCT (μm)	573.3 (38.5)	573.4 (37.4)
IOP0 (mmHg)	24.9 (2.71)	23.4 (1.60)
PSD (dB)	1.91 (0.21)	2.00 (0.52)
VCD	0.39 (0.19)	0.32 (0.14)
Follow-up IOP
Mean (mmHg)	21.36 (3.44)	19.53 (2.46)
SD (mmHg)	2.27 (0.98)	2.22 (0.92)
Variance of residuals*	4.73 (4.50)	3.73 (3.53)
Follow-up visits (N, %)
3	11 ( 0.8%)	19 ( 2.4%)
4	16 ( 1.1%)	14 ( 1.7%)
≥5	1397 (98.1%)	773 (95.9%)
POAG (N, %)	134 (9.4%)	88 (10.9%)

^*From simple linear regression models fit to each individual

• Since these continuous baseline covariates are measured in quite different scales, they are standardized to have mean 0 and variance 1 throughout the remainder of this paper. As such, their coefficients in the regression models represent the effect per 1-SD change.

• Informative dropout may be an issue in both studies because participants with higher risk of POAG tend to drop out earlier due to diagnosis of POAG. For example, a great majority (26 out of 27 in OHTS, and 27 out of 33 in EGPS) of subjects with 3 or 4 visits have developed POAG. Although these with 3 or 4 visits are only a small fraction of the overall data (1.9% for OHTS and 4.1% for EGPS), excluding them could result in serious biased estimates because they account for 19.4% and 30.6% of the individuals developed POAG in OHTS and EGPS respectively.

3. Joint Models of follow-up IOP and time to POAG

3.1 Notation

Suppose there are N subjects and each subject has n_i pre-POAG follow-up visits. For longitudinal data, let Y_ij denote the post-randomization IOP measured at time t_ij for ith individual, with i =1, 2, …N, and j=1, 2, …n_i. Because high IOP is an eligibility criterion in both studies, the intercept (initial level) in mixed model is more likely suffering from “regression to the mean”. To alleviate such an influence, the time 0 is chosen as 1 year after randomization in this paper. Because post-randomization IOPs are measured approximately every 6 months in both studies, a common measuring time is used for all individuals, with{t_ij}= {−0.5, 0, 0.5,1, …}. For survival data, let T_i=minimum(D_i, C_i) be the observed time for ith subject, where D_i is the time to POAG and C_i represents the censoring time which is assumed independent of D_i. Let Δ_i be the corresponding event indicator, with Δ_i=1 if POAG is observed and Δ_i=0 otherwise. Finally, we denote the baseline covariates predictive of longitudinal and survival processes as X_i and Z_i respectively, which may or may not be the same.

3.2 Joint models

Our goal is to jointly model follow-up IOP and time to POAG, with a special attention to the effect of IOP fluctuation on the risk of developing POAG. In the past decade, many authors have studied the joint analysis of longitudinal and survival data (Pauler and Finkelstein, 2002; Tsiatis and Davidian, 2004; Vonesh et al, 2006; Wulfsohn and Tsiatis, 1997). In most joint models, longitudinal data are delineated by a conventional linear mixed model assuming homogeneous within-subject variance. However, such a homogeneity assumption automatically precludes the assessment of the question whether individuals with different levels of IOP variability have different susceptibility to POAG.

In the proposed model, the IOP trajectory is described by a linear mixed model that incorporates patient-specific variance (Lyles et al, 1999),

$$\begin{array}{c}{Y}_{ij}=f_1(\beta ,X_i,t)+I_i+S_i{t}_{ij}+e_{ij}=f_1(\beta ,X_i,t)+W_{1i}+e_{ij},\\ \text{with}{\text{I}}_i\sim N(0,{\sigma }_{\text{I}}^2),{\text{S}}_i\sim N(0,{\sigma }_{\text{S}}^2),\\ e_{ij}\sim N(0,{\text{V}}_{\text{i}}),\text{and}log({\text{V}}_i)\sim N({\mu }_v,{\sigma }_{\text{v}}^2),\end{array}$$ (1)

where β is a vector of parameters for fixed effects, I_i and S_i are the patient-specific intercept and slope as in the conventional linear mixed model (Laird and Ware, 1982), and V_i represents the “true” within-subject variability which follows a log-normal distribution with mean μ_v and variance ${\sigma }_{\text{v}}^2$. The term f₁(β, X_i, t) is a known function describing the mean response, W_1i = I_i+ S_it_ij can be viewed as the “true” individual-level trajectory after adjusting the overall mean response, and the patient-specific variance V_i reflects individual’s fluctuation around the predicted (possibly non-linear) trend over time.

Turning to the survival sub-model, the risk of developing POAG for individual i at time t is specified as a proportional hazards form,

$${\lambda }_i(t)={\lambda }_0(t)exp(f_2(\alpha ,Z_i)+W_{2i}(\gamma ,I_i,S_i,log(V_i),t)),$$ (2)

where λ₀(t) is the baseline hazard when all covariates are 0, f₂(α, Z_i) is a known function representing the effects of baseline covariates, and the term W_2i(γ, I_i, S_i, log(V_i), t) incorporates patient-specific random effects from model (1). To obtain a fairly flexible λ₀(t), we break the survival time annually into K subintervals and assume λ₀(t) being a step-function with height λ_k at each interval (t_k, t_k+1), for k=1, 2, …, K. Hence, model (2) yields a semi-parametric piecewise exponential distribution for the time to POAG. Regarding the function W_2i(γ, I_i, S_i, log(V_i), t), 7 different forms are considered in this paper, namely,

• W_2i = 0 (association induced only via shared baseline covariates);

• W_2i =γ₁I_i;

• W_2i =γ₁I_i +γ₂S_i;

• $W_{2i}={\gamma }_3{Y}_{ik}^{\ast }(t)$;

• W_2i =γ₁I_i +γ₄ log(V_i);

• $W_{2i}={\gamma }_3{Y}_{ik}^{\ast }(t)+{\gamma }_{4}log(V_i)$;

• W_2i =γ₁I_i +γ₂S_i +γ₄ log(V_i);

where $Y_{ik}^{\ast }(t)=I_i+S_i(t_k-1)$ is a time-dependent variable and represents individuals’ deviation from the systematic trend at each subinterval (t_k, t_k+1), for k=1, 2, …, K.

The piecewise exponential model permits an easy incorporation of time-dependent effects. In the event that only time-independent variables are involved in the best model, however, a full parametric model of Weibull (λ₀(t) = ρt ^(ρ−1)) or Exponential (λ₀(t) = 1) distribution is also explored, where ρ is the Weibull shape parameter with ρ>1 for a monotone increasing hazard and ρ<1 for a monotone decreasing hazard. We seek this change because, if it works, a parametric λ₀(t) will be more convenient for computation and more efficient for prediction. It is also scientifically reasonable for λ₀(t) to take a smooth form. In addition, our previous analysis (unpublished study on parametric survival) has shown that, without time-dependent covariates, a parametric Weibull model can adequately fit the OHTS data.

Finally, to facilitate an easy prediction of future cases (whose treatment information may be absent), we assume that the effect of treatment is only signified via post-randomization IOP. That is, the hypotensive medication modifies IOP evolution which in turn influences the time to POAG. Therefore, the latent quantities I_i and S_i within W_2i(γ, I_i, S_i, log(V_i), t) have to be adjusted according to the functional form of f₁(β, X_i, t) in model (1). In the presence of a significant interaction (β₂, say) between randomization group (TRT) and time, for example, a treatment-modified slope $S_i^{\ast }$ rather than S_i will be actually used in model (2), with $S_i^{\ast }-{\beta }_2•{\text{TRT}}_{\text{i}}+{\text{S}}_{\text{i}}$.

3.3 Parameter estimation and model selection

The joint distribution of follow-up IOP, Y, and time to POAG, T, can be specified in the form of

$$f(Y,T\mid {\theta }_1,{\theta }_2)=\int f(Y\mid {\theta }_1,{\eta }_i)f(T\mid Y,{\eta }_i,{\theta }_2)f({\eta }_i)d{\eta }_i,$$

with the corresponding likelihood function being

$$L(Y,T\mid {\theta }_1,{\theta }_2)=\prod _{i=1}^N\int f(Y\mid {\theta }_1,{\eta }_i)f{(T\mid Y,{\eta }_i,{\theta }_2)}^{{\mathrm{\Delta }}_i}{(1-F(T\mid Y,{\eta }_i,{\theta }_2))}^{1-{\mathrm{\Delta }}_i}f({\eta }_i)d{\eta }_i,$$

where η_i = {I_i, S_i, V_i} represents the shared underlying stochastic process, ${\theta }_1=\{\beta ,{\sigma }_I^2,{\sigma }_S^2,{\mu }_v,{\sigma }_v^2\}$ and θ₂={α,γ, λ_k} are the population parameters as given in models (1) and (2), and f ( ) and F ( ) denote the probability density function and cumulative distribution function respectively. The parameters in the model are estimated using Markov chain Monte Carlo (MCMC) method with Gibbs sampling (Gelman, 2003). Specifically, a random sample for each unknown parameter is generated from the full conditional posterior distribution given all other parameters, and the process will be iterated till its convergence to the target distribution.

To analyze data from a Bayesian perspective, the prior distributions for all unknown parameters must be specified. We use a proper prior distribution for each parameter, but the hyper-parameters in a prior are chosen so that the prior will have high variability (non-informative prior). In this paper, the choice of priors is aided by a preliminary data analysis in OHTS (Gao et al, 2011). Following prior distributions are specified and all the unknown parameters are assumed to be mutually independent,

$$\begin{array}{c}\alpha ,\beta ,\gamma ,{\mu }_{\text{v}}\sim \text{N}(0,1000),\\ {\lambda }_k\sim \text{G}(0.1,1),\\ \rho \sim \text{G}(1,1),\\ \text{and}{\sigma }_I^2,{\sigma }_S^2,{\sigma }_v^2\sim \text{IG}(0.01,0.01),\end{array}$$

where N (a, b) denotes a Normal distribution with mean a and variance b, G(a, b) represents a Gamma distribution with mean a/b and variance a/b², and x ~ IG(a, b) means that x follows an Inverse Gamma distribution or 1/x has a Gamma distribution with meann a/b and variance a/b².

The best model is selected using Deviance Information Criterion (DIC) which is a Bayesian generalization of Akaike’s Information Criterion (Spiegelhalter et al, 2002). DIC consists of two components, DIC= D̄ + ρD. The first term D̄ is the posterior mean of deviance and measures the goodness-of-fit. The second term ρD measures model complexity and is defined as the difference between the posterior mean of deviance ( D̄ ) and the point estimate of deviance obtained at the posterior mean of parameters{θ̄₁,θ̄₂}. In normal hierarchical model, ρD is approximately the trace of the “hat” matrix that maps the observed data to their fitted values and thus can be viewed as the expected effective number of parameters in the model. Since a smaller D̄ indicates a better fit and a smaller ρD indicates a parsimonious model, the model with smallest DIC is preferred and the best model is selected following the guidelines by Gelman et al (2003).

The parameter estimation is implemented using the noncommercial statistical software WinBUGS (http://www.mrc-bsu.cam.ac.uk/bugs/). We use three parallel MCMC sampling chains with different starting values. The convergence of each chain is monitored by the trace plots and the diagnostic statistics of Gelman et al (2003). The posterior mean of the parameters and the 95% credible intervals are based on 15,000 iterations following a 15,000-iteration of burn-in period.

4.Results

4.1 Separate analysis of longitudinal data

In order to fully specify the mean response f (β, X_i, t), first we analyze the longitudinal data using model (1) alone. Taking advantage of the fact that the conventional linear mixed model and model (1) produce almost identical estimates for fixed effects (Manatunga et al, 2005), we initially analyze IOP using SAS PROC Mixed to avoid intensive computation of MCMC methods. The results show that all the second-order interactions between treatment and the other 5 covariates plus time are not statistically significant (with the likelihood ratio tests of X²=10.2, df=6, p=0.12, and X²=5.7, df=6, p=0.46 for OHTS and EGPS, respectively). The results also reveal that adding quadratic time can significantly improve the model fit in the OHTS (X²=49, df=1, p<0.001) but not in the EGPS (X²=0.5, df=1, p=0.48). Therefore, the mean response f (β, X_i, t) is chosen as $f_1={\beta }_0+{\beta }_1{\mathit{TRT}}_i+{\beta }_2{t}_{ij}+{\beta }_3{t}_{ij}^2+{\beta }_4{\mathit{AGE}}_i+{\beta }_5{\mathit{CCT}}_i+{\beta }_6\mathit{IOP}{0}_i+{\beta }_7{\mathit{PSD}}_i+{\beta }_8{\mathit{VCD}}_i$

and f₁=β₀+β₁TRT_i+β₂t_ij+β₃AGE_i+β₄CCT_i+β₅IOP0_i+β₆PSD_i+β₇VCD_i for OHTS and EGPS respectively.

Table 2 presents the posterior means and 95% credible intervals for the population parameters in model (1). In OHTS, the initial (more precisely, 1-year after randomization) IOP level in the treatment group is significantly lower than that in the observation group (19.7 versus 24.3 mmHg). The estimates of β₂ and β₃ show that, on average, the follow-up IOP decreases over time but the trend is not linear. It displays a fast decrease initially and then slows down gradually as time goes by. Among the 5 baseline covariates, only CCT and IOP0 are significantly associated with follow-up IOP. It is noteworthy that the estimated ${\sigma }_v^2$ (0.53 with a 95% interval of 0.48–0.59) supports the assumption of heterogeneous variance for follow-up IOP. For the EGPS data, the difference of initial IOP levels between active treatment and placebo is much smaller (19.7 versus 20.8 mmHg) and the IOP decreases over time linearly about 0.5 mmHg per year. The result also reveals an ample dissimilarity between OHTS and EGPS with respect to the follow-up IOP. For example, baseline CCT is a significant predictor in OHTS but not in EGPS.

Table 2.

Estimated regression coefficients (β) and 95% credible intervals (CI) for IOP trajectory in OHTS and EGPS, where only the longitudinal data are analyzed.

Parameters	OHTS		EGPS
	β	95% CI	β	95% CI
Fixed Effects
Intercept	24.297	(24.130, 24.460)	20.794	(20.600, 20.990)
TRT	−4.629	(−4.840, −4.401)	−1.137	(−1.407, −0.866)
Time	−0.410	(−0.459, −0.362)	−0.477	(−0.533, −0.419)
Time*Time	0.035	(0.027,0.043)	--	(--, --)
AGE	0.010	(−0.105, 0.124)	0.029	(−0.114, 0.175)
CCT	0.172	(0.060, 0.286)	0.038	(−0.098, 0.171)
IOP0	1.151	(1.043, 1.263)	1.185	(1.043, 1.327)
PSD	0.053	(−0.061, 0.175)	−0.180	(−0.328, −0.035)
VCD	−0.076	(−0.189, 0.040)	0.058	(−0.084, 0.200)
Random Effects
${\sigma }_I^2$	3.739	(3.396, 4.091)	3.183	(2.801, 3.595)
${\sigma }_S^2$	0.111	(0.096, 0.127)	0.409	(0.345, 0.480)
μv	1.421	(1.377, 1.466)	1.275	(1.213, 1.335)
${\sigma }_v^2$	0.531	(0.478, 0.585)	0.452	(0.374, 0.541)

The posterior distributions for patient-specific random effects are also obtained from model (1) and the posterior means are calculated as a point estimate for each individual. Although it is almost certain that these point estimates tend to have a smaller variability than they should have (over-shrinkage), they provide tangible quantities to explore the relationship between longitudinal and survival processes and thus facilitate investigations to gain insight with respect to joint analysis.

4.2 Separate analysis of survival data

Next we analyze survival data using model (2) alone, with λ₀(t) totally unspecified (Cox model). We take the widely used two-step approach to determine whether IOP fluctuation is independently predictive of POAG. Specifically, simple summary statistics (mean and variance) of the post-randomization IOP are calculated for each individual and used in the Cox model as if they were observed at baseline. Since the conventional sample-based variance is more likely influenced by the systematic trend over time, we use the variance of residuals, from the linear regression model fit to each individual, as a surrogate for the “true” within-subject variability. The covariate effect f₂(α, Z_i) is chosen after the well- established meta-analysis of OHTS and EGPS (Gordon et al, 2007), with the same functional form f₂(α, Z_i)=α₁TRT_i+α₂ AGE_i+α₃CCT_i+α₄IOP0_i+α₅PSD_i+α₆VCD_i for both studies.

Table 3 shows the estimated hazard ratios (HRs) and their 95% confidence intervals from the Cox models. In OHTS, results show that the mean post-randomization IOP is a significant risk factor to POAG, with high IOP level indicating a poor prognosis. After incorporating follow-up IOP, as expected, the effect of treatment is masked and no longer independently predictive of POAG. Possibly due to the same reason, the effect of baseline IOP is not significant either. Similar results are obtained in the analysis of EGPS data. A rather surprising observation is that the HRs of IOP variability in both OHTS (HR=0.79) and EGPS (HR=0.74) are significantly smaller than 1, indicating that subjects with higher IOP fluctuation are less likely to develop POAG. Although this finding is contradictory to the usual clinical expectation, it is consistent with the trend of a previous analysis in EGPS (HR=0.87, 95% CI 0.70–1.09), which took a two-step approach and used standard deviation as a time-dependent surrogate for the “true” within-subject variability (Miglior et al, 2007b).

Table 3.

Estimated hazard ratios (HR) and 95% confidence intervals (CI) for time to POAG in OHTS and EGPS, where only the survival data are analyzed and the effect of IOP variability is assessed using a naïve two-step approach.

Parameters	OHTS		EGPS
	HR	95% CI	HR	95% CI
Effects of Baseline Covariates
TRT	1.458	(0.843, 2.521)	1.178	(0.754, 1.840)
AGE	1.245	(1.037, 1.494)	1.441	(1.142, 1.820)
CCT	0.542	(0.451, 0.651)	0.747	(0.609, 0.917)
IOP0	0.893	(0.742, 1.075)	1.071	(0.854, 1.342)
PSD	1.157	(0.967, 1.384)	1.199	(0.984, 1.460)
VCD	1.725	(1.417, 2.101)	1.531	(1.234, 1.898)
Effects of Follow-up IOP
Mean	1.316	(1.228, 1.410)	1.183	(1.078, 1.298)
log(Vi)*	0.794	(0.663, 0.951)	0.738	(0.607, 0.897)

^*logarithm transformed variance of residuals from simple linear models fit to each individual, one subject (ID=505) excluded from EGPS data due to zero variance.

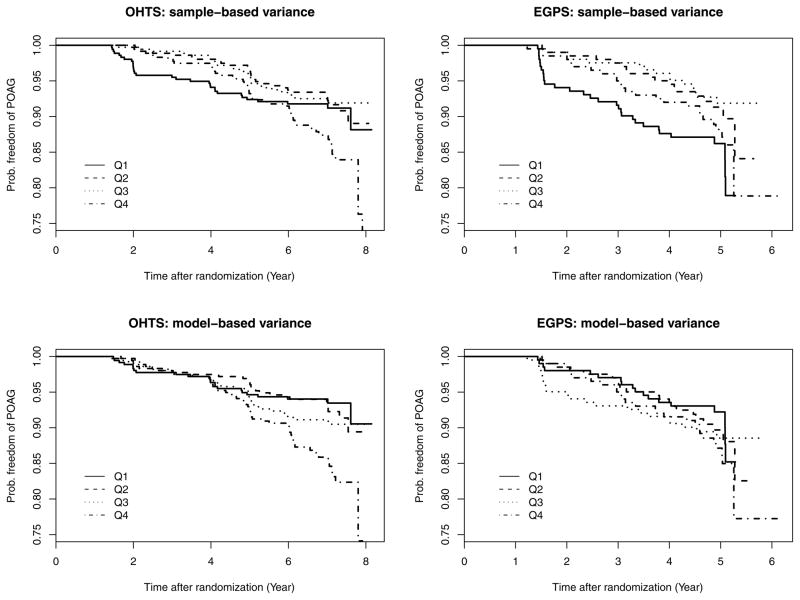
Figure 1 graphically explores the relationship between IOP variability and time to POAG in OHTS and EGPS. For each study, subjects are first ranked into 4 equal-size groups by the variance of residuals from the ordinary linear model fit to each individual, and then a Kaplan-Meier curve of time to POAG is drawn for each group (Upper panel of Figure 1). The survival curves in the group with least variability (Q1) show a sharp decrease shortly after randomization, whereas the curves in other 3 groups are in an acceptable (though not perfect) order (i.e., the higher the IOP variability, the greater the risk of developing POAG). This phenomenon is mainly caused by the informative dropout. As mentioned earlier, our data only include pre-POAG IOP values. Consequently, these subjects with the highest risk are more likely to fall out of study earlier and thus deprived the chance to show fluctuation. Actually this is exactly one of the major reasons to call for joint analysis, known for its ability to handle informative dropout (Henderson et al, 2000). Similar Kaplan-Meier curves are also prepared using the model-based variance (the posterior mean of patient-specific variance from the mixed models in Section 4.1). Interestingly, the problem of informative dropout is alleviated dramatically even before we attack this issue via joint analysis (Lower panel Figure 1).

Figure 1.

The Kaplan-Meier curves of time to POAG stratified by the estimated variance, where “Sample-based variance” means the variance of residuals from the ordinary linear model fit to each individual, “Model-based variance” refers to the posterior means of the patient-specific variances from linear mixed models, and Q1–Q4 represent the 4 groups based on quartile of variance within each study.

4.3 Joint analysis of post-randomization IOP and time to POAG

Table 4 reports the total DIC from the 9 candidate joint models for each study. Among the first 7 models with a piecewise exponential sub-model, Model 3 and Model 7 have similar performance and provide the best fit to the OHTS data. Because γ₄ (which is absent in Model 3) is significantly different from 0 and the two models produce almost identical estimates in all other parameters, Model 7 is chosen as the best fit to the OHTS data. For the EGPS data, all the first 7 models have similar performance and none of the 4 parameters (γ₁, γ₂, γ₃, γ₄) for follow-up IOP is significantly different from 0. For comparison with OHTS, however, we choose Model 7 as the best fit to EGPS. Since only time-independent covariates get involved in the best models, two additional joint models are further constructed, one with λ₀(t) being a Weibull distribution (Model 8) and the other using an Exponential distribution (Model 9). Interestingly, though Model 8 is chosen as the final model based on DIC, Models 7–9 produce similar results for these parameters of special interest (α, β, γ).

Table 4.

Deviance Information Criterion (DIC) of the candidate joint models for the OHTS and EGPS data.

Model ID	λ0(t)	W1i	W2ia	Total DIC
				OHTS	EGPS
1	λk	Ii, Si, Vi	0	80967.9	32194.2
2	λk	Ii, Si, Vi	γ1I*i	80929.7	32197.3
3	λk	Ii, Si, Vi	γ1I*i + γ2Si	80890.3	32193.0
4	λk	Ii, Si, Vi	γ3Y*ik	80909.4	32196.2
5	λk	Ii, Si, Vi	γ1I*i + γ4log(Vi)	80927.0	32193.3
6	λk	Ii, Si, Vi	γ3Y*ik + γ4log(Vi)	80907.8	32194.7
7	λk	Ii, Si, Vi	γ1I*i + γ2Si + γ4log(Vi)	80888.2	32194.4
8	ρt (ρ−1)	Ii, Si, Vi	γ1I*i + γ2Si + γ4log(Vi)	80494.1	32015.7
9	1	Ii, Si, Vi	γ1I*i + γ2Si + γ4log(Vi)	80559.9	32050.7

^a: $I_i^{\ast }={\beta }_1•{\mathit{TRT}}_i+I_i$, treatment-modified random intercept

^a: $Y_{ik}^{\ast }=I_1^{\ast }+S_i•(t_k-1)$, deviation from the systematic trend at interval (t_k, t_k+1)

Table 5 presents the posterior means and 95% credible intervals for the population parameters in Model 8. For the longitudinal component, the parameter estimates from joint models are almost identical as these shown in Table 2. For the survival component, the joint model and two-step analysis reach consistent conclusion for most baseline covariates. Regarding the impact of IOP variability on POAG, however, the joint models result in a conclusion quite different from that in Table 3. In OHTS, the joint model shows that IOP fluctuation (γ₄ =0.379, 95% CI 0.100 – 0.688), as well as the initial level (γ₁ =0.184, 95% CI 0.121 – 0.246) and the trend over time (γ₂ =1.576, 95% CI 0.796 – 2.388), are all independently predictive of POAG. In EGPS, the effect of IOP variability on POAG is not significantly different from 0 (with γ₄ =0.396, 95% CI −0.095 – 0.870).

Table 5.

Posterior means and 95% credible intervals (CI) of parameters from the final joint model of longitudinal and survival data for the OHTS and EGPS data.

Parameters	OHTS		EGPS
	Estimates	95% CI	Estimates	95% CI
Longitudinal Sub-model
Intercept (β0)	24.301	(24.130, 24.460)	20.797	(20.590, 21.020)
TRT (β1)	−4.631	(−4.854, −4.415)	−1.148	(−1.433, −0.863)
Time (β2)	−0.405	(−0.452, −0.358)	−0.473	(−0.532, −0.418)
Time*Time (β3)	0.036	(0.028, 0.044)	--	(--, --)
AGE (β4)	0.012	(−0.108, 0.129)	0.029	(−0.122, 0.185)
CCT (β5)	0.166	(0.054, 0.278)	0.036	(−0.098, 0.179)
IOP0(β6)	1.160	(1.051, 1.270)	1.188	(1.036, 1.335)
PSD (β7)	0.048	(−0.068, 0.167)	−0.181	(−0.323, −0.035)
VCD (β8)	−0.065	(−0.176, 0.047)	0.065	(−0.073, 0.207)
${\sigma }_I^2$	3.741	(3.410, 4.096)	3.182	(2.805, 3.588)
${\sigma }_S^2$	0.113	(0.097, 0.131)	0.406	(0.3474, 0.472)
μv	1.424	(1.379, 1.469)	1.281	(1.219, 1.343)
${\sigma }_v^2$	0.533	(0.478, 0.590)	0.449	(0.376, 0.533)
Survival Sub-model
Shape (ρ)	2.041	(1.791, 2.317)	2.101	(1.664, 2.543)
Intercept(α0)	−7.233	(−7.966, −6.434)	−6.303	(−7.398, −5.293)
AGE (α1)	0.231	(0.043, 0.427)	0.331	(0.100, 0.566)
CCT (α2)	−0.620	(−0.817, −0.421)	−0.321	(−0.549, −0.102)
IOP0(α3)	0.198	(0.025, 0.370)	0.145	(−0.063, 0.349)
PSD (α4)	0.207	(0.010, 0.396)	0.145	(−0.060, 0.340)
VCD (α5)	0.564	(0.351, 0.772)	0.413	(0.184, 0.634)
F/U IOP
$I_i^{\ast }({\gamma }_1)$	0.184	(0.121, 0.246)	0.067	(−0.055, 0.186)
Si (γ2)	1.576	(0.796, 2.388)	0.089	(−0.453, 0.624)
log(Vi) (γ4)	0.379	(0.100, 0.688)	0.396	(−0.095, 0.870)

$I_i^{\ast }={\beta }_1•{\mathit{TRT}}_i+I_i$: treatment-modified random intercept

5. Discussion

In this paper, we propose a joint analysis approach to assess whether variability of a biomarker is independently predictive of clinical outcomes. Using data from two long-term clinical trials of the efficacy of IOP lowering medication in the prevention of glaucoma, we determine if long-term IOP fluctuation is independently predictive of POAG. The trajectory of IOP is described by a linear mixed model incorporating patient-specific variance, and its association with the time to POAG is assessed using both semi-parametric and full parametric survival models. Interestingly, the results show that the Weibul model produces similar estimates of the relative risk as those in the piecewise exponential model. This will reduce the computational burden and facilitate an easy prediction.

The joint analysis offers attractive features for modeling the effect of biomarker variability. First, compared to the frailty framework for patient heterogeneity (Henderson et al, 2000), such a regression approach is relatively straightforward to interpret and the effect of biomarker variability on outcome can be readily quantified as hazard ratio which is familiar to clinical investigators. Second, since the parameters describing longitudinal data and time-to-event data are estimated simultaneously, informative dropout and measurement error can be accounted and the relationship between these two stochastic processes can be more accurately estimated. Thirdly, the availability of the full posterior estimates of the random effects provides a useful tool to gain insight into the model construction and permits the possibility of a patient-specific prediction (Pauler and Finkelstein, 2002). Finally, the Deviance Information Criterion (DIC) facilitates an easier comparison among various complex but realistic models that do not need to be nested.

The naïve two-step approach, though convenient to use and widely applied, should be used with caution. Possibly because of measurement error and/or informative dropout, the estimates based on two-step analysis are very sensitive to the data selection (personal communications with Dr. David Musch on his unpublished data on IOP variability). In the OHTS and EGPS data, for example, the current two-step analysis shows that subjects with a higher IOP variability are significantly less likely to develop POAG, but another analysis taking the two-step approach (result not presented in the paper) produces non-significant effects in both studies after we exclude those subjects with 3 visits (who only account for less than 2% of the total study cohort). In contrast, the joint models produce consistent results across different datasets.

Substantively, our results show that IOP variability is independently predictive of POAG in OHTS, and the subjects with high IOP fluctuation have an increased risk of developing POAG. Though this conclusion is not justified by the data from EGPS, the result in EGPS shows a trend consistent with that in OHTS. Note that, in both studies, the estimated within-subject variability actually consists of two components, the biologic fluctuation and the pure measurement error. In the current analysis we have not sought to make such a distinction, but the non-specificity of fluctuation may attenuate the potential association between biomarker variability and clinical outcome.

A limitation of the joint model is its intensive computation. The analysis of OHTS data (N=1424) with a parametric Weibull baseline hazards, for example, required approximately 5 hours per model when using 3 parallel chains with 30,000 iterations each. This makes it difficult to use the joint model as a real-time, web-based tool to predict prognosis. One possible solution is the joint latent class model (Proust-Lima and Taylor, 2009), where the latent classes can be determined by the patterns of IOP trajectory. In future work, we will investigate ways to incorporate the post-treatment IOP and to enhance the predictive accuracy of the existing web-based OHTS-EGPS Glaucoma Risk Calculator.