Abstract
Adaptations of large arteries to sustained alterations in hemodynamics that cause changes in both caliber and stiffness are increasingly recognized as important initiators or indicators of cardiovascular risk to high flow, low resistance organs such as the brain, heart, and kidney. There is, therefore, a pressing need to understand better the underlying causes of geometric and material adaptations by large arteries and the associated time courses. Although such information must ultimately come from well designed experiments, mathematical models will continue to play a vital role in the design of these experiments and their interpretation. In this paper, we present a new multilayered model of the time course of basilar artery growth and remodeling in response to sustained alterations in blood pressure and flow. We show, for example, that single- and multi-layered models consistently predict similar changes in caliber and wall thickness, but multilayered models provide additional insight into other important metrics such as the residual stress related opening angle and the axial prestress, both of which are fundamental to arterial homeostasis and responses to injury or insult.
Keywords: Constrained mixture model, Evolving Microstructure, Residual Stress, Finite elasticity, Adaptation, Hypertension
1. Introduction
The arterial wall is a multilayered composite structure organized in layers that consist of different mixtures of cells and extracellular matrix proteins (Humphrey (2002)). Specifically, the normal wall consists of three layers: intima, media, and adventitia. In young healthy individuals, the innermost layer, or intima, consists primarily of a monolayer of endothelial cells adherent to a thin basement membrane that consists of collagen IV and laminin; it is thought that this layer normally supports little mechanical load. With increasing age, however, the intimal layer thickens due to the accumulation of smooth muscle cells and fibrillar collagens (types I and III), and with the development of atherosclerosis there is a further accumulation of lipids, cells, collagen, calcium, and necrotic debris within the intima. Hence, the intimal layer can evolve to play a major role in load bearing. The middle layer, or media, typically consists of layers of smooth muscle cells, elastic fibers, fibrillar collagens, and proteoglycans. The percentage of smooth muscle cells, elastin, and collagen varies along the arterial tree and can change dramatically in disease. For example, hypertension is characterized by a marked increase in medial smooth muscle and collagen whereas aneurysms are characterized by dramatic decreases in smooth muscle (via the process known as apoptosis) and elastic fibers, the latter of which often become damaged mechanically or degraded proteolytically. Finally, the outermost layer, or adventitia, consists primarily of type I collagen with admixed elastic fibers, proteoglycans, and nerves. Although it is thought by many that the adventitial layer serves primarily as a stiff sheath in healthy arteries that protects smooth muscle cells from acute over-extensions in response to transient increases in blood pressure, this layer adapts during the formation of an aneurysm so as to provide most of the structural integrity of the wall.
Biomechanical modeling of the layered structure of the arterial wall dates back at least three decades (e.g., von Maltzahn et al. (1981), Vito and Demiray (1982)), and transmural variations in material properties are known to play important roles in arterial homeostasis (e.g., Holzapfel et al. (2000), Taber and Humphrey (2001), Stergiopulos et al. (2001)). Nevertheless, most prior mathematical models of arterial growth and remodeling (G&R) focus on either a homogenized or a thin wall (e.g., Taber (1998); Rachev (2000), Gleason et al. (2004); Tsamis et al. (2009); Valentín et al. (2009); Wan et al. (2010)). To gain a deeper understanding of both normal arterial mechanobiology and arterial pathobiology in diverse diseases, there is a need for models that account for the evolution of a thick, layered wall. In this paper, we extend the recent 3-D homogenized model of arterial G&R by Karšaj et al. (2010) to account for the multilayer construction of the normal wall. For illustrative purposes, we focus on the basilar artery, one of the primary arteries that supplies blood to the brain.
Intracranial arteries differ from most other large arteries in that they have a prominent internal elastic lamina that separates the intima from the media, but no external elastic lamina separating the media from the adventitia. Moreover, the overall percentage of elastin is low compared to most similarly sized extracranial arteries. Nonetheless, elastin plays important roles in intracranial arteries, which are of the muscular-type, meaning that the media consists largely of smooth muscle and the media and adventitia occupy similar portions of the wall. We simulate adaptations of basilar arteries to alterations in blood pressure (e.g., hypertension) and flow (increased and decreased), focusing on associated short- and long-term changes in the caliber, wall thickness, residual stress related opening angle, and axial prestress. The so-called opening angle is identified experimentally by introducing a radial cut in an excised, traction-free arterial ring; the opening of the ring into a sector reveals the underlying existence of residual stress, which is thought to result from nonuniform growth and to help homogenize the transmural distribution of stress in the wall (Fung (1990)). The axial prestress, on the other hand, results from an associated prestretch that appears to arise primarily during development and maturation and to depend primarily on elastin. In particular, load-bearing elastin is incorporated within the arterial wall during the perinatal period and has an extremely long half-life (~ 40 years in humans; Arribas et al. (2006)), hence it is stretched as the blood vessel increases in size during overall tissue growth. The residual stress and the axial prestress thus appear to work together to establish a favorable mechanical micro-environment for the intramural cells under normal conditions (Cardamone et al. (2009)). Indeed, it appears that these cells work hard to reorganize or refashion the arterial wall when this mechanical state is perturbed from normal. The focus of this paper is to present a theoretical framework to model mathematically such cell-mediated G&R of the arterial wall in response to perturbations of local stress from normal due to gross changes in the hemodynamics.
2. Methods
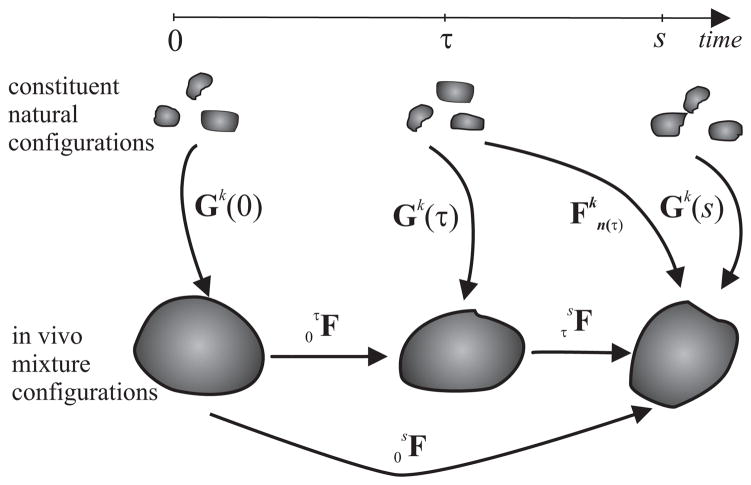
We adopt the general approach of Humphrey and Rajagopal (2002) and thus assume that arterial tissue can be modeled as a constrained mixture wherein individual constituents (k = 1, 2,…n, as, for example, elastin, multiple families of locally parallel collagen fibers, and smooth muscle) must deform together with the arterial wall (i.e., xk ≡ x at all times), but can possess individual mass fractions, material properties, and natural (stress-free) configurations (Figure 1). Another fundamental assumption is that elastin does not turnover in maturity whereas collagen and smooth muscle turnover continuously, the rates of which are governed by deviations in stress from homeostatic values. Finally, it is assumed that newly produced constituents are incorporated within the extant matrix at preferred, or homeostatic, values of stress or stretch; we model this via a deposition stretch denoted by Gk(τ), where τ ∈ [0, s] is the G&R time at which the constituent was deposited, 0 is the time at which G&R commenced in response to an alteration in loading, and s is the current G&R time.
Figure 1.
Schema of configurations important in arterial growth and remodeling (G&R). The constituent natural configurations represent the individual stress-free configurations associated with the time of deposition of that constituent. The in vivo configurations are for the arterial wall as a whole, here at mean arterial pressure.
2.1. Kinematics
Let the linear transformations and quantify, respectively, mappings from either intermediate loaded-mixture configurations or constituent-natural configurations to the current loaded mixture configuration at G&R time s (Figure 1). Moreover, let possible linear transformations from current to unloaded mixture configurations be denoted simply by F. An advantage of using an in vivo configuration as a reference is that the clinically available in vivo configuration (F = I) is convenient both computationally and biologically (Cardamone et al. (2009a)). Although one could select in vivo diastolic, systolic, or other configurations, we use the in vivo configuration at mean arterial pressure.
Because the total mass density of the mixture appears to remain constant despite G&R, that is, ρ(τ) ≈ ρ (0), we have
| (1) |
whereby J(τ) represents local changes in volume within the current in vivo configuration for any instant τ ∈ [0, s].
2.2. Kinetics of G&R
The mass of each constituent at any particular G&R time depends on that originally present at time 0, its normal half-life, and subsequent production and removal. We assume that production and removal can both depend on the local mechanical environment experienced by the cell, which via mechanotransduction influences its gene expression. To account for the possible evolution of mass for constituent k, we let (cf. Baek et al. (2006))
| (2) |
where Mk(s) is the total mass of constituent k existing at G&R time s, Qk(s) ∈ [0, 1] accounts for fractions of material produced at or before time τ = 0 that survive to time τ = s, with Qk(0) = 1 by definition, mk(τ) > 0 is the true mass production rate, and qk(s – τ) ∈ [0, 1] is a survival function that accounts for fractions of material produced at time τ that survive to time τ = s. The functions Qk are determined from qk via integration over τ ∈ [0, s]. Clearly, the mass production rates and survival functions must be prescribed constitutively based on data on cell responses to changes in mechanical stimuli. Here in, we use functions suggested by Valentín et al. (2009), namely
| (3) |
where is the basal production rate, is a gain-type rate parameter that models wall stress-mediated changes, and is a gain-type parameter that models vasoactive molecule mediated changes. Moreover,
| (4) |
| (5) |
where σ(τ) is a scalar metric of intramural wall stress, τw(τ) is wall shear stress, Cs is a material parameter, and the ‘h’ denotes a homeostatic (or, target) value. In particular, changes in wall shear stress experienced by endothelial cells regulate their production of vasoactive molecules (e.g., the dilator nitric oxide and the constrictor endothelin-1), which also affect smooth muscle proliferation rates and their production of collagen. Also from Valentín et al. (2009), we assume a first-order-type kinetic decay of all constituents, namely
| (6) |
where Kk(τ̃) are rate-type parameters for mass removal with units of day−1 that may depend on the level of tension in the constituent (see Humphrey (2008a)), and τ̃ is a dummy variable of integration.
2.3. Constitutive Formulation and Stress Analysis
Arteries exhibit nonlinear, anisotropic, passive responses over finite deformations. Using a rule of mixtures, the stored energy function for passive behaviors is decomposed conceptually as W = Σk φkŴk where φk denote constituent mass fractions. The stored energy for a constituent k can be written (Baek et al. (2006))
| (7) |
where is the right Cauchy-Green tensor, which accounts for the deformation experienced by constituent k relative to its natural configuration defined at time τ when that constituent was produced. A neo-Hookean response is often used for elastin (Dorrington and McCrum (1977)), hence
| (8) |
where c1 is a material parameter. To account for possible nonlinear spatial distributions of elastin prestretches Ge(r) built in during development and maturation, we use following relation (Cardamone et al. (2009))
| (9) |
where K governs the ‘deposition rate’ (e.g., K = 0 implies constant deposition through the wall, K = 1 a linear distribution, and so forth), and ro and ri denote outer and inner radii of the arterial wall in loaded configurations.
Exponential behaviors are typically assumed for fibrillar collagen, as is usual, as well as for passive smooth muscle (Cardamone et al. (2009)). Hence, let
| (10) |
where and are associated material parameters and , where mk(s) denotes the orientation of fiber family k. Finally, active stress generation by the smooth muscle in the circumferential direction is modeled via (Rachev and Hayashi (1999)),
| (11) |
where TM is the maximum actively generated stress, having units kPa, λM is the circumferential stretch at which active stress is maximum, λ0 is the circumferential stretch at which active stress goes to zero, C(s) is the aforementioned net ratio of constrictors to dilators, and with rm(active)(s) evolving via a first order rate equation (Baek et al. (2007)). See Table 1 for related parameters. Of course, other models of SMC activation could be used similarly (cf. Nardinocchi and Teresi (2007)).
Table 1.
Parameter values used to simulate G&R of a basilar artery. Note that ‘h’ denotes homeostatic.
| Geometry and Applied Loads | ri = 1.42 mm, ρs = 1050 kg/m3, Ph = 95 mmHg, Qh = 3.075 mL/s | |
| Muscle Activation Parameters | TM = 150 kPa, λM = 1.1, λ0 = 0.4, CB = 0.68, CS = 20 · CB | |
| Material Parameters |
|
|
| G&R parameters |
|
2.4. Global equilibrium
Having identified constitutive relations for arterial growth and remodeling, we now assume that G&R is a quasi-static process and thus consider a sequence of equilibrium problems corresponding to a pressurized and axially loaded thick-walled cylinder, a reasonable approximation for the basilar artery. In our previous work (Karšaj et al. (2010)), we used a single layer model wherein all constituents were uniformly dispersed through the wall. Modeling the layered structure of the wall (i.e., the intima, media, and adventitia) promises to reveal more insight into, among other aspects of the mechanics, the residual stress related opening angle and axial stretch. Thus, taking as unknowns the inner radius ri, and either the outer radius ro or the wall thickness h, we use following statement of equilibrium for an axisymmetric cylinder
| (12) |
where P is the transmural (or distending) pressure and rm and ra demarcate, respectively, the radii at the intimal - medial and medial - adventitial borders. In this way, we can endow each of the three layers with individual distributions (e.g., mass fractions) of the three primary structurally significant constituents (elastin, collagen, and smooth muscle). The total axial force L is computed similiarly as a sum for each layer
| (13) |
Of course, for a 2-layer model we have 2 integrals and for a 1-layer model we have a single integral in Equations 12 and 13. A third equation defines balance of the mass, namely
| (14) |
where Jm is a mass change function (Karšaj et al. (2010)), l is the length of the deformed artery, and ρ(τ) is the mass density of the wall, which is assumed to be constant during the G&R; trr, tθθ and tzz are radial, circumferential, and axial components of the Cauchy stress, respectively.
3. Illustrative Material Parameters and Cases
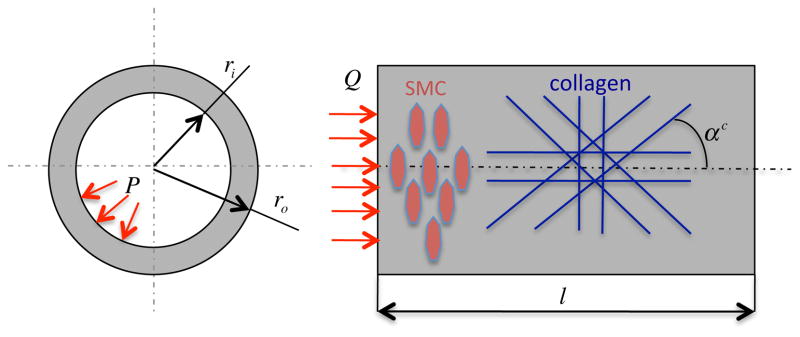
We simulated G&R for a basilar artery, one of the key vessels supplying blood to the brain, because we already have verified results for a single layer formulation to which to compare (Karšaj et al. (2010)). Note, again, that we assume that the collagen may be oriented axially, circumferentially, or symmetric diagonally about the axial direction, and the smooth muscle is always oriented circumferentially (Figure 2). Material parameters are taken from Valentín et al. (2009), or calculated to satisfy equilibrium and ensure normal tissue maintenance, Table 1. Please note that material parameters for collagen and SMC are the same for all three cases presented below whereas the material parameter c1 for elastin is determined for each case (see below).
Figure 2.
Geometry of a basilar artery and orientations of the smooth muscle (circumferential) and four general families of collagen (axial, circumferential, and symmetric diagonal) used for computations. P denotes the transmural pressure and Q the volumetric flow rate, both of which are measurable clinically.
Experimental findings reveal that the opening angle ranges from 70 to 90 degrees in passive basilar arteries (H. Wagner, personal communication); SMC activation often increases this angle further (Humphrey (2002)). Aiming to achieve a comparable value with our three layer model, we first let the intima be 4%, the media 56%, and the adventitia 40% of wall volume. Mass fractions for the individual of specific constituents in each layer are given by Table 2 (Lee (1995)). Because we prescribe both the homeostatic (target) intramural stress and the deposition stretches, we cannot prescribe all material parameters independently. To ensure consistency amongst these selections, the material parameter for elastin was computed to be c1 = 116.6 kPa, well within the expected range, for this case. Elastin prestretches and their distributions are also important determinants of opening angle values. Thus while keeping fixed mass fractions in each layer, we varied the distribution of elastin prestretches parametrically until we obtained a reasonable value of the passive opening angle. Ultimately, we let at inner radius ri and at outer radius ro together with linear distribution in between (K = 1) as defined by Equation 9. With these parameters values we found an initial passive opening angle (TM = 0 kPa) of 69.2° and an initial active opening angle (TM = 150 kPa) of 135.2°.
Table 2.
Initial mass fractions of each of the three structurally significant constituents within the three-layered model. Recall that the intima is defined from ri to rm, the media from rm to ra, and the adventitia from ra to ro.
| Mass Fractions | Intima | Media | Adventitia |
|---|---|---|---|
| Elastin | 100% | 4% | 10% |
| Collagen | 0% | 25% | 90% |
| SMC | 0% | 71% | 0% |
Second, we checked the efficiency of the model having two layers (i.e. media and adventitia). For this simulation, we let the media within the two-layer model be a merged intima and media from the three-layer model. Thus, the media constituted 60% and adventitia 40% of arterial wall thickness. Merging mass fractions of each constituent shown by Table 2, we get the two-layer data listed in Table 3. Aiming to obtain a similar passive opening angle (73.6°), we used the following elastin prestretches: at the inner radius and at the outer radius together with a distribution described with parameter K = 0.5. The associated active opening angle was 135.2° and the material parameter for elastin in this two-layer model was computed to be c1 = 88.1 kPa, which again was well within the expected range.
Table 3.
Initial mass fractions of each of the three structurally significant constituents within the two-layered model. Recall that the media is defined from ri to ra, and the adventitia from ra to ro.
| Mass Fractions | Media | Adventitia |
|---|---|---|
| Elastin | 10.4% | 10% |
| Collagen | 23.3% | 90% |
| SMC | 66.3% | 0% |
Finally, we built a one-layer model, similar to that which was already verified in our previous work (Karšaj et al. (2010)). One layer data were computed by merging the intima, media, and adventitia from the three-layer model. We assumed the mass fractions for the structurally significant constituents shown in Table 4. When keeping mass fractions unchanged while changing elastin prestretches, we could barely simulate the experimentally measured passive opening angle values. The best agreement we obtained was 87° for elastin prestretches of at the inner radius and at the outer radius for a distribution described by equation 9 with parameter K = 2. In this case, the active opening angle was 96.6°, which differed significantly from values for the three- and two-layer models. Here we computed c1 = 120.1 kPa.
Table 4.
Similar to Tables 2 and 3, initial mass fractions in the one-layer model were prescribed as shown here.
| Mass Fractions | Artery Wall |
|---|---|
| Elastin | 10.2% |
| Collagen | 50% |
| SMC | 39.8% |
Test Cases for G&R presented below will demonstrate further the different behaviors of the multi-layer models on artery responses. Case I simulates hypertension (i.e. 50% increased blood pressure), Case II a 10% increased blood flow, and Case III a 30% reduced blood flow. In Case IV, we consider a two-layer model subjected to an increased pressure of 50% together with 25% larger values of the growth parameters Kσ and KC in the adventitia, which emphasizes that mechanobiological responses by smooth muscle cells in the media and fibroblasts in the adventitia need not be the same.
Diverse observations of arterial responses to altered pressure and flow provide an easy check of geometric results from G&R simulations (Humphrey (2008b)). Considering mean values of wall shear stress and circumferential wall stress, homeostatic (h) values are
| (15) |
| (16) |
If perturbations in blood flow and pressure are given by Q = εQh and P = γPh, and both wall shear stress and circumferential stress return to homeostatic values, then stress-mediated G&R must produce specific changes in geometry: and h = γε1/3hh. For example, when blood flow is 30% below its homeostatic (normal) value, ε = 0.7 and it is expected that inner radius and thickness should both change as 0.71/3 = 0.8879 of homeostatic values. Whereas these simple relations provide insight into final values of geometric changes, they do not inform us with regard to the evolution of these changes. Let us now consider predictions of the present G&R model for insights into the evolution.
4. Results
Case I - 50% Increase in Pressure
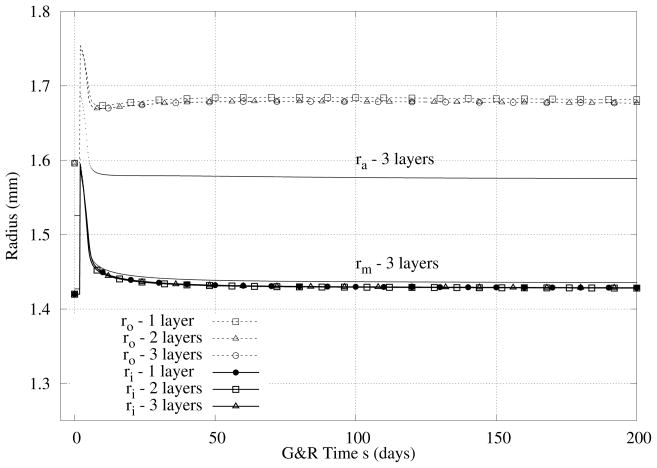
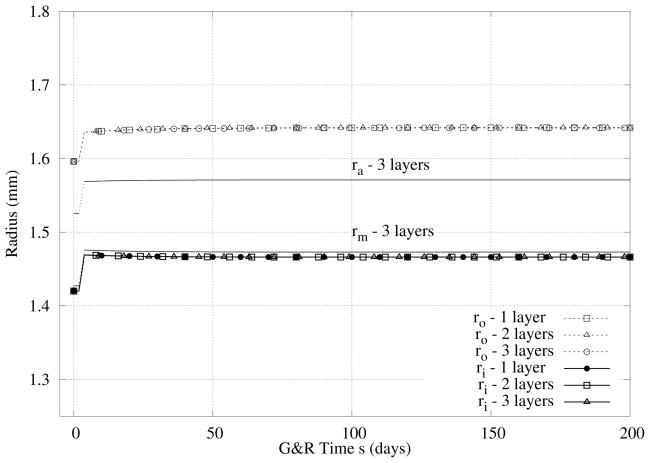
Three different models are compared, i.e., the three-layer, two-layer, and one-layer models. In Figure 3, we see that there are no significant differences in the predicted evolution of the inner radius by the different models although a slightly larger thickness is predicted by the one-layer model. Note that the immediate increase in inner radius, with a concomitant isochoric decrease in thickness, was an expected nonlinearly elastic response to the prescribed step increase in pressure. More importantly, the rapid return of the inner radius toward normal and the associated thickening of the wall were emergent G&R responses that restored the wall shear stress and mean circumferential wall stress to near normal values (cf. equations 15 and 16). Because the rapid return of the inner radius to near normal occurs biologically via an increased contraction of smooth muscle (cf. equation 11), mediated via an increase in vasoconstrictors produced by the endothelial cells, mass production rates increased due to both stress and constrictor mediation (cf. equation 3), which there by worked together. We checked also the change in intima/media/adventitia ratio, Table 5 and Figure 3. As it can be seen, thickening occurred via comparable changes in the media and adventitia with little variation in the intima.
Figure 3.
Case I - Predicted evolution of radii in response to an abrupt (at s = 0) but sustained 50% increase in pressure. Note the initial pressure-induced distension, but return of the inner radius toward normal within the first few weeks. Note too the thickening and similiar results for the 3-, 2-, and 1-layer models.
Table 5.
Case I - Predicted evolution of intimal (I), medial (M), and adventitial (A) thickness in response to an abrupt but sustained 50% increase in pressure.
| G&R Time (Days) | Thickness (%)I/M/A | (%) I/M/A |
|---|---|---|
| 0 | 4/56/40 | 100/100/100 |
| 5 | 3.3/56.8/39.9 | 95.7/117.2/115.5 |
| 200 | 2.8/56.4/40.8 | 100/142/143.7 |
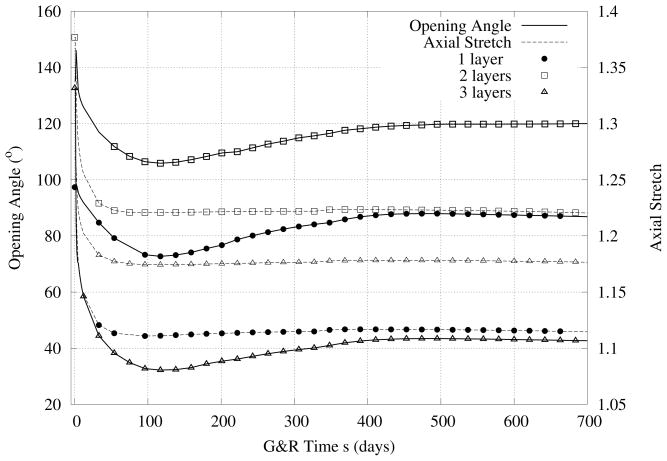
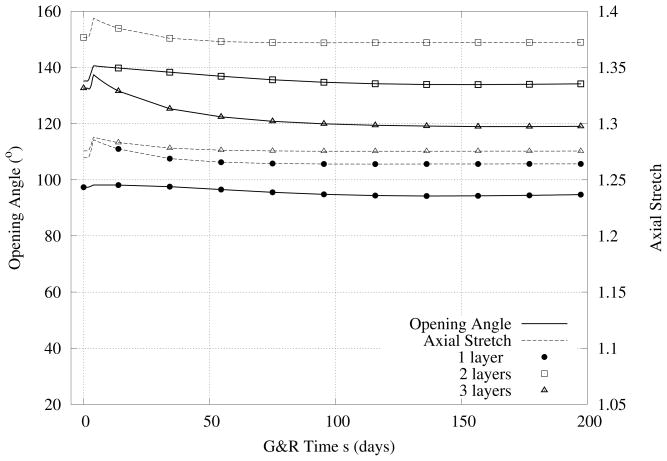
Furthermore, we give results for changes in the active (i.e., with basal smooth muscle tone, that is, TM = 150 kPa) opening angles over 700 days after increasing the pressure by 50% (Figure 4). These predictions all show the same qualitative behaviors - namely, a rapid increase in opening angle followed by a slower decrease back toward original values and a monotonic decrease in axial stretch. Both findings are consistent with general reports in the literature (Fung (1990), Humphrey (2002)) even though there are no comparable data specifically for basilar arteries.
Figure 4.
Case I - Predicted evolution of the opening angle (left ordinate) and in vivo axial stretch ratio (right ordinate) associated with Figure 3, a 50% increase in pressure. Note the differences for the three different models in contrast to Figure 3.
Case II - 10% Increase in Blood Flow
In Figure 5 we see again that there are no significant differences in the predicted evolution of the values of inner radius by the different models although a slightly larger thickness was predicted by the one-layer model. In this case, inner radius increased to restore wall shear stress to near normal (via vasodilator activity by the endothelial cells), which of course would increase mean circumferential wall stress. It is for this reason that the G&R also produced a thicker wall. Changes in opening angle and axial stretch are also shown in Figure 6.
Figure 5.
Case II - Similiar to Figure 3 except for a 10% increase in flow. Again, results for the three models are similiar.
Figure 6.
Case II - Similiar to Figure 4 except for a 10% increase in flow. Note the much smaller predicted changes in both opening angle and axial stretch when compared to the case of increased pressure.
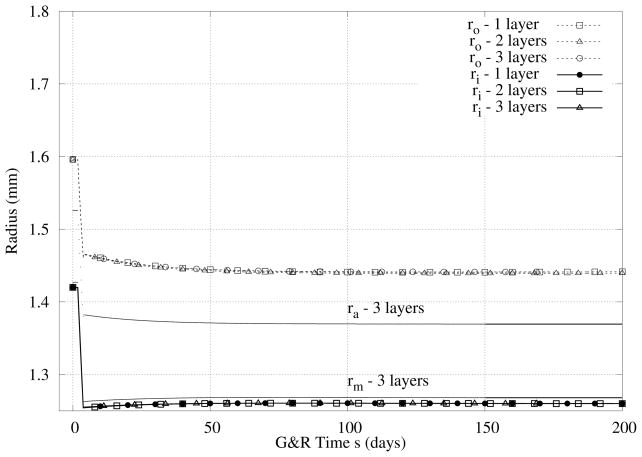
Case III - 30% Decreased Blood Flow
Figures 7 and 8 show overall similar results for the case of decreased flow, noting that a decrease in blood flow causes a reduction in the inner radius to restore wall shear stress toward normal and similarly a slight reduction in wall thickness to restore the mean circumferential stress toward normal. Note that, because the prescribed increase (Figure 5) and decrease (Figure 7) in flow were moderate, the initial vasoactive response was able to restore wall shear stress toward normal quickly in both cases.
Figure 7.
Case III - Similiar to Figure 5 except for the case of a 30% decrease in flow.
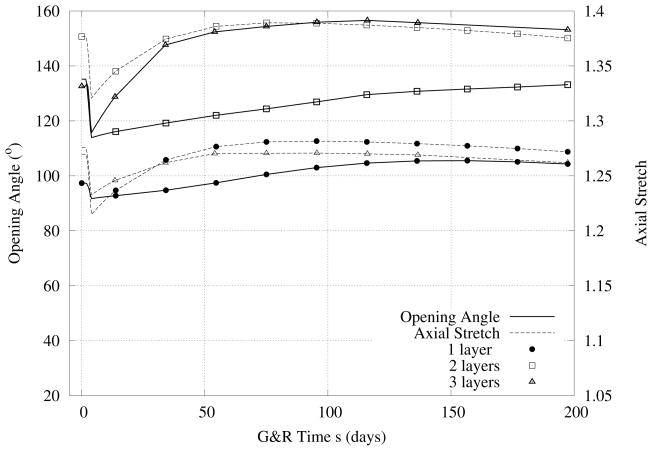
Figure 8.
Case III - Similiar to Figure 6 except for a 30% decrease in flow. Note the initial decreases, then increases back toward normal values of axial stretch.
Case IV - Hypertension and Different Growth Parameters
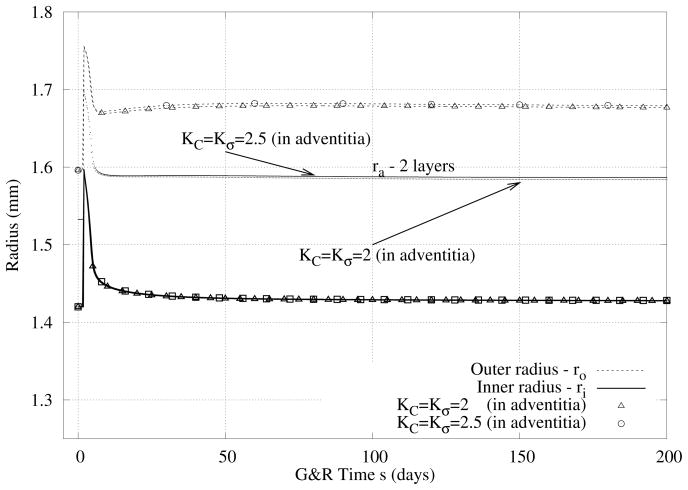
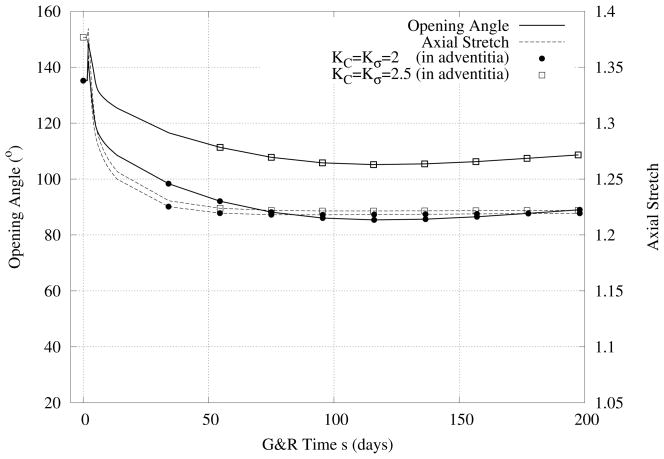
In Figure 9 we compare predicted evolutions of inner and outer radii in response to hypertension (i.e., a 50% increase in pressure) when the smooth muscle cells of the media and the fibroblasts of the adventitia respond differently to changes in stress. As it can be seen, increased values of the production parameters (cf. equation 3) in the adventitia resulted in a slightly thicker wall. Although there are no significant differences in the relative thicknesses of the media and adventitia, there were more pronounced differences in the predicted evolution of opening angle and axial stretch (Figure 10).
Figure 9.
Case IV - Similiar to prior results except for the combined case of 50% increase in pressure and different rates of cell response in the media (SMC) and adventitia (fibroblasts).
Figure 10.
Case IV - Similiar to Figure 9 except for opening angle and axial stretch.
5. Discussion
As noted earlier, most models of arterial growth and remodeling have neglected the multilayered structure of the wall. In many cases, this assumption is justifiable because simpler models can provide information on time-courses of change in both geometry (caliber and wall thickness) and overall stiffness, the two metrics of most importance in many clinical assessments of vascular health or disease (Valentín et al. (2009)). Nevertheless, to exploit the rapidly increasing information on vascular cell mechanobiology and pathobiology, mathematical models of arterial G&R should account for the multilayered construction of the wall and, in particular, the different compositions of each layer. Indeed, many diseases and responses to injury are restricted primarily to particular layers; notable examples include atherosclerosis and restenosis following angioplasty, both of which involve primarily the intima albeit mediated by SMC migration from the media.
In contrast to others who have considered transmural heterogeneities in arterial properties (e.g., Alford et al. (2008); Machyshyn et al. (2010); Schmid et al. (2010)), we focused on the basilar artery, a muscular artery important for supplying blood to the brain. Our present model extends our prior 3-D thick-walled model of this artery by allowing the percentage of load-bearing constituents and deposition stretches to vary transmurally (Tables 2 – 4). From Figures 3, 5, and 7, we can see that there were negligible differences in the predictions of evolving radii for the three different models. This finding both gives us confidence that the multilayer models are accurate (recall that the one-layer model in Karšaj et al. (2010) was verified independently) and reveals that gross predictions of evolving geometry are not particularly sensitive to some aspects of the modeling. On the other hand, there were significant differences in the predicted evolution of opening angle and axial stretch (Figures 4, 6, and 8). This finding reminds us that model validation should be based on as many different metrics as possible, which for arterial G&R should include changes in geometry, wall stiffness, opening angle, and axial prestress at the minimum. Of course, data on evolving mass fractions within the different layers would provide a further means to validate or re-fine a model. Whereas we focused on abrupt, sustained changes in pressure and flow (which is appropriate to many experimental and clinical situations, including surgery and device implantation), we showed earlier that allowing such changes to occur gradually over time (as in exercise or diseases such as hypertension) tends to affect only the time course, not the extent of G&R (Karšaj et al. (2010)). More data on time courses of change in loading and response are also needed for model building and validation.
In conclusion, whereas we and others have begun to address transmural variations in arterial wall properties, there is a need to focus such modeling on human pathological cases wherein such variations are particularly important. Among these, intimal thickening due to aging and atherosclerosis are both important and relevant. For example, Holzapfel et al. (2007) presented excellent layer-specific data on residual strains in human aorta, ranging in age from 36 to 74 years. Testing competing hypotheses on the long-term growth and remodeling processes that result in age-related differences in arterial composition, structure, and properties that describe such data promises to increase our understanding greatly and must be pursued. We submit that the present or similar models of G&R that account for multilayered differences will be fundamental to such investigations.
Acknowledgments
This work was supported, in part, via NIH grants HL-086418 and HL-105297.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Igor Karšaj, Email: ikarsaj@fsb.hr.
Jay D Humphrey, Email: jay.humphrey@yale.edu.
References
- Alford PW, Humphrey JD, Taber LA. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech Model Mechanobiol. 2008;7 (4):245–62. doi: 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arribas SM, Hinek A, González MC. Elastic fibres and vascular structure in hypertension. Pharmacol Ther. 2006;111 (3):771–91. doi: 10.1016/j.pharmthera.2005.12.003. [DOI] [PubMed] [Google Scholar]
- Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng. 2006;128 (1):142–149. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- Baek S, Valentín A, Humphrey JD. Biochemomechanics of cerebral vasospasm and its resolution: Ii. constitutive relations and model simulations. Ann Biomed Eng. 2007;35 (9):1498–509. doi: 10.1007/s10439-007-9322-x. [DOI] [PubMed] [Google Scholar]
- Cardamone L, Valentín A, Eberth JF, Humphrey JD. Origin of axial prestretch and residual stress in arteries. Biomech Model Mechanobiol. 2009;8 (6):431–446. doi: 10.1007/s10237-008-0146-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorrington KL, McCrum NG. Elastin as a rubber. Biopolymers. 1977;16 (6):1201–22. doi: 10.1002/bip.1977.360160604. [DOI] [PubMed] [Google Scholar]
- Fung Y. Biomechanics: motion, flow, stress, and growth. Springer Verlag; NY, NY: 1990. [Google Scholar]
- Gleason RL, Taber LA, Humphrey JD. A 2-d model of flow-induced alterations in the geometry, structure, and properties of carotid arteries. J Biomech Eng. 2004;126 (3):371–81. doi: 10.1115/1.1762899. [DOI] [PubMed] [Google Scholar]
- Holzapfel G, Gasser T, Ogden R. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61 (1):1–48. [Google Scholar]
- Holzapfel GA, Sommer G, Auer M, Regitnig P, Ogden RW. Layer-specific 3d residual deformations of human aortas with non-atherosclerotic intimal thickening. Ann Biomed Eng. 2007;35 (4):530–45. doi: 10.1007/s10439-006-9252-z. [DOI] [PubMed] [Google Scholar]
- Humphrey J. Cardiovascular solid mechanics: cells, tissues, and organs. Springer Verlag; NY: 2002. [Google Scholar]
- Humphrey J, Rajagopal K. A constrained mixture model for growth and remodeling of soft tissues. Mathematical Models and Methods in Applied Sciences. 2002;12 (3):407–430. [Google Scholar]
- Humphrey JD. Mechanisms of arterial remodeling in hypertension: coupled roles of wall shear and intramural stress. Hypertension. 2008a;52 (2):195–200. doi: 10.1161/HYPERTENSIONAHA.107.103440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochem Biophys. 2008b;50 (2):53–78. doi: 10.1007/s12013-007-9002-3. [DOI] [PubMed] [Google Scholar]
- Karšaj I, Sorić J, Humphrey JD. A 3-D framework for arterial growth and remodeling in response to altered hemodynamic loads. International Journal of Engineering Science. 2010;48:1357–1372. doi: 10.1016/j.ijengsci.2010.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee R. Morphology of cerebral arteries. Pharmac Ther. 1995;66:149–173. doi: 10.1016/0163-7258(94)00071-a. [DOI] [PubMed] [Google Scholar]
- Machyshyn IM, Bovendeerd PHM, van de Ven AAF, Rongen PMJ, van de Vosse FN. A model for arterial adaptation combining microstructural collagen remodeling and 3D tissue growth. Biomech Model Mechanobiol. 2010;9 (6):671–87. doi: 10.1007/s10237-010-0204-z. [DOI] [PubMed] [Google Scholar]
- Nardinocchi P, Teresi L. On the active response of soft living tissues. Journal of Elasticity. 2007;88 (1):27–39. [Google Scholar]
- Rachev A. A model of arterial adaptation to alterations in blood flow. Journal of Elasticity. 2000;61 (1):83–111. [Google Scholar]
- Rachev A, Hayashi K. Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions in arteries. Ann Biomed Eng. 1999;27 (4):459–68. doi: 10.1114/1.191. [DOI] [PubMed] [Google Scholar]
- Schmid H, Watton PN, Maurer MM, Wimmer J, Winkler P, Wang YK, Röhrle O, Itskov M. Impact of transmural heterogeneities on arterial adaptation: application to aneurysm formation. Biomech Model Mechanobiol. 2010;9 (3):295–315. doi: 10.1007/s10237-009-0177-y. [DOI] [PubMed] [Google Scholar]
- Stergiopulos N, Vulliémoz S, Rachev A, Meister JJ, Greenwald SE. Assessing the homogeneity of the elastic properties and composition of the pig aortic media. J Vasc Res. 2001;38 (3):237–46. doi: 10.1159/000051052. [DOI] [PubMed] [Google Scholar]
- Taber LA. A model for aortic growth based on fluid shear and fiber stresses. J Biomech Eng. 1998;120 (3):348–54. doi: 10.1115/1.2798001. [DOI] [PubMed] [Google Scholar]
- Taber LA, Humphrey JD. Stress-modulated growth, residual stress, and vascular heterogeneity. J Biomech Eng. 2001;123 (6):528–535. doi: 10.1115/1.1412451. [DOI] [PubMed] [Google Scholar]
- Tsamis A, Stergiopulos N, Rachev A. A structure-based model of arterial remodeling in response to sustained hypertension. J Biomech Eng. 2009;131 (10):101004. doi: 10.1115/1.3192142. [DOI] [PubMed] [Google Scholar]
- Valentín A, Cardamone L, Baek S, Humphrey JD. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J R Soc Interface. 2009;6 (32):293–306. doi: 10.1098/rsif.2008.0254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vito R, Demiray H. A two-layered model for arterial wall mechanics. Proceed 35th ACEMB Meeting; Philadelphia, USA. 1982. [Google Scholar]
- von Maltzahn WW, Besdo D, Wiemer W. Elastic properties of arteries: a nonlinear two-layer cylindrical model. J Biomech. 1981;14 (6):389–97. doi: 10.1016/0021-9290(81)90056-7. [DOI] [PubMed] [Google Scholar]
- Wan W, Hansen L, Gleason RL., Jr A 3-D constrained mixture model for mechanically mediated vascular growth and remodeling. Biomech Model Mechanobiol. 2010;9 (4):403–19. doi: 10.1007/s10237-009-0184-z. [DOI] [PMC free article] [PubMed] [Google Scholar]