A new dependence parameter approach to improve the design of cluster randomized trials with binary outcomes

Abstract

Background and Purpose

Power and sample size calculations for cluster randomized trials require prediction of the degree of correlation that will be realized among outcomes of participants in the same cluster. This correlation is typically quantified as the intraclass correlation coefficient (ICC), defined as the Pearson correlation between two members of the same cluster or proportion of the total variance attributable to variance between clusters. It is widely known but perhaps not fully appreciated that for binary outcomes, the ICC is a function of outcome prevalence. Hence the ICC and the outcome prevalence are intrinsically related, making the ICC poorly generalizable across study conditions and between studies with different outcome prevalences.

Methods

We use a simple parametrization of the ICC that aims to isolate that part of the ICC that measures dependence among responses within a cluster from the outcome prevalence. We incorporate this parametrization into sample size calculations for cluster randomized trials and compare our method to the traditional approach using the ICC.

Results

Our dependence parameter, R, may be less influenced by outcome prevalence, and has an intuitive meaning that facilitates interpretation. Estimates of R from previous studies can be obtained using simple statistics. Comparison of methods showed that the traditional ICC approach to sample size determination tends to overpower studies under many scenarios, calling for more clusters than truly required.

Limitations

The methods are developed for equal-sized clusters, whereas cluster size may vary in practice.

Conclusions

The dependence parameter R is an alternative measure of dependence among binary outcomes in cluster randomized trials that has a number of advantages over the ICC.

Introduction

In a cluster randomized trial, natural groups or “clusters” of individuals such as medical practices, school classrooms or communities are randomized to study conditions, and outcomes are measured on individuals within clusters. Cluster randomized trials are a key tool in intervention and clinical research and have become widely used in recent years [1, 2].

In cluster randomized trials, the outcomes of individuals within the same cluster are statistically dependent rather than independent [2, 3]. Sample size and power calculations for such trials generally require prediction of the degree of correlation among observations that will be realized in the final completed trial data. The degree of correlation is typically quantified by the intraclass correlation coefficient (ICC), commonly denoted ρ. For example, one widely used approach is to determine the sample size required for a trial with independent subjects and inflate this number by a factor of 1 + (m − 1)ρ, where m is the cluster size (see, for example, [3–5]). The quantity 1 + (m − 1)ρ represents overdispersion due to clustering and is called the variance inflation factor or design effect [6–8].

The value of the ICC used for sample size and power calculations is of utmost importance because small differences in ICC values can yield substantial differences in the sample size required to achieve the desired power [3, 8]. Given this sensitivity, there is a serious risk that a study will be underpowered if the ICC realized in the completed data is higher than the value assumed at the design stage, or overpowered if the realized ICC is lower. Hence it is essential to deal adequately with intracluster correlation in the planning stages of a study. Recent reviews have emphasized the importance of ICC estimates for sample size and power calculations for cluster randomized trials [1, 9, 10].

In practice, investigators often perform power and sample size calculations using ICC values from previous studies that are deemed to be similar [3, 11]. Investigators using this approach have benefited from an increase in recent years in the number of papers reporting ICC values [10], consistent with calls for better reporting [12]. However, empirical investigations have found wide variation in ICC values in data collected in similar circumstances. Adams et al. [13] reanalyzed data from 31 cluster-based studies in primary care. They estimated the ICC for 1,039 variables (binary, continuous and ordinal) and found widely varying ICCs for the same outcome variable, even after adjusting for individual- and cluster-level characteristics. They concluded that the magnitude of the ICC for a given measure can rarely be estimated in advance. Other authors have also noted that ICC values from one context often have poor generalizability to other contexts [14]. Overall, these reports raise serious concerns about the practice of using ICC values from previous studies to power future studies.

In this work, we focus on one factor which may help to explain the lack of generalizability of the ICC between seemingly similar studies. It is widely known but perhaps not fully appreciated that for binary outcomes, the ICC, variously defined as the Pearson correlation between two members of the same cluster or the proportion of the total variance in the outcome attributable to the variance between clusters, is a function of the outcome prevalence. Given this functional relationship, it follows quite naturally that ICC values will generally not transfer well between studies with different outcome prevalences.

To address this problem, we propose to use a simple parametrization that aims to isolate that part of the ICC that measures the degree of dependence among responses within a cluster from the outcome prevalence. The parametrization involves a parameter R that quantifies the association among observations within clusters independent of the outcome prevalence. Our work is motivated in part by Rosner [15] and Stefanescu and Turnbull [16]. We develop sample size formulae for cluster randomized trials for binary outcomes that use R rather than the ICC, to mitigate dependence on the outcome prevalence. The parameter R also has an intuitive meaning that can facilitate interpretation. We show how estimates of R can be obtained from prior studies and used in the design of a future study.

The paper is organized as follows. First, we describe the common correlation model and variance inflation rubric for sample size estimation, show that the ICC is a function of the outcome prevalence and propose a parametrization of the ICC involving the parameter R. We show how to obtain estimates of R from previous studies using simple statistics and discuss specification of R values for sample size calculations. We incorporate the parametrization into sample size formulae and compare the new R-based approach to the traditional ICC-based approach for sample size determination. We end with a discussion of advantages and limitations.

Methods

The common correlation model

We base our method on the common correlation model [17–19]. Consider a set of c clusters of size m. Let X_ij denote the binary response of individual i = 1, …, m in cluster j = 1, …, c. The possible values of X_ij are success and failure, coded as 1 and 0, respectively. The probability of success, which we can think of as outcome prevalence in the context of a health study, is assumed to be the same for all individuals; specifically, Pr(X_ij = 1) = π for all i, j. (We introduce a second set of clusters with a different outcome prevalence later.) The responses of individuals from different clusters are assumed to be independent, while within each cluster, the correlation between any pair of responses (X_ij, X_i′j), i ≠ i′, is ρ, the ICC, which takes values in [−1, 1]. The case of ρ = 0 corresponds to independence among cluster members. An unbiased estimator of the outcome prevalence is $\widehat{\pi }=\frac{1}{\mathit{\text{mc}}}{\displaystyle {\sum }_{i=1}^m{\displaystyle {\sum }_{j=1}^c}{X}_{\mathit{\text{ij}}}}$ [20]. It can be shown (see, e.g., [6]) that the variance of this estimator is

$$\mathit{\text{Var}}(\widehat{\pi })=\frac{\pi (1-\pi )}{\mathit{\text{mc}}}[1+(m-1)\rho ]$$ (1)

Since the variance of the estimator under independent observations would be $\frac{\pi (1-\pi )}{\mathit{\text{mc}}}$, the quantity 1 + (m − 1)ρ is the variance inflation due to clustering and is known as the variance inflation factor or design effect [6–8].

The common correlation model is the basis for the much-used variance inflation rubric for sample size and power calculation for cluster randomized trials. In the simplest of these approaches, one determines the sample size required assuming independent observations then inflates this number by the design effect to account for clustering [3–5]. For example, suppose that we wish to have at least 100(1-β) power to detect a difference in two proportions π₁ and π₂ using a two-sided test with Type I error rate α. The number of subjects required per condition, assuming equal-sized groups and independent subjects, is given by

$$n=\lceil \frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2[{\pi }_1(1-{\pi }_1)+{\pi }_2(1-{\pi }_2)]}{{({\pi }_1-{\pi }_2)}^2}\rceil$$ (2)

where ⌈x⌉ is the ceiling function giving the smallest integer ≥ x and z_p denotes the pth quantile of the standard normal distribution; see, for example, [21–23]. To account for clustering, n is multiplied by an inflation factor 1 + (m − 1)ρ and we take ⌈n/m⌉ clusters per condition. The variance inflation rubric for sample size determination has been extended to methods for varying cluster size [24–27] and matched-pair, stratified and other study designs [3].

The ICC is a function of the outcome prevalence

Under the common correlation model, the ICC is defined as the Pearson pairwise correlation between observations in a cluster. Beginning with the definition of the Pearson correlation, we can derive the following equivalent expressions for the ICC:

$$\rho =\frac{\mathit{\text{Cov}}(X_{\mathit{\text{ij}}},X_{i\prime j})}{\sqrt{\mathit{\text{Var}}(X_{\mathit{\text{ij}}})\mathit{\text{Var}}(X_{i\prime j})}}=\frac{E(X_{\mathit{\text{ij}}}{X}_{i\prime j})-{\pi }^2}{\pi (1-\pi )}=\frac{P(X_{\mathit{\text{ij}}}=1,X_{i\prime j}=1)-{\pi }^2}{\pi (1-\pi )}$$ (3)

for i ≠ i′. Further simplification can be obtained by noting that P(X_ij = 1, X_i′j = 1) = P(X_i′j = 1)P(X_ij = 1|X_i′j = 1) = πP(X_ij = 1|X_i′j = 1), which leads to the expression

$$\rho =\frac{P(X_{\mathit{\text{ij}}}=1|X_{i\prime j}=1)-\pi }{1-\pi }.$$ (4)

This expression reveals that ρ is a function of the outcome prevalence π and the conditional probability P(X_ij = 1|X_i′j = 1). Two important consequences follow from the functional relationship between ρ and π. First, it provides a basis for expecting that ICC values will be poorly generalizable between studies with different outcome prevalences. For this reason, it would be very useful to have a measure of the degree of dependence among responses within clusters that does not depend on outcome prevalence, and hence would be more “portable” between studies with different outcome prevalences. Secondly, since outcome prevalence will differ by study condition, we might expect the ICC to also generally differ by study condition. This suggests that we should use sample size and power calculation methods for trials with correlated binary outcomes that allow the ICC to differ by study arm.

Proposed parametrization of the ICC

To address these issues, our approach is to develop a parametrization of ρ that aims to isolate that part of the ICC that measures the degree of dependence among responses within cluster from the outcome prevalence. To this end, we focus on the conditional probability P(X_ij = 1|X_i′j = 1), which is the component of ρ in (4) that encodes the degree of dependence among observations within clusters, and develop a parametrization for this conditional probability.

A useful parametrization of this conditional probability was proposed by Rosner [15] in the context of ophthalmologic studies, in which individuals may contribute two eyes worth of data, whose values may be correlated. Rosner proposed a model in which P(X_ij = 1) = π for eye i in person j, and P(X_ij = 1|X_3−i,j = 1) = Rπ, i = 1, 2 for some constant R. The constant R is a measure of dependence between the two eyes of the same person. If R = 1, the two eyes are completely independent, while if P(X_ij = 1|X_3−i,j = 1) = Rπ = 1, the eyes are completely dependent. We note that the assumption of constant success probability, P(X_ij = 1) = π, in Rosner's model is consistent with the common correlation model, which we have been using as our basic probability model.

We propose the parametrization P(X_ij = 1|X_i′j = 1) = Rπ as an empirically useful parametrization for quantifying dependence among outcomes within clusters in cluster randomized trials with binary outcomes. Incorporating this parametrization into expression (4) for the ICC, we obtain

$$\rho =\frac{(R-1)\pi }{1-\pi }.$$ (5)

Inspection of this expression shows that if R = 1, then ρ = 0 and the observations are independent. If $1<R\le \frac{1}{\pi }$, then 0 < ρ ≤ 1 and the ICC is positive. R < 1 would correspond to negative intraclass correlation, which is thought to be rare in cluster randomized trials [2, 3, 19]. We will call R the dependence parameter.

An appealing aspect of this parametrization is that R provides an intuitive quantification of how much more or less likely a member of a cluster is to have the outcome given that another member of the cluster has the outcome. If R = 1, a participant is uninfluenced by the outcomes of other cluster members; the observations are independent. If R > 1, other “successes” in the cluster make it more likely that a subject in that cluster will also be a “success.” For example, if R = 1.05, the participant would be 5% more likely to be a success if a randomly chosen other cluster member is a success. In the rare situation in which R < 1, other successes make a participant less likely to be a success.

Unlike the ICC, R is not an overt function of π. The bounds on R do depend on π, but these bounds will rarely be approached in practice. The upper bound for R is $\frac{1}{\pi }$; this upper bound corresponds to perfect positive correlation of ρ = 1, and the magnitude of the correlation in most cluster randomized trials is well below this level. The lower bound for ρ in the common correlation model is not −1 but rather, as shown by Prentice [28], is

$$\frac{-1}{(m_{\mathit{\text{max}}}-1)}+\frac{\omega (1-\omega )}{m_{\mathit{\text{max}}}(m_{\mathit{\text{max}}}-1)\pi (1-\pi )}$$ (6)

where m_max is the maximum cluster size, ω = m_maxπ − int(m_maxπ) and int(·) denotes the integer part [17, 28]. Hence negative values are possible for small clusters, and ρ → 0 as m_max → ∞. As mentioned previously, negative ICC is thought to be rare; designing a trial with an assumption of negative ICC runs a risk of underpowering the study and is not recommended [2]. Hence although both the upper and lower bounds for R depend on π, in most trials, unless cluster size is very large, these bounds will not be approached.

Rosner [15] did not use the parametrization P(X_ij = 1|X_i′j = 1) = Rπ for study design but rather proposed it as a means of adjusting for intraclass correlation in inference. Rosner's parametrization has been used in the context of a sensitivity analysis for the design of a cluster randomized trial [16]. The objective of the PRECISE trial was to test the hypothesis that a daily nutritional supplement of selenium would reduce cancer incidence [29]. In the study, households would be randomized to selenium supplements or placebo, with the primary endpoint being total cancer incidence within 5 years. Investigators wished to compare a one person per household design to a clustered sampling design in which each participant would invite one or more members of the same household to also participate. Stefanescu and Turnbull [16] describe the use of Rosner's parametrization to conduct a sensitivity analysis. Assuming clusters of size 2, they used the formula ρ = (Rπ − π)/(1 − π) to estimate the design effect of the clustered sampling scheme, computing the design effect for a range of π and R values. They concluded that the design effect would be minimal, motivating the investigators to proceed with the clustered design.

Obtaining estimates of R from prior studies

Since investigators typically have access only to summary statistics from previous studies, from published literature, we present a method of obtaining estimates of R using only summary statistics. Point estimates of R from previous studies can be obtained using point estimates of ρ and π for each condition:

$${\widehat{R}}_k=1+\frac{{\widehat{\rho }}_k(1-{\widehat{\pi }}_k)}{{\widehat{\pi }}_k}$$ (7)

where k indexes study condition. Maximum likelihood estimation of R based on individual-level data is briefly discussed in Rosner [15].

Equation (7) relating R̂ and ρ̂ implies that estimates of R will be less biased than estimates of ρ. Specifically, suppose that on average ρ̂ overestimates ρ by, say, 10%. Then E(ρ̂) = ρ + 0.1ρ and a direct calculation shows E(R̂) = R + 0.1(R − 1), implying that

$$E\left(\frac{\widehat{R}-R}{R}\right)=\frac{0.1(R-1)}{R}=0.1\left(1-\frac{1}{R}\right)<0.1,$$ (8)

since R is positive. This suggests that if the estimate ρ̂ has an upward bias, then the corresponding upward bias of R̂ is always smaller in percentage terms. Similarly, if ρ̂ has downward bias, R̂ will have less downward bias in percentage terms.

Is R Independent of Outcome Prevalence?

We propose R as an useful parameter that, unlike the ICC, is not an overt function of the outcome prevalence. Since values of R are empirically determined, it is not possible to present a mathematical proof that R does not depend on outcome prevalence. Rather, this can only be verified by observation. If R is indeed describing some inherent dependence among observations in a cluster that does not depend on the outcome prevalence, then values of R computed on the same clusters for the same outcome but that have different prevalences should be similar. Comparing R values in such a setting, in which all else is held constant except prevalence, would constitute a test of the empirical validity of the R parameter. In practice, it is difficult to find data meeting these conditions to see whether this holds empirically. However, some suitable data are provided by Hade et al. [30], who published ICC estimates for cancer screening outcomes for various levels of aggregation (e.g., physician, clinic, county). For some settings, ICCs were obtained for both “ever screened” and “screened within guidelines” on the same set of subjects. “Screened within guidelines” subjects are a subset of the “ever screened” subjects, and thus the proportion screened within guidelines is lower than the proportion ever screened. Hence these settings resemble a situation in which all else is constant except prevalence.

We found 10 instances in Table 2 of Hade et al. [30] in which both screened within guidelines and ever screened proportions were reported for what appeared to be exactly the same individuals (matching study, cancer site, group, method of ascertaining outcome, number of groups and average number of members per group), and computed corresponding R values. These data (Table 1) show that in all but one instance, higher prevalence is associated with a higher ICC, helping to validate the association between prevalence and ICC. In addition, the values of the two ICCs were generally quite different. In contrast, in most cases, the values of the two Rs were quite close. This small-scale empirical study lends support to the notion that values of R represent some inherent measure of intracluster dependence that is not as subject to change with changing prevalence as the ICC.

Table 1.

Estimates of prevalence π, intraclass correlation ρ and dependence parameter R for 10 clustered binary data settings that differ only in prevalence. Subscripts: 1 = screened within guidelines, 2 = ever screened. Data from Hade et al [30].

Setting and outcome	π1	π2	ρ1	ρ2	R1	R2
Self-reported Papanicolaou test, community setting, 8 clusters, average of 202 members/cluster [31]	0.806	0.918	0.1001	0.1772	1.02	1.02
Self-reported Papanicolaou test, community setting, 8 clusters, average of 200 members/cluster [31]	0.764	0.893	0.1911	0.2920	1.06	1.04
Self-reported mammography, clinic setting, 25 clusters, average of 18 members/cluster [32]	0.685	0.951	0.0449	0.0006	1.02	1.00
Self-reported colonoscopy, clinic setting, 25 clusters, average of 21 members/cluster [32]	0.674	0.773	0.0005	0.0214	1.00	1.01
Self-reported mammography, community setting, 8 clusters, average of 202 members/cluster [31]	0.665	0.815	0.0281	0.0607	1.01	1.01
Self-reported mammography, community setting, 8 clusters, average of 200 members/cluster [31]	0.650	0.755	0.0694	0.1080	1.04	1.04
Self-reported prostate specific antigen test, clinic setting, 25 clusters, average of 12 members/cluster [32]	0.599	0.784	0.0139	0.0203	1.01	1.01
Chart audit verified colonoscopy, clinic setting, 25 clusters, average of 21 members/cluster [32]	0.490	0.554	0.0460	0.0961	1.05	1.08
Chart audit verified mammography, clinic setting, 25 clusters, average of 18 members/cluster [32]	0.357	0.674	0.1444	0.2166	1.26	1.11
Chart audit verified prostate specific antigen test, clinic setting, 25 clusters, average of 12 members/cluster [32]	0.355	0.572	−0.0151	0.1181	0.97	1.09

It is worth noting that the values of R and ρ calculated from the same data can give very different impressions of the level of dependence among responses. For example, the first row of Table 1 has R of 1.02, a low value near independence, while the ICCs are 0.10 and 0.18, which give the impression of substantial correlation. Because $\rho =\frac{(R-1)\pi }{1-\pi }$, the situation of low R but high ρ occurs when prevalence is high.

New approach to sample size determination using the dependence parameter R

We now develop a sample size formula for cluster randomized trials with binary outcomes that uses R rather than the ICC, first covering some preliminaries. Due to the functional relationship between ρ and π, we suggest that ρ should be allowed to vary by study condition, which we index by k:

$${\rho }_k=\frac{P(X_{\mathit{\text{ijk}}}=1|X_{i\prime \mathit{\text{jk}}}=1)-{\pi }_k}{1-{\pi }_k}=\frac{R_k{\pi }_k-{\pi }_k}{1-{\pi }_k}=\frac{(R_k-1){\pi }_k}{1-{\pi }_k},$$ (9)

k = 1, 2. If the two arms have similar degrees of dependence within a cluster, then one can set R₁ = R₂. Different R values would be used when the study conditions will have different effects on the dependence among responses within cluster. This may occur if, for example, the intervention fosters interactions among cluster members and the control condition does not. Interventions entailing interactions among cluster members include group educational sessions and group therapy (e.g., [33–36]). We provide an example below.

Parametrization (9) leads to expressions for the variances of the outcome prevalences

$$\mathit{\text{Var}}({\widehat{\pi }}_k)=\frac{{\pi }_k(1-{\pi }_k)}{\mathit{\text{mc}}}[1+(m-1){\rho }_k]=\frac{{\pi }_k(1-{\pi }_k)}{\mathit{\text{mc}}}\left[1+\frac{(m-1)(R_k-1){\pi }_k}{1-{\pi }_k}\right],$$ (10)

k = 1, 2. A general expression that can be used to derive sample size or power in the case of a two-arm trial with binary outcomes is (Chow et al. [22], page 87):

$$\frac{|{\pi }_1-{\pi }_2|}{\sqrt{\mathit{\text{Var}}({\widehat{\pi }}_1)+\mathit{\text{Var}}({\widehat{\pi }}_2)}}-z_{1-\alpha /2}\approx z_{1-\beta }$$ (11)

Into this expression we can substitute expression (10) and assuming equal allocation, we obtain the following formula for the number of clusters per study arm:

$$c=\lceil \frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2\{{\pi }_1[1-{\pi }_1+(m-1)(R_1-1){\pi }_1]+{\pi }_2[1-{\pi }_2+(m-1)(R_2-1){\pi }_2]\}}{m{({\pi }_1-{\pi }_2)}^2}\rceil$$ (12)

This formula can be inverted and solved for power. An alternative derivation of the same formula is to begin with a sample size formula that allows different ICCs in the different study arms [2]:

$$c=\lceil \frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2\{{\pi }_1(1-{\pi }_1)[1+(m-1){\rho }_1]+{\pi }_2(1-{\pi }_2)[1+(m-1){\rho }_2]\}}{m{({\pi }_1-{\pi }_2)}^2}\rceil$$ (13)

and substitute ρ_k = (R_k − 1)π_k/(1 − π_k), k = 1, 2 into this formula.

Note that invariance of R across study conditions does not imply that the ICC will be constant across conditions; rather, in such cases, the ICCs would generally differ due to the difference in outcome prevalence. Because $\frac{\pi }{1-\pi }$ is a monotonically increasing function in π, if we have R₁ = R₂ = R > 1, then we will have ${\rho }_1=\frac{(R-1){\pi }_1}{(1-{\pi }_1)}<{\rho }_2=\frac{(R-1){\pi }_2}{(1-{\pi }_2)}$ when π₁ < π₂, i.e., the ICC will be higher in the study condition with higher outcome prevalence when R is constant (see Table 1 for empirical examples). In addition, the ICC increases rapidly as π increases. For a fixed π, the ICC increases linearly as R increases.

Specification of R Values

Sample size formula (12) involves R₁ and R₂, corresponding to the dependence parameters for each study condition. Thus in order to use this formula to design a study, we need to prespecify likely values of R₁ and R₂. The choice of a single R versus R varying by study arm will depend on whether or not the study conditions are anticipated to have different effects on the dependence among responses within a cluster. If the intervention involves interactions among participants in the same cluster whereas the control condition does not, we might expect a higher R in the intervention condition. In the absence of such differences, we may choose R to be constant across conditions.

We present examples from previous studies to guide the selection of a single R versus (R₁, R₂) and the magnitude of R values. Estimates of R from previous studies with similar designs in conjunction with careful consideration of the population, intervention, setting and primary outcome of the future planned trial, can be used to predict the value of R that is likely to be observed in the future data. Rather than using a single value, it would be prudent to conduct a sensitivity analysis using a range of plausible values of R.

Example 1: Our first example is from the National Institutes of Health-funded study “Increasing Colorectal Cancer Screening in High Risk Individuals” (NIH CA7536701). In this study [37], clusters consisting of first-degree relatives (adult siblings and children) of 1,280 colorectal cancer cases identified through the California Cancer Registry were randomized to intervention and control conditions, with intervention assignees receiving personalized print materials and telephone counseling about colorectal cancer screening and control assignees receiving usual care. The primary endpoint was self-reported receipt of colorectal cancer screening at follow-up. Clustering of observations was by family. Subjects were age-eligible older adults and were generally not living in the same household. Study staff communicated with trial participants singly by telephone and mail.

In this study, since cluster members were generally not in the same physical location and the intervention did not foster interaction among family members, we might expect the dependence of outcomes within clusters to be relatively low and similar for the intervention and control conditions. The ICCs for the intervention and control arms were ρ̂₁ = 0.028 and ρ̂₂ = 0.020, respectively, and the outcome proportions were π̂₁ = 0.39 and π̂₂ = 0.30, yielding estimates of R̂₁ = 1.044 and R̂₂ = 1.047. Hence a similar study might be designed using a value of R of about 1.05, constant across study conditions. This represents a relatively low degree of dependence among responses within clusters.

Note that while the ICC was higher in the intervention condition than the control condition, the dependence parameters were essentially equal. The difference in ICC across conditions appears to be attributable to the difference in the outcome proportions.

Example 2: Our second example is from the Breast Cancer Education Program for Samoan Women [33, 38], a cluster randomized trial designed to increase rates of mammogram usage in women of Samoan ancestry funded by the California Breast Cancer Research Program (4BB-1400) and the National Center for Minority Health and Health Disparities (P60MD000532). This study randomized 61 Samoan churches in southern California to intervention and control conditions. These churches serve as community centers for members of the Samoan American community, and members within churches tend to be socially connected. Women at churches assigned to the intervention arm participated in an interactive culturally tailored breast cancer education program delivered in four sessions over several weeks. Women in the control arm received usual care. The primary endpoint was self-reported receipt of a mammogram at follow-up.

In this study, the ICCs for the intervention and control arms were 0.34 and 0.06, respectively, and the outcome proportions were 0.47 and 0.39. The corresponding dependence parameters were R̂₁ = 1.39 and R̂₂ = 1.09. These parameters contrast with those from previous example in several ways. First, they are greater in magnitude, even in the control condition. This may be attributable to the fact that this study involved subjects who were inherently cohesive due to preexisting social networks. Secondly, R was dramatically higher in the intervention condition. This is consistent with the intervention inducing additional correlation due to its highly interactive nature. In intuitive terms, we could interpret the R values to mean that in the absence of the intervention, a participant was about 9% more likely to obtain a mammogram if another member of her church, chosen at random, obtained a mammogram. The intervention increased this conditional probability by 30 percentage points.

Example 3: Our third example is from a randomized controlled trial conducted at a veterans affairs medical center [39]. In this study, health care providers in the intervention arm attended a workshop on colorectal cancer screening and received periodic feedback on screening rates and training to improve communication with patients. The control condition was usual care. The primary endpoint was colorectal cancer screening. Chart review revealed screening completion rates of 0.413 in the intervention and 0.324 in the control arm. This study does not report ICCs but does report the design effect in the two arms separately. Since the design effect is equal to 1 + ρ(m − 1), where m is average cluster size, we were able to estimate the ICCs as 0.082 in the intervention and 0.035 in the control arm. (Average cluster sizes were 16.9 and 18.2 patients, respectively.) The corresponding dependence parameters are R̂₁ = 1.12 and R̂₂ = 1.07. This provides another example of a differential level of dependence across study conditions, and the control value might be taken as a typical example of the level of dependence among patients with the same provider in this setting.

Comparison of Performances of R-Based and ICC-Based Approaches for Sample Size Determination

We compared the performance of our proposed approach using R to traditional approaches to sample size calculation using the ICC as follows. We assumed that the study to be planned will be a balanced trial with c clusters of equal size m in each condition. Summary statistics from a previous study deemed to be similar are available and are used to compute parameters for use in the sample size calculation. Using the R-based approach, the investigators compute R₁ and R₂ based on the values of π₁, ρ₁, π₂ and ρ₂ in the previous study using equation (7), then use these R values in equation (12), along with the values of the π's expected in the new study, to calculate the number of clusters needed in each condition. We considered two ICC-based approaches. ICC approach A allows for different ICCs in each arm; the investigators obtain values of ρ₁ and π₂ from the previous study and use them in sample size formula (13), along with the values of the π's expected in the new study, to calculate the required number of clusters per condition. ICC approach B uses a single overall ICC, which is currently the most common approach; the investigators get the overall ICC ρ_comb from the previous study, then use the traditional formula [3]

$$c=\lceil \frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2[{\pi }_1(1-{\pi }_1)+{\pi }_2(1-{\pi }_2)][1+(m-1){\rho }_{\mathit{\text{comb}}}]}{m{({\pi }_1-{\pi }_2)}^2}\rceil ,$$ (14)

to calculate the required number of clusters per condition. Comparisons among these three approaches allow one to evaluate the impact of a single ICC assumption versus an arm-specific ICC assumption versus an R-based assumption in a step-by-step manner. We specified power of 0.8 and α of 0.05 for all approaches. We compared the samples size estimates under each approach and calculated the actual achieved power, assuming that the R parameters accurately described the dependence in the future study and that the assumed prevalences in the sample size calculation were realized, and that the outcome analysis used a cluster-level analysis comparing the means of the cluster-level proportions in the two groups using a two-sample t-test [3], which is consistent with equation (11).

Previous study scenarios were constructed by specifying (π₁, π₂) and (R₁, R₂). From these values one can compute ρ₁ and ρ₂ using equation (5), which are needed to get the variances in (11). The value of ρ_comb is also determined by (π₁, π₂, R₁, R₂) and was obtained as follows. Under the assumption of equal-sized clusters, the classical estimator of the Pearson correlation coefficient over all pairs of observations within groups is [17]:

$${\widehat{\rho }}_k=\frac{1}{{\widehat{\pi }}_k(1-{\widehat{\pi }}_k)}\left[\frac{{\displaystyle {\sum }_{j=1}^c}{Y}_{\mathit{\text{jk}}}^2-\mathit{\text{cm}}{\widehat{\pi }}_k}{\mathit{\text{cm}}(m-1)}-{\widehat{\pi }}_k^2\right]$$ (15)

where Y_jk is the number of successes in cluster j in condition k and ${\widehat{\pi }}_k=\frac{1}{\mathit{\text{cm}}}{\displaystyle {\sum }_{j=1}^c}{Y}_{\mathit{\text{jk}}}$, the overall proportion of successes in condition k. The combined ICC, calculated over both conditions, can thus be expressed as:

$${\widehat{\rho }}_{\mathit{\text{comb}}}=\frac{1}{\widehat{\pi }(1-\widehat{\pi })}\left[\frac{{\displaystyle {\sum }_{j=1}^c}{Y}_{j1}^2+{\displaystyle {\sum }_{j=1}^c}{Y}_{j2}^2-2\mathit{\text{cm}}\widehat{\pi }}{2\mathit{\text{cm}}(m-1)}-{\widehat{\pi }}^2\right]$$ (16)

where π̂ = (π̂₁ + π̂₂)/2, which can be shown to simplify to

$${\widehat{\rho }}_{\mathit{\text{comb}}}=\frac{{\widehat{\rho }}_1(1-{\widehat{\pi }}_1)+{\widehat{\rho }}_2(1-{\widehat{\pi }}_2)}{2\widehat{\pi }(1-\widehat{\pi })}.$$ (17)

We expected that our approach would yield results most different from the ICC-based approaches when the prevalence levels in the previous study and new study were different. We examined four prevalence-change scenarios: moving from a high prevalence setting of (π₁, π₂) = (0.7, 0.5) in the previous study to a moderate prevalence setting of (π₁, π₂) = (0.5, 0.3) in the planned study, from moderate (π₁, π₂) = (0.5, 0.3) to low (π₁, π₂) = (0.3, 0.1), from low to moderate, and from moderate to high. We also compared the methods under no prevalence change scenarios. We considered a range of values of R₁ and R₂, and considered R₁ = R₂, R₁ < R₂ and R₁ > R₂. Cluster sizes were 5, 20 and 50.

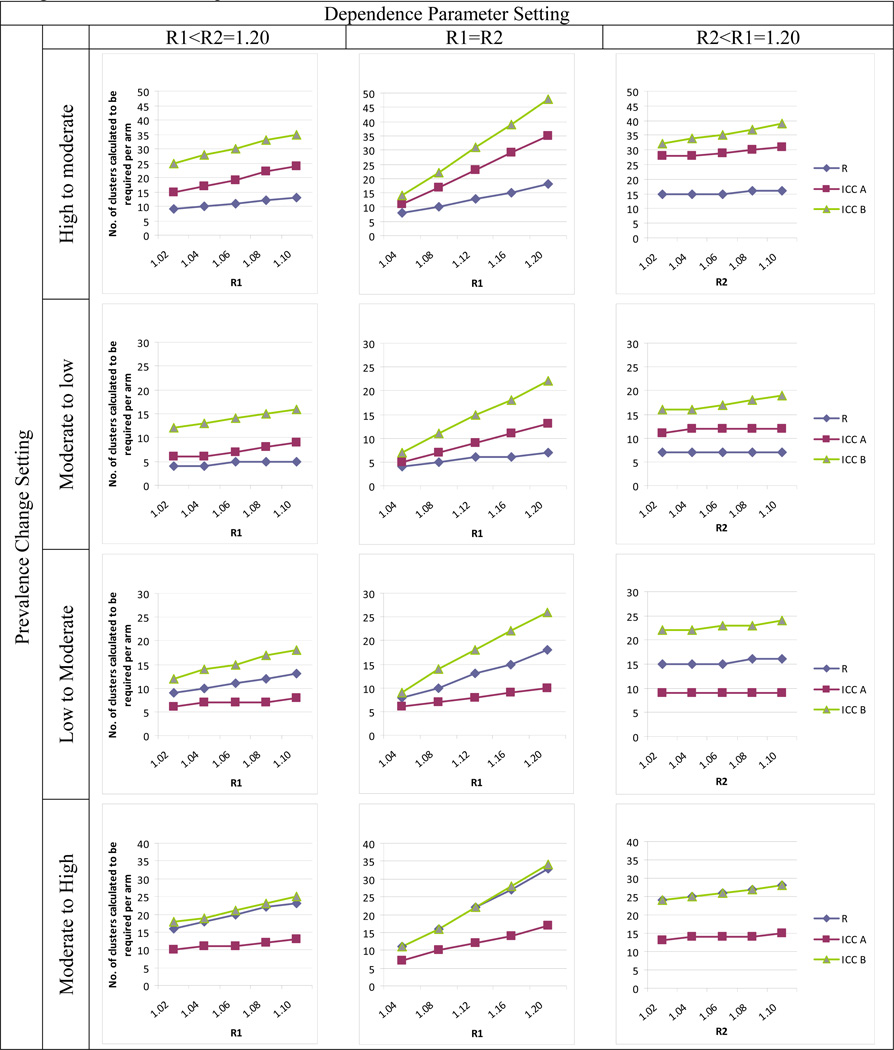
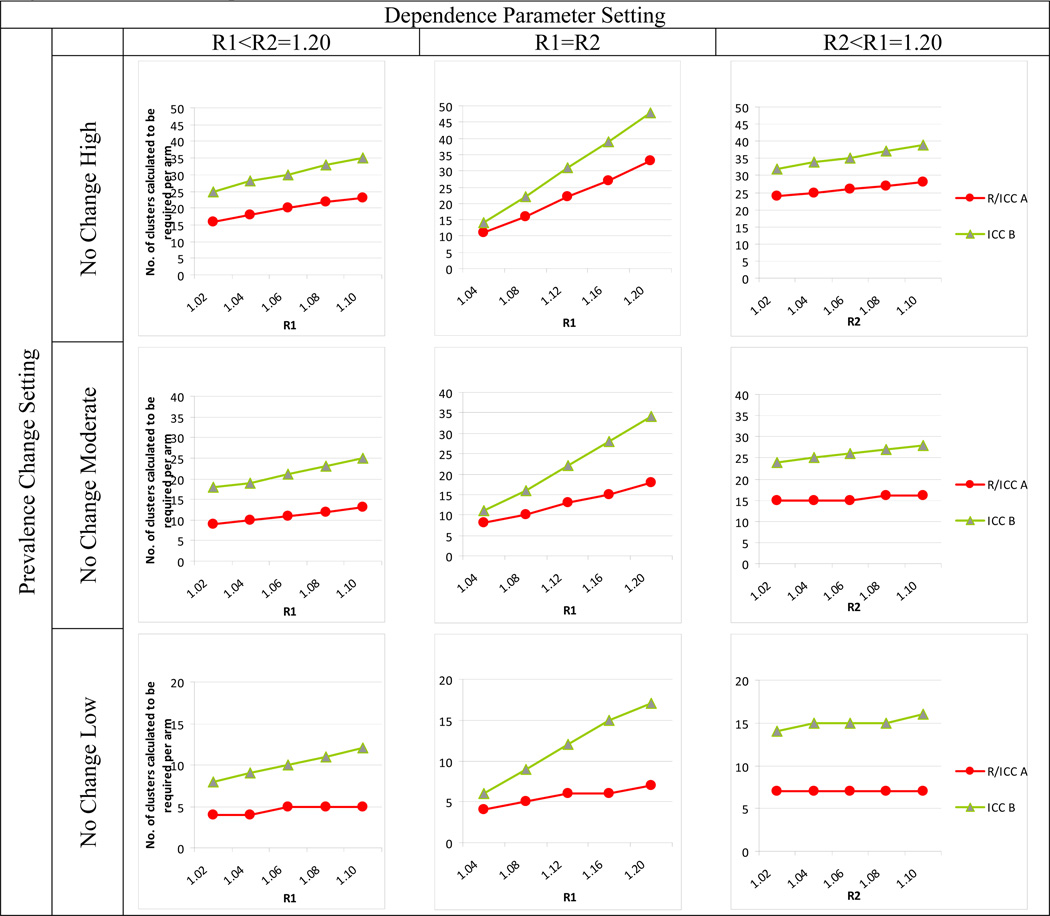
Results for clusters of size 20 are provided in Figures 1 and 2. Full results in tabular form are provided in the online appendix accompanying this article.

Figure 1.

Comparison of R- and two ICC-based approaches to sample size calculation when prevalence setting changes between previous and future study. R method uses R1 and R2 for Arms 1 and 2, respectively, and equation 13. ICC method A uses ICC1 and ICC2 for Arms 1 and 2 and equation 14. ICC method B uses a single overall ICC and equation 15. See text for additional details.

Figure 2.

Comparison of R- and two ICC-based approaches to sample size calculation when prevalence setting does not change between previous and future study. R method uses R1 and R2 for Arms 1 and 2, respectively, and equation 13. ICC method A uses ICC1 and ICC2 for Arms 1 and 2 and equation 14. ICC method B uses a single overall ICC and equation 15. See text for additional details.

The results show that when moving from high to moderate or from moderate to low prevalence (Figure 1, top two rows), the ICC approaches can grossly overpower the study, calling for many more clusters than required to achieve desired power. ICC approach A performs better than ICC B, due to the fact that the combined ICC provides a more inflated estimate of correlation - it is generally either higher than either arm-specific ICC or closer to the higher value - but ICC A still overpowers the study substantially. Overpowering is expected, since the ICCs in the new study will be lower than in the previous study due to reduced prevalence, all else being equal. When R₁ = R₂, the overestimation worsens with increasing R.

The bottom two rows of Figure 1 show that when moving to a higher prevalence setting, ICC A underpowers the study. This occurs because this approach underestimates the ICC in the new study; the ICC is expected to increase as the prevalences increase, a phenomenon that simply transferring the previous ICC to the new study does not take into account. The R method takes this into account. ICC B overpowers studies when moving from a low to a moderate prevalence setting (Figure 1, third row), but tends to size the study fairly well when moving from moderate to high prevalence (Figure 1, fourth row). Here, the fact that the combined ICC is an inflated measure of correlation provides a protective effect against underpowering.

Figure 2 shows results when prevalence is unchanged. In these cases, the R and ICC A methods are equivalent. ICC B, however, causes overpowering, due again to the fact that the combined ICC inflates the correlation.

Discussion

The dependence of the ICC on the outcome prevalence in clustered binary data is not commonly recognized and may account for some of the lack of generalizability of ICCs between contexts. In this work, we have proposed a simple parametrization of the ICC that helps to isolate that part of the ICC that measures dependence among responses within a cluster from the outcome prevalence. Our approach has a number of advantages. The value of the dependence parameter R may be more portable between studies with different outcome prevalences, and hence may be more suitable as a freestanding measure of the magnitude of dependence among responses within cluster. The parametrization is simple and has an intuitive meaning that facilitates interpretation and elicitation. In addition, estimates of R can be obtained directly from simple statistics from previous studies, and these estimates may be less susceptible to bias than estimates of the ICC. If R values do indeed transfer between studies, our approach performs much better than ICC-based approaches in terms of achieving desired power.

Code to implement these methods, written in R software (freeware available at http://www.r-project.org/), is available from the first author. The code includes power and sample size calculation functions as well as a graphics module that produces plots of power vs. sample size and other common plots. The graphics module also facilitates sensitivity analyses by taking as input a range of parameter values, so that investigators can evaluate sample size requirements and power under varying assumptions. The code enforces the lower and upper bounds on R that are implied by the bounds on ρ.

Abbreviations

ICC

intracluster (or intraclass) correlation coefficient