Mathematical Equivalence of Two Common Forms of Firing-Rate Models of Neural Networks

Abstract

We demonstrate the mathematical equivalence of two commonly used forms of firing-rate model equations for neural networks. In addition, we show that what is commonly interpreted as the firing rate in one form of model may be better interpreted as a low-pass-filtered firing rate, and we point out a conductance-based firing rate model.

At least since the pioneering work of Wilson and Cowan (1972), it has been common to study neural circuit behavior using rate equations – equations that specify neural activities simply in terms of their rates of firing action potentials, as opposed to spiking models, in which the actual emissions of action potentials or “spikes” are modeled. Rate models can be derived as approximations to spiking models in a variety of ways (e.g. Aviel and Gerstner 2006, Ermentrout 1994, La Camera et al. 2004, Mattia and Del Giudice 2002, Ostojic and Brunel 2011, Shriki et al. 2003, Wilson and Cowan 1972; reviewed in Ermentrout and Terman 2010, Chapter 11; Gerstner and Kistler 2002, Chapter 6; Dayan and Abbott 2001, Chapter 7)).

Two forms of rate model most commonly used to model neural circuits are the following, which we will refer to as the v-equation and r-equation respectively:

$$\tau \frac{d\mathbf{v}}{dt}=-\mathbf{v}+\stackrel{\sim }{\mathbf{I}}+\mathbf{Wf}(\mathbf{v})$$ (1)

$$\tau \frac{d\mathbf{r}}{dt}=-\mathbf{r}+\mathbf{f}(\mathbf{Wr}+\mathbf{I})$$ (2)

Here, v and r are each vectors representing neural activity, with each element representing the activity of one neuron in the modeled circuit. v is commonly thought of as representing voltage, while r is commonly thought of as representing firing rate (probability of spiking per unit time). f(x) is a nonlinear input-output function that acts element-by-element on the elements of x, i.e. it has i^th element (f(x))_i = f(x_i) for some nonlinear function of one variable f. f typically takes such forms as an exponential, a power law, or a sigmoid function, and f(v_i) is typically regarded as a static nonlinearity converting the voltage of the i^th cell v_i to the cell’s instantaneous firing rate. W is the matrix of synaptic weights between the neurons in the modeled circuit. Ĩ and I are the vectors of external inputs to the neurons in the v or r networks, respectively, which may be time dependent. In the Appendix, we illustrate a simple heuristic “derivation” of the v-equation, starting from the biophysical equation for the voltages v. Along the way, we also point to a conductance-based version of the rate equation.

When developing a rate model of a network, it can be unclear which form of equation to use or whether or not it makes a difference. Here we demonstrate that the choice between Eqs. 1 and 2 makes no difference: the two models are mathematically equivalent, and so will display the same set of behaviors. It has been noted previously (Beer 2006) that, when I is constant and W is invertible, then the two equations are equivalent under the relationship v = Wr + I, Ĩ = I. We generalize this result to demonstrate the equivalence of the two equations when W is not invertible and inputs may be time dependent.

The v-equation is defined when we specify the input across time, Ĩ (t), and the initial condition v(0); we will call the combination of these and Eq. 1 a v-model. The r-equation is defined when we specify I(t) and r(0); we will call the combination of these and Eq. 2 an r-model. We will show that any v-model can be mapped to an r-model and any r-model can be mapped to a v-model such that the solutions to Eqs. 1–2 satisfy v = Wr + I.

As we will see, the inputs in equivalent models are related by $\stackrel{\sim }{\mathbf{I}}=\mathbf{I}+\tau \frac{d\mathbf{I}}{dt}$, or $\tau \frac{d\mathbf{I}}{dt}=-\mathbf{I}+\stackrel{\sim }{\mathbf{I}}$. That is, I is a low-pass filtered version of Ĩ. Note that there is an equivalence class of I, parametrized by I(0), that all correspond to the same Ĩ under this equivalence. We assume that the equivalence class has been specified, i.e. Ĩ has been specified (if I has been specified, Ĩ can be found as $\stackrel{\sim }{\mathbf{I}}=\mathbf{I}+\tau \frac{d\mathbf{I}}{dt}$). Then a v-model is defined by specifying v(0), while an r-model is defined by specifying the set {r(0), I(0)}. If W is D × D, then v(0) is D-dimensional, while {r(0), I(0)} is 2D-dimensional, so we can guess that the map from r to v takes a D-dimensional space of r-models to a single v-model, and conversely the map from v to r takes a single v-model back to a D-dimensional space of r-models, and we will show that this is true.

We first show that if r evolves according to the r-equation, then Wr + I evolves according to the v-equation. Setting v = Wr + I, we find:

$$\tau \frac{d\mathbf{v}}{dt}=\mathbf{W}\tau \frac{d\mathbf{r}}{dt}+\tau \frac{d\mathbf{I}}{dt}=\mathbf{W}(-\mathbf{r}+f(\mathbf{Wr}+\mathbf{I}))+\tau \frac{d\mathbf{I}}{dt}$$ (3)

$$=-(\mathbf{v}-\mathbf{I})+\mathbf{W}f(\mathbf{v})+\tau \frac{d\mathbf{I}}{dt}$$ (4)

$$=-\mathbf{v}+\stackrel{\sim }{\mathbf{I}}+\mathbf{W}f(\mathbf{v})$$ (5)

Therefore, if v evolves according to the v-equation and r evolves according to the r-equation and v(0) = Wr(0) + I(0), then – since the v-equation propagates Wr + I forward in time − v = Wr + I at all times t > 0. We will thus have established the desired equivalence if we can solve v(0) = Wr(0) + I(0) for any v-model, specified by v(0), or for any r-model, specified by {r(0), I(0)}.

Note that, as expected, a D-dimensional space of r-models converges on the same v-model. Since {r(0), I(0)} forms a 2D-dimensional space, which is constrained by the D-dimensional equation v(0) = Wr(0)+I(0), the D-dimensional subspace of r-models {r(0), I(0)} that satisfy this equation all converge on the same v-model.

To go from an r-model to a v-model is straightforward: we simply set v(0) = Wr(0) + I(0).

To go from a v-model to an r-model, we first define some useful notation:¹

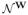• is the nullspace of W, i.e. the subspace of all vectors that W maps to zero. P_N is the projection operator into .

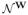• ${\mathcal{N}}_{\perp }^{\mathbf{W}}$ is the subspace perpendicular to 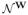. This is the subspace spanned by the rows of W. P_N⊥ is the projection operator into ${\mathcal{N}}_{\perp }^{\mathbf{W}}$.

• ℛ^W is the range of W, i.e. the subspace of vectors that can be written Wx for some x. This is the subspace spanned by the columns of W. P_R is the projection operator into ℛ^W.

• ${\mathcal{R}}_{\perp }^{\mathbf{W}}$ is the subspace perpendicular to ℛ^W, also called the left nullspace. P_R⊥ is the projection operator into ${\mathcal{R}}_{\perp }^{\mathbf{W}}$.

For any vector x, we define x_N ≡ P_N x, x_N⊥ ≡ P_N⊥x, x_R ≡ P_Rx, x_R⊥ ≡ P_R⊥x. We rely on the fact that x = x_N + x_N⊥ = x_R + x_R⊥.

Given a v-model, the equation v(0) = Wr(0)+I(0) has a solution if and only if v(0)−I(0) ∈ ℛ^W, which is true if and only if v_R⊥ (0) − I_R⊥ (0) = 0,² so we must choose

$${\mathbf{I}}_{R\perp }(0)={\mathbf{v}}_{R\perp }(0)$$ (9)

Letting D_R be the dimension of ℛ^W and D_N the dimension of 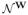the fundamental theorem of linear algebra states that D_R + D_N = D. So I_R⊥ (0) has dimension D_N. This leaves unspecified I_R(0), which has dimension D_R.

To solve for r_N⊥ (0), we note that the equation v = Wr + I can equivalently be written v = Wr_N⊥ + I (because Wr_N = 0, so Wr = Wr_N⊥). That is, knowledge of v only specifies r_N⊥. We define W⁻¹ to be the Moore-Penrose pseudo-inverse of W. This is the matrix that gives the 1-to-1 mapping of ℛ^W into ${\mathcal{N}}_{\perp }^{\mathbf{W}}$ that inverts the 1–1 mapping of ${\mathcal{N}}_{\perp }^{\mathbf{W}}$ to ℛ^W induced by W, and that maps all vectors in ${\mathcal{R}}_{\perp }^{\mathbf{W}}$ to zero.³ The pseudoinverse has the property that W⁻¹W = P_N⊥ while WW⁻¹ = P_R. Then we can solve for r_N⊥ (0) as

$${\mathbf{r}}_{N\perp }(0)={\mathbf{W}}^{-1}(\mathbf{v}(0)-\mathbf{I}(0))={\mathbf{W}}^{-1}({\mathbf{v}}_R(0)-{\mathbf{I}}_R(0))$$ (10)

This is a D_R-dimensional equation for the 2D_R-dimensional set of unknowns {r_N⊥ (0), I_R(0)}, so it determines D_R of these parameters and leaves D_R free. For example, it could be solved by freely choosing I_R(0) and then setting r_N⊥ (0) = W⁻¹(v_R(0) − I_R(0)), or by freely choosing r_N⊥ (0) and then setting I_R(0) = v_R(0) − Wr_N⊥ (0).

Equations 10 and 9 together ensure the equality v(0) = Wr(0) + I(0). Applying W to both sides of Eq. 10 yields v_R(0) = Wr_N⊥ (0)+I_R(0) = Wr(0)+I_R(0). This states that the equality hold within the range of W; orthogonal to the range of W, we have P_R⊥ Wr = 0 and v_R⊥ (0) = I_R⊥ (0). Together these yield v(0) = Wr(0) + I(0).

Finally, we can freely choose r_N (0), which has no effect on the equation v(0) = Wr(0) + I(0). r_N (0) has D_N dimensions, so we have freely chosen D_R + D_N = D dimensions in finding an r-model that is equivalent to the v-model. That is, we have found a D-dimensional subspace of such r-models, those that satisfy v(0) = Wr(0) + I(0).

To summarize, we have established the equivalence between r-models and v-models. For each fixed choice of W, τ, and Ĩ(t), an r-model is specified by {r(0), I(0)} and Eq. 2, while a v-model is specified by v(0) and Eq. 1. The equivalence is established by setting v(0) = Wr(0) + I(0), which yields a D-dimensional subspace of equivalent r-models for a given v-model. Under this equivalence, v obeys Eq. 1, r obeys Eq. 2, and the two are related at all times by v = Wr+ I, with $\tau \frac{d\mathbf{I}}{dt}=-\mathbf{I}+\stackrel{\sim }{\mathbf{I}}$. To go from an r-model to its equivalent v-model, we simply set v(0) = Wr(0)+I(0). To go from a v-model to one of its equivalent r-models, we set I_R⊥ (0) = v_{R ⊥} (0); freely choose r_N (0); and freely choose {r_N⊥ (0), I_R(0)} from the D_R-dimensional subspace of such choices that satisfy r_N⊥ (0) = W⁻¹(v_R(0) − I_R(0)), where W⁻¹ is the pseudoinverse of W.

Finally, note that Eq. 2 can be written $\tau \frac{d\mathbf{r}}{dt}=-\mathbf{r}+\mathbf{f}(\mathbf{v})$. That is, if we regard v as a voltage and f(v) as a firing rate, as suggested by the “derivation” in the Appendix, then r is a low-pass-filtered version of the firing rate, just as I is a low-pass-filtered version of the input Ĩ.

Appendix

As an example of an unsophisticated and heuristic derivation of these equations (more sophisticated derivations can be found in the references in the main text), the v-equation can be “derived” as follows: we start with the equation for the membrane voltage of the i^th neuron:

$$C_i\frac{{dv}_i}{dt}=\sum _j{g}_{ij}(E_{ij}-v_i)$$ (11)

where C_i is the capacitance of the i^th neuron and g_ij is the j^th conductance onto the neuron, with reversal potential E_ij. We assume that the g_ij’s are composed of an intrinsic conductance, $g_i^L$, with reversal potential $E_i^L$; extrinsic input $g_i^{\text{ext}}$ with reversal potential $E_i^{\text{ext}}$; and within-network synaptic conductances, with g̃_ij representing input from neuron j with reversal potential Ẽ_ij. Dividing by Σ_k g_ik and defining τ_i(t) = C_i/Σ_k g_ik gives

$${\tau }_i(t)\frac{{dv}_i}{dt}=-v_i+\frac{g_i^L{E}_i^L+g_i^{\text{ext}}{E}_i^{\text{ext}}+{\sum }_j{\stackrel{\sim }{g}}_{ij}{\stackrel{\sim }{E}}_{ij}}{g_i^L+g_i^{\text{ext}}+{\sum }_k{\stackrel{\sim }{g}}_{ik}}$$ (12)

We now make a number of further simplifying assumptions. We assume that g̃_ij is proportional to the firing rate r_j of neuron j, with proportionality constant W̃_ij ≥ 0: g̃_ij = W̃_ijr_j. This ignores synaptic time courses, among other things. We assume that r_j is given by the static nonlinearity r_j = f(v_j) (e.g., see Hansel and van Vreeswijk 2002, Miller and Troyer 2002, Priebe et al. 2004 for such a relationship between firing rate and voltage averaged over a few 10’s of milliseconds). We assume synapses are either excitatory with reversal potential E_E or inhibitory with reversal potential E_I, and linearly transform the units of voltage so that E_E = 1 and E_I = −1. We define W_ij = W̃_ijE_j: this is now a synaptic weight that is positive for excitatory synapses and negative for inhibitory synapses. We define ${\stackrel{\sim }{I}}_i\equiv g_i^L{E}_i^L+g_i^{\text{ext}}{E}_i^{\text{ext}}$ and define $g_i\equiv g_i^L+g_i^{\text{ext}}$. This yields the “conductance-based rate equation”:

$${\tau }_i(t)\frac{{dv}_i}{dt}=-v_i+\frac{{\stackrel{\sim }{I}}_i+{\sum }_j{W}_{ij}f(v_j)}{g_i+{\sum }_k\mid W_{ik}\mid f(v_k)}$$ (13)

with τ_i(t) = C_i/ (g_i + Σ_k |W_ik|f(v_k)).

Finally, we assume that the total conductance, represented by the denominator in the last term of Eq. 13, can be taken to be constant, e.g. if $g_i^L$ is much larger than synaptic and external conductances, or if inputs tend to be “push-pull”, with withdrawal of some inputs compensating for addition of others. We absorb the constant denominator into the definitions of Ĩ_i and W_ij, and note that this also implies that τ_i is constant, to arrive finally at the v-equation:

$${\tau }_i\frac{{dv}_i}{dt}=-v_i+\sum _j{W}_{ij}f(v_j)+{\stackrel{\sim }{I}}_i$$ (14)