Improving Peak Capacity in Fast On-Line Comprehensive Two-Dimensional Liquid Chromatography with Post First Dimension Flow-Splitting

Abstract

The use of flow splitters between the two dimensions in on-line comprehensive two dimensional liquid chromatography (LC×LC) has not received very much attention in comparison to their use in GC×GC where they are quite common. In principle, splitting the flow after the first dimension column and performing on-line LC×LC on this constant fraction of the first dimension effluent should allow the two dimensions to be optimized almost independently. When there is no flow splitting any change in the first dimension flow rate has an immediate impact on the second dimension. With a flow splitter one could for example double the flow rate into the first dimension column and do a 1:1 flow split without changing the sample loop size or the sampler’s collection time. Of course, the sensitivity would be diminished but this can be partially compensated by use of a larger injection; this will likely only amount to a small price to pay for this increased resolving power and system flexibility. Among other benefits, we found a 2-fold increase in the corrected 2D peak capacity and the number of observed peaks for a 15 min analysis time by using a post first dimension flow splitter. At a fixed analysis time this improvement results primarily from an increase in the gradient time resulting from the reduced system re-equilibration time and to a smaller extent it is due to the increased peak capacity achieved by full optimization of the first dimension.

INTRODUCTION

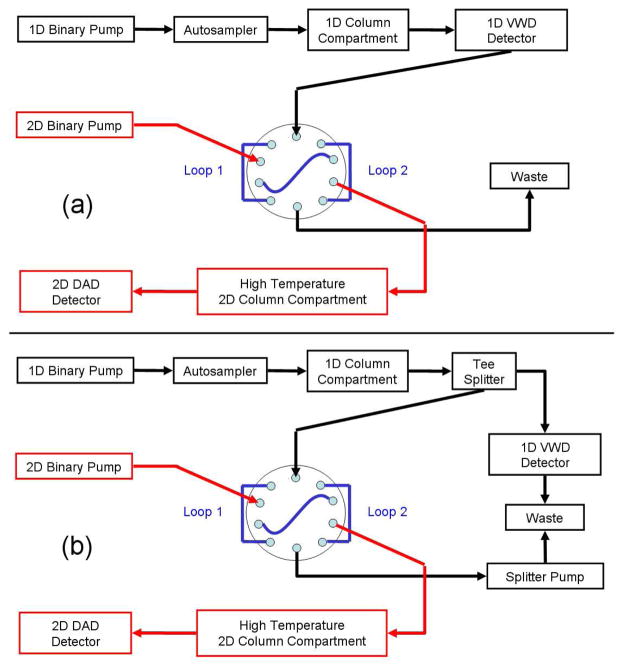
Since its introduction in 1991 the use of flow-splitting as part of the modulator between the first and second dimensions in multidimensional gas chromatography has become quite common¹. More recently the various benefits of flow splitting were discussed by Tranchida et al². However, we have only seen a few references to the use of post first dimension flow-splitting in on-line LC×LC^{3, 4}; in none of them was the flow-splitting used for independently optimizing the first dimension. Block diagrams of on-line LC×LC systems without and with post first dimension flow-splitting as implemented in this work are shown in Figs. 1(a) and (b) respectively.

Fig. 1.

Block diagrams of the instruments used in the on-line LC×LC separations for (a) split-less and (b) split modes.

In both systems a comprehensive chromatogram is acquired; with use of a post first dimension flow splitter only a fraction of the total effluent of the first dimension column is collected and delivered to the second dimension. This fraction is uniform and completely representative of the total effluent from the first dimension. This differs from the kind of sampling described by Seeley³ where the duty cycle did not continuously collect the effluent coming from the first dimension, rather discrete fractions were acquired at regular time periods.

The principal motivation for our interest in flow-splitting in on-line LC×LC is best explained by our experiences in prior work. Previously we and others have shown that in this form of LC×LC there is necessarily an optimum sample acquisition time^{4, 5}. In on-line LC×LC this sampling time (t_s) must be equal to the second dimension cycle time (²t_c). Thus the volume of sample collected when there is no splitter is:

$$V_s={}^{1}F·{{}^{2}t}_c$$ (1)

It is evident that once the sampling time, which is equal to the second dimension cycle time, has been chosen, any change in the first dimension flow rate (¹F) must result in a change in the sample volume with the split-less system shown in Fig. 1(a). If a splitter were used as shown in Fig. 1(b), eq. (1) can be generalized to:

$$V_s=\rho {}^{1}F·{{}^{2}t}_c$$ (2)

Where ρ is the “split ratio”. Obviously the smaller is the split ratio the greater will be the dilution of the sample. This dilution effect in multi-dimensional separations has been studied by Schure⁶ and more recently by Horvath et al.⁷ The overwhelming chief virtue of this type of flow splitter is that it allows the two dimensions to be operated essentially independently. However, there are numerous other possible benefits including, we believe, a significant enhancement in the resolving power of on-line LC×LC.

Giddings’s peak capacity⁸ has become the most important metric of separating power in multi-dimensional separations. It also has been shown, at least for 1D-LC, that the peak capacity is proportional to the average resolution⁹. Ideally, the two dimensional peak capacity (n_{c, 2D}) is defined by the product of the peak capacities of the first (¹n_c) and second (²n_c) dimensions (the so-called product rule):

$$n_{c,2D}={{}^{1}n}_c\times {{}^{2}n}_c$$ (3)

It is well known that this equation overestimates the practical peak capacity of the system and corrections must be applied to account for the under-sampling of the first dimension^{5, 10, 11} and for the lack of “orthogonality” of the separation mechanisms in the two dimensions¹².

The product rule can be corrected for under-sampling by use of the Davis-Stoll-Carr factor^{11, 13}:

$$\langle \beta \rangle =\sqrt{1+3.35{\left(\frac{{{}^{2}t}_c}{{}^{1}w}\right)}^2}=\sqrt{1+3.35{\left(\frac{{{}^{2}t}_c{{}^{1}n}_c}{{{}^{1}t}_g}\right)}^2}$$ (4)

Where β is the under-sampling correction factor, ¹w and ¹t_g are the first dimension 4σ peak width and gradient time respectively. By applying this correction factor to eq. (3) we obtain the corrected two dimensional peak capacity (n′_c,2D):

$${n^{\prime }}_{c,2D}=\frac{{{}^{1}n}_c\times {{}^{2}n}_c}{\langle \beta \rangle }\approx \frac{{{}^{1}t}_g\times {{}^{2}n}_c}{{}^{1}w\sqrt{1+3.35{\left(\frac{{{}^{2}t}_c}{{}^{1}w}\right)}^2}}$$ (5)

We feel that using the corrected two dimensional peak capacity provides a more accurate measure of the real resolving power and reasonably incorporates the effect of under-sampling.

As on-line LC×LC becomes more widely adopted for quantitative analysis, replicate analyses and high throughput will become more important. In this respect the analysis time needs to be as short as possible. The system re-equilibration time (t_re-eq) plays a key role in setting the gradient time (t_g) for a certain analysis time (t_an) and must be considered for optimization since no separation takes place during re-equilibration. The concept of the fraction of the analysis time devoted to the separation (λ) has been defined by Horvath et al. for the second dimension of a 2D-LC separation^{13, 14}. With the same objective in mind we define its analog for the first dimension of 2D-LC as:

$${}^1\lambda =\frac{{{}^{1}t}_g}{{{}^{2}t}_{an}}=\frac{{{}^{1}t}_g}{{{}^{1}t}_g+{{}^{1}t}_{re-eq}}$$ (6)

This relationship will be used to represent the fraction of the analysis time that is devoted to the separation in the first dimension. Obviously as the first dimension re-equilibration time occupies a smaller fraction of the total first dimension analysis time, ¹λ approaches unity.

In this work we will compare the time-based performance of the two system configurations (split and split-less) in terms of the corrected 2D peak capacity as defined by eq. (5). We also report the number of observed peaks in a complex maize extract sample as a complementary metric of the performance of the systems. These two metrics are very important in that the instrumental configuration that yields the larger total corrected 2D peak capacity should also yield (for the same peak distribution) the larger number of observed peaks¹¹. The corrected 2D peak capacity production rate is also calculated as it is especially important in high throughput analysis.

EXPERIMENTAL

Chemicals

The origin of most of the indolic standards used to determine the peak capacities is described in previous work¹⁵; however, indole-5-carbonitrile, 4-indolyl acetate, as well as nitroethane and nitropropane were purchased from Sigma-Aldrich (St. Louis, MO) as reagent grade or better. Thiourea was reagent grade purchased from Matheson Coleman & Bell (East Rutherford, NJ, USA). Chromatographic grade water and acetonitrile were obtained from Fisher Scientific (Pittsburg, PA, USA). perchloric acid reagent grade was purchased from Sigma-Aldrich (St. Louis, MO, USA). All materials were used as received. All mobile phases were prepared gravimetrically (± 0.01 g) and used without any further filtration.

Samples Preparation

Two samples were used in this experiment. A standard mixture and a maize extract. The standard mixture contained the following compounds: Thiourea (33.9 μg/mL), 5-hydroxyL-tryptophan (151 μg/mL), indole-3-acetyl-L-aspartic acid (27.1 μg/mL), indole-3-acetyl-L-glutamic acid (265 μg/mL), tryptophan (91.6 μg/mL), anthranilic acid (33.9 μg/mL), indole-3-acetyl-L-glycine (80.8 μg/mL), 5-hydroxy-tryptamin (22.9 μg/mL), indole-3-acetyl-ε-L-lycine (33.9 μg/mL), indole-3-acetyl-β-D-glucose (54.9 μg/mL), indole-3-acetamide (74.6 μg/mL), indole-3-carboxylic acid (91.6 μg/mL), indole-3-acetyl-L-isoleucine (61.8 μg/mL), indole-3-propionic acid (33.9 μg/mL), indole-3-ethanol (72.9 μg/mL), tryptamine (40.7 μg/mL), indole-3-butyric acid (133 μg/mL), indole-3-acetonitrile (102 μg/mL), indole-5-carbonitrile (48.5 μg/mL), 4-indolyl acetate (18.1 μg/mL), nitroethane (10.4 μg/mL) and nitropropane (9.9 μg/mL). The final solvent composition of the standard mixture was water with less than 1% in volume of acetonitrile. The maize seed used for the maize extract preparation was Silver Queen (Burpee, Warminster, PA) and a detailed procedure for its preparation has been given⁴. The samples were filtered through 0.45 um PTFE membrane before injection and the injected volumes are reported in Table 1.

Table 1.

First dimension operational parameters and peak capacities.

	Analysis Time [min]
	15		30		60
Split Mode	split-less	split	split-less	split	split-less	split
1tg [min] a	6	12.4	19	25	43	52.1
1tre-eq [min] b	9	2.6	11	5	17	7.9
1λ c	0.40	0.82	0.63	0.83	0.72	0.87
1λ Ratio d	2.05		1.31		1.20
1L [cm] e	5	20	10	30	25	40
1F [μL/min] f	100	570	100	380	100	290
Vinjection [μL] g	1.5	8.57	1.5	5.7	1.5	4.35
Injection Delay [min]	4.9	0.86	4.9	1.29	4.9	1.69
1φi h	0	0	0	0	0	0
1φf i	0.81	0.49	0.62	0.50	0.63	0.47
1wave.[s]	9.7	4.99	12.9	8.28	16.1	13.4
1wave.Ratio j	1.94		1.55		1.20
1nc, pred k	46	228	94	275	149	317
1nc, pred Ratio l	5.0		2.9		2.1
1nc, measured m	37	149	88	181	157	232
1nc, measured Ratio n	4.0		2.1		1.5

Column is Zorbax SB-C3 2.1 mm i.d. 3.5 μm particles. Temperature is 40 °C.

^aGradient time;

^bRe-equilibration time;

^cFraction of the analysis time devoted to the separation;

^dRatio of ¹λ value for split to split-less mode;

^eColumn length;

^fFlow rate;

^gInjection volume;

^hInitial eluent strength;

ⁱFinal eluent strength;

^jRatio of average peak width for split-less to split mode;

^kPredicted peak capacity obtained with the optimization procedure;

^lRatio of predicted peak capacity for split to split-less mode;

^mMeasured peak capacity calculated with eq. (7) using average peak widths;

ⁿRatio of measured peak capacity ratio for split to split-less mode.

It is most important to note that the injection volume for the standard mixture and maize extract samples were chosen to hold constant the number of moles of sample transferred from the first to the second dimension. For example, at an analysis time of 15 min using the split-less mode the injection volume was 1.5 μL and the entire sample was transferred to the second dimension; the flow rate in the first dimension was fixed at 100 μL/min delivering a sample volume of 20 μL and 34 μL for the 12 s and 21 s cycle times respectively. In the split mode the first dimension optimized flow rate was 570 μL/min but the splitting pump was set to a flow rate of 100 μL/min. To compensate for the split-flow, 8.57 μL (1.5 μL×570/100) of sample were injected into the first dimension so that the same amount of moles of sample would be delivered to the second dimension in both modes. This was done to ensure that peak counting was not affected by a change in sensitivity when the flow is split. In addition, in preliminary work (not shown) the amount injected was deliberately varied to test for column overload. We are confident that the first dimension was not overloaded in either mode.

LC×LC Instrumentation - First Dimension

The system used an Agilent in-line Micro Vacuum Degasser (G1379), and an Agilent 1200 SL binary pump (G1312) where the original mixer was replaced by a JetWeaver V100 also from Agilent. This allowed us to reduce both the flush-out volume to 700 μL and the delay volume of the system to 610 μL. This helps minimize the system flush-out time which is part of the first dimension re-equilibration time. The sample was introduced with an Agilent 1290 Infinity Autosampler (G4226A) equipped with a 40 μL loop cartridge. The chromatographic column was placed in an Agilent 1200 SL Thermostatted Column Compartment (G1312B). The detector used was an Agilent 1100 VWD (G1314A) equipped with a 1 μL, 5 mm path micro flow cell. When the system was configured in the split-less mode, the flow from the first dimension was fixed at 100 μL/min and all the effluent was collected after the detector as shown in Fig. 1(a); when the system was configured in the split mode, the flow was divided into two streams using a stainless steel ‘tee’ U-428 from IDEX Corp (Lake Forest, Il, USA). One of the outputs was connected to the Agilent 1100 VWD (G1314A) UV Detector equipped with a 1 μL, 5 mm path micro flow cell and then connected to the waste line. The other output was connected to a 10 port / 2 position (VICI CHEMINERT 110-0063H, Valco Instruments, Houston, TX, USA) valve for sampling the first dimension as shown in Fig. 1(b). The flow path after the 10 port valve was connected to an Agilent 1290 Pump (G4220A) which controls the flow of the incoming effluent at a flow rate of 100 μL/min. A 100 cm by 0.0025 in i.d. length of PEEK-Sil tubing was connected at the output of the pump to provide backpressure for the check valves to operate properly. The 10 port valve was pneumatically actuated using helium at 80 psi. The two sample loops (loop 1 and loop 2 in Fig. 1) were made of 37.5 cm long 0.01 in. i.d. PEEK tubing for the 12 s cycle time and 137 cm long 0.007 in. i.d. PEEK tubing for the 21 s cycle time; the volume of each set of loops is listed in Table 2.

Table 2.

Second dimension operational parameters and peak capacities.

	Cycle Time [s]
	12	21
2tg [s] a	9	18
2tre-eq [s] b	3	3
2L [cm] c	3.3	3.3
2F [mL/min] d	3.0	3.0
Vloop [μL] e	20	34
2φi f	0	0
2φf g	1.0	1.0
2nc, measured h	24	32

Column is 3.3 cm long by 2.1 mm i.d. packed with ZirChrom-CARB 3 μm particles. Temperature is 110 °C.

^aGradient time;

^bRe-equilibration time;

^cColumn length;

^dFlow rate;

^eSample loop volume;

^fInitial eluent strength;

^gFinal eluent strength;

^hSecond dimension peak capacity calculated by eq. (8) using measured average peak width.

The separation columns used for the first dimension were ZORBAX SB-C3 2.1 mm i.d. with 3.5 μm particles from Agilent and columns of 5, 10, 15 and 25 cm length were connected to achieve the desired column length according to the optimization protocol. Operational conditions used in both the split and split-less modes and peak capacities for the first dimensions are given in Table 1.

LC×LC Instrumentation - Second Dimension

An Agilent 1290 binary pump (G4220A) configured with a JetWeaver V35 mixer was used in the second dimension of the on-line LC×LC system. The solvent in channel A was 10 mM aqueous phosphoric acid and the solvent in channel B was acetonitrile. The second dimension gradient time was either 9 or 18 s, with a fixed re-equilibration time of 3 s regardless of the gradient time. The corresponding second dimension cycle times were 12 and 21 s. An Agilent DAD detector (G4220A) equipped with a 1 μL, 6 mm path micro flow cell with a sampling rate of 80 Hz; data were acquired at a wavelength of 220 nm. The slit width was set to 4 nm and the reference wavelength set to off.

The second dimension separations were carried out on 2.1 × 33 mm columns packed in-house with 3.0 μm ZirChrom CARB particles (ZirChrom Separations Inc. Anoka, MN, USA). The column was operated at 110 °C and a flow rate of 3.0 mL/min, corresponding to a maximum system pressure of about 400 bar during gradient elution. An eluent pre-heater and column heating system from Systec Inc. (New Brighton, MN, USA) was used to maintain the second dimension column at 110 ± 0.1 °C. Columns with a small inner diameter (2.1 mm) were used to minimize thermal mismatch peak broadening¹⁶. The small dimensions of this column together with the high flow rate ensures a short system dwell time and fast column re-equilibration^{17, 18}. ZirChrom CARB was chosen as the second dimension stationary phase for its good chemical and mechanical stability at high temperature and highly different selectivity relative to most RP stationary phases¹⁹. Operational conditions used for the second dimensions are in Table 2.

Data Acquisition and System Control

All Agilent modules were configured and controlled using Agilent Chemstation B.04.03[16] (Agilent Technologies Inc, USA). The binary pump used for the second dimension and the 10 ports valve were coordinated by LabVIEW 9.0 software via a PCI 6024E data acquisition board (National Instruments Inc. Austin, TX, USA) using a simple in-house program.

Data Processing

The data were acquired by the Chemstation software as a single run for each 2D experiment, were then exported as a comma separated file and processed using Matlab 7.10 (R2010b, The Mathworks Inc, MA, USA) with in-house programs.

Optimization and Calculation of Peak Capacities

A computational method for a priori optimization of gradient elution peak capacity was developed by Wang et al.⁹. This method maximizes the peak capacity through the prediction of gradient peak widths and retention times based on the LSST theory²⁰. For a given gradient time, column i.d., particle size and maximum pressure available, the optimum column length, linear velocity and final gradient composition are calculated to maximize the peak capacity. The indolic standard analytes were used to calibrate the optimization procedure. We believe that the indolic standard mixture is a good representative of the key components in the maize sample extract¹⁵. We followed this approach to optimize the first dimension for both the split and split-less modes. When the split-less mode is used the flow rate was fixed at 100 μL/min allowing only the column length and final gradient composition to be optimized. For the second dimension we have experimentally shown⁴ that an optimum sampling time exists. Accordingly we decided to use two cycle times (12 and 21 s) which closely bracket the optimum for the current experiments.

We decided to use 2.1 mm columns for the first dimension in both modes. This was done because this column diameter works well at the sub-optimum flow rate of 100 μL/min needed in the split-less mode. In the split mode we could have accommodated a larger (e.g. 4.6 mm) diameter column. In order to make a conservative and simpler comparison of the two modes we decided to keep the diameter constant. Use of a 4.6 mm i.d. column in the split mode offers two advantages over the use of a 2.1 mm column. First, at the same linear velocity the higher flow rate would diminish the system flush out time thereby increasing ¹λ even further (see below). Second, 4.6 mm columns generally offer more plates than do 2.1mm columns.

Peak Capacity Measurement

The first dimension peak capacity in optimized gradient conditions was measured using the indolic standard mixture. The peak capacity was calculated according to eq. (7).

$${{}^{1}n}_c=\frac{(t_{R,\mathit{last}}-t_{R,\mathit{first}})}{w_{\mathit{avg}.}}$$ (7)

Where t_{R, last} and t_{R, first} are the retention times of the last and first peaks observed in the separation space and w_avg is the average 4σ peak width of all well resolved peaks.

Because delayed injection was used in this work and the first peak in the samples always eluted near the column hold up time, t_{R, first} was taken as t₀. A very important consideration is that use of delayed injection also allows us to combine the time needed to flush the instrument dwell volume with part of the column flush-out/re-equilibration time. Thus for a long series of injections we do not need to consider the instrument dwell. By use of delayed injection the flushing of the system dwell is effectively combined with the re-equilibration of the column. For all these reasons we believe that in a fair comparison of the split and split-less modes one should exclude the instrument dwell time as that time is only paid once in a series of runs and is rapidly amortized. The operational conditions were optimized such that the last peak in our standard mixture eluted near the end of the gradient; t_{R, last} was set equal to t₀ + t_g. The peak width in eq. (7) was taken as the average 4σ peak width of all well resolved compounds in the standard mixture.

The second dimension peak capacity was calculated based on the average of the observed 4σ peak widths of representative well formed second-dimension peaks in the on-line LC×LC separations of the maize extract. These second dimension peaks were carefully chosen to avoid broad peaks caused by sample overloading, specific chemical interactions between the column and samples, and unresolved peaks. The peak capacity was then calculated according to:

$${{}^{2}n}_c=\frac{{{}^{2}t}_g}{w_{\mathit{avg}.}}$$ (8)

In eq. (8), ²t_g is the second dimension gradient time, which is t_s - 3 s in our experiments and w_avg. is the average 4σ peak width of the second dimension separation.

The corrected 2D peak capacities at the specified first and second dimension gradient time combinations were calculated according to eq. (5) and are reported in Table 3.

Table 3.

Effect of split mode, analysis time and second dimension cycle time on corrected 2D peak capacity and corrected 2D peak capacity production rate.

a) 12 s		Analysis Time [min]
		15		30		60
	Split Mode	split-less	split	split-less	split	split-less	split
	1nc, measured a	37	149	88	181	157	232
	2nc, measured b	24	24	24	24	24	24
	<β> c	2.5	4.5	2.0	2.8	1.7	1.9
	n′c, 2D d	360	793	1073	1534	2257	2912
	n′c, 2D / tan [peaks/min] e	24	53	36	51	38	49
b) 21 s		Analysis Time [min]
		15		30		60
	Split Mode	split-less	split	split-less	split	split-less	split
	1nc, measured a	37	149	88	181	157	232
	2nc, measured b	32	32	32	32	32	32
	<β> c	4.1	7.8	3.1	4.7	2.5	3.0
	n′c, 2D d	291	614	899	1221	1975	2456
	n′c, 2D / tan [peaks/min] e	19	41	30	41	33	41

^aFirst dimension peak capacity calculated by eq. (7) using measured average peak width;

^bSecond dimension peak capacity calculated by eq. (8) using measured average peak;

^cFirst dimension peak broadening factor calculated by eq. (4);

^dCorrected 2D peak capacity calculated by eq. (5);

^eCorrected 2D peak capacity production rate relative to analysis time.

Number of Peaks Observed in the Maize Extract. To confirm the trend in the results obtained with the corrected 2D peak capacity as a measure of the resolving power in 2D-LC we counted the number of peaks observed in the maize extract. The procedure is based on a painstaking visual inspection of each individual second dimension chromatogram and the manual merging of peaks that correspond to the same first dimensional peak. This procedure has been described in detail⁴.

RESULTS AND DISCUSSION

2D-LC can be used either to generate very large peak capacities or to generate reasonably large peak capacities in a relatively short time^21–23. While off-line LC×LC^{24, 25} is clearly the best way to generate very high peak capacities (but it is very expensive in terms of analysis time), on-line LC×LC is surely the best way to generate large peak capacities in a relatively short analysis time²² (15–30 min). In both on-line and off-line modes many restrictions apply such as compatibility of mobile phases between both dimensions^{26, 27}, limits on volume of sample injected in the second dimension²⁸ and the strength of the sampled solvent from the first dimension^{29, 30}.

In on-line LC×LC another restriction applies since the second dimension analysis time must be equal to the sampling time (unless parallel columns are used) because the samples are sequentially analyzed in real time. This imposes a serious constraint since both are tightly coupled. As a result the peak capacity of each dimension is severely diminished. The second dimension needs to be very fast to reduce the deleterious effect of under-sampling the first dimension but it must have an acceptable separating power i.e. peak capacity. This also affects the first dimension because flow rates much lower than optimum must be used to avoid injecting too large a sample volume into the second dimension. To reduce this effect some researchers have used long capillary columns in the first dimension but still run them at flow rates lower than optimum^31–33. With this strategy both the instrument and column re-equilibration times are greatly increased.

Different approaches have been used to reduce this problem. Stoll et al. used a pre-first dimension flow splitter with a split ratio of 10:1 to reduce the pumping system flush-out time ²³. The pump was working at a flow rate of 1000 μL/min while the column received only 100 μL/min which was also below its optimum flow rate. Occasionally a post-first dimension flow splitter had been used to reduce the volume of sample collected in the loops without optimizing the flow rate which was usually below the optimum^{10, 34}.

In those publications where a post-first dimension flow splitter had been used the split ratio was invariably implemented by using a ‘tee’ with the appropriate tubing lengths and i.d.s of the two branches chosen to create the desired relative flow resistances and thus the desired split ratio. We refer to this technique as passive flow-splitting. In passive flow-splitting the split ratio under gradient conditions is affected by the viscosity of the fluid and thus is determined by the eluent composition and its temperature. Our approach is much less sensitive to fluctuations or differences in composition or temperature.

To the best of our knowledge, post first dimension flow-splitting has never been used to maximize the peak capacity of the first dimension in on-line LC×LC. The novelty of this work is that using post first dimension flow-splitting controlled by a metering pump has allowed us to fully optimize the first dimension conditions independent of the second dimension and precisely control the split ratio. We refer to this as active flow-splitting. Using active flow-splitting the split ratio is not affected by viscosity or temperature. It is important to note that in the approach used here the first dimension separation is not affected by any change in the split ratio in contrast any change in the flow ratio of a pre-first dimension flow splitter must alter the first dimension retention time. Using a pumping system to accurately control the flow rate of the branch that connects to the 10 port sampling valve allows accurate control of the sample introduced in the second dimension and the flexibility to change the split ratio as needed.

It has been shown that the first dimension separation power is less important to the overall peak capacity than is the second dimension^{22, 35, 36}, unless the gradient time is also increased. In this work we predict and confirm an important improvement in the corrected 2D peak capacity using post first dimension active flow-splitting (see Tables 3 and 4).

Table 4.

Effect of analysis time, split mode and second dimension cycle time on corrected 2D peak capacity and number of observed peaks.

a) 12 s		Analysis Time [min]
		15		30		60
	Split Mode	split-less	split	split-less	split	split-less	split
	n′c, 2D a	360	793	1073	1534	2257	2912
	n′c, 2D Ratio b	2.20		1.43		1.29
	# Observed Peaks	36	113	111	158	165	213
	# Peaks Ratio c	3.14		1.42		1.29
b) 21 s		Analysis Time [min]
		15		30		60
	Split Mode	split-less	split	split-less	split	split-less	split
	n′c, 2D a	291	614	899	1221	1975	2456
	n′c, 2D Ratio b	2.11		1.36		1.24
	# Observed Peaks	43	80	103	128	154	184
	# Peaks Ratio c	1.86		1.24		1.19

^aCorrected 2D peak capacity calculated by eq. (5);

^bRatio of measured corrected 2D peak capacity for split to split-less mode;

^cRatio of the number of observed peaks for split to split-less mode.

Our calculations (see Table 1) using post first dimension column flow-splitting predicted a 5-fold increase in the peak capacity of the first dimension (see 15 min. analysis time) by fully optimizing not just the column length and final eluent composition as was done in the split-less mode, but use of the splitter also allows the optimization of the flow rate with its concomitant effect on column length and final effluent composition. The experimental results show a 4-fold increase in the observed first dimension peak capacity (see Table 1). However, not all this gain is actually realized in n″_c,2D because such an increase in the first dimension peak capacity (and thus a reduction in peak width in time units) is accompanied by an increase in the under-sampling effect (see eq. 5) as shown by Davis et al¹¹.

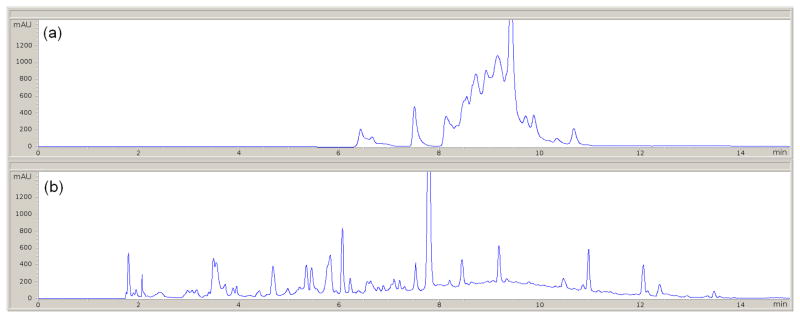
At longer analysis times (results shown for 30 and 60 min) the improvement is not as big as for the 15 min case. This is because in both the split and split-less modes the fraction of the time devoted to the gradient is larger relative to the time spent re-equilibrating the system as shown by ¹λ in Table 1. The peak capacity increases as ¹λ approaches unity. This effect can be easily observed in the chromatograms of the first dimension of the LC×LC experiments. In Fig. 2(a) and (b) the analysis time is 15 min and the time devoted for the separation is about half that for the split-less mode (see Table 1). As the analysis time was increased, the relative difference between the gradient and re-equilibration time becomes smaller but is still significant.

Fig. 2.

Chromatograms of the maize extract for 15 min analysis time as acquired by the first dimension detector for (a) split-less and (b) split modes. Experimental conditions described in Table 1.

There are two factors that contribute to the increase in the first dimension peak capacity shown in Table 1. First, the flow splitter allows a very significant increase in ¹t_g at the same analysis time, that is, an increase in ¹λ. Second, the flow splitter allows us to work at a fully optimized flow rate, column length and eluent composition. This results in a decreased average peak width (see Table 1).

The question arises -- which effect has the greater impact on the corrected 2D peak capacity? The question is not easily answered. Inspection of Table 1 shows that the ¹λ and ¹w ratios are about equal at all three analysis times suggesting that both factors contribute equally to the improved corrected 2D peak capacity but this is misleading.

Examination of eq. 5 clearly shows that when under-sampling is fairly strong, that is <β> is larger than unity (see Table 1) then a decrease in ¹w due to system optimization is almost cancelled by the increase in the under-sampling effect. The increase in <β> upon change from the split-less to the split mode is quite large (see Table 3). Some simple computations using the form of the right in eq. 5 show that at 15 minutes the increase in the corrected 2D peak capacity due solely to the increase in ¹t_g amounts to a factor of 2.07 whereas the increase due to only the decrease in ¹w is a factor of 1.07. The product of the two factors gives an increase of 2.20 in almost exact agreement with the observed increase in n_c,2D. Clearly the dominant effect is the increase in ¹t_g and the concomitant improvement in ¹λ.

It is also important to note (see Table 1) the lower final organic solvent composition in the gradient when the flow rate is optimized. This gives better focusing on the second dimension column. Another point as shown in Table 4 at analysis times less than 60 min a cycle time of 12 s gives higher corrected 2D peak capacities and numbers of observed peaks than does a cycle time of 21 s. Actual 2D chromatograms are shown in Fig. 3.

Fig. 3.

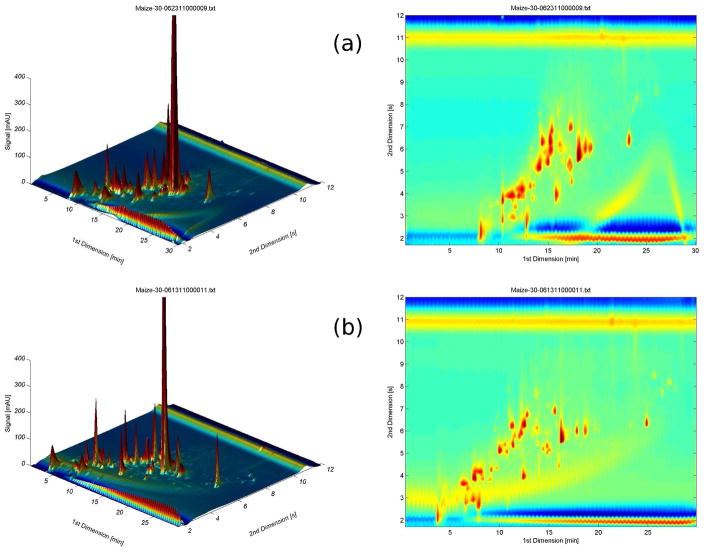
3D and contour plots of the maize extract in the (a) split-less and (b) split modes. Analysis time is 30 min with 12 s cycle time.

We chose to show results at an analysis time of 30 min because the rate of production of peak capacity is almost as high as at an analysis time of 15 min but the total peak capacity is a good bit higher. It is evident in both the 3D and contour plots of Fig. 3 that the peaks are distributed over a wider range in first dimension space in the runs with the flow splitter.

CONCLUSIONS

In this work we have shown the benefits of using a post first dimension column active flow-splitter to optimize the first dimension conditions and improve the separation power in on-line LC×LC. The key conclusions are the following:

1. The ability to optimize the first dimension independently from the second dimension allowed us to increase the corrected 2D peak capacity and the number of observed peaks by a factor of more than 2 at a 15 min analysis time.

2. This improvement is made possible primarily by reducing the system re-equilibration time and thus increasing the time allowed for the separation of the first dimension. A small secondary effect is the decrease in peak width that results from the optimization of the flow rate, column length and final mobile phase composition.

3. The flow splitter should allow the use of wider columns in the first dimension (e.g. 4.6 mm i.d.) which will result in even better usage of the time devoted to the separation in the first dimension increasing the overall separation power of on-line LC×LC.

4. Using an active flow-splitter gives the extra benefit of flexibility to precisely control the amount of sample transferred into the second dimension. This can be automated and adjusted as needed.

5. Since the flow-splitter is implemented after the first dimension column, the reproducibility of the separation in the first dimension is not affected by any change in the split ratio.