Zero-inflated and Hurdle Models of Count Data with Extra Zeros: Examples from an HIV-Risk Reduction Intervention Trial

INTRODUCTION

In controlled clinical trials, outcome variables often take the form of integers or counts, such as number of symptoms or number of risk behaviors during some defined time period (e.g. episodes of drug use, episodes of risky sex per month). These generally are not normally distributed. Ordinary least squares models, of which t-tests, ANOVA and ANCOVA are special cases, assumes that the outcome is normally distributed and may yield a biased estimate of the effect of a treatment (and of other factors) if that assumption is violated. What this means, in practical terms, is that the size of the effect of treatment and its statistical significance are either over-estimated or underestimated, neither of which is good.

The last several decades have therefore seen the growing availability in standard statistical packages of parametric models (i.e., Mplus, R, SAS, Splus, Stata) for non-normally distributed data, including Poisson, negative binomial, zero-inflated, and hurdle models. These models have all the flexibility and power of parametric models, handling repeated measures, multiple covariates, and various configurations of fixed and random effects, while assuming that the outcome has different than normal distribution (Poisson, negative binomial, etc). Previous reports have compared Poisson, negative binomial, zero-inflated and hurdle models applied to various outcomes, including counts of adverse events related to a vaccine (2), hospital stays (3) (4), and traffic accidents (5). The purpose of this paper is to illustrate the differences between these distributions and models and to explore how to compare different models using data from a multi-site clinical trial of behavioral interventions to reduce episodes of HIV risk behavior (CTN-0019) conducted through the National Institute on Drug Abuse Clinical Trials Network (1).

Poisson, Negative Binomial, Zero-Inflated, and Hurdle Models

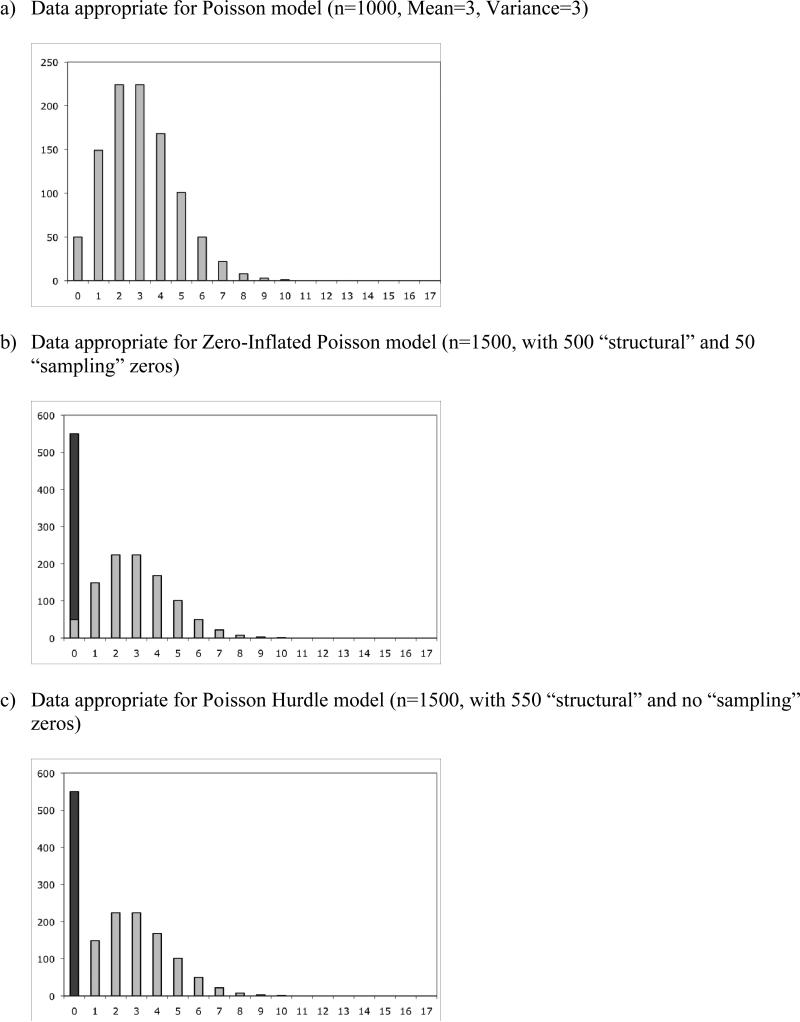
The shape of distribution of data appropriate for the Poisson, zero-inflated Poisson, and Poisson hurdle models are illustrated in Figure 1. Data appropriate for the negative binomial, zero-inflated negative binomial and negative binomial hurdle models are distributed similarly as the distribution of the three corresponding models with Poisson distribution in Figure 1 with extreme values spread further away from zero.

Figure 1.

Example of models with Poisson distribution

Note: Three models with the negative binomial distribution were not shown because they would appear similar to the corresponding models with Poisson distribution and would be hard to distinguish visually from the Poisson distribution.

Poisson distribution

The number of events occurring in a fixed period of time by definition follows the Poisson distribution. The classic example of such distribution is a count. When the mean count is low, then the data consists of mostly low values (e.g. counts of 0, 1, 2) and less frequently higher values (illustrated by a long right tail). As the mean count increases, the skewness diminishes, and the distribution becomes approximately normal. For non-negative count outcomes, a model with Poisson distribution is much more appropriate than an ordinary least-squares linear model (6).

Over-dispersion and Zero-inflation

Unlike the normal distribution, the variance of a Poisson random variable depends on the mean, with the mean equal to the variance. Count data frequently depart from the Poisson distribution due to a larger frequency of extreme observations resulting in spread (variance) greater than the mean in the observed distribution. This is called “over-dispersion”.

In practice, the distribution of counts, such as episodes of substance use or other risk behaviors, often has a much larger than expected number of observed zeros than assumed by Poisson distribution, called “zero-inflated”. For instance, many patients may already be abstaining or not having unprotected sexual occasions. This may be particularly common in effectiveness trials, where the effort is to maximize generalizability of the study by minimizing exclusionary criteria that might otherwise put a floor on the severity of problems at baseline.

Negative Binomial distribution

The negative binomial distribution is an alternative to the Poisson model (6, 7) and is especially useful for count data whose sample variance exceeds the sample mean (i.e., data with over-dispersion). The negative binomial distribution looks superficially similar to the Poisson but with a longer, fatter tail to the extent that the variance exceeds the mean. If the observed outcome is suspected to have variance larger than mean, the negative binomial distribution of the outcome is more appropriate than either the Poisson or normal distributions.

Zero-inflated and Hurdle Models

Zero-inflated (8) and “hurdle” (7) models (each assuming either the Poisson or negative binomial distribution of the outcome) have been developed to cope with zero-inflated outcome data with over-dispersion (negative binomial) or without (Poisson distribution) (see Figures 1b and 1c). Both (zero-inflated and hurdle) models deal with the high occurrence of zeros in the observed data but have one important distinction in how they interpret and analyze zero counts.

A zero-inflated model assumes that the zero observations have two different origins: “structural” and “sampling”. Figure 1b shows a zero-inflated Poisson model with the zero observations split due to their structural (dark grey portion of the zero bar; let's call them “structural zeros”) or sampling origin (light grey portion of the zero bar; let's call them “sampling zeros”). The sampling zeros are due to the usual Poisson (or negative binomial) distribution, which assumes that those zero observations happened by chance. Zero-inflated models assume that some zeros are observed due to some specific structure in the data. For example, if a count of high-risk sexual behaviors is the outcome, some participants may score zero because they do not have a sexual partner; these are the structural zeros since they cannot exhibit unprotected sexual behavior. Others participants have sexual partners but score zero because they have eliminated their high-risk behavior. That is, their risk behavior is assumed to be on a Poisson or negative binomial distribution that includes both zero (the “sampling zeros”) and non-zero counts.

In contrast, a hurdle model (see Figure 1c for illustration of a Poisson hurdle) assumes that all zero data are from one “structural” source. The positive (i.e., non-zero) data have “sampling” origin, following either truncated Poisson (Figure 1c) or truncated negative-binomial distribution (7). For example, consider a study of cocaine users in which a secondary outcome is a number of tobacco cigarettes smoked during last month. In this case, it is safe to assume that only non-smokers will smoke zero cigarettes during the last month and smokers will score some positive (non-zero) number of cigarettes during last month. Hence the zero observations can come from only one “structural” source, the non-smokers. If a subject is considered a smoker, they do not have the ‘ability’ to score zero cigarettes smoked during the last month and will always score a positive number of cigarettes in a hurdle model with either truncated Poisson or truncated negative binomial distributions.

The distinction between structural and sampling zeros, and hence between zero-inflated and hurdle models, may seem subtle. However, one or the other models may be more appropriate depending on the nature of the experimental design and the outcome data being observed (2). The different models can yield different results with very different interpretations.

METHODS

Participants

Data were drawn from a national, multi-site randomized clinical trial (CTN-0019) conducted through the National Institute on Drug Abuse Clinical Trials Network to test the effectiveness of a 5-session safer sex skills building (SSB) group intervention compared against a 1-session standard HIV education intervention (HE). Details of the methods and the primary outcome analysis have been previously published (1). The participants were 515 women recruited from community-based drug treatment programs who met eligibility criteria for being at heightened risk for HIV/STI heterosexual transmission, defined as having at least one unprotected occasion with a male partner in the prior 6 months.

Measurement

Primary Outcome

The number of unprotected sexual occasions (USO) with male partner(s) in the 3 months prior to each assessment. Sexual risk behaviors were collected via an audio computer-assisted self-interview (ACASI) format version of the Sexual Experiences and Risk Behavior Assessment Schedule (SERBAS, 9).

Treatment

The SSB intervention is an HIV prevention program for women was previously demonstrated to be effective by Exner, Seal and Ehrhardt (10). The SSB intervention consists of five group sessions cultivating HIV risk assessment, problem-solving to overcome obstacles to safer sex, condom use, negotiation skills, and assertiveness. The HE control intervention consists of one 60-minute informational group session designed to simulate standard HIV prevention offered within substance abuse treatment programs.

Data Analysis

Poisson, negative binomial, zero-inflated Poisson, zero-inflated negative binomial, Poisson hurdle, and negative binomial hurdle models were each fit to the data with mixed-effects modeling (MEM), using PROC NLMIXED in SAS 9.2 (SAS, 11) on the intent-to-treat sample of all randomized participants. The dependent variable was the count of unprotected sexual occasions, measured at 3 and 6 month follow-up points. Independent variables were the intervention condition (SSB versus HE), time (assumed to be categorical variable), count of unprotected sexual occasions at baseline, and age. Because other demographic variables, such as racial/ethnic group, education, and marital status, were not significantly associated with the outcome variable in the primary outcome paper (1), they were not included in this analysis. The interaction of time-by-treatment was included in all the models. Missing outcomes were assumed to be missing at random, while random effects estimated within-subject correlation from repeated measurements (12,13).

Various statistical tests were applied to evaluate over-dispersion and compare model fit. Over-dispersion in the Poisson regression was tested by the Lagrange multiplier statistic (14). For negative binomial models, the dispersion parameters were tested for difference from zero with t-statistics. To compare goodness of fit between pairs of models, likelihood ratio tests (LR; for full and nested models), Akaike's information criterion (AIC; for non-nested models) (15) (16), and Vuong statistics (for non-nested models) (17) were calculated.

RESULTS

Of the 515 randomized patients, 250 were assigned to Safer Sex Skills Building (SSB) and 265 to the Health Education (HE) control condition. At baseline, the average number of unprotected sexual occasions (USO) in the past 3 months was 18.6 (SD=27.8, range=0-191) for SSB and 20.0 (SD=33.4, range=0-325) for HE. As previously reported (1), neither the covariates nor the follow-up rates differed by treatment group.

The observed mean and variance in the number of USO across all participants and time points were 13.6 and 744.6, respectively. The observed variance to mean ratio is 54.8, clearly indicating over-dispersion. After controlling for covariates (treatment, time, age, baseline USO, interaction between time and treatment) in the Poisson model, the Lagrange multiplier remained highly significant (chi-square = 8753.6, d.f. = 1, p < .0001), suggesting overdispersion.

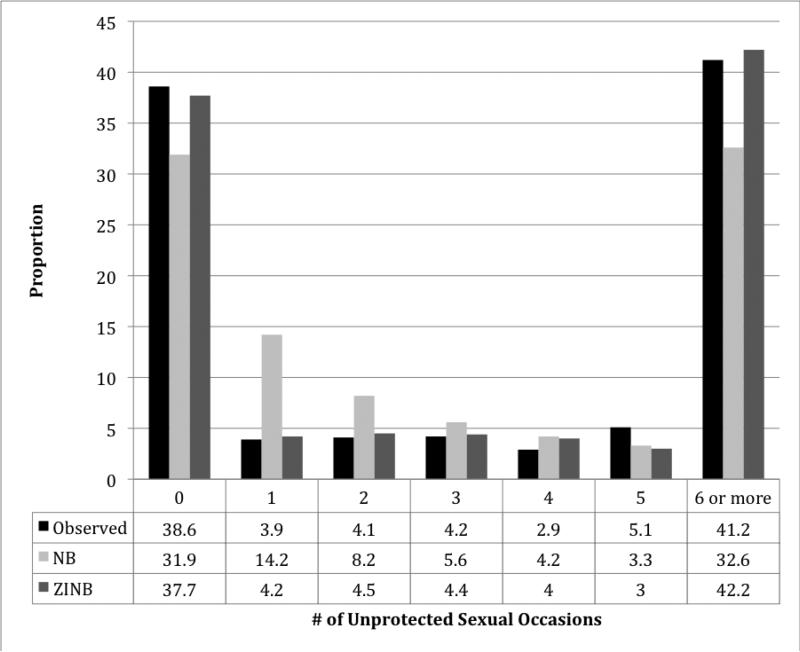
To explore zero-inflation in the outcome data, we first examined the observed distribution of the count of USO (see Figure 2). On inspection, the negative binomial model (NB) appears to underestimate zero counts, overestimate counts of 1 to 3, and underestimate counts in the higher ranges of 6 or more. In contrast, the zero-inflated negative binomial model (ZINB) fits the data closely in terms of the higher count of zeros and the greater dispersion of non-zero values.

Figure 2.

Observed and modeled distribution of the count of unprotected sexual occasions in a clinical trial of an HIV-risk reduction intervention, according to negative binomial (NB) and zero-inflated negative binomial (ZINB) models.

Table 1 summarizes the statistics comparing goodness of fit of the models. The likelihood ratio (LR) was used in χ² tests to compare pairs of full and nested models (i.e. NB vs. Poisson, ZINB vs. ZIP and NBH vs. PH); the differences in AIC and Vuong statistics were computed for all pairs of non-nested models (i.e., PH vs. NB, NBH vs. ZINB). Significant values of χ² LR test (always positive) suggest that model in the column fits the observed USO data significantly better than model in the row. Positive differences in AIC and Vuong statistics suggest that the model in the column fits better than the model in the row. Negative differences mean that the model in the row fits better than the model in the column. Stars denote significance of one model better fitting over another.

Table 1.

Criteria for evaluating goodness of fit and model selection among six different models for analyzing the outcome of counts of high risk sexual behavior in a randomized clinical trial of an HIV-risk reduction intervention. Values in the table are chi-square (χ2) statistics for likelihood ratios (LR) comparing models, differences between Akaike's information criterion (AIC) for models being compared, and Vuong statistics^a comparing models. Positive numbers mean that the model in the column fits better than the model in the row. Negative numbers mean that the model in the row fits better than the model in the column.

	Differences in Fit statistics	Poisson	Negative Binomial (NB)	Zero-inflated Poisson (ZIP)	Zero-inflated Negative Binomial (ZINB)	Poisson Hurdle (PH)	Negative Binomial Hurdle (NBH)
Poisson	χ2 (LR) AIC Vuong	---	1825.2***	880.6 4.25***	1956.3 5.09***	758.1 2.61**	1873.6 3.32***
NB	χ2 (LR) AIC Vuong		----	-942.6 -1.31	133.1 18.49***	-1065.1 -2.58**	50.4 -5.90***
ZIP	χ2 (LR) AIC Vuong			----	1075.7***	-122.5 -10.43***	993 0.66
ZINB	χ2 (LR) AIC Vuong				----	-1198.2 -4.22***	-82.7 -27.27***
PH	χ2 (LR)					----	1117.5***

^aVuong statistics are referred to a standard normal distribution

^**refers to significant difference at p<.01.

^***refers to significant difference at p<.001.

Two main patterns emerge from the Table 1:

1. The zero-inflated negative binomial model shows superior fit compared to the other models, with all positive numbers in its row and all negatives in its column; the Poisson distribution is inferior to the other models as shown by all negative numbers in its row and all positives in its column; and zero-inflated models fit better than their corresponding non-zero inflated counterparts; this suggests the best fitting model needs to account for both over-dispersion and zero-inflation in the observed data.

2. Based on the AIC and Vuong tests, the zero-inflated Poisson and zero-inflated negative binomial models fit better than their corresponding Poisson hurdle and negative binomial hurdle models; this suggests the zero counts were best modeled as being due to both structural and sampling zeroes, not only from structural zeroes as in the hurdle models.

Tables 2a, 2b, and 2c show the parameter estimates for independent predictors: treatment, time, the time-by-treatment interaction, and other covariates. For the zero-inflated and hurdle models (Tables 2b and 2c), there are two sets of columns for each model, first showing the chances that the particular independent variable affected the “structural” zeros and the second showing the model for the “sampling” counts themselves. Across models, the effect of treatment manifests as a time-by-treatment interaction, consistent with the previously reported finding in the primary outcome paper in which a Poisson model was applied that the SSB intervention reduced episodes of unprotected sex compared to the HE intervention, mainly at the 6-month time point (1). The Poisson models (Poisson, zero-inflated Poisson, and Poisson hurdle) yield substantially greater time-by-treatment interactions compared to the corresponding negative binomial models, possibly suggesting that failure to account for overdispersion by the Poisson models leads to over-estimation of the effect of treatment. The negative binomial and zero-inflated negative binomial models yield similar estimates of the time-by-treatment interaction (both with p-value < 5%). Finally, the negative binomial hurdle model fails to detect a significant time-by-treatment interaction, suggesting that considering all zeros to be “structural” may bias against detecting an effect of treatment in this sample.

Table 2a.

The Poisson and negative binomial models on unprotected sexual occasions (USO) at 3-month and 6-month follow-up in a randomized clinical trial of an HIV-risk reduction intervention, Safer Sex Skills Building (SSB) versus a Health Education (HE) control condition

	Poisson		Negative Binomial (NB)
	beta	s.e.	beta	s.e.
USO at baseline	0.68***	0.08	0.68***	0.08
AGE>=40	-0.57**	0.22	-0.60**	0.21
Treatment (SSB vs. HE)	-0.33	0.22	-0.41+	0.24
Time (3-month follow-up vs. 6-month)	-0.35***	0.03	-0.22	0.15
Time-by-treatment interaction	0.33***	0.05	0.46*	0.23
Fit Statistics:
Overdispersion			1.10***	0.15
-2 Loglikelihood	5798.8		3973.6
AIC	5812.8		3989.6

⁺refers to p<.1.

^*refers to p<.05.

^**refers to p<.01.

^***refers to p<.001.

Table 2b.

The Zero-inflated Poisson and Zero-inflated Negative Binomial models on unprotected sexual occasions (USO) at 3-month and 6-month follow-up in a randomized clinical trial of an HIV-risk reduction intervention, Safer Sex Skills Building (SSB) versus a Health Education (HE) control condition

	Zero-inflated Poisson (ZIP)				Zero-inflated Negative Binomial (ZINB)
	Probability on having zero USO		Number of USO		Probability on having zero USO		Number of USO
	beta(1)	s.e.(1)	beta(2)	s.e.(2)	beta(1)	se(1)	beta(2)	se(2)
USO at baseline	-0.61***	0.14	0.51***	0.06	-0.71***	0.18	0.49***	0.06
AGE	0.48	0.36	-0.45**	0.15	0.53	0.45	-0.46**	0.15
Treatment (SSB vs. HE)	0.46	0.42	-0.31*	0.15	0.50	0.52	-0.30+	0.17
Time(3-month follow-up vs. 6-month)	0.06	0.34	-0.35***	0.03	0.12	0.39	-0.22*	0.11
Time-by-treatment interaction	-0.60	0.50	0.38***	0.05	-0.72	0.59	0.30*	0.17
Fit Statistics:
Overdispersion							0.39***	0.06
-2 Loglikelihood	4902.2				3824.5
AIC	4932.2				3856.5

⁺refers to p<.1.

^*refers to p<.05.

^**refers to p<.01.

^***refers to p<.001.

Table 2c.

The Poisson Hurdle and Negative Binomial Hurdle models on unprotected sexual occasions (USO) at 3-month and 6-month follow-up in a randomized clinical trial of an HIV-risk reduction intervention, Safer Sex Skills Building versus a Health Education (HE) control condition

	Poisson Hurdle (PH)				Negative Binomial Hurdle(NBH)
	Probability on having zero USO		Number of USO		Probability on having zero USO		Number of USO
	beta(1)	s.e.(1)	beta(2)	s.e.(2)	beta(1)	se(1)	beta(2)	se(2)
USO at baseline	-0.49***	0.08	0.30***	0.05	-0.46***	0.07	0.35***	0.05
AGE	0.44+	0.23	-0.30*	0.14	0.39+	0.21	-0.35*	0.15
Treatment(SSB vs. HE)	0.40	0.29	-0.33*	0.14	0.39	0.27	-0.26	0.17
Time (3-month follow-up vs. 6-month)	0.08	0.26	-0.35***	0.03	0.09	0.25	-0.23+	0.12
Time-by-treatment interaction	-0.51	0.38	0.38***	0.05	-0.49	0.36	0.28	0.18
Fit Statistics:
Overdispersion							0.54***	0.09
-2 Loglikelihood	5028.7				3911.2
AIC	5054.7				3939.2

⁺refers to p<.1.

^*refers to p<.05.

** refers to p<.01.

^***refers to p<.001.

DISCUSSION

We considered six different models involving either the Poisson or negative binomial distributions for analyzing clinical trials outcome data. The negative binomial distribution better accommodates overdispersion in the outcome data compared to Poisson distribution. Zero-inflated and hurdle models account for over-representation of zero counts in the outcome data. We fit each of these models to the data from a controlled clinical trial of a skills-oriented HIV-risk reduction intervention (1), in which the outcome variable was the count of unprotected sexual occasions. Inspection of the observed data, as well as fit statistics, suggested that the distribution of the outcome variable was both overdispersed and zero-inflated. The fit statistics for the models (Table 1) showed that the zero-inflated negative binomial model provided the best fit. Models using the negative binomial distribution fit better than their corresponding models using the Poisson distribution, while zero-inflated and hurdle models fit better than their respective counterparts (Poisson, negative binomial). Taken together, these suggest the importance of accounting for both over-dispersion and zero-inflation in modeling the outcome data.

The estimates of the effect of treatment, in the form of the time-by-treatment interactions, differed in magnitude between models. Of particular note, the Poisson models estimated larger effects of treatment than the corresponding negative binomial models, suggesting that failure to account for overdispersion in the model results in overestimation of the treatment effect in this particular case. This makes intuitive sense since ignoring greater dispersion in the data, in essence, suppresses variance. This illustrates the risk of falsely identifying a significant effect of treatment if the model chosen does not model the spread of the data correctly.

Across both zero-inflated and hurdle models, effects of time-by-treatment interaction or main effect of treatment were not detected to significantly influence the chances of “structural” zero outcomes. Thus, treatment reduced the magnitude of counts of high-risk sex but not the frequency of scoring zero. This illustrates the potential advantage of such models to provide a more precise interpretation of the data when the process that generates zero values differs from the process that generates non-zero counts. In the present example, it may mean that the SSB treatment affected the number of unprotected sexual occasions of some participants but did not significantly affect the number of those participants who had no sexual partners.

Zero-inflated models fit better than the corresponding hurdle models. Zero-inflated models consider two sources of zero observations, “sampling zeros” that are part of the underlying sampling distribution (Poisson, or negative binomial) and “structural zeros” that cannot score anything other than zero. In the present example, it may be that while some participants scored zero unprotected sexual occasions because they had no sexual partners, others had sexual partners but scored zero because they did not engage in high-risk sex. The SSB intervention focuses on promoting safe sex among those with partners and should, if effective, drive the rate of unsafe sex to zero in at least some of those participants. The hurdle model considers all zeros to be “structural zeros”. The negative binomial hurdle model failed to detect a significant treatment effect, suggesting that truncating such “sampling” may have biased against finding treatment effect, perhaps by diluting the ability to show that SSB drove high risk sex to zero in some at-risk participants.

Taken together, the data suggest the importance for any given data set of finding the most appropriate model for outcome data in order to arrive at the most accurate estimate of the effect of a treatment intervention and how an inadequately fitting model can bias either in the direction of overestimating or underestimating an effect of treatment. The process illustrated here of finding the best fit can proceed empirically without a priori hypothesis about the distribution of the data. However, investigators designing clinical trials should be encouraged to hypothesize in advance the distribution of the outcome counts based on their knowledge of the population and the intervention being tested, as well as prior data. This could then guide the choice of model in the event that fit statistics do not identify a clear best fit.