Designer Magnetoplasmonics with Nickel Nanoferromagnets

Abstract

We introduce a new perspective on magnetoplasmonics in nickel nanoferromagnets by exploiting the phase tunability of the optical polarizability due to localized surface plasmons and simultaneous magneto-optical activity. We demonstrate how the concerted action of nanoplasmonics and magnetization can manipulate the sign of rotation of the reflected light’s polarization (i.e., to produce Kerr rotation reversal) in ferromagnetic nanomaterials and, further, how this effect can be dynamically controlled and employed to devise conceptually new schemes for biochemosensing.

Nanoplasmonics—the physics of nanoconfined collective oscillations of the charge carriers, induced by incoming electromagnetic (EM) radiation—is a burgeoning research field. The strong localization and the sensitivity toward the surrounding medium allow a multitude of potential applications from nanophotonics^1,2 to optical biochemosensing.(3) Virtually any nearly free electron metal would support such resonances in the optical region of the EM spectrum, and it is thus not surprising that concepts from nanoplasmonics increasingly spill over to the research in nanomagnetism,(4) leading to a range of intriguing effects. Large magnetic field-dependent modulation of particle transparency has been observed in Co/Au core/shell microparticles due to spin-dependent interface effects.(5) Diamagnetic plasmonic materials can also develop magneto-optical (MO) activity.(6) In chiral nickel microstructures the direction of magnetization can be tracked by surface plasmons through magnetization-induced second harmonic generation.(7) An anomalous magneto-optic Kerr effect (MOKE) due to resonant excitation of localized and/or propagating plasmonic modes has been reported in various systems: Au/Co/Au nanosandwiches,^8,9 bilayer systems of perforated Au and uniform bismuth iron garnet films,^10,11 gold-coated maghemite nanoparticles,(12) Ni nanowires,(13) Co or Au/iron garnet films perforated with holes,^14,15 ferrimagnetic garnet films incorporating Au particles,(16) Co/Ag core–shell nanoparticles,(17) or Co/Pt multilayers deposited on arrays of polystyrene spheres.(18)

Differently from the studies of propagating surface plasmons in ferromagnetic systems,(19) or the combination of plasmonic and ferromagnetic materials into hybrid nanostructures, here we explore the opportunities arising from direct excitation of localized surface plasmons (LSPs) in purely ferromagnetic nanostructures, namely, nickel nanodisks. Notably, so far, the use of LSPs in ferromagnets has been hampered by the notion of the high Ohmic losses in these materials. Here we show how LSPs can be exploited to achieve a controlled manipulation of the MO response of Ni nanostructures. The ferromagnetic nature of the material allows investigating MO phenomena, whereas the plasmonic nature allows exploring intrinsic features of the polarizability and its strong dependence on the external dielectric medium, to control plasmon-modified MO response.

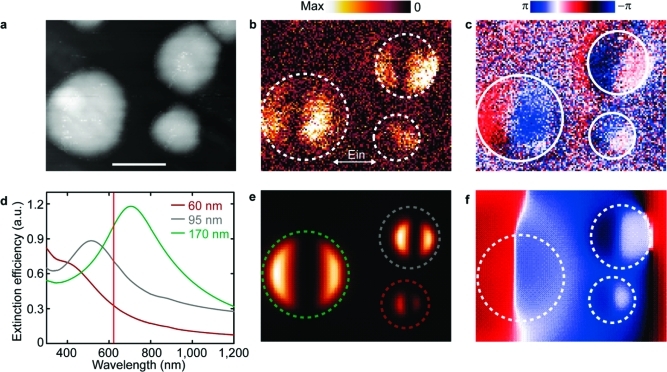
To address the LSPs in Ni nanostructures, we use a scattering-type (apertureless) scanning near-field optical microscopy (s-SNOM)^4,20,21 that allows real-space probing of amplitude and phase of the resonant LSPs.(22) Figure 1a overviews a system of nickel nanodisks with three diameters of 60, 95, and 170 nm (same thickness of 30 nm), combined on the same glass substrate, fabricated using hole–mask colloidal lithography(23) (see Supporting Information). In this way the phase of LSP resonances of the three different nanodisks types become directly comparable(24) (Figure 1b,c). Three separate systems comprising exclusively nanodisks of the same size (60, 95, and 170 nm) are also prepared to collect the far-field extinction efficiencies (Figure 1d). Both experimental (Figure 1b,c) and simulated (Figure 1e,f) images show the amplitude and phase of the vertical near-field component. Two bright spots in the amplitude are visible for all three types of Ni nanodisks. They are aligned along the polarization direction of the incident light and are out of phase by π. Such a pattern is clear evidence of the dipole mode of the plasmon oscillation.^4,20 Interestingly, the dipoles of 60 and 95 nm disks oscillate with roughly similar phase, whereas the dipole of 170 nm disks shows a phase shift of about π/2. Naturally, in nanoplasmonic systems the amplitude and the phase of the dipolar LSP mode directly define the position of the optical resonance,(25) here visualized as the far-field extinction efficiency of the three nanodisks systems (Figure 1d). Convincingly, the near-field phase shift observed for the 170 nm disks reflects the LSP resonance crossing the excitation light wavelength (633 nm) in the far-field.

Figure 1.

(a) Topography image of nickel nanodisks with diameters of 60, 95, and 170 nm, combined on the same glass substrate. Scale bar, 100 nm. (b, c) s-SNOM-near-field amplitude and phase images, recorded simultaneously with topography. (d) Far-field extinction efficiencies of three separate systems of Ni nanodisks of sizes 60 (brown), 95 (gray), and 170 nm (green). The vertical red line marks excitation at 633 nm. Finite-difference time-domain (FDTD) calculated near-field amplitude (e) and near-field phase (f) at 633 nm. The white or correspondingly colored (60 nm, brown; 95 nm, gray; 170 nm, green) circles in (b), (c), (e), and (f) outline the nickel nanodisk dimensions.

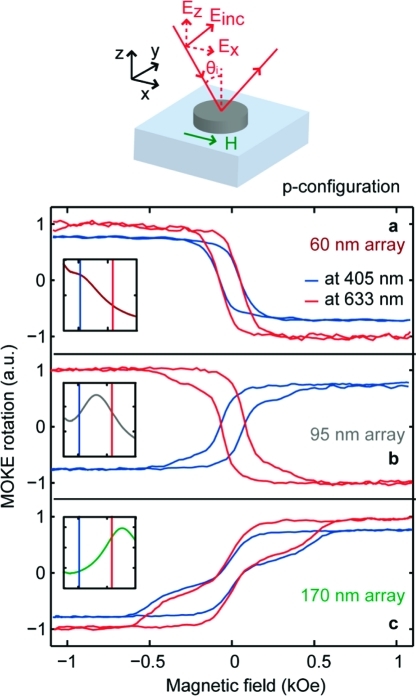
Given the ferromagnetic nature of nickel, we further explore the MO activity of the system, in particular the interplay between LSPs and MO phases. In magnetic materials the off-diagonal components of the dielectric tensor give rise to the polarization change in the reflected linearly polarized light, denoted as complex Kerr rotation (Φ_K + iΨ_K).(26) In plasmonic materials the proper choice of an applied magnetic field, H, perpendicular to disk surface (polar configuration) and perpendicular to the illuminating linearly polarized light leads to the Lorentz force acting on the excited oscillating charge density. This results in effective rotation of the plasmonic dipole, which is manifested in a weak MO activity in disks of purely diamagnetic materials such as Au.(6) The polar configuration is also the one used to investigate MO enhancement in noble-metal/ferromagnet “sandwiches”.^8,9 In these studies the MO enhancement requires optical and MO polarizabilities being both in the “sandwich” plane, so that their relative phase is determined only by the wavelength dependence of the intrinsic optical and MO parameters of the material. In the case of Ni plasmonic nanomagnets we present a different strategy, namely, using the longitudinal Kerr with the incident light in p- and s-polarizations.(27) With the oblique light incidence and applied H in the nanodisk plane (see schematics in Figure 2 and Figure S1 in the Supporting Information), we exploit the polarizability anisotropy in nanodisk geometry (in plane vs out of plane) to tune the phase difference between the optical and MO polarizabilities beyond what is offered by intrinsic material properties. We collect the longitudinal MOKE rotation Φ_K for all three nanodisks types, each with a characteristic LSP resonance (cf., Figure 1d), using two different excitation wavelengths, namely 405 and 633 nm, in p-polarization configuration. The resulting MOKE magnetization loops as a function of the applied H are shown in Figure 2. The shape of the MOKE loops shows clear single magnetic domain state for the smallest nanodisks (diameter 60 nm), while it suggests the nucleation of a vortex configuration at low fields during the magnetization reversal in the larger ones. This is in agreement with previous works on similar nanomaterials.(28) A striking fact is evident from these figures: the change of sign in the MOKE loops is immediately noticeable when comparing the measurements done on the Ni nanodisks at the different wavelengths. While the sign of the MOKE rotation in each particular experiment is defined by the combination of the incoming and reflected polarizations, and different signs are typically attributed to a clockwise or an anticlockwise rotation of the axes of the polarization ellipse viewed along the reflected direction, here the inversion is detected in the same incoming polarization configuration when changing the wavelength of the incoming light. A closer view at the nanoplasmonic resonances of the respective disks in relation to the employed laser line in each MOKE experiment (insets in Figure 2) reveals that the inversion appears when the plasmon resonance spans across the excitation light wavelength. Nickel nanodisks with LSPs at one side of a given excitation line produce the same MOKE loop sign whereas those on the opposite sides are effectively inverted (Figure 2). Importantly, the loop inversion is not related to intrinsic material properties, i.e., in the absence of excited LSPs. Namely, the MOKE results obtained on a continuous Ni film (codeposited on the same substrate) (see Figure S2 in Supporting Information) rule out the possibility that the inversion is related to a photon energy dependence of the MO coefficient resulting in a change of sign of Φ_K.(29)

Figure 2.

Normalized p-polarization MOKE on nickel nanodisks of 60 (a), 95 (b), and 170 nm (c), employing two different excitation wavelengths (405 nm (graphs in blue) and 633 nm (graphs in red)). Sketch on top is schematic of L-MOKE in p-configuration. The loops measured at 405 nm have been scaled by 80% for clarity of presentation. The insets schematically show far-field extinction spectra for the corresponding nanodisk types in relation to the two excitation wavelengths of MOKE experiments.

Similarly, the MOKE loop reversal is detected in s-configuration (see Figure S1 in Supporting Information) where the oscillating charge density of LSP and external H are orthogonal and thus efficiently coupled by Lorentz force, as in polar MOKE configuration. However, the previously reported increase in MOKE signal(30) is not evident here. Therefore, a direct plasmon–magnetization coupling is not prerequisite and the observed Kerr rotation reversal in nickel nanoferromagnets rather represents a fundamental feature of nanoconfined ferromagnetic materials.

This remarkable magnetoplasmonic effect in nickel nanoferromagnets can be intuitively explained considering the Lorentz torque that acts on a metallic nanoparticle of polarizability α illuminated by a linearly polarized incident light beam and in the presence of field H. A similar explanation has been often used as simple model for the change of the reflected light polarization in the MO Kerr effect.(31) Such torque can be viewed as simplification of the appearance in the reflected beam of a p-component for an s-polarized incident beam and vice versa.(26)

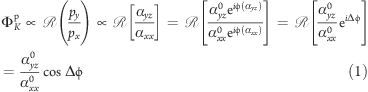
Similarly to the approach in ref (6). and following the coordinate system sketched in Figure 2 (p-polarization) and Figure S1 in Supporting Information (s-polarization), because of H the net induced dipole in the nanoparticle oscillates at an angle Φ_K with respect to the incident light’s electric field in both p and s-configurations

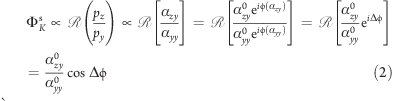where the superscripts p and s in Φ_K indicate the polarization state of the incident light and p_i represents the light induced dipole expressed as function of the polarizability α of the system. Equations 1 and 2 show how the Kerr rotation Φ_K is directly related to the ratio of the off-diagonal (related to MO) and the diagonal (from LSPs) elements of the polarizability α in both s and p configurations. Writing α in exponential notation shows clearly how the change in Kerr phase is determined by the difference Δϕ between the phases of the α_yz (or α_zy) and α_ii components.

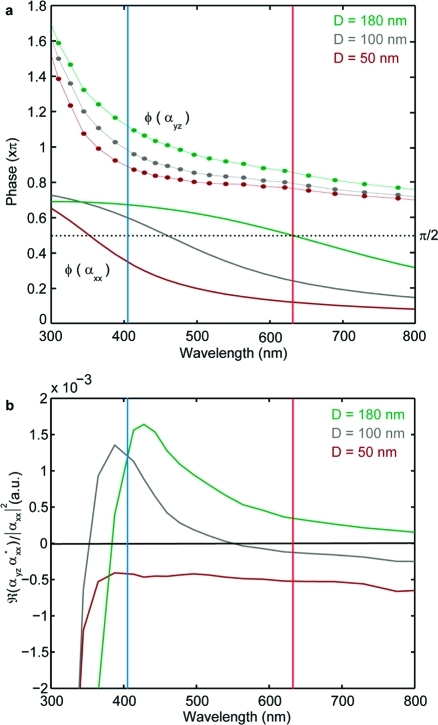
This intuitive model is confirmed by calculating the phases of the off-diagonal α_yz and the diagonal α_xx components of the polarizability tensor (Figure 3a) and evaluating Φ_K through eq 2 (Figure 3b; see Supporting Information for simulations details). In this way we consider the pure local (near-field) effect, i.e., the sign change of Kerr rotation, that involves the dipolar plasmon resonance and the magneto-optical coupling. We do not reproduce the absolute values of the spectrally resolved Kerr rotation though, for which an effective medium approach would be required in order to estimate properly reflection effects and account for the differences between far- and near-field spectral signatures.(4)

Figure 3.

(a) Calculated phases of the diagonal α_xx (solid lines) and off-diagonal α_yz (circular symbols with a guiding line) polarizability components for three nickel nanodisks types (50 nm, brown; 100 nm, gray; 180 nm, green). (b) Calculated Kerr rotation (see Supporting Information) for the three nickel nanodisks types. Blue and red lines mark excitation at 405 and 633 nm, respectively.

Clearly, α_yz and α_xx show sizably different wavelength-dependence (anisotropic polarizability). Consequently, independently of their initial phase difference, by properly selecting the incoming light’s wavelength it is possible to cause a relative phase change between α_ij and α_ii enough to produce a Φ_K reversal, i.e., crossing the π/2 value. Interestingly, Φ_K shows strong wavelength sensitivity at shorter wavelength ranges. Further, this clarifies the similar behavior observed in p and s configurations, since for a circular disk α_xx = α_yy and α_yz = −α_zy. In the exemplary case of three Ni nanodisks systems, corresponding differences in the initial phases of diagonal and off-diagonal terms of the polarizability (Figure 3a) result in the Kerr effect reversal for 95 nm nanodisks (gray curve in Figure 3b and MOKE loops in Figure 2b). On the other hand, 60 and 170 nm nanodisks, though having opposing Kerr rotation signs, do not experience the Kerr effect reversal upon crossing 405 and 633 nm excitation light lines (brown and green curves in Figure 3b and MOKE loops in Figure 2a,c). It is worth mentioning that the reversal of the Kerr rotation does not necessarily occur at the peak of absorption. Though the two are naturally related through the diagonal components of the polarizability, it is only the interplay between the diagonal and off-diagonal components that determines the Kerr rotation reversal.

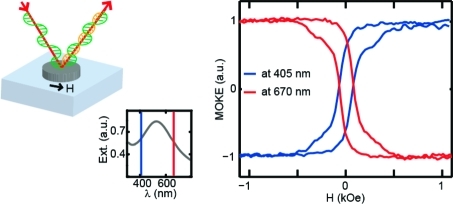
We now explore this central property of nanoconfined ferromagnetic materials to obtain a dynamically tunable magnetoplasmonic system. The fundamental dependence of plasmonic nanoparticle polarizability on the external dielectric medium is well-known and has given rise to a range of applications of nanoplasmonics in various refractive index (RI) sensing schemes. We utilize this characteristic property of LSPs to reversibly shift the phase of the polarizability by modifying the external dielectric medium. We use Ni nanodisks (supported on 15 nm silica spacer to boost their refractive index sensitivity(32)) of 140 nm in diameter, designed to display the LSP resonance on the short-wavelength side of the MOKE excitation laser line of 633 nm (Figure 4a, inset, far-field optical spectrum of the system). By subjecting the nanodisks to a medium with refractive index 1.49 (that of spin-coated poly(methyl methacrylate), PMMA), we shift the nanoplasmonic resonance across the 633 nm line (Figure 4b, inset). Remarkably, the MOKE loop follows this transition evidencing the inversion (Figure 4b). Further, by removing PMMA layer, we recover the initial nanoplasmonic resonance position, along with the original MOKE loop sign (Figure 4c), thus effectively devising a magnetoplasmonic system that allows the dynamic tuning of the reflected light polarization rotation. Note that, in accordance with calculated spectroscopic MOKE data (Figure 3b), the strategy of dynamic Kerr rotation manipulation for the present set of nickel nanostructures would be the most effective toward the shorter wavelengths. Indeed, steep features around the 405 nm line suggest that proper design of nanoferromagnets with red-shifted intrinsic nanoplasmonic resonances would earn a system able to drastically switch the polarization rotation sign. Straightforwardly, with nanoplasmonic systems such resonance red shift is realized by increasing the lateral dimensions of the nanostructure.

Figure 4.

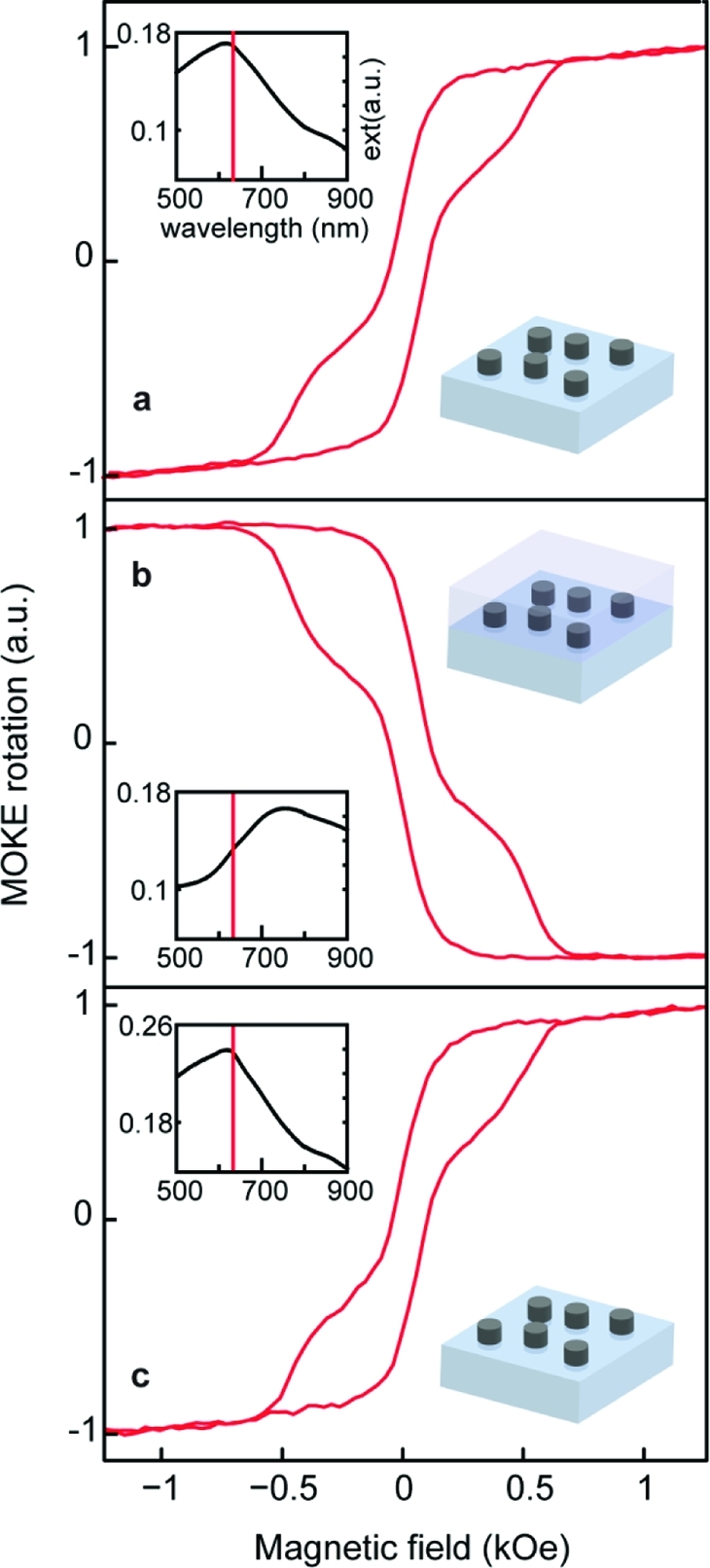
s-polarization MOKE on nickel nanodisks (nominal diameter, 140 nm): pristine system (a), system immersed in PMMA (b), and after removal of PMMA (c). Insets: far-field extinction of the corresponding systems with marked excitation line at 633 nm.

It is further very appealing to explore the possibilities of magnetoplasmonic RI sensing with nanoferromagnets. It is common to evaluate the RI sensitivity of nanoplasmonic biochemosensors as a resonance shift per refractive index unit (RIU). With Ni nanoferromagnets, featured in Figure 4, experimentally measured RI sensitivity amounts to 297 nm per RIU at 608 nm resonance (in air). Note that already with this simple experiment nickel nanostructures display twice higher plasmon sensitivity as compared to similar Au nanoplasmonic sensors (about 150 nm per RIU at 600 nm resonance with silica-supported Au nanodisks(32)). Further, our modified spheroid theory calculations estimate surface-supported nickel nanostructures sensitivity of 377 nm per RIU at 628 nm resonance with the correction for the substrate contribution of 48% in the effective RI.(32) As discussed above, Kerr rotation in nickel nanoferromagnets experiences reversal that is sensitive to the surrounding RI. Indeed, spectroscopic MOKE experiment that follows the PMMA deposition on the array of 95 nm Ni nanoferromagnets provides direct manifestation of the functionality of such magnetoplasmonic RI sensor (Figure 5a). Note also good correspondence of the MOKE spectroscopic data to the calculated one of Figure 3b. The point of zero-crossing of the MOKE spectroscopic curve remarkably red shifts in response to the change of the surrounding RI. Naturally, we can define the inverse value of the Kerr rotation 1/Φ_K that in turn reacts significantly on the variation of the surrounding refractive index (Figure 5b). As a consequence, we essentially devised a MOKE RI nanosensor that relies on purely nanoferromagnetic materials. Having the 1/Φ_K resonance at 585 nm, we obtain the sensitivity for surface-supported nanoferromagnetic system of 122 nm per RIU (compare to the sensitivity of surface-supported Au nanodisks of about 80 nm per RIU at this resonance(32)). Importantly, this sensitivity is accompanied by virtually unlimited value for the figure-of-merit (FOM), defined as the resonance shift divided on full width at half-maximum of the resonance. The resonance of 1/Φ_K is produced by Kerr rotation zero-crossing, earning sharply defined singularity that is experimentally best defined with highest spectroscopic resolution of MOKE. Through the model employed to calculate spectroscopic MOKE rotation, we can predict potentially extremely high RI sensitivity (inset of Figure 5b) if we consider an optimized structure where the substrate contribution is only 20% (similarly to nanopillar-supported Au plasmonic nanosensors). This hints that nanoferromagnet-based sensors might represent a viable ultrahigh sensitivity alternative to the presently actively developed noble-metal based ones. Our study introduces a completely new and versatile method of detection that can be employed not only in pure ferromagnetic systems but also in hybrid and pure noble structures where the presence of a magneto-optical activity has been largely proved.^6,30

Figure 5.

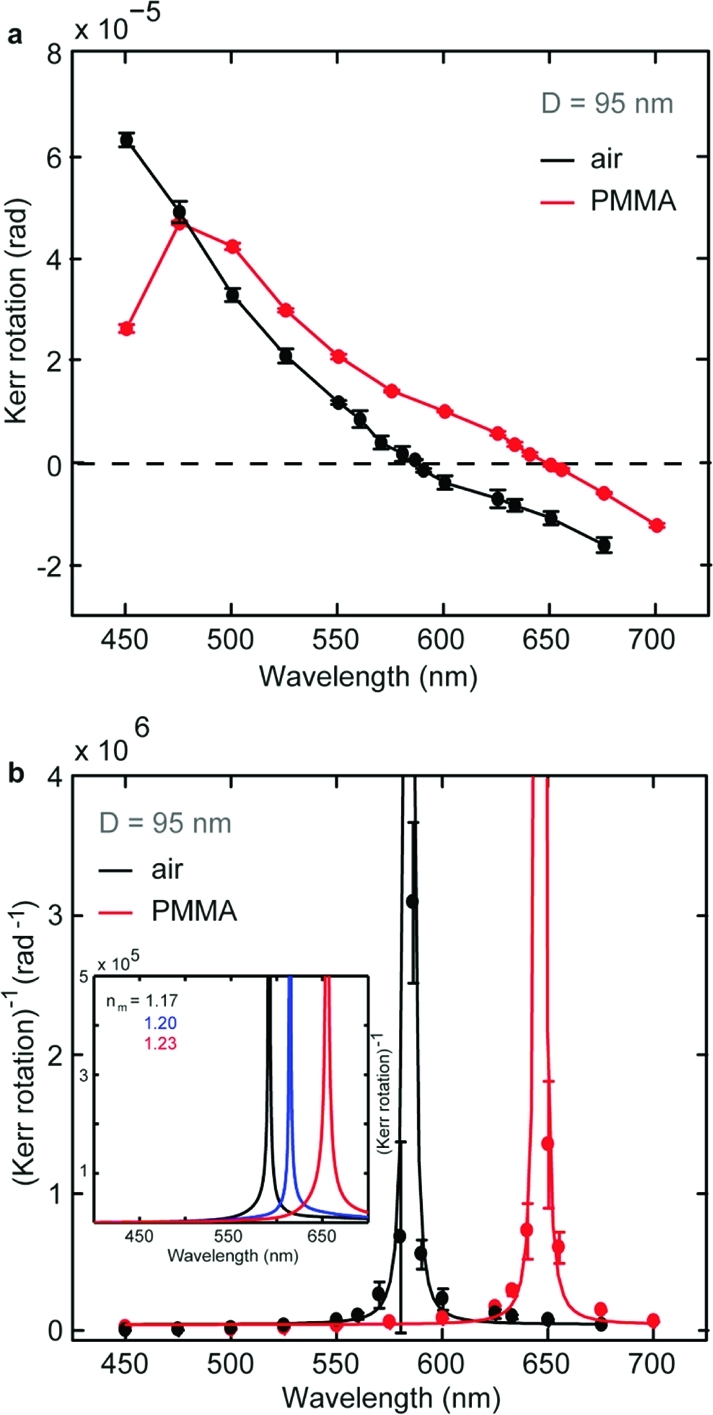
(a) Experimental wavelength dependence of the Kerr rotation on 95 nm nickel disks in air (black symbols) and immersed in PMMA (red symbols). (b) Corresponding experimental inverse Kerr rotation for 95 nm nanodisks in air (black symbols) and in PMMA (red symbols). The lines are guide for eyes. The inset shows the calculated inverse Kerr rotation in media with three different surrounding refractive indices (n_m = 1.17 (black), 1.20 (blue), 1.23 (red)) for nickel nanodisks with diameter 100 nm and thickness 30 nm.

We demonstrate that nickel nanoferromagnets act as a magnetoplasmonic material, showing strong and tunable correlation between the localized plasmons and magneto-optics, i.e., the polarizability and the sign of Kerr rotation Φ_K. A strongly wavelength-dependent phase shift in Φ_K can be produced by the combination of the anisotropic polarizability and the MO in the nanostructured ferromagnetic medium. Indeed, the presence of nanoplasmonic excitations in other ferromagnetic materials like cobalt(14) and iron(33) points toward the generality of the reported phenomenon. This fundamental finding brings a new impulse to the exploration of mutual relations between magnetism, MO activity, and localized electronic excitations. In particular, it points to the possibility of devising plasmon-controlled polarization-resolved MO light modulation. We also foresee the use of such magnetoplasmonic nanomaterials in biology and medicine, where, separately, magnetic and plasmonic nanoparticles are increasingly finding a broad spectrum of applications. Given the strong response of the Kerr rotation to the surrounding RI change, highly sensitive biochemodetectors are envisaged. Combining both properties in a magnetoplasmonic nanomaterial combines the benefits: ease of spatial manipulation due to magnetism, functionality for remote optical sensing with the possibility for multiplexing due to polarization- and wavelength-sensitive MO, and active and highly localized thermal management due to nanoplasmonics in these materials.

Supporting Information Available

Detailed experimental procedures and supplementary figures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^¶ Contributed equally.