Structural Analysis of Macromolecular Assemblies by Electron Microscopy

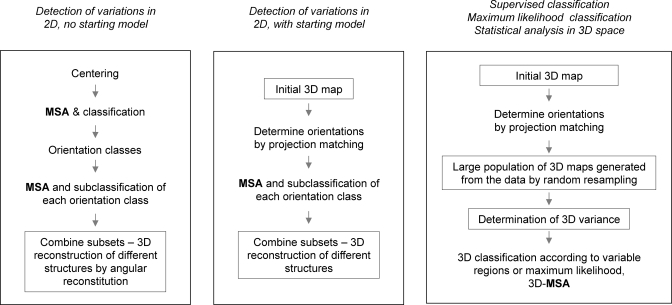
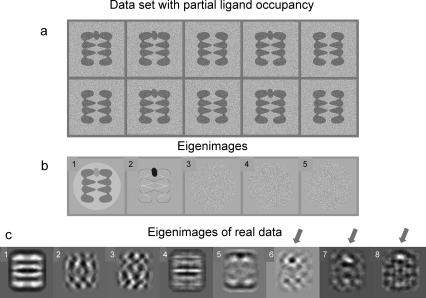
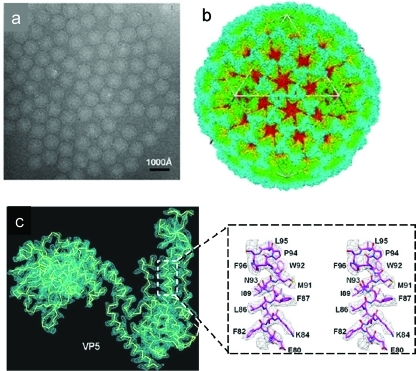
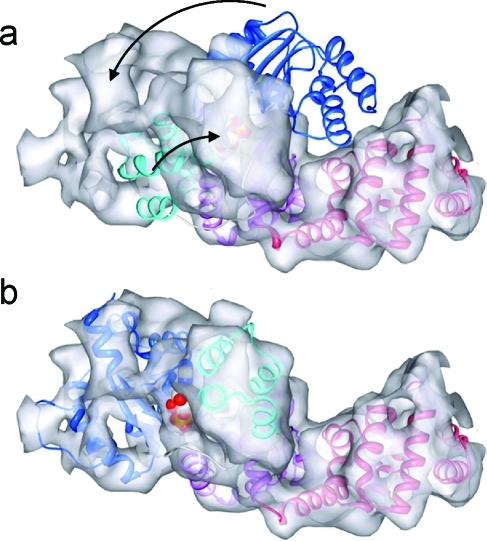
1. Introduction

1.1. Light and Electron Microscopy and Their Impact in Biology

To fully understand biological processes from the metabolism of a bacterium to the operation of a human brain, it is necessary to know the three-dimensional (3D) spatial arrangement and dynamics of the constituent molecules, how they assemble into complex molecular machines, and how they form functional organelles, cells, and tissues. The methods of X-ray crystallography and NMR spectroscopy can provide detailed information on molecular structure and dynamics. At the cellular level, optical microscopy reveals the spatial distribution and dynamics of molecules tagged with fluorophores. Electron microscopy (EM) overlaps with these approaches, covering a broad range from atomic to cellular structures. The development of cryogenic methods has enabled EM imaging to provide snapshots of biological molecules and cells trapped in a close to native, hydrated state.^1,2

Because of the importance of macromolecular assemblies in the machinery of living cells and progress in the EM and image processing methods, EM has become a major tool for structural biology over the molecular to cellular size range. There have been tremendous advances in understanding the 3D spatial organization of macromolecules and their assemblies in cells and tissues, due to developments in both optical and electron microscopy. In light microscopy, super-resolution and single molecule methods have pushed the resolution of fluorescence images to ∼50 nm, using the power of molecular biology to fuse molecules of interest with fluorescent marker proteins.(3) X-ray cryo-tomography is developing as a method for 3D reconstruction of thicker (10 μm) hydrated samples, with resolution reaching the 15 nm resolution range.(4) In EM, major developments in instrumentation and methods have advanced the study of single particles (isolated macromolecular complexes) in vitrified solution as well as in 3D reconstruction by tomography of irregular objects such as cells or subcellular structures.^1,5−7 Cryo-sectioning can be used to prepare vitrified sections of cells and tissues that would otherwise be too thick to image by transmission EM (TEM).^8,9

In parallel, software improvements have facilitated 3D structure determination from the low contrast, low signal-to-noise ratio (SNR) images of projected densities provided by TEM of biological molecules.¹⁰⁻¹⁴ Alignment and classification of images in both 2D and 3D are key methods for improving SNR and detection and sorting of heterogeneity in EM data sets.(14) The resolution of single-particle reconstructions is steadily improving and has gone beyond 4 Å for some icosahedral viruses and 5.5 Å for asymmetric complexes such as ribosomes, giving a clear view of protein secondary structure elements and, in the best cases, resolving the protein or nucleic acid fold.^15,16

1.2. EM of Macromolecular Assemblies, Isolated and in Situ

A variety of molecular assemblies of different shapes, sizes, and biochemical states can be studied by TEM, provided the sample thickness is well below 1000 nm. There is a range of sample types typified by two extreme cases: biochemically purified, isolated complexes (single particles or ordered assemblies such as 2D crystals) and unique, individual objects such as tissue sections, cells, or organelles. From preparations of isolated complexes with many identical single particles present on an EM grid, many views of the same molecule can be obtained, so that their 3D structure can be calculated. Near-atomic resolution maps were first obtained from samples in ordered arrays such as 2D crystals and helices.^17,18 Membrane proteins can be induced to form 2D crystals in lipid bilayers, although examples of highly ordered crystals leading to high-resolution 3D structures are still rare. If membrane-bound complexes are large enough, they can also be prepared as single particles using detergents or in liposomes. In general, the single-particle approach is widely applicable and has caught up with the crystallographic one. This approach is applicable to homogeneous preparations of single particles with any symmetry and molecular masses in the range of 0.5–100 MDa (e.g., viruses, ribosomes) and can reveal fine details of the 3D structure.(15) The study of single particles by cryo-EM in the 0.1–0.5 MDa size range still needs great care to avoid producing false but self-consistent density maps. In addition, the single-particle approach can be used to correct for local disorder in ordered arrays, improving the yield of structural information. Regarding the quality of this structural information, the resolution of cryo-EM is steadily improving, and comparisons of cryo-EM results with X-ray crystallography or NMR of the same molecules indicate that cryo-EM often provides faithful snapshots of the native structure in solution. A detailed account of the basic principles of imaging and diffraction can be found in ref (19).

For cells, organelles, and tissue sections, electron tomography provides a wealth of 3D information, and methods for harvesting this information are in an active state of development. Automated tomographic data collection is well established on modern microscopes. A major factor limiting resolution in cryo-electron tomography is radiation damage of the specimen by the electron beam during acquisition of a tilt series. At the forefront of this field are efforts to optimize contrast at low electron dose, in order to locate and characterize macromolecular complexes within tomograms of cells and tissues. At present, complexes must be well over 1 MDa to be clearly identifiable in an EM tomographic reconstruction. Examples of important biological structures characterized by electron tomography include the nuclear pore complex(20) and the flagellar axoneme.(21) For thicker, cellular samples, X-ray microscopy (tomography) provides information in the 15–100 nm resolution range, bridging EM tomography and fluorescence methods.

The above developments have led to a flourishing field enabling multiscale imaging to link atomic structure to cellular function and dynamics. In this Review, we aim to cover the theoretical background and technical advances in instrumentation, software, and experimental methods underlying the major developments in 3D structure determination of macromolecular assemblies by EM and to review the current state of the art in the field.

2. EM Imaging

2.1. Sample Preparation

Electron imaging is a powerful technique for visualizing 3D structural details. However, because electrons interact strongly with matter, the electron path of the microscope must be kept under high vacuum to avoid unwanted scattering by gas molecules in the electron path. Consequently, the EM specimen must be in the solid state for imaging, and special preparation techniques are necessary to either dehydrate or stabilize hydrated biological samples under vacuum.(22)

2.1.1. Negative Staining of Isolated Assemblies

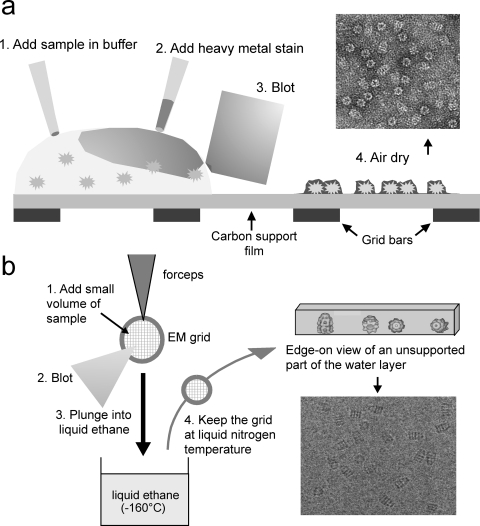
The simplest method for examining a solution or suspension of isolated particles such as viruses or other macromolecules is negative staining, in which a droplet of the suspension is spread on an EM support film and then embedded in a heavy metal salt solution, typically uranyl acetate, blotted to a thin film and allowed to dry^23,24 (Figure 1a). Although uranyl acetate is the most widely used stain and gives the highest contrast, some structures are better preserved in other stains such as tungsten or molybdenum salts.^25,26 The heavy metal stain is deposited as a dense coat outlining the surfaces of the biological assembly, giving information about the size, shape, and symmetry of the particle, as well as an overview of the homogeneity of the preparation. The method is called negative staining because the macromolecular shape is seen by exclusion rather than binding of stain. The method is quick and simple, although not foolproof. Some molecules are well preserved in negative stain, but fragile assemblies can collapse or disintegrate during staining and drying. In general, the 3D structure becomes flattened to a greater or lesser degree, and the stain may not cover the entire molecule, so that parts of the structure may be distorted or absent from the image data. Therefore, it is normally preferable to use cryo-methods for 3D structure determination. The exception is for small structures, below ∼100–200 kDa, for which the signal in cryo-EM may be too weak for accurate detection and orientation determination. For such structures, 3D reconstruction is done from negative stain images and can provide much useful information.

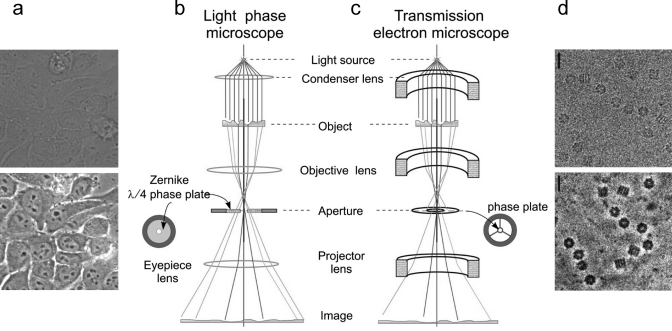
Figure 1.

Negative stain and cryo EM sample preparation. (a) Schematic view of sample deposition, staining, and drying, with an example negative stain image. (b) Schematic of plunge freezing and of a vitrified layer, and an example cryo EM image. Panel (b) is adapted with permission from ref (24). Copyright 2000 International Union of Crystallography.

2.1.2. Cryo EM of Isolated and Subcellular Assemblies

Macromolecules and cells are normally in aqueous solution, and hydration is necessary for their structural integrity. Cryo EM makes it possible to stabilize samples in the native, hydrated state, even under high vacuum. The main technical effort of cryo EM is to keep the specimen cold and free of surface contamination in an otherwise warm microscope while retaining mechanical and thermal stability. Rapid freezing is used to bring the sample to the solid state without dehydration or ice crystallization, and the sample is maintained at low temperature during transfer and observation in the EM. The method widely used for freezing aqueous solutions is to blot them to a thin layer and immediately plunge into liquid ethane or propane (−182 °C) cooled by liquid nitrogen for rapid heat transfer from the specimen^1,27 (Figure 1b(24)). Cooling by plunging into liquid ethane is much faster than plunging directly into liquid nitrogen because liquid ethane is used near to its freezing point rather than at its boiling point, so it does not evaporate and produce an insulating gas layer. Rapid cooling traps the biological molecules in their native, hydrated state embedded in glass-like, solid water, vitrified ice, and prevents the formation of ice crystals, which would be very damaging to the specimen. There are two tremendous advantages of cryo EM: the sample, which is kept around −170 °C, near liquid nitrogen temperature (−196 °C), is trapped in a native-like, hydrated state in the high vacuum of the microscope column, and the low temperature greatly slows the effects of electron beam damage.

An important consideration in cryo EM sample preparation is the type of support film. Some samples adhere to the carbon support film, but continuous carbon films contribute additional background scattering and reduce the image contrast. Therefore, perforated films are often used, in which the sample is imaged in regions of ice suspended over holes in the support film. Home-made holey films provide a random distribution of holes. Nanofabricated grids (e.g., Quantifoil grids, Quantifoil Micro Tools GmbH; C-flat grids, Protochips, Inc.) with regularly arranged holes are used for automated and manual data collection. A significantly higher sample concentration is usually needed for good particle distribution in holes. The ice thickness is extremely critical for achieving good contrast while preserving the integrity of the structure. It takes some experience to adjust the blotting so that the ice is an optimal thickness for each sample. The general rule is to have the ice as thin as possible without squashing the molecules of interest.

In addition to thermal stability, a major issue is sample conductance; ice unsupported by carbon film is an insulator, and charging effects caused by the electron beam can seriously degrade the image, especially at high tilt. This problem is lessened by including an adjacent carbon layer in the illuminated area. New support materials with higher conductivity than carbon are being investigated.^28,29

The single-particle approach can be applied to preparations of isolated objects such as particles in aqueous solution or membrane complexes in detergent solution. EM is experimentally more difficult in detergent, which may give extra background and change the properties of the ice. Membrane complexes can also be imaged in lipid vesicles,^30,31 in a variant of single-particle analysis in which the particle images are excised from larger assemblies.

There is a lower size limit for single-particle analysis, because the object must generate enough contrast to be detected and for its orientation to be determined. Single-particle cryo-EM becomes very difficult when the particle is less than a few hundred kDa in mass. The size limit is affected by the shape of the particle; an extended structure with distinct projections in different directions will be much easier to align than a compact spherical particle of similar mass. For small particles, negative stain EM is used. A hybrid approach to sample preparation, cryo-negative staining, has been developed.^22,32,33 The sample is embedded in stain solution and then vitrified, after partial drying. This method allows smaller complexes to be studied by cryo EM, but has the disadvantage that the sample is in a high concentration of heavy metal salt, far from physiological conditions.

2.1.3. Stabilization of Dynamic Assemblies

As molecular biology moves toward studies of more complex systems, the focus of interest has moved toward more biochemically heterogeneous samples. Although there are computational methods for sorting particles with structural variations (section 9), the success of the experiment depends critically on the quality of the biochemical preparation. One approach for dealing with unstable, heterogeneous assemblies is to use protein cross-linkers such as glutaraldehyde to stabilize complexes during density gradient separation, a procedure termed GraFix.^22,34 Promising results have been obtained with very difficult samples such as complexes in RNA editing,(35) but it should be noted that cross-linkers may also introduce artifacts in flexible assemblies.

2.1.4. EM Preparation of Cells and Tissues

2.1.4.1. High Pressure Freezing

Most cellular structures are too thick for TEM imaging, and samples are prepared as thin sections. Standard chemical fixation has provided the classical view of cell structure, in which the sample is cross-linked with fixatives and then dehydrated and embedded in plastic resin so that it can be readily sectioned for EM examination. Plastic-embedded sections are contrasted with heavy metal staining. Although this treatment can lead to extensive rearrangement and extraction of cell and tissue contents, the great majority of cell structure information at the EM level has been derived from such material.

High-pressure freezing has made it possible to avoid chemical fixation so that cell and tissue sections can be imaged in the vitreous state.³⁶⁻³⁸ To vitrify specimens thicker than a few micrometers, it is necessary to do the rapid freezing at high pressures, around 2000 bar, because the freezing rate in thicker samples at ambient pressure is not high enough to prevent ice crystal growth. Instruments for high-pressure freezing (HPF)(36) were first developed in the 1960s and are widely used in cell preparation, in combination with freeze-substitution (see section 2.1.4.2). The specimen is introduced into a pressure chamber at room temperature and rapidly pressurized, with cooling provided by liquid N₂ flow through the metal sample holder. Samples such as yeast or bacterial cells in 100–200 μm thick pellets or pastes can readily be vitrified by HPF. Samples with higher water content, such as embryonic or brain tissue, are more difficult to vitrify in this manner, because water is a poor thermal conductor, and thinner tissue slices (≤100 μm) must be used. For the same reason, aqueous media surrounding the sample must be supplemented by antifreeze agents such as 1-hexadecene(39) or 20% dextran before vitrification by HPF.(40)

2.1.4.2. Freeze-Substitution

Freeze-substitution (FS) eliminates some of the artifacts of chemical fixation and dehydration and provides greatly improved structural preservation, while retaining the ease of working with plastic sections and room temperature microscopy.(41) The sample is initially vitrified as for cryo-sectioning, but then gradually warmed for substitution of the water with acetone, followed by staining and resin embedding at −90 to −50 °C (see, for example, ref (42)). Some resins can be polymerized by UV illumination at low temperature, so that all processing is completed at low temperature. With this treatment, cytoplasmic contents such as ribosomes are retained and rearrangement of cell structures is reduced(36) (Figure 2a). However, small ice crystals form during FS processing, and staining is not uniform, so that the results are not reliable on the molecular scale.

Figure 2.

Slices of single axis tomograms of yeast cell sections prepared by freeze-substitution (a) and cryo-sectioning of vitrified samples (b). The black dots are mainly ribosomes. R, ribosomes; N, nucleus; V, vacuole; MT, microtubules (ring shaped cross sections); M, mitochondrion; ER, endoplasmic reticulum. Panel (b) was produced by Dan Clare.

Importantly, antigenicity is often conserved in FS material, so that immunolabeling or other chemical labeling can be done on the sections.(36) This is a major advantage over vitreous sectioning, for which antibody labeling is impossible. FS is an important adjunct to cryo-sectioning for tomography of cell structures, because large volumes are far more readily imaged and structures of interest tracked in the 200–300 nm thick sections that can be examined with FS. In addition, the fluorescence of GFP is retained in the freeze-substituted sections, facilitating correlative fluorescence/EM.(43) A chemical reaction of the GFP chromophore with diaminobenzidine produces an electron dense product, allowing GFP tags to be precisely localized in EM sections.(44) Therefore, the combination of cryo-sectioning and freeze-substitution on the same sample can provide an overview of the 3D structure, chemical labeling, and detailed structural information on regions of interest.

2.1.4.3. Cryo-Sectioning of Frozen-Hydrated Specimens

Sectioning removes the restriction of cryo EM to examination of only the thinnest bacterial cells or cell extensions. After a long period of development, vitreous sectioning has started to become generally accessible.^8,9 The vitrified block is sectioned at −140 to −160 °C with a diamond knife. Compression of the sections along the cutting direction and crevasses on the surface of thicker sections present mechanical artifacts. Nevertheless, HPF and cryo-sectioning currently provide the best view into the native structures of cells and tissues (Figure 2b). Because the native structures are preserved, macromolecular structures can be imaged in vitrified sections. Therefore, cryo-ET is an important step toward the ultimate goal of understanding the atomic structure of the cell.(45)

Cryo-sections must be around 50–150 nm thick, to find the best compromise between formation of crevasses (thicker) and section compression (thinner). Because of the low contrast and the tiny fraction of cell volume sampled in such thin sections, it can be very hard to locate the object of interest, unless the structure is large and very abundant, or associated with large-scale landmarks, such as membranes or large organelles. For this reason, and also for biochemical identification, a very important recent development is correlative cryo-fluorescence and EM.(46) Cryo stages are being developed for fluorescence microscopes, and if the signal is strong, the fluorescence can be first mapped out on the cryo section or cell culture on an indexed (“finder”) grid, and then the same grid can be examined by cryo EM.

2.1.4.4. Focused Ion Beam Milling

An alternative to cryo-sectioning currently being explored is focused ion beam milling, in which material is removed from the surface of a frozen specimen by irradiation with a beam of gallium ions, until the sample is thin enough for TEM.^47,48 Milling is done under visual control in a cryo-scanning EM, followed by cryo-transfer to the TEM for tomography. Preliminary work suggests that the thinned layer remains vitrified, without noticeable effects of the ion beam exposure. The method produces a smooth surface, importantly, without section compression or crevasses, thus avoiding the mechanical artifacts of cryo-sectioning.

2.2. Interaction of Electrons with the Specimen

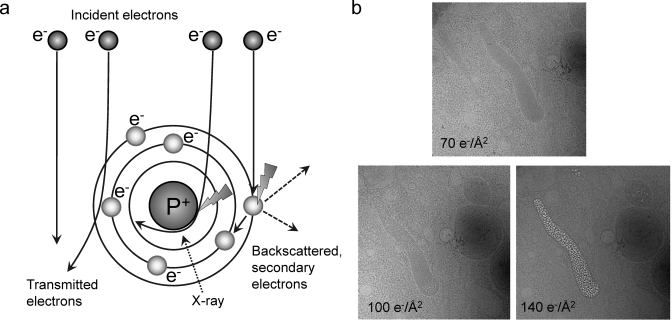
Imaging with electrons provides the advantage of high resolution, due to their short wavelength. However, the strong interaction of electrons from the primary electron beam with the sample causes radiation damage in the sample. The nature of the interaction of the electrons with the sample depends on the electron energy and sample composition.(49) Some electrons pass through the sample without any interactions, others are deflected by the electrostatic field of the nucleus, screened by the outer orbital electrons of specimen atoms, and some electrons may collide or nearly collide with the atomic nuclei, suffering high angle deflections or even backscattering. Of the interacting electrons, some are scattered without energy loss (elastic scattering), but others transfer energy to the specimen (inelastic scattering) (Figure 3a). Energy transfer from incident electrons can ionize atoms in the specimen, induce X-ray emission, chemical bond rearrangement, and free radicals, or induce secondary electron scattering, all of which change the specimen structure. Radiation damage of specimens is a significant limitation in high-resolution imaging of biological molecules. Prolonged exposure to an intense electron beam in an EM produces a level of damage comparable to that caused to living organisms exposed to an atomic explosion.(50) Typical values of electron exposure used for biological samples range from 1 to 20 electron/Ų. Although biological specimens can tolerate an exposure of 100–500 e^–/Ų, depending on specimen temperature and chemical composition, the highest resolution features of the specimen are already affected at electron exposures of 10 e^–/Ų or less.(51) Therefore, radiation damage dictates the experimental conditions and limits the resolution of biological structure determination, especially for cryo-tomography. To reduce radiation damage during area selection, alignment, and focusing, special “low dose” systems are used to deflect the beam until the final step of image recording.^52,53 An example of electron beam damage is shown in Figure 3b.(54) Lower electron doses can be used for two-dimensional (2D) crystals than for single particles, because the signal from all unit cells is averaged in each diffraction spot. Therefore, the diffraction spots are visible even when the unit cells are not visible in the image.^55,56

Figure 3.

Interaction of the electron beam with the sample. (a) Schematic of elastic and inelastic electron scattering. Collision of beam electrons with atomic electrons or nuclei leads to energy loss (inelastic scattering), while deflection by the electron cloud does not change the energy of the electron (elastic scattering). (b) Effect of electron beam damage on a cryo image of a cell. The electron dose is shown on the images. Increasing dose causes damage to cellular structures, but different cell regions and materials show the effects of damage at different levels of radiation. In this case, damage first appears on the Weibel Palade bodies. Reproduced with permission from ref (54). Copyright 2009 National Academy of Sciences.

2.3. Image Formation

The basic principle of electron optical lenses is the deflection of electrons, negatively charged particles of small mass, by an electro-magnetic field. Similar to a conventional light microscope, the EM consists of an electron source, a series of lenses, and an image detecting system, which can be a viewing screen, a photographic film, or a digital camera. Electron microscopy has made it possible to obtain images at a resolution of ∼0.8 Å for radiation-insensitive materials science samples,(57) 1.9 Å for electron crystallography of well-ordered 2D protein crystals,(58) 3.3 Å for symmetrical biological single-particle macromolecular complexes,(15) and 5.5 Å for the ribosome.^16,17

2.3.1. Electron Sources

The standard electron source is a tungsten filament heated to 2000–3000 °C. At this temperature, the electron energy is greater than the work function of tungsten. The thermally emitted electrons are accelerated by an electric field between the anode and filament. Another common electron source is a LaB₆ crystal, which produces electrons from a smaller effective area of the crystal vertex whose emitting surface is at a lower temperature because of a lower work function. This beam has higher coherence and current density. At present, the most advanced electron source, used in high performance microscopes, is the field emission gun (FEG).(59) The FEG beam is still smaller in diameter, more coherent, and ∼500× brighter, with a very small spread of energies.(59) This is achieved by using single crystal tungsten sharpened to give a tip radius ∼10–25 nm, as compared to 5–10 μm for LaB₆ crystals. The tip is coated with ZrO₂, which lowers the work function for electrons. Thermally emitted electrons are extracted from the crystal tip by a strong potential gradient at the emitter surface (field emission), and then accelerated through voltages of 100–300 kV.

2.3.2. The Electron Microscope Lens System

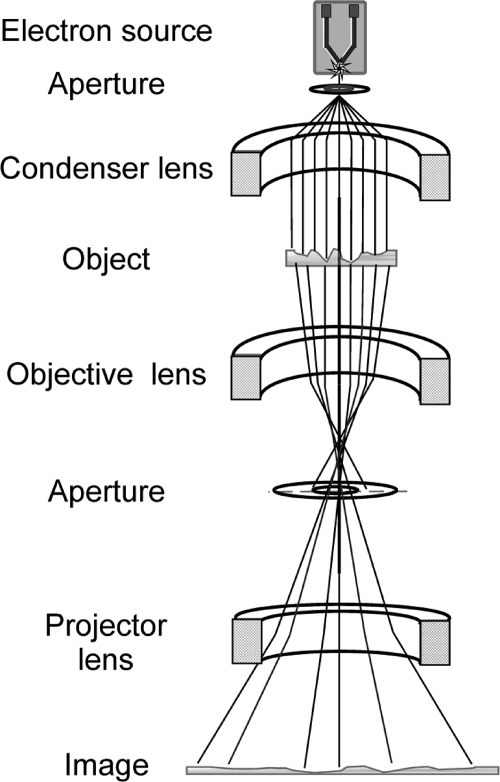
As in light microscopy, condenser lenses convert the diverging electron beam into a parallel one illuminating the specimen (Figure 4). The specimen in modern electron microscopes is located in the middle of the objective lens, fully immersed in the magnetic field. An objective aperture is placed in the back focal plane of this lens; the aperture prevents electrons scattered at high angles from reaching the image plane, thus improving the image contrast. The objective lens provides the primary magnification (20–50×) and is the most important optical element of the electron microscope. Its aberrations play a key role in imaging. The image is further magnified by intermediate and projector lenses before the electrons arrive at the detector. Alternatively, the electron diffraction pattern at the back focal plane of the objective can be recorded after being magnified.

Figure 4.

Simplified schematic representation of an electron microscope.

2.3.3. Electron Microscope Aberrations

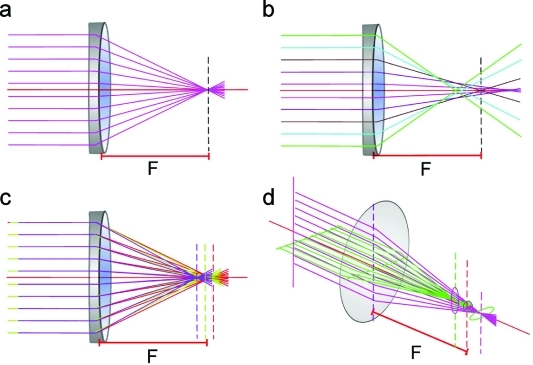
Electromagnetic lenses have the same types of defects as optical lenses, spherical and chromatic aberrations, curvature of the field, astigmatism, and coma,(60) of which the most significant are spherical, chromatic, and astigmatic aberrations (Figure 5). The quality of the beam source is essential for coherence of the electron beam needed for high-resolution imaging. Spherical aberration is an image distortion due to the dependence of the ray focus on the distance from the optical axis (Figure 5b). Rays passing through the periphery of the lens are refracted more strongly than paraxial rays. Chromatic aberration is caused by the lens focusing rays with longer wavelengths more strongly so that part of the image is formed in a plane closer to the object, resulting in “colored” halos around edges in the images (Figure 5c). Chromatic aberration in electron microscopes results from variations in electron energy caused by voltage variation in the electron source, electron energy spread in the primary beam, and energy loss inelastic events in the sample, and blurs the fine details in images. Astigmatic aberration is produced by deviation from axial symmetry in the lens, so that the lens is slightly stronger in one direction than in the perpendicular direction. Astigmatism in electron microscopes is caused by an asymmetric magnetic field in the lenses and can be compensated by stigmator coils. It results in two different image planes corresponding to these directions so that the image of a point becomes an ellipse (Figure 5d). The aberrations described here are the major ones that affect the images, although there are also other, higher order aberrations, which must be considered for high-resolution analysis.(61)

Figure 5.

Ray diagrams of lens aberrations: (a) perfect lens, (b) spherical, (c) chromatic, and (d) astigmatic aberration. F is the focal length of the lens.

2.4. Contrast Transfer

Normally, images represent intensity variations caused by regional variations in specimen transmission. These variations are recorded by a detector system; the image contrast Cont_im is defined as the ratio of the difference between brightest ρ_max and darkest ρ_min points in the image and the average intensity ρ̅ of the whole image:

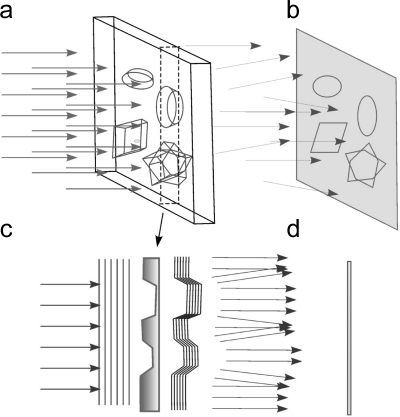
The image contrast resulting from absorption of part of the incident beam is known as amplitude contrast (Figure 6). Because only a small fraction of the electrons is actually absorbed by the biological specimen in inelastic interactions, the amplitude contrast can also be increased by using the objective lens aperture to eliminate electrons scattered at high angles.(59)

Figure 6.

Amplitude contrast. (a) An amplitude object illuminated by a parallel beam. (b) The image resulting from interaction of the beam with the sample. (c) A cross section of the object outlined by the dashed lines in (a); some of the rays are absorbed in the sample. Arrows show the changes in the wavefront after interaction with the sample. (d) Intensity of the rays creating the image in the region of the cross section. Black dots in the image correspond to areas of beam absorption (c).

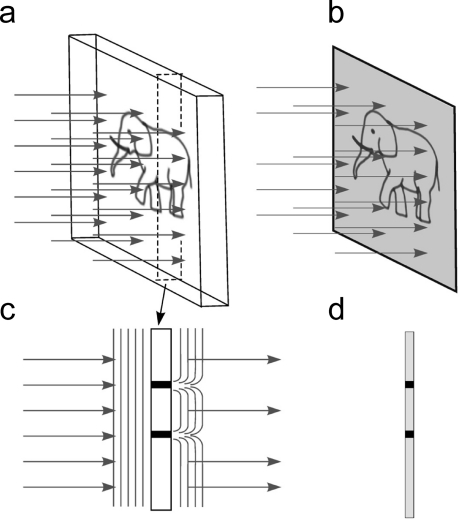
One of the difficulties of biological electron microscopy is that biological molecules produce very little amplitude contrast. They consist of light atoms (H, O, N, and C) and do not absorb electrons from the incident beam but rather deflect them, so that the total number of electrons in the exit wave immediately after the specimen remains the same. That means that the specimens do not produce any intensity modulation of the incident beam and the image features are not visible. Yet these specimens still change the exit wave because electrons interact with the material. Electrons undergo scattering at varying angles so they have different path lengths through the specimen, giving phase contrast (Figure 7). One can say that they experience a location-dependent phase shift. These phase variations encoded in the exit wave are made visible by being converted into amplitude variations that are directly detectable by a sensor. In practice, this is achieved by introducing a 90° phase shift between incident and scattered waves.

Figure 7.

Phase contrast. (a) A phase object illuminated by a parallel beam. (b) The resulting image shows only weak features. (c) A cross section of the object outlined by dashed lines in (A). Arrows show the changes in the wavefront (parallel lines) after interaction with the sample. The intensity is not changed, but the wavefront becomes curved. (D) Intensity of the rays creating the image in the region of the cross section. Note that the intensity differences are small.

2.4.1. Formation of Projection Images

In the case of elastic scattering, the scattering angle is proportional to the electron potential of the atom (the higher is the atomic number, the higher is its electron potential). The exit wave that has passed through the sample can be described as

where Ψ_sam is the exit wave emerging from the specimen; Ψ₀ is the incident wave; σ = m_eλ/(2πℏ²); m_e is electron mass; λ is electron wavelength; ℏ = h/2π; h is Planck’s constant; and φ_pr(r⃗) = ∫_–t/2^+t/2 φ(r⃗,z) dz is the specimen potential projected along the z direction, which coincides with the optical axis of the microscope, r⃗ is a vector in the image plane, and t corresponds to the thickness of the sample.

Because biological specimens in general are weak electron scatters, the phase shift introduced by the sample is small; that is, the exponent term in eq 2 is close to unity, which makes it possible to describe the exit wave by the following approximation:

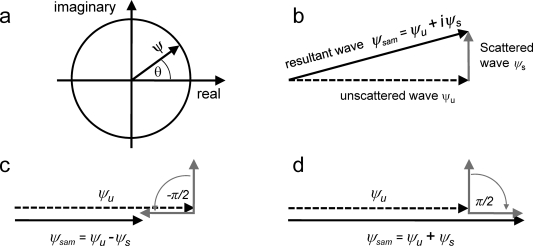
The transmitted wave Ψ_sam(r⃗) consists of two parts: the first term corresponds to the unscattered wave, and the second term, corresponding to the deflected (scattered) electrons, is linearly proportional to the specimen potential. The second term Ψ_s = Ψ₀iσφ_pr(r⃗) has a phase shift of 90°, because it corresponds to the imaginary part of the expression indicated by the factor i (Figure 8a and b). In the following discussion, we assume that the amplitude of the incident wave Ψ₀ = 1.

Figure 8.

Graphical representation of phase contrast. (a) Complex plane representation of a wave vector ψ with phase θ. (b) Vector representation of the scattered wave ψ_s, unscattered wave ψ_u, and resultant wave ψ_sam = ψ_u + iψ_s. Amplitudes (vector lengths) of ψ_sam and ψ_u are very similar, resulting in low image contrast. (c) −π/2 phase shift of the scattered wave leads to a noticeable decrease in the resultant wave amplitude relative to the unscattered wave (negative phase contrast). (d) π/2 phase shift of the scattered wave increases the amplitude of the resultant wave relative to the unscattered wave (positive phase contrast).

2.4.2. Contrast for Thin Samples

The image is formed by all electrons, both scattered and unscattered, giving very little contrast for thin, unstained biological specimens. This is known as phase contrast, which results from interference of the unscattered beam with the elastically scattered electrons (Figures 7 and 8). Thin transparent samples scatter electrons through small angles and are described as weak phase objects.(59) The intensity distribution observed in the image plane will be given by

where “*” denotes the complex conjugate. However, the magnitude of (σφ_pr(r⃗))² is ≪1, so the image will have practically no contrast. To increase the contrast, it is necessary to change the phase of the scattered beam φ_pr(r⃗) by 90° (Figure 8c and d), which changes the exit wave as follows:

The intensity in the image plane then can be approximated by the following expression:

Here, the intensity becomes proportional to the projection of the electron potential of the sample, and the magnitude of 2σφ_pr(r⃗) will be much greater than (σφ_pr(r⃗))². Therefore, the phase shift of the scattered beam transfers the invisible “phase” contrast into amplitude contrast that can be recorded. How in practice can the contrast be increased? One method is to use substances that increase the scattering, such as negative stains. Another possibility is to utilize imperfections of the microscope such as spherical aberration.

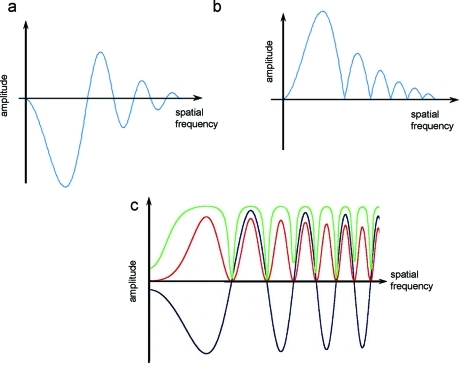
In practice, the image contrast obtained depends on the operating conditions of the microscope such as the level of focus and aberrations. Multiple scattering of electrons within thick specimens obscures the relation between object and image. There are several factors that affect the appearance and contrast of an EM image including lens aberrations, limited incident beam coherence, quantum noise because of the discrete nature of electrons (shot noise), radiation stability of the sample, instabilities in the microscope, and environment, for example, vibrations, stray electromagnetic fields, temperature changes, and imperfect mechanical stability of the EM column. Instabilities and limited coherence of the electron beam cause falloff of the signal transfer by the microscope for fine image details, leading to blurring of small features. In simple terms, a sharp dot will not be imaged as a dot but as a blur. The link between the original dot and its image is described by the point spread function (PSF) of the imaging device, in our case of the electron microscope. The PSF is a function that describes the imperfections of the imaging system in real space. However, a convenient way to describe the influence of these factors on the image is to use Fourier (diffraction) space:

where F{Ψ_obs} is the Fourier transform of the observed image; R⃗ is spatial frequency (Fourier space coordinate); F{Ψ_sam} is the Fourier transform of the specimen; CTF(R⃗) is the contrast transfer function of the microscope; and E(R⃗) is an envelope function. E(R⃗) describes the influence of various instabilities and specimen decay under the beam.(62) The envelope decay can be partly compensated by weighting, for example, with small angle scattering curves (see section 8.3). The optical distortions are usually approximated as a product of functions attributed to individual damping factors (e.g., lens current instability). The link to the PSF is given by the following equation:

The amplitude and phase changes arising from objective lens aberration, or CTF(R⃗), are usually described by the function exp(iγ), where γ describes the phase shift arising from spherical aberration and image defocus:(59)

where γ is the phase shift caused by aberrations, R⃗ is spatial frequency, a vector in the focal plane of the objective lens, C_s is the coefficient of spherical aberration, λ is the wavelength of the electron beam, and Δ is the defocus, the distance of the image plane from the true focal plane.

It was found that the image contrast of biological objects could be improved by the combined effects of spherical aberration and image defocus, moving the image plane away from exact focus.(63) The basis for the contrast enhancement is that spherical aberration combined with defocus induces a phase shift between scattered and unscattered electrons. The greater phase shift between scattered and unscattered rays leads to stronger image contrast.

The diffraction pattern of the image (image plane of the microscope) is given by

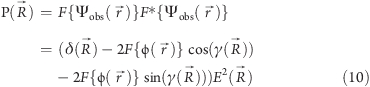where δ(R⃗) is the Dirac delta function.

In the plane of the image, the amplitude contrast is described by 2 cos γ and the phase contrast by 2 sin γ (for a more detailed description of image formation, see refs (60) and (63)). For phase objects, the sine term of eq 10 has the major influence. It describes an additional phase shift due to spherical aberration and changes in the image contrast depending on defocus. The major effect of the CTF on images of weak phase objects arises from oscillations of the sin γ term that reverse the phases of alternate Thon rings in the Fourier transform of the image(64) (Figure 9). For thin cryo specimens, the amplitude contrast for 120 keV electrons has been estimated at 7%, whereas for negatively stained samples the amplitude contrast can rise to 25%.(53) For 300 keV cryo images, it drops to ∼4%.(65)

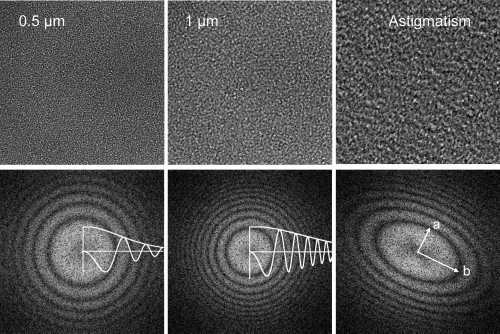
Figure 9.

Images of carbon film and their diffraction patterns, showing Thon rings and corresponding CTF curves. The left image was obtained at 0.5 μm defocus, and the middle image was at 1 μm defocus. The Thon rings of the second image are located closer to the origin and oscillate more rapidly. The rings alternate between positive and negative contrast, as seen in the plotted curves. An example of an astigmatic image and its diffraction pattern is shown in the right panel. The largest defocus is along axis a, and the smallest is along axis b.

2.5. Phase Plates and Energy Filters

The very small phase shifts induced by biological samples in the scattered electrons result in poor image contrast. In phase contrast light microscopy, the imaging of phase objects is enabled by the use of a quarter-wave phase plate,(66) which produces visible contrast by shifting the phase of the scattered light relative to that of the transmitted beam by 90°, leading to constructive interference (Figure 10a,b(67)). An equivalent solution for electron microscopy was pioneered by Boersch.(68)

Figure 10.

Phase contrast in optical and electron microscopy. (a) Bright field (upper panel) and phase contrast (lower panel) images of a field of cells. The cells are approximately 50 μm in length. Panel (a) was provided by Maud Dumoux and Richard Hayward. (b) Schematic representation of the light microscope. (c) Schematic representation of the electron microscope for comparison, showing the major lenses. The positions of phase plates are indicated. (d) Images of GroEL taken without (upper panel) and with the phase plate (lower panel). Scale bars, 20 nm. Image (d) is reproduced with permission from ref (67). Copyright 2008 Royal Society Publishing.

An early attempt to create a device to change the phase of the central beam relative to the scattered rays was done by Unwin, who devised a simple electrostatic phase plate that was inserted into the optical system.(69) He used a thin poorly conducting cylinder (a spider’s thread) over a circular aperture inserted in the back focal plane of the objective lens (where the electron diffraction pattern is formed). This cylinder partly obstructed the central beam and became charged when illuminated by the electron beam, thus creating an electrostatic phase plate. The first experiments with negatively stained samples clearly demonstrated increased contrast.

The practical realization of this idea has only recently become feasible. Microfabrication has allowed the construction of the first miniature phase plates, which are positioned in the back focal plane of the objective lens (Figure 10c,d). The phase plate functions as an electrostatic lens and is placed in the path of the scattered electrons, shifting their phase by 90° so that contrast is improved when they recombine with the unscattered electrons in the image plane of the TEM.^67,70−72 The resulting large increase in contrast over a wide resolution range, especially at low resolution, is particularly useful for electron cryo-tomography.(73)

An additional approach to improving image contrast is energy filtering. A fraction of the electrons reaching the objective lens are inelastically scattered, having lost energy by interaction with the sample atoms. The lower energy (corresponding to longer wavelength) of these electrons causes them to be focused in different planes from the elastically scattered electrons, in other words, chromatic aberration. Therefore, inelastic electrons degrade the recorded image with additional background and blurring, in addition to damaging the sample. Energy filters can be used to stop these electrons from contributing to the image after their interaction with the specimen. Filtering works on the basis that electrons of different wavelength can be deflected along different paths, and the filter can be either in the column (Ω filter) or post column (GIF). The use of energy filtering to improve the contrast of cryo EM images was introduced by Trinick and Berriman(74) and Schröder.(75) Energy filtering is most important for tomography, because of the long path length of the beam through the tilted sample. An in-column filter has recently been used to obtain very high-quality images of actin filaments,(76) and the authors attribute a significant part of the contrast improvement to the filtering.

3. Image Recording and Preprocessing

3.1. Electron Detectors

3.1.1. Photographic Film

Until recently, the conventional image detector was photographic emulsion. The light-sensitive components in films are microscopic silver halide crystals embedded in a gelatin matrix. Absorption of incident radiation by the crystals induces their transition into a metastable state, thus recording the image. The image remains hidden until photographic developer transforms silver halide into visible silver grains. The optical density OD = log(1/T), where T is the transmission of the film. The OD of the film in response to illumination dose, the number of photons/electrons per unit area, initially increases linearly with dose, then starts to saturate and eventually reaches a plateau at high dose, although it is S-shaped for light. At low energy (10–80 keV), optical density is directly proportional to electron energy, and the peak sensitivity is around 80–100 keV. Within the current working range of electron energy (100–300 keV), the speed of EM films is inversely related to the electron energy: higher-energy electrons interact less with the silver halide crystals, leading to lower OD for the same irradiation dose. Therefore, emulsions produced for electron microscopy are optimized for sensitivity to 100–300 keV electrons, with large grain size and high silver halide content. The film mainly used for TEM is Kodak SO-163, which provides good contrast at low dose.(77) The advantage of photographic film is the extremely fine “pixels” and the large image detection area. Photographic film is still the most effective electron detector, in terms of spatial resolution over a large area (number of effective pixels) and cost. The inconveniences of using films are that they introduce an additional load on the microscope vacuum system due to the presence of adsorbed water and they need chemical processing, drying, and digitization.

3.1.2. Digitization of Films

Films must be digitized for computer analysis. To convert the optical densities of the film into digital format, the film is scanned with a focused bright beam of light. The transmitted light is focused on a photo diode connected to a photo amplifier that produces an electrical signal. The intensity of the current is converted into a number related to the optical density of the film. The densitometer measures the average density within square elements (pixels) whose size is determined by the sampling resolution. Linear CCD detectors are used to measure a line of pixels in parallel.

Digitisation does not provide a faultless transfer of optical density into digital format. The accuracy is determined by the quality of the optical system and the sensitivity of the photo detectors and amplifiers. Densitometer performance can be described in terms of the modulation transfer function (MTF), which is defined as the modulus of the densitometer’s transfer function.(78) The output image is considered as the convolution of the input image with the point spread function of the densitometer. The dependence of MTF on spatial frequency describes the quality of signal transfer. A strong falloff of the MTF at high frequencies indicates the loss of fine details in the digitized images. Densitometer characteristics and assessments have been described in several articles.^79,80

3.1.3. Digital Detectors

Digital imaging has practically replaced recording on films in photography and is widely used in EM due to developments in automated data collection and tomography methods. The most popular cameras are based on charge-coupled device (CCD) sensors that convert the analogue optical signal into digital format. The CCD was invented in 1969 by W. S. Boyle and G. E. Smith at Bell Telephone Laboratories (Nobel prize, 2009).(81) The physical principle of this device is analog transformation of photon energy (light) into a small electrical charge in a photo sensor and its conversion into an electronic signal. CCD chips consist of an array or a matrix of photosensitive elements (wells) that converts light into electric charge accumulated in the wells (Figure 11). “Charge-coupled” refers to the readout mechanism, in which charges are serially transferred between neighboring pixels to a readout register, amplified, and converted to a digital signal. The readout is done through one or several ports, which determines the speed of CCD image recording.

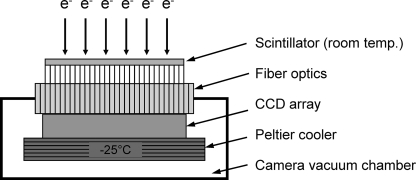
Figure 11.

Diagram of a CCD detector for EM. The incident electrons are converted to photons by the scintillator. Fiber optics transmit the image to the CCD (charge coupled device) sensor where the photons generate electrical charge (CCD electrons). The charge is accumulated in parallel registers. During readout, this charge is shifted line by line to the serial register from where it is transferred pixel by pixel to the output analog-to-digital converter. Image reproduced with permission from H. Tietz.

Because high-energy electrons irreversibly damage the photosensitive wells in CCDs, currently available devices employ mono- or polycrystalline scintillators to convert the electrons to photons, which are then relayed to the CCD chip (Figure 11). Although the graininess of the scintillator and electron-to-photon conversion add noise to the images, the use of a scintillator greatly extends the usable life of a CCD chip. This detection scheme works quite well for accelerating voltages up to 120 kV. At higher voltages, the camera sensitivity decreases, and, to compensate, thicker scintillator layers are needed to improve the electron detection efficiency. In addition, image quality is degraded because the higher-energy electrons are scattered in the scintillator, reducing image resolution.

The CCD is a very sensitive and effective electron detector with remarkably linear response and very large dynamic range (16 bit resolution). This allows recording of both low contrast images and electron diffraction patterns in which diffraction intensities can range over several orders of magnitude. The disadvantage of this type of camera is the high cost and limited sensor size. CCD chips of 5 × 5 cm² (4k × 4k pixels) are now widely used, and digital cameras with 8k × 8k sensors and 12 cm in diameter are available. The typical size of current CCD pixels is 14–15 μm, which imposes additional restrictions on the minimal magnification used to record images, because the image sampling by the CCD should be finer than the target resolution by about a factor of 4 (see section 8). Examples of successful use of CCD imaging for high-resolution cryo-EM at 300 kV are shown by Chen with coauthors(82) and Clare and Orlova.(83)

The current generation of digital detectors for electron microscopy includes a direct detection device (DDD), which can be exposed directly to the high energy electron beam. Hybrid pixel detectors such as Medipix2 are direct electron detectors that count individual electrons, rather than producing a signal proportional to the accumulated charge.(84) Another type of new DDD is the monolithic active pixel sensor (MAPS), in which the signal is proportional to the energy deposited in the sensitive element.(85) The DDD uses a radiation-hardened monolithic active-pixel sensor developed for charged particle tracking and imaging and smaller pixel size (5 μm).^86,87 These detectors are being combined with the CMOS (complementary metal–oxide–semiconductor) design, in which the amplifiers are built into each pixel, enabling local conversion from charge to voltage and thus faster readout. Direct exposure to the incident electron beam significantly improves the signal-to-noise ratio in comparison to a CCD. This type of sensor has high radiation tolerance and allows for capture of electron images at 200 and 300 keV. A comparison of digital detectors demonstrated that DDD in combination with CMOS can provide good DQE, MTF, and improved signal-to-noise ratio at low dose.^87,88

Design of digital cameras in EM continues to improve: the latest cameras are able to register electrons over a broad energy range and cover large areas with smaller pixels so that the detector area (16k × 16k pixels) becomes comparable to or bigger than EM films.^84,87,89

3.2. Computer-Controlled Data Collection and Particle Picking

The goal of automated data collection is to replace the human operator in time-consuming, repetitive operations such as searching for suitable specimen areas and recording very large data sets, including low-dose operation, particle selection, and obtaining tilt data.(90) Most EMs now have computer-controlled operation for lens settings and stage movement, along with basic image analysis operations such as FTs. Essential steps to control are settings for illumination, stage position, magnification, tilt, and focus. The automation system must be able to recognize the same region at different magnification scales, so that objects selected in a lower magnification overview can be located for data collection, in particular after stage movements. The software must compensate for inaccuracies in mechanical stage positioning. This compensation is done by collecting overview images and finding the areas of interest by cross-correlation with previously recorded images, so that the selected area can be positioned with sufficient precision for high-magnification recording. For all of these operations, electronic image recording is essential, and the availability of high-resolution CCD cameras has enabled the development of automation. Several automation systems have been developed, both by academic users (e.g., Leginon;(90) JADAS(91)) and by EM suppliers (FEI, JEOL systems). Some of them are coupled to data processing pipelines that extend the automation through the stages of particle picking and image processing (e.g., Appion(92)). Serial EM is a widely used system that provides semiautomated procedures for manually selecting a series of targets for subsequent unsupervised collection of tomograms and can also be used for single-particle data.(93)

In single-particle EM, data processing begins with particle selection. Conventionally, the particles are identified by shape and characteristic features that are often difficult to recognize for a new complex. Even for known complexes, manual selection of ∼100 000 single-particle images is prohibitively time-consuming and tedious. Not surprisingly, the idea of automating particle selection has been a focus of research efforts. The first computational methods were based on template matching,^94,95 and more sophisticated approaches were subsequently based on pattern recognition.(96) A comparative evaluation of different programs can be found in the review by Zhu and coauthors,(97) and other programs have been developed more recently.(98)

3.3. Tomographic Data Collection

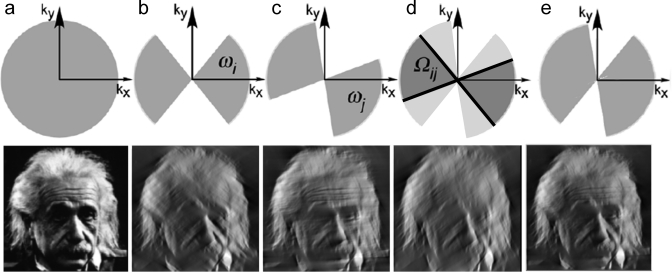
The purpose of electron tomography is to obtain a 3D reconstruction of a unique object, such as a cell section, isolated subcellular structure, or macromolecular complex, that can take up a variety of different structures. A series of images of the same region is recorded over the largest possible range of tilt angles, up to −70° to 70°. The limitation on tilt is ultimately due to the increased path length of the beam through the sample, although the specimen holder may also limit the tilt. Electron tomograms will therefore be missing information from a 40–60° wedge of space, resulting in some distortion to the 3D map (Figure 12(99)).

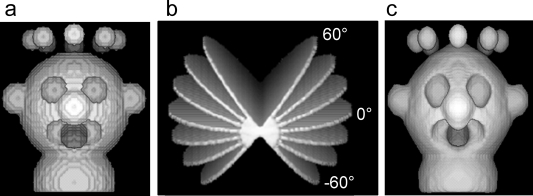
Figure 12.

Distortions caused by the missing wedge. (a) A model object. (b) Set of image planes at different angles from a tilt series. The limitation on maximum tilt angle results in a missing wedge of data. (c) Reconstruction of the object showing elongated features due to the missing wedge. Reproduced with permission from ref (99). Copyright 1998 Elsevier Inc.

The high tilt, especially of thicker specimens, increases the inelastic scattering and multiple elastic scattering, therefore reducing the fraction of coherent electrons useful in image formation, in the scattered beam. The energy-loss electrons can be removed from the image by an energy filter, which is particularly important for improving contrast in tomography.

For plastic sections, the initial exposure to the beam causes thinning of the sections, but subsequently the sample changes little during data collection. Therefore, data collection with fine angular steps is possible. Room temperature tomography also facilitates dual-axis data collection, in which a second tilt series is collected after 90° rotation of the specimen in the plane of the stage, so that the missing wedge is reduced to a missing pyramid. Therefore, data collection can be optimized for plastic sections, but dehydration and staining do not preserve molecular detail. However, as mentioned above, sections up to 300 nm thick can be used to give a 3D overview of larger structures.

On the other hand, in electron cryo-tomography, the molecular structure is preserved in the frozen-hydrated sample, but it is hard to get beyond 3–4 nm resolution. The resolution of cryo-tomography is severely limited by radiation damage, because at least 50–100 images must be collected of the same area for the tilt series. These conflicting requirements for low dose and many exposures mean that the images are recorded with extremely low electron dose and therefore very low SNR, and the accumulated damage changes the structure during the tilt series. The thicker is the sample, the more views are needed to reach a given resolution. In addition, the limitation on maximum tilt angle leaves a missing wedge of data. These problems make processing of cryo-tomograms more difficult. The best resolution is obtained by averaging subregions of cryo-tomograms containing multiple occurrences of the same object, for example, viral spikes (see section 4.4). This method is called subtomogram averaging.

Automation is indispensable for electron tomography.(100) Well-developed tomography software is available from both academic and commercial sources (SerialEM;(93) UCSF Tomo;(101) Protomo;(102) TOM;(103) Xplore3D;(104) IMOD^105,106). Leginon incorporates tomographic and other tilt data collection protocols such as conical tilt (section 6.1).(107)

3.4. Preprocessing of Single-Particle Images

Although theoretical and technical progress in electron microscopy has improved the imaging of weak phase objects, defocusing complicates the interpretation of the image because features in some size ranges will have reversed contrast. Imaging of biological objects requires a compromise between contrast enhancement and minimization of image distortions.

The intensity distribution in the EM image plane is related to the projected electron potential by

where sin γ is the phase contrast transfer function and γ is defined by eq 9. F^–1{sin γ} defines the shape of the image of a point in the object plane formed by the microscope optics, the point spread function (PSF) of the microscope. Therefore, the real image is distorted, because the ideal object image is convoluted with the PSF, and is not directly related to the density distribution in the original object. To restore the image, so that it corresponds to the projected electron potential of the sample, the image must be corrected for the effect of contrast modulation by sin γ, the microscope phase contrast transfer function (CTF). The CTF, modified by an envelope decay, and the PSF of a microscope are related by Fourier transformation. For weak phase objects, deconvolution with the PSF of the microscope is necessary for complete restoration of image data. The procedure of eliminating the effects of the CTF is called CTF correction.

3.4.1. Determination of the CTF

For a given microscope setup, the voltage and spherical aberration are constant, but the defocus varies from image to image because of variations in lens settings, sample height, and thickness. There are two main approaches for determination and correction of the CTF. In the first one, the images are CTF-corrected before structural analysis. In the second approach, structural analysis is done separately on each micrograph, and determination and correction of the CTF are performed on the structures obtained. Each approach has its own advantages and disadvantages.

If CTF correction is done first, data can be combined from many different micrographs and subsequently processed together. The second method is applicable if each micrograph has a sufficient number of particles to calculate a 3D reconstruction. This method works well for particles at high concentration and has the advantage that CTF determination is more accurate because of the high SNR in the reconstruction, in which the images have been combined. However, with fewer particles and lower symmetry, it will not be possible to get a good reconstruction of the object from a single micrograph, so that the first approach is more practical.

Manual CTF determination(108) involves calculation of the rotationally averaged power spectrum (diffraction intensity) of a set of 2D images, which can only be done in the absence of astigmatism. The amplitude profile (square root of the intensities) is compared to a model CTF. The model defocus is varied to find the best match between the two profiles. The value corresponding to the match is then used as the defocus for that particular set of images. It is also possible to include additional processing steps such as band-pass filtering to remove background and provide smoothing for more accurate detection of the positions of the CTF minima.

The rotational averaging used in the above method assumes good astigmatism correction. Software developed by Mindell and Grigorieff (CTFFIND3(109)) searches for the best match of experimental with theoretical CTF functions calculated at different defoci. This software includes the determination of astigmatism in the images, assuming that its effect on the CTF can be approximated by an ellipse (valid for small astigmatism), with averaging of the profiles over sectors of the ellipse. Scripts can be used to automate the search and correction.

In some studies, statistical analysis has been employed to sort power spectra of particle images (squared amplitudes of the image Fourier transform) into groups with similar CTF. Class averages of the spectra provide a higher SNR for CTF determination.(110) Other, more sophisticated approaches that take into account background and noise are described by Huang(111) and Fernández and coauthors.(112) A fully automated program, ACE, implemented in Matlab, incorporates a model for background noise and uses edge detection to define the elliptical shape of the Thon rings.(113)

3.4.2. CTF Correction

The representation of the object of interest is considered as faithful if the EM images corresponding to its projections are corrected for the effects of the microscope CTF. A full restoration of the specimen spectrum requires division of the F{Ψ_sam(r⃗)} (eq 7) by the CTF, sin γ. However, this operation is not possible because of the CTF zeroes, and the spectrum cannot be restored from images taken at a single defocus. To fully restore the information, it is necessary to use images taken at different defocus values, so that zeroes of each particular CTF will be filled by merging data from images with different defoci (Figure 13).

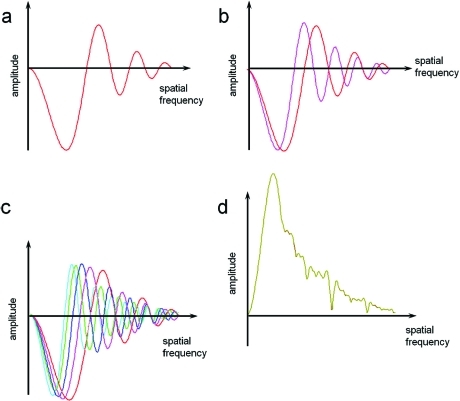
Figure 13.

CTF curves, for a single defocus (a), overlaid for two different defocus values (b). The red curve corresponds to a closer to focus image, and oscillates more slowly. Image (c) shows multiple defocus values. The cyan/green curves correspond to the images with the highest defocus, and the red curve is closest to focus. (d) The sum of amplitude absolute values of all curves in (c), showing the overall transfer of spatial frequency components in a data set with the defocus distribution shown. Images courtesy of Neil Ranson.

3.4.2.1. Phase Correction

The simplest method of CTF correction is to flip the image phases in regions of the spectra where sin γ reverses its sign. In many cases, this produces reliable reconstructions because a large number of images with different defoci are merged together, leading to restoration of information lost in individual images in the vicinity of CTF zeroes. Practically all EM image analysis software packages have options for this type of CTF correction.

3.4.2.2. Amplitude Correction and Wiener Filtration

A more advanced method of information restoration is correction of both amplitude distortions and phases of the image spectra. This correction usually takes into account not only CTF oscillations but also compensates for the amplitude decay at high spatial frequencies. In theory, the following operation should be sufficient:

where Im is the recorded image, PSF is the point spread function of the microscope, the Fourier transform of which is CTF, and Im_cor is the corrected image. If there were no noise in the image spectra, reliable correction could be done everywhere except for points where the CTF is zero. In practice, small CTF values suppress signal transfer in these regions, and noise unaffected by the CTF dominates the spectra there. Thus, simply dividing the image spectra by the CTF would lead to preferential amplification of noise. To avoid this, a Wiener filter(114) is used to take account of the SNR and perform an optimal filtration to correctly restore the spectra:

where c is a function of SNR: c = 1/(SNR).

Multiplication of the Fourier transform of the image by the CTF corrects the image phases, while division by CTF² + 1/(SNR) provides the amplitude correction. Addition of 1/(SNR) to the denominator is necessary to avoid division by values close to zero(115) (Figure 14). Amplitude correction has been implemented in EMAN,(116) SPIDER,(117) Xmipp,(118) and other software packages. To visualize high-resolution details, it is also important to correct the envelope decay of image amplitudes at high spatial frequencies (see section 8.3).

Figure 14.

(a) CTF curve from uncorrected data, (b) after phase correction, and (c) overlay of original (black), the square of the curve after rescaling (red), and amplitude correction (green). Panel (c) courtesy of Stephen Fuller.

3.4.3. Image Normalization

After CTF correction, the image of a weak phase object can be considered as a reasonable approximation of the 2D projection of the 3D object, except for the regions affected by CTF zeros, where the signal is low. This allows the process of image analysis to progress toward determination of the 3D density distribution for the object. Nonetheless, some important steps of preprocessing are necessary.

Even with the same EM settings during data acquisition, variations in specimen particle orientation, support film thickness, and film processing conditions lead to differences in image contrast. In addition, structural analysis requires the merging of image data collected during multiple EM sessions. Optimization of data processing requires standardization of images known as normalization. It is conventional in EM image processing to set the mean density of all particle images to the same level, usually zero, and to scale the standard deviation of the densities to the same value for all images, which is important for the alignment procedure.

Images are normalized using the formula:

σ_old is the standard deviation of the original image, and σ_new is the target standard deviation in the data.

The mean density ρ̅ of the images is defined as

where I and J are dimensions of the image array, and ρ_i,j is the density in the image pixel with coordinates i and j. σ_old is defined as

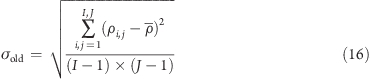The normalization sets all images to the same standard deviation and a mean density of zero.

4. Image Alignment

The information we wish to extract from EM images, the signal, is the projected density of the structure of interest. The recorded images contain, in addition to the signal, fluctuations in intensity caused by noise from many different sources. Sources of noise include background variations in ice or stain, damage to the molecule from preparation procedures or radiation, and detector noise. The signal-to-noise ratio (SNR) is defined as

where P_signal is the energy (the integral of the power spectrum after normalization) of the signal spectrum, and P_noise is the energy of the noise.

Many views of the particle are recorded in different orientations, but each individual image has a low SNR. The main task in extracting the 3D structural information is to determine the relative positions and orientations of these particle images so that they can be precisely superimposed. Alignment is done by finding shifts and rotations that bring each image into register with a reference image. Cross correlation is the main tool for measuring similarity of images, but it is not very reliable at low SNR. In practice, alignments are iterated so that successive averages contain finer details, which in turn improve the reference image, for subsequent rounds of refinement.

4.1. The Cross-Correlation Function

The correlation function is widely used as a measure of consistency or dependency between two values or functions. In image analysis it is used for assessment of similarity between images. Cross correlation compares two different images.

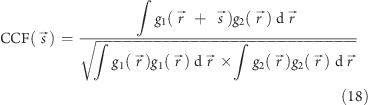Equation 18 defines the normalized cross correlation function (CCF) between two functions, g₁(r⃗) and g₂(r⃗), where r⃗ is a vector in space, and s⃗ is the shift between images. In our case, images are the 2D functions being compared, and r⃗ and s⃗ are vectors in the image plane. The images are normalized to a mean value of zero, to avoid influence of the background level. Without normalization of the images, the CCF would be offset by a constant proportional to the product of the mean values of the images.

The normalized cross-correlation function is maximal when the two images are identical and perfectly aligned, and the displacement s⃗_p of the correlation peak from the origin gives the displacement of image g₁ with respect to image g₂. It is quicker to calculate the CCF in Fourier space, because the FT of the correlation integral is the product of the complex conjugate of the first image FT with the second image FT.

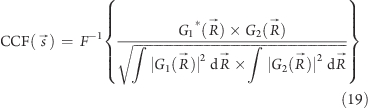where R⃗ is a vector in Fourier space, and G₁ and G₂ are FTs of g₁ and g₂.

The cross-correlation of an image with itself is the autocorrelation function (ACF). In crystallography, the ACF is known as the Patterson function, which is obtained by Fourier transformation of intensities in diffraction patterns and gives a map of interatomic distances (correlation peaks between pairs of atoms).

4.2. Alignment Principles and Strategies

Faced with a data set of images of an unknown structure, we do not have an a priori reference for alignment. A suitable reference can be generated from the data by approaches known as reference-free alignment. In one such approach, the first step in alignment of preprocessed images is to center the particles in their selected boxes. Particles can be centered either by shifting the center of mass of the image to the center of the image frame or by a few iterations of translational alignment to the rotationally averaged sum of all images.(119) In another version of reference-free alignment, a series of arbitrarily selected images are used in turn as references to align all of the other images.(120)

If the signal is weak, or the reference image does not match the data, noise can be correlated to the reference image during alignment. Therefore, to avoid bias, it is important to start a new analysis with reference-free alignment. The problem of reference bias is illustrated by tests in which pure noise data sets are aligned to a reference image.^121,122 Because the correlation is sensitive to the SNR in the image data, the accuracy of the correlation measure can be improved by weighting the correlation of Fourier components according to their SNR.(122)

Alignment of a single-particle data set is accomplished by a series of comparisons in which alignment parameters are determined on the basis of correlations of each raw image with one or a set of reference images. The major information for alignment comes from the stronger, low-frequency components of the images. Because of the low SNR in cryo-images, it is important to maximize the contribution of the signal to the correlation measurement by reducing noise. There are two ways to reduce noise in the images. In real space, a mask around the particle serves to exclude background regions outside the particle. In reciprocal space, a band-pass filter can be applied to exclude low-frequency components related to background variations over distances greater than the maximum extent of the particle and high-frequency components beyond the resolution of the analysis. In later iterations of alignment, it is useful to increase the contribution of higher-frequency components.

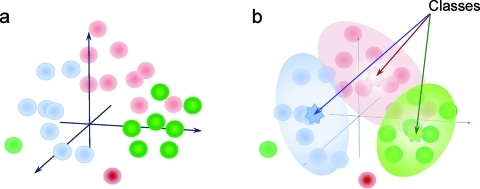
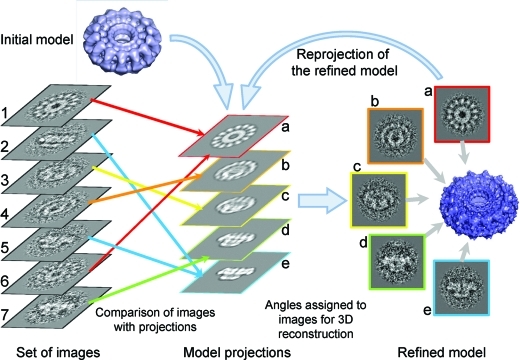
In addition to their arbitrary positions and orientations in the plane of the image projection, the particles may have different out-of-plane orientations, which will give rise to different projections. To sort the images into groups with common orientations, statistical analysis and classification are essential tools (see next section) in “alignment by classification”.(12) Initial class averages selected from a first round of classification can serve as references to bring similar images to the same in-plane position and orientation and to separate different out-of-plane views. A few iterations of these alignment and classification steps provide good averages representing the characteristic views in the data set.

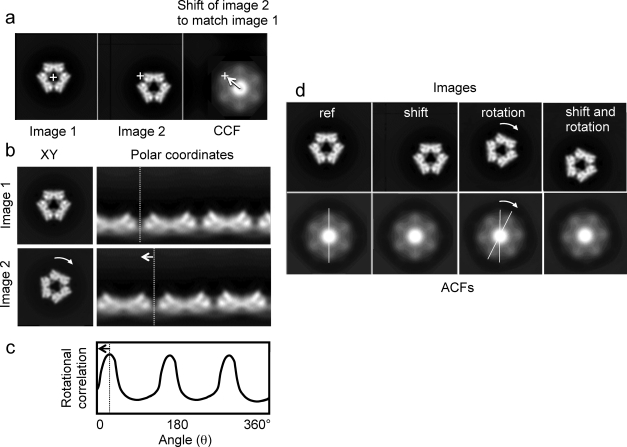
Various protocols have been developed for translational and rotational alignment of image data sets. Tests on model data suggest that, after initial centering, iterations of rotational followed by translational alignment to the reference images are effective^12,123,124 (Figure 15). The quality of the result also depends on the accuracy of the interpolation procedures, because the digital images must be rotated and shifted by non integral pixel values during alignment.(125)

Figure 15.

Alignment using translational and rotational cross correlations and autocorrelation. (a) Two images to be aligned, with the second shifted off center. The right panel shows the cross-correlation function (CCF) of the second image with the first. The crosses indicate the image centers. The arrow indicates the shift that must be applied to image 2 to bring it into alignment with image 1, according to the CCF maximum. (b) Two images, related by a 25° rotation, shown in Cartesian (left) and polar coordinates (right). The curved arrow shows the rotation in the Cartesian coordinate view, and the dashed line shows the corresponding shift of a feature in the polar coordinate representation. (c) Plot of the rotational correlation between the two images in (b). The arrow shows the angular shift required to align image 2 to image 1. (d) Images and their corresponding autocorrelation functions (ACF). When the image is shifted (second panel), the ACF is unchanged (translationally invariant). The reference image (ref) has 3-fold symmetry, but its ACF is 6-fold because of the centrosymmetric property of ACFs. Rotation of the image causes the same rotation of the ACF, but has an ambiguity of 180°. A possible alignment strategy is to use the ACF first for rotational alignment, using the property of translational invariance. The CCF then can be used for translational alignment, checking both 0° and 180° rotational positions.

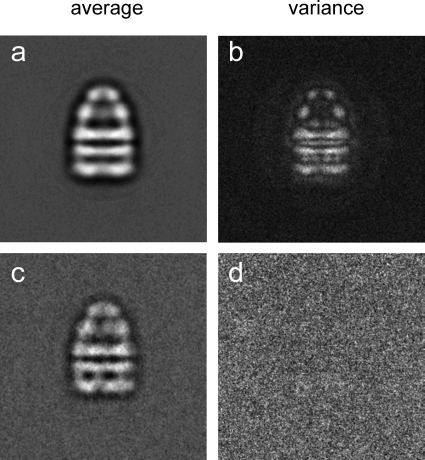
The progress of an alignment can be evaluated by examining the average and variance images (Figure 16). The average of an aligned set of similar images should improve in contrast and visible detail during refinement, and the variance should decrease. In addition, the cross-correlation (CC; maximum value of the normalized CCF) between references and raw images should increase during refinement.

Figure 16.

Average and variance for an image set of particles whose orientations are distributed by rotation around the symmetry axis (a,b) and for an image set of particles in a single orientation (c,d). The average in (a) contains images of particles in different orientations, resulting in significant variation of image features (b). Panel (d) is featureless, because all of the particles in the average (c) have the same orientation, so that the projections only differ in the noise background. Figure courtesy of Neil Ranson.

4.2.1. Maximum Likelihood Methods

For alignment of an image data set to a set of references, each image is assigned the alignment parameters of the single reference image with which it has the highest CC. The maximum likelihood approach uses the whole set of CC values between each image and all of the references to define a probability distribution of orientation parameters for the image being aligned.^126,127 For clusters of references giving similar CC values, this approach is likely to provide more reliable alignment parameters than would be obtained just taking account of the highest CC, but it is computationally very expensive.

4.3. Template Matching in 2D and 3D

So far, we have considered alignment of 2D images to references, but there is also a need to detect known features (motifs) in noisy and distorted image data in both 2D and 3D. In 2D, motif detection is used for automated particle picking in raw micrographs. In 3D, the task is to search for occurrences of known molecular complexes in tomograms. These tasks represent 2D and 3D versions of a search for a known, or approximately known, structural motif in image data. In automated particle picking from micrographs, individual particles with low SNR are located by a cross-correlation search of the whole micrograph with one or more template images, references derived from the data, a model, or a related structure. In 3D, if a known structural motif is expected to be present in the reconstructed volume, the 3D map of that motif can be used to search for occurrences of related features in the tomogram. The main problem is reliable identification of motifs in noisy data. In the case of template matching, a small region of the whole micrograph or 3D structure is searched by cross-correlation with the template. If the image or structure is normalized as a whole (global normalization), the cross-correlation between the template and each small, local region will be influenced by many features outside the region of interest. On the other hand, if the image or structure is normalized just in the local region at each step of the search, the resulting correlation values will give more reliable results reflecting the local match with the template. A locally normalized correlation approach was developed by Roseman and is widely used.^124,128,129

4.4. Alignment in Tomography

4.4.1. Alignment with and without Fiducial Markers

The accuracy of tomographic reconstruction depends on the alignment of successive tilt views. Alignment is done by tracking the displacements of marker particles (fiducial markers) across the image as a function of tilt angle. Dense particles such as colloidal gold beads or quantum dots (semiconductor particles that are both fluorescent and electron dense) are used for this purpose. For plastic sections, these markers are applied to the surfaces. With a good distribution of fiducial markers and a stable specimen, it is possible to obtain accurate alignment and even to correct for local distortions. Alignment can sometimes be improved by restricting it to subregions of interest, which move coherently through the tilt series.(130)

For cryo-tomography, fiducial markers can be mixed into cell suspensions before freezing. Alternatively, a method for depositing fiducial markers onto sections at cryo-temperatures has been published.(131) In cryo-tomography, the requirement to limit the total dose means that the SNR in each view is very low.(132) In addition, cumulative radiation damage and tilting change the image from one view to the next. These problems reduce the success rate of alignment, especially for vitreous sections.

With sufficient contrast of image features, markerless alignment can be used. A method has been developed in which a large array of randomly chosen points is tracked by cross-correlation.(133) Because of the continually changing images, tracking is done through many overlapping short trails. The markers are checked for consistency to search for useful ones.

4.4.2. Alignment of Subregions Extracted from Tomograms

Tomographic reconstructions of irregular objects such as subcellular regions often contain multiple copies of molecular complexes. If these complexes can be recognized and extracted from the tomogram, they can be aligned and classified as single particles in 3D, giving substantial improvements in SNR. The main difference with single-particle analysis in 2D is that the tomogram has a wedge of missing data (section 3.4). For each occurrence of the object, this wedge of missing data will be in a different direction, depending on the orientation of the object in the original tomogram. To avoid bias to the orientation of the missing wedge, each pairwise correlation must include only the regions of Fourier space common to both images(134) (Figure 17). Subtomogram averaging has been used to study paracrystals of filaments, viral particles, and their substructures such as surface spikes.^102,135

Figure 17.

Diagrams of angular coverage and the corresponding images, to illustrate alignment of subtomograms taking account of the missing wedge. (a) The original image with no missing data. (b) The effect of a missing wedge along the y axis on the image. Only projections within the gray sector ω_i are used to produce the image. Some features of the face (wrinkles and eyes) are not resolved. (c) Another set of projections ω_j with the missing wedge in a different orientation causes different features to be lost. (d) If only the data common to the two images (b) and (c) are present (Ω_ij), the image is more distorted. Nevertheless, alignment of the two images (b and c) can be based on this overlapping information. Otherwise, the alignment would be biased by the missing wedge. (e) After alignment, the two data sets (b) and (c) can be combined to give a better angular coverage, so that the reconstruction more closely resembles the original object. Modified with permission from ref (134). Copyright 2008 Elsevier Inc.

5. Statistical Analysis of Images

As discussed in section 4, the structural features of the object of interest in an EM image are typically corrupted by noise resulting from counting noise in the number of electrons per image element, sensitivity of individual channels in the image sensor, radiation damage to the specimen, and fluctuations in local concentrations of buffer chemical components. In addition, rapid freezing can trap biological complexes in different structural states that must be separated. How can a large image data set be transformed into a system with fewer parameters that adequately represents different projections of the same molecules as well as their different biological states?

Assuming that the noise is not correlated to the structure, it can be suppressed by averaging many images of the particles, thereby enhancing the structural information. For averaging, it is essential that the particle images are brought into register so that similar features superimpose in their average. In general, the alignment is an iterative process beginning with coarse features of the data set, for example, center of mass of each particle image, followed by grouping and averaging of individual images. Averaging improves the SNR by a factor of √N, where N is the number of averaged images. This in turn facilitates the determination of relative orientations of the different group averages (“characteristic views”). Analysis of images followed by classification into different groups (clusters) according to their features is the basis of the statistical approach.(136) Statistical analysis was introduced into EM image analysis around 1980.^137,138 Several methods are used for analysis of variations, such as principal component, multivariate, or covariance analysis. Classification can done by hierarchical or K-means clustering.

5.1. Principal Component Analysis

Each image of I × J pixels can be represented as a vector in (I × J)² dimensional hyperspace with coordinates defined by the density values of the image pixels. So a set of images can be considered as set of vectors or, equivalently, as a cloud of points (ends of the vectors) in the hyperspace (Figure 18).

Figure 18.

Schematic of a data cloud illustrating the principles of multivariate statistical analysis and classification. (a) Each image is represented by a color-coded dot in a multidimensional data cloud, which has been subjected to MSA. (b) The dots are sorted into three classes according to color and position. Several outlying dots (represented by inconsistency between color and position) are not assigned to major classes and represent classes composed only by one dot, and are not considered as representative classes.

Similar images will correspond to points that are close to each other within the cloud. However, a pairwise comparison of all images would be very slow because it requires pixel-by-pixel evaluation of the differences for all possible shifts and rotations. The essence of the statistical approach is to reduce the number of variables describing the data set and to find a smaller set of uncorrelated variables, called principal components. Multivariate statistical analysis (MSA) identifies the largest variations in a big data set and changes the coordinate system in the hyperspace using these major components as new axes. The axes are oriented along the directions of these variations and are orthogonal (and therefore uncorrelated) to each other. Principal component analysis (PCA) uses the eigenvectors of the covariance matrix (pairwise comparison of all images) as principal components (for explanation, see ref (139)). Typically, only a subset of new coordinates is used with directions corresponding to largest variations in the data set. In image analysis, eigenvectors are presented as eigenimages, which show the regions of major density variations in the image data set. The smaller variations are usually attributed to noise components of the data. The reduction of dimensionality of the space leads to a compressed representation of the data set without much loss of information. This compression is achieved by representing each image as a linear combination of the principal components (see details in ref (140)). Evaluation of the image similarities then can be carried out as a comparison of vectors with a reduced number of components.

5.2. Hierarchical Clustering

The principal components of the data cloud can be used to sort the images into groups by a clustering procedure. To decide how to group the images (or elements of the data set), the distance between them, or their similarity, must be estimated. There are two main approaches for clustering that differ in their starting point: In the agglomerative, or ascendant, hierarchical classification, each point in the data hyperspace is initially considered as a group (class) followed by merging the most similar (closely spaced) points into the requested number of clusters. The divisive approach initially places all of the data in one cluster, which must be separated into smaller groups according to their dissimilarity. Depending on the distance of each data point from the existing clusters, that element will either join the nearest cluster or form the seed of a new cluster.(139)

The principal difference between the currently used algorithms is the definition of the distances between elements (metric) in the hyperspace. The metrics typically used are Euclidian distances, chi-square metrics (χ²), or modulation distances.(139) The smaller is the distance between the points, the greater is the correlation (similarity) between the corresponding images. The simple Euclidean distance measure is sensitive to differences in scaling (normalization) between the images. Thus, two images with densities that are proportional to each other could incorrectly end up in different clusters using this metric. Therefore, the χ² measure incorporates normalization by the average of all images, and the modulation measure scales the images by their standard deviations, allowing for more robust classification schemes.

The algorithm implemented in IMAGIC(141) is based on minimization of the intraclass variance in a cluster (between the members of the cluster) and maximization of the interclass variance between the centers of mass of the clusters.^139,142 In SPIDER, there are options to use either correspondence analysis based on chi-square metrics (χ²), which requires all data to be positive, or PCA, which does not have that requirement.(124)

5.3. K-Means Clustering and the Maximum Likelihood Method

K-means is a clustering (partition) method, which starts with a predefined number (K) of points randomly selected from the data as seeds. Each data point is assigned to a cluster nearest to one of the K points, and the center of the created cluster is redefined. As further points are added, the algorithm iteratively reorganizes the clusters until the sum of intracluster distances is minimized. The results of classification by K-means usually depend on the initial center assignment. This approach works best with a small number of clusters.

The maximum likelihood method can be used to cluster images with low SNR.^127,128 This approach is based on random selection of K subsets of the data from which seeds of clusters are created, followed by the optimization of the clusters. Seed positions are reassessed during formation of the clusters. The maximum likelihood method along with K-means clustering has been implemented in Xmipp.(118)

The use of statistical analysis and classification of images is important for discriminating variations from any source, differences in defocus, different particle orientations that reflect different 2D projections of a 3D structure, structural variations within an orientation group, and eventually conformational changes of the complexes.

6. Orientation Determination

To calculate the 3D map from a set of projection views, the relative orientations of the 2D projections must be determined. There are two general approaches to this problem. An experimentally based approach involves the collection of images of the same particles at different tilt angles.(144) This method is particularly applicable for particles that adopt a preferred orientation on the support grid. The other approach is computationally based, in which untilted images are collected. For the second approach, it is essential to collect a range of views distributed over different orientations.^145−147 The biggest challenge in orientation determination is to get the first set of assignments for a data set corresponding to an unknown 3D structure, especially if it is asymmetric. Once an initial model (starting model) is available, the orientations can be refined. A significant problem in single-particle analysis is that an incorrect starting model can bias the result or even completely invalidate it, and there are examples in the literature of dissimilar or completely different EM structures for the same biological complex. In such cases, further information is needed from biochemical, biophysical, or genetic experiments to help validate the resulting structure.

6.1. Random Conical Tilt

Radermacher^148,149 developed the method of random conical tilt that provided the first reconstructions of macromolecular assemblies without using symmetry (50S ribosome and RyR channel.^148−150 Images are taken in pairs, so that the same field of particles is recorded first at high tilt (45–60°) and then untilted (Figure 19). The image pairs are tracked by aligning the two fields via recognizable point features. The method has mainly been used with negative stain EM, because cryo-EM is more difficult at high tilt angles. It is most straightforward if the particles have a preferred orientation on the carbon support film. In that case, all of the untilted images will be the same, except for in-plane rotation, and the tilted images will correspond to projections lying on a cone of orientations. The position on the cone for each tilted view is determined by the in-plane orientation (azimuthal angle) of the corresponding untilted view. If the particles do not all have the same in-plane view, the untilted images must first be sorted out into groups of similar views by classification, so the tilted views can be grouped according to their corresponding in-plane orientations. This information is sufficient to define the orientations of the tilted particles, and a first 3D map, or set of maps for different in-plane orientation classes, can be calculated. In principle, the method is simple and reliable, and indeed it is widely used for getting a starting model.

Figure 19.

Conical tilt geometry. (a) The original object, with arrows indicating the angular directions of the data projections. (b) Representation of the sections in Fourier space corresponding to data projections collected within this cone of angles. A central cross section of the planes in Fourier space is shown in (c). (d) A surface view of the resulting conical tilt reconstruction, surrounded by the eight projections corresponding to the original view directions. Reproduced with permission from ref (99). Copyright 1998 Elsevier Inc.

However, the conical tilt approach has some limitations. It is technically difficult to get good quality images at high tilt, because of specimen thickness and microscope stage stability, especially for cryo-EM. The tilted images will have a gradient of defocus, although with continuous carbon film it is possible to determine the defocus and correct for it.^149,151 A more difficult problem is incomplete staining, in which particles are not fully embedded in stain and the highest regions of the structure are missing from the images. Partial staining can be avoided by placing the stained particles between two carbon films, but this task is experimentally more difficult, and very thin carbon films are needed to avoid excessive loss of contrast. Current microscopes make it more feasible to avoid these problems by using cryo-EM for conical tilt. Finally, the limit on maximum tilt angle imposed by the specimen holder and thickness of the tilted specimen results in a missing cone of data, limiting the resolution in z. This problem can be rectified if there are different particle orientations in the untilted image, so that different conical tilt reconstructions can be merged to compensate for missing cones.

The orthogonal tilt strategy provides an elegant approach to 3D reconstruction from tilted views.(152) Unlike conical tilt, this method requires well distributed out-of-plane orientations. Pairs of images are collected at −45° and 45° tilts. Suppose there are two particles with out-of-plane orientations 90° apart. If the rotation axes coincide, a −45° tilt of one particle will correspond to a +45° tilt of the other. The problem is to find equivalent views in tilt images arising from particles that are orthogonal at 0° tilt. Combining such tilt views from particles with different in-plane orientations will generate a tomographic series around the common axis and can be used to generate a 3D reconstruction with no missing cone (see Figure 1 of Leschziner and Nogales(152)).

6.2. Angle Assignment by Common Lines in Reciprocal Space

For any set of 2D projections of a given 3D structure, there are relationships between the projections that can be used to determine their relative orientations (Figure 20). Each pair of 2D projections has at least one 1D (line) projection in common.^153,154 In Fourier space, 2D projections correspond to planes passing through the origin of Fourier space, and 1D line projections become radial lines in the transform. The common line between two projections in Fourier space is the line of intersection of the corresponding two planes in Fourier space (Figure 21).

Figure 20.

Relationships between images and projections in real and Fourier space. The 3D structure can be projected onto planes to give 2D projections, which can in turn be projected in different directions to yield 1D (line) projections, indicated by the operator of summation ∑. The complete set of line projections is known as the Radon transform. A sinogram is a set of line projections of the 2D projection or a section of the 3D Radon transform. In the reverse direction, the set of line projections can be combined to reconstruct the 2D image and the set of 2D projections combined to reconstruct the 3D object, indicated by the operator of stretching. The image information can be equivalently represented in reciprocal space, in the form of Fourier amplitudes and phases (right column). Fourier transforms (F) of the 2D projections correspond to central sections of the 3D transform (extraction), and the line projections correspond to lines passing through the origin of Fourier space (central lines). Therefore, the object can also be reconstructed by combining (filling) the set of central sections into the 3D transform followed by inverse 3D Fourier transformation. Adapted with permission from ref (12). Copyright 2000 Cambridge University Press.

Figure 21.

Surface rendered views, projections, and transform sections of a structure, with a common line intersection illustrated in reciprocal space. The structure has rotational symmetry, and there are several symmetry-related common lines. From the angles between common line projections of different views, the relative Euler-angle orientations of a set of projections can be determined. Adapted with permission from ref (24). Copyright 2000 International Union of Crystallography.

With only two images, the angle between the two intersecting planes cannot be determined because only one common line exists, but with three images there are three common lines, and angles between any two common lines can be found with respect to the third one, so that all of the orientations are fixed. Determination of common lines from individual raw images is difficult, but the presence of symmetry provides many more constraints and results in multiple common lines, both from the same image (self-common lines) and between image pairs (cross common lines). Icosahedral viruses provide the most favorable case, and Crowther(145) developed the application of common lines for determining the relative orientations of virus particles in Fourier space. Using their icosahedral symmetry, he was able to find the common lines and to determine the particle orientations. Because the searching is done in reciprocal space, the radial lines of the image transforms are compared and the common lines identified by minimizing the sum of phase residuals between pairs of common lines. Fuller(155) introduced a weighting scheme to make the common lines method more effective for use with cryo EM images of icosahedral particles. The phase residual comparison depends on particle orientation: the common lines are less well separated in views around the symmetry axes, and fewer independent values of the transform are compared. At low SNR, this difference in the number of comparisons means that the probability of finding views near symmetry axes must be downweighted.(156)

6.3. Common Lines in Real Space

The Radon transform (discussed in section 7) is the set of all 1D (line) projections of an N-dimensional function. This concept is useful in considering the relationships between a 3D object and its projections. In particular, a 2D section of the Radon transform of a 3D function corresponds to the set of 1D projections of the 2D projection. On the basis of this concept, a common lines approach in real space for arbitrary symmetry was developed by van Heel and colleagues and implemented in IMAGIC.^{12,154,157,158} For each 2D image, a set of 1D projections is calculated and presented as an image (sinogram) whose lines are formed of the series of 1D projections from 0° to 360°. It is important to note that centering of images is essential for angle assignment by common lines, because shifting the 2D image shifts the 1D projections. In the search for common lines in Fourier space, the images are centered by the phase minimization procedure, because the common lines must be centrosymmetric.

The task is to find the best matching lines for each pair of images being compared, by cross correlation between their sinograms (Figure 22). Especially with low symmetry structures, the low SNR makes this comparison very difficult with sinograms obtained directly from the raw images. An important innovation making it possible to work with lower symmetries was use of class averages (see section 5) rather than individual raw images for the common lines search. It is advisible to make several trials to get an initial 3D reconstruction by angular reconstitution and to check the consistency of the results, especially with asymmetric structures. Once a consistent initial 3D map has been obtained, the structure can be refined by further cycles of alignment, classification, and common line searching.

Figure 22.

Sinograms and sinogram correlation functions for a model structure. Three projections (numbered 1–3) are shown of a model composed of three Gaussian dots with different densities. S1, S2, and S3 are sinograms or sets of 1D projections of the corresponding 2D projections. CSC12 and CSC32 represent cross-sinogram correlation functions between projections 1 and 2 and projections 3 and 2, respectively. Each point of the sinogram correlation function contains the correlation coefficient of a pair of lines from the two sinograms. Solid lines indicate the common lines between projections 2 and 1, while the dashed lines indicate the common lines between projections 2 and 3. Each CSC has two peaks because projections from 180° to 360° mirror those from 0° to 180°. The angular distance between the common lines (solid and dashed) gives the angle between projections 1 and 3.

6.4. Projection Matching

The procedure of projection matching is much easier to understand in principle, but it needs an initial model. Once a 3D structure is available, even at very low resolution, it can be used to generate reprojections at all possible orientations. The set of reprojections can then serve as reference images, in a systematic comparison of each image in the data set (or set of class averages) with all of the reference images (Figure 23).(159) In projection matching, for each image in turn, the Euler angles of the reference image that gives the best cross correlation are assigned to the raw image or class average. For each comparison, all possible in-plane alignments must be tested, so that this is a very lengthy calculation. Once the Euler angles are assigned, a new 3D map can be calculated and the procedure iterated with the new set of reprojections (Figure 23). Real-space projection matching is implemented in EMAN,(116) IMAGIC,(141) and SPIDER.(117) The program FREALIGN does the projection matching search in reciprocal space, giving some advantages in speed and providing an option for refining defocus of each particle.(160) Another projection matching method, PFT (polar Fourier transforms), was developed by Baker and colleagues for refinement of icosahedral structures^146,161 (Baker and Cheng, 1996, Sinkovits and Baker, 2009). An alternative approach uses wavelet expansions to compare images and reprojections, demonstrating improvements in speed and robustness to noise.(162)

Figure 23.

Projection matching procedure. A set of images is compared to a set of references from an initial model (low resolution). Once the best match is found between the image and one of the references (reprojections), based on the height of the correlation peak, the shift relative to the matching reference and angles of that reference are assigned to the image. Images 1 and 6 have the best correlation with model projection a (red arrows), while images 2 and 5 match image e (blue arrows). Image 3 corresponds to the tilted view c (yellow arrow). A new 3D map is calculated using images with the assigned angles. The refined 3D reconstruction is then reprojected with a smaller angular increment to generate new references for the next iteration of refinement.

6.5. Molecular Replacement

As in protein crystallography, it is usually much quicker and easier to determine a structure if a sufficiently similar starting model is already available. In many cases, the objective is to determine the structure of a complex with a ligand or with localized conformational changes. If the structure of the initial complex is known, it can be used to generate reprojections that can be used for projection matching or common lines search in real or reciprocal space. The resulting new model can be used for subsequent refinement. The initial result of projection matching usually resembles the starting model, but after a few rounds of refinement the new features of the data set should become stronger. However, if the relationship between model structure and data is not well established, the possibility of reference bias needs to be carefully checked.

Conversely, EM maps can be used as molecular replacement models to phase X-ray structures.^163−165 For this approach, there must be overlap in resolution ranges between the EM and X-ray data. So far, phasing from EM has mainly been used with large complexes or viruses for which it is difficult to obtain heavy-metal derivatives.

7. 3D Reconstruction

In EM, we are dealing with 2D images that can be considered as 2D projections of the 3D electron potential of the specimen, after restoration of the image information by CTF correction. Several alternative approaches have been developed for reconstruction of a 3D object from its projections.(166) These methods fall into two major groups. Methods that perform the reconstruction in real space include back-projection and algebraic methods. In the other group, the reconstruction is done in Fourier space. The current trend is toward automation of all of the image processing steps, from particle picking to 3D reconstruction.(167) For icosahedral particles, which are easier to process because of their shape and their high symmetry, the reconstruction steps are more readily automated.^168,169

7.1. Real-Space Methods

The Austrian mathematician Johann Radon demonstrated in 1917 that an N-dimensional function can be restored from its integrals over the continuum of straight lines, which represent its one-dimensional projections.(153) The continuous set of line projections is known as the Radon transform of the N-dimensional function. 2D sections of Radon transforms (sinograms) are used in orientation determination (see section 5). The inverse of the complete (N-dimensional) Radon transform defines the distribution of densities of the object. However, there are difficulties in numerical implementation of the inverse Radon transform for structural analysis, and several other implementations are used to approximate this transform.

7.1.1. Back Projection

The digital projection P_l^α at angle α of a two-dimensional function is the sum of densities along one pixel wide parallel rays (Figure 24a):

where i and j are the object pixel indices, k is the projection pixel index, and δ(1_k – L⃗·r⃗_i,j) is a line (or plane) over which the summation is performed, L⃗ is a unit vector that defines the projection direction at angle α, and l_k is the projection coordinate. Back-projection works by stretching the projection back over the volume (array) to be reconstructed along the projection direction. Pixels of a projection being stretched form lines that are called ray sums (RS). An estimate of the density in a given pixel of the reconstruction with coordinates i,j is the sum of all RSs that pass through that pixel (Figure 24b). However, this simple technique does not accurately reconstruct the original object; details are smeared over some distance or surrounded by a halo (Figure 24C and D). These distortions arise because the reconstruction is convoluted with a broad PSF, which has a falloff of 1/r in 2D and 1/r² in 3D space:

or where ⊗ is the convolution operator and r⃗ is the real space vector.^124,170

Figure 24.

Back-projection algorithm. (a) Projections P_l^α1, P_l^α2, and P_l^α3 are obtained experimentally from an object containing two dots of different density. α1, α2, and α3 are the angles of the different projection directions, and L_α1, L_α2, and L_α3 are the unit vectors of the corresponding projection directions (eq 20). (b) Back projection is done by stretching projections back through the area to be reconstructed along the original projection directions, or in other words by creating rays of pixels with the density of the corresponding projection pixel. This is shown as light and dark gray lines from projections 1, 2, and 3. The rays are summed in the reconstructed area, providing information on the dot positions. (c) The more projections that are used, the better defined are the dots. (d) An artifact of the technique is that each point is surrounded by a background halo. The intensity of the halo is proportional to the density of the dot.

7.1.2. Filtered Back-Projection or Convolution Methods

Filtered back-projection is a modified version of the back-projection algorithm, which corrects for the blurring introduced by the PSF function mentioned in section 7.1.1 (Figure 25). The operation can be performed in either real or Fourier space. In Fourier space, the correction is achieved by applying a filter corresponding to the inverse of the PSF. For 1/r, this function is proportional to the spatial frequency and is called a ramp filter.

Figure 25.

Filtered back projection. The original object contains two dots of different densities. The upper panel represents reconstructions by back projection of these dots using 7, 15, 45, and 180 projections, respectively. Although the radial streaks are eliminated by using more projections, this method leaves a halo around the reconstructed dots. The bottom panels show reconstructions from the same projections using filtering. Reduction of the halo is most pronounced on the reconstructions with more projections.

A variety of filters can be used in real space. One type of filter used for correcting back projection is the Laplace operator, which is applied to the projections for prefiltering. These reconstruction algorithms are based on functions that approximate the inverse Radon transform; they perform back-projection reconstruction on the preprocessed projections.^171−173 The preprocessing modifies the projections using window (apodizing) functions (Hamming window), which are equal to zero outside a chosen distance interval and enhance the signal within the interval.(170) In some packages, the filtering is performed in 3D space on the reconstruction obtained by back-projection.

Filter characteristics in addition to the 1/r term depend on the distribution of projections and their noise level, as well as the symmetry of the object.^149,174,175 Most published filter functions have been derived analytically from theoretical considerations.^170,173

7.1.3. Algebraic Methods

The development of algebraic methods has been stimulated by medical tomography. In this case, reconstruction of the 3D object is based on determination of successive planar slices of the object (patient), so that the problem is reduced to a set of 2D reconstructions from 1D projections. We will explain the methods in 2D space, because the concept of reconstruction can be easily extended to 3D space.

This technique requires that the object is described by a positive function over a finite region (the object is of limited size) and can be represented as a digital I × J array of densities. An element of the array with coordinates i, j is the pixel ρ_i,j. The projection P_l^α is defined as in eq 20:

where i = 1, 2, ..., I; j = 1, 2, ..., J; = 1, 2, ..., L.

Equation 22 is linear, with I unknowns. For M projections, there will be L × M linear equations. Solution of the complete set of equations would give the reconstruction of the object. The problem arises from the fact that a number of unknowns I × J (the size of the array {ρ(r⃗_i,j)}) can be larger than number of equations in the set (L·M), and that the number of unknowns increases dramatically with image dimensions. If L × M < I × J, the set of equations can have more than one solution. Moreover, in reality, projections may not be consistent with each other because of noise. Even for an image of 50 × 50 pixels, the number of variables to be determined is 2500 in the 2D case and grows to 625 000 in 3D space. In practice, the images are bigger than this, so that direct solution of the equation set becomes unfeasible. Therefore, alternative approaches are needed, based on reasonable approximation of the object rather than on exact solution.

In algebraic techniques, the value of ρ_i,j can be estimated as the sum of all RSs from M projections P_l^αm that intersect at the point (i,j), multiplied by a weighting factor, where each RS is one pixel wide.

where passes through (i,j)th pixel. The weight factor W_i,j^m represents the contribution of the (i,j)th pixel to the th RS. The whole problem can be described as minimization of the differences between original (measured) and calculated projections:

Various algebraic techniques use different criteria to estimate these errors and to apply corrections. They can be subdivided into four groups: ART, algebraic reconstruction technique;(176) SIRT,(177) simultaneous iterative reconstruction technique; SART, simultaneous algebraic reconstruction technique;(177) and RMLE, relaxation methods for linear equations.^170,178,179

7.1.3.1. Algebraic Reconstruction Technique

In ART, the initial array (the first approximation) is blank: ρ_i,j = 0, and eq 24 is solved iteratively:

where R^k denotes the kth approximation (R^k=0 = 0); P_measured^αm is the measured mth projection, and P_{calculated^αm} is the calculated projection in the same direction; and W is the weight matrix. Corrections are made after adding each successive projection.(180)

This is a simple method, but the result depends on the starting projection. The process may become unstable because of amplification of inconsistencies in noisy projections. Different implementations of ART vary in weighting matrix specification and using additional constraints such as density thresholding and zero density outside of the object. There is a version of multiplicative ART in which the initial approximation is defined as R^k=0 = ρ_i,j = 1, and

7.1.3.2. Simultaneous Iterative Reconstruction

As in additive ART, one can start with a blank (zero) reconstruction, or with R^k=0 = 1 if the multiplicative correction approach is used. The main distinction between ART and SIRT techniques is in how the reconstruction correction is performed in an iteration step: in ART, differences between the currently used projection and corresponding reprojection are calculated, and the current reconstruction R^k (calculated on the basis of the limited set of projections used so far) is immediately modified; in SIRT, all projections are used to create the current reconstruction R^k before calculating reprojections and corresponding differences are used to calculate an overall corrective matrix for the next iteration:

where A and B are weighting parameters.(181) Results of SIRT do not depend on the starting projection. Although SIRT converges more slowly than ART, it produces better results.(182)

7.1.3.3. Simultaneous Algebraic Reconstruction

This approach combines the best features of ART and SIRT. The technique, introduced by Andersen and Kak,(183) uses bilinear interpolation for the reconstruction and projection steps and restricts the area of reconstruction to a circle (sphere in 3D). This restriction simplifies the weighting scheme of projections: partial weights are assigned only to the individual RS points that intersect with the circle covering the area of reconstruction; inside the circle, the RSs are used with full weight, while weights are set to zero outside of that area. To further reduce the noise resulting from unavoidable inconsistencies with real projection data, the correction terms are simultaneously applied for all of the rays in one projection as in SIRT. In SART, reconstructions are obtained by bilinear interpolation.

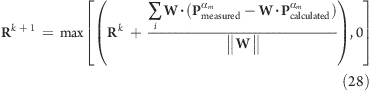Another implementation of the algebraic technique is RMLE, or relaxation methods for linear equations. This method applies additional constraints depending on the object data types and uses any a priori information on the object, such as positive density in the object, density thresholds, and location of the object. Such additional constraints improve the convergence of iterative approaches (see details in ref (170)).

7.2. Fourier Methods

7.2.1. Fourier Inversion

Intuitively, Fourier methods are very close to X-ray or electron crystallography, where data are collected to fill Fourier space so that the inverse Fourier transform generates the 3D map of the object in real space.^184,185 In single-particle analysis, the inverse Fourier approach is based on the theorem that a projection of an object corresponds to the central section of the FT of that object (central section theorem, Figure 21). FTs of particle images yield a set of central sections in the corresponding directions. These sections are part of the 3D object FT, but the information is incomplete and must be rebuilt by interpolation between the sections. The inverse transform will then reproduce the electron density distribution of the object. Symmetry of the object allows for better and more even sampling of the object FT with fewer images. Inverse Fourier techniques were the first methods used for 3D reconstruction.^186−188

7.2.2. Fourier–Bessel Reconstruction

A modified version of the inverse Fourier approach has been extensively used in the analysis of complexes with helical or icosahedral symmetry. The advantage of helical or icosahedral particles is in their high symmetry, which means that each image is equivalent to many symmetry-related projections. The number of related projections depends on the symmetry of the complex. Thus, one image of an icosahedral structure corresponds to 59 other symmetry-related views, while for helical symmetry the number of equivalent views is defined by the number of particles per helical repeat and the length of the helix. In the ideal situation, a single image of a helix provides sufficient views of the asymmetric unit to obtain a 3D reconstruction.^145,189,190

If the molecular complex has rotational or helical symmetry, its density distribution is conveniently described in cylindrical polar coordinates. In this case, the Fourier transform of the object can be expressed as a Fourier–Bessel transform. The advantage of using polar coordinates in Fourier space (Bessel functions) is that the dimensionality of the transform can be reduced to a set of Z-planes (normal to the helical axis) each containing concentric rings of different radii, thus reducing the interpolation to just one dimension (Figure 26a and b; for details see ref (145)). EM images of helical structures provide only restricted sampling of the amplitudes and phases along these rings because of the limited number of projections, and helical symmetry is used to determine cylindrical functions G_n that define 3D FT of the complex. Once the 3D FT is filled, the inverse can be computed to obtain the 3D reconstruction of the complex.(145)

Figure 26.

Fourier Bessel reconstruction. (a) A helical structure with a sinusoidal density profile of pitch P. (b) The Fourier transform of the helix (a) constitutes two planes on which the amplitudes are represented as concentric rings with phases alternating between 0° and 180°. The amplitudes of the rings are described by Bessel functions. (c) Reconstruction of a microtubule complexed with the kinesin-5 motor at a resolution 9 Å. Enlargement of the boxed area shows the fit of the X-ray structure into the EM map. Parts (a) and (b) are based on earlier figures by Moody.(19) Part (c) is reproduced with permission from ref (197). Copyright 2010 Elsevier Inc.

Helical bacteriophage tails were the first structures to be reconstructed in 3D from EM images.(187) The methods remain important due to the large number of helical polymers found in biology. Unfortunately, in reality most helical assemblies are flexible and distorted, which restricts the application of Fourier–Bessel methods. Early approaches to overcome this problem involved the straightening of bent helices,^191−193 but a more effective solution was subsequently suggested using the single-particle approach. The image of the helical object is divided into short, overlapping segments, which are aligned as separate images relative to reference projections calculated from a model, followed by reconstruction. In an approach developed by Egelman,(194) the helical parameters and the quality of the reconstruction are assessed by minimization of differences between symmetry-related elements in the reconstruction. The density differences are assessed for a range of axial rise and azimuthal rotation values. The best parameters are used to create a model for further iterations of projection matching. In addition to local disorder, some helical structures such as microtubules have a break (seam) in the packing of their constituent protofilaments, leading to breakdown in helical symmetry. Ruby-Helix software developed by Kikkawa enables the analysis of such asymmetric helices by assessment of distortions in the diffraction phases caused by the seam^195−197 (Figure 26c). Successful application of the new methods in studies of helical viruses, actin filaments, pili, and other biological polymers revealed a variety of possible distortions present in these structures, highlighting the need for further development of the techniques to improve the resolution.

7.3. Distribution of Projections

The quality of the reconstruction depends not only on the image quality and implementation of the algorithms, but also on the angular distribution of projections. In principle, reconstruction methods assume that there are an infinite number of projections that are evenly distributed around the Euler sphere. The Euler sphere is an imaginary sphere whose origin is at the center of mass of the object. The intersection of a projection direction with the sphere defines a point on its surface that denotes the projection orientation (Figure 27a). The distribution of these points demonstrates the distribution in angular space of projections of the object under study (Figure 27b). Orlov(174) demonstrated that a reconstruction of an object can be obtained with isotropic resolution if the set of projections is distributed along any curve connecting opposite poles of the Euler sphere. Nonetheless, this condition assumes an infinite number of projections along such curves. Unfortunately, even under cryo conditions, biomolecular complexes often display preferred orientations, so that the projections are unevenly distributed in space and the condition required for complete reconstruction is not satisfied. In this case, the resolution becomes anisotropic due to the absence of information in certain directions. Examples are complexes with strongly charged or hydrophobic surface regions that adsorb to the air–water interface, or flat complexes adsorbed to a support film, resulting in preferred orientation in cryo-EM.(99)

Figure 27.

Euler sphere and distribution of projections. (a) The Euler sphere is an imaginary sphere of unit radius with the object located at its center. The points on its surface represent view directions of the object. A projection direction is shown by the vector from the center to the viewpoint on the sphere surface, so the angles of the projection are described by the vector direction. In this figure, the angle convention is as in IMAGIC α, β, and γ, corresponding to SPIDER angles ψ, θ, and φ, with ψ = 90° – α; θ = β; φ = γ – 90°. (b) An example of the angle distribution of a single-particle data set on the Euler sphere shown in elliptical (Mollweide) projection. This representation shows the angle of projection directions relative to the z axis (β angle) and around it (γ angle), but the rotation in the image plane is not shown. These figures are normally used to examine the angular distribution of images used for reconstruction, to assess the uniformity of spatial coverage in the data set.

7.4. Electron Crystallography

Important work in the development of high-resolution EM of biological samples used electron crystallography of 2D crystals.(198) This method was pioneered by Unwin and Henderson(55) in the first direct demonstration of α-helical densities in a membrane protein. The structure of bacteriorhodopsin was subsequently determined by electron crystallography to 3.5 Å(199) and then 3 Å resolution.(200) These results stimulated the development of molecular structure determination methods in EM.(201) The basic idea of electron crystallography is very similar to X-ray crystallography but has the advantages that the phases are determined from the images of crystals and that lattice distortions can be corrected in the images. Because the crystal lattice has only one or two layers, its scattering is continuous along the direction perpendicular to the crystal plane. Therefore, the diffraction spots are extended into lattice lines. Either images or electron diffraction patterns can be collected from 2D crystals. To fill in the 3D information, the lattice lines are sampled at different heights by collecting data at different tilt angles^55,202 (Figure 28). The electron diffraction pattern intensities are not affected by the CTF of the microscope, but CTF-corrected images provide the phases of the reflections.

Figure 28.

Electron crystallography. (a) Schematic diagram of lattice lines from a 2D crystal and their intersection with a tilted plane of data. Adapted from ref (198). Copyright 1982 Pergamon Press. (b) 3D electron diffraction pattern of a tubulin crystal. Plane A shows the untilted electron diffraction pattern, and planes B and C restore the lattice lines from the tilt series. The missing wedge can be seen on plane C (dashed lines). Unit vectors h and k indicate the position of the origin. Part (b) is reproduced with permission from ref (202). Copyright 2010 Elsevier Inc.

Typically both electron diffraction patterns and images from 2D crystals are collected from crystals tilted relative to the incident electron beam. However, the EM grid cannot be tilted more than ∼70° because the bars of the support grid obstruct the beam and also because the sample becomes too thick along the beam direction. Restriction to ±70° means that information is missing along the z-axis, normal to the plane of the crystal. This “missing wedge” of information results in an anisotropic PSF that is elongated in the z direction. The resulting 3D density map is distorted by convolution of the original structure with the PSF. If the tilt data are collected from crystals in arbitrary orientations on the grid, the missing wedge is reduced to a missing cone. The influence of the anisotropic PSF (missing cone) depends on the individual structural features and orientation of the protein in the crystal. In bacteriorhodopsin(199) and most other α-helical membrane proteins, the helices are mainly parallel to the z (vertical) axis, so they are not greatly distorted by the PSF. However, structural elements with orientations parallel to the plane of the crystal will be more poorly resolved.

There are some problems in common with X-ray crystallography, notably that crystal disorder reduces the resolution of the electron density map. Because the crystals are two-dimensional, they are easily bent and distorted during EM specimen preparation. Small distortions can be computationally corrected by “unbending” based on the correlation map between a small crystalline patch and the whole crystal. Deviations of the correlation peak positions from those of a perfect crystallographic lattice show how the unit cells must be moved back to recreate the perfect lattice. The FT of the corrected lattice provides better defined reflections with more accurate phases.

Combination of reflection amplitudes from electron diffraction and phases from the images permits restoration of the FT of the crystal in 3D. The inverse FT generates the 3D structure of the unit cell. The technique is benefiting from software development and automated data collection.^203,204 One of the best results obtained by electron diffraction of a biological specimen is the 1.9 Å resolution structure of lens-specific aquaporin-0 (AQP0), a water channel forming junctions between lens fiber cells.(58) The structure reveals details of the distribution of lipids around the aquaporin tetramers.

7.5. Tomographic Reconstruction

Electron tomography is used for 3D analysis of individual, large structures such as single cells or their components.^7,20 The principle is the same as in medical tomography, in which the sections of a patient’s body are reconstructed slice by slice from images collected at different angles. Accordingly, the word “tomography” originates from two Greek words: “tomos” meaning “to slice”, and “graph” meaning “image”. Electron tomography also has some features in common with electron crystallography, in which the samples are tilted around axes perpendicular to the electron beam. For specimens with the typical slab geometry, the longer path length of the beam through the sample at high tilt and technical constraints in tilting range of specimen holders imposes a limitation on maximum tilt angle, so that part of space is not sampled. Consequently, there is a “missing wedge” in the data. This wedge (or pyramid for dual-tilt tomography) results in worse resolution in the “vertical” (incident electron beam) direction (Figure 17).

The resolution achievable in cryo-tomographic reconstruction is limited by radiation damage. The total dose is the main factor defining the quality of the reconstruction, but the dose per image in a tilt series must be sufficiently high to allow accurate alignment of images in the series.^52,205 Another limitation in electron tomography is the deterioration of image quality at high tilt, due to the increased electron path length mentioned above. This increases electron scattering by the sample, in particular inelastic scattering, which reduces image intensity and contrast. Longer exposure times can compensate for lower contrast at high tilt, but this increases the dose per image and consequently the radiation damage.(52)

Although there are several programs for automated tilt series data collection, the raw images collected are not perfectly aligned relative to each other. Therefore, as in single-particle image processing, these images must be accurately aligned before proceeding to 3D reconstruction. Image alignment in tomography is performed in real space using cross-correlation and fiducial markers.^6,105 Projection matching can be used for refinement.(102) The images are usually aligned starting from low tilt angles, and the alignment progressively includes higher tilts. Because EM images correspond essentially to 2D projections of the object along the electron beam, the images collected from the same area at different tilt angles correspond to the set of object projections at different but known orientations. Once the images are aligned within a tilt series, a 3D reconstruction of the object can be readily obtained using back projection or algebraic techniques.^6,7,102

Recent developments have extended the applicability of cryo-electron tomography and have led to improvements in data processing. In addition to large, irregular assemblies such as Herpes simplex virus and subcellular organelles, cell and tissue sections can be imaged in the vitreous state (see section 2.1.3). If multiple copies of a structure are present in the reconstructed volume, subtomogram averaging (described in section 4.4.2) can be used to improve SNR and, if the structure is present in different orientations, to fill in the missing wedge, thus improving the resolution of the averaged volumes.

CTF correction is difficult in tomograms, because the very low dose in each tilt view does not give sufficient signal to measure the Thon rings, and also because the defocus varies across tilted images. Nevertheless, several approaches have been developed, such as correcting in bands parallel to the tilt axis, where the width of the band decreases with increasing tilt angle,^{102,151,206,207} and two approaches have been compared for estimating the defocus in a tilt series: correcting by the average defocus of the whole tilt series, or determining defocus from the very small changes in magnification caused by changes in defocus.

8. Evaluation of Reconstruction Quality and Reliability

It is not straightforward to verify that a single-particle reconstruction is correct and then to evaluate its resolution. There are examples in the literature of different maps of the same object. The match between input images and reprojections is necessary but not sufficient to ensure that the map is correct. It is also essential that the class members resemble the class averages and that the characteristic views are recognizable in the raw data. Note that resolution can be very anisotropic, especially with tilt data, and that it can vary between different regions of a structure. For example, rigid regions will be more accurately represented than flexible ones, and peripheral regions will be more affected by orientation errors than central ones.

To evaluate map reliability, an approach somewhat equivalent to the free R factor in crystallography has been proposed. The idea is to collect some tilt pairs, with relatively low tilt (10–30°), and to determine the particle orientations by projection matching to the final map.(208) This procedure provides a check on the consistency of the map with independent data, and allows for hand determination, but can be very difficult at low resolution if the structure does not have strongly asymmetric features.

The point-to-point resolution of an image is defined by the minimum distance between two distinguishable density maxima. However, the accuracy of locating the center of mass of a density maximum is 3–5 times better than the point to point resolution (Figure 29). If the map shows features of secondary structure, its correctness can be verified by fitting of components with known atomic structures.

Figure 29.

Resolution definition by separation of features. (a) When two points are far apart, there is a deep trough of density between them. (b) Two points are regarded as just resolved when the peak of one point spread function overlaps the first minimum of the other (Rayleigh criterion), see ref (60). (c) The point spread functions of two dots close together overlap to form one maximum, so that the points are not resolved.

8.1. Causes of Resolution Loss

Structure information can be lost or distorted at all stages of the data collection and analysis, depending on instrumentation, experimental, and computational skills. Poor electron optical alignment, drift, detector noise, magnification variations, inaccurate defocus determination, errors in alignment, sample heterogeneity, flexibility, incomplete angular coverage, and radiation damage can all combine to give dramatic falloff of the high-resolution information.^10,208,209 Inaccuracy of alignment leads to the blurring of each point in the image, which can be described by as a point spread function (PSF) with a Gaussian distribution. Better alignment leads to a sharper PSF. Conversely, a broad PSF leads to errors in determination of angular orientations and slows the refinement procedure, increasing the number of iterations in the alignment–reconstruction loop.

8.2. Resolution Measures

The measurement of resolution should quantify the level of reliable detail detectable in the final map. In practice, the detectability of features at a given resolution is determined by the SNR in that frequency range of the data. To quantify resolution, the SNR must be estimated as a function of spatial frequency. With crystallographic data, the signal is concentrated in diffraction peaks, whereas the noise is distributed continuously over reciprocal space. Therefore, the SNR in any given frequency range is readily estimated by comparing the diffraction peak to the surrounding region, and the resolution is determined by the spatial frequency of the highest resolution diffraction peaks clearly detectable (typically 3× higher) over background noise.

In single-particle and tomography data, both signal and noise are distributed over the whole spectrum, and there is no simple way to estimate the resolution. The most widely used method for determining the resolution of a single-particle reconstruction is Fourier ring (in 2D) or Fourier shell correlation (FSC).^210,211 The data set is split into two equivalent halves, usually by separating odd- and even-numbered images from the data stack. Separate reconstructions are calculated from the two halves, and their 3D FTs (F₁, F₂) are compared by cross-correlation in spatial frequency shells (k, Δk). The average correlation for each shell is plotted and typically shows a falloff from a correlation of 1 at low resolution down to 0 at high resolution.

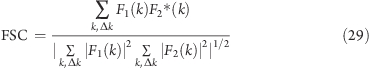The spatial frequency at 0.5 correlation is commonly taken as the resolution estimate, but other criteria, for example, comparison to the noise level, or 0.143 have been proposed on the basis of SNR estimates.^208,211 Systematic errors that affect both halves of the data set equally will not be detected in the FSC, which will therefore be overoptimistic. If a sharp-edged mask is used around the maps, or if noise becomes correlated with the signal during refinement,(122) spurious high-resolution correlation can be generated, so that the correlation falls to a minimum and then rises again at high resolution, reflecting good correlation between the masks applied to the reconstructions. The FSC can be derived from the SNR from the relationship between SNR and the cross correlation (CC).(212)

Another method, first proposed for 2D averages and subsequently extended to 3D structures, is the spectral signal-to-noise ratio (SSNR).^213−215 In this case, the signal is estimated to be the reprojections of the map, and the noise is estimated by taking the difference between input images and the corresponding reprojections. This approach does not require the data set to be divided into halves. Like the FSC, the SSNR requires the aligned input images. It should be noted that a good resolution value does not guarantee that the map is correct.

For resolution assessment of tomograms, Cardone et al. proposed two methods.(216) The simpler method is directly equivalent to the single-particle FSC, using tomograms calculated from even and odd projections. A more accurate method that is computationally more expensive is based on averaging a series of Fourier ring correlations between a given projection and the corresponding reprojection of the tomogram calculated from all of the other projections.

A further method has been proposed, R-measure.(217) It does not require the input data, but uses the final map itself, along with the surrounding region of the reconstruction outside the particle, for the resolution estimation. This method examines the correlations between adjacent pixels in the FT of the reconstruction. For a map containing pure noise, adjacent transform pixels are uncorrelated. Background masking introduces such correlations, which can be predicted, and the structure itself introduces further correlations. From these correlations and from an estimate of the noise measured on the region surrounding the particle, the FSC curve can be predicted without access to the input data. This is clearly an advantage, but requires the map to be provided without tight masking of the structure.

Although these various criteria are available, most work currently uses the 0.5 FSC criterion. What matters is not a number, small or large, giving the resolution. The important thing is what the map shows. If α-helices are resolved, the resolution must be better than ∼9 Å. β-Strands require it to be better than 4.5 Å. Moreover, there are many examples in the literature of much lower resolution maps that give important biological insights.

8.3. Temperature Factor and Amplitude Scaling (Sharpening)

Advances in single-particle analysis mean that cryo EM structures increasingly reach subnanometer resolutions, revealing not only domain organization of molecular complexes but also their secondary structural elements. It is therefore important that cryo EM maps show the features necessary for interpretation of these structural elements. Methods of alignment, averaging, and reconstruction usually result in overweighting of the low-resolution information. Consequently, the fine details in the map are obscured. The loss of details can be described by the temperature factor, or B-factor, which represents the loss of signal with resolution as the smearing out of atoms by thermal vibrations. The falloff of signal with reciprocal spacing can be described by a plot of ln F against 1/r², where F is the spherically averaged scattering amplitude and r is the real space coordinate.(208) The curve is linear at low spatial frequencies, and its slope is proportional to the radius of gyration of the scattering object (the Guinier region in small angle scattering). It is a standard procedure to make the high-frequency details more visible by scaling the experimental maps either by applying a filter to reduce the contribution of low frequency components or by rescaling the amplitude decay according to the amplitude spectrum of a reference atomic structure, effectively sharpening the map. This correction has been done by using X-ray solution scattering curves to scale the Fourier amplitudes computed from the EM reconstruction.^218,219 Amplitude scaling can therefore uncover fine details in the structure. This change in scaling of the FT amplitudes does not affect the measured resolution of the structure, but its effects can be observed by examining the rotationally averaged power spectrum of the map. Figure 30 shows an example comparing an EM map of TMV before and after amplitude scaling and sharpening.

Figure 30.

Effects of full CTF correction and amplitude scaling on the appearance and resolution of an EM map of TMV. (a) Surface view and two orthogonal central sections of an EM map of TMV, with the fitted atomic structure shown on the sections (ref (23)). (b) Enlargement of the boxed region in (a), of a map obtained only with phase correction but not amplitude correction or scaling. (c) The same map region after full amplitude correction. (d) The map region after full amplitude correction and B-factor scaling. (e) Rotationally averaged power spectra of the maps with phase correction (blue), amplitude and phase correction (red), of a map calculated from the atomic structure fit (green), and of the fully corrected and B-factor scaled map (purple). (f) FSC curves for the phase and amplitude corrected maps, colored as in (e). Reproduced with permission from ref (83). Copyright 2010 Elsevier Inc.

9. Heterogeneity in 2D and 3D

9.1. Sources of Heterogeneity

The resolution of macromolecular structure determination by cryo EM is more often limited by conformational variation of the structure than by problems with microscopy or image processing. Images of a biological complex in solution will reflect the different states of the complex captured during vitrification.(220) Sample heterogeneity can arise from several sources: (i) partial occupancy of a ligand in a molecular complex,(221) (ii) structural dynamics that is reflected in a few distinct reaction states or by a gradual transformation through intermediate states,^222−225 and (iii) multiple oligomeric states of different symmetry and/or size.^30,226 Ideally, distinct conformations should be trapped biochemically before EM imaging (e.g., ref (223)), but in many cases this is not possible.

9.2. Methods for Computational Sorting of Mixed Structures

Three main approaches have been developed for computational separation of mixed structures(220) (Figure 31). In the first category, recognition of heterogeneity and initial sorting are done in 2D only, prior to any 3D reconstruction. This “a priori” group of methods is based primarily on MSA of features in the 2D images to detect structural variations and discriminate them from orientation differences. The images are sorted according to their major variations, which are reflected in the low order eigenimages. To separate images with variable occupancy of a substrate, two stages of MSA and classification can be used. In the first step, images are separated according to features showing global variance due to orientation differences, while the second classification is based on localized differences induced by substrate binding. These steps do not require angular orientation determination, so the technique is independent of any initial 3D model. The technique was shown to discriminate overall size variations as small as 5%.^226,227 This approach has been used to separate ribosome–EF-G complexes and chaperonin–substrate complexes^228,229 (Figure 32).

Figure 31.

Three main approaches currently used to identify and sort molecular heterogeneity. The first approach (left panel) is based on statistical analysis of 2D images (a priori analysis) to detect the heterogeneity of the sample in its images. The initial sorting is done prior to any 3D reconstruction. The second approach (middle panel) requires an initial 3D map to separate the images into subsets according to their orientation. Analysis of structural heterogeneity is done in 2D for each orientation subset. The third method (a posteriori analysis) is based on examination of variations in multiple 3D maps (right panel). Reproduced with permission from ref (220). Copyright 2010 Elsevier Inc.

Figure 32.

Statistical analysis to detect variable ligand occupancy. A model data set with variable ligand occupancy, simplified to show only one orientation (a), and the corresponding eigenimages (b). The first eigenimage is the sum of all images. The area corresponding to the ligand has density proportional to the occupancy (50%) of the ligand in the complex. The second eigenimage shows a very dark spot located in the area of the ligand. This feature reflects the major variation present in the data set. The remaining eigenimages reflect variations related to noise in the images. (c) Real eigenimages from a data set of GroEL with variable binding of non-native malate dehydrogenase. Eigenimages 2 and 3 show variations mainly related to different orientations around the rotation axis. Eigenimage 4 indicates small variations in tilt around a horizontal axis. Eigenimages 5–8 mainly reveal variations related to occupancy and location of the ligand in the complex (arrows). Reproduced with permission from ref (229). Copyright 2007 Elsevier Inc.

In the second category of sorting methods, an initial 3D map is required to separate the images into subsets containing images of a molecular complex in similar orientations. Analysis of heterogeneity is then done in 2D for each image subset. This minimizes orientation variation within classes, and as a result facilitates recognition of conformational variations. The approach has been applied to the reconstruction of heterogeneous ribosome complexes^224,230 and to icosahedral viruses with symmetry mismatches or partial occupancy of some components.(231)

The third category is based on a posteriori analysis of 3D reconstructions by considering a population (as many as possible) of 3D reconstructions to determine the variance in 3D. Many 3D maps are reconstructed for the variance analysis; the most representative ones are then used as initial models for refinement. In the so-called “bootstrap” technique,^232,233 3D maps are calculated from randomly selected subsets of images whose spatial orientations were determined by projection matching to an initial 3D map. The evaluation of variance in the resulting 3D maps and localization of regions with high variance allows assessment of the heterogeneity, and estimation of covariance in the population enables classification of 3D maps. Once the region of major variation is localized in the 3D maps and in the corresponding 2D projections, images are sorted into subgroups according to average pixel density in the high variance region.(232) Another idea is the maximum likelihood-based classification of 3D maps that identifies conformational variability within the maps and then separates the different molecular states.(143)

10. Map Interpretation

10.1. Analysis of Map Features

Once the map of a new structure is obtained, it should be possible to estimate the molecular mass and oligomeric state, in conjunction with other biochemical and biophysical data on the sample. The map should be examined at a contour level that encloses the approximate molecular mass. Mass measurements by scanning transmission EM can be very useful for interpretation, although access to specialized scanning transmission EM facilities is limited. The map, normally contoured at 1 σ, should show continuous density well above background noise (obviously checked before masking) because disconnected pieces of density would not make sense for a single complex. Density sections of the map should be viewed in gray scale representation, to check for inconsistencies such as regions of anomalously high density, which would not be noticed in an isosurface representation.

With a map at 4 Å resolution or better, it may be possible to build an atomic model with the methods used in X-ray crystallography(15) (Figure 33). In the case of EM, the density is fully determined (assuming sufficient angular sampling) from the recorded images, which contain both amplitude and phase information. Therefore, an important difference between model building in crystallography and in EM is that the atomic model is not required to refine the EM map. For tomograms of cells or subcellular structures, segmentation is used to identify substructures such as membranes and cytoskeletal elements.

Figure 33.

High-resolution single-particle EM of Aquarheovirus. (a) Raw images of viruses in vitreous ice. (b) 3D reconstruction colored according to radius. (c) Structure of subunit VP5 with the backbone model and enlargement to show side-chain detail. Reproduced with permission from ref (15). Copyright 2010 Elsevier Inc.

10.2. Atomic Structure Fitting

Docking of known or related atomic structures of components into the EM map of an assembly is the main tool for interpretation.^234−236 Most single-particle maps are in the 7–30 Å resolution range, so that they cannot be independently interpreted in terms of molecular structure. In this resolution range, it is not possible to build atomic structures, nor is it always possible to unambiguously identify the positions of known domains. In the low resolution range (20–30 Å), large domains may be recognizable by their shapes. In the 6–9 Å resolution range, α-helical secondary structures are resolved. The individual β-strands are seen with a resolution beyond 4.5 Å. Side-chain detail is only present in exceptionally high-resolution structures, such as the aquareovirus particle shown in Figure 33, but docking into lower resolution density maps often provides good predictive value for probing mechanisms and designing mutants.

Over the whole resolution range, map interpretation is almost always facilitated by the availability of known or related atomic structures for components that can be used for fitting (Figure 34). The basic principle of fitting is density correlation. A target density map is calculated from the atomic structure, at the same resolution as the EM map, and a cross correlation search in 3D is used to align the two densities. The search can be done in either real or reciprocal space. For a small object being docked into a larger map, the method of local correlation was developed (section 4.3(128)), giving a more sensitive measure of fit. Even at modest resolution, if the subregion has an asymmetric shape, it may be possible to position the structure with an accuracy of a few angstroms. Fitting a set of small, separate subunits into a large map at low resolution is very difficult, unless information on subunit interfaces is available. Labeling experiments are very helpful if an accessible position can be identified for insertion of a binding site, for example, a unique cysteine for binding a derivatized gold particle, or fusion of a protein domain such as GFP. However, gold labels can bind nonspecifically or disassemble fragile complexes.

Figure 34.

Flexible fitting of the crystal structure of the N-terminal part of the human apopotosome (domains NBD, HD1, WHD, and HD2) into the corresponding segmented cryoEM map at 9.5 Å resolution (ref (239)). (a) Initial fit before adjustment of the structure. (b) Result of flexible fitting. Figure courtesy of Shujun Yuan.

Often there are hinge movements when molecules assemble into larger complexes, so that the original search object does not match the density as a rigid body. For this case, flexible fitting approaches are used (Figure 34).^{235,237−241} The molecules are allowed to bend in designated hinge regions, or multiple conformations are generated by normal-mode analysis and then used for fitting. For these methods, there is a danger of overinterpretation with unjustified details, especially with low resolution maps. If major refolding of the atomic structure is suggested, it is important to use biochemical or biophysical experiments to provide supporting data, for example, interatomic distance measures by spectroscopy or cross-linking. The more constraints are available, the more reliable is the final result.

10.3. Biological Implications

Ultimately, the most important questions are: Does the structure make sense? What new biological insight does it provide? With sufficient resolution, the structure can be used to predict effects of mutations or sites of potential cross-links, and these predictions can be tested in molecular biological experiments. 3D EM analysis increasingly forms a part of molecular and cell biology studies. The future prospect is to combine 3D information over the whole range, to understand the operation of macromolecular machines in cells and tissues. An example of a cryo-tomogram of a section of skin tissue, from which the intercellular desmosome junctions were extracted, aligned, and averaged to reveal the 3D density corresponding to cadherin molecules that could be fitted with an atomic model is shown in Figure 35.(242)

Figure 35.

From a section of skin tissue to molecular shape of cadherin. (a) Segmented, rendered image showing the different cellular components in the reconstructed tissue section. (b) Tomogram slice. D, desmosome; IF, intermediate filaments; Nu, nucleus; ER, endoplasmic reticulum; NE, nuclear envelope; Mi, mitochondrion. (c) Desmosome extracted from the area in the red dashed box in (b), with an inset of the averaged image. (d) Sub tomogram average with fitted cadherins. Reproduced with permission from ref (242). Copyright 2007 Macmillan Press.

With the concurrent progress in macromolecular crystallography, it is often possible to derive a pseudoatomic model of large assemblies by docking atomic structures of components into EM maps. Advances resulting from these hardware and software improvements are helping to reveal the mechanisms of operation of macromolecular machines by providing snapshots of their different functional states. The 3D EM field, following macromolecular crystallography, is maturing, with an international database of EM density maps (EMDatabank.org) linked to the PDB, currently containing over 1000 entries and growing steadily.

Biographies

Helen Saibil obtained her B.Sc. in Biophysics from McGill University in Montreal and Ph.D. at Kings College London. After postdoctoral grants at Kings College and at the Centre d’Etudes Nucleaires, Grenoble, followed by an academic post at Oxford University, she joined the Crystallography Department at Birkbeck College London, where she presently holds the Bernal Chair of Structural Biology. She has been elected as a Fellow of the Royal Society and a member of the European Molecular Biology Organization. Her research interests cover the actions of macromolecular machines such as molecular chaperones, involved in protein folding and misfolding, as well as protein refolding during membrane pore formation. She has built up a cryo-electron microscopy laboratory at Birkbeck, to study macromolecular complexes as well as cellular structures using single particle and tomography approaches.

Elena Orlova received her B.Sc. and M.Sc. in Physics from Moscow Physical-Technical University, and her Ph.D. degree in Physics and Mathematics from the Institute of Crystallography in Moscow. After working in the laboratories of Professors B. K. Vainshtain and N. A. Kiselev in Moscow, she worked in the laboratories of W. Chiu (Houston) and M. van Heel (Berlin and London). Presently, she is a professor at Birkbeck College (London). Her research interests are in structural analysis of biomacromolecular complexes using cryo electron microscopy imaging and in methods development. Her group has analyzed a range of different molecular complexes starting from symmetrical and asymmetrical huge viral assemblies to very small regulatory proteins such as the tumour suppressor p53.