Abstract
Severe burns are among the most common causes of death from unintentional injury. The induction and resolution of the burn-induced systemic inflammatory response are mediated by a network of factors and regulatory proteins. Numerous mechanisms operate simultaneously, thus requiring a systems level approach to characterize their overall impact. Towards this goal, we propose an in silico semi-mechanistic model of burn-induced systemic inflammation using liver specific gene expression from a rat burn model. Transcriptional responses are coupled with extracellular signals through a receptor mediated indirect response (IDR) and transit compartment model. The activation of the innate immune system in response to the burn stimulus involves the interaction between extracellular signals and critical receptors which triggers downstream signal transduction cascades leading to transcriptional changes. The resulting model consists of fifteen (15) coupled ordinary differential equations capturing key aspects of inflammation such as pro-inflammation, anti-inflammation and hypermetabolism. The model was then evaluated through a series of biologically relevant scenarios aiming at revealing the non-linear behavior of acute inflammation including: investigating the implication of effect of different severity of thermal injury; examining possible mechanistic dysregulation of IKK-NFκB system which may reflect secondary effects that lead to potential malfunction of the response; and exploring the outcome of administration of receptor antagonist or anti-body to significant cytokines.
Keywords: thermal injury, trauma, inflammation, hypermetabolism, modeling, liver, rat
Introduction
In the United States, over 1.2 million burn injuries are reported annually [1] and despite significant advances in patient care morbidity and mortality remain high in those patients [2; 3]. Responses to thermal injury are both local and systemic, involving cellular protection mechanisms, hypermetabolism, prolonged catabolism, organ dysfunction and immune-suppression [4]. Innate immune cell activation leads to the production and release of proinflammatory cytokines, which are proximal mediators of the systemic inflammatory response. Changes in energy expenditure following burn injury have been attributed to processes such as gluconeogenesis, ureagenesis, fatty acid synthesis and catabolism, processes relating to the need to compensate for the increased loss of body heat through the injured skin, as well as changes in the circulating levels of plasma proteins primarily synthesized in the liver [5].
Though much is known about the molecular and physiological pathways of the acute inflammatory response induced by thermal injury, this knowledge has not led to effective therapies. One reason may be that the complex nature of the response renders targeting isolated components an ineffective strategy [6]. Thus, the complex dynamics of burn-induced inflammation make appealing system, model-based, approaches that explore simultaneously multiple hypotheses for deciphering complex modes of action [7]. Therefore, it has been hypothesized that mathematical modeling may provide insights into the global dynamics of the inflammatory process [8].
A number of excellent prior studies [6; 8; 9; 10; 11] have placed significant emphasis on simulating inflammation based on the kinetics of well accepted constituents of the acute inflammatory response. A key feature in these models is the a priori postulation of particular components that are consistent with biological knowledge and play a major role in triggering the inflammatory response. Because such computational integration can offer significant insight on how such components interact, combinations of in silico and in vivo approaches are emerging as a viable analysis strategy [12].
However, how to identify representative biological features that can adequately represent the complex dynamics of a host undergoing an inflammatory response is a big challenge. Therefore, there is emphasis on reducing the complexity of the unified inflammatory response by identifying a limited number of time-dependent interactions of key elements that are highly sensitive to specific modes of initiation and modulation of the inflammatory response. Recently, we proposed a computational methodology which effectively decomposes the dynamics of the response from DNA microarray data into an elementary set that can serve as a surrogate for predicting the collective behavior of the system [13]. Based on this, we have proposed a model for endotoxin-induced systemic inflammation using an indirect response model (IDR) in Foteinou et al [14] which describes the dynamics of LPS-induced inflammation, as well as evaluates effectiveness of corticosteroid therapy under various treatment schedules establishing an in silico zone of therapeutic opportunity [15].
Despite the aforementioned advances no major efforts have been undertaken towards the development of dynamic models of burn-induced inflammation. It is therefore the aim of the present study to discuss a liver-specific physicochemical model of burn inflammation based on in vivo data. The focus on liver is driven by the fact that it is the organ that undertakes the burden of producing the majority of circulating cytokines in response to the thermal injury. We begin by extracting a critical set of liver-specific transcriptional signatures and then outline the development of a semi-mechanistic model of thermal injury- induced acute inflammation in rat liver that aims at coupling extracellular signals with essential transcriptional responses through a combination of receptor mediated indirect response (IDR) [16] and transit compartment [17] models. We hypothesize that the inflammatory response is activated when trauma-induced products are recognized by appropriate recognition receptors. Tumor necrosis factor-alpha (TNF) is a key product released following a cutaneous thermal injury [18] and is a key mediator of local and systemic inflammation [19; 20]. Thus, we assume that the circulating levels of TNF will act as a prototypical “invader” activating the inflammatory response. Our model describes the kinetic interaction between the ligand (TNF) and its signaling receptor (TNFR1) coupled with the activation of transcriptional factor (NFκB) which triggers the stimulation of expression of the essential transcriptional motifs identified through the analysis of the corresponding gene expression data. Based on the analysis of rat liver microarray data following burn injury, we hypothesize that the essential components include the early, intermediate and late pro-inflammatory responses associated with increased expression of proinflammatory cytokines and chemokines; the anti-inflammatory response that serves as the immuneregulation of the host defense system; and an anabolism response characterized by the increased expression of genes that participate in cell growth and metabolism. Such thermal injury-induced models could potentially emerge as critical enablers towards understanding the connectivity and relationship of the critical components in the innate immune system, which offers opportunities for unraveling the control mechanisms of the onset and resolution of systemic inflammation. The potential of our model is demonstrated by investigating the implications of varying the severity of the thermal injury; examining possible mechanistic dysregulation which may reflect secondary effects that lead to potential malfunction of the response leading to highly activated inflammation; and evaluating the impact of administration of receptor antagonists or antibodies of important cytokines.
Identification and Functional Characterization of Essential Transcriptional Responses
Rat Thermal Injury Model
Male Sprague-Dawley rats were subjected to a full skin thickness scald burn injury of the dorsum which is calculated to be ~20% of the rat’s total body surface area (TBSA) as previously described in [21]. Liver samples were obtained at 5 time points (0, 1, 4, 8 and 24 h post burn) and RNA extracted from liver samples was isolated and subsequently hybridized on an Affymetrix U34A GeneChip that had 8,799 probes represented on each chip. Thus the control for this experiment is the measurement labeled “Time 0” which was obtained prior to the thermal injury. The data are available with accession number GSE802 at the Gene Expression Omnibus (GEO).
Identification of Essential Transcriptional Responses
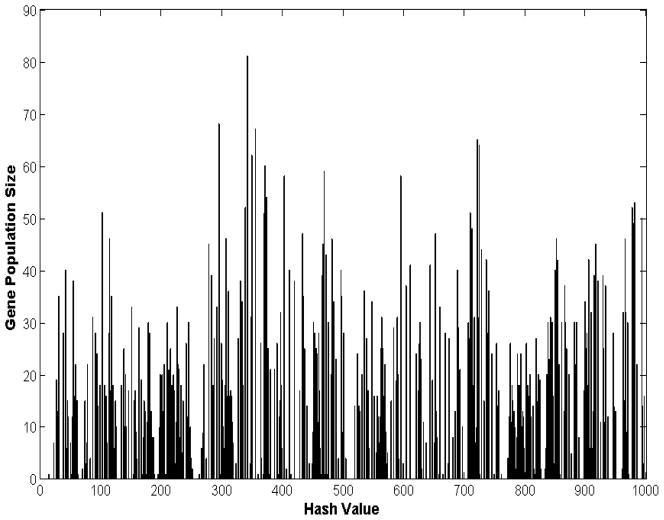
A 20% TBSA thermal injury to rats elicits a complex dynamic transcriptional response altering the expression level of numerous liver-specific genes. Our aim is to unravel a critical set of “informative” temporal responses that are characterized as the “blueprints” of the orchestrated dynamics of the perturbed biological system which will serve as surrogate for modeling. Based on our previous work, a micro-clustering approach is applied first, which is based on a symbolic transformation of time series data assigning a unique integer identifier (hash value) to each expression motif [13]. Hashing allows us to uniquely characterizing the overall dynamic response of each transcriptional profile through a single integer number. Expression motifs are composed of the probe sets which are very similar in shape and hashed to the same value. Therefore, the expression values of thousands of genes can be assigned to unique expression motifs. A distribution of motif values for all the available probes is produced by the symbolic transformation of the expression motifs and the subsequent assignment of hash values to each expression profile [13] as seen in Figure 1.
Figure 1.
Expression motifs of inflammatory transcriptional signatures in rat liver. 8,799 probe sets are micro-clustered to 492 expression motifs.
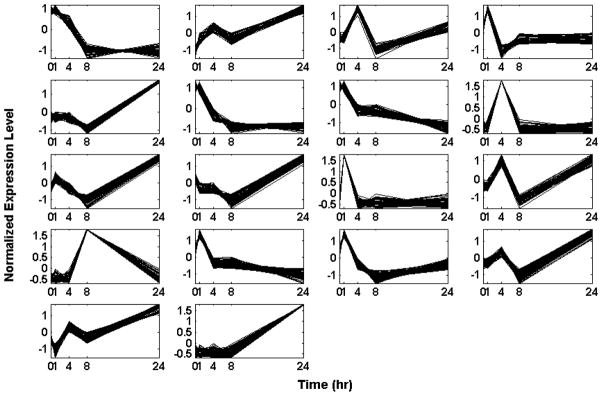
We further process the data by calculating a p-value based on the cluster size and filtering out those expression motifs which are highly likely to be generated by a random model. Reshuffling of the original gene expression data is used to generate random background data in order to estimate a p-value for each expression motif. The analysis identifies a sub-set of 18 transcriptional motifs which are considered to be statistically significant and these are depicted in Figure 2.
Figure 2.
Temporal profiles of statistically significant expression motifs: Normalized Signal Intensity of expression motifs with P, 0.0020 vs. time
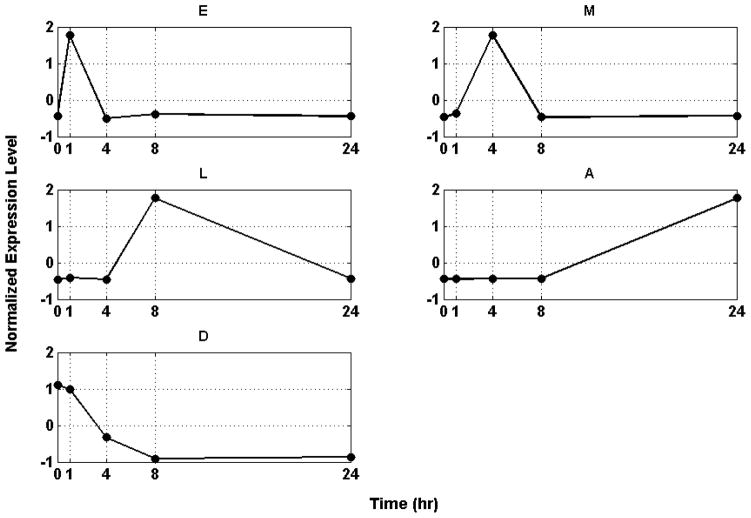
The set of motifs is further lumped by identifying a discriminating set of critical temporal shapes that best characterizes the intrinsic dynamic response of the system utilizing the concept of Transcriptional State (TS) we previously introduced in [13]. The TS of the system is defined as the overall distribution of expression values at a specific time point by quantifying the deviation of the system at each time point versus a baseline distribution (t=0 h) applying a Kolmogorov- Smirnov (K-S) test [22]. Our quantifying metric is the summation of all the estimated K-S values over time. Therefore, the aim here is selecting a set of expression motifs whose corresponding transcriptional state deviates maximally from the baseline (distribution of expression values at time t=0h). Given the aforementioned metric we are interested in identifying the minimum number of expression motifs which characterize the maximum deviation of the Transcriptional State of the system. The selection is a combinatorial optimization problem for which we apply a stochastic optimization algorithm, based on simulated annealing (SA)[23]. The maximum deviation from homeostasis is obtained when we select 5 motifs, whereas further addition of motifs reduced the deviation indicating the addition of less critical responses. We therefore hypothesize the existence of a distinct critical set of temporal responses that best capture the intrinsic dynamics of the host response to thermal injury, Figure 3.
Figure 3.
Essential Transcriptional Elements of the Inflammatory Response. (E) Early pro-inflammatory response, (M) Intermediate pro-inflammatory response, (L) Late pro-inflammatory response, (A) Anti- inflammatory response and (D) Anabolism
The first response (E) is characterized by an early up-regulation during the first hour following the thermal injury whereas the second (M) and the third (L) essential response represent later up-regulation events at about 4h and 8h post-injury respectively. All three responses return to base line within the first 24h. The fourth response (A) exhibits a later, yet persistent up-regulation after 24h. Finally, the fifth response (D) is characterized by persistent down-regulation during the time course of the experiment and deviation from baseline. 59, 54, 62, 81 and 52 probe sets are included in E, M, L, A, D respectively.
Functional Characterization of Essential Responses
Once the inflammatory signal is de-convoluted into its essential components, it is hypothesized that genes whose transcriptional signatures are highly correlated with the essential motifs participate in relevant inflammatory pathways. This enables us to gain a biologically relevant understanding of the systemic response with respect to the thermal injury. We characterize the biological relevance of the intrinsic responses by evaluating the enrichment of the corresponding subsets in thermal injury-induced inflammation –specific pathways by using ARRAYTRACK [24].
The “E” response displays an early peak in up-regulation within the first hour following the burn injury and contains genes which are primarily responsible for the early pro-inflammatory response. Genes in this major temporal class are involved in Gap junction (Raf1, Csnk1d, and Drd2) as well as in Adipocytokine signaling pathway (TNF, Acs14, Adipor2, and G6pc). It is reported that activation of Kupffer Cells in vivo or in vitro resulted in formation of Gap Junction and plays a critical role during liver inflammation [25]. Adipose tissue secretes a large number of physiologically active peptides that often share structural properties with cytokines and are therefore referred to collectively as adiocytokines [26]. The adipokines or adipocytokines are a group of cytokines (cell-to-cell signaling proteins) secreted by adipose tissue including chemerin, interleukin-6 (IL-6), TNF et.al. Moreover, we identified genes (TNF) which are critical in activating transcription factors that act as important initial mediator of pro-inflammatory response. TNF is an important mediator of the production of acute phase proteins (APP), is one important proinflammatory cytokine, acting via cytokine-receptor interactions, intracellular signaling pathways, and ultimately influencing transcription factors, these cytokines are able to modulate the promoter regions of multiple acute phase proteins [27; 28]. TNF’s primary role is in the regulation of immune cells. We should discriminate the TNF as the initiator of the overall response and that in the “E”. Under assumption, circulating TNF released immediately following thermal injury triggers overall response. This early, or “alarm”, cytokine has pleiotropic activity and act both locally and distally. Distally, immune cells such as Kupffer cells begin to synthesize and release their own particular set of cytokines within particular tissues such as liver. Although some of these cytokines may have been released earlier by the monocytes, it is this secondary wave that augments the homeostatic signal and initiates the cellular and cytokine cascade that are involved in the complex process of APR [5]. Thus, the transcriptional expression of TNF in “E” stands for the activation of acute response of hepatic cells in response to circulating TNF.
The “M” response represents an intermediate, middle, pro-inflammatory actions and is associated with genes involved in P38 MAPK signaling pathway (Interleukin-1alpha, (IL-1α), Map3k12 (p38mapk), cxcl14) essential in regulating the pro-inflammatory response. P38MAPK is known to play a central role in the cellular response to external stress and mediate proinflammatory cytokine production [29]. Activated p38MAPK results in downstream activation of proapoptotic transcription factors such as p53 and stimulates robust proinflammatory cytokine production of IL-6, interleukin-1 beta (IL-1β), and TNF [30; 31]. Moreover, we identified the late increased expression of IL-1a and Cxcl14 which is assumed to be indicative of pro-inflammatory response.
The “L” response represents a late pro-inflammatory reaction. Motif “L” is enriched in genes which are mainly involved in the late pro-inflammatory response, such as complement and coagulation cascades (C1qb, C1s, C3, and C4a) associated with the innate and adaptive immune systems. The end result of this activation cascade is massive amplification of the response and activation of the cell-killing membrane attack complex. Due to the fast response of the component complement cascade following thermal, this may reflect a restoration of the levels to normal due to the exhaustion of complement at the time of injury. In addition, other genes which code significant pro-inflammatory cytokines are also found such as IL-1β, IL-18, IFN-γ and cxcl2. It is widely accepted that IL-1β is one of the most important proinflammatory cytokines following thermal injury [32]. In addition, IL-18 is a TH-1 inducing, proinflammatory cytokine and member of the IL-1 family [33]. Similarly, IFN-γ is considered as a proinflammatory cytokine because it augments TNF activity and induces nitric oxide (NO)[32].
The “A” response is found to be associated with the anti-inflammatory component. Genes in this major temporal class are important in ribosome (RPL/RPS family) and proteomes (psma1, psma2, psma6) which can be interpreted as characteristic of a change in protein synthesis patterns, more specifically an increase in the synthesis of the positive acute phase proteins and important anti-inflammatory cytokines as well as a decrease in the synthesis of negative acute phase proteins and the constituent proteins. In addition, the genes coding important positive acute phase proteins such as FGA, KGA, and A2m are also present in this motif. Acute phase proteins are considered as important ‘diffusible’ anti-inflammatory mediators [34]. Moreover, the genes which code important anti-inflammatory cytokines such as IL-10, IL-1ra, IL-1r2, Il-1r2β [35] are also identified.
Finally, the “D” response is identified to be related to anabolism. Genes in this major temporal class are important in the JAK-STAT (Bcl211, IL13, and IL9, jak1, socs2 and stat5a), MAPK signaling pathways (Map2k1, Map2k5, Map3ka, Map4k4, Mapk14 and mapkapk3) and VEGF signaling pathways (Map2k1, Mapk14, Mapkapk3). In addition, many growth factors are found in this motif, such as IGF-1, EGF, HGF, Fgfr2 which are considered to be important in regulation of anabolic effects such as stimulating the synthesis of protein, glucose and lipid, cell growth, proliferation. STAT5 is used to regulate certain hepatocyte functions, particularly in response to growth hormones. VEGF regulates several endothelial cell functions, including proliferation, differentiation, permeability, vascular tone, and the production of vasoactive molecules. Signaling cascades that have been implicated in VEGF action include Src, PLC-g, MAPK, as well as STAT3 and STAT5. Synthesis of nutrients, cell growth and proliferation can be considered as anabolism, since the growth and proliferation of cells do need synthesis of new proteins, lipid and glucose. Therefore, the down regulation represents the opposite effect, i.e., catabolism, which induces hypermetabolism following thermal injury. This motif could be seen as the indicator of the metabolic status of the hepatic cells. The deviation from normal levels is the representative of damage to the body.
These transcriptional responses effectively represent the overall dynamics and define the constitutive elements of the overall response. We hypothesize that they correspond to the cellular signatures in response to thermal injury and manifest the integrated systemic response and, subsequently, we explore the possibility of developing a model describing the dynamics of these responses.
Modeling Burn Injury Induced Acute Inflammation
Putative structure of the network of interacting components
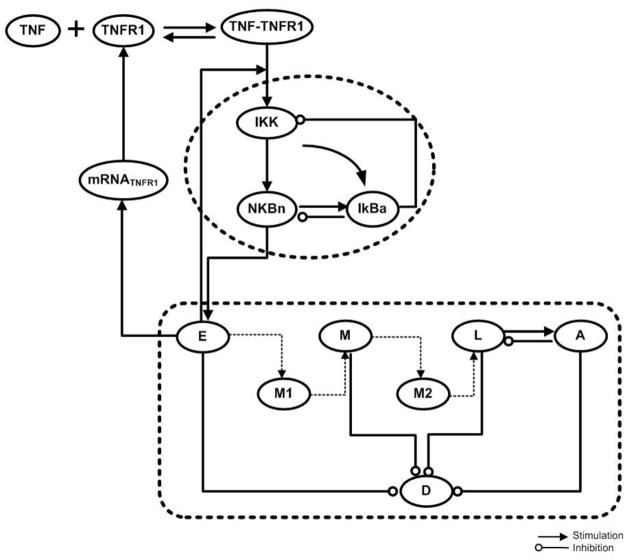
It is believed that the cells of the innate immune system are activated by alarm/danger molecules released from injured or stressed cells, such as those exposed to pathogens, toxins, or mechanical, physical, or physiological stimuli [36]. We hypothesize that the inflammatory response is activated when trauma-induced products are recognized by appropriate receptors. Tumor necrosis factor (TNF) is a key product released following a cutaneous thermal injury [18]. TNF, a cytokine with a relative molecular mass of 17,000, is produced by activated macrophages in response to pathogens and other injurious stimuli, and is a necessary and sufficient mediator of local and systemic inflammation [19; 20]. Administration of TNF to humans reproduces many acute physiologic and metabolic responses to injury, including inflammatory response and energy substrate mobilization. TNF induces a net catabolic state by mediating increased catabolism, causing anorexia, and activating the hypothalamic – pituitary- adrenal axis in both humans and animals [37; 38; 39; 40]. Furthermore, the metabolic effects following TNF administration are dose-dependent and dose increases result in enhanced energy expenditure, increased hepatic gluconeogenesis, increased whole body protein breakdown, activation of the hypothalamic-pituitary-adrenal axis and increased whole body lipolysis; all features of the metabolic response to thermal injury. In even larger doses, TNF triggers potentially catastrophic tissue injury and lethal shock [20; 41]. Therefore, TNF is assumed to be initiator of overall response.
The combination of the prototypical initiator, i.e., TNF, and its receptor (R), i.e., TNFR1, on the membrane of hepatic cells triggers a series of intracellular events that ultimately result in the activation of major transcription factors, such as NF-κB [42] known to regulate the expression of inflammatory cytokines, chemokines, immunoreceptors, and cell adhesion molecules. Due to its role and significance, NF-κB has often been termed a central mediator of the human immune response [43]. Therefore, we assume that it is the translocation of NF-κB from the cytoplasm to the nucleus that stimulates the production of the proinflammatory response. Although numerous signaling molecules and reactions participate in NF-κB signaling pathway [44], sensitivity analysis has shown that the activity of NF-κB is maximally modulated by a reduced set of three basic signaling molecules (IKK, IκBα and NF-κB) [45].
The activated transcriptional factor NF-κB will indirectly stimulate the production rate of “E” the early pro-inflammatory response. ”E” is characterized as the ‘first line’ transcriptional response that is triggered upon the recognition of the extracellular ligand (TNF) by its pattern recognition receptors (TNFR1). Since “E” denotes early pro-inflammation it serves as the signal that will further stimulate downstream processes associated with the intermediate response “M”, further activating late pro-inflammatory response ”L”. The activation of this pro-inflammatory cascade of responses in known to involve a number of interrelated steps forming a complex signal transduction cascade [34; 46; 47]. This is also evident but the transient up-regulation of each component of the pro-inflammatory family of responses with a characteristic peak at different points in time. In order to best simulate the time delays we hypothesize the existence of transit compartments between each leading response, namely “E”, “M” and “L”, [17]. We assume the existence of one compartment between each successive step, (M1) and (M2), used to describe the time delay between the components of the pro-inflammatory response.
Once the pro-inflammatory response has mounted it serves as a subsequent signal for stimulating the anti-inflammatory component “A” [5; 34; 48; 49]. Given the temporal dynamics of “A” and “L”, we assume that “L” is activated as soon as the pro-inflammatory response has reached its peak, as expressed by the maximal activation of “L”. Therefore, we assume a direct inhibitory link between “A” and “L” aiming at dampening the response [50].
Several studies have shown that increased pro-inflammatory cytokine synthesis contributes to hypermetabolism and catabolism [51; 52]. Therefore, the pro-inflammatory response, “E”, “L” and “M”, are expected to inhibit anabolism, i.e., increase catabolism, “D”. Furthermore, up-regulation of the expression of acute phase proteins, component of “A”, will further increase hypermetabolism [53; 54; 55]. The metabolic rate in burns is extremely high; energy requirements are immense and are met by the mobilization of proteins and amino acids. Increased protein turnover, degradation (as expressed by an increase in “A” response), and negative nitrogen balance leading to the enhanced metabolic requirements which causes catabolism [56]. Therefore, the anti-inflammatory response “A” will further inhibit anabolism “D”.
All the aforementioned qualitative relations are depicted in the form of a network in Figure 4.
Figure 4.
Qualitative Structure of the Thermal Injury Induced Model Detailed explanations are in the text.
A Quantitative model of burn induced inflammation
The mathematical model is succinctly presented in equations (1–15). Specifically, the components represented in the model are the following:
Circulating TNF dynamics and primary activating signal formation
In order to model the primal instigator, in the form of a rapid release of TNF due to the burn injury, we adopted the formalism of Vodovotz et al [9]. Equation (1) is therefore used to describe the effect of trauma expressed as an exponential decay of influence after an initial insult. It represents possible released cellular material, assumed to be TNF, which can trigger inflammation. The parameters TRon, tTR, xTR determine the peak value of TNF. Circulating TNF is recognized by its appropriate surface receptor TNFR1. The corresponding ligand-receptor equilibrium is expressed in equations (2) and (3). The rate of translation of mRNATNFR1 to the corresponding surface protein describes the dynamic evolution of synthesis of new receptors and is described by equation (4). The dynamic profile of mRNATNFR1 in (4) is characterized by a 0th order synthesis and 1st order degradation, whereas the expression is stimulated by “E” (early pro-inflammatory) [57] using the principles of IDR.
NFκB dynamics
In order to model the dynamics of the activation of NFκB we pursue a simplified model as suggested in our earlier work [15] as expressed in equation (5–8). Qualitatively, the IKK activity corresponds to its intracellular concentration and it serves as the input signal for the subsequent activation of NFκB signaling module. The activation of kinase activity IKK is induced by the cellular surface complex TNF-TNFR1. In order to achieve a oscillation and bistability [58] response in the dynamics of the explored system which could lead to constrained response or unconstrained one, a non-linear function of Hill- type is assumed. In chronic inflammatory diseases several cytokines might be responsible for perpetuating and amplifying the inflammatory reaction through the critical node IKK [59]. Therefore, such an interaction is simulated by the presence of a positive feedback loop between (E) and (IKK) in equation (5). NFκBn is used to denote both the fraction of cytoplasmic concentration in nucleus and nuclear activity in this study. Thus, the term (1- NFκBn) denotes the available free cytoplasmic concentration of NFκB. The dynamics of nuclear concentration of NFκBn is depicted in equation (6). The import rate of cytoplasmic NFκB into the nucleus depends on the availability of its free cytoplasmic concentration (1- NFκBn) stimulated by the kinase activity, IKK. However, its degradation rate depends on the presence of its primary inhibitor IκBα as the latter retrieves nuclear concentrations of NFκB by forming an inactive complex in the cytoplasmic region. The dynamics of the gene transcript of mRNAIκBα in equation (7), are characterized by a zero order production rate kin,IκBα and a first order degradation rate kout,IκBα which is stimulated by NFκBn. The protein inhibitor of NF-κB, IκBα, is synthesized based on the translation from its gene transcript mRNAIκBα with rate kI,1 and it degraded at a rate kI,2 which is stimulated by the kinase activity (IKK) as seen in equation (8). Based on the premise that IκBα forms a complex with the available cytoplasmic NFκB [60], mathematically we expressed it as the product(1− NFκBn)× IκBa. From a modeling point of view, in order to achieve a zero steady state for the protein inhibitor IκBα we need the additional negative term − kI,1.
Dynamics of intrinsic transcriptional responses
The core of the cellular dynamics representing the activation of cellular responses is described in equations (9–15). The dynamics of “E”, “M”, “L”, “A” and “D” basically follow the basic principles of modeling a cellular response using a 0th order synthesis and a 1st order degradation dynamics. Both are appropriately stimulated and/or inhibited by appropriate terms as described next. The dynamics of “E”, the early pro-inflammatory response is given in (9). At the transcriptional response level, we assume the nuclear activity of NFκB serve as the “active signal” that indirectly stimulates the production rate of “E” by enhancing the expression of the associated genes. Mathematically the stimulation effect of the nuclear activity NFκB is expressed by the linear function(1+ kE,NFκBn × NFκBn). The link between the various components of the pro-inflammatory response is, as explained earlier, quantified by means of a compartmentalized signal transduction cascade with intermediate signals denoted by M1 and M2. In (11) the indirect response model is used to model the dynamics of “M” which is stimulated by the upstream signal M1 with rate kM,M1 and coefficient γ1. Similarly, the late pro-inflammatory response signal “L” is activated by the intermediate transduction process M2 with rate kL,M2 coefficient γ2 as shown in equation (13). In (10) and (12) the transduction processes M1 and M2 are modeled using the transit compartment model; these steps will propagate stimulatory effects from “E” to “M” and from “M” to “L” with transit times τ1 and τ2 respectively. The anti-inflammatory signal “A” is stimulated by the activated late proinflammatory response “L” and decays with rate kout,A as shown in equation (14). Finally, both the pro-inflammatory and anti-inflammatory responses would inhibit the anabolism, thus the modifying functions in denominator decreases kin,D the production rate of “D” as shown in (15).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Results and Discussion
Estimation of Relevant Parameters
The model depends on the values of 40 parameters. However, 15 are obtained either from literature or estimated in relation to other model parameters. Specifically:
The half-life of TNF has been estimated to be 70 ± 11 min [61], and then we speculate the initial normalized concentration of the inflammatory stimulus (TNF) quickly decays so that it completely clears at about 1 hour to 80 min. Thus the parameters describing the dynamics of TNF in equation (1), TRon, tTR and xTR, are set to 1, 0.3 and 0.5 respectively.
The dynamics of the TNF receptor (R) based on equation (2) depend on the ratio of dissociation/association parameters of the ligand–receptor interaction whose corresponding parameters k2 and k1 are assumed to be related k2 =1.5*k1 [62].
For a 20% TBSA burn injury, all rats are expected to survive and eventually fully recover [63]. Therefore, all the immune responses will eventually resolve and return to homeostasis. As a result a number of relations exist between kinetic parameters based on the system dynamics. Detailed relationships between those parameters are derived and presented in the Appendix.
A basic qualitative characteristic of the model is that, in the absence of any external therapeutic intervention, it should posses the ability to generate two possible outcomes (steady states) based on the severity of the primary burn injury. Namely, the subject are expected to either recover and return to the prior to injury homeostatic state, or attain a level of persistent inflammatory activation [64]. The central control in the proposed model centers on the dynamics of NFkB regulation. A thorough parametric analysis identify the critical role of k4 (5), kI,1 (8), kI,2 (8) in controlling the manifestation of the two steady states. Thus, in order to assure the model have the switch like behavior, k4 (5), kI,1 (8), kI,2 (8) are determined to assume the values 2, 1.4 and 1.48 respectively.
Once the released initiator TNF is recognized by its specific receptor TNFR1, the concentration of the free receptor should decrease at the beginning due to the increased occupation and subsequently increase because of the degradation of the initiator TNF and decomposition of the complex (TNF·TNFR1). Thus, consistent with this fact, the set of the parameters controlling the dynamics of the receptor in equation (2), ksyn, k1, k2 and kdeg should be chosen such that the qualitative characteristics of the receptor are similar to what was previously described.
As a result of the aforementioned analysis, only 25 independent parameters need to be estimated. However, identification of a unique set of appropriate parameter values is precluded based on the complex and nonlinear nature of the model [65] and the limited number of available experimental data [66]. This limitation could be overcome by applying widely used and robust resampling approaches, such as bootstrapping which can provided estimates for the parameter values and confidence interval using the resulting empirical distribution of parameters [67].Given the nature of the data used for the estimation of the relevant model parameters, the sampling is based on the probe sets constituting each essential cluster. Each expression motif used for the model calibration is composed of a number of probe sets, as earlier described. For each bootstrap run sampling with replacement is performed on the original set of probe sets. Each bootstrap sample is used for estimating a set of parameters. The resampling process is repeated a number of times (1000 in our case) and mean of multiple bootstrap estimated model parameters is reported as the most likely parameter estimate [68]
| (16) |
where i denotes bootstrap iteration. The relevant kinetic parameters are shown in Table 1, and the performance of the model in reproducing the recorded responses is shown in Figure 5.
Table 1.
Estimated values of the parameters based on self- limited response data
| Index | Parameter | Value | min | max | 5%quantile | 95%quantile |
|---|---|---|---|---|---|---|
| 1 | TRon | 1 | ||||
| 2 | tTR | 0.3 | ||||
| 3 | xTR | 0.5 | ||||
| 4 | ksyn | 0.0178 | 0.0001 | 0.1907 | 0.0009 | 0.0237 |
| 5 | kdeg | 0.0178 | ||||
| 6 | k1 | 2.9835 | 2.6402 | 3.1860 | 2.7806 | 3.1419 |
| 7 | k2 | 0.0448 | ||||
| 8 | kin, mRNA,TNFR1 | 0.0892 | 0.0025 | 0.1962 | 0.0771 | 0.0955 |
| 9 | kout, mRNA, TNFR1 | 0.2447 | ||||
| 10 | kTNFR1,E | 1.7439 | 1.6189 | 1.8659 | 1.6463 | 1.8363 |
| 11 | k3 | 4.9924 | 4.6696 | 5.2970 | 4.7187 | 5.2616 |
| 12 | k4 | 2 | ||||
| 13 | kNFκB,1 | 16.2767 | 15.3150 | 17.2588 | 15.3907 | 17.1419 |
| 14 | kNFκB,2 | 1.0124 | 0.2565 | 1.2480 | 0.9484 | 1.1187 |
| 15 | kin,IκBα | 0.5019 | 0.3686 | 2.7546 | 0.4370 | 0.7228 |
| 16 | kIκBα,1 | 13.2824 | 12.4863 | 14.0660 | 12.5927 | 14.0074 |
| 17 | kout,IκBα | 0.5019 | ||||
| 18 | kI,1 | 1.4 | ||||
| 19 | kI,2 | 1.48 | ||||
| 20 | kin,E | 1.3944 | 1.1954 | 1.6907 | 1.2758 | 1.4831 |
| 21 | kE,NFκB | 7.2374 | 6.7439 | 7.6585 | 6.8332 | 7.5813 |
| 22 | kout,E | 1.3944 | ||||
| 23 | τ1 | 1.2208 | 1.1429 | 2.2262 | 1.1562 | 1.2986 |
| 24 | kin,M | 0.1895 | 0.14406 | 0.5711 | 0.16058 | 0.2033 |
| 25 | kout,M | 0.8693 | ||||
| 26 | kM, M1 | 3.5872 | 3.3779 | 3.8097 | 3.3999 | 3.7865 |
| 27 | γ1 | 1.5505 | 1.3912 | 2.2236 | 1.4310 | 1.8318 |
| 28 | τ2 | 9.7784 | 9.1848 | 10.3504 | 9.2556 | 10.2919 |
| 29 | kin,L | 0.1679 | 0.1386 | 0.2758 | 0.1489 | 0.2210 |
| 30 | kout,L | 0.2524 | ||||
| 31 | kL, M2 | 0.5193 | 0.2501 | 0.6325 | 0.3277 | 0.5728 |
| 32 | γ2 | 3.9989 | 3.5282 | 4.2362 | 3.7943 | 4.1953 |
| 33 | kin,A | 0.0021 | 0.0007 | 0.0069 | 0.0009 | 0.0027 |
| 34 | kout,A | 0.0452 | ||||
| 35 | kA,L | 20.5386 | 19.3222 | 21.7660 | 19.4349 | 21.6616 |
| 36 | γ3 | 1.5684 | 1.4025 | 2.2521 | 1.4370 | 2.0230 |
| 37 | kin,D | 3.3369 | 3.1351 | 3.5332 | 3.1592 | 3.5165 |
| 38 | kout,D | 0.2709 | ||||
| 39 | kD,L | 1.1756 | 1.0955 | 1.2469 | 1.1103 | 1.2359 |
| 40 | kD,A | 4.6662 | 4.3858 | 4.9442 | 4.4139 | 4.9180 |
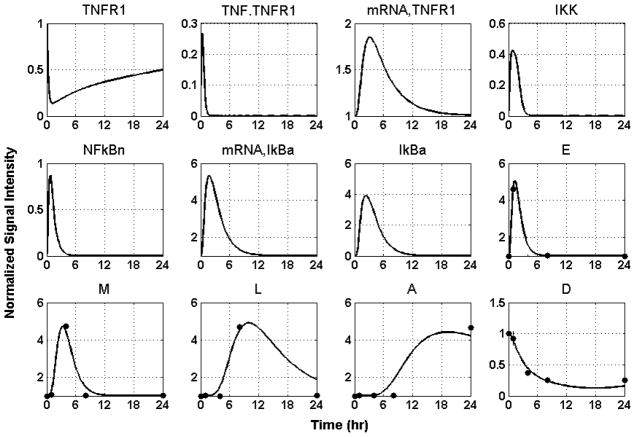
Figure 5.
Model Building Results: Dynamic profiles of the elements that constitute the mechanistic model of thermal injury-induced inflammation. Experimentally measured normalized mRNA transcript levels are denoted by symbols (●); solid lines (-) are the model predictions.
Confidence interval by bootstrap percentiles
The percentile method is explored in order to estimate confidence intervals for the estimated parameters. The estimated interval is denoted as
| (17) |
where subscript l and u respectively denote the lower and the upper limits of the vector of true model parameters β which is approximated by α central confidence interval.
The 100(α/2) and 100 (1−α/2) percentile values of the bootstrap distribution are used as the upper and lower confidence limits for a parameter. The probability α (0<α<1) indicates a 100α% confidence that β∈[β̂l, β̂u]. In this study, α is chosen as 5, then 95% confidence limits for β based on 1000 bootstrap replications are given by β̂l = 25th and β̂u = 976th largest estimates of β [68]. The confidence intervals for parameter are also shown in Table 1. Histograms of 1000 bootstrap replications of 4 parameters are presented in Figure 6. All histograms are roughly Gaussian in shape, suggesting that confidence interval evaluation based on bootstrap percentile is a reasonable approach.
Figure 6.
Histograms of 1000 bootstrap estimates of 4 parameters. The bars represent frequency. The average bootstrap estimator values of parameters are indicated by a dashed line and its lower and upper confidence limits and respectively, are represented by dotted lines.
Sensitivity analysis
Sensitivity analysis is performed to gain an insight in the model’s dependence on all the parameters. The sensitivity coefficients [45] are calculated as:
| (18) |
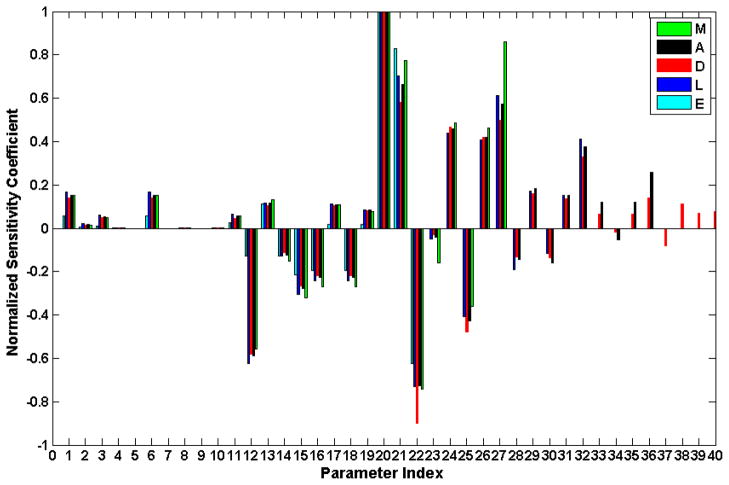
where p denotes the parameter whose sensitivity is to be estimated. In order to obtain a broader view of the model sensitivities, the analysis is performed with respect to each of the five essential responses individually. The target response, m, is thus defined as the maximum over the 24hr period following the burn injury of E, M, L, A and the minimum of D. Normalized sensitivity coefficients are depicted in Figure 7. The parameters showing negative normalized sensitivity coefficient are either the ones directly modulate the degradation rate of components such as k4 (12), kNFκB,2 (14), kout,E (22), kout,M (25) kout,L (30), kout,A (34) or the ones that indirectly inhibit the signaling activity of NFkBn such as kin,IκBα (15), kIκ Bα,1 (16), kI,1 (18). Perturbations of the parameters labeled 37–40 (kin,D (37), k out,D (38), kD,L (39), kD,A (40)) which only modulate the dynamics of D, anabolism, have, as expected, low impact on upstream model components. Similarly, perturbation of the parameters labeled 33–36 (kin, A (33), kout, A (34), kA,L (35), γ3 (36)), 29–32(kin,L (29), kout,L (30), kL,M2 (31), γ2 (32)), 24–27 (kin,M (24), kout,M (25), kM,M1 (26), γ1 (27) will only affect A/D, A/D/L, A/D/L/M respectively. The sign and absolute value of normalized sensitivity coefficients for the parameters labeled 1–22 are almost identical for all 5 responses indicating that the perturbation of any of those parameters will have similar influence to all transcriptional responses. Sensitivity analysis predicts that the most sensitive parameters are the ones related to the IKK-NFkB-IkBa system and the pro-inflammation system. Parameters involved in the dynamics of IKK (k4 (12)), mRNAIKBA (kin,IκBα (15), kIκ Bα,1 (16)) and IkBa (kI,1 (18)) which combine together to control the magnitude of the NFkB signal in the activation of downstream components. Parameters governing the behavior of the early response (kin,E (20), kE,NFκB (21), and kout,E (22)), intermediate (kin,M (24), kout,M (25), kM,M1 (26), and γ1 (27)), and late proinflammatory responses (kin,L (29), γ2 (32)) also have high sensitivities since they directly determines the intensity and duration of the pro-inflammatory response.
Figure 7.
Sensitivity analysis on the model parameters. Sensitivity coefficients are calculated by using Eq. (18) with δ p= 0.01. Normalization is obtained by dividing the raw sensitivity coefficient by the maximum one for each response. The numbered labels on the x-axis correspond to the parameter in Table 1.
Increasing the severity of thermal injury
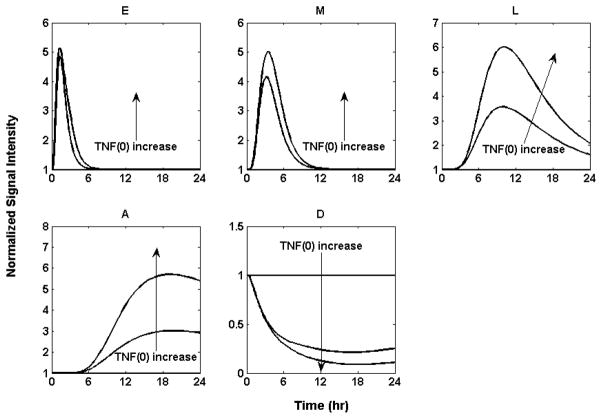
It is reported that burn size determines the robustness of the inflammatory and hypermetabolic responses [64]. An increase in burn size is associated with increased hypermetabolism, persistent inflammation, catabolism and organ dysfunction. We simulate the increases in the severity of the injury by increasing the initial condition of the initiator TNF and thus inferring in silico progression of the inflammatory trajectory. We used the model to predict the outcome under different initial value of the initiator TNF, as seen in Figure 8.
Figure 8.
Implications of different severities of thermal injury. 1) TNF (0) =0: All the profiles stay at baseline. 2) TNF (0) =0.6: Thermal injury triggers a stronger response for every profile. All the pro-inflammatory responses (E), (M) and (L) and the anti-inflammatory response (A) ultimately abate and return to the baseline while the anabolism response (D) increases and returns to baseline. 3) TNF (0) = 1.2: A much stronger response for every profile is observed. In addition, due to the increased initiator, the time the late-inflammatory response (L), anti-inflammatory response (A) and anabolism response (D) return to the baseline is postponed.
The situation in which the initial level of TNF is 0 mimics a sham burn scenario and the result is, as expected, no deviation from homeostasis. Since in our model we assume that the arbitrary initial concentration of TNF of 1 correspond to 20% TBSA burn, values lower than that would correspond to reduced injury severity and higher values to increase injury severity. Figure 8 depicts typical predictions for varying levels of burn injury. A heightened response and slower return to homeostasis is observed. These findings are in agreement with prior studies [64] in which it was observed that larger burns cause a marked inflammatory response and elevation in catecholamines, both of which are associated with increased metabolic rate.
The nominal condition of TNF (0) =1 represents the 20% TBSA burn injury which is tolerated by the animals. Our model, however, predicts that an initial condition of TNF(0)=2.1, which corresponds to approximately 40% TBSA and is known to be detrimental [64], results in sustained synthesis of positive acute phase proteins and persistent turnover of the constitute proteins leading to prolonged hypermetabolism. Heightened levels of the inflammatory insult therefore leads an amplification of the immune response [69] followed by a dysregulation in the host defense intrinsic dynamics leading to an unconstrained inflammatory response. Moreover, the anti-inflammatory response becomes highly activated which will further inhibit anabolism. Persistent down-regulation of anabolism (thus causing increased catabolism) is consistent with chronic hypermetabolism. In all, these results show that switch between healthy state (recovery/survival) and unhealthy state (sepsis/morbidity and mortality) in burned patients is burn size dependent [64]. Thus our model has the ability to predict the existence of two possible steady states corresponding to a resolved and unresolved inflammatory states depending on the extend of the injury.
Dysregulation of intracellular controls
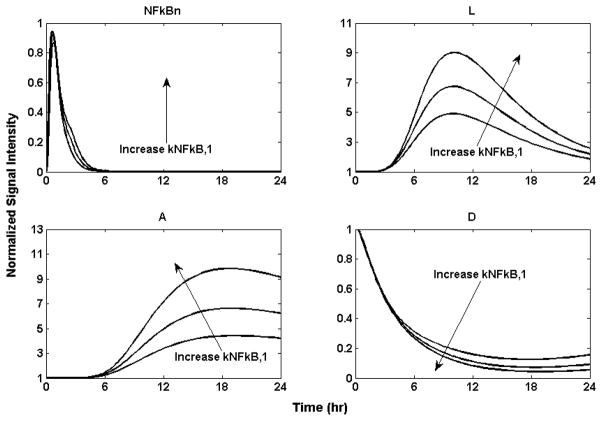
The cellular host response to injury plays a pivotal role in determining the intensity and duration of the inflammatory response. NF-κB, a ubiquitous nuclear transcription factor, plays a key role in regulating inflammation as well as other immune responses. Consistent with this role, incorrect regulation of NF-κB has been implicated with cancer, inflammatory and auto-immune diseases, septic shock, viral infection, and improper immune development [70]. It is considered that aberrant NF-κB activity could be caused by defects in the regulatory mechanisms controlling NF-κB activation[71]. Our model allows us to investigate the response dynamics emerging from alterations in the IKK-NFκB dynamics. We explore the effect of increasing the activation rate of the kinase NFκB quantified through increases in the rate of activation NFκB by IKK signal, by increasing kNFkB,1 in equation (6), by 50% and 100% respectively. This “mutation” would result in a persistently elevated output signal from the NFκB module, leading to persistently elevated responses for “A” and “D” as depicted in Figure 9. The result illustrates the implications of aberrant regulation of NFκB [72] leading to improper immune response. The increase systemic sensitivity to the tight regulation of NFkB dynamics could render an, otherwise, self-limited to an aberrant, detrimental response The central role of NFkB signaling renders it a critical regulator of the inflammatory response [73].
Figure 9.
Implication of dysregulation of NF-κB activity by increasing the activation rate of NF-κB by IKK signal kNFκ B,1 by 50% and 100% respectively. It leads to persistently elevated responses for “A” and “D”. The larger the NF-κB activation rate kNFκB,1, the higher the response will be for (L) the proinflammatory response, (A) the anti-inflammatory, and (D) the anabolism.
Implication of Administration of Receptor Antagonists or Antibodies Targeting Pro-Inflammatory Cytokines
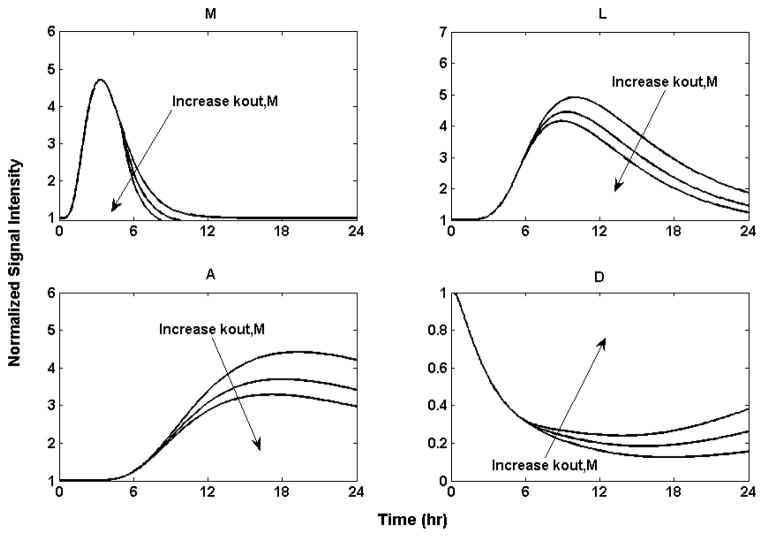
The thermal injury-induced severe sepsis, persistent hypermetabolism and surprisingly high morbidity and mortality call for effective mechanistic-based treatments. Our model indicates that persistent hypermetabolism and catabolism following severe thermal injury are linked to the release of proinflammatory mediators which will trigger, broaden and deepen downstream immune responses. Thus, blocking and neutralizing the pro-inflammatory cytokines with administration of receptor antagonists or antibodies post burn might be an effective strategy to prevent overactivation of downstream responses as well as deduce mitigating hypermetabolism through injection of receptor antagonists or antibodies of proinflammatory cytokines, such as monoclonal antibodies against TNF-α, soluble TNF receptors, IL-1 receptor antagonists and soluble IL-1 receptors [74]. We explore the influence of administrating a receptor antagonist against IL-1 (a prototypical representative marker of the “M” response) as a potential target for therapeutic intervention [75]. Blocking and neutralizing IL-1 with through soluble IL-1 receptor antagonists are simulating by increasing the degradation rate of “M” through kout,M which represents accelerated lost of effective IL-1 signals. The administration of a receptor antagonist at 5 hours postburn is depicted in Figure 10. The administration of IL-1RA could reduce the effective signal of ‘M’ which will ultimately attenuate subsequent responses and reduce hypermetabolism. This result is in agreement with recent observations that administration IL-1RA has the ability to favorably influence chronic inflammatory diseases supporting the hypothesis that blocking a single mediator of the immune response may have clinical impact [76].
Figure 10.
Implication of administration of IL-1 receptor antagonist by decreasing concentration of (M) through increasing the degradation rate constant. Increase kout,M by 20% and 40% respectively from the 5th hour. The larger the degradation rate of (M), the lower the response will be for (M) the intermediate proinflammatory response, (L) the proinflammatory response, (A) the anti-inflammatory, and (D) the anabolism. All the responses, including the anabolism, returned to baseline after a period of time.
It is worth noting that for antibody and antagonist therapies the “window of opportunity” determines the therapeutic effect [77]. The administration of the antibody before the full onset of the response will have a beneficial result while no effect will be observed if the injection occurs too early or too late. In our model, ‘M’, the intermediate response peaks at 4 hour post burn, and declines slowly until it returns to baseline at about 12 hour post-thermal injury. Thus, it is predicted by our model that administration of the IL-1RA 12 hour postburn will have no effect in controlling the response.
Concluding Remarks
The proposed response model describes a sequence of intracellular inflammatory responses and nuclear transcriptional events in response to a thermal injury. The physicochemical, mechanistic-based indirect response model allows us to intuitively explore the relationship between the significance of inflammatory responses and the severity of thermal injury which directly determines the outcomes. The model allows the design of a number of in silico experiments aiming at deciphering complex interactions between constitutive elements, such as signaling components and mediator blocking trough receptor antagonists, and the severity of the injury. A better understanding of complexities of burn-induced inflammatory responses trough modeling could be a significant step forward towards the discovery of improved treatment options and strategies.
Acknowledgments
The authors acknowledge support from NIH GM082974
Appendix
Steady-State Equations
In order to obtain the baseline dynamics within 24 hours post burn injury, steady state equations were derived as follows:
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Church D, Elsayed S, Reid O, Winston B, Lindsay R. Burn wound infections. Clin Microbiol Rev. 2006;19:403–34. doi: 10.1128/CMR.19.2.403-434.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wibbenmeyer L, Danks R, Faucher L, Amelon M, Latenser B, Kealey GP, Herwaldt LA. Prospective analysis of nosocomial infection rates, antibiotic use, and patterns of resistance in a burn population. J Burn Care Res. 2006;27:152–60. doi: 10.1097/01.BCR.0000203359.32756.F7. [DOI] [PubMed] [Google Scholar]
- 3.Wurtz R, Karajovic M, Dacumos E, Jovanovic B, Hanumadass M. Nosocomial infections in a burn intensive care unit. Burns. 1995;21:181–4. doi: 10.1016/0305-4179(95)80005-9. [DOI] [PubMed] [Google Scholar]
- 4.Dasu MR, Cobb JP, Laramie JM, Chung TP, Spies M, Barrow RE. Gene expression profiles of livers from thermally injured rats. Gene. 2004;327:51–60. doi: 10.1016/j.gene.2003.11.015. [DOI] [PubMed] [Google Scholar]
- 5.Baumann H, Gauldie J. The acute phase response. Immunol Today. 1994;15:74–80. doi: 10.1016/0167-5699(94)90137-6. [DOI] [PubMed] [Google Scholar]
- 6.Vodovotz Y, Chow CC, Bartels J, Lagoa C, Prince JM, Levy RM, Kumar R, Day J, Rubin J, Constantine G, Billiar TR, Fink MP, Clermont G. In silico models of acute inflammation in animals. Shock. 2006;26:235–44. doi: 10.1097/01.shk.0000225413.13866.fo. [DOI] [PubMed] [Google Scholar]
- 7.Rumbaugh KP, Colmer JA, Griswold JA, Hamood AN. The effects of infection of thermal injury by Pseudomonas aeruginosa PAO1 on the murine cytokine response. Cytokine. 2001;16:160–8. doi: 10.1006/cyto.2001.0960. [DOI] [PubMed] [Google Scholar]
- 8.Kumar R, Clermont G, Vodovotz Y, Chow CC. The dynamics of acute inflammation. J Theor Biol. 2004;230:145–55. doi: 10.1016/j.jtbi.2004.04.044. [DOI] [PubMed] [Google Scholar]
- 9.Chow CC, Clermont G, Kumar R, Lagoa C, Tawadrous Z, Gallo D, Betten B, Bartels J, Constantine G, Fink MP, Billiar TR, Vodovotz Y. The acute inflammatory response in diverse shock states. Shock. 2005;24:74–84. doi: 10.1097/01.shk.0000168526.97716.f3. [DOI] [PubMed] [Google Scholar]
- 10.Day J, Rubin J, Vodovotz Y, Chow CC, Reynolds A, Clermont G. A reduced mathematical model of the acute inflammatory response II. Capturing scenarios of repeated endotoxin administration. J Theor Biol. 2006;242:237–56. doi: 10.1016/j.jtbi.2006.02.015. [DOI] [PubMed] [Google Scholar]
- 11.Reynolds A, Rubin J, Clermont G, Day J, Vodovotz Y, Bard Ermentrout G. A reduced mathematical model of the acute inflammatory response: I. Derivation of model and analysis of anti-inflammation. J Theor Biol. 2006;242:220–36. doi: 10.1016/j.jtbi.2006.02.016. [DOI] [PubMed] [Google Scholar]
- 12.Munster AM, Smith-Meek M, Dickerson C, Winchurch RA. Translocation. Incidental phenomenon or true pathology? Ann Surg. 1993;218:321–6. doi: 10.1097/00000658-199309000-00011. discussion 326–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang EH, Almon RR, Dubois DC, Jusko WJ, Androulakis IP. Identification of global transcriptional dynamics. PLoS One. 2009;4:e5992. doi: 10.1371/journal.pone.0005992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. Modeling endotoxin-induced systemic inflammation using an indirect response approach. Math Biosci. 2009;217:27–42. doi: 10.1016/j.mbs.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. In silico simulation of corticosteroids effect on an NFkB- dependent physicochemical model of systemic inflammation. PLoS One. 2009;4:e4706. doi: 10.1371/journal.pone.0004706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Krzyzanski W, Jusko WJ. Mathematical formalism for the properties of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1997;25:107–23. doi: 10.1023/a:1025723927981. [DOI] [PubMed] [Google Scholar]
- 17.Sun YN, Jusko WJ. Transit compartments versus gamma distribution function to model signal transduction processes in pharmacodynamics. J Pharm Sci. 1998;87:732–7. doi: 10.1021/js970414z. [DOI] [PubMed] [Google Scholar]
- 18.Clark RA, Nielsen LD, Welch MP, McPherson JM. Collagen matrices attenuate the collagen-synthetic response of cultured fibroblasts to TGF-beta. J Cell Sci. 1995;108(Pt 3):1251–61. doi: 10.1242/jcs.108.3.1251. [DOI] [PubMed] [Google Scholar]
- 19.Tracey KJ, Fong Y, Hesse DG, Manogue KR, Lee AT, Kuo GC, Lowry SF, Cerami A. Anti-cachectin/TNF monoclonal antibodies prevent septic shock during lethal bacteraemia. Nature. 1987;330:662–4. doi: 10.1038/330662a0. [DOI] [PubMed] [Google Scholar]
- 20.Tracey KJ, Beutler B, Lowry SF, Merryweather J, Wolpe S, Milsark IW, Hariri RJ, Fahey TJ, 3rd, Zentella A, Albert JD, et al. Shock and tissue injury induced by recombinant human cachectin. Science. 1986;234:470–4. doi: 10.1126/science.3764421. [DOI] [PubMed] [Google Scholar]
- 21.Vemula M, Berthiaume F, Jayaraman A, Yarmush ML. Expression profiling analysis of the metabolic and inflammatory changes following burn injury in rats. Physiol Genomics. 2004;18:87–98. doi: 10.1152/physiolgenomics.00189.2003. [DOI] [PubMed] [Google Scholar]
- 22.Lampariello F. On the use of the Kolmogorov-Smirnov statistical test for immunofluorescence histogram comparison. Cytometry. 2000;39:179–88. doi: 10.1002/(SICI)1097-0320(20000301)39:3<179::AID-CYTO2>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 23.Kirkpatrick S, Gelatt CD, Jr, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 24.Tong W, Cao X, Harris S, Sun H, Fang H, Fuscoe J, Harris A, Hong H, Xie Q, Perkins R, Shi L, Casciano D. ArrayTrack--supporting toxicogenomic research at the U.S. Food and Drug Administration National Center for Toxicological Research. Environ Health Perspect. 2003;111:1819–26. doi: 10.1289/ehp.6497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eugenin EA, Gonzalez HE, Sanchez HA, Branes MC, Saez JC. Inflammatory conditions induce gap junctional communication between rat Kupffer cells both in vivo and in vitro. Cell Immunol. 2007;247:103–10. doi: 10.1016/j.cellimm.2007.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lyon CJ, Law RE, Hsueh WA. Minireview: adiposity, inflammation, and atherogenesis. Endocrinology. 2003;144:2195–200. doi: 10.1210/en.2003-0285. [DOI] [PubMed] [Google Scholar]
- 27.Huang JH, Liao WS. Synergistic induction of mouse serum amyloid A3 promoter by the inflammatory mediators IL-1 and IL-6. J Interferon Cytokine Res. 1999;19:1403–11. doi: 10.1089/107999099312867. [DOI] [PubMed] [Google Scholar]
- 28.Moshage H. Cytokines and the hepatic acute phase response. J Pathol. 1997;181:257–66. doi: 10.1002/(SICI)1096-9896(199703)181:3<257::AID-PATH756>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 29.Wang M, Sankula R, Tsai BM, Meldrum KK, Turrentine M, March KL, Brown JW, Dinarello CA, Meldrum DR. P38 MAPK mediates myocardial proinflammatory cytokine production and endotoxin-induced contractile suppression. Shock. 2004;21:170–4. doi: 10.1097/01.shk.0000110623.20647.aa. [DOI] [PubMed] [Google Scholar]
- 30.Dillman JF, 3rd, McGary KL, Schlager JJ. An inhibitor of p38 MAP kinase downregulates cytokine release induced by sulfur mustard exposure in human epidermal keratinocytes. Toxicol In Vitro. 2004;18:593–9. doi: 10.1016/j.tiv.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 31.Wu GS. The functional interactions between the p53 and MAPK signaling pathways. Cancer Biol Ther. 2004;3:156–61. doi: 10.4161/cbt.3.2.614. [DOI] [PubMed] [Google Scholar]
- 32.Dinarello CA. Proinflammatory cytokines. Chest. 2000;118:503–8. doi: 10.1378/chest.118.2.503. [DOI] [PubMed] [Google Scholar]
- 33.Dinarello CA. IL-18: A TH1-inducing, proinflammatory cytokine and new member of the IL-1 family. J Allergy Clin Immunol. 1999;103:11–24. doi: 10.1016/s0091-6749(99)70518-x. [DOI] [PubMed] [Google Scholar]
- 34.Tracey KJ. The inflammatory reflex. Nature. 2002;420:853–9. doi: 10.1038/nature01321. [DOI] [PubMed] [Google Scholar]
- 35.Opal SM, DePalo VA. Anti-inflammatory cytokines. Chest. 2000;117:1162–72. doi: 10.1378/chest.117.4.1162. [DOI] [PubMed] [Google Scholar]
- 36.Lagoa CE, Bartels J, Baratt A, Tseng G, Clermont G, Fink MP, Billiar TR, Vodovotz Y. The role of initial trauma in the host’s response to injury and hemorrhage: insights from a correlation of mathematical simulations and hepatic transcriptomic analysis. Shock. 2006;26:592–600. doi: 10.1097/01.shk.0000232272.03602.0a. [DOI] [PubMed] [Google Scholar]
- 37.Oliff A, Defeo-Jones D, Boyer M, Martinez D, Kiefer D, Vuocolo G, Wolfe A, Socher SH. Tumors secreting human TNF/cachectin induce cachexia in mice. Cell. 1987;50:555–63. doi: 10.1016/0092-8674(87)90028-6. [DOI] [PubMed] [Google Scholar]
- 38.Michie HR, Sherman ML, Spriggs DR, Rounds J, Christie M, Wilmore DW. Chronic TNF infusion causes anorexia but not accelerated nitrogen loss. Ann Surg. 1989;209:19–24. doi: 10.1097/00000658-198901000-00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Starnes HF, Jr, Warren RS, Jeevanandam M, Gabrilove JL, Larchian W, Oettgen HF, Brennan MF. Tumor necrosis factor and the acute metabolic response to tissue injury in man. J Clin Invest. 1988;82:1321–5. doi: 10.1172/JCI113733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tracey KJ, Wei H, Manogue KR, Fong Y, Hesse DG, Nguyen HT, Kuo GC, Beutler B, Cotran RS, Cerami A, et al. Cachectin/tumor necrosis factor induces cachexia, anemia, and inflammation. J Exp Med. 1988;167:1211–27. doi: 10.1084/jem.167.3.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tracey KJ, Lowry SF, Fahey TJ, 3rd, Albert JD, Fong Y, Hesse D, Beutler B, Manogue KR, Calvano S, Wei H, et al. Cachectin/tumor necrosis factor induces lethal shock and stress hormone responses in the dog. Surg Gynecol Obstet. 1987;164:415–22. [PubMed] [Google Scholar]
- 42.Chen G, Goeddel DV. TNF-R1 signaling: a beautiful pathway. Science. 2002;296:1634–5. doi: 10.1126/science.1071924. [DOI] [PubMed] [Google Scholar]
- 43.Pahl HL. Activators and target genes of Rel/NF-kappaB transcription factors. Oncogene. 1999;18:6853–66. doi: 10.1038/sj.onc.1203239. [DOI] [PubMed] [Google Scholar]
- 44.Hoffmann A, Levchenko A, Scott ML, Baltimore D. The IkappaB-NF-kappaB signaling module: temporal control and selective gene activation. Science. 2002;298:1241–5. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- 45.Ihekwaba AE, Broomhead DS, Grimley RL, Benson N, Kell DB. Sensitivity analysis of parameters controlling oscillatory signalling in the NF-kappaB pathway: the roles of IKK and IkappaBalpha. Syst Biol (Stevenage) 2004;1:93–103. doi: 10.1049/sb:20045009. [DOI] [PubMed] [Google Scholar]
- 46.Plackett TP, Colantoni A, Heinrich SA, Messingham KA, Gamelli RL, Kovacs EJ. The early acute phase response after burn injury in mice. J Burn Care Res. 2007;28:167–72. doi: 10.1097/BCR.0b013E31802CB84F. [DOI] [PubMed] [Google Scholar]
- 47.Sparkes BG. Immunological responses to thermal injury. Burns. 1997;23:106–13. doi: 10.1016/s0305-4179(96)00089-7. [DOI] [PubMed] [Google Scholar]
- 48.Dinarello CA. The role of the interleukin-1-receptor antagonist in blocking inflammation mediated by interleukin-1. N Engl J Med. 2000;343:732–4. doi: 10.1056/NEJM200009073431011. [DOI] [PubMed] [Google Scholar]
- 49.Dinarello CA. Interleukin-1 and its biologically related cytokines. Adv Immunol. 1989;44:153–205. doi: 10.1016/s0065-2776(08)60642-2. [DOI] [PubMed] [Google Scholar]
- 50.Fiorentino DF, Zlotnik A, Mosmann TR, Howard M, O’Garra A. IL-10 inhibits cytokine production by activated macrophages. J Immunol. 1991;147:3815–22. [PubMed] [Google Scholar]
- 51.Van den Berghe G, de Zegher F, Veldhuis JD, Wouters P, Awouters M, Verbruggen W, Schetz M, Verwaest C, Lauwers P, Bouillon R, Bowers CY. The somatotropic axis in critical illness: effect of continuous growth hormone (GH)-releasing hormone and GH-releasing peptide-2 infusion. J Clin Endocrinol Metab. 1997;82:590–9. doi: 10.1210/jcem.82.2.3736. [DOI] [PubMed] [Google Scholar]
- 52.Frost RA, Lang CH, Gelato MC. Transient exposure of human myoblasts to tumor necrosis factor-alpha inhibits serum and insulin-like growth factor-I stimulated protein synthesis. Endocrinology. 1997;138:4153–9. doi: 10.1210/endo.138.10.5450. [DOI] [PubMed] [Google Scholar]
- 53.De Maio A, Mooney ML, Matesic LE, Paidas CN, Reeves RH. Genetic component in the inflammatory response induced by bacterial lipopolysaccharide. Shock. 1998;10:319–23. doi: 10.1097/00024382-199811000-00002. [DOI] [PubMed] [Google Scholar]
- 54.Livingston DH, Mosenthal AC, Deitch EA. Sepsis and multiple organ dysfunction syndrome: a clinical-mechanistic overview. New Horiz. 1995;3:257–66. [PubMed] [Google Scholar]
- 55.Selzman CH, Shames BD, Miller SA, Pulido EJ, Meng X, McIntyre RC, Jr, Harken AH. Therapeutic implications of interleukin-10 in surgical disease. Shock. 1998;10:309–18. doi: 10.1097/00024382-199811000-00001. [DOI] [PubMed] [Google Scholar]
- 56.Rennie MJ. Muscle protein turnover and the wasting due to injury and disease. Br Med Bull. 1985;41:257–64. doi: 10.1093/oxfordjournals.bmb.a072060. [DOI] [PubMed] [Google Scholar]
- 57.Ware CF, Crowe PD, Vanarsdale TL, Andrews JL, Grayson MH, Jerzy R, Smith CA, Goodwin RG. Tumor necrosis factor (TNF) receptor expression in T lymphocytes. Differential regulation of the type I TNF receptor during activation of resting and effector T cells. The Journal of Immunology. 1991;147:4229. [PubMed] [Google Scholar]
- 58.Nelson DE, Ihekwaba AE, Elliott M, Johnson JR, Gibney CA, Foreman BE, Nelson G, See V, Horton CA, Spiller DG, Edwards SW, McDowell HP, Unitt JF, Sullivan E, Grimley R, Benson N, Broomhead D, Kell DB, White MR. Oscillations in NF-kappaB signaling control the dynamics of gene expression. Science. 2004;306:704–8. doi: 10.1126/science.1099962. [DOI] [PubMed] [Google Scholar]
- 59.Barnes PJ, Karin M. Nuclear factor- B-a pivotal transcription factor in chronic inflammatory diseases. New England Journal of Medicine. 1997;336:1066–1071. doi: 10.1056/NEJM199704103361506. [DOI] [PubMed] [Google Scholar]
- 60.Barnes PJ, Karin M. Nuclear factor-kappaB: a pivotal transcription factor in chronic inflammatory diseases. N Engl J Med. 1997;336:1066–71. doi: 10.1056/NEJM199704103361506. [DOI] [PubMed] [Google Scholar]
- 61.Waage A, Brandtzaeg P, Halstensen A, Kierulf P, Espevik T. The complex pattern of cytokines in serum from patients with meningococcal septic shock. Association between interleukin 6, interleukin 1, and fatal outcome. J Exp Med. 1989;169:333–8. doi: 10.1084/jem.169.1.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bajzer Z, Myers AC, Vuk-Pavlovic S. Binding, internalization, and intracellular processing of proteins interacting with recycling receptors. A kinetic analysis. J Biol Chem. 1989;264:13623–31. [PubMed] [Google Scholar]
- 63.LaLonde C, Hennigan J, Nayak U, Demling R. Energy charge potential and glutathione levels as predictors of outcome following burn injury complicated by endotoxemia. Shock. 1998;9:27–32. doi: 10.1097/00024382-199801000-00004. [DOI] [PubMed] [Google Scholar]
- 64.Jeschke MG, Mlcak RP, Finnerty CC, Norbury WB, Gauglitz GG, Kulp GA, Herndon DN. Burn size determines the inflammatory and hypermetabolic response. Crit Care. 2007;11:R90. doi: 10.1186/cc6102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zenker S, Rubin J, Clermont G. From inverse problems in mathematical physiology to quantitative differential diagnoses. PLoS Comput Biol. 2007;3:e204. doi: 10.1371/journal.pcbi.0030204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Koh G, Teong HF, Clement MV, Hsu D, Thiagarajan PS. A decompositional approach to parameter estimation in pathway modeling: a case study of the Akt and MAPK pathways and their crosstalk. Bioinformatics. 2006;22:e271–80. doi: 10.1093/bioinformatics/btl264. [DOI] [PubMed] [Google Scholar]
- 67.Chrysikopoulos CV, Hsuan PY, Fyrillas MM. Bootstrap estimation of the mass transfer coefficient of a dissolving nonaqueous phase liquid pool in porous media. Water Resources Research. 2002;38 [Google Scholar]
- 68.Efron B, Tibshirani R. An Introduction to the Bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]
- 69.Munford RS. Severe sepsis and septic shock: the role of gram-negative bacteremia. Annu Rev Pathol. 2006;1:467–96. doi: 10.1146/annurev.pathol.1.110304.100200. [DOI] [PubMed] [Google Scholar]
- 70.Karin M, Greten FR. NF-kappaB: linking inflammation and immunity to cancer development and progression. Nat Rev Immunol. 2005;5:749–59. doi: 10.1038/nri1703. [DOI] [PubMed] [Google Scholar]
- 71.Li Q, Verma IM. NF-kappaB regulation in the immune system. Nat Rev Immunol. 2002;2:725–34. doi: 10.1038/nri910. [DOI] [PubMed] [Google Scholar]
- 72.Lawrence T, Bebien M, Liu GY, Nizet V, Karin M. IKKalpha limits macrophage NF-kappaB activation and contributes to the resolution of inflammation. Nature. 2005;434:1138–43. doi: 10.1038/nature03491. [DOI] [PubMed] [Google Scholar]
- 73.Karin M, Ben-Neriah Y. Phosphorylation meets ubiquitination: the control of NF-[kappa]B activity. Annu Rev Immunol. 2000;18:621–63. doi: 10.1146/annurev.immunol.18.1.621. [DOI] [PubMed] [Google Scholar]
- 74.Minnich DJ, Moldawer LL. Anti-cytokine and anti-inflammatory therapies for the treatment of severe sepsis: progress and pitfalls. Proc Nutr Soc. 2004;63:437–41. doi: 10.1079/pns2004378. [DOI] [PubMed] [Google Scholar]
- 75.Dinarello CA. Biologic basis for interleukin-1 in disease. Blood. 1996;87:2095–147. [PubMed] [Google Scholar]
- 76.Freeman BD, Buchman TG. Interleukin-1 receptor antagonist as therapy for inflammatory disorders. Expert Opin Biol Ther. 2001;1:301–8. doi: 10.1517/14712598.1.2.301. [DOI] [PubMed] [Google Scholar]
- 77.Clermont G, Bartels J, Kumar R, Constantine G, Vodovotz Y, Chow C. In silico design of clinical trials: a method coming of age. Crit Care Med. 2004;32:2061–70. doi: 10.1097/01.ccm.0000142394.28791.c3. [DOI] [PubMed] [Google Scholar]