Abstract
Protein-protein binding events mediate many critical biological functions in the cell. Typically, functionally important sites in proteins can be well identified by considering sequence conservation. However, protein-protein interaction sites exhibit higher sequence variation than other functional regions, such as catalytic sites of enzymes. Consequently, the mutational behavior leading to weak sequence conservation poses significant challenges to the protein-protein interaction site prediction. Here, we present a phylogenetic framework to capture critical sequence variations that favor the selection of residues essential for protein-protein binding. Through the comprehensive analysis of diverse protein families, we show that protein binding interfaces exhibit distinct amino acid substitution as compared with other surface residues. Based on this analysis, we have developed a novel method, BindML, which utilizes the substitution models to predict protein-protein binding sites of protein with unknown interacting partners. BindML estimates the likelihood that a phylogenetic tree of a local surface region in a query protein structure follows the substitution patterns of protein binding interface and non-binding surfaces. BindML is shown to perform well compared to alternative methods for protein binding interface prediction. The methodology developed in this study is very versatile in the sense that it can be generally applied for predicting other types of functional sites, such as DNA, RNA, and membrane binding sites in proteins.
Keywords: Protein-protein interaction, protein interaction site prediction, phylogenetic substitution model, mutation pattern, sequence analysis
Introduction
Protein-protein interactions (PPIs) mediate many critical biological processes in the cell. The complexity of the interactions can be seen through the recent construction of large-scale PPI maps, which reveal the intricate functional interplay between many proteins in pathways and the formation of oligomeric complexes1–3. At the same time, genome sequencing projects and the structural genomic initiatives are rapidly accumulating individual protein sequences and structures4;5. With the increasing availability of individual protein data and their interactions, it is becoming more essential to locate protein binding interfaces (PBIs) of many interacting proteins to bridge the gap between the global view of PPI networks and high-resolution scrutiny of amino acids that structurally form protein complexes. PBI prediction is indispensable toward this end, where it can help substantiate PPI data as a critical platform for enhanced molecular recognition research and experimental design.
Various ideas have been explored in predicting PBI in proteins, which utilize structural- and/or sequence-based features. Several structure-based methods use relative area of solvent accessibilities based on the observation that interacting residues are generally more exposed on the protein surface6–10. The other structural features used include surface shape7;10;11, the crystallographic temperature factors6, and the propensity of the secondary structure at PBI6. Several studies utilize specific physiochemical properties and energetic features. These features include desolvation energies12 and complementary residue-residue charges that establish salt bridges across interfaces13. These features have been used by machine learning techniques such as neural networks14;15 and naive Bayesian classifiers6 for PBI site prediction. The increasing value of sequence and structural features employed by PBI site prediction methods are discussed in recent reviews16,17.
Although amino acid composition at the PBI is biased compared to non-PBI (NPBI) sites7;13;18;19, it was reported that PBI sites are less conserved than protein cores and functional sites in proteins, such as ligand binding sites and catalytic sites20;21. Hence, conventional sequence conservation can be used as one of the features of PBI sites20–22, but it is not sufficient to be used alone for prediction21;23. Other than sequence conservation, phylogenetic information24 and correlated mutation25 has been used for predict PBI but only for specific biological instances.
Here, we have developed a novel PBI site prediction method, named Binding site prediction by Maximum Likelihood (BindML), which utilizes mutational constraints that are found in known PBI and NPBI sites. The mutation patterns of known PBI sites and NPBI sites are captured in the form of amino acid substitution models (i.e. amino acid similarity matrices). BindML uses these substitution models with a likelihood-based phylogenetic tree inference method to compute and compare the likelihood that the mutation pattern of a local protein surface patch follows that of PBI and NPBI by constructing trees. There exist methods that employ phylogenetic trees to predict protein functional sites24;26–28. A class of such methods use phylogenetic trees to examine residue conservation within and across subfamilies26;29–31. Another class of methods identifies regions with a constrained mutation pattern as functional sites using phylogenetic trees27;28. In contrast, our method, BindML, specifically determines whether a multiple sequence alignment (MSA) taken from a local surface patches on the structure of the query protein exhibit mutation patterns that follow PBI or NPBI, which is achieved by evaluating the likelihood that phylogenetic trees constructed for the MSA of the local patch follow the sequence evolution of PBI or NPBI substitution models. Remarkably, BindML performs well in comparison to existing methods, which combine various sequence and structural information into machine learning frameworks. The impact of our method is broad, since it can be easily extended for predicting other specific types of functional sites, such as DNA, RNA, or membrane binding sites in proteins if such functional sites have characteristic amino acid mutation patterns that are distinguishable from other sites. The conceptual novelty of this method is that it detects constrained sequence variations rather than conventional conservation in protein family sequences, thus aimed to open a new direction in protein sequence analysis.
Materials and Methods
Dataset of Protein-Protein Complexes
Multiple sequence alignments (MSAs) of protein complexes were taken from the iPFAM database of protein-protein interactions, which provided an initial dataset of 2733 pair-wise protein-protein interactions in the PFAM database (rel. 12.0)32. The interactions in iPFAM are based on structural evidence found from complexes in the Protein Data Bank (PDB). We applied the following eight criteria to filter the iPFAM entries: (1) the unaligned seed sequences for each corresponding PFAM family were used. (2) We selected PFAM families with 20 to 100 seed sequences yielding 748 PFAM families. (3) PFAM families consisting domain sequences were replaced with their corresponding full-length sequences from UniProt33. A representative PDB structure was then selected from each PFAM family given by the association in iPFAM. When a PFAM family has more than one structure representative, we selected one of them arbitrarily. (4) Protein structures that do not have any observable interacting partners in their PDB files were removed. (5) Complexes were eliminated if they are classified as monomers bound by crystal contacts in the PQS definition34. (6) Proteins with their PDB entries that have nonstandard amino acids, too small proteins where the entire structure are part of PPI sites, short protein sequences (shorter than 40 amino acids), and obsolete PDB files were filtered out. (7) PDB structures with antibody-antigen and protein-DNA/RNA interactions were removed. (8) In the final dataset, PFAM families with redundant representative structures with ≥35% sequence identity were filtered out. Given that MSAs in PFAM may not have the PDB structure as a part of the alignment, we employed MUSCLE (ver. 3.6)35 with default parameters to compute MSAs from PFAM unaligned sequences and one sequence from the selected PDB structure. This procedure forms the final MSA dataset of 505 families. The dataset can be accessed at http://kiharalab.org/bindml/families.tar.gz.
In addition, we have also tested the performance of BindML to proteins in unbound conformations. 107 proteins with bound and unbound conformations are selected from 112 structures in the protein-protein docking benchmark dataset ver. 4.036, which have MSAs in the PFAM database.
Amino Acid Substitution Models
Amino acid substitution models (matrices) reflect the ratio of pair-wise amino acid substitutions observed in MSAs and the same amino acid pairs appearing by chance. Substitution models for PBI and NPBI were constructed from the MSAs in the filtered iPFAM dataset. Protein surface residues were defined as those which have larger than 10% of the relative solvent accessible area in comparison with the value in the tripeptide with glycines on both sides37. Among the protein surface, residues at PBI were defined as those that are closer than 5Å to any residues in the protein docking partner, otherwise residues were defined as NPBI. The observed substitutions for PBI and NPBI were counted at gapless positions in the set of pairwise set of alignments following the JTT procedure38. The values in the substitution matrices were calculated using the BLOSUM method39. The PBI and the NPBI substitution models are given Table 1A and 1B, respectively.
Table 1.
Log odds matrices for PBI and NPBI.
| (A) PBI model. | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PBI | A | R | N | D | C | Q | E | G | H | I | L | K | M | F | P | S | T | W | Y | V |
| A | 3 | −2 | −1 | −1 | −1 | −1 | −1 | −1 | −2 | −2 | −2 | −1 | −1 | −2 | −1 | 0 | 0 | −3 | −2 | 0 |
| R | −2 | 3 | −1 | −2 | −2 | 0 | −1 | −2 | −1 | −2 | −2 | 1 | −2 | −3 | −2 | −1 | −2 | −2 | −2 | −2 |
| N | −1 | −1 | 4 | 0 | −1 | −1 | −1 | −1 | 0 | −2 | −3 | 0 | −2 | −2 | −2 | 0 | −1 | −3 | −2 | −2 |
| D | −1 | −2 | 0 | 3 | −3 | −1 | 1 | −1 | −1 | −3 | −3 | −1 | −3 | −3 | −2 | −1 | −1 | −4 | −3 | −3 |
| C | −1 | −2 | −1 | −3 | 6 | −2 | −3 | −2 | −2 | −2 | −2 | −2 | −1 | −1 | −3 | 0 | −1 | −2 | −1 | −1 |
| Q | −1 | 0 | −1 | −1 | −2 | 4 | 0 | −2 | 0 | −2 | −1 | 0 | −1 | −3 | −2 | −1 | −1 | −2 | −2 | −2 |
| E | −1 | −1 | −1 | 1 | −3 | 0 | 3 | −2 | −2 | −3 | −2 | 0 | −2 | −3 | −2 | −1 | −1 | −3 | −3 | −2 |
| G | −1 | −2 | −1 | −1 | −2 | −2 | −2 | 3 | −2 | −4 | −3 | −2 | −3 | −3 | −2 | −1 | −2 | −3 | −3 | −3 |
| H | −2 | −1 | 0 | −1 | −2 | 0 | −2 | −2 | 4 | −2 | −2 | −1 | −2 | −1 | −2 | −1 | −2 | −2 | 0 | −2 |
| I | −2 | −2 | −2 | −3 | −2 | −2 | −3 | −4 | −2 | 3 | 0 | −2 | 0 | −1 | −2 | −2 | −1 | −3 | −2 | 1 |
| L | −2 | −2 | −3 | −3 | −2 | −1 | −2 | −3 | −2 | 0 | 3 | −2 | 1 | 0 | −2 | −2 | −2 | −2 | −1 | 0 |
| K | −1 | 1 | 0 | −1 | −2 | 0 | 0 | −2 | −1 | −2 | −2 | 3 | −1 | −3 | −2 | −1 | −1 | −3 | −2 | −2 |
| M | −1 | −2 | −2 | −3 | −1 | −1 | −2 | −3 | −2 | 0 | 1 | −1 | 4 | −1 | −3 | −1 | −1 | −2 | −2 | 0 |
| F | −2 | −3 | −2 | −3 | −1 | −3 | −3 | −3 | −1 | −1 | 0 | −3 | −1 | 4 | −3 | −2 | −2 | 0 | 1 | −1 |
| P | −1 | −2 | −2 | −2 | −3 | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −3 | −3 | 4 | −1 | −1 | −3 | −3 | −2 |
| S | 0 | −1 | 0 | −1 | 0 | −1 | −1 | −1 | −1 | −2 | −2 | −1 | −1 | −2 | −1 | 3 | 0 | −2 | −2 | −2 |
| T | 0 | −2 | −1 | −1 | −1 | −1 | −1 | −2 | −2 | −1 | −2 | −1 | −1 | −2 | −1 | 0 | 3 | −3 | −2 | 0 |
| W | −3 | −2 | −3 | −4 | −2 | −2 | −3 | −3 | −2 | −3 | −2 | −3 | −2 | 0 | −3 | −2 | −3 | 6 | 0 | −2 |
| Y | −2 | −2 | −2 | −3 | −1 | −2 | −3 | −3 | 0 | −2 | −1 | −2 | −2 | 1 | −3 | −2 | −2 | 0 | 4 | −2 |
| V | 0 | −2 | −2 | −3 | −1 | −2 | −2 | −3 | −2 | 1 | 0 | −2 | 0 | −1 | −2 | −2 | 0 | −2 | −2 | 3 |
| (B)NPBI model. | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NPBI | A | R | N | D | C | Q | E | G | H | I | L | K | M | F | P | S | T | W | Y | V |
| A | 3 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −2 | −1 | 0 | 0 | −2 | −2 | 0 |
| R | −1 | 3 | −1 | −2 | −2 | 0 | −1 | −2 | 0 | −2 | −1 | 1 | −1 | −2 | −2 | −1 | −1 | −2 | −2 | −2 |
| N | −1 | −1 | 3 | 0 | −2 | −1 | −1 | −1 | 0 | −2 | −2 | 0 | −2 | −2 | −2 | 0 | 0 | −3 | −1 | −2 |
| D | −1 | −2 | 0 | 3 | −3 | −1 | 0 | −1 | −1 | −3 | −3 | −1 | −2 | −3 | −1 | −1 | −1 | −3 | −2 | −2 |
| C | −1 | −2 | −2 | −3 | 6 | −2 | −3 | −2 | −1 | −1 | −1 | −2 | −1 | −1 | −2 | −1 | −1 | −1 | −1 | −1 |
| Q | −1 | 0 | −1 | −1 | −2 | 3 | 0 | −2 | 0 | −2 | −1 | 0 | −1 | −2 | −1 | −1 | −1 | −2 | −2 | −1 |
| E | −1 | −1 | −1 | 0 | −3 | 0 | 2 | −2 | −1 | −2 | −2 | 0 | −2 | −3 | −1 | −1 | −1 | −3 | −2 | −2 |
| G | −1 | −2 | −1 | −1 | −2 | −2 | −2 | 3 | −2 | −3 | −3 | −2 | −2 | −3 | −2 | −1 | −2 | −3 | −3 | −3 |
| H | −1 | 0 | 0 | −1 | −1 | 0 | −1 | −2 | 4 | −2 | −1 | −1 | −2 | −1 | −2 | −1 | −1 | −1 | 1 | −2 |
| I | −1 | −2 | −2 | −3 | −1 | −2 | −2 | −3 | −2 | 4 | 1 | −2 | 1 | 0 | −2 | −2 | −1 | −2 | −1 | 2 |
| L | −1 | −1 | −2 | −3 | −1 | −1 | −2 | −3 | −1 | 1 | 3 | −2 | 1 | 0 | −2 | −2 | −1 | −1 | −1 | 0 |
| K | −1 | 1 | 0 | −1 | −2 | 0 | 0 | −2 | −1 | −2 | −2 | 3 | −1 | −2 | −1 | −1 | −1 | −3 | −2 | −2 |
| M | −1 | −1 | −2 | −2 | −1 | −1 | −2 | −2 | −2 | 1 | 1 | −1 | 5 | 0 | −2 | −1 | 0 | −1 | −1 | 0 |
| F | −2 | −2 | −2 | −3 | −1 | −2 | −3 | −3 | −1 | 0 | 0 | −2 | 0 | 4 | −3 | −2 | −2 | 1 | 2 | −1 |
| P | −1 | −2 | −2 | −1 | −2 | −1 | −1 | −2 | −2 | −2 | −2 | −1 | −2 | −3 | 4 | −1 | −1 | −3 | −2 | −2 |
| S | 0 | −1 | 0 | −1 | −1 | −1 | −1 | −1 | −1 | −2 | −2 | −1 | −1 | −2 | −1 | 3 | 0 | −2 | −2 | −1 |
| T | 0 | −1 | 0 | −1 | −1 | −1 | −1 | −2 | −1 | −1 | −1 | −1 | 0 | −2 | −1 | 0 | 3 | −2 | −2 | 0 |
| W | −2 | −2 | −3 | −3 | −1 | −2 | −3 | −3 | −1 | −2 | −1 | −3 | −1 | 1 | −3 | −2 | −2 | 6 | 1 | −2 |
| Y | −2 | −2 | −1 | −2 | −1 | −2 | −2 | −3 | 1 | −1 | −1 | −2 | −1 | 2 | −2 | −2 | −2 | 1 | 4 | −1 |
| V | 0 | −2 | −2 | −2 | −1 | −1 | −2 | −3 | −2 | 2 | 0 | −2 | 0 | −1 | −2 | −1 | 0 | −2 | −1 | 3 |
The BindML Algorithm
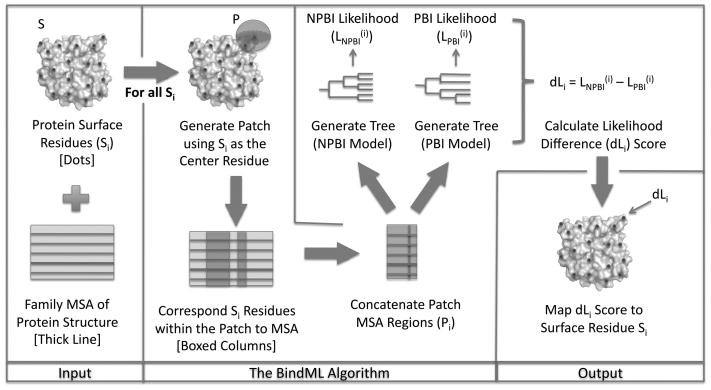
A flow chart of the BindML algorithm is illustrated in Figure 1. The method takes a PDB structure of a target protein and a MSA of its family including the target sequence. For each surface residue, a patch is defined as neighboring residues that are within the sphere of a certain radius. The β-carbon of a given amino acid (α-carbon is used for glycine) is selected as the representative point when computing the distance between amino acids. For a patch, all corresponding residues in the MSA are concatenated together. As will be shown later in Results, the radius of 15Å was found to perform the best.
Figure 1.
Flowchart of the BindML algorithm.
We employed our modified version of the PHYML (ver. 2.4.5) program40 to compute the likelihood that a patch MSA comes from PBI and NPBI by constructing phylogenetic trees with either the PBI or NPBI substitution models. PHYML is a maximum likelihood method that builds a phylogenetic tree for a given MSA and adjusts the topology and branch length simultaneously. The algorithm starts from an initial tree constructed by the BIONJ method41, a fast distance-based algorithm, and improves it by branch-length optimization and tree swapping procedures. BIONJ has been shown to outperform other distance-based tree inference methods42. To compute the likelihood of a surface patch as PBI/NPBI, we feed PHYML with the MSA of the patch and select the PBI/NPBI substitution model and the amino acid frequency distribution of PBI/NPBI, which is used as the equilibrium frequencies. Values in the PBI/NPBI substitution model are shifted so that all the values in the matrices are positive, which is required by PHYML.
Due to the large number of residue points on the protein surface that are needed to compute the likelihood values, we used the initial tree topology computed by BIONJ rather than the optimized tree with the maximized likelihood. This shortcut speeds up the computation dramatically, by about 15 times, and nevertheless, the prediction accuracy did not deteriorate significantly. PHYML computes the likelihood of having the input patch MSA following the PBI/NPBI substitution model given the initial tree topology. Finally, the difference of the likelihood under PBI and NPBI substitution models provides a score used to predict PPI sites. For a patch MSA, Pi, which has residue i at the center,
| (1) |
| (2) |
| (3) |
where MNPBI and MPBI is the substitution model of NPBI and PBI, respectively, and TNPBIi and TPBIi are tree generated with MNPBI and MPBI, respectively, for the input patch MSA. Note that TNPBIi and TPBIi are not necessarily identical. The distance likelihood (dL) score is the difference between the log likelihood of the patch MSA being NPBI and PBI (Eqn. 3). Once the dL scores for all surface residues are computed, these scores are recast into Z-scores and a threshold is placed. Lower (negative) Z-scores indicate more likelihood of PBI mutation patterns, while higher Z-scores correspond to less likelihood of following the PBI substitution model. Any residues with a dL score that is equal to or smaller than a given Z-score threshold value are predicted to be included in a PPI site. Thus, BindML determines whether the mutation pattern of a given local surface patch is more likely to occur from PBI site or NPBI site. A web server implementation and stand-alone program for BindML is available at http://kiharalab.org/bindml/.
Evaluation of the Prediction Performance
The prediction performance of PBI residues was evaluated mainly using the area under the curve (AUC) of the receiving operator characteristic (ROC)43. A ROC curve plots the false positive rate relative the true positive rate over various scoring threshold values of a method. The overall AUC of a method was computed as the average of ROCs for every protein family in the dataset. In addition to the AUC, we also provide the sensitivity, the specificity, and the positive predictive value (PPV). True positives (TP) are the true binding interfaces residues predicted correctly, true negatives (TN) are non-protein-protein interactions sites correctly classified, false positives (FP) are false predictions of protein-protein interaction sites, and false negatives (FN) are protein-protein binding sites that are not predicted. The sensitivity is the fraction of correctly predicted PBI residues over all the true PBI residues. The specificity is the fraction of true negatives among all residues predicted to be NPBI. PPV is defined as the true positives among those residues predicted to be PBI. The Matthews Correlation Coefficient (MCC) measures the correlation between observed and predicted PBI and NPBI, where a value of −1 represent inverse prediction, 0 mean random prediction, and 1 is a perfect prediction.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Other Methods used for Comparison
We compared BindML with two existing methods, ProMate6 and cons-PPISP15. ProMate is based on a naïve Bayesian method that uses a combination of various sequence-based (single amino acid distribution, amino acid pairs distribution, and evolutionary conserved positions) and structural-based properties (non-regular secondary structure length, secondary structure, hydrophobic patch rank, and water molecules). Cons-PPISP uses sequence conservation and relative solvent accessibilities of residues as features in a consensus neural network, which is a combination of multiple differently parameterized neural networks. Web servers of the two methods were used (ProMate: http://bioinfo.weizmann.ac.il/promate/; cons-PPISP: http://pipe.scs.fsu.edu/ppisp.html). We disregarded entries in the iPFAM dataset when either ProMate or cons-PPISP servers did not return prediction results by batch processing. Thus, 449 entries in the iPFAM dataset were used for the performance comparison with BindML.
Results
Comparison of PBI and NPBI Substitution Models
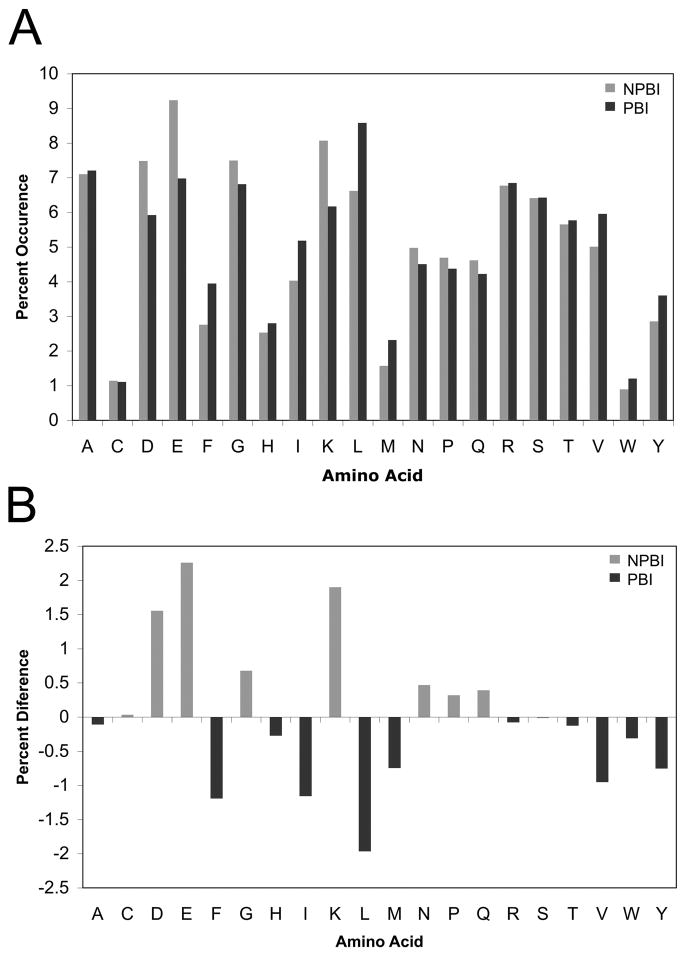
BindML exploits the differences in the amino acid substitutions at PBI and those at NPBI for protein binding site prediction. First, we compared the amino acid frequency at PBI and NPBI sites. Differences in the amino acids frequencies at PBI and NPBI were counted in multiple sequence alignments (MSAs) in the iPFAM dataset (Fig. 2A & 2B). Several amino acids showed noticeable differences in frequency at PBI and NPBI. Aromatic residues and hydrophobic residues were more abundant at PBI than NPBI. On the other hand, NPBI sites were richer in charged residues as compared with PBI sites. These results are consistent with previous studies6;7;18;23.
Figure 2.
A, Distribution of the frequencies of the standard amino acids in the dataset used in this study. Black bars correspond to known protein binding interfaces (PBI) and gray bars represent non-protein binding interfaces (NPBI). B, The difference of the amino acid frequency at the NPBI and the PBI. The percentage occurrence of each amino acid at PBI is subtracted from the corresponding value at NPBI.
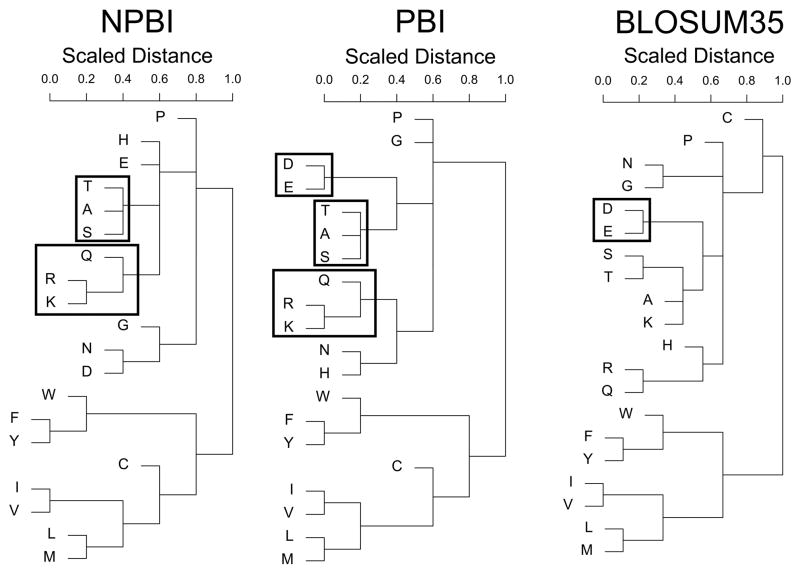
Next, we compared amino acid substitutions at PBI and NPBI sites (Fig. 3). We also included the BLOSUM35 matrix39 in comparison to clarify the distinction between the newly constructed NPBI and PBI substitution models. Among the series of BLOSUM matrices, we chose BLOSUM35 because it is generated with a 35% sequence identity threshold, which is the same similarity cutoff that we used to compute the PBI and the NPBI models.
Figure 3.
Cluster dendrograms of amino acid substitutions from the NPBI and PBI models, as well as BLOSUM35. Common subclasses of the hydrophilic substitutions are in shown in boxes.
Although the PBI and the NPBI models were more correlated with each other (a correlation coefficient of 0.906) relative to the BLOSUM35 (the correlation coefficient values with the PBI and the NPBI are 0.721 and 0.726, respectively), they were different with statistical significance when subject to a Kolmogorov-Smirnov distribution test (D=0.171, p=0.004)44. In Figure 3, the three substitution models were compared by complete linkage clustering of the log-odd values of the substitution models. To compute the distance of an amino acid pair, the log-odds score of the pair was negated and shifted by a constant value to have all the positive distances. Then, the distance values were normalized to a range between 0 and 1.
All three models showed clear division of aromatic and hydrophobic amino acids from the rest of the residues. Hydrophobic amino acids on protein surfaces appeared to have conservative mutations between each other (i.e. a smaller distance) even at NPBI sites, implying that they could possibly correspond to other types of functionally important regions that may not directly involve PPI45. BLOSUM35 classified cysteine with the polar groups, while NPBI and PBI placed cysteine in the hydrophobic cluster of residues. The similarities between the NPBI and PBI models were observed for the sub-classification of polar amino acid substitutions. The clustering of polar residues in the NPBI and PBI models had common arginine↔lysine↔gluatamine and threonine↔alanine↔serine substitution marked in boxes in Figure 3. When comparing PBI with BLOSUM35, there was only one instance of a common subcluster, aspartic acid glutamic acid, which did not appear in the NPBI.
There were several differences between overall NPBI and PBI. The two common subtrees, arginine↔lysine↔gluatamine and threonine↔alanine↔serine, were grouped with different amino acids in the PBI and NPBI. There was also clear distinction in the substitution preference of asparagines and glycine. Taken together, we observed distinct amino acid substitutions found at protein binding interfaces, which would be useful in identifying protein binding regions of the protein surface.
Example of Protein Binding Site Prediction by BindML
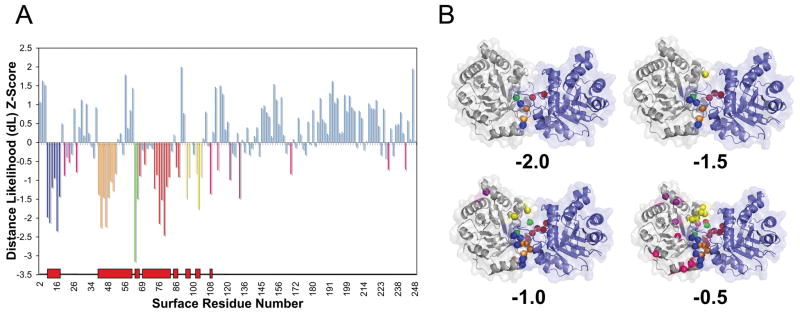
To begin with discussing PBI prediction results, we present an example of protein binding site prediction by BindML for a homo-dimer structure, triosephosphate isomerase (PDB ID: 7TIMA). A MSA for this protein was taken from the PFAM database 46 (PFAM ID: PF00121). In Figure 4A, the Z-score of each surface amino acid is indicated as a vertical bar, where smaller Z-scores are more likely to be included in PBI. To illustrate how the predicted residues change with different threshold values, predictions made using four Z-score threshold values, −2.0, −1.5, −1.0, and −0.5 are shown.
Figure 4.
An example of protein binding interface prediction by BindML (PDB ID: 7TIMA). (A) The colored vertical bars in the graph show residues predicted with a Z-score value at or below threshold values, −2.0, −1.5, −1.0, or −0.5. Each range of sequence signals colored in green, red, blue, orange, and yellow bars corresponds to the first, second, third, forth, and fifth highest scoring regions, respectively. The red blocks along the x-axis indicate the correct interface regions. (B) The predicted residues using the four different threshold values are shown in the same colors on the structure.
As shown in the mapped structures (Fig. 4B), using the Z-score −2.0 and −1.5 did not yield any over predictions. The specificity was 1.0 for the two cases, and the sensitivity was 0.212 and 0.303 for the Z-score value of −2.0 and −1.5, respectively. Increasing the Z-score threshold to −1.00 resulted in predicting more residues at the true interface (sensitivity: 0.636, specificity: 0.984) with a single false positive residue. Further increasing the Z-score threshold to −0.50 provided a good trade-off in the sensitivity (0.849) and the specificity (0.893). Obviously, more residues were predicted as PBI when the Z-score threshold was raised, however, predictions were mostly concentrated on the true PBI sites. The strongest signal (colored in green with the lowest Z-score of −3.151 corresponding to glutamine 64) was located at the most central part of the true PBI. The second strongest signals (including a significant Z-score of −2.455 for asparagine 78) spanned over the residue range from 68 to 87 (with some gaps) colored in red, which corresponds to a protruding binding loop. The third significant region, residue 12–17 (blue) and the fourth, residue 43–46, 48, 49, 51, 52 (orange) with the strongest Z-score of −2.230, corresponded to loop regions, which bind the protruding loop of the symmetrically bound partner (this loop is an equivalent region that was previously shown in red). Finally, the fifth signal included phenylalanine 102 (colored in yellow with the Z-score of −1.751), which is a part of a loop that follows a short six-residue helix. Overall, the prediction performance on 7TIM showed an outstanding AUC value of 0.936.
Effect of different alignment and prediction sphere sizes
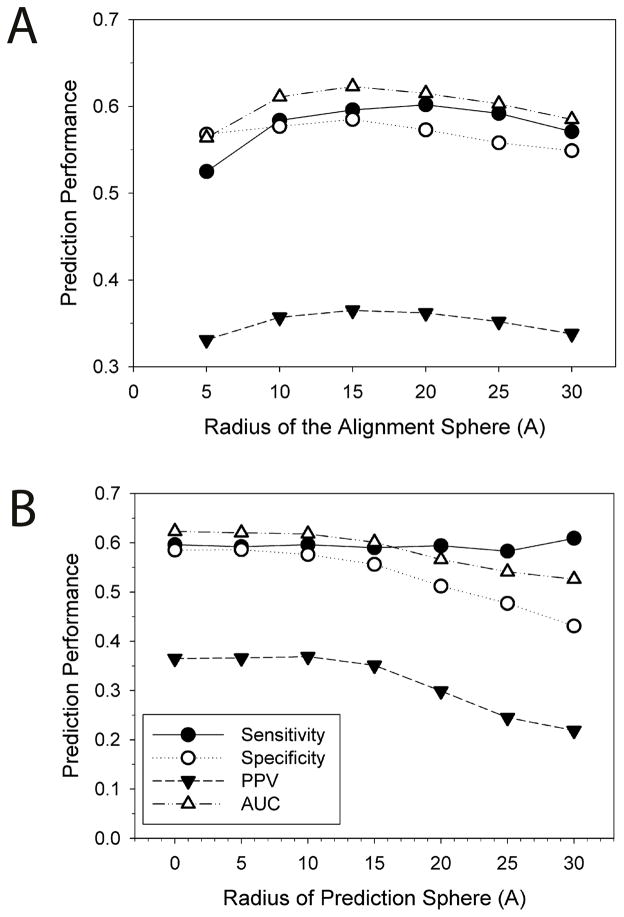
BindML extracts partial MSAs by employing a sphere that is centered at a particular surface residue (the alignment sphere) and another sphere to map the final PBI prediction to residues within it (the prediction sphere). Figure 5 shows the effect of the changing sphere sizes.
Figure 5.
AUC relative to the size of the alignment sphere (A) and the prediction sphere (B). One entry, 1AVZ-C, is discarded from the iPFAM dataset because the use of a sphere of 30 Å radius centered at every surface residue captures the entire protein. The 35% sequence identity was used as the threshold values for computing the PBI/NPBI substitution models. These results show the optimal Z-score threshold value is chosen for each prediction sphere size that gives the closest point to the true positive and the false positive rate of 1 and 0 on the ROC curve, respectively. Therefore, the sensitivity does not simply increase when larger prediction sphere sizes are used.
The radius of the alignment sphere was changed from 5 to 30 Å (Fig. 5A). Approximately two residues were included when the radius of five is used, while it increased to 25 and 101 residues for the radius of 15 and 30 Å, respectively. The best prediction performance was observed when using a sphere size of 15 Å in terms of all the performance metric we used except for the sensitivity. A sphere of 15 Å radius covered roughly 700 Å2 of the protein surface area, which corresponded to about one third of the average PBI surface area in the iPFAM dataset (2200 Å2).
Figure 5B shows the performance of BindML with different prediction sphere sizes. With the prediction sphere size of 0 Å, PBI prediction was assigned just to the center residue of the sphere. With larger sphere sizes, all the residues included in the sphere were predicted as a PBI site. The results showed that simply assigning prediction to the center residue (i.e. sphere size of 0 Å) performed the best in terms of the AUC value (0.623). Based on these results, we used the alignment sphere of 15 Å radius and the prediction sphere of 0 Å in the subsequent benchmark studies.
Prediction performance of BindML
We benchmarked BindML by a five-fold cross validation using the iPFAM dataset. The whole dataset of 505 proteins are randomly split into five subsets. The list of proteins in the five subsets is provided in the supplementary materials (Table S1), which is made available at http://kiharalab.org/bindml/suppl.pdf. The training set, which consists of four fifth of the entire dataset, was used to compute the PBI and the NPBI substitution models and also to determine the optimal sequence identity threshold value of sequence pairs for computing the substitution models. Sequences which are closer than the threshold value to any other sequence in the dataset were pruned out. Then, the computed PBI/NPBI substitution models were used in making predictions on the remaining one fifth of the dataset (testing set). This process was repeated five times by changing the testing and training sets.
Both training and testing sets yielded an average AUC value of 0.624, indicating that the PBI and the NPBI models were very well generalized for protein-protein binding site prediction. The AUC values for each of the five training and the corresponding testing sets were given in Table 2. The sequence identity threshold values used to compute the substitution models was optimized for each training set. The threshold values for the five training datasets were consistent, where 35% worked best for the three training sets and 30% was optimal for the remaining two sets. Further, to eliminate the influence of similar proteins more thoroughly, we strictly excluded proteins in the control dataset with equal to or higher than 25% in the sequence identity to those found in the training dataset, which still resulted in very consistent AUCs between the control (0.623) and training (0.624) datasets (the two rightmost columns in Table 2). We have also compared the global (built using the entire iPFAM dataset, Table 1) and each substitution model built using each training dataset. We found that they are very consistent, showing an average correlation coefficient of 0.9988 for PBI and 0.9836 for NPBI models.
Table 2.
Performances of each of the five cross validation datasets.
| Dataset | Sequence Identity Threshold (%) | Control AUC | Training AUC | Control AUC (25% cutoff) a) | Training AUC (25% cutoff) |
|---|---|---|---|---|---|
| 1 | 35 | 0.643 | 0.617 | 0.637 | 0.617 |
| 2 | 35 | 0.599 | 0.630 | 0.597 | 0.630 |
| 3 | 35 | 0.625 | 0.627 | 0.622 | 0.627 |
| 4 | 30 | 0.658 | 0.616 | 0.662 | 0.616 |
| 5 | 30 | 0.596 | 0.631 | 0.596 | 0.631 |
|
| |||||
| Average | 0.624 | 0.624 | 0.623 | 0.624 | |
Proteins in the control dataset which have equal to or more than 25% sequence identity to any of proteins in the training set were strictly removed.
In Table 3, we examined the effect of sequence identity threshold values used to compute the substitution models on the prediction performance of BindML. As the purpose was to investigate the effect of the parameter, the entire iPFAM dataset was used. Raising the threshold value increased the number of sequences included in each family, while lowering the threshold eliminated more sequences. The sensitivity and the specificity was computed using a threshold Z-score which gave the closest point in the ROC curve to the true positive and the false positive rate of 1 and 0 (i.e. the corner of the ROC curve). A 35% sequence identity yielded the highest predictive performance with the highest AUC value (0.623), the positive predict value (0.365), and the sensitivity (0.596). Because of its best performance, we have chosen 35% sequence identity in the subsequent analyses.
Table 3.
Effect of different sequence identity percentage cutoff values for PBI and NPBI Substitution Models.
| Percent Identity | Sensitivity | Specificity | PPV | AUC |
|---|---|---|---|---|
| 60 | 0.496 | 0.486 | 0.276 | 0.481 |
| 55 | 0.464 | 0.490 | 0.265 | 0.463 |
| 50 | 0.546 | 0.445 | 0.277 | 0.482 |
| 45 | 0.571 | 0.435 | 0.283 | 0.489 |
| 40 | 0.516 | 0.487 | 0.282 | 0.489 |
| 35 | 0.596 | 0.585 | 0.365 | 0.623 |
| 30 | 0.596 | 0.581 | 0.363 | 0.622 |
| 25 | 0.584 | 0.584 | 0.361 | 0.617 |
| 20 | 0.585 | 0.584 | 0.362 | 0.617 |
| 15 | 0.584 | 0.586 | 0.362 | 0.617 |
| 10 | 0.585 | 0.585 | 0.362 | 0.618 |
Patches on the surface are generated using a scanning sphere size of 15Å and a defining instance of a given predicted site as the single central residue in the sphere. Line in bold text highlights parameters used with the best threshold value.
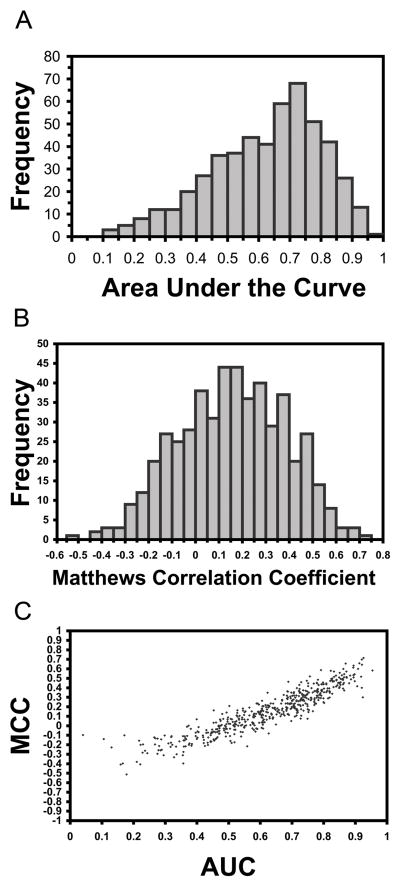
Distribution of Individual Performances
On closer inspection of individual predictions by BindML, we analyzed the distribution of AUCs for all proteins in the iPFAM dataset (Fig. 6A). The AUC values were taken from the testing dataset in the cross validation (Table 2). Although we reported an average AUC of 0.624 in the previous section, the performance of individual prediction distributed widely from almost perfect prediction, 0.956, to predictions below 0.5 (Fig. 6A). The peak of the AUC distribution was between 0.70 and 0.75 (consisting 68 proteins), and the second most frequent AUC values were in the range of 0.75 to 0.80 (51 proteins). Predictions above AUC of 0.5 shared 86.9%. In addition, we computed the distribution of MCC values using a Z-score threshold of −0.5, which provided good balance of sensitivity and specificity for many proteins in the iPFAM benchmark dataset (Figure 6B). The average MCC value was 0.156. As shown in Figure 6C, AUC and MCC correlate well with a correlation coefficient of 0.918. Thus, MCC of the predictions essentially provides the same picture as the AUC distribution.
Figure 6.
Distribution of performances for proteins in the iPFAM dataset for A, the AUC values; B, the MCC values; C, the correlation between AUC and MCC values.
The distribution revealed that there were cases where BindML predicted poorly. The cause of poor predictions depends on cases: In the case of cellular receptor HVEA/HVEM interacting with an envelope glycoprotein of herpes simplex virus (1JMAB), the sequence profile at the binding interface was too conserved for BindML to detect PBI specific interaction pattern. Also, it is not easy for BindML to predict PBI sites that are too small or narrow, given that it uses an alignment sphere of 15 Å radius. An example for this case (1S70A) will be discussed in the next section.
We further examined prediction performance by BindML on homo- and hetero-protein complexes, because several studies have shown differences in the sequence and structural composition of homo- and hetero-complexes7;11;47–49. 65% of our dataset are composed of homo-complexes, whereas the remaining 35% are hetero-complexes. The PBI prediction performance for homo-complexes was higher (AUC: 0.638) than hetero-complexes (AUC: 0.599). Thus, BindML can pick up PBI sites for both using a general PBI/NPBI substitution model, but provides better performance for homo- than hetero-complexes.
Prediction Examples
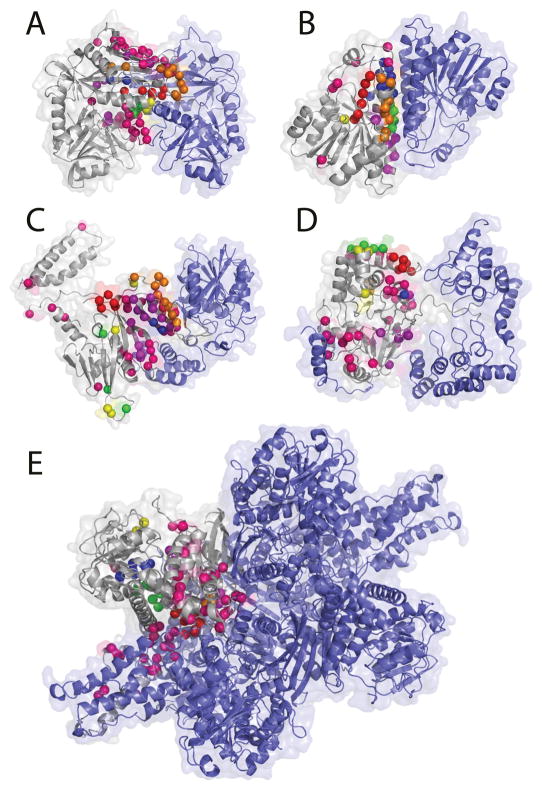
Figure 7 provides five examples of BindML’s predictions. We used a Z-score threshold of −0.5. These five structural complexes from heterogeneous protein families consist of one complex taken from the iPFAM dataset (Fig. 7A, 1KT8A), two targets used in the Critical Assessment of Prediction of Interactions (CAPRI)50 (Figs. 7C & E, 2B3TB and 1HWZA), and two other additional structural examples (Figs. 7B & D, 1A4UA, 1S70A). The first two shown are successful examples of enzymes (Figs. 7A & B). Figure 7A is the result for amino acid transferase (1KT8A), which forms a homo-dimer complex. The AUC value of this prediction was high, 0.847, and the sensitivity and the specificity are 0.636 and 0.859, respectively. In Figure 7B, binding sites for the homo-dimer alcohol dehydrogenase (1A4UA) is shown. The predicted residues corresponded very well at the α-helical regions of the dimer interface (AUC: 0.800, sensitivity: 0.569, specificity: 0.889). The next example, Figure 7C, is peptide chain release factor 1 complexed with methyltransferase hemK (2B3T). The prediction is made for peptide chain release factor 1 (2B3TB). Several false positives on the opposite side from the binding interface were observed but the overall performance was decent with an AUC value, sensitivity, specificity value of 0.656, 0.444, and 0.777, respectively. We also show the prediction for serine/threonine phosphatase (1S70A), a CAPRI target (T14) structure, where BindML did not perform well (Fig. 7D). BindML prediction was reasonably specific, with the specificity of 0.667; however, a poor sensitivity (0.225) dropped the overall AUC value to 0.476. The main reason for the poor result comes from prediction at the binding region to the N-terminal tail of binding partner, myosin phosphatase, which wraps around the phosphatase structure. The interacting region to the tail forms an elongated shape, which is not advantageous for BindML to scan by using a sphere. The last example is the prediction on a large homo-hexameric complex of Glutamate dehydrogenase (1HWZA) (Fig. 7E). The A-chain interacts with the B, D, E, F chains forming the binding interface of 64 residues. BindML predicts this large binding interface well with the AUC value of 0.711 and the specificity of 0.789.
Figure 7.
Additional prediction examples. A, amino acid transferase (PDB: 1KT8A); B, alcohol dehydrogenase (1A4UA); C, peptide chain release factor 1 complexed with methyltransferase hemK (2B3TB); D, protein serine/threonine phosphatase complexed with smooth muscle myosin phosphatase (1S70A); E, hexameric glutamate dehydrogenase (1HWZA). The target chain subject to the prediction is shown in gray. The same color scheme is used to rank the strength of the cluster of signals as in Figure 4.
Comparing highly conserved regions to BindML predictions
To illustrate that BindML is not simply identifying conserved regions, we compare BindML prediction with those by considering naive sequence conservation (the percentage of conserved residues at each position in the MSA) and also with prediction by the ConSurf method51. ConSurf utilizes a phylogenetic tree to calculate conservation rate along the evolution for a MSA of a protein family. We employed the web server implementation of ConSurf (http://consurf.tau.ac.il/). For ConSurf predictions, we only considered solvent exposed residues. ConSurf was employed here as an example of methods that essentially captures residue conservation.
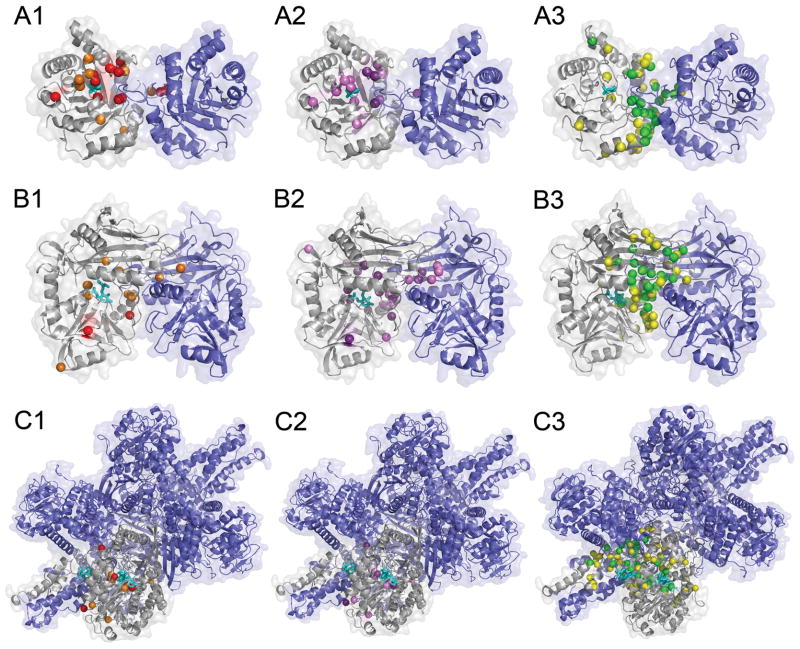
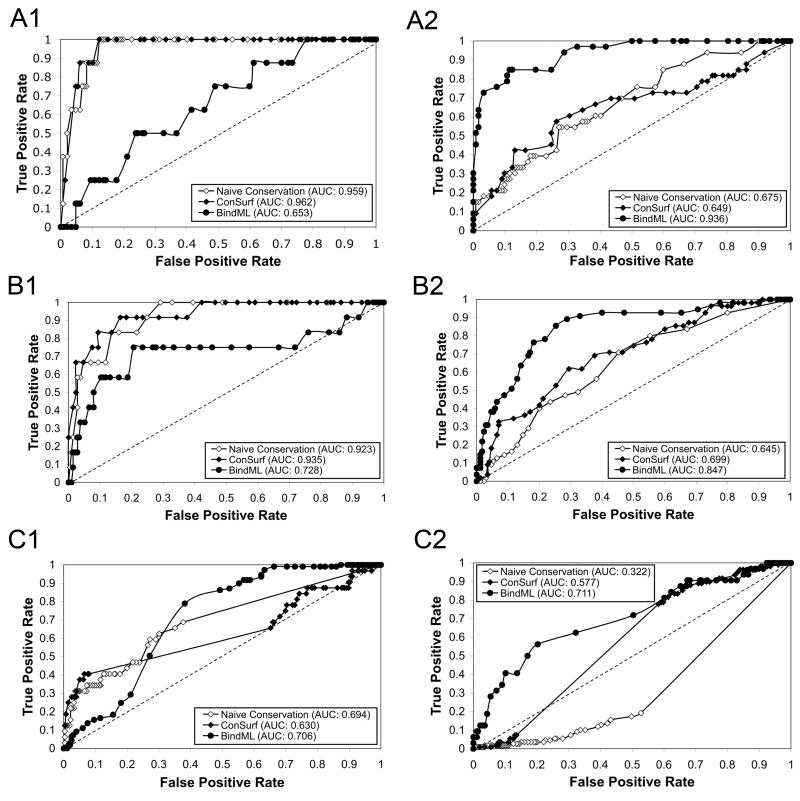
Figure 8 shows predictions by the three methods. The first protein, triosephosphate isomerase homo-dimer (7TIM), binds phosphoglycolohydroxamate (PGH) at its well conserved ligand binding pocket. Thus, strong sequence conservation selected mostly residues in contact with the ligand or residues surrounding the binding site (Fig. 8A1). This is also true for the ConSurf prediction (Fig. 8A2). Both methods do not identify almost any PBI site residues. In contrast, predictions provided by BindML concentrated on residues at PBI site (Fig. 8A3). With the Z-score of −1.0, the prediction was very specific to the PBI site, with a specificity of 0.992 and a sensitivity of 0.516. Raising the Z-score threshold to −0.5 yielded an increased in sensitivity of 0.849 (specificity: 0.885).
Figure 8.
Comparison of residues selected by naive sequence conservation, ConSurf, and BindML. A, triosephosphate isomerase homo-dimer (7TIM); B, amino acid transferase homo-dimer (1KT8); C, glutamate dehydrogenase (1HWZ). Ligand molecules binding to these proteins are shown in cyan. For the three proteins, residues which are assigned with a significantly high score by the three methods are shown. A1, B1, C1, residues with high conservation; A2, B2, C2, residues with a high score by ConSurf; A3, B3, C3, residues identified by BindML. For sequence conservation, residues which are conserved in more than 90% (70%) of sequences are shown in red (orange) (A1, B1, C1). As for ConSurf, residues detected with a Z-score of −1.3 (−1) or lower is shown in purple (violet) (A2, B2, C2). Residues identified with a Z-score of −1 (−0.5) or lower by BindML are shown in gree (yellow) (A3, B3, C3).
The next examples are predictions for amino acid transferase homo-dimer (1KT8) which bind N-[O-phosphono-pyridoxyl]-isoleucine in the ligand binding cavity. Again, naive conservation predictions (Fig. 8B1) as well as ConSurf (Fig. 8B2) identified ligand binding residues and not PBI site residues. In comparison, the predicted residues by BindML were located in different places in the structure, where they were mostly covering PBI sites (Fig. 8B3). Using the Z-score threshold value of −1.0, the sensitivity and the specificity were 0.40 and 0.941, respectively. Further increasing the Z-score threshold to −0.5 resulted in increased sensitivity (0.636) and specificity (0.859).
The difference in predictions by BindML relative to the other two methods of sequence conservation is further apparent when the AUC value of the ROC curve for ligand binding residues and PBI site residues are compared (Fig. 9). For both of the cases of triosephosphate isomerase (Fig. 9A) and amino acid transferase (Fig. 9B), BindML showed lower AUC value for ligand binding residues compared to naive sequence conservation and ConSurf (Figs. 9A1 & 9B1). BindML’s AUC value for ligand binding sites for the second case remained high (0.728) (Fig. 9B1), but this is due to six residues that were located at the PBI site that also interact with the ligand molecule. When the AUC value for PBI sites were computed (Figs. 9A2 & 9B2), BindML showed significantly higher predictive performance than the other two methods.
Figure 9.
ROC curves of ligand binding residue prediction and PBI residue prediction by naive sequence convervation (open diamonds), ConSurf (filled diamonds) and BindML (filled circles). A, triosephosphate isomerase homo-dimer (7TIM); B, amino acid transferase homo-dimer (1KT8); C, glutamate dehydrogenase (1HWZ). A1, B1, C1, ligand binding site; A2, B2, C2, PBI site prediction. Ligand binding residues are defined as those which are within 5.0Å to the ligand molecule.
The last examples in Figure 9 are predictions for hexameric glutamate dehydrogenase (1HWZ). This six-chain complex has three ligands bound to the active site, NADPH, glutamate, and GTP. Ligand binding residues for all three ligands were evaluated for the chain A. Although the sensitivity was low, the naive residue conservation and ConSurf identified ligand binding residues very specifically. The specificity by the naive sequence conservation and ConSurf was 0.978 and 0.996 with the threshold value of 70% and −1.0, respectively. On the other hand, prediction by BindML provided more PBI site residues. Again, the predictive difference by BindML is obvious by considering the ROC curves (Fig. 9C). The ROC curve of naive sequence conservation (Fig. 9C) indicates that the PBI site of this protein chain is not conserved at all in comparison to the other surface residues.
In summary, Figures 8 and 9 clearly illustrate that BindML identifies the mutation patterns of PBI sites, which cannot be simply captured by the methods of sequence conservation. Naive sequence conservation (and ConSurf) can evidently identify ligand binding sites well, but not PBI sites.
Comparison with other existing PBI prediction methods and sequence conservation
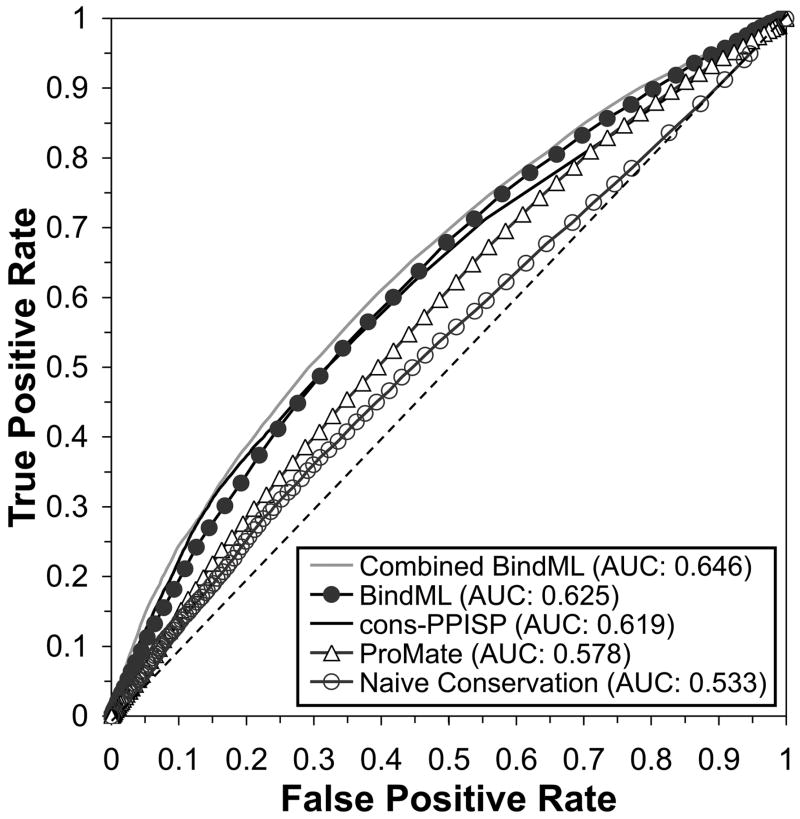
In this section we compare BindML with two existing PBI prediction methods (cons-PPISP15 and ProMate6) and naive sequence conservation on the iPFAM dataset (Fig. 10). The results for BindML were taken from the cross-validation test of the entire iPFAM dataset. For the false positive rates between 0.00 and 0.30, cons-PPISP performed slightly higher than BindML with approximately 1 percent difference in the true positive rate. Therefore, the AUC up to 20 percent false positives (AUC20) shows the following order of cons-PPISP, BindML, ProMate, and naive conservation with 0.043, 0.035, 0.027, and 0.026 respectively. However, overall, BindML showed the highest ROC value, 0.625. Cons-PPISP, ProMate, and naive conservation followed in this order with an AUC value of 0.619, 0.578, and 0.533, respectively. The AUC value of BindML is significantly higher than that of cons-PPISP when subject to a Hanley and McNeil test (p-value: 4×10−5) 52. This is remarkable because BindML primarily uses sequence mutation patterns, while the cons-PPISP and ProMate methods both combine sequence and structural information using a more elaborate machine learning framework. Naive sequence conservation performed worst in predicting PBI sites confirming that BindML does not simply identify conserved regions in MSAs.
Figure 10.
ROC performances for BindML, cons-PPISP, ProMate, and the naïve conservation on the iPFAM dataset. Combined BindML is an ensemble approach that combines BindML and cons-PPISP. The dashed diagonal line is the expected performance of random predictions (AUC value of 0.5).
As illustrated in the previous section with Figures 8 & 9, naive conservation captured more ligand binding residues than BindML. Using 174 proteins that have both ligands and PBI sites in the dataset, AUC computed for residues which bind ligands but not at PBI sites was 0.582 for naive conservation while 0.549 for BindML.
To seek for further improvement of the prediction accuracy, we took an ensemble approach53–55 (or meta-server approach), which integrates independent prediction by BindML and cons-PPISP. The score of the ensemble approach, named Combined BindML in Figure 10, is simply the average of the rescaled BindML score and the cons-PPISP score. The new Combined BindML method performed with consistently higher true positive rate at all false positive rate values across the entire ROC Curve in comparison to the original BindML and the other methods in the figure. The AUC of the Combined BindML is 0.646, which is higher than that of original BindML (0.625) and cons-PPISP (0.619) with statistical significance (p-value < 0.000001). Moreover, the AUC20 of Combined BindML is 0.047, highest among the methods compared.
Prediction results for unbound structures
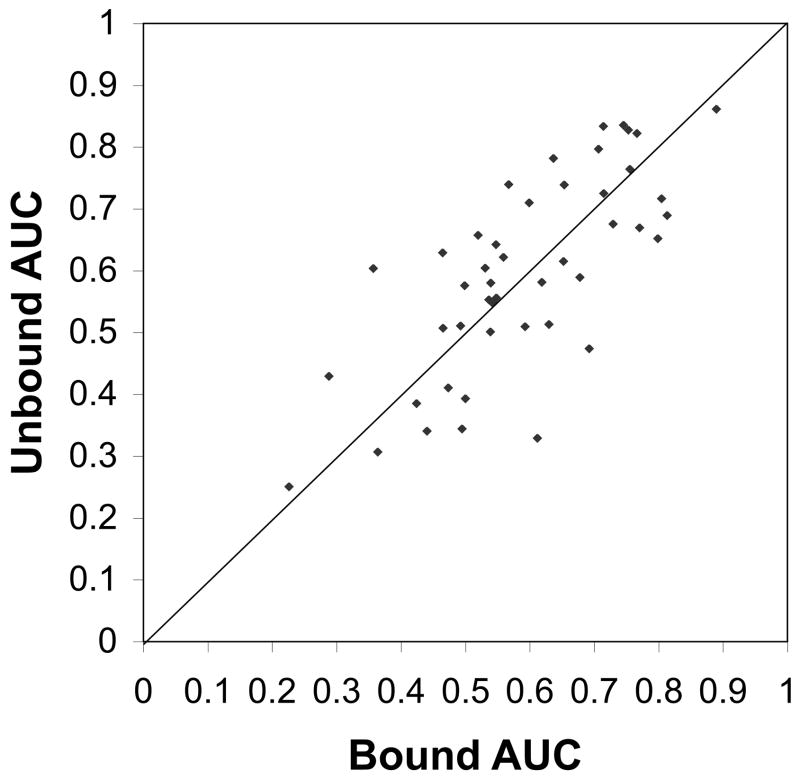
Finally, we apply BindML to predict PBI sites of proteins in unbound conformation. Out of 112 structures of bound and unbound form of protein structures in a protein-protein docking benchmark dataset ver. 4.0 compiled by Z. Weng group36, 46 pairs were selected, whose sequence are not included in the MSAs in the iPFAM dataset used to determine parameters and to compute PBI and NPBI substitution models. PBI residues were defined on the bound form of proteins. The average root mean square deviation (RMSD) of PBI sites between bound and unbound form of the proteins was 1.43Å.
Figure 11 compares the AUC values of bound and unbound conformation of each protein in the dataset. Overall, the prediction for unbound structures does not deteriorate, rather, showing even slightly better results for the unbound form than bound form in this dataset. The average AUC for bound form structures was 0.587 while that of unbound form was 0.596. Out of the total of 46 cases, 26 unbound predictions (56.5%) are better than bound case predictions. Thus, BindML, is tolerant to usual level of conformation change from unbound to bound forms, partly because it is using a large alignment sphere of the 15Å radius to extract a MSA of a surface region. As an example, we compared corresponding surface patches between bound and unbound conformations of cysteine protease ATG4B complexed with microtubule-associated proteins (1A/1B) (bound structure: 2Z0E; unbound: 1V49A & 2D1IA). The RMSD of the bound and unbound structures at the interaction interface is 2.15Å, and the AUC of predicted PBI site was very similar, 0.781 and 0.782 (the average of ligand and receptor proteins) for bound and unbound structures, respectively. For this complex, the bound and unbound structures have 239 corresponding surface patches, each of which contains on average 22.6 residues. As expected, the conformation change does not have significant impact to the residues included in corresponding patches between bound and unbound conformation: Among the 239 corresponding patches, 86.2% has less than 5 residue difference, and 69.0% has less than 3 residue difference. Results of more detailed analysis for this protein complex and another one were put in the supplemental material (http://kiharalab.org/bindml/suppl.pdf). Of course it is still possible that proteins that undergo significant conformational changes from unbound to bound forms may pose challenges to BindML. However, note that such drastic conformational change is rather rare according to our current knowledge based on the structure database. The average RMSD of PBI sites between bound and unbound form of structures in another independent dataset of 124 bound and unbound complexes56 is 1.36Å, which is consistent with the dataset we used.
Figure 11.
Comparison of AUC of PBI prediction for bound and unbound form of proteins. 46 structures from the protein-protein docking benchmark dataset 4.0 were used.
Discussion
We have reported a novel computational method, BindML, for predicting PBI sites by capturing their characteristic mutation patterns. BindML extracts the MSA of local surface patch on the query protein structure and computes phylogenetic trees using PBI and NPBI substitution models, whose likelihood scores are then compared. A great advantage of BindML is that the procedure is very general; therefore it can be readily applied for identifying other types of sites in proteins that have distinctive mutation patterns. For example, interaction sites to other molecules, such as DNA, RNA, or membrane can be predicted by computing site specific substitution models from known structural complexes.
Obviously BindML is not able to make prediction for proteins that have no sequence homologs, where no MSA can be constructed for input of BindML. Also the quality of the MSA can potentially affect the accuracy of PBI predictions.
Further improvement of prediction accuracy is expected by several future developments. More sensitive PBI/NPBI substitution models could be obtained by employing sophisticated sequence weighting scheme57;58 and pseudo-counts59, rather than the current scheme, which simply uses the BLOSUM method39 on a sequence set pruned out by the global sequence identity. Instead of the BLOSUM procedure, utilizing thorough techniques for maximizing the likelihood of phylogenetic trees can further optimize the estimation of the amino acid replacement rates60–62. Lastly, including additional structural and/or energetic features of PBIs, such as residue accessible surface area, surface shape, the secondary structure, by using machine learning framework is certainly expected to improve the accuracy of detection of PBI sites.
The present method was developed and evaluated based on our current knowledge of protein-protein interaction sites obtained from the databases. However, there may be many interactions of proteins that are not yet known. Therefore, it is possible that the false positives evaluated in our predictions may actually capturing unknown interacting surface regions. The limitation of our current knowledge is an inevitable problem for developing and evaluating prediction methods. It will be necessary to reevaluate and retune our method as well other existing methods a few years later when we have more information about protein-protein interaction.
As protein sequence and structure information continue to accumulate at an increasing rate, there is an urgent need for developing methods for annotating functions to new proteins and specifically to their local sites, where these functions are carried out. Most of the popular existing methods are still based on the traditional principle of conservation in sequences and structures. In this work we showed that mutation patterns forms a rich source of information for identifying functional sites of proteins. In contrast to finding conserved regions, through the development of BindML we propose new direction of sequence analysis, which aims to capture mutational constraints or structure of variation in protein sequences. Thus, the current work is conceptually very different from the conventional methods and has broader applicability, where specific local mutational signatures can be classified for newly sequenced proteins. Introducing new directions for sequence analyses will become more crucial as the amount of sequence information awaiting our interpretation continues to rapidly grow particularly by recent new generation sequencing techniques. We believe turning our attention to analyzing hidden structures of sequence variation will open up new directions for biological sequence analysis.
Supplementary Material
Acknowledgments
We thank Dr. Michael Zanis for his lecture on phylogenetic likelihood analysis, which inspired this work. We are grateful to Dr. Vishwesh Venkatraman for fruitful discussions. This work was supported in part by the National Institute of General Medical Sciences of the National Institutes of Health (R01 GM075004). DK also acknowledges funding from the National Science Foundation (DMS800568, IIS0915801, EF0850009).
Reference List
- 1.Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, Qureshi-Emili A, Li Y, Godwin B, Conover D, Kalbfleisch T, Vijayadamodar G, Yang M, Johnston M, Fields S, Rothberg JM. A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae. Nature. 2000;403:623–627. doi: 10.1038/35001009. [DOI] [PubMed] [Google Scholar]
- 2.Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc Natl Acad Sci U S A. 2001;98:4569–4574. doi: 10.1073/pnas.061034498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Giot L, Bader JS, Brouwer C, Chaudhuri A, Kuang B, Li Y, Hao YL, Ooi CE, Godwin B, Vitols E, Vijayadamodar G, Pochart P, Machineni H, Welsh M, Kong Y, Zerhusen B, Malcolm R, Varrone Z, Collis A, Minto M, Burgess S, McDaniel L, Stimpson E, Spriggs F, Williams J, Neurath K, Ioime N, Agee M, Voss E, Furtak K, Renzulli R, Aanensen N, Carrolla S, Bickelhaupt E, Lazovatsky Y, DaSilva A, Zhong J, Stanyon CA, Finley RL, Jr, White KP, Braverman M, Jarvie T, Gold S, Leach M, Knight J, Shimkets RA, McKenna MP, Chant J, Rothberg JM. A protein interaction map of Drosophila melanogaster. Science. 2003;302:1727–1736. doi: 10.1126/science.1090289. [DOI] [PubMed] [Google Scholar]
- 4.Todd AE, Marsden RL, Thornton JM, Orengo CA. Progress of structural genomics initiatives: an analysis of solved target structures. J Mol Biol. 2005;348:1235–1260. doi: 10.1016/j.jmb.2005.03.037. [DOI] [PubMed] [Google Scholar]
- 5.Chandonia JM, Brenner SE. The impact of structural genomics: expectations and outcomes. Science. 2006;311:347–351. doi: 10.1126/science.1121018. [DOI] [PubMed] [Google Scholar]
- 6.Neuvirth H, Raz R, Schreiber G. ProMate: a structure based prediction program to identify the location of protein-protein binding sites. J Mol Biol. 2004;338:181–199. doi: 10.1016/j.jmb.2004.02.040. [DOI] [PubMed] [Google Scholar]
- 7.Jones S, Thornton JM. Analysis of protein-protein interaction sites using surface patches. J Mol Biol. 1997;272:121–132. doi: 10.1006/jmbi.1997.1234. [DOI] [PubMed] [Google Scholar]
- 8.Tjong H, Qin S, Zhou HX. PI2PE: protein interface/interior prediction engine. Nucleic Acids Res. 2007;35:W357–W362. doi: 10.1093/nar/gkm231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Porollo A, Meller J. Prediction-based fingerprints of protein-protein interactions. Proteins. 2007;66:630–645. doi: 10.1002/prot.21248. [DOI] [PubMed] [Google Scholar]
- 10.Bradford JR, Westhead DR. Improved prediction of protein-protein binding sites using a support vector machines approach. Bioinformatics. 2005;21:1487–1494. doi: 10.1093/bioinformatics/bti242. [DOI] [PubMed] [Google Scholar]
- 11.Jones S, Thornton JM. Prediction of protein-protein interaction sites using patch analysis. J Mol Biol. 1997;272:133–143. doi: 10.1006/jmbi.1997.1233. [DOI] [PubMed] [Google Scholar]
- 12.Fernandez-Recio J, Totrov M, Skorodumov C, Abagyan R. Optimal docking area: a new method for predicting protein-protein interaction sites. Proteins. 2005;58:134–143. doi: 10.1002/prot.20285. [DOI] [PubMed] [Google Scholar]
- 13.Xu D, Tsai CJ, Nussinov R. Hydrogen bonds and salt bridges across protein-protein interfaces. Protein Eng. 1997;10:999–1012. doi: 10.1093/protein/10.9.999. [DOI] [PubMed] [Google Scholar]
- 14.Fariselli P, Pazos F, Valencia A, Casadio R. Prediction of protein--protein interaction sites in heterocomplexes with neural networks. Eur J Biochem. 2002;269:1356–1361. doi: 10.1046/j.1432-1033.2002.02767.x. [DOI] [PubMed] [Google Scholar]
- 15.Chen H, Zhou HX. Prediction of interface residues in protein-protein complexes by a consensus neural network method: test against NMR data. Proteins. 2005;61:21–35. doi: 10.1002/prot.20514. [DOI] [PubMed] [Google Scholar]
- 16.Ezkurdia I, Bartoli L, Fariselli P, Casadio R, Valencia A, Tress ML. Progress and challenges in predicting protein-protein interaction sites. Brief Bioinform. 2009;10:233–246. doi: 10.1093/bib/bbp021. [DOI] [PubMed] [Google Scholar]
- 17.La D, Kihara D. Predicting binding interfaces of protein-protein interactions. In: Li XL, Ng SK, editors. Biological Data Mining in Protein Interaction Networks. Philadelphia: IGI-GLobal; 2010. pp. 64–79. [Google Scholar]
- 18.Cho KI, Lee K, Lee KH, Kim D, Lee D. Specificity of molecular interactions in transient protein-protein interaction interfaces. Proteins. 2006;65:593–606. doi: 10.1002/prot.21056. [DOI] [PubMed] [Google Scholar]
- 19.Hu Z, Ma B, Wolfson H, Nussinov R. Conservation of polar residues as hot spots at protein interfaces. Proteins. 2000;39:331–342. [PubMed] [Google Scholar]
- 20.Capra JA, Singh M. Predicting functionally important residues from sequence conservation. Bioinformatics. 2007;23:1875–1882. doi: 10.1093/bioinformatics/btm270. [DOI] [PubMed] [Google Scholar]
- 21.Caffrey DR, Somaroo S, Hughes JD, Mintseris J, Huang ES. Are protein-protein interfaces more conserved in sequence than the rest of the protein surface? Protein Sci. 2004;13:190–202. doi: 10.1110/ps.03323604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jones S, Thornton JM. Searching for functional sites in protein structures. Curr Opin Chem Biol. 2004;8:3–7. doi: 10.1016/j.cbpa.2003.11.001. [DOI] [PubMed] [Google Scholar]
- 23.Bordner AJ, Abagyan R. Statistical analysis and prediction of protein-protein interfaces. Proteins. 2005;60:353–366. doi: 10.1002/prot.20433. [DOI] [PubMed] [Google Scholar]
- 24.Lichtarge O, Bourne HR, Cohen FE. Evolutionarily conserved Galphabetagamma binding surfaces support a model of the G protein-receptor complex. Proc Natl Acad Sci U S A. 1996;93:7507–7511. doi: 10.1073/pnas.93.15.7507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Halperin I, Wolfson H, Nussinov R. Correlated mutations: advances and limitations. A study on fusion proteins and on the Cohesin-Dockerin families. Proteins. 2006;63:832–845. doi: 10.1002/prot.20933. [DOI] [PubMed] [Google Scholar]
- 26.Lichtarge O, Bourne HR, Cohen FE. An evolutionary trace method defines binding surfaces common to protein families. J Mol Biol. 1996;257:342–358. doi: 10.1006/jmbi.1996.0167. [DOI] [PubMed] [Google Scholar]
- 27.La D, Livesay DR. Predicting functional sites with an automated algorithm suitable for heterogeneous datasets. BMC Bioinformatics. 2005;6:116. doi: 10.1186/1471-2105-6-116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Livesay DR, La D. The evolutionary origins and catalytic importance of conserved electrostatic networks within TIM-barrel proteins. Protein Sci. 2005;14:1158–1170. doi: 10.1110/ps.041221105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lichtarge O, Sowa ME. Evolutionary predictions of binding surfaces and interactions. Curr Opin Struct Biol. 2002;12:21–27. doi: 10.1016/s0959-440x(02)00284-1. [DOI] [PubMed] [Google Scholar]
- 30.Sankararaman S, Sjolander K. INTREPID--INformation-theoretic TREe traversal for Protein functional site IDentification. Bioinformatics. 2008;24:2445–2452. doi: 10.1093/bioinformatics/btn474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rausell A, Juan D, Pazos F, Valencia A. Protein interactions and ligand binding: from protein subfamilies to functional specificity. Proc Natl Acad Sci U S A. 2010;107:1995–2000. doi: 10.1073/pnas.0908044107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Finn RD, Marshall M, Bateman A. iPfam: visualization of protein-protein interactions in PDB at domain and amino acid resolutions. Bioinformatics. 2005;21:410–412. doi: 10.1093/bioinformatics/bti011. [DOI] [PubMed] [Google Scholar]
- 33.Uniprot Consortium. The Universal Protein Resource (UniProt) in 2010. Nucleic Acids Res. 2010;38:D142–D148. doi: 10.1093/nar/gkp846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Henrick K, Thornton JM. PQS: a protein quaternary structure file server. Trends Biochem Sci. 1998;23:358–361. doi: 10.1016/s0968-0004(98)01253-5. [DOI] [PubMed] [Google Scholar]
- 35.Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hwang H, Vreven T, Janin J, Weng Z. Protein-protein docking benchmark version 4.0. Proteins. 2010;78:3111–3114. doi: 10.1002/prot.22830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Miller S, Janin J, Lesk AM, Chothia C. Interior and surface of monomeric proteins. J Mol Biol. 1987;196:641–656. doi: 10.1016/0022-2836(87)90038-6. [DOI] [PubMed] [Google Scholar]
- 38.Jones DT, Taylor WR, Thornton JM. The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- 39.Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci U S A. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Guindon S, Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol. 2003;52:696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
- 41.Gascuel O. BIONJ: an improved version of the NJ algorithm based on a simple model of sequence data. Mol Biol Evol. 1997;14:685–695. doi: 10.1093/oxfordjournals.molbev.a025808. [DOI] [PubMed] [Google Scholar]
- 42.Hollich V, Milchert L, Arvestad L, Sonnhammer EL. Assessment of protein distance measures and tree-building methods for phylogenetic tree reconstruction. Mol Biol Evol. 2005;22:2257–2264. doi: 10.1093/molbev/msi224. [DOI] [PubMed] [Google Scholar]
- 43.Gribskov M, Robinson NL. Use of receiver operating characteristic (ROC) analysis to evaluate sequence matching. Comput Chem. 1996;20:25–33. doi: 10.1016/s0097-8485(96)80004-0. [DOI] [PubMed] [Google Scholar]
- 44.Tseng YY, Liang J. Estimation of amino acid residue substitution rates at local spatial regions and application in protein function inference: a Bayesian Monte Carlo approach. Mol Biol Evol. 2006;23:421–436. doi: 10.1093/molbev/msj048. [DOI] [PubMed] [Google Scholar]
- 45.Kelly MD, Mancera RL. A new method for estimating the importance of hydrophobic groups in the binding site of a protein. J Med Chem. 2005;48:1069–1078. doi: 10.1021/jm049524q. [DOI] [PubMed] [Google Scholar]
- 46.Coggill P, Finn RD, Bateman A. Identifying protein domains with the Pfam database. Curr Protoc Bioinformatics. 2008;Chapter 2(Unit) doi: 10.1002/0471250953.bi0205s23. [DOI] [PubMed] [Google Scholar]
- 47.Venkatakrishnan AJ, Levy ED, Teichmann SA. Homomeric protein complexes: evolution and assembly. Biochem Soc Trans. 2010;38:879–882. doi: 10.1042/BST0380879. [DOI] [PubMed] [Google Scholar]
- 48.Landgraf R, Xenarios I, Eisenberg D. Three-dimensional cluster analysis identifies interfaces and functional residue clusters in proteins. J Mol Biol. 2001;307:1487–1502. doi: 10.1006/jmbi.2001.4540. [DOI] [PubMed] [Google Scholar]
- 49.Levy ED, Pereira-Leal JB, Chothia C, Teichmann SA. 3D complex: a structural classification of protein complexes. PLoS Comput Biol. 2006;2:e155. doi: 10.1371/journal.pcbi.0020155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mendez R, Leplae R, Lensink MF, Wodak SJ. Assessment of CAPRI predictions in rounds 3–5 shows progress in docking procedures. Proteins. 2005;60:150–169. doi: 10.1002/prot.20551. [DOI] [PubMed] [Google Scholar]
- 51.Landau M, Mayrose I, Rosenberg Y, Glaser F, Martz E, Pupko T, Ben-Tal N. ConSurf 2005: the projection of evolutionary conservation scores of residues on protein structures. Nucleic Acids Res. 2005;33:W299–W302. doi: 10.1093/nar/gki370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 53.Fischer D. Servers for protein structure prediction. Curr Opin Struct Biol. 2006;16:178–182. doi: 10.1016/j.sbi.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 54.Pawlowski M, Gajda MJ, Matlak R, Bujnicki JM. MetaMQAP: a meta-server for the quality assessment of protein models. BMC Bioinformatics. 2008;9:403. doi: 10.1186/1471-2105-9-403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hu J, Yang YD, Kihara D. EMD: an ensemble algorithm for discovering regulatory motifs in DNA sequences. BMC Bioinformatics. 2006;7:342. doi: 10.1186/1471-2105-7-342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hwang H, Pierce B, Mintseris J, Janin J, Weng Z. Protein-protein docking benchmark version 3.0. Proteins. 2008;73:705–709. doi: 10.1002/prot.22106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Sunyaev SR, Eisenhaber F, Rodchenkov IV, Eisenhaber B, Tumanyan VG, Kuznetsov EN. PSIC: profile extraction from sequence alignments with position-specific counts of independent observations. Protein Eng. 1999;12:387–394. doi: 10.1093/protein/12.5.387. [DOI] [PubMed] [Google Scholar]
- 58.Pei J, Grishin NV. AL2CO: calculation of positional conservation in a protein sequence alignment. Bioinformatics. 2001;17:700–712. doi: 10.1093/bioinformatics/17.8.700. [DOI] [PubMed] [Google Scholar]
- 59.Sjolander K, Karplus K, Brown M, Hughey R, Krogh A, Mian IS, Haussler D. Dirichlet mixtures: a method for improved detection of weak but significant protein sequence homology. Comput Appl Biosci. 1996;12:327–345. doi: 10.1093/bioinformatics/12.4.327. [DOI] [PubMed] [Google Scholar]
- 60.Holmes I. Using evolutionary Expectation Maximization to estimate indel rates. Bioinformatics. 2005;21:2294–2300. doi: 10.1093/bioinformatics/bti177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Klosterman PS, Uzilov AV, Bendana YR, Bradley RK, Chao S, Kosiol C, Goldman N, Holmes I. XRate: a fast prototyping, training and annotation tool for phylo-grammars. BMC Bioinformatics. 2006;7:428. doi: 10.1186/1471-2105-7-428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Arvestad L. Efficient methods for estimating amino acid replacement rates. J Mol Evol. 2006;62:663–673. doi: 10.1007/s00239-004-0113-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.