Population-based proband-oriented pedigree information system: application to hypertension with population-based screening data (KCIS No. 25)

Abstract

Objective

To develop a population-based proband-oriented pedigree information system that can be easily applied to various diseases in genetic epidemiological studies, making allowance for the capture of theoretical family relationships.

Designs and Measurements

A population-based proband-oriented pedigree information system with ties of consanguinity based on both population-based household registry data and Keelung Community Integrated Screening data was proposed to build a comprehensive extended family pedigree structure to accommodate a series of genetic studies on different diseases. We also developed an algorithm to efficiently assess how well theoretical family relationships affecting the occurrence of diseases across three generations with respect to the relative relationship score, a quantitative indicator of genetic influence, were captured.

Results

We applied this population-based proband-oriented pedigree information system to estimate the rate of hypertension with various relative relationships given the selection of probands. The degree of capturing complete familial relationships was assessed for three generations. The risk for early onset of hypertension was proportional to the proband-oriented relative relationship score with 2% increased risk and 1% correction for incomplete capture.

Conclusions

The population-based proband-oriented pedigree information system is powerful and can support various genetic descriptive and analytic epidemiological studies.

Introduction

A variety of genetic epidemiological designs (including family aggregation studies, linkage analysis, and association studies) have been proposed to assess the relationship between genetic influence and environmental factors using different types of family pedigree information.¹ With proband changes from study to study, different familial relations are often identified in different studies under the same family tree, due to either different sampling schemes or different disease outcomes. The feasibility and efficiency of this type of research, particularly regarding genomic studies, would be enhanced by exploring of the possibility of sharing information by integrating genomic data (including familial relations) into personal health records obtained from health check-ups² or questionnaires on environmental factors. Therefore, population-based family pedigree systems need to be constructed to accommodate proband-oriented familial relations.

The two main hurdles to achieving this objective have been highlighted in a report by Malin.³ First, the construction of a population-based genealogical database requires a great deal of effort to identify and validate family structure if all family members are to be identified and their relevant variables of interest collected. Second, because the possible combinations of the degree of relative relationships increase with the number of family members in a population-based family pedigree database, the complete capture of full information on all possible theoretical combinations is rarely possible.

The Keelung Community-based Integrated Screening (KCIS) program is a population-based multiple screening program that collects information on multiple outcomes after follow-up for various conditions including a variety of cancers and chronic diseases.⁴ This project provides a comprehensive population database on community-based individual-specific health information and epidemiological risk factors but with un-identified familial relations. Fortunately, the population-based household registry in Taiwan allows the construction of a population-based family pedigree system by ties of consanguinity. By linking the two databases, we constructed a proband-oriented pedigree information system across generations and households. We then estimated relative relationship scores based on the selected proband and developed a novel algorithm to assess incomplete capture of screening data that leads to biased relative relationship scores. We applied the population-based proband-oriented family-based pedigree information system together with all of the proposed methods to study familial aggregation of hypertension in relation to genetic influence based on relative relationship scores and environmental factors.

Material and methods

Population-based proband-oriented pedigree infrastructure

To develop a population-based family pedigree information system, we used two population-based data sources: a population household registration system and primary data obtained from KCIS. The procedure for using two population-based datasets is illustrated in figure 1. We borrowed the method of presenting the system construction from the Malin report,³ even though our methods and datasets were completely different. We retrieved and updated the database for the Keelung population household registry using the annual nationwide population household registry between 1999 and 2006 for local Keelung residents (updated census). We then used this Keelung population household registry to develop a unique three-generation genealogical structure with ties of consanguinity across households with household number, spouse relationships, and parents' names (family structure). Family members living in the same household were identified by a unique household number. The spouse relationship in each household enables extension to paternal and maternal pedigrees. Parents' birth names allow the siblings of the mother and father to be identified, even when they live in different households (see figure 1; the details of the algorithm and an example are given below). Through their personal identification number, individuals listed in the KCIS database were further validated in several ways: by the Keelung population household registry to identify whether they took part in any screening programs; by the national death registry; by the nationwide cancer registry; and by any other nationwide registry-related systems, such as the diabetes registry (validation). Data from the population-based KCIS dataset were linked to the population-based family pedigree information system by personal identification numbers to obtain relevant health information, such as health outcomes, particularly regarding cancer and chronic diseases, genomic data, phenotypes, and other risk factors (link). The linkage between KCIS and the population-based family pedigree system yielded the population-based proband-oriented pedigree information system (TRIPIS). Names and any personal identification were removed from TRIPIS for privacy if data were shared for research purposes.

Figure 1.

Population-based proband-oriented pedigree information system (TRIPIS). KCIS, Keelung Community-based Integrated Screening program.

Population-based household registration

The population-based household registration system in Taiwan was developed by merging personal identification registration data with household registration data. Both have been recorded since 1947 and have been in an electronic format since 1985.⁵ The former registration system contains each person's unique personal identification number (similar to the social security number in Western countries), name, gender, and current address, which are all recorded on a personal identification card. In Taiwan, unique personal identification numbers with 10 digits have been recorded in the population household registry system since 1965. The first digit using a capital English letter indicates the location (county) where the subject was born. The second digit stands for gender (‘1’ for male and ‘2’ for female). Under the auspices of the Ministry of the Interior, a specific algorithm is used to randomly generate the last eight digits that can be used to verify key-in and coding errors when data entry is needed and also to detect errors when data linkage is required. In addition to personal data, personal identification registration also records the full names of spouses, fathers, and mothers as well as information on marriage or divorce, adoption, and date of death. Parents' names allow identification of siblings living in different households (figure 1; details of the algorithm are given below).

At household registration, each household is provided with a booklet containing a unique household number, names, dates of birth, and personal identification numbers, which are recorded in the personal registration system mentioned above. One member, not necessarily but often the father of the family, is assigned as the master of the household. The relationships between the master and other family members are recorded, including their spouse, first-degree and second-degree or higher relatives (including parents, grandparents, offspring, etc), adoptees, and tenants. Step relationships (stepmother, stepfather, and stepchild) are also recorded. Spouse and step relationships and linkage by ties of consanguinity through parents' names allow for the construction of polygamous family pedigrees. However, we did not include this type of pedigree in TRIPIS.

The status of household registration is updated by both active and passive methods. In the active method, household registration is updated by the master or other household members in case of immigration, emigration, death, marriage, birth, adoption, new tenants, or changing accommodation. Passive surveillance for updating household registration is implemented by police in a population census every 5 years in Taiwan.

Both population and household registration have been centralized to the Department of Population and Household Centre, which is part of the Ministry of the Interior of Taiwan. Data are further decentralized to the Population and Household Center in each local county and district. The Keelung Health Bureau can update the data at 6-month intervals upon request due to the healthcare provided under the KCIS program. All procedures followed government regulations on data security and were approved by the relevant central and local governments.

Community-based integrated screening

The second set of data was derived from the community-based integrated screening program in Keelung, the northernmost county of Taiwan. The KCIS program was initiated on January 1, 1999⁴ and provides both disease screening and a platform for research purposes. Databases on the KCIS program are managed by an health information management system, which supplies validation, database linkage, and referral management.⁶ The KCIS program provides a screening package every year for five types of cancer (cervical, breast, oral, liver, and colorectal) and three types of chronic disease (hypertension, diabetes, and hyperlipidemia) according to evidence-based screening guidelines in the literature. The program design and rationale for KCIS have been fully described in previous studies.^{4 6 7}

Algorithm for constructing the three-generation pedigree

Three procedures were followed to construct population-based pedigrees in TRIPIS by combining population-based household registration data with KCIS information. In addition to validating and structuring the data, to reduce the repeated procedure of building up the pedigree for different genetic association studies, we developed a proband-oriented pedigree system to ascertain other relatives. In the same family pedigree, the proband may change from study to study due different probands being selected under different topics. The relative relationships of the proband are therefore also changed. We linked the population-based household registry system with the KCIS data to develop TRIPIS with the incorporation of disease outcomes, risk factors, genome data, and phenotypes, as illustrated in figure 1. Standard symbols and a pictorial method were adopted to illustrate how the algorithm was developed to ascertain pedigree data across households. Personal identification number and names in TRIPIS are removed to maintain privacy if the data are used for research purposes.⁸ Figure 2 gives an example of constructing such a pedigree. It also shows the proband-oriented relative relationships expressed by relative relationship scores (table 1) when different probands in the same pedigree are selected: (b) in figure 2A, (e) in figure 2B, and (h) in figure 2C. The procedure for developing such a population-based proband-oriented pedigree information system is described below. To quantify the degree of relative relationships of family members to the proband, we borrowed the idea of degree of relative relationship from Thomas⁹ with some modifications. The relative relationship score used in table 1 represents the degree of relative relationship between the proband and his/her family members. The score was weighted from 1 to 8 in accordance with the degree of relationship as traditionally used in genetic pedigree studies, with higher scores assigned to closer blood relationships.

Figure 2.

Demonstration of proband-oriented and trans-generational algorithm. DBP, diastolic blood pressure; HTN, hypertension; SBP, systolic blood pressure.

Table 1.

Definition of relative relationship scores

Code	Relative	Score (Y)
X8	Parent (father/mother)	8
X7	Offspring (son/daughter)	7
X6	Sibling (brother/sister)	6
X5	Paternal grandfather/grandmother	5
X4	Maternal grandfather/grandmother	4
X3	Grandson/granddaughter (son's)	3
X2	Grandson/granddaughter (daughter's)	2
X1	Spouse	1

Algorithm for relative relationships within a household

Using the population-based proband-oriented pedigree information system, we can assess the degree of relative relationships, particularly parent–offspring and spouse relationships, based on the selected proband within the household together with information on whether they attended the KCIS program. In figure 2, parent–offspring and spouse relationships in three different households are shown together with information on household number, names of members, and screening uptake. The spouses of probands (b), (e), and (h) are (a), (d), and (i), respectively. The corresponding offspring are (c), (f), and (g), and (j) and (k). The (j) and (k) members of family-C4300004, who are denoted by dotted lines, do not have information on screening data because they did not attend the KCIS program.

Algorithm for relative relationships across households

We assessed relative relationships across households by linkage through the names of the mother and father recorded in the population-based household registration system. As the maximum number of generations in our study was three, we developed pedigrees across households from the founder to their grandchildren. Siblings sharing common parents were ascertained through linkage to the population-based household registry from the first to third generations. As shown in figure 2, subjects (b), (e), and (h) were selected as probands. We identified three siblings of (b), (e), and (h) listed in different generations across households who were descended from the same parents. Pedigree can be further expanded across households and generations by ascertaining offspring through spouse relationships identified in the first stage. The three-generation pedigree was constructed using an algorithm. To quantify kindred relationships, we assigned a series of codes (X₁–X₈) to the corresponding score denoted by a random variable, Y, to indicate the degrees of relative relationship between probands and their relatives (see table 1). Higher scores indicate closer kinship with the proband. Recall that TRIPIS accommodates the changing relative relationship as the selected proband is changed.

Proband-oriented relative relationship score

The proband-oriented method can be used to assess the proband-oriented relative relationship score. Supposing that there are k members in a family, we can ascertain different relative relationship scores by selecting different probands. The relative relationship score for the ith proband can be calculated by summing each score of the other k−1 members following the codes in table 1. Figure 2 provides an example of the three types of relative relationship scores calculated with our algorithm by changing the probands (b), (e), and (h) (corresponding to figure 2A–C, respectively). The sums for each proband in different generations were 32 (1+7+7+5+5+7), 43 (8+8+6+1+7+7+6), and 29 (8+8+6+6+1) for (b), (e) and (h), respectively.

Theoretical family relationships

Incomplete capture of the degree of family relationship is a possibility when collecting screening data for the construction of the family pedigree system. In light of the relationship of family members across three generations, we used the following codes to derive the formula for the probabilities of different combinations of family members with different relationships categorized by X₁–X₈. Theoretical relationships between relatives and the selective proband across different generations were derived. Therefore, we can deduce theoretical combinations for different numbers of relatives in each generation. The numbers of relatives are subject to the social norms of relative relationships. This means some theoretical combinations (eg, spouse≥2) are inadmissible. Based on the expected members and finite relationships, we developed a generalized formula of theoretical combinations across different generations. The detailed mathematics for deriving theoretical relative relationship scores given the possible combinations of family members by selecting the proband across three generations are given in the appendix. Table 2 compares the distributions of relative relationship scores obtained from the theoretical condition and empirical screening data. In addition to the relative relationship score, the derivation of theoretical combinations can also be used to check the degree of capture (see the final column of table 2). Theoretical combinations and empirical ascertainment from screening data are compared in online supplementary tables S1–S3.

Table 2.

Comparison of relative relationship scores between the theoretical method and empirical screening data by generations and family members

Generation	Number of other family members	Theoretical method				Empirical screening data				Capture rate (B/A)
		Types of combination (A)	Range	Mean (SD)	Median	Types of combination (B)	Range	Mean (SD)	Median
First*	1	5	(1–7)	3.8 (2.6)	3.0	(see second generation)
	2	14	(3–14)	8.0 (3.4)	8.0	5	(8–14)	9.6 (2.6)	8.0	35.7%
	3	30	(5–21)	12.3 (4.3)	12.0	10	(11–21)	16.2 (2.5)	15.0	33.3%
	4	55	(7–28)	16.7 (5.2)	17.0	12	(14–28)	22.7 (2.7)	22.0	21.8%
	5	91	(9–35)	21.2 (6.1)	21.0	8	(22–35)	30.0 (2.8)	29.0	8.8%
	6	140	(11–42)	25.6 (7.0)	25.5	9	(24–42)	35.2 (5.7)	36.0	6.4%
	7	204	(13–49)	30.1 (7.9)	30.0	6	(33–49)	44.2 (5.5)	44.0	2.9%
	8	285	(13–49)	28.0 (8.4)	28.0	2	(34–42)	38.0 (5.7)	38.0	0.7%
Second†	1	4	(1–8)	5.5 (3.1)	6.5	4	(1–8)	3.0 (2.8)	1.0	100.0%
	2	9	(7–16)	12.0 (3.2)	13.0	6	(7–16)	11.3 (3.4)	12.0	66.7%
	3	15	(13–23)	18.4 (3.2)	19.0	12	(13–23)	17.6 (3.4)	18.0	80.0%
	4	21	(19–30)	24.9 (3.3)	25.0	17	(19–30)	23.5 (3.2)	24.0	81.0%
	5	27	(25–37)	31.3 (3.4)	31.0	20	(25–35)	29.5 (3.0)	29.0	74.1%
	6	33	(31–44)	37.8 (3.5)	38.0	21	(31–43)	35.0 (2.8)	35.0	63.6%
	7	39	(37–51)	44.3 (3.6)	44.0	19	(37–48)	41.9 (2.6)	42.0	48.7%
	8	45	(37–50)	43.2 (3.6)	43.0	7	(43–51)	46.3 (2.6)	45.5	15.6%
	9	51	(37–49)	42.5 (3.6)	42.0	4	(51–58)	53.8 (3.1)	53.0	7.8%
Third‡	1	5	(1–8)	4.8 (2.6)	5.0	–	–	–	–
	2	14	(5–16)	10.1 (3.1)	10.0	2	(12–13)	12.5 (0.5)	12.0	14.3%
	3	27	(9–22)	15.5 (3.4)	16.0	8	(13–21)	19.9 (1.7)	21.0	29.6%
	4	40	(14–28)	21.1 (3.5)	21.0	9	(20–27)	26.1 (1.3)	27.0	22.5%
	5	49	(19–34)	26.7 (3.6)	27.0	6	(26–33)	31.9 (1.7)	33.0	12.2%
	6	51	(20–32)	25.5 (3.1)	25.0	2	(33–34)	33.8 (0.4)	34.0	3.9%

^*Parents (X₈) not included.

^†Grandchildren not included.

^‡Offspring not included.

Applications

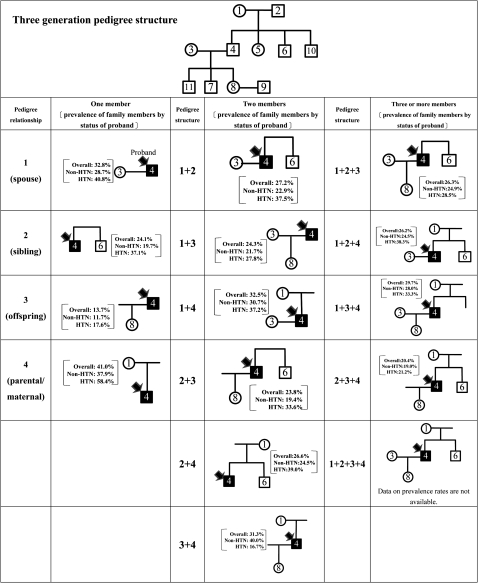
TRIPIS can be applied to various genetic epidemiological designs, including descriptive and analytic studies, once unique personal identification numbers and names have been removed. Here, we used hypertension as an example to demonstrate the two applications. The first application was to estimate the prevalence rate of hypertension among family members given the selected proband. Figure 3 shows the construction of various pedigree structures ascertained from TRIPIS, starting with one, then two, and, finally, three or more family members. The prevalence rates of hypertension could be estimated for family members by the status of the proband. In addition, information in table 2 can be used to check how well theoretical family relationships have been captured.

Figure 3.

Hypertension (HTN) prevalence rates in family members based on the selected proband under various pedigree structures.

For analytic studies, we demonstrate the relationship between the relative relationship score and age at onset of hypertension, with adjustment for environmental factors. The proportional hazards regression model was used to estimate the HRs for each factor. Age was censored at entry to screening for normal cases and age at onset of hypertension was treated as the time of the event. A p value of 0.05 was considered statistically significant for entry and removal criteria. All models were adjusted for independent variables, such as gender, educational level, alcohol consumption, smoking, and betel nut chewing. To examine the difference in the relative relationship scores between the theoretical method and the empirical data (table 2), we adjusted the mean value of each category of family member in three generations using the ratio of SD to the mean (coefficient of variation). Using the second case as an example (the second row in table 2), the corrected mean value was 6.1 by using 8.0 multiplied by the ratio of the SD of the empirical data (2.6) to that of the theoretical method (3.4). A similar procedure was applied to other categories. The adjusted HRs were corrected by the ratio of the average of the corrected mean value to the corresponding value of the uncorrected mean from empirical data. A p value of 0.05 was considered statistically significant.

Data sources

Data used for the de-identified pedigree were derived from 94 275 residents aged over 20 years participating in the KCIS program from 1999 to 2006. Information was obtained from a comprehensive semi-structured questionnaire, anthropometric measurements, blood bioassay, and urinary tests. All participants gave informed consent before screening.

Anthropometric measurements were performed by public health nurses or doctors. Systolic (SBP) and diastolic blood pressure (DBP) were measured twice with an interval of at least 20 min. The lower of the two measurements was taken as the individual's blood pressure. The definition of hypertension follows our previous study in light of JNC7 criteria.⁷ Those with a previous history of hypertension were also considered hypertensive. Body mass index (BMI) was calculated by multiplying weight by the square of height, with 25 kg/m² or above defined as obesity. We also used central waist circumference as another indicator of obesity: a central waist measurement above 90 cm for males or 80 cm for females was considered central obesity in accordance with the Asian obesity definition of the WHO.¹⁰

Blood and urine samples were taken when the questionnaire was administered. All tests were carried out by certified biotechnical laboratories. The venous blood sample was taken after a fast of 12 h and was used to measure general blood counts, fasting blood glucose, triglyceride, total cholesterol, high density lipid, uric acid, and hepatitis antigen.

Results

To build the population-based proband-oriented pedigree information system to ascertain other relatives, we linked mass screening data with the population household registry database based on our trans-generational approach (see figure 2). In addition to assessing the relative relationship scores following selection of different probands, these three-generation pedigree data allowed us to estimate the prevalence rate of hypertension by generation and the prevalence rate of family members of the proband.

As shown in table 3, a total 68 068 subjects among 94 275 residents had one or more relatives who attended the screening program in Keelung, including 30 609 males and 37 459 females. The proportions of spouses and first, second, and third generations were 39.0%, 10.7%, 49.8%, and 0.5%, respectively. The corresponding mean ages were 51.9 (±14.1), 60.6 (±10.4), 45.4 (±14.8), and 26.2 (±5.2), respectively. The prevalence rates of hypertension were 31.4%, 41.1%, 24.3%, and 8.6% for spouses (mainly including first and second generation members) and first, second, and third generations, respectively. No statistically significant differences were observed between females and males in generation distribution or age distribution, but the hypertension prevalence rate of males was higher than that of females regardless of generation.

Table 3.

Distributions of age and prevalence rate of hypertension by gender and generation

Generation	Male		Female		Total		Mean age, years			Prevalence rate of hypertension
	No.	%	No.	%	No.	%	Male (SD)	Female (SD)	Total	Male	Female	Total
Spouse only	12 602	41.2%	13 928	37.2%	26 530	39.0%	54.8 (14.6)	49.3 (13.1)	51.9 (14.1)	39.2%	24.3%	31.4%
First generation	3053	10.0%	4249	11.3%	7302	10.7%	62.5 (10.2)	59.3 (10.3)	60.6 (10.4)	46.2%	37.5%	41.1%
Second generation	14 793	48.3%	19 078	50.9%	33 871	49.8%	45.3 (14.7)	45.5 (14.9)	45.4 (14.8)	30.0%	19.8%	24.3%
Third generation	161	0.5%	204	0.5%	365	0.5%	27.1 (5.6)	25.5 (4.8)	26.2 (5.2)	16.2%	2.5%	8.6%
Total	30 609	100.0%	37 459	100.0%	68 068	100.0%	50.8 (15.5)	48.4 (14.5)	49.5 (15.0)	35.3%	23.4%	28.8%

By using the proposed formula for theoretical combinations based on a three-generation pedigree, the types of combination for each generation could be used to determine each relative relationship score. The scores ranged between 5 and 285 for different relatives (see table 2). The distributions of the relative relationship scores are listed in table 2 with the mean, SD, and median. The corresponding figures based on empirical data are also presented in table 2. The second-generation combinations were more comprehensive than those of other generations. Therefore, the chance of incomplete capture was higher in the first and third generations than in the second generation. For example, with three other family members, the probabilities of complete capture were 33.3% in the first generation, 80.0% in the second generation, and 29.6% in the third generation.

Figure 3 shows the hypertension prevalence rates in spouse, siblings, parents, and offspring based on the proband's disease status, and also shows the variants for the four combinations using the comprehensive pedigree infrastructure (top panel of figure 3). In the pedigree with only one member and a spouse proband, the prevalence rate of hypertension in the other spouse was 40.8% among disease probands, which was higher than the 28.7% for non-disease probands. These descriptive results with various pedigree structures also reveal the relative contributions of genetic influence (eg, sibling) and environmental effects (eg, spouse) to the prevalence rates in these relatives. The different prevalence rates between spouse probands and sibling probands were greater for non-disease probands than for disease probands. Examination of the pedigrees of siblings, parents, and offspring, shows the family member from disease proband had a 1.5–2-fold increased risk for hypertension compared with that from non-disease proband from the first to the third generation. Figure 3 shows prevalence rates for various pedigree structures. The descriptive results become more complicated with increasing numbers of family members. For example, when the pedigree involved two or more family members, the prevalence rate of family members was the result of a mixture of a series of simplified pedigree structures. The degree of incomplete capture can also be assessed by comparing the types in figure 3 with those derived using the theoretical method (see table 2). For example, the pedigree structures in figure 3 lack empirical data on grandchild relationships. For example, subjects 1 and 8 under one member structure in Figure 3 may not be available from our screening program. Data on four members of the pedigree structure were also unavailable (see 1+2+3+4 in figure 3) from screening data.

We analyzed the effect of the relative relationship score on the age at onset of hypertension by regarding the relative relationship score as an interval-scale property and also a categorical property using the Cox proportional hazards regression model. After controlling for gender, educational level, and environmental factors, the adjusted HR of the relative relationship score on the age at onset of hypertension using a liner relationship was 1.02 (95% CI 1.01 to 1.03). When the relationship score was stratified as <6, 6–7.9, 8–14.9, and over 15, the adjusted HR values were 1.05 (95% CI 1.01 to 1.09), 1.35 (95% CI 1.28 to 1.43), and 1.72 (95% CI 1.55 to 1.90) compared with the baseline group (<6). The trend test for the relative relationship score was statistically significant (see table 4).

Table 4.

Effects of genetic influence and environmental risk factors on age at onset of hypertension

Variable	Classification	Coefficient	HR (95% CI)
Relative relationship score	6–7.9/<6	0.0488*	1.05 (1.01 to 1.09)
	8–14.9/<6	0.3018***	1.35 (1.28 to 1.43)
	≥15/<6	0.5395***	1.72 (1.55 to 1.90)
		p value for trend test: p<0.0001
Number of relatives		−0.1206***	0.89 (0.86 to 0.92)
Gender	Male/female	−0.2818***	0.75 (0.73 to 0.78)
Education level	Middle/high	0.6954***	2.00 (1.94 to 2.07)
	Low/high	1.0129***	2.75 (2.63 to 2.89)
Alcohol consumption	Quit/never	0.0538	1.06 (0.98 to 1.14)
	Current/never	0.4051***	1.50 (1.44 to 1.56)
Betel nut chewing	Quit/never	0.9424***	2.57 (2.37 to 2.78)
	Current/never	1.0186***	2.77 (2.55 to 3.00)
Body mass index	≥25/<25 kg/m2	0.4932***	1.64 (1.59 to 1.69)
Triglyceride level	≥200/<200 mg/dl	0.2511***	1.29 (1.24 to 1.33)

*0.01≤ p<0.05.

***p<0.0001.

When the difference in the relative relationship score distribution between theoretical and empirical screening data was considered, the mean relative relationship score corrected with the coefficient of variance method was 16.6, which was lower than the corresponding value of 27.9 from empirical screening data without correction. The adjusted HR of the relative score corrected by the factor of 0.59 (6.6/27.9) was deflated to 1.01 (95% CI 1.00 to 1.02) (table 4). The corresponding adjusted HRs (table 4) with correction for three high levels of the relative relationship score based on categorical classifications were 1.04 (95% CI 1.00 to 1.08), 1.29 (95% CI 1.23 to 1.34), and 1.59 (95% CI 1.48 to 1.70).

Discussion

In contrast to the conventional pedigree information approach,¹¹ our method uniquely demonstrates how to use population-based screening data and a population household registry to create a population-based proband-oriented pedigree information system to provide information for various genetic studies. The changing relative relationship scores are readily available for genetic epidemiological applications with the selection of different probands under our system, which dispenses with repeated procedures for obtaining pedigree information in each study. Our study also developed a novel algorithm for elucidating the degree of incomplete capture associated with the TRIPIS pedigree. Our system has a wide application potential for different diseases and events. In our study, we have demonstrated the usefulness of applying TRIPIS to assess the prevalence rate of hypertension based on different probands. In addition, we modeled the effect of the relative relationship score on the age at onset of hypertension, making allowances for environmental factors. Our findings have significant implications for the role of heritability in hypertension. It is well known that family history is the key factor for the development of hypertension. This has been demonstrated in a previous study using the same data but without the pedigree information collected in TRIPIS.⁷ Familial aggregation of hypertension either through shared environment or genetic components is also well recognized. However, reporting a positive association between family history and hypertension cannot capture heritability and familial aggregation studies cannot distinguish heritability from environmental influence. To capture both, we used TRIPIS by assigning a relative relationship score (the degree of relationship) to capture heritability and also by collecting environmental factors to separate their influence from genetic factors with a proportional hazards regression model by taking age at onset of hypertension as the outcome. Note that the earlier the onset of hypertension, the higher the contribution from genetics. The results show that, taking environmental factors into account, the independent contribution of genetic influence to the risk of developing hypertension was statistically significant as the dose–response relationship of the relative relationship score demonstrates in table 4. The higher the relative score, the higher the risk for having hypertension at an earlier age. Our study provided evidence consistent with the hypothesis of the heritability of hypertension.

Several other merits of TRIPIS are noteworthy. The TRIPIS-based screening database approach has advantages compared to other methods because it is based on the general registry system. The Swedish Family Cancer Database study reported the interval between first and second cancer cases in individual families, revealing that the second case was usually found shortly after the first cancer was diagnosed. There was a higher chance of detecting a second cancer (in another family member) after the first cancer diagnosis, regardless of whether the proband was a parent or a sibling.¹² This phenomenon is related to ‘selection bias’ and might inflate the risk of familial aggregation compared with control proband relatives. Our system can dispense with this bias by using population-based screening data to enroll family members by changing different probands to case or control probands.

Incomplete capture of family relatives due to truncation from using restricted data is common in family-based pedigree studies.¹³ We generated a formula for combinations of family relatives according to different numbers of families given the selected proband. Our study demonstrates that information about probands from the second generation was more complete than from the first and third generations. With the high variation embedded in theoretical distribution, we postulate that an exaggerated effect of the relative relationship score on the age at onset of hypertension would be expected if the empirical data are used without correction for such incomplete capture. The effects were deflated after correction with the coefficient of variation method.

For epidemiological research of diseases, information on family history provides a useful and convenient tool for public health applications.¹⁴ In addition to recall bias, there is one concern about the definition of ‘family history’, which can include father or mother¹⁵ or first- or second-degree relatives.¹⁶ Although self-report surveys are feasible, sensitivity varies with disease.^{17 18} Our TRIPIS system helps to clarify the role of family history by collecting data on the type and number of family members¹⁹ and the ages at disease onset for family members that represent different baseline risks for disease.²⁰ We also collected environmental factors for each subject through a community-based screening project. Such comprehensive information contributes to the study of genetic and environmental influences on chronic diseases, such as hypertension and diabetes.

TRIPIS has significant implications for the design of several types of genetic studies, including pedigree, sib-pair, and case–control proband studies. However, results have been inconsistent with different approaches, which might be partly due to inadequate selection of subjects and insufficient sample sizes.²¹ Although the affected sib-pair study is popular for this application, the design does not fully identify genetic penetrance in different generations. A simulation study on heritability based on three empirical family studies demonstrated that the pedigree structure influences the results compared with a trimmed incomplete pedigree and original family pedigree.²² Extended family studies not only consider the quantitative genetic trait but also identify environmental factors for application in genetic studies. Information on extended family pedigrees requires more time and effort to collect than small or nuclear family information. Therefore, the algorithm developed in TRIPIS contributes to the collection of extended family pedigrees based on a population approach. Our results on the disease prevalence rate in family members in various pedigree structures (figure 3) are tailored for such a purpose. Estimating the prevalence rate in family members is also helpful for sample size determination when different genetic study designs are adopted.

Several large-scale population-based family studies for various cancers through local population registries have been established, including the Utah Population Database in the USA,²³ the Multigenerational Register and Swedish Family Cancer Database in Sweden,^24–26 and the genealogy database of multiple cancers from the Icelandic Cancer Registry.²⁷ Although these studies demonstrate the usefulness of such large databases for familial research on a variety of cancers, they are limited to interactions between genetic influence and personal attributes or environmental risk factors, both of which often rely on primary studies of surveys or screening rather than archival data. Therefore, the TRIPIS system based on population-based screening data and household data facilitates a more efficient approach.

Malin's study extracted information from death records in public online sources and further validated it by using the Social Security Death Index (SSDI) to re-identify familial databases by name and link them with genomic data.³ By contrast, we used the population-based household registry to construct an extended family structure rather than a simple nuclear family structure because the household number and the names of the father, mother, and spouse are recorded by the system, in addition to a personal identifier, if available. Both father's and mother's names can yield more siblings, and identification of the spouse relationship can also extend the pedigree structure to link paternal or maternal family members together. Our system is more comprehensive and extensive for constructing a familial database for sharing the information used for epidemiological and molecular researches. The family pedigree under TRIPIS provides a significant opportunity to examine the heritability of certain diseases (eg, hypertension) across three family generations.

From a biomedical and health perspective, issues in constructing TRIPIS focus on the representativeness of the group subject to screening, the validity of the linkages created, and the accuracy of the familial relationships identified. Accordingly, several concerns should be noted. First, we did not construct family pedigrees that included polygamous relationships in TRIPIS, although our population-based household registry system can provide sufficient information to do this. Polygamous relationships are still rare in Chinese society. However, extension of TRIPIS to cover this aspect should be considered in the future on several grounds. Family relationships between monogamous and polygamous family structures have been studied in clinical and genetic research, particularly on general mental health in full and half siblings; Elbedour et al proved that the shared family environment plays a crucial role in the similarity in general mental ability in Bedouin full and half siblings.²⁸ The identification of exact family relationships in siblings and half siblings also contributes to linkage analysis using DNA markers.²⁹ Moreover, multiple marriage (polygamous) relationships have been also covered in a computer-aided medical pedigree drawing system.³⁰ Second, there is a risk of error due to duplicate records caused by linkage across datasets using the same name, but the chance of error still depends on the matching criteria. By linking the vital statistics registry and the population registry in Calgary, Canada using surname, first name, sex, and date of birth, Li et al found that correct linkage rates of 98.5% could be achieved.³¹ In our study, we used Chinese names from both parents to identify the relationships of siblings. According to the 2006 household registry in Keelung, the maximum duplication rate of a single Chinese name was 0.000185, which implies the potential misclassification rate for siblings, namely for the pair of parents, was very low (approximately 3.42×10⁻⁸), assuming marriage is independent of name. Third, the ability to construct a pedigree structure based on genetics in our study is due to the availability of information on the parents' birth names and spouse relationships recorded on the population-based personal identification card. Information on siblings living in different households was also obtained from the population-based household registry. These unique population-based registry features in the Taiwanese population may limit the generalization of our method to other countries without such information.

In conclusion, we developed a population-based proband-oriented pedigree information system to identify changing and trans-generational relative relationships by developing an algorithm to ascertain family structure (from nuclear family to extended family), while making allowances for incomplete capture of family relationships. We applied this system to assess genetic and environmental influences on hypertension. Such a population-based proband-oriented family-based pedigree information system provides a platform for future genetic studies of different diseases in various disciplines.

Appendix.

The derivation of theoretical combinations of relative relationships by proband-oriented generation

Proband from the first generation

The possible relative relationships with the proband selected from the first generation include X₁ (spouse), X₂ (grandchildren, daughter's), X₃ (grandchildren, son's), X₆ (sibling), and X₇ (offspring), as defined in table 1. If Z_j (j=1,2,3,6,7) represents the number of relative relationships derived from the proband and the number of families among the identified pedigree is denoted by k, we have a linear equation:

$$Z_1+Z_2+Z_3+Z_6+Z_7=k-1.$$

Let r stand for the maximum probable relative relationships, which changes depending on the generation the proband is selected from. When the proband is selected from the first generation, r is equal to 5.

From the mathematical definition of combination, we obtain:

$$H_{k-1}^r=C_{r-1}^{\left(r-1\right)+\left(k-1\right)}$$

with the following constraints:

$$Z_1\le 1\text{and}0\le Z_j\le k-1.$$

The number of theoretical combinations subject to the constraints r and k can be expressed as:

$$H_{\left(k-1\right)}^r-H_{\left(k-1\right)-2}^r$$ (1)

Proband from the second generation

The possible relative relationships with the proband selected from the second generation include X₁ (spouse), X₆ (sibling), X₇ (offspring), and X₈ (parents). We can use the linear equation:

$$Z_1+Z_6+Z_7+Z_8=k-1$$

with the following constraints:

$$Z_1\le 1,Z_8\le 2,\text{and}0\le Z_j\le k-1.$$

The number of theoretical combinations subject to the constraints, r (=4) and k are expressed as follows:

$$H_{k-1}^r-H_{\left(k-1\right)-2}^r-\left(H_{\left(k-1\right)-3}^r-H_{\left(k-1\right)-\left(2+3\right)}^r\right)$$ (2)

Proband from the third generation

The possible relative relationships with the proband selected from the third generation include X₁ (spouse), X₄ (grandparent(s), maternal), X₅ (grandparent(s), paternal), X₆ (sibling), and X₈ (parents). Another linear equation can described:

$$Z_1+Z_4+Z_5+Z_6+Z_8=k-\mathrm{1,}$$

with the following constraints:

$$Z_1\le 1,Z_8\le 2,Z_4\le 2,Z_5\le 2,\text{and}0\le Z_j\le k-1.$$

The number of theoretical combinations subject to the constraints, r (=5) and k are expressed as follows:

$$H_{k-1}^r-H_{\left(k-1\right)-2}^r-3\times \left(H_{\left(k-1\right)-3}^r-H_{\left(k-1\right)-\left(2+3\right)}^r\right)$$ (3)