Non-technical summary
The fastest contracting vertebrate muscle known is found in toadfish. This muscle surrounds the gas-filled swimbladder of males and contracts and relaxes at 100–200 times per second, producing a mating call. Because calcium ions, the trigger for muscle contraction, must be released and taken up (‘pumped’) on each contraction, this muscle would seem to require a prodigious rate of Ca2+ pumping. Previous work, however, indicates that (1) the pumping proteins in toadfish are not particularly fast, and (2) the mating calls are short (400 ms), interleaved with long (5–15 s) intercall intervals. The present study shows that the Ca2+ pumping paradox is solved in two ways: (1) the amount of Ca2+ released per stimulus is reduced (which also avoids running out of Ca2+), and (2) the muscle's high concentration of the protein parvalbumin binds released Ca2+ during a call, thereby allowing most pumping to occur during the intercall interval.
Abstract
Abstract
Superfast fibres of toadfish swimbladder muscle generate a series of superfast Ca2+ transients, a necessity for high-frequency calling. How is this accomplished with a relatively low rate of Ca2+ pumping by the sarcoplasmic reticulum (SR)? We hypothesized that there may not be complete Ca2+ saturation and desaturation of the troponin Ca2+ regulatory sites with each twitch during calling. To test this, we determined the number of regulatory sites by measuring the concentration of troponin C (TNC) molecules, 33.8 μmol per kg wet weight. We then estimated how much SR Ca2+ is released per twitch by measuring the recovery oxygen consumption in the presence of a crossbridge blocker, N-benzyl-p-toluene sulphonamide (BTS). The results agreed closely with SR release estimates obtained with a kinetic model used to analyse Ca2+ transient measurements. We found that 235 μmol of Ca2+ per kg muscle is released with the first twitch of an 80 Hz stimulus (15oC). Release per twitch declines dramatically thereafter such that by the 10th twitch release is only 48 μmol kg−1 (well below the concentration of TNC Ca2+ regulatory sites, 67.6 μmol kg−1). The ATP usage per twitch by the myosin crossbridges remains essentially constant at ∼25 μmol kg−1 throughout the stimulus period. Hence, for the first twitch, ∼80% of the energy goes into pumping Ca2+ (which uses 1 ATP per 2 Ca2+ ions pumped), but by the 10th and subsequent twitches the proportion is ∼50%. Even though by the 10th stimulus the Ca2+ release per twitch has dropped 5-fold, the Ca2+ remaining in the SR has declined by only ∼18%; hence dwindling SR Ca2+ content is not responsible for the drop. Rather, inactivation of the Ca2+ release channel by myoplasmic Ca2+ likely explains this reduction. If inactivation did not occur, the SR would run out of Ca2+ well before the end of even a 40-twitch call. Hence, inactivation of the Ca2+ release channel plays a critical role in swimbladder muscle during normal in vivo function.
Introduction
Male toadfish (Opsanus tau) produce a loud, hooting mating call, commonly described as a ‘boatwhistle’, to attract females to their nest (Skoglund, 1961; Fine, 1978). The call frequency, which depends on ambient water temperature, is 80–100 Hz at 15°C, rising to 250 Hz or more at 25°C (Fine, 1978; Edds-Walton et al. 2002). Calling is accomplished by vibration of the swimbladder in response to unfused, high frequency contractions of the surrounding superfast muscle. These high frequency contractions are made possible by a number of adaptations, including an extraordinarily fast detachment rate constant of myosin crossbridges (Rome et al. 1999), an extremely brief Ca2+ transient, and, probably, a fast off-rate of Ca2+ from troponin (Rome et al. 1996; Rome, 2006).
Superfast muscle might be expected to use ATP at a superfast rate to permit rapid cycling of the force-generating crossbridges and rapid release and re-uptake of SR Ca2+. However, previous work indicates that the rate of ATP utilization per kg muscle of maximally activated swimbladder fibres which were skinned with saponin (to permeablize the plasma membrane, but leave the SR intact) is no higher than that of fast-twitch fibres (Rome & Klimov, 2000). The lower than expected rate of crossbridge ATP utilization (measured in the presence of the SR Ca2+ pump blockers 2′,5′-di(tert-butyl)-1,4-benzohydroquinone (TBQ) and cyclopiazonic acid (CPA)) appears to be due to the large increase in the crossbridge detachment rate constant g, without a parallel increase in the attachment rate constant f. This results in the rapid crossbridge detachment needed for fast relaxation but also results in a low force production and a relatively low ATP utilization rate (Rome et al. 1999).
How a high-frequency train of superfast Ca2+ transients is accomplished with a relatively low rate of ATP utilization by the SR Ca2+ pump (and thus a low Ca2+ pumping rate), however, is puzzling. If enough Ca2+ is released and re-sequestered with each twitch to saturate and desaturate troponin C (TNC), then, with a troponin site concentration previously estimated indirectly to be 70 μmol kg−1 (Young et al. 2003), a calling frequency of 100 Hz would appear to require a SR Ca2+ pumping rate of 7 mmol kg−1 s−1 (15°C). The maximal SR-Ca2+ pumping rate, however, is only 2 mmol kg−1 s−1 (measured in the presence of the crossbridge blocker, N-benzyl-p-toluene sulphonamide (BTS)) (Young et al. 2003).
Two mechanisms, which may be additive, could explain this seeming paradox. Mechanism no. 1: during each twitch of a call, there may not be complete saturation and desaturation of troponin with Ca2+; rather the troponin occupancy level may rise and fall only slightly while the fibre operates on a steep portion of the curve relating force vs. troponin occupancy. This could permit considerable reduction in the average Ca2+ release and reuptake per stimulus. Mechanism no. 2: since toadfish call with a low duty cycle (vocalization duration/(vocalization + intercall interval durations)), most of the Ca2+ released during a typical call (lasting 0.4–1 s) could temporarily bind to parvalbumin (Parv; with Ca2+-binding sites present at up to 3 mmol kg−1) (Hamoir et al. 1980; Appelt et al. 1991; Tikunov & Rome, 2009) and be pumped back into the SR during the much longer (5–10 s) intercall interval (i.e. only after the muscle has relaxed). Postponement of most of the Ca2+ pumping would permit a lower time-averaged SR-Ca2+ pumping rate (Rome & Klimov, 2000; Young et al. 2003).
Evidence supporting both mechanisms was obtained in this study, in which we estimated how much Ca2+ is released per twitch in intact, normally functioning swimbladder fibres activated at a physiological calling frequency and for a physiological duration. To do so, we developed a novel technique based on recovery oxygen consumption (Kushmerick & Paul, 1976; Rome & Kushmerick, 1983). We also analysed myoplasmic Ca2+ transients measured (from other swimbladder fibres) with a Ca2+ indicator dye. SR Ca2+ release was then estimated with a kinetic model that incorporates biochemical information on the concentrations and reaction kinetics of the major myoplasmic Ca2+ buffers, including troponin, parvalbumin and the SR Ca2+ pumps (Baylor & Hollingworth, 2007). Good agreement was observed between these two approaches. As the approaches are based on fundamentally different assumptions, this concurrence provides strong support for the validity of the results and for the approaches that generated them. Preliminary reports of this work were published (Harwood et al. 2001; Tikunov et al. 2003).
Methods
Animals
Experiments were performed at both The Marine Biological Laboratory and The University of Pennsylvania. In both cases, toadfish were housed in seawater tanks maintained at 15°C and fed ad libitum.
Preparation of intact muscle bundles
In accordance with federal recommendations and with the approval of the Institutional Animal Care and Use Committees at both institutions, toadfish were sedated by lowering their temperature on ice until they became unresponsive. They were then given a blow to the head, after which their spinal column was severed and their brain and spinal cord were destroyed (double pithing). As described previously (Young & Rome, 2001), the swimbladder was isolated quickly and placed in a dish containing chilled Ringer solution (composition in mm: NaCl 132, KCl 2.6, MgCl2 1, CaCl2 2.7, imidazole 10, sodium pyruvate 10, pH 7.7 at 15°C), where it was cut in half longitudinally. The swimbladder muscle, which is pure in fibre type, was dissected quickly into four to six strips. One of these strips was dissected further into a thinner preparation, ≤1 mm thick, and mounted vertically in a chamber on a custom-made muscle holder to which oxygen can diffuse from all sides. The muscle holder was attached to the chamber lid made of Macor (Corning Inc, Corning, New York, USA a machinable ceramic that does not absorb or resorb significant amounts of O2; Rome & Kushmerick, 1983). One end of the preparation was fixed onto the holder by a stainless steel clamp; the other was tied to a gold chain that traversed a vertical hole in the chamber lid.
Muscle mechanics measurements
The muscle holder and lid assembly were placed inside a water-jacketed, glass chamber containing oxygenated Ringer solution. The other end of the gold chain was attached to a force transducer (Model FS2-A, Konigsberg Instruments Inc., Pasadena, CA, USA) and sarcomere length, measured by laser diffraction, was set to 2.3 μm (Rome et al. 1999). To assess whether the preparations were healthy, a series of isometric twitches and brief tetani (e.g. a 1 s tetanus at 150 Hz) were performed to determine isometric force. Preparations with low forces and/or slow twitch kinetics were rejected (Young & Rome, 2001).
Use of recovery oxygen consumption to estimate the Ca2+ release per stimulus in intact muscle
Recovery O2 consumption measurements have been described previously (Kushmerick & Paul, 1976; Rome & Kushmerick, 1983). The rationale is that the extra O2 consumed during and following a stimulus will be proportional to the extra ATP consumed by the muscle in response to that stimulus. This is so even though high energy phosphate (∼P) production lags ATP use, provided that O2 consumption is measured over a time period sufficient for the pre-stimulus state of the muscle to be restored. In this case, crossbridges return to their resting state, released Ca2+ is returned to the SR, and ∼P is replenished by oxidative phosphorylation, so that the only detectable difference between the pre-stimulus muscle and the muscle at the end of the recovery oxygen measurement is that a small amount of substrate (e.g. glycogen) has been utilized and oxygen consumed (Kushmerick & Paul, 1976). Here we describe a new application of recovery O2 measurements to the estimation of the amount of Ca2+ released during stimulation. The next sections describe the steps required for this estimate and the supporting experimental evidence.
Estimating SR Ca2+ release from ATP consumption of SR Ca2+ pumps
Extra ATP consumption due to contractile activity is associated mainly with two processes, the cycling of crossbridges and the pumping of released calcium back into the SR (see also Discussion). If crossbridge cycling is eliminated, then most of the remaining ATPase utilization can be associated with the SR Ca2+ pump (e.g. Young et al. 2003; Barclay et al. 2007, 2008). Two Ca2+ ions are returned to the SR per ATP molecule consumed by the pump (Weber et al. 1966), so the amount of Ca2+ released can be estimated from the ATP consumption associated with pumping this released Ca2+ back into the SR. The time course of release is not obtained since there are lags between Ca2+ release and Ca2+ pumping and between Ca2+ pumping and ∼P restoration. This approach to estimating release is very different from that based on measurements of the free Ca2+ transient (see below), which relies on concentration and kinetic information about the myoplasmic Ca2+ buffers to obtain estimates of the amount and time course of release.
Use of BTS to knock out crossbridge ATP utilization
To eliminate myosin-associated ATPase activity, we blocked crossbridge activity with N-benzyl-p-toluene sulphonamide (BTS; Cheung et al. 2002). We have previously shown in skinned swimbladder fibres that 25 μm BTS blocks more than 95% of the crossbridge force and crossbridge ATPase (Young et al. 2003). The recovery O2 measurements, however, require use of bundles of fibres up to 1 mm in thickness that contain several hundred fibres. Preliminary studies showed that 25 μm BTS reduced force (and therefore crossbridge ATP utilization) from the bundles by more than 96% provided that several hours were allowed for BTS to diffuse into the bundles. Because of this long diffusion time, we sometimes left the bundles in BTS overnight at a reduced temperature. We obtained similar results whether the muscle bundle was exposed for several hours or overnight, and data obtained after both exposure times were combined.
O2 consumption measurements
Recovery O2 consumption was measured as the change in O2 partial pressure (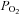 ) in our closed chamber. The
) in our closed chamber. The 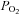 change was measured with a Radiometer polarographic electrode (E5046), consisting of a combined platinum- and silver–silver chloride electrode mounted in an electrode jacket and covered by a 20 μm thick membrane of polyethylene. The electrode was polarized at about –0.63 V and the current output had a temperature coefficient of 3%°C−1. Temperature in the chamber, which was monitored continuously by a glass encapsulated thermistor, was controlled by using a Neslab refrigerated circulator (Model RTE-211, Thermo Neslab Inc, Newington, NH, USA) maintained at 15 ± 0.01oC that circulated water through the glass jacket surrounding the chamber. Data with uncertainties larger than 10% due to temperature fluctuations were not included in the analysis. A stirrer, constructed from Macor and located in the bottom of the chamber, stirred the Ringer solution continuously. The Ringer solution volume in the chamber was 9.2 ml as measured by weight. The salinity of the Ringer solution was calculated to be 9.125 parts per thousand. At 15oC, the molar solubility of oxygen in the Ringer solution is 15.24 mol O2 ml−1 kPa−1 at STPD (standard temperature and pressure, dry) (Cameron, 1986).
change was measured with a Radiometer polarographic electrode (E5046), consisting of a combined platinum- and silver–silver chloride electrode mounted in an electrode jacket and covered by a 20 μm thick membrane of polyethylene. The electrode was polarized at about –0.63 V and the current output had a temperature coefficient of 3%°C−1. Temperature in the chamber, which was monitored continuously by a glass encapsulated thermistor, was controlled by using a Neslab refrigerated circulator (Model RTE-211, Thermo Neslab Inc, Newington, NH, USA) maintained at 15 ± 0.01oC that circulated water through the glass jacket surrounding the chamber. Data with uncertainties larger than 10% due to temperature fluctuations were not included in the analysis. A stirrer, constructed from Macor and located in the bottom of the chamber, stirred the Ringer solution continuously. The Ringer solution volume in the chamber was 9.2 ml as measured by weight. The salinity of the Ringer solution was calculated to be 9.125 parts per thousand. At 15oC, the molar solubility of oxygen in the Ringer solution is 15.24 mol O2 ml−1 kPa−1 at STPD (standard temperature and pressure, dry) (Cameron, 1986).
As illustrated in Fig. 1, the pre-stimulation basal O2 consumption rate was recorded for 10–20 min. The muscle was then subjected to a stimulation protocol (see below) during and after which it consumed extra O2 (ΔO2). Following this recovery period, O2 consumption again reached a constant rate and this post-stimulation basal oxygen consumption rate was recorded for another 15–25 min. ΔO2 was calculated as the difference between tangents drawn to the pre- and post-stimulation basal O2 consumption rates (Fig. 1). During periods of basal O2 consumption, rates of ATP consumption and ATP production are equal.
Figure 1. Recovery oxygen record for a 5 s tetanus.
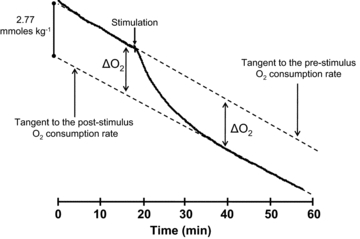
The oxygen consumption measurement is made with a  electrode in a closed chamber and is expressed in m moles of O2 consumed per kilo gram of muscle based on the solubility coefficient of oxygen and the volume of the chamber. The drop in
electrode in a closed chamber and is expressed in m moles of O2 consumed per kilo gram of muscle based on the solubility coefficient of oxygen and the volume of the chamber. The drop in 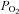 is due entirely to O2 consumption by the muscle (i.e. the electrode and chamber consume very little O2). The ΔO2 measurements determine the extra amount of oxygen consumed to replenish the extra ATP used during and immediately after the contraction. Because the pre-stimulus resting O2 consumption rate approximately equals the late post-relaxation rate, the ΔO2 is simply the vertical distance between the tangents. Because of small differences in the pre- and post-stimulation tangents, the ΔO2 is measured just before the stimulus and after recovery and the values are averaged. A stimulus artifact is seen: these appear in some experiments and not in others, but had no effect on the measurement of ΔO2. Preparation weight was 157 mg. In these experiments, swimbladder fibre length was generally 25–30 mm. Fibre diameter is approximately 38 μm (Appelt et al. 1991)
is due entirely to O2 consumption by the muscle (i.e. the electrode and chamber consume very little O2). The ΔO2 measurements determine the extra amount of oxygen consumed to replenish the extra ATP used during and immediately after the contraction. Because the pre-stimulus resting O2 consumption rate approximately equals the late post-relaxation rate, the ΔO2 is simply the vertical distance between the tangents. Because of small differences in the pre- and post-stimulation tangents, the ΔO2 is measured just before the stimulus and after recovery and the values are averaged. A stimulus artifact is seen: these appear in some experiments and not in others, but had no effect on the measurement of ΔO2. Preparation weight was 157 mg. In these experiments, swimbladder fibre length was generally 25–30 mm. Fibre diameter is approximately 38 μm (Appelt et al. 1991)
Relation between ΔO2 and ATP consumption
The measured ΔO2 was converted to ATP utilization by multiplying by 6, the assumed ratio of high-energy phosphate production to oxygen consumption (∼P/O2). Literature values for the ∼P/O2 ratio range from ∼4 to 6.3. In isolated mouse sartorius muscle (Crow & Kushmerick, 1982), the apparent ∼P/O2 ratio is over 6. In contrast, the predicted maximum ratio based on detailed evaluation of the mechanism for oxidative metabolism in isolated mitochondria provides a value of about 5.3 (Hinkle et al. 1991). Recently, NMR combined with other spectroscopic techniques provided a value of 5.4 for human muscle (Amara et al. 2008). If the ∼P/O2 ratio in swimbladder is less than 6, then the actual release of Ca2+ will be less than calculated.
Anaerobic metabolism of swimbladder muscle
A potential difficulty of the method is that anaerobic glycolysis could be a significant contributor to the ATP production. For instance in frog sartorius muscle the anaerobic contribution was found it to be ∼10% even under very high oxygen tensions (Rome & Kushmerick, 1983). To investigate this issue, muscle lactate production (Δlactate) was measured as a change in chamber lactate concentration (see the online Supplemental Material).
ΔLactate was too low to measure accurately during our typical 80 stimulus contractions, and hence we stimulated 400 times (i.e. a 5 s tetanus at 80 Hz). Figure 2 shows that, even with this strong stimulus, no more than ∼5% of the total ATP generation came from anaerobic sources. Because all other experiments reported in this study used only 80 stimuli, which, except for the 1 s tetanus, were spread out over tens or hundreds of seconds (see below), the proportional anaerobic contribution to these stimulus trains is expected to be extremely small and was ignored.
Figure 2. Anaerobic contribution to high energy phosphate production.
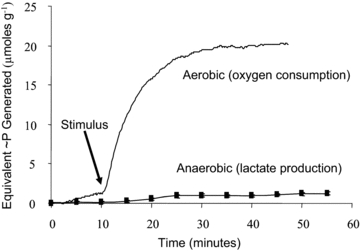
The contributions of aerobic (upper trace labelled O2 consumption) and anaerobic (lower trace labelled lactate production) metabolism for 400 stimuli given over 5 s (i.e. at 80 Hz) are shown. This is 5 times more stimuli than given during our other experimental protocols (80 stimuli). Lactate measurements are means from 5 different muscles. Recovery O2 consumption and lactate production were converted into units of high-energy phosphate (∼P) using conversion factors of 6.0 (ΔO2) and 1.5 (Δlactate). As illustrated here, the anaerobic contribution was about 5%.
Signal averaging of ΔO2 measurements
A second potential limitation of the ΔO2 measurement is sensitivity, as we found that we could not accurately measure the ΔO2 for a single twitch. Instead, to determine how much Ca2+ is released during a twitch (equivalently, the first stimulus of a call), we gave the muscle 80 twitches separated by a fixed time interval. The interval was determined empirically to avoid inactivation of the Ca2+ release channels (Baylor et al. 1983; Schneider & Simon, 1988; Jong et al. 1995; Hollingworth & Baylor, 1996), which might reduce Ca2+ release in some of the twitches. Figure 3 shows the results of stimulating a bundle 80 times with the fixed intervals between stimuli ranging from 12.5 ms (80 Hz stimulation) to 2 s (0.5 Hz stimulation). As the interval between stimuli increased, ΔO2 increased until a maximum was reached at ∼500 ms; no further increase in ΔO2 was observed with longer intervals. Thus, when 80 twitches were given over a period of 40 s (500 ms between stimuli), the measured value of ΔO2 after a 20 min recovery was divided by 80 to yield the average ΔO2 for a single twitch.
Figure 3. ΔO2 for 80 stimuli as a function of time between stimuli (interpulse interval).
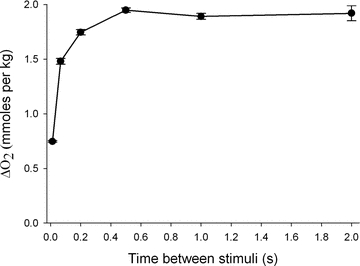
Eighty stimuli given within 1 s (80 Hz or interpulse interval of 0.0125 s) consumed an average of 0.747 μmol g−1 O2 but as the interpulse interval increases, the ΔO2 increased about 2.6-fold until a maximum was reached at the interpulse interval of 0.5 s (2 Hz). The ΔO2 remained constant thereafter as the interpulse interval increased. Hence, for these experiments we used an interpulse interval of 0.5 s to determine the ΔO2 (and ATP utilization) for the first twitch. Error bars shown are ±SEM. n = 6–11 for all points except for 0.5 Hz where n = 4. These measurements were performed in the absence of BTS, and hence include the crossbridge ATP utilization. In another set of experiments where ΔO2 was measured in the presence of BTS, ΔO2 rose 4.13-fold from 0.378 ± 0.026 μmol g−1 (n = 4) at 80 Hz to 1.56 ± 0.021 μmol g−1 (n = 4) at 2 Hz.
Stimulus protocol
To determine the Ca2+ release per stimulus as a function of stimulus number, we again stimulated the muscle a total of 80 times, but adjusted the stimuli (80 Hz) per train and the number of trains accordingly. For instance to determine the average Ca2+ release during stimuli nos 2–4 of an 80 Hz train, we gave the muscle 20 trains of four stimuli each, allowing sufficient recovery time (20 s) between trains. By this procedure the total ΔO2 measured can be divided by 20 to yield the ΔO2 for a train of four stimuli. By subtracting the cost for the first twitch from the cost of the first four twitches, we obtained the total cost of twitch nos 2–4. Division by 3 provides the average cost per stimulus. We used this procedure iteratively to determine the cost per stimulus for various twitches in the train.
Data acquisition, analysis and statistics
Throughout the recovery O2 experiments, chamber  , temperature, and stimulation were captured and analysed on-line via an A to D data card (Keithly Instruments, Cleveland, OH, USA) and software written in Testpoint (Capitol Equipment Corp., Billerica, MA, USA). On the completion of each experiment, the length of the preparation was measured. The preparation was then taken off the muscle holder, the tendons were removed with the aid of a dissecting microscope and, after blotting, the wet weight of the preparation was determined. The cross-sectional area of the preparation was determined from the weight of the preparation, the fibre length, and an assumed density of 1.05 g cm−3. Force, normalized for cross-section, provided isometric stress. Recovery O2 consumption and lactate production were normalized for mass. Unless noted, results are reported as sample means ± SEM (standard error of the mean). All statistical tests were made utilizing SigmaStat software (Systat Software Inc., San Jose, CA, USA), with the significance level set to P < 0.05 unless otherwise noted. Student's paired t test was performed where possible; otherwise unpaired t tests were done. Analysis of variance (ANOVA) was also used for two tests (see legend of Fig. 5).
, temperature, and stimulation were captured and analysed on-line via an A to D data card (Keithly Instruments, Cleveland, OH, USA) and software written in Testpoint (Capitol Equipment Corp., Billerica, MA, USA). On the completion of each experiment, the length of the preparation was measured. The preparation was then taken off the muscle holder, the tendons were removed with the aid of a dissecting microscope and, after blotting, the wet weight of the preparation was determined. The cross-sectional area of the preparation was determined from the weight of the preparation, the fibre length, and an assumed density of 1.05 g cm−3. Force, normalized for cross-section, provided isometric stress. Recovery O2 consumption and lactate production were normalized for mass. Unless noted, results are reported as sample means ± SEM (standard error of the mean). All statistical tests were made utilizing SigmaStat software (Systat Software Inc., San Jose, CA, USA), with the significance level set to P < 0.05 unless otherwise noted. Student's paired t test was performed where possible; otherwise unpaired t tests were done. Analysis of variance (ANOVA) was also used for two tests (see legend of Fig. 5).
Figure 5. Twitch by twitch Ca2+ release and ATP utilization by SR-Ca+2 pumps and crossbridges during simulated calling by toadfish.

The Ca2+ release per twitch (red bars, calibrated at right) was determined by ΔO2 measured in the presence of BTS. During the first twitch, 235 μmol kg−1 of Ca2+ was released and this amount dropped quickly in subsequent twitches, so that by the 10th twitch it was down to about 48 μmol kg−1 and remained constant throughout the rest of the physiological range (up to 1 s). This value is below the concentration of Ca2+ binding sites on TNC (67.6 μmol kg−1, red horizontal dashed line). Correspondingly, the ATP used by the SR Ca2+ pumps (left-hand axis), from which Ca2+ release was calculated, also drops dramatically with subsequent twitches. The total ATP utilized per twitch (black bars) was determined in the absence of BTS in a different group of muscles. Crossbridge ATP utilization (green bars) was determined by subtracting the BTS values from the total values measured in the absence of BTS. For muscle in BTS (Red), n = 9 except for 21–80 where n = 4. For muscle in absence of BTS (Black), n = 6. Error bars shown are ±SEM. The error bars for the crossbridge ATPase are calculated as the SE of the difference between two means [Total ATP utilization (no BTS) – Ca2+ pump ATP utilization (in BTS)]. There was a significant fall in Ca2+ release with increasing twitch number up to about the 10th twitch, i.e. a significant drop between groups up to and including twitches 11–20 (ANOVA, P < 0.001). Thereafter, release remained constant, i.e. there was no significant difference between twitches 11–20 and 21–80 (pairwise comparison gave a P = 0.89). The overall data relationship was well fitted by a 3-parameter hyperbolic decay: Release (μmol Ca2+ per kg muscle) = 43.3 + (2068 × 0.1019)/(0.1019 + twitch number), r2 = 0.91. There did not appear to be a relationship between twitch number and crossbridge ATP utilization per twitch, i.e. there was no significant difference between the groups (ANOVA, P = 0.595). A similar result was obtained using two-way ANOVA (individual preparation, twitch number). Measurements were made on 80 (one-twitch trains), 20 (four-twitch trains), 8 (10-twitch trains), 4 (20-twitch trains) and 1 (80-twitch train). The calculations were as follows: Twitch 2–4 is the difference between the four-twitch train and the one-twitch train. Twitch 5–10 is the difference between the 10-twitch train and the four-twitch train, twitch 11–20 is the difference between the 20-twitch train and the 10-twitch train, and twitch 20–80 is the difference between the 80-twitch train and the 20-twitch train. Note that in a smaller group of muscles (n = 7) we measured ΔO2 for 80 twitches at 2 Hz in the absence and presence of BTS. The proportions for the crossbridges (∼12%) and the SR Ca2+ pumps (88%) in this group are consistent with those obtained for the first twitch in the larger comparison shown in this figure.
Troponin C determination
The concentration of troponin C was measured using quantitative protein analysis as previously described (Tikunov et al. 2001; Tikunov & Rome, 2009). Briefly, muscle proteins were completely extracted by biochemical and mechanical means, and TNC was separated on SDS-PAGE gels calibrated with molecular weight markers. The TNC band was cut out of the gel, TNC was eluted on a custom micro-elution device and the protein content in the elution buffer was then determined by a protein assay that was calibrated for TNC (Tikunov et al. 2001).
Fluorescence indicator dye measurements
Furaptra (Raju et al. 1989), a rapidly responding low-affinity Ca2+ indicator with some sensitivity to Mg2+, was used to measure changes in myoplasmic free [Ca2+] (Δ[Ca2+]) and changes in myoplasmic free [Mg2+] (Δ[Mg2+]) in individual swimbladder fibres. Δ[Ca2+] was then used as an input to a kinetic model to estimate SR Ca2+ release (last section of Methods).
The furaptra measurement techniques, which were similar to those described previously with furaptra in other fibre types (e.g. Konishi et al. 1991; Baylor & Hollingworth, 2003), were applied to swimbladder fibres stimulated to give single action potentials and brief high-frequency trains of action potentials (67–100 Hz) (Rome et al. 1996). Briefly, a small bundle of swimbladder fibres was dissected in the Ringer solution described above and mounted at 16oC in a temperature-controlled chamber on an optical bench apparatus. To reduce movement artifacts in the optical records, the bundle was stretched to a sarcomere length of ∼3 μm and lowered onto a pair of supporting pedestals. One fibre within the bundle was gently pressure-injected with the membrane-impermeant (K+-salt) form of furaptra. Fibres were studied only if they gave stable, all-or-nothing changes in fluorescence (ΔF) in response to brief supra-threshold stimuli from a pair of extracellular electrodes. The fluorescence excitation and emission filters passed light of 410 ± 20 nm and 530 ± 60 nm, respectively. ΔF and resting fluorescence (FR) were recorded in all experiments, with signal properties analysed as ΔF/FR. The furaptra concentration at the measurement site (denoted [DT], with concentration units referred to the myoplasmic water volume; see below) was typically ≤0.2 mm; this is sufficiently small that Δ[Ca2+] is not expected to be perturbed significantly due to Ca2+ buffering by the indicator (e.g. Konishi et al. 1991).
Calibration of myoplasmic Ca2+ and Mg2+ signals from furaptra
For analysis, the recorded furaptra ΔF/FR signal was first scaled by 1.46. This factor (see Supplemental Material) is based on the estimate that ∼31% of FR comes from indicator in the ‘core’ region of a swimbladder fibre (the central zone devoid of myofilaments and t-tubules), which is unlikely to experience the brief ΔF associated with action potential stimulated Ca2+ release in the ‘myofibrillar’ region of the fibre (where contractile activity occurs). As described in the next section, ΔF/FR is thought to consist of a large Ca2+-related component, which is brief and returns to a small baseline offset after each stimulus, and a small but distinguishable Mg2+-related component, which develops slowly. The components of ΔF/FR were converted to Δ[Ca2+] and Δ[Mg2+] as follows:
- The Ca2+-related component was converted to ΔfCaD, the change in the fraction of furaptra in the Ca2+-bound form, with the equation:
(Hollingworth et al. 1996; Baylor & Hollingworth, 2003). Equation (1) assumes that fMgD, the fraction of furaptra in the Mg2+-bound form, at rest is 0.086 (see below and Konishi et al. 1993). ΔfCaD was converted to Δ[Ca2+] with the equation: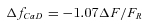
(1)
with a value of 96 μm for KD,Ca, furaptra's apparent dissociation constant for Ca2+ in the myoplasm (Konishi et al. 1991; Baylor & Hollingworth, 2003).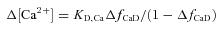
(2) - The Mg2+-related component was converted to ΔfMgD, the change in the fraction of furaptra in the Mg2+-bound form, with the equation:
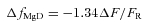
(3)
Equation (3) is based on the in vitro observation that, with 410 nm excitation, the change in furaptra's fluorescence due to Mg2+ binding is 0.80 times that due to Ca2+ binding (Konishi et al. 1991). ΔfMgD was converted to Δ[Mg2+] with the equation:
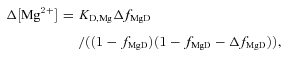 |
(4) |
with values of 10.6 mm for KD,Mg (furaptra's apparent dissociation constant for Mg2+ in the myoplasm) (Konishi et al. 1991) and 0.086 for fMgD, the value expected if resting free [Mg2+] is 1 mm. Equation (4) follows from the 1:1 binding equation under the assumptions that furaptra's Mg2+ reaction is not rate-limited and that Ca2+ binding by furaptra can be ignored. These assumptions are reasonable given that the major portion of the furaptra Mg2+ signal (next section) appears to develop slowly and at a time when [Ca2+] is small.
Decomposition of the furaptra signal into Ca2+- and Mg2+-related components
Figure 4 shows an example of the ΔF/FR signal recorded from a swimbladder fibre stimulated by a single stimulus (Fig. 4A) and 10 stimuli at 83.3 Hz (Fig. 4B). The fibre was sufficiently immobilized that the furaptra signal appeared to be almost free of movement artifacts. In response to the single stimulus, ΔF/FR reaches a negative peak of –0.243 at 5.5 ms after stimulation, then decays quickly almost to baseline, reaching a negative minimum of –0.003 at ∼25 ms; ΔF/FR then becomes increasingly negative during the remainder of the sweep. As in muscle fibres from frog (Konishi et al. 1991) and mouse (Hollingworth et al. 1996), the large early furaptra signal is thought to be due almost entirely to Δ[Ca2+]. Interestingly, a distinct slowly developing negative change like that seen in Fig. 4A is not seen in frog or mouse fibres. The amplitude of ΔF/FR at 120 ms is –0.009, which is about 3 times larger than that at 25 ms. A similar slow component of the furaptra signal elicited by a single stimulus was seen in all swimbladder experiments in which the fibre bundle appeared to be well immobilized for a single twitch (n = 4).
Figure 4. Furaptra fluorescence responses in a swimbladder fibre stimulated by either a single stimulus or a 10-stimulus, 83.3 Hz train.
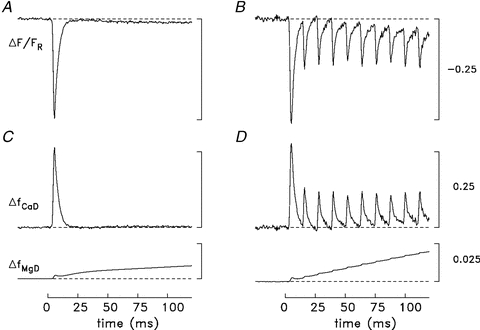
A and B, original records of ΔF/FR after scaling by the factor 1.46 as described in Methods; the records in A and B are an average of 3 and 2 sweeps, respectively. Fibre diameter, 35 μm; sarcomere spacing, 2.7 μm; [DT], 0.2 mm in A and 0.1 mm in B. C and D, the ΔF/FR records were separated into their putative contributions from Δ[Ca2+] and Δ[Mg2+] as described in Methods; these components were then converted to ΔfCaD and ΔfMgD with eqns (1) and (3), respectively. In both C and D, ΔfCaD goes slightly below baseline at t≈ 25 to 30 ms. This is likely to indicate a slight contamination of the ΔF/FR records with a small movement artifact. The calibration bars in B and D also apply in A and C.
The slow component of the furaptra signal is thought to be due to Δ[Mg2+] and not to Δ[Ca2+] because (i) SR Ca2+ release elicited by an action potential likely ceases within a couple of milliseconds after its initiation, and (ii) the model calculations described in Results (Fig. 6) reveal a slow increase in myoplasmic [Mg2+] that, if converted to a ΔF/FR waveform, has an amplitude and time course similar to that of the slow component of ΔF/FR. In frog and mouse fast-twitch fibres, furaptra signals elicited by a single stimulus are also thought to contain a Mg2+-related component (Konishi et al. 1991), which, as in swimbladder fibres, is thought to be due primarily to the presence of parvalbumin (see below). The Mg2+ signal is small in frog and mouse fibres, however, and does not appear as a distinct kinetic component (probably due to the smaller parvalbumin content of these fibres); thus it can usually be ignored. In contrast, in swimbladder fibres the signal is larger, appears as a distinct kinetic component, and interferes with the estimation of Δ[Ca2+] during a tetanus. Therefore a method was developed to separate ΔF/FR into its Ca2+- and Mg2+-related components.
Figure 6. Measured and modelled responses of a swimbladder fibre to a 10-stimulus 83.3 Hz stimulus.
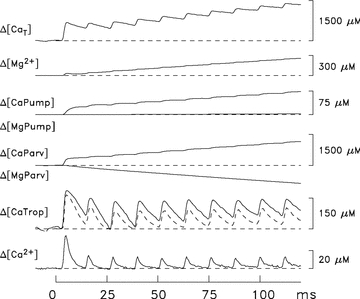
The Δ[Ca2+] trace was calculated from the ΔfCaD trace in Fig. 4B with eqn (2) and used to drive the Ca2+ model, which used standard parvalbumin kinetics and a concentration of Ca2+ pumps of 190 μm (Model 1). The dashed trace displayed with Δ[CaTrop] is the calculated change for troponin if only troponin molecules having both regulatory sites bound with Ca2+ are considered. Δ[MgPump] is small because the large concentration of Mg2+ released by parvalbumin leads to a substantial Δ[Mg2+] (second trace from top); this increases Mg2+ binding to the pump slightly even though Ca2+ binding to the pump increases markedly (as expected) because of Δ[Ca2+]. The top trace, Δ[CaT], estimates the concentration of Ca2+ released from the SR due to the 10 stimuli. The flux of Ca2+ release due to each stimulus, was also estimated as (d/dt)Δ[CaT] (not shown). With each stimulus, the full duration at half-maximum (FDHM) of the flux was ∼1 ms.
To achieve the decomposition, ΔF/FR was initially assumed to be due entirely to Δ[Ca2+]. ΔF/FR was then converted to Δ[Ca2+] with eqns (1) and (2) and used as input to the model described in the next section. The Δ[Mg2+] waveform generated by the model was converted to ΔF/FR units with the inverse forms of eqns (3) and (4), which yielded the initial estimate of the Mg2+-related component of ΔF/FR. This component was subtracted from the original ΔF/FR waveform to yield a revised estimate of the Ca2+-related component of ΔF/FR. This process was repeated three more times after which changes to the estimates of the Ca2+- and Mg2+-related components were negligible. Based on this decomposition, ΔfCaD in Fig. 4C returns close to baseline by 20 ms after stimulation and remains near baseline thereafter. In contrast, ΔfMgD has two distinguishable phases, a small early increase whose time of peak matches that of ΔfCaD and a larger more slowly developing increase that is still rising slightly at the end of the sweep. According to the modelling (next section and Results), the fast kinetic component of ΔfMgD is due to the Mg2+ released to the myoplasmic pool from ATP in mass-action exchange for bound Ca2+ whereas the slower component is due primarily to Mg2+ released from parvalbumin in a similar mass-action exchange. While this method of decomposition of ΔF/FR is clearly empirical, it is reasonable given that SR Ca2+ release is likely to cease shortly after action potential repolarization. Moreover, the main conclusions from the modelling are not highly sensitive to the exact method used to separate the smaller Mg2+-related component of ΔF/FR from the larger Ca2+-related component.
With high-frequency stimulation (Fig. 4B), a rapid Ca2+-related component of ΔF/FR occurs in response to each stimulus, although the amplitudes of the peaks elicited by the stimuli after the first are considerably smaller than the initial amplitude. Figure 4B also reveals that the minimum return value of ΔF/FR after each stimulus becomes increasingly offset from the baseline with later stimuli in the train. As in Fig. 4A, this slowly increasing offset of ΔF/FR is thought to be due to a slowly developing Δ[Mg2+] caused primarily by the release of Mg2+ from parvalbumin. The ΔF/FR in Fig. 4B was also decomposed in terms of its putative Ca2+ and Mg2+ components by the method used in Fig. 4A and C. Figure 4D shows the result after conversion of these components to ΔfCaD and ΔfMgD with eqns (1) and (3). While ΔfCaD returns close to baseline after each stimulus, ΔfMgD continues to increase throughout the stimulus period. By the end of the sweep, ΔfMgD is 0.0198, which is 2.2-fold larger than in Fig. 4C. These values correspond to Δ[Mg2+] values of 257 and 118 μm, respectively (eqn. (4)).
Ca2+ release modelling
The Δ[Ca2+] signals from furaptra were analysed with a single-compartment (‘spatially averaged’) kinetic model to estimate the total concentration of Ca2+ released by the SR (denoted Δ[CaT]) with each stimulus. The model, which was adapted from an analogous model for mouse fast-twitch fibres (Baylor & Hollingworth, 2007), assumes that Δ[CaT] is given by the sum of seven changes: Δ[Ca2+] itself; the change in the concentration of Ca2+ bound to the Ca2+ regulatory sites on troponin (Δ[CaTrop]) and to the metal sites on ATP (Δ[CaATP]), parvalbumin (Δ[CaParv]), the SR Ca2+ pump (Δ[CaPump]), and furaptra (Δ[CaDye]); and the change in concentration of Ca2+ pumped by the SR Ca2+ pumps (Δ[CaPumped], which, on the ∼0.1 s time scale of the calculations, is a small fraction of Δ[CaT]). Ca2+ binding by ADP and by inorganic phosphate (Pi) were ignored because of the small myoplasmic concentrations of these molecules ([ADP] < 1 mm, [Pi]≈ 1 mm; (Godt & Maughan, 1988; Chase & Kushmerick, 1995)). Similarly, Ca2+ uptake by the mitochondria was ignored because of their small content in swimbladder fibres, ∼4% by volume, and their central location (Appelt et al. 1991; see also Baylor & Hollingworth, 2007). As for [DT], the concentration units of all variables are referred to the myoplasmic water volume (Baylor et al. 1983).
Most of the reaction schemes and parameter values were identical to those in the mouse model (Tables I–II and Fig. 2 of Baylor & Hollingworth, 2007). The following changes were made to take into account the unique features of swimbladder fibres.
The myoplasmic concentration of troponin molecules was set to 106 μm based on the troponin content measured in this study, 33.8 μmol (kg wet weight)−1, and the factor 3.13 derived in the Supplemental Material to convert the latter units to μmoles per litre of water in the myofibrillar region. The result is slightly smaller than the value in the mouse model (120 μm). The reaction of Ca2+ with the two regulatory sites on each troponin molecule (total site concentration, 212 μm), followed an independent (rather than a cooperative) binding scheme. The dissociation constant of each site for Ca2+ was 3.9 μm, achieved with on- and off-rate constants of 0.885 × 108m−1 s−1 and 345 s−1, respectively (Rome et al. 1996).
The myoplasmic concentration of parvalbumin was set to 2670 μm (rather than 750 μm). This value is based on the most recent – and probably most reliable – determination of the parvalbumin content of swimbladder fibres (see Supplemental Material). As in the mouse model, each parvalbumin molecule is assumed to have two identical Ca2+/Mg2+ binding sites, which yields a total parvalbumin site concentration of 5340 μm.
Two different concentrations of SR Ca2+ pump molecules were considered: 190 μm and 980 μm (see Supplemental Material). These values are 1.6 times (Feher et al. 1998) and 8 times (Appelt et al. 1991), respectively, the value for the pump concentration in the mouse model (120 μm). As before, each pump molecule has two Ca2+/Mg2+ binding sites, with unique reaction kinetics for each divalent-ion binding step.
The reactions of Ca2+ and Mg2+ with the metal site on ATP explicitly included competition between Ca2+ and Mg2+ (rather than the reduced ‘equivalent’ reaction that considered just Ca2+ binding under the assumption that resting free Mg2+, [Mg2+]R, is constant). This permitted estimation of the concentration of Mg2+ released to the myoplasmic pool by ATP in response to Ca2+ binding. The on- and off- rate constants were 1.5 × 108m−1 s−1 and 30,000 s−1 for Ca2+ and 1.5 × 106m−1 s−1 and 150 s−1 for Mg2+ (16°C; Baylor & Hollingworth, 1998).
- As in the mouse model, [Mg2+]R was 1 mm; however, changes in [Mg2+] during activity were allowed in the swimbladder model because of the large parvalbumin concentration and the expected large exchange of Ca2+ for Mg2+ on the parvalbumin sites during sustained activity (cf. Irving et al. 1989). Δ[Mg2+] was calculated from Δ[Mg]T (the change in the total concentration of Mg2+ released to the myoplasmic pool due to the competitive reactions of Ca2+ and Mg2+ on parvalbumin, ATP, and the SR Ca2+ pump) with a linear buffering approximation:
BFMg, the myoplasmic buffering factor for Mg2+, was set to 0.35 (Baylor et al. 1985) under the assumptions that (i) phosphocreatine is the major myoplasmic Mg2+ buffer for changes near the resting level (Irving et al. 1989), (ii) the myoplasmic concentration of phosphocreatine is 50 mm, the value estimated in frog twitch fibres (Curtin & Woledge, 1978; Godt & Maughan, 1988), and (iii) phosphocreatine's dissociation constant for Mg2+ is 25 mm (O'Sullivan & Perrin, 1964).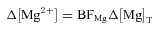
(5)
Results
Troponin C concentration
By biochemical extraction and calibrated gels, we determined that the TNC concentration was 33.8 ± 1.6 μmol kg−1 (SEM; n = 9), giving a Ca2+ regulatory site concentration of 67.6 μmol kg−1.
Oxygen consumption and SR Ca2+ release per twitch
As described in Methods, recovery O2 consumption measurements in the absence and presence of the crossbridge ATPase blocker BTS permit estimation of the ATP consumption by the crossbridges and the SR Ca2+ pumps associated with specific stimulation protocols. Figure 5 summarizes the results from nine preparations in the presence of BTS and an additional six preparations in the absence of BTS. The bundles were stimulated a total of 80 times, but the stimuli (80 Hz) per train and the number of trains were adjusted accordingly. The values measured in the presence of BTS (red bars; see also Table 1 part A) reflect ATP utilization by the SR Ca2+ pumps, whereas the difference in the values measured in the absence (black bars) and presence of BTS reflects ATP consumption due to the crossbridges (green bars). With the first twitch, 235 ± 9.2 μmol Ca2+ kg−1 (SEM, n = 9) is pumped, and was therefore previously released, by the SR (right-hand calibration); this amount is 3.5 times the amount of TNC Ca2+ regulatory sites. With subsequent twitches, the amount of Ca2+ released declines dramatically, such that, beginning with about the 10th twitch, Ca2+ release is only about 48 μmol kg−1 per twitch. This level is well below that required to fully saturate and desaturate the regulatory sites on troponin (horizontal dashed line, which intersects the right-hand ordinate at 67.6 μmol kg−1). Release then remains approximately constant throughout the rest of the stimulation period (up to 80 twitches in 1 s), which includes the full range of call durations recorded in the natural environment (Edds-Walton et al. 2002). These results provide strong evidence that Ca2+ release per twitch during most of a call is well below the number of TNC sites.
Table 1.
Estimated concentration of SR Ca2+ release per twitch during high-frequency stimulation of toadfish swimbladder fibres (15–16°C)
| Stim no. 1 (μm) | Stim no. 2–4 (μm) | Stim no. 5–10 (μm) | Stim no. 11 20 (μm) | |
|---|---|---|---|---|
| A. Recovery O2 measurements | ||||
| (80 Hz; n = 9) | 735 ± 81 | 339 ± 100 | 252 ± 81 | 152 ± 41 |
| B. Ca2+ modelling (83.3 Hz) | ||||
| 1. Model 1 (see Fig. 6) | 683 | 222 | 180 | — |
| 2. Model 2 (see Fig. 7A) | 732 | 242 | 196 | — |
| 3. Model 3 (see Fig. 7B) | 790 | 339 | 236 | — |
| C. Ca2+ modelling (67–100 Hz) | ||||
| Model 1 (n = 5) | 701 ± 54 | — | — | — |
| Model 2 (n = 5) | 764 ± 65 | — | — | — |
| Model 3 (n = 5) | 819 ± 40 | — | — | — |
All concentrations refer to the myoplasmic water volume in the myofibrillar space (see Methods). In A, the values are means ± SD from the 9 experiments summarized in Fig. 5; to convert to μM units, results in μmoles per kg of muscle were multiplied by 3.13 (see Methods and Supplemental Material). In B, the values are from the single experiment discussed in connection with Figs. 6 and 7; the values for stimuli after the first have been averaged over the indicated number of stimuli. See Results for differences between Models 1–3. In C, the entry gives the mean ± SD for the first-stimulus release in the five experiments discussed in the last section of Results; in three of these fibres, a movement artifact prevented an accurate estimate of release for stimuli after the first. Three t tests did not reveal a statistical difference between the Ca2+ released for the first stimulus estimated by recovery oxygen measurements (A) and that estimated by Models 1, 2 or 3 (C), that is the P values (0.421, 0.507, 0.053, respectively) were greater than the significance level (adjusted to 0.017 by the Bonferroni correction for multiple comparisons).
Figure 5 also shows that, in contrast to ATP utilization by the SR Ca2+ pumps, crossbridge ATP utilization is approximately constant at 25 μmol kg−1 per twitch during stimulation of up to 1 s. Given that the myosin and myosin head concentrations are 34.5 and 69 μmol kg−1 (Rome et al. 1999), respectively, this is equivalent to just under 1 ATP split per myosin molecule during each twitch. A consequence of the fall in the Ca2+ pump ATP utilization but constant crossbridge ATP utilization per twitch is that the percentage of the energy that goes into pumping Ca2+ changes during isometric contractions, starting at about 80% for the first twitch, but declining to about 50% by the 10th and subsequent twitches up to the maximum duration of a call (<1 s). These results contrast with previous results from other fibre types using different approaches, in which Ca2+ pumping during isometric contractions is reported to use only 20–50% of the total energy and is similar for both twitches and tetani (Homsher et al. 1972; Smith, 1972; Rall, 1982; Barclay et al. 2007).
Ca2+ release modelling
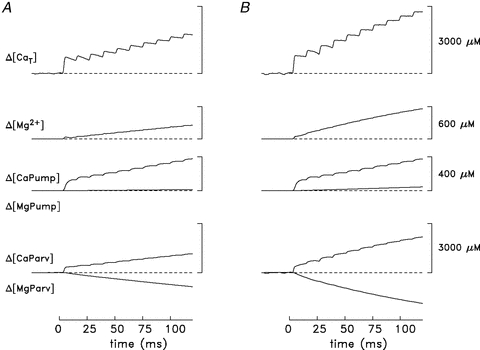
Figure 6 shows myoplasmic Ca2+ and Mg2+ movements estimated when the computational model described in Methods is applied to the furatpra Ca2+ signal elicited by a 10-stimulus, 83.3 Hz train of stimuli. For this calculation, the ΔfCaD signal in Fig. 4D was converted to Δ[Ca2+] (lowermost trace in Fig. 6) with eqn (2). Δ[Ca2+] was then used to drive the model, thereby yielding estimates of the other Ca2+-related changes that contribute to Δ[CaT]. The concentration of the SR Ca2+ pumps was set to 190 μm (‘Model 1’), the smaller of the two estimates available from the literature. The most relevant of the Ca2+-related changes are shown in Fig. 6: Δ[CaTrop], shown as a continuous trace; Δ[CaTrop2] (unlabelled dashed trace), which considers only the contribution to Δ[CaTrop] from those troponin molecules that become doubly occupied with Ca2+ ions (i.e. the troponin molecules that are likely to be functionally important for activation of the fibre's mechanical response); Δ[CaParv]; Δ[CaPump]; and Δ[CaT] itself (uppermost trace). Not shown are Δ[CaATP] (which is ∼3.4 times Δ[Ca2+]; see Baylor & Hollingworth, 2007); Δ[CaDye] (= ΔfCaD×[DT]); and Δ[CaPumped] (whose contribution to Δ[CaT] is small, 19 μm at 120 ms). The model also yields estimates of the changes in concentration of Mg2+ bound to three constituents: ATP (not shown), parvalbumin (Δ[MgParv]), and the SR Ca2+ pump (Δ[MgPump]). The negative sum of these three changes yields Δ[Mg]T (not shown), from which the Δ[Mg2+] trace (second from top) was estimated with eqn (5).
To estimate the concentration of SR Ca2+ released by any particular stimulus in Fig. 6, the peak value of Δ[CaT] was determined during the period when Δ[CaT] was changing due to that stimulus and, from this, the value of Δ[CaT] just prior to onset of this period was subtracted. The estimated concentrations of Ca2+ released during the 120 ms 83.3 Hz train are summarized in Table 1B1. These estimates are similar to, although slightly smaller than, those obtained with the oxygen-consumption measurements for an 80 Hz stimulus (Table 1A), and they show the same pattern of fractionally smaller releases with later stimuli in the train.
It is also of interest in Fig. 6 to consider what percentage of the released Ca2+ ions are bound to troponin. With stimuli 2–4, the average peak change in the concentration of Ca2+ bound to troponin is 115 μm (continuous trace in Fig. 6 labelled Δ[CaTrop]); this represents 52% of the average increase in Δ[CaT] per action potential (222 μm). With stimuli 5–10, the average peak change is 89 μm, which represents 49% of the average increase in Δ[CaT] per action potential (180 μm). Most of this bound Ca2+ serves to increase the occupancy of troponin molecules with two bound Ca2+ ions (dashed trace in Fig. 6). With stimuli 2–4, the average peak change in the concentration of Ca2+ associated with doubly occupied troponin molecules is 89 μm and, with stimuli 5–10, is 82 μm. The corresponding peak percentages of the troponin molecules that are doubly occupied with Ca2+ during the high-frequency train are 42 and 39%, respectively.
Model calculations were also carried out with the larger estimate of the SR pump concentration, 980 μm (‘Model 2’). Figure 7A displays the traces in Fig. 6 that are affected by the change in the pump concentration (Δ[CaT], Δ[Mg2+], Δ[CaPump] and Δ[MgPump]) as well as Δ[CaParv] and Δ[MgParv] (which are included for comparison with the calculations in Fig. 7B, described below). As expected, the concentration of Ca2+ bound by the pump in Fig. 7A is larger than that in Fig. 6, in proportion to the increase in the pump concentration. Nevertheless, in Fig. 7A the concentration of Ca2+ captured by the pump at t = 120 ms is small relative to that captured by parvalbumin (377 vs. 1151 μm). The amount of Ca2+ returned to the SR by the Ca2+ pump at 120 ms is also relatively small, 98 μm. Table 1B2 lists the estimated concentrations of Ca2+ released by the 10 stimuli for this calculation. These values are in reasonable agreement with (within 1 SD of) the SR release estimates obtained with the oxygen-consumption measurements; however, additional data would be necessary to make statistical inferences. Because the majority of the released Ca2+ is captured by parvalbumin in both Model 1 and Model 2, the large increase in pump concentration has a relatively small effect on the release estimates.
Figure 7. Responses like those in Fig. 6 for two other versions of the swimbladder model.
In both A and B, the model was also driven by the Δ[Ca2+] trace shown in Fig. 6 but the pump concentration was 980 rather than 190 μm (Model 2; see text). In B, the rate constants for the reactions of Ca2+ and Mg2+ with parvalbumin were 3-fold larger than the standard values (Model 3; see text). For both models, the FDHM of each release flux was ∼1 ms. The calibration values in B also apply in A.
An expectation of an accurate model of myoplasmic Ca2+ movements is that the increments in Δ[CaT] due to the individual stimuli in a train should increase when release is active and remain constant thereafter. This follows provided that Δ[CaT] includes the change in concentration of Ca2+ complexed with all significant myoplasmic Ca2+ buffers as well as the released Ca2+ that is returned to the SR by the SR Ca2+ pumps. With both Models 1 and 2, however, the increments in Δ[CaT] are not maintained; rather, each increment reaches a peak and then decays somewhat prior to onset of the increment elicited by the next stimulus. While this problem is somewhat smaller in Model 2, where the rates of decay of Δ[CaT] elicited by the individual stimuli are ∼20% smaller than in Model 1, it is still present. Additional calculations were therefore performed in an attempt to understand the possible source of this problem.
Influence of parvalbumin's kinetics on modelling results
Taken at face value, the decays in the Δ[CaT] waveforms in Figs 6 and 7A imply that Ca2+ either binds more rapidly to one or more of the modelled myoplasmic buffer sites or is removed from the myoplasm by an unknown mechanism. Figure 7B explores the first of these possibilities in a calculation with the 980 μm pump concentration that additionally includes a 3-fold increase in the on- and off-rate constants of the reactions of Ca2+ and Mg2+ with parvalbumin (‘Model 3’). This change in parvalbumin kinetics was chosen because preliminary stopped-flow experiments to investigate the kinetics of parvalbumin's reactions with Ca2+ (J. P. Davis, B. Tikunov and L. Rome, unpublished observations) indicate that the Ca2+ off-rate constant of swimbladder parvalbumin may be severalfold larger than that of frog parvalbumin, on which the modelling in Figs 6 and 7A is based (Baylor et al. 1983). With this change in kinetics, parvalbumin captures Ca2+ more rapidly during the falling phase of Δ[Ca2+], when Ca2+ is dissociating from troponin and ATP, with the result that the problematic decays of Δ[CaT] between stimuli are largely eliminated (cf. top trace in Fig. 7B). At t = 120 ms, the concentration of Ca2+ captured by parvalbumin is 2177 μm in Fig. 7B (vs. 1151 μm in Fig. 7A). Given this improved behaviour of the model, it would clearly be of value to investigate the possibility of faster parvalbumin kinetics in swmbladder muscle in a more complete set of stopped-flow experiments that also included measurement of the Mg2+ reaction rate constants.
The Ca2+ release estimates for the model of Fig. 7B are summarized in Table 1B3 (Model 3). These values are in very good agreement with the estimates from the oxygen-consumption measurements (Table 1A). Although use of the faster parvalbumin kinetics largely resolves the modelling problem identified in Figs 6 and 7A, it does so at the expense of introducing a new problem, namely, the amplitude of the Δ[Mg2+] waveform in Fig. 7B is no longer consistent with the amplitude of the ΔfMgD component in Fig. 4D. For example, Δ[Mg2+] in Fig. 7B is 561 μm at t = 120 ms (vs. 257 and 254 μm in Figs 6 and 7A, respectively). This difficulty would be resolved if BFMg (the Mg2+ buffer factor in eqn. (5)) is ∼0.16 rather than 0.35 (see Methods); however, the basis of a BFMg value as small as 0.16 is not understood. Although the larger pump concentration used in Fig. 7 in combination with the reaction scheme used to model the pump kinetics (Hollingworth et al. 2006) is consistent with the rates of Ca2+ pumping measured in skinned swimbladder fibres (Young et al. 2003), it is nevertheless possible that alterations of the pump reaction scheme might also help resolve the inconsistencies identified above in the model calculations. Such alterations were not explored.
In summary, all the modelled Ca2+ release estimates in this experiment support the conclusion from the recovery O2 consumption measurements that the first stimulus of a high-frequency train elicits a very large release of SR Ca2+, ca 700–800 μm, and that the subsequent releases are much smaller, in the range 25–45% of the initial release.
Estimates of SR Ca2+ release in other fibres and at other stimulus frequencies
The experiment of Figs 6–7 was the only one in which a furaptra signal that was virtually free of movement artifacts was recorded from a fibre stimulated at 83.3 Hz, a frequency similar to that used in the oxygen-consumption measurements summarized in Fig. 5 and Table 1A (80 Hz). Similar furaptra signals were successfully recorded at two other stimulus frequencies: 100 Hz (in the same fibre as in Figs 6 and 7) and 67 Hz (in a different fibre). Results from analysis of the 67 and 100 Hz measurements are in excellent agreement with those summarized in Table 1. For example, with the model used in Fig. 7B, the values of Δ[CaT] elicited by 10 stimuli at 100 Hz are 783 μm for the first stimulus, 243–287 μm for stimuli nos 2–4 (mean, 270 μm), and 189–269 μm for stimuli nos 5–10 (mean, 228 μm). At 67 Hz, the values are 847 μm, 410–479 μm (mean, 448 μm), and 245–356 μm (mean, 296 μm), respectively. As expected, the values with the first stimulus are similar to that in Table 1B3 (790 μm); for the later stimuli, the mean values estimated for the 100 and 67 Hz stimuli are somewhat smaller and larger, respectively, than the corresponding values of Table 1B3 (Model 3). These differences are in the directions expected given that greater and lesser degrees of inactivation of the SR Ca2+ release system, respectively, are expected during a stimulus train with stimuli separated by 10 and 15 ms compared to 12 ms.
Three other fibres revealed qualitatively similar responses to repetitive stimulations (67–100 Hz), including the much smaller Ca2+ transients elicited by stimuli after the first. While the presence of a movement artifact in these experiments ruled out a quantitative analysis of the responses to all stimuli, the artifact did not interfere with the release estimates elicited by the first stimulus. These estimates are in good agreement with the first-stimulus release estimates mentioned above. For example, with Model 3, the first-stimulus releases in these fibres are 763, 810 and 854 μm (see also the statistical summary in Table 1C)
Discussion
Estimate of Ca2+ release per twitch by recovery O2 consumption in the presence of BTS
The quantity of SR Ca2+ released during normal muscle function is of critical importance for understanding Ca2+ regulation and muscle design. The energetic cost of pumping Ca2+ is also an important input to optimization models of locomotion. Prior to this study, the most widely used method to estimate Ca2+ release during normal function is to measure the Ca2+ transient with a Ca2+ indicator dye and, from that, estimate the Ca2+ release waveform with a model that incorporates concentration and binding kinetics of the various Ca2+ buffers (e.g. Baylor et al. 1983; Melzer et al. 1987), including the SR Ca2+ pump (Pape et al. 1990; Baylor & Hollingworth, 2007). As explained in the Methods (and Supplemental Material), detailed information about the Ca2+ buffers and the morphology of the fibres in question is necessary to model the Ca2+ release waveform accurately. However, in most muscles, knowledge of the concentrations and kinetics of the various Ca2+ buffers is either incomplete or involves some uncertainty. Further, the measurement of the change in the myoplasmic free [Ca2+] is subject to optical and chemical limitations that vary with the Ca2+ indicator employed (e.g. Baylor & Hollingworth, 2011).
To estimate Ca2+ release in swimbladder fibres, we have addressed the limitations of the above method in two ways. First, for kinetic modelling, we have determined the amounts of two of the major Ca2+ buffers in swimbladder fibres, Parv (Tikunov & Rome, 2009) and troponin (this study), and, through the use of morphological information (Appelt et al. 1991), have determined geometric factors to express biochemical concentrations in terms of the myoplasmic water volume (see Supplemental Material). Clearly, the more detailed and accurate the information that goes into the model, the more reliable will be the estimate of the amount and rate of Ca2+ release.
Second, we developed a novel recovery-oxygen approach for estimating release, which does not depend on the same assumptions used in the kinetic modelling. Indeed, this second approach has permitted us to estimate SR Ca2+ release for different twitches that likely occur in a toadfish boatwhistle without any knowledge of the concentration and kinetics of Ca2+ buffers, nor indeed of the morphological structure of the muscle. In consequence, the recovery oxygen approach provides an independent method to estimate Ca2+ release per twitch (see also below).
The six assumptions made in our recovery-oxygen estimates of SR Ca2+ release per twitch (Fig. 5) may slightly overestimate, but probably not underestimate, the actual release values (see Supplemental Material for analysis). Indeed, because of likely small contributions from the crossbridge ATPase and the Na+–K+ pump, the actual values for Ca2+ pumping may be ∼2% lower for the first stimulus and up to about 10% lower for the 10th (and subsequent) stimulus than those in Fig. 5, which further reduces the amount of Ca2+ estimated to be pumped (and hence released) during calling. This supports our conclusion that, by the 10th twitch, the amount is well below that required to saturate and desaturate TNC.
Comparison of Ca2+ release per twitch estimated from recovery O2 consumption and Ca2+ transient modelling
In this study we found good agreement between two completely independent methods for estimating SR Ca2+ release: recovery-oxygen consumption and Ca2+ transient modelling. The independence of the two techniques is based on the fact that neither the measurements nor the underlying assumptions of the analysis overlap. Both approaches showed a similarly sized Ca2+ release on the first stimulus (ca 700–800 μm, Table 1), with a large drop on subsequent stimuli (only about 30% of the first release by the 10th stimulus). Excellent agreement was also observed between the methods for estimating the total Ca2+ released over the first 10 twitches; 1.03 mmol Ca2+ kg−1 by the recovery oxygen approach (see Supplemental Material) compared to 0.78, 0.84 and 1.03 mmol kg−1, for release models 1, 2, and 3, respectively.
This agreement over the large drop from the first stimulus to the 10th supports the general validity of both approaches. Results based on both approaches, however, give the most complete information. A major strength of the kinetic model is that it provides estimates on a millisecond time scale of the Ca2+ movements during and following Ca2+ release. However, to estimate similar results in a novel fibre type requires a large amount of information on both the concentrations and kinetics of the various myoplasmic Ca2+ buffers. The recovery oxygen-consumption measurement in the presence of BTS can, without buffer information, provide an estimate of the amount of Ca2+ release against which the Ca2+ transient modelling can be compared. If significant disagreements between the estimates occur, this would suggest a need for improved Ca2+ buffer information for the model. By its nature, the recovery oxygen-consumption technique, which integrates over time, does not provide the detailed time course information about all underlying Ca2+ movements as the Ca2+ modelling approach does.
Combining biochemical and physiological information of the type obtained in this study can provide unique insights into molecular design, e.g. how are Ca2+ buffer concentrations and kinetics set to produce the mechanical response needed for a given activity. For instance, as discussed later, having a very high Parv concentration with faster Ca2+ and Mg2+ kinetics (cf. Fig. 7B and associated text) is likely to be an important adaptation to permit toadfish swimbladder to function as it does. Even with the new buffer information that we have obtained, there are still important unknowns in toadfish swimbladder muscle, such as the concentration and kinetics of the SR Ca2+ pumps. Interestingly, the Ca2+ modelling shows that the 5-fold difference between the SR Ca2+ pump concentrations as estimated by morphological (Appelt et al. 1991) and biochemical methods (Feher et al. 1998) does not strongly influence the release estimates (cf. Model 1 and 2 in Table 1B). This situation arises because of the dominant role that parvalbumin plays during relaxation from each twitch (see below).
The mechanism for reduction in Ca2+ release per stimulus
There are two mechanisms that could explain the marked decline in Ca2+ release during the first 10 stimuli (Figs 5–7). First, depletion of SR Ca2+ could limit release. We have evidence against this possibility from a parallel study, that showed that the total Ca2+ in the SR is approximately 6 mmol kg−1 at rest (Rome, 2006). By the 10th stimulus of the measurements reported here, less than 20% of this value, 1.03 mmol kg−1 (see Supplemental Material), had been released (Fig. 5). Over the same period, the Ca2+ release per stimulus had declined 5-fold (from 235 to 48 μmol kg−1). Hence dwindling SR Ca2+ levels play, at best, only a minor role in this decline of Ca2+ released per stimulus.
The second mechanism, a Ca2+-dependent inactivation of release (Baylor et al. 1983; Schneider & Simon, 1988; Jong et al. 1995; Pape et al. 1995), is likely to explain the majority of the decline in Ca2+ release per twitch. In frog cut fibres, paired stimuli experiments have shown that the size of the Ca2+ release declines dramatically with a second action potential if it is given shortly after the first (Jong et al. 1995). The time constant of recovery from this inactivation is calculated to be about 28 ms at 15°C. A similar time constant, 25 ms at 16oC, has been estimated for swimbladder fibres (Hollingworth & Baylor, 1996). As the swimbladder fibres for the oxygen measurements of this study were stimulated with a 12.5 ms interval between stimuli (80 Hz), considerable inactivation would be expected; moreover, the degree of inactivation should be larger at higher frequencies. Consistent with this expectation, the total amount of Ca2+ released for 10 twitches calculated with Ca2+ transient modelling (e.g. Fig. 7B) was 8% less for a 100 Hz stimulus compared with an 83 Hz stimulus (0.95 mmol kg−1vs. 1.03 mmol kg−1). Similarly the stimulation frequency used for the recovery-oxygen consumption experiments, 80 Hz, could result in Ca2+ release values 1–3% higher than those determined in the Ca2+ modelling approach at a slightly higher frequency, 83.3 Hz (cf. Table 1B).
The role of Ca2+ release channel inactivation during in vivo muscle function
Swimbladder muscle provides a unique model for examining the importance of specific muscle properties for in vivo function. The swimbladder muscle is pure in fibre type and the muscle as a whole is controlled in an all or none manner (Rome, 2006). Further, in swimbladder, there is a one-to-one relationship between sound pulses and muscle stimuli. Therefore, by recording toadfish calls in the field with a hydrophone, the stimulation frequency and stimulus number can be deduced (Edds-Walton et al. 2002). Because our measurements were made on an intact swimbladder preparation using a stimulation frequency and number of stimuli that occur physiologically during mating calls, these measurements provide a unique opportunity to assess the significance of Ca2+ release channel inactivation for normal in vivo function of muscle. Our results show that this inactivation plays a critical role in the superfast muscle's ability to produce the mating call which is observed. If inactivation did not occur and the Ca2+ release per twitch were the same for the whole call (40–80 twitches) as it is for the first twitch (235 μmol kg−1; Fig. 5), then the muscle could not function in the intended way. With the first 40 twitches, the muscle would have released approximately 9.4 mmol (kg muscle)−1. With a maximum SR-Ca2+ pumping rate of 2 mmol s−1 kg−1 (Young et al. 2003), over that 0.5 s time period, the SR Ca2+ pumps could not return more than 1 mmol kg−1 to the SR. Hence, the net release (8.4 mmol (kg muscle)−1) would be substantially more Ca2+ than is actually available in the SR (6 mmol kg−1) (Rome, 2006). This amount of Ca2+ would also saturate all of the Ca2+ binding sites in the myoplasm (i.e. Parv sites + TNC sites = ∼3 mmol kg−1 (Appelt et al. 1991; Tikunov & Rome, 2009, this paper), and, if unchecked, the free [Ca2+] might rise to the near millimolar range, which could tetanize and possibly severely damage the muscle. In contrast, we measured that the total Ca2+ released for the first 20 twitches was 1.6 ± 0.1 mmol kg−1 (n = 10) and we calculate that, for a typical 40 twitch (500 ms) call, 2.6 mmol kg−1 would be released, which is within the myoplasmic buffering capacity of the muscle. By reducing the Ca2+ released on a twitch-by-twitch basis to a level below that necessary to fully saturate and desaturate troponin, the SR can control [Ca2+] at a safe level, permitting the muscle to perform its vital function. Inactivation also reduces the amount of Ca2+ that ultimately must be pumped back into the SR, and hence reduces the energetic cost of producing calls. For example, we estimate that the Ca2+-pump uses 1.3 mmol ATP kg−1 for a 40-twitch call. Without Ca2+ release channel inactivation, it would be about 3.5-fold higher (or 4.6 mmol kg−1), which could tax the ability of the metabolic system to supply the extra ATP.
In swimbladder muscle, the reduced Ca2+ exchange per twitch during a stimulus train accounts for some of the discrepancy posed in the Introduction between the maximum SR Ca2+ pumping rate and the product of TNC binding sites and stimulus frequency (see Mechanism no. 1). This reduction is supported by our kinetic modelling, which indicates that slightly less than half of the troponin sites exchange Ca2+. Nevertheless, if the SR Ca2+ release in an 80 Hz stimulus is ∼48 μmol kg−1 per twitch (for twitches after the 10th, Fig. 5), to keep up with Ca2+ release in real time, the pumps would still need to pump faster (3.8 mmol kg−1 s−1) than their maximum measured rate, 2 mmol kg−1 s−1. This implies the importance of another ‘removal system’.
Mechanism no. 2: role of parvalbumin during calling in toadfish
Previous results (Tikunov & Rome, 2009) suggested that Parv plays an important role in explaining the remainder of the discrepancy identified in the previous paragraph, and evidence from the Ca2+ transient model also provides support for this conclusion. For instance, of the total Ca2+ released in a 10-twitch train, ∼70% is ultimately bound to Parv (Fig. 7B). Another portion is bound to the Ca2+ pump but very little is actually pumped during the 120 ms stimulus (31 μmoles (kg muscle)−1; Fig. 7B). Consistent with this, high energy phosphate measurements indicate that very little Ca2+ is pumped in the first 400 ms of a high frequency stimulus (Tikunov et al. 2003; Tikunov, Klimov and Rome, unpublished findings). Thus Parv undoubtedly plays a critical role in binding Ca2+ and thereby lowering free [Ca2+] during a call.
Continuous calling in midshipman without parvalbumin
Midshipman (Porichthys notatus) is another sound producing fish. Like toadfish, they call at 80–100 Hz and have a maximum SR Ca2+ pumping rate of 2 mmol kg−1 (Young et al. 2003). Unlike toadfish, midshipman call with a 100% duty cycle for hours, and, accordingly, have very low [Parv]; hence Parv cannot help reduce the disparity noted above (Tikunov & Rome, 2009). In midshipman, reducing the Ca2+ exchange per twitch by inactivation of the Ca2+ release channels and optimizing Ca2+ binding by troponin is likely to play key roles in permitting high frequency contractions (80–100 Hz) with modest Ca2+ pumping.
Crossbridge ATP utilization per isometric twitch
Our experiments show that under isometric conditions, the crossbridge ATP utilization per twitch of swimbladder muscle is about 25 μm kg−1. Given that the myosin head concentration is 69 μmol kg−1, on average a bit less than one out of every two myosin heads hydrolyses an ATP molecule per twitch. This is remarkably similar to that found in mouse papillary muscle, despite the cardiac muscle being at least 25-fold slower than swimbladder muscle (Widen & Barclay, 2006). While it is necessary for swimbladder fibres to shorten and do work to produce sound, the amount of shortening and work produced are exceedingly small. In workloop experiments at 80 Hz, the optimal muscle strain is only 1% and the maximum work per cycle is only 0.08 J kg−1 (Young & Rome, 2001). If the efficiency of work production from ATP is 50%, this would increase ATP usage per twitch by only about 5 μm kg−1, and hence would result in only small increases in the proportion of the total ATP used by crossbridges during calling (cf. Fig. 5.)
As noted in connection with Fig. 5, the proportion of ATP usage (crossbridges: SR-Ca2+ pumps) for isometric twitches in intact swimbladder fibres is 20:80 for the first twitch and about 50:50 for later twitches in an 80 Hz train. These proportions are quite different from the 67:33 ratio that we previously observed in saponin-skinned swimbladder fibres, a ratio that is similar to that observed with heat measurements for isometric twitches and tetani of amphibian muscles (e.g. Homsher et al. 1972; Smith, 1972; Rall, 1982). In the case of skinned swimbladder fibres at high [Ca2+], the ratio simply depends on the maximum rates of ATP usage by the crossbridges and the SR Ca2+ pumps. In contrast, in intact swimbladder fibres, the ratio depends on the amount of Ca2+ release and, hence, the number and timing of the applied stimuli. Moreover, the crossbridge ATP utilization rate is larger in intact swimbladder fibres than that in skinned fibres, 2.2 mmol s−1 kg−1 (this study) vs. 0.77 mmol s−1 kg−1 (Rome & Klimov, 2000). This difference is consistent with the observation that crossbridge ATPase (in both intact and skinned fibres) slows during contraction (West et al. 2003). In the case of swimbladder, we are comparing short contractions (<1 s) in intact fibres to long contractions (∼5–20 s) in skinned fibres, so a difference in the observed direction is to be expected. Hence, measurement conditions, e.g. transient twitches in intact fibres vs. maximal sustained activation in skinned fibres, can certainly affect the observed proportions.
These proportions have become of interest to the field of motor control. With improvement of musculoskeletal modelling approaches (e.g. OpenSim; Delp et al. 2007) motor control scientists seek to understand the role of various muscles that have redundant actions around a joint (Cheng & Loeb, 2008). Optimization algorithms are used to partition the actions of these different muscles, and energetics, (e.g. the cost of pumping Ca2+and crossbridge action) is one of the factors that should be included in the optimization algorithms (Loeb et al. 2002). To date, scientists have used fixed proportions based on isometric heat measurement. The results of the present study show that at least in some muscles, the cost is not fixed, with the value depending on the duration and timing of stimuli.
Acknowledgments
This work was supported by the Wellcome Trust UK (C.L.H.), MBL summer fellowships (I.S.Y.) and NIH grants AR38404 (L.C.R.), AR46125 (L.C.R.), and GM 086167 (S.M.B.). The authors thank Professor Peter Petriatis for expert statistical advice. This paper is dedicated to the memory of our colleague and friend, Dr Boris A. Tikunov. His enthusiasm for muscle biology as well as his great skill in accurately quantifying the concentrations of different proteins in minute samples, has made our physiological study of swimbladder muscle possible.
Glossary
Abbreviations
- BTS
N-benzyl-p-toluene sulphonamide
- SR
sarcoplasmic reticulum
- TNC
troponin C
Author contributions
All authors contributed to the design and execution of the experiments, analysis of the data and the writing of the ms. Experiments were conducted in the Biology and the Physiology Departments at the University of Pennsylvania and in the Whitman Center at the Marine Biological Laboratory. All authors except for BAT approved the final version.
Authors' present addresses
C. L. Harwood: University of Liverpool, School of Dental Studies, Liverpool Dental School, Liverpool, UK.
I. S. Young: Faculty of Veterinary Science, University of Liverpool, Liverpool, UK.
Supplementary material
SUPPLEMENTAL DATA
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors
References
- Amara CE, Marcinek DJ, Shankland EG, Schenkman KA, Arakaki LS, Conley KE. Mitochondrial function in vivo: spectroscopy provides window on cellular energetics. Methods. 2008;46:312–318. doi: 10.1016/j.ymeth.2008.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Appelt D, Shen V, Franzini-Armstrong C. Quantitation of Ca ATPase, feet and mitochondria in super fast muscle fibers from the toadfish, Opsanus tau. J Musc Res Cell Mot. 1991;12:543–552. doi: 10.1007/BF01738442. [DOI] [PubMed] [Google Scholar]
- Barclay CJ, Lichtwark GA, Curtin NA. The energetic cost of activation in mouse fast-twitch muscle is the same whether measured using reduced filament overlap or N-benzyl-p-toluenesulphonamide. Acta Physiol (Oxf) 2008;193:381–391. doi: 10.1111/j.1748-1716.2008.01855.x. [DOI] [PubMed] [Google Scholar]
- Barclay CJ, Woledge RC, Curtin NA. Energy turnover for Ca2+ cycling in skeletal muscle. J Muscle Res Cell Motil. 2007;28:259–274. doi: 10.1007/s10974-007-9116-7. [DOI] [PubMed] [Google Scholar]
- Baylor SM, Chandler WK, Marshall MW. Sarcoplasmic reticulum calcium release in frog skeletal muscle fibres extimated from Arsenazo III calcium transients. J Physiol. 1983;344:625–666. doi: 10.1113/jphysiol.1983.sp014959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor SM, Hollingworth S. Model of sarcomeric Ca2+ movements, including ATP Ca2+ binding and diffusion, during activation of frog skeletal muscle. J Gen Physiol. 1998;112:297–316. doi: 10.1085/jgp.112.3.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor SM, Hollingworth S. Sarcoplasmic reticulum calcium release compared in slow-twitch and fast-twitch fibres of mouse muscle. J Physiol. 2003;551:125–138. doi: 10.1113/jphysiol.2003.041608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor SM, Hollingworth S. Simulation of Ca2+ movements within the saromere of fast-twitch mouse fibres stimulated by action-potentials. J Gen Physiol. 2007;130:283–302. doi: 10.1085/jgp.200709827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor SM, Hollingworth S. Calcium indicators and calcium signalling in skeletal muscle fibres during excitation-contraction coupling. Prog Biophys Mol Biol. 2011;105:162–179. doi: 10.1016/j.pbiomolbio.2010.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor SM, Quinta-Ferreira ME, Hui CS. Isotropic components of antipyrylazo III signals from frog skeletal muscle fibers. In: Rubin RP, Weiss G, Putney JW Jr, editors. Calcium in Biological Systems. New York: Plenum Publishing Corp; 1985. pp. 339–349. [Google Scholar]
- Cameron JN. Principles of Physiological Measurement. San Diego: Academic Press; 1986. p. 257. [Google Scholar]
- Chase PB, Kushmerick MJ. Effect of physiological ADP concentrations on contraction of single skinned fibers from rabbit fast and slow muscles. Am J Physiol Cell Physiol. 1995;268:C480–C489. doi: 10.1152/ajpcell.1995.268.2.C480. [DOI] [PubMed] [Google Scholar]
- Cheng EJ, Loeb GE. On the use of musculoskeletal models to interpret motor control strategies from performance data. J Neural Eng. 2008;5:232–253. doi: 10.1088/1741-2560/5/2/014. [DOI] [PubMed] [Google Scholar]
- Cheung A, Dantzig JA, Hollingworth S, Baylor SM, Goldman YE, Mitchison TJ, Straight A. A small-molecule inhibitor of skeletal muscle myosin II. Nature Cell Biology. 2002;4:83–88. doi: 10.1038/ncb734. [DOI] [PubMed] [Google Scholar]
- Crow MT, Kushmerick MJ. Chemical energetics of slow- and fast-twitch muscle of the mouse. J Gen Physiol. 1982;79:147–166. doi: 10.1085/jgp.79.1.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtin NA, Woledge RC. Energy changes and muscular contraction. Physiol Rev. 1978;58:690–761. doi: 10.1152/physrev.1978.58.3.690. [DOI] [PubMed] [Google Scholar]
- Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54:1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- Edds-Walton P, Mangiamele L, Rome LC. Boatwhistles from oyster toadfish (Opsanus tau) around Waquoit Bay, Massachusetts. J Bioacoust. 2002;13:153–173. [Google Scholar]
- Feher JJ, Waybright TD, Fine ML. Comparison of sarcoplasmic reticulum capabilities in toadfish (Opsanus tau) sonic muscle and rat fast twitch muscle. J Musc Res Cell Motil. 1998;19:661–674. doi: 10.1023/a:1005333215172. [DOI] [PubMed] [Google Scholar]
- Fine ML. Seasonal and geographical variation of the mating call of the oyster toadfish Opsanus tau L. Oecologia. 1978;36:45–57. doi: 10.1007/BF00344570. [DOI] [PubMed] [Google Scholar]
- Godt RE, Maughan DW. On the composition of the cytosol of relaxed skeletal muscle of the frog. Am J Physiol Cell Physiol. 1988;254:C591–C604. doi: 10.1152/ajpcell.1988.254.5.C591. [DOI] [PubMed] [Google Scholar]
- Hamoir G, Gerardin-Otthiers N, Focant B. Protein differentiation of the superfast swimbladder muscle of the toadfish Opsanus tau. J Mol Biol. 1980;143:155–160. doi: 10.1016/0022-2836(80)90129-1. [DOI] [PubMed] [Google Scholar]
- Harwood CL, Young IS, Rome LC. Cheap twitches in in superfast toadfish swimbladder (SB) muscle. Biophys J. 2001;80:(1), 271a. (abstract) [Google Scholar]
- Hinkle PC, Kumar MA, Resetar A, Harris DL. Mechanistic stoichiometry of mitochondrial oxidative phosphorylation. Biochemistry. 1991;30:3576–3582. doi: 10.1021/bi00228a031. [DOI] [PubMed] [Google Scholar]
- Hollingworth S, Baylor SM. Sacroplasmic reticulum (SR) calcium release in intact superfast toadfish swimbladder (TSB) and fast frog twitch fibers. Biophys J. 1996:A235. (abstract) [Google Scholar]
- Hollingworth S, Chandler WK, Baylor SM. Effect of tetracaine on voltage-activated calcium sparks in frog intact skeletal muscle fibers. J Gen Physiol. 2006;127:291–307. doi: 10.1085/jgp.200509477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollingworth S, Zhao M, Baylor SM. The amplitude and time course of the myoplasmic free [Ca2+] transient in fast-twitch fibers of mouse muscle. J Gen Physiol. 1996;108:455–469. doi: 10.1085/jgp.108.5.455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homsher E, Mommaerts WF, Ricchiuti NV, Wallner A. Activation heat, activation metabolism and tension-related heat in frog semitendinosus muscles. J Physiol. 1972;220:601–625. doi: 10.1113/jphysiol.1972.sp009725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irving M, Maylie J, Sizto NL, Chandler WK. Simultaneous monitoring of changes in magnesium and calcium concentrations in frog cut twitch fibers containing antipyrylazo III. J Gen Physiol. 1989;93:585–608. doi: 10.1085/jgp.93.4.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jong DS, Pape PC, Baylor SM, Chandler WK. Calcium inactivation of calcium release in frog cut muscle fibers that contain millimolar EGTA or Fura-2. J Gen Physiol. 1995;106:337–388. doi: 10.1085/jgp.106.2.337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konishi M, Hollingworth S, Harkins AB, Baylor SM. Myoplasmic calcium transients in intact frog skeletal muscle fibers monitored with the fluorescent indicator furaptra. J Gen Physiol. 1991;97:271–301. doi: 10.1085/jgp.97.2.271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konishi M, Suda N, Kurihara S. Fluorescence signals from the Mg2+/Ca2+ indicator furaptra in frog skeletal muscle fibers. Biophys J. 1993;64:223–239. doi: 10.1016/S0006-3495(93)81359-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kushmerick MJ, Paul RJ. Relationship between initial chemical reactions and oxidative recovery metabolism for single isometric contractions of frog sartorius muscle at 0°C. J Physiol. 1976;254:711–727. doi: 10.1113/jphysiol.1976.sp011254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeb GE, Brown IE, Lan N, Davoodi R. The importance of biomechanics. Adv Exp Med Biol. 2002;508:481–487. doi: 10.1007/978-1-4615-0713-0_54. [DOI] [PubMed] [Google Scholar]
- Melzer W, Rios E, Schneider MF. A general procedure for determining the rate of calcium release from the sarcoplasmic reticulum in skeletal muscle fibers. Biophys J. 1987;51:849–863. doi: 10.1016/S0006-3495(87)83413-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Sullivan WJ, Perrin DD. The stability constants of metal-adenine nucleotide complexes. Biochemistry. 1964;3:18–26. doi: 10.1021/bi00889a005. [DOI] [PubMed] [Google Scholar]
- Pape PC, Jong DS, Chandler WK. Calcium release and its voltage dependence in frog cut muscle fibers equilbrated with 20 mM EGTA. J Gen Physiol. 1995;106:259–336. doi: 10.1085/jgp.106.2.259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pape PC, Konishi M, Hollingworth S, Baylor SM. Perturbation of sarcoplasmic reticulum calcium release and phenol red absorbance transients by large concentrations of fura-2 injected into frog skeletal muscle fibers. J Gen Physiol. 1990;96:493–516. doi: 10.1085/jgp.96.3.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raju B, Murphy E, Levy LA, Hall RD, London RE. A fluorescent indicator for measuring cytosolic free magnesium. Am J Physiol Cell Physiol. 1989;256:C540–C548. doi: 10.1152/ajpcell.1989.256.3.C540. [DOI] [PubMed] [Google Scholar]
- Rall JA. Energetics of Ca2+ cycling during skeletal muscle contraction. Fed Proc. 1982;41:155–160. [PubMed] [Google Scholar]
- Rome LC. Design and function of superfast muscles: new insights into the physiology of skeletal muscle. Annu Rev Physiol. 2006;68:193–221. doi: 10.1146/annurev.physiol.68.040104.105418. [DOI] [PubMed] [Google Scholar]
- Rome LC, Cook C, Syme DA, Connaughton MA, Ashley-Ross M, Klimov AA, Tikunov BA, Goldman YE. Trading force for speed: Why superfast crossbridge kinetics leads to superlow forces. Proc Natl Acad Sci U S A. 1999;96:5826–5831. doi: 10.1073/pnas.96.10.5826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rome LC, Klimov AA. Superfast contractions without superfast energetics: ATP usage by SR-Ca2+ pumps and crossbridges in the toadfish swimbladder muscle. J Physiol. 2000;526:279–298. doi: 10.1111/j.1469-7793.2000.t01-1-00279.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rome LC, Kushmerick MJ. The energetic cost of generating isometric force as a function of temperature in isolated frog muscle. Am J Physiol Cell Physiol. 1983;244:C100–C109. doi: 10.1152/ajpcell.1983.244.1.C100. [DOI] [PubMed] [Google Scholar]
- Rome LC, Syme DA, Hollingworth S, Lindstedt SL, Baylor SM. The whistle and the rattle: the design of sound producing muscles. Proc Natl Acad Sci U S A. 1996;93:8095–8100. doi: 10.1073/pnas.93.15.8095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider MF, Simon BJ. Inactivation of calcium release from the sarcoplasmic reticulum in frog skeletal muscle. J Physiol. 1988;405:727–745. doi: 10.1113/jphysiol.1988.sp017358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skoglund CR. Functional analysis of swim-bladder muscle engaged in sound production by toadfish. J Biophys Biochem Cytol. 1961;10:187–200. doi: 10.1083/jcb.10.4.187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith IC. Energetics of activation in frog and toad muscle. J Physiol. 1972;220:583–599. doi: 10.1113/jphysiol.1972.sp009724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tikunov BA, Klimov AA, Rome LC. Using post-relaxation SR-Ca2+ pump ATP Use (SR-ATPase) to probe the magnitude and kinetics of parvalbumin (PARV) function in intact toadfish swimbladder muscle (TSB) Biophys J. 2003;84:389a. (abstract) [Google Scholar]
- Tikunov BA, Rome LC. Is high concentration of parvalbumin a requirement for superfast relaxation? J Muscle Res Cell Motil. 2009;30:57–65. doi: 10.1007/s10974-009-9175-z. [DOI] [PubMed] [Google Scholar]
- Tikunov BA, Sweeney HL, Rome LC. Quantitative electrophoretic analysis of myosin heavy chains in single muscle fibers. J Appl Physiol. 2001;90:1927–1935. doi: 10.1152/jappl.2001.90.5.1927. [DOI] [PubMed] [Google Scholar]
- Weber A, Herz A, Reiss I. Study of the kinetics of calcium transport by isolated fragmented sarcoplasmic reticulum. Biochem Z. 1966;345:329–369. [Google Scholar]
- West TG, Curtin NA, Ferenczi MA, He ZH, Sun YB, Irving M, Woledge RC. Actomyosin energy turnover declines while force remains constant during isometric muscle contraction. J Physiol. 2003;555:27–43. doi: 10.1113/jphysiol.2003.040089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widen C, Barclay CJ. ATP splitting by half the cross-bridges can explain the twitch energetics of mouse papillary muscle. J Physiol. 2006;573:5–15. doi: 10.1113/jphysiol.2006.104992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young IS, Harwood CL, Rome LC. Cross-bridge blocker BTS permits the direct measurement of Ca2+ pump ATP utilization in skinned toadfish swimbladder muscle fibers. Am J Physiol Cell Physiol. 2003;285:C781–C787. doi: 10.1152/ajpcell.00025.2003. [DOI] [PubMed] [Google Scholar]
- Young IS, Rome LC. Mutually exclusive muscle designs: the power output of the locomotory and sonic muscles of the oyster toadfish (Opsanus tau) Proc. R. Soc. Lond. B. 2001;268:1965–1970. doi: 10.1098/rspb.2001.1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


