A Model for the Effect of Homologous Recombination on Microbial Diversification

Abstract

The effect of homologous recombination (HR) on the evolution of microbial genomes remains contentious as competing hypotheses seek to explain the evolutionary dynamics of microbial species. Evidence for HR between microbial genomes is widespread, and this process has been proposed to act as a cohesive force that can constrain the diversification of microbial lineages. We seek to characterize the evolutionary dynamics of sympatric populations to explore the impact of HR on microbial speciation. We describe a simple equation for quantifying the cohesive effect of HR on microbial populations as a function of their nucleotide divergence, μ/ρ = π_g10 ^{− 20 π_g}. The model was verified using a forward-time microbial population simulator that can explore the evolutionary dynamics of sympatric populations in nonoverlapping niche space. The model was also evaluated using multilocus sequence data from a range of microbial species, providing criteria for dividing them into either cohesively recombining or clonally diverging lineages. We conclude that models of microbial diversification that appear contradictory can be explained in a unified manner as the natural and predictable consequence of variation in a small number of population parameters.

Introduction

Widespread evidence of horizontal gene transfer (HGT) among bacteria and archaea has provoked ongoing debate as to whether genetic clusters in these organisms represent species or simply represent points along a continuum of genetic exchange. A variety of evolutionary forces have been invoked in these debates, but chief among them are periodic selection, genetic drift, and the effects of both homologous recombination (HR) and nonhomologous recombination (NR). Several different models have been proposed to explain the evolution of microbial species (Fraser et al. 2009). The ecotype model, for example, predicts that periodic selection and genetic drift act together to create isolated genetic clusters that represent ecologically distinct groups or “ecotypes” (Cohan 2002). The ecotype model explains well the patterns of divergence observed in Bacillus spp. from Evolution Canyon, Israel, where distinct genetic clusters occur in ecologically distinct locations within the canyon (Cohan and Perry 2007). However, organisms like Neisseria meningitidis, Streptococcus pneumoniae, and Helicobacter pylori have high rates of gene exchange (Feil et al. 2000; Falush et al. 2001), and the application of the ecotype model to such recombining populations is complicated by the reshuffling of genes made possible by HR. Consequently, a variety of competing species models have been proposed and reviewed (Stackebrandt et al. 2002; Gevers et al. 2005; Konstantinidis et al. 2006; Nesbo et al. 2006; Whitaker 2006; Achtman and Wagner 2008; Fraser et al. 2009).

Although HGT can act as a diversifying force when it involves the acquisition of new genes and traits, HGT can also act as a cohesive force by mediating homologous replacement of existing genes (Fraser et al. 2007). HR involves the nonreciprocal unidirectional transfer of a homologous segment of DNA from a donor to a recipient (analogous to interallelic gene conversion in eukaryotes). Because this form of HR is nonreciprocal, it decreases nucleotide divergence between donor and recipient, with the net change in similarity being a function of the sequence divergence prior to replacement. The HR rate depends on the similarity of the donor and recipient in the stretch of DNA to be combined. This relationship likely depends upon local sequence similarity at the ends of recombination tracts referred to as minimum efficiently processed segment (MEPS) (Shen and Huang 1986; Hsieh et al. 1992; Rao and Radding 1995; Majewski and Cohan 1999b). The dependence of HR rate on local sequence similarity has been described as ρ × 10^−20π, where π is the nucleotide divergence between the donor and the recipient stretch involved in recombination, ρ is the rate at which recombination events are initiated, and −20 is the distance factor of recombination used to modify the success rate of recombination events based on the value of π (Fraser et al. 2007).

We describe a simple equation that can be used to quantify the cohesive effect of HR on microbial populations and to make predictions about their evolutionary dynamics. Predictions generated from this equation are verified with the use of a microbial population simulation. The simulation is used to test predictions from the equation, we describe and to determine whether the cohesive effects of HR are sufficient to prevent core genome divergence between sympatric populations. We seek to define the range of mutation and recombination rates that promote the divergence or convergence of sympatric populations, values of relevance to models of microbial speciation. We use the terms convergence and divergence to indicate a change in sequence similarity across the loci of the core genome. It is important to note that HR can serve as a mechanism for adaptation and differentiation (Levin and Cornejo 2009; Shapiro et al. 2009), but because our framework is not designed to account for the effects of selection and adaptation, these effects are not considered. Although simplifying assumptions were made in both theory and simulation, the framework we present provides a simple null model that can be used to make predictions about the evolutionary dynamics of microbial populations and species.

Materials and Methods

In Results and Discussion, we describe equations that we developed from theory to determine the impact of HR on the evolutionary dynamics of microbial populations. Predictions from these equations were tested using a new population simulator called bactsimDF (for bacterial simulation different and fixed) that we developed to model the evolution of microbial populations forward in time. The bactsimDF program simulates two coexisting neutral populations that start at a user-specified level of interpopulation nucleotide divergence and population size. Individuals in each population have equal access to DNA from both populations without respect to population boundaries (at a rate modified by the level of nucleotide divergence). However, after each round of recombination, the new generation for each population is sampled at random from within each population. This allows drift to act independently on each population and prevents a multiple population simulation from turning into a single population simulation with a recent common ancestor. In this way bactsimDF simulates ecologically isolated sympatric populations and approximates the conditions required for divergence via the ecotype model, in which an adaptive mutation permits a subpopulation to occupy a new ecological niche and to escape the effects of selection and drift in the ancestral population (Cohan 2002).

The bactsimDF simulator was modified from the algorithm and code of the forward in time population simulator forwsim (Padhukasahasram et al. 2008). The algorithm used by forwsim to increase simulation speed is detailed elsewhere (Padhukasahasram et al. 2008), so we will only describe it briefly here. The populations being modeled are neutral Wright–Fisher populations that are constant in size. Individual chromosomes are modeled as collections of polymorphic sites, allowing new mutations to appear only at nonpolymorphic sites. Mutations are tracked by their location on the chromosome. Further information is not necessary, as the simulation works on a pseudoinfinite sites assumption. To improve the speed of the program, forwsim simulates the future genealogy of the population in the next eight generations and tracks all individuals still in the population at that time and any individuals that have recombined with any of those present individuals in that span of time. Mutations or recombination events that occur between individuals that do not contribute to future generations are not simulated. The user may also specify the number of generations after which homogenous features of the population are purged, that is, if a mutation goes to fixation or extinction, it is no longer necessary to include that polymorphic site in every individual's chromosome and is removed. If a mutation is no longer carried in the population, then it is removed from the list of existing mutations, and new mutations may again enter the population at that site (i.e., that location becomes nonpolymorphic).

The bactsimDF simulation program is modified substantially from forwsim in order to model HR (i.e., interallelic gene conversion) instead of crossing over. In addition, the mean tract length has been modified to be user specified with the tract length of individual events realized as a draw from a geometric distribution, as in the coalescent simulation ms (Hudson 2002). The probability of individual recombination events is determined as, R = ρ10^−dπ, where ρ is the recombination rate, π is the average nucleotide divergence, and d is the distance factor of recombination. The distance factor of recombination (i.e., the degree to which recombination rate declines with increasing sequence divergence) is the empirically defined value for the slope of the log-linear line that describes the relationship between R, ρ, and π (as described in Fraser et al. 2007). For the purpose of modeling individual recombination events, the value of π is calculated between each individual donor and recipient. The program calculates nucleotide divergence between populations every 500 generations by comparing a user-specified number of individuals in both populations. User input includes effective population size, sample (output) size, genome length, total number of generations, the number of generations between deletions of homogenous features, recombination rate, mutation rate, tract length, and the distance factor. The simulations we describe used the following parameters: effective population size, 2,000 (1,000 in each population); sample size, 200; genome length, 500,000; total generations, 25,000,000; mutation rate, 5 × 10⁻⁵ individual⁻¹ generation⁻¹; recombination rate, variable; time between deletions, 50 generations; tract length, 500; distance factor, −20. bactsimDF source code and precompiled binaries are freely available at https://sites.google.com/site/doroghazi/.

Multilocus sequence data were used to estimate values of μ/ρ and π for a range of microbial species in order to evaluate these parameter estimates in the context of our model. Multilocus sequence data and ClonalFrame output files from Vos and Didelot (2009) were graciously provided by Dr Michiel Vos. Nucleotide diversity was calculated with a Perl script. Values for μ/ρ and π are provided in supplementary table S1 (Supplementary Material online).

Results and Discussion

Results Produced from Theory

We sought to characterize the impact of HR on microbial speciation and we will first consider a pair of populations with equal mutation and recombination rates, with no barriers to recombination. In the absence of HR, we would expect the populations to diverge over time due to mutation. The effect of mutation in this case is straightforward, as mutations accumulate in each lineage at the mutation rate of individuals in the population (Kimura 1968), thus, we naturally expect that two isolated populations will diverge at twice their mutation rate or 2μ. Estimating the effect of HR on a population, however, is somewhat more complex. The HR rate for any given fragment of DNA is expected to vary as a log-linear function of the nucleotide divergence between donor and recipient. The effect of sequence similarity on HR rate has been quantified in Escherichia coli (Vulic et al. 1997), S. pneumoniae (Majewski et al. 2000), Bacillus subtilis, and Bacillus mojavensis (Zawadzki et al. 1995) as roughly R = ρ10^−20π, where R is the modified recombination rate, ρ is the recombination rate when there are no differences between sequences, π is the nucleotide divergence between sequences, and −20 is the distance factor of recombination (Fraser et al. 2007).

To quantify the cohesive effect of HR between two populations, we start by assuming that the two populations will converge due to HR at the rate 2ρπ_g10 ^{− 20π_g}, where ρ is the recombination rate and π_g is the average nucleotide divergence between the populations (i.e., the average nucleotide divergence between any two sequences which are chosen at random from each of the two populations). In the simplest terms, this result is obtained by considering each HR event as a type of mutation that has the ability to reduce nucleotide divergence between populations (due to gene conversion). Unlike the rate of point mutation, however, which is assumed to be constant, the HR rate is strongly influenced by the nucleotide similarity between donor and recipient (as described above). In addition, the number of nucleotide changes introduced by each HR event is a function of the nucleotide divergence between the donor and the recipient for the DNA fragment being exchanged.

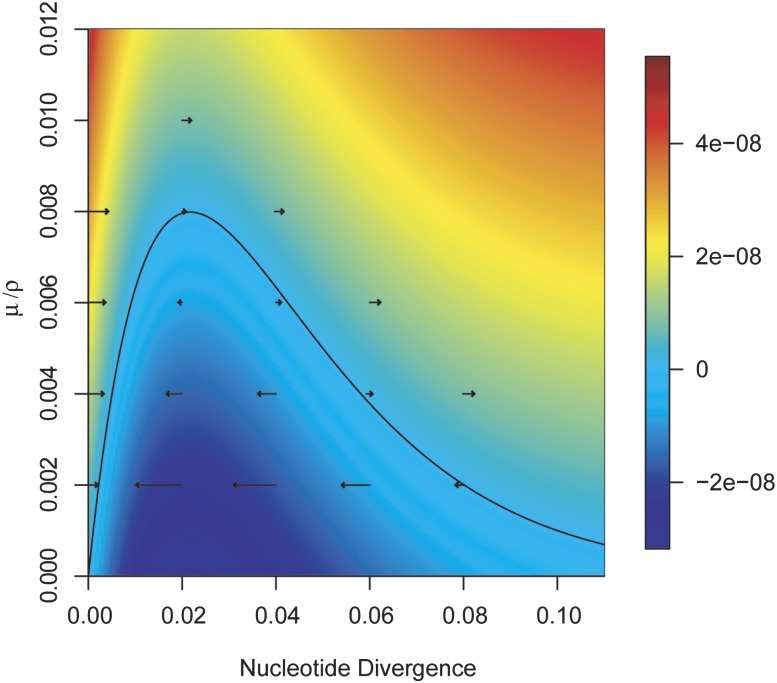
Given the above, the forces of mutation and HR between two populations are equal when 2μ = 2ρπ_g10 ^{− 20π_g}, and thus, we find that μ/ρ = π_g10 ^{− 20 π_g}. This equation describes a line that represents the threshold of cohesive recombination between any two populations (fig. 1). We can see that two populations will diverge when μ/ρ>π_g10 ^{− 20π_g} and converge when μ/ρ<π_g10 ^{− 20π_g}. Thus, pairs of populations with values of μ/ρ and π_g that fall below the threshold will be cohesive, whereas populations above the threshold will be free to diverge clonally through the random accumulation of mutations. With a simple rearrangement of the equation, we can calculate the per generation change in nucleotide divergence between the populations as Δ = 2μ−2ρπ_g10 ^{− 20π_g}, and this rate is indicated by the heat map in figure 1 for a range of values μ/ρ and π_g (It is important to note that ρ is the per-site frequency of recombination, combining the rate of occurrence of recombination events and the tract lengths of those events.). Calculating the rate of change between populations requires us to assume a mutation rate, and the heat map depicted figure 1 assumes a mutation rate of 1 × 10⁻¹⁰ nucleotide⁻¹ generation⁻¹. Lowering or raising the mutation rate will vary the rate of change between populations (i.e., the scale of the heat map) but not the direction of change (i.e., convergence or divergence) because the threshold of cohesive recombination is defined as a function of the ratio of mutation and recombination.

Fig. 1.—

The ratio of mutation to HR is expressed as a function of mean interpopulation nucleotide divergence for sympatric populations that are free to recombine. The line (described by the function μ/ρ = π_g10 ^{− 20 π_g}) represents the predicted threshold that bounds populations subject to the cohesive effects of recombination. Pairs of populations below the curve are predicted to convergence due to HR, whereas populations above the curve are clonal and free to diverge. The heat map predicts the rate of change between two populations, calculated as Δ = 2μ−2ρπ_g10 ^{− 20π_g}, where ▵ is the change in nucleotide divergence per generation. Each arrow indicates the results from a different bactsimDF simulation run with distinct initial values for μ/ρ and π_g. Initial values for each simulation are indicated by the origin of each arrow. Arrow tips show the level of nucleotide divergence resulting after 25 million generations.

Forward in Time Simulations

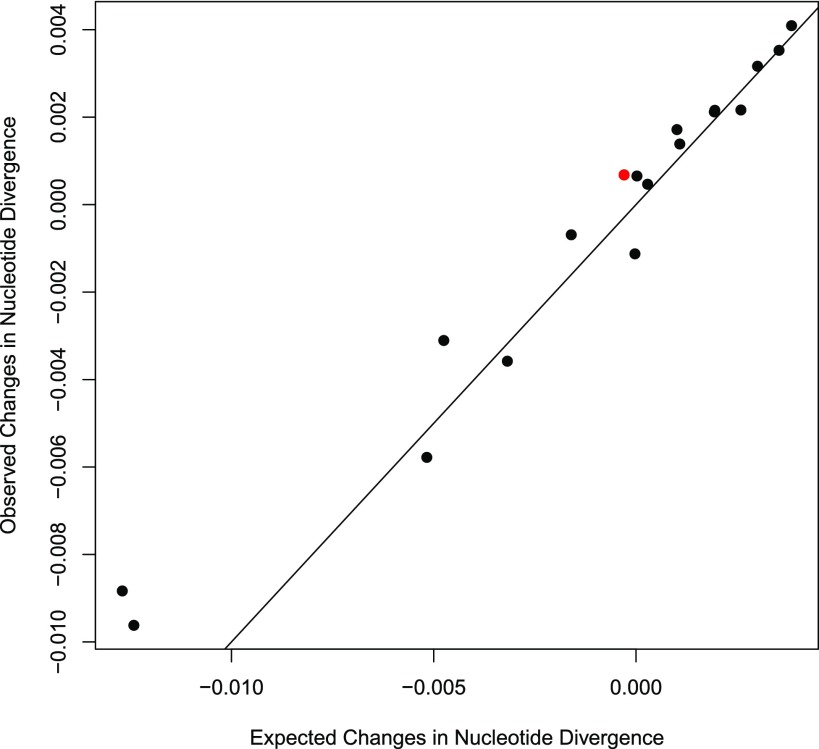
We developed the population simulator bactsimDF to test the ability of the equation described above to model the evolutionary dynamics of populations as a function of their interpopulation nucleotide divergence (π_g) and the ratio of mutation and recombination (μ/ρ). When evaluated across a wide range of parameter values, the results from simulations were in close agreement with predictions calculated directly from theory using the equation 2μ−2ρπ_g10 ^{− 20π_g} (figs. 1 and 2). Simulations run with population parameters that fall above the cohesive threshold were observed to diverge, whereas those below the threshold converged (fig. 1). There was a single exception where a simulation initiated with parameters that fell below the curve resulted in net divergence (as indicated by the arrow below the curve which points to the right, fig. 1, seen as the outlier in fig. 2). This outlier likely results from stochastic variation due to the proximity of the initial simulation parameters to an unstable equilibrium between the forces of recombination and mutation.

Fig. 2.—

Observed changes in nucleotide divergence (as depicted in fig. 1) compared with expected changes calculated using recurrent application of the formula Δ = 2μ−2ρπ_g10 ^{− 20π_g}. The line shown has an intercept of 0 and a slope of 1; identical observations and expectations should fall exactly on this line. The outlier, shown in red, is the one simulation that diverged and oscillated instead of converging.

Fig. 3.—

Change in nucleotide divergence between two recombining populations that differ in size. Circle area is proportional to effective population size with 1800 individuals in the large population and 200 in the small population. The simulation was started with π_g of 0.04 and μ/ρ of 0.00035.

For the purposes of testing the equation we describe, output from the simulation is evaluated only with respect to the overall genomic similarity between two populations. Output from the simulation, however, can also be used to analyze changes in smaller genomic regions. Such analysis could be especially useful in considering, for example, the fragmented speciation theory of Retchless and Lawrence (2007). The simulation can also be used for modeling allopatric populations because geographical isolation would be represented in the simulation by using an interpopulation recombination rate of zero.

The model we describe can be extended to evaluate recombination between populations that differ in effective population size by accounting for the change in interpopulation recombination rate due to the different probability of encountering DNA from an individual from the other population (this relates to propinquity and the effect should also be influenced by differences in census population size). For equal sized populations, ρ₁π_g10 ^{− 20π_g} + ρ₂π_g10 ^{− 20π_g} = 2ρ₁π_g10 ^{− 20π_g} but for populations that differ in size the individual interspecies recombination rate must be calculated for each population. To simulate coexisting populations of unequal population size, we modified bactsimDF to include populations of size 1800 and 200 (fig. 3). When averaged across all individuals in both populations the recombination rate for populations of unequal size and for those of equal size was the same (5 × 10⁻⁴ individual⁻¹ generation⁻¹ with a tract length of 500), but when examined with respect to the different populations, it was determined that the smaller population realized a mean interpopulation recombination rate of 4.74 × 10⁻⁴, 5.2 times higher than that realized for the larger population. As a result, the smaller population is swamped with DNA from the larger population, drifting 33.2 times closer to the large population than the large moved toward the small (fig. 3).

In the simulations described above, sequence similarity was calculated over the tract being recombined to assess the probability of recombination. For comparison, we also ran a simulation in which two identical 22-bp regions at the start and end of the recombination tract were required for a recombination event to occur (as suggested by Majewski and Cohan 1999b), and a simulation in which a 44-bp stretch of identity was required at one end of the recombination tract (as described in Rao and Radding 1995; Reddy et al. 1995). These different approaches to assessing recombination probability did not significantly alter simulation results (supplementary fig. S1A, Supplementary Material online). The requirement for short regions of identity (MEPS) at the termini of recombination tracts results in a relative recombination rate that is indistinguishable from the rate obtained when calculating the success of recombination as a function of sequence similarity, modified by the distance factor of −20, across entire recombination tract (supplementary fig S1B, Supplementary Material online).

Relevance to Microbial Species

We have examined above the effect of HR on two sympatric yet ecologically isolated populations. We can also use this framework to make hypotheses about the dynamics of core genome evolution for individual microbial species. We assume that the level of nucleotide divergence for the entire species is greater than or equal to the level of interpopulation nucleotide divergence for any two populations within the species (i.e., π_g ≤ π). We further accept the simplifying assumptions that there is complete mixing of individuals, constant population size, and lack of selection among the individuals in the species (assumptions common to models of population genetics). Starting from these assumptions, we can calculate values of μ/ρ and π from multilocus sequence data collected for strains representing a particular microbial lineage and use these parameter estimates to make a hypothesis about whether the homologous genes in any two populations within the lineage are free to diverge through clonal processes or are constrained by the cohesive effects of HR. Obviously, violation of assumptions will impact the accuracy of these predictions, but a framework for making such null hypotheses provides a valuable tool for exploring the evolutionary forces that drive the diversification of microbial lineages.

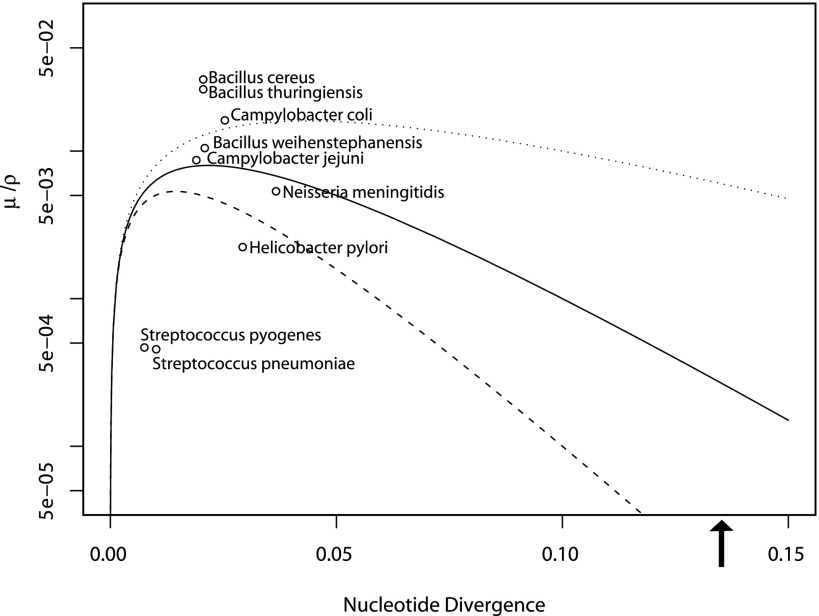
We examined the biological relevance of our model by calculating μ/ρ and π for a range of bacterial and archaeal species (fig. 4 and supplementary table S1, Supplementary Material online). For this purpose, we used multilocus sequence data that has been described previously (Vos and Didelot 2009). We also chose to examine the impact that varying the distance factor of recombination has on the threshold of cohesive recombination (fig. 4). Although the distance factor has been estimated at −20 in laboratory experiments, the degree to which this term varies across the domains of life remains poorly characterized. For example, a distance factor between −29 and −44 was estimated for recombination among Ferroplasma in acid mine drainage (Eppley et al. 2007). Different values for the distance factor of recombination may result from unique aspects of the recombination machinery in acidophilic Ferroplasma or due to fitness costs associated with insertion of divergent DNA (Eppley et al. 2007). The population parameters for a wide range of microorganisms can be seen to span the threshold that separates recombining and clonal populations regardless of the distance factor (fig. 4). Our model locates the species Bacillus thuringiensis, Bacillus weihenstephanensis, and Bacillus cereus well above the threshold of cohesive recombination (fig. 4). The model predicts that species with these parameters will evolve along clonal trajectories, having subpopulations able to diverge on separate evolutionary trajectories as described by the ecotype model. In contrast, H. pylori, N. meningitidis, and S. pneumoniae, which are known to be highly recombining (Feil et al. 2000; Falush et al. 2001), fall under the threshold of cohesive recombination (It should be noted that although H. pylori has an exceptionally high recombination rate, this species also has an exceptionally high mutation rate which causes the ratio μ/ρ to be somewhat higher than that observed for species with lower rates of recombination [e.g., S. pneumonia]). The model predicts that the evolution of species having these parameters will be dominated by the cohesive effects of recombination. Although the evolutionary significance of HR differs dramatically for the species described above, we can see that these differences arise as manifestations of simple underlying principles.

Fig. 4.—

Values of nucleotide diversity, HR rate, and mutation rate estimated from strains that belong to a range of microbial species plotted in relation to the equilibrium threshold for cohesive recombination (values plotted on a log scale to allow all points to be visualized). These values are intended as estimates of values that may occur between different populations within the named species. The recombination distance factor was varied to demonstrate the impact of this value on the threshold of cohesive recombination. The distance factors that were used are −20 for the solid line (as presented in fig. 1), −10 for the dotted line, and −30 for the dashed line. Values for μ/ρ are calculated as π (r/m)⁻¹ from the values of r/m in Vos and Didelot (2009) and π is calculated from the same data sets provided by Dr Michiel Vos. A larger set of values and species names are given in supplementary table S1 (Supplementary Material online). The arrow shows the average nucleotide divergence between Campylobacter coli and Campylobacter jejuni based on MLST loci (Dingle et al. 2005) values for C. coli were calculated from Lang et al. (2009) as described in supplementary table S1 (Supplementary Material online).

Implications and Further Discussion

The bactsimDF population simulator was designed to test the equations we developed to explain the evolutionary dynamics of sympatric microbial populations. A limitation of the model is the small size of the populations being modeled. This constraint was imposed by computational limitations in order to allow simulations to run in a reasonable period of processor time. The value we used for population size was selected to be large enough to capture dynamics due to genetic drift and yet small enough to allow robust simulation. It should also be noted that given the simplifying assumptions used in bactsimDF the census population size is equal to effective population size. In real microbial populations, the effective population size is expected to be vastly smaller than census population size. Previous models for evaluating the evolution of microbial population have used effective population sizes in the range of 500–2000 (Falush et al. 2006) and as small as 20 (Vetsigian and Goldenfeld 2005). In our simulation, an increase in population size by an order of magnitude (to 20,000 individuals) did not noticeably impact simulation results beyond the expectations of stochastic variation (supplementary fig. S1A, Supplementary Material online).

The simulations we describe have important implications for the ability of ecotype model to explain the divergence of sympatric lineages. In the ecotype model, a new ecotype forms when the acquisition of an adaptive mutation allows a derived population to invade a new ecological niche and escape from the effects of drift and selection imposed by the ancestral population. We show that the HR rates estimated for a variety of microbial species are high enough to prevent lineage diversification through the ecotype mechanism (fig. 4). Populations under the threshold of recombination (fig. 1) would be sufficiently cohesive such that, in the absence of barriers to gene exchange, derived populations would be unable to diverge across the homologous loci of the core genome. Furthermore, the period during which a nascent ecotype is formed from an ancestral population would, by necessity, be characterized by inequality in population size, and this difference in population size would serve to decrease the ability of the derived population to escape the impact of HR from the ancestral population (as described in fig. 3). We would predict that populations that fall below the cohesive threshold of recombination would be unlikely to diverge as described by the ecotype model. Application of the ecotype concept would still have utility for characterizing the divergence of populations found above the threshold line for cohesive recombination, such as those of Bacillus species. We might speculate that, in recombining populations, niche expanding mutations might be found in the auxiliary genome and their exchange within the population governed by propinquity. An example of this may be observed in Vibrio cholerae in which the genes of the core genome are mixing globally within species, but auxiliary genes associated with integrons cross species boundaries and show strong dependence on the geographic location from which the strains were isolated (Boucher et al. 2011).

Although we have restricted our analyses to the effects of HR, NR also serves as a powerful force of evolutionary change. NR contrasts with HR in that the former will lead to gene acquisition rather than gene replacement, and as a result, we would expect that NR will generally manifest as a diversifying rather than as a cohesive force and have its greatest impacts on the auxiliary genome. Niche expansion by the acquisition of adaptive genes can promote divergence of populations above the threshold of cohesive recombination consistent with the ecotype model. Our model predicts that the acquisition of niche expanding genes would not be expected to promote sympatric divergence within a cohesively recombining population unless somehow the acquisition also created a barrier to gene exchange. In this case, it would be the barrier to gene exchange, rather than escape from periodic selection, that would be expected to drive lineage divergence. It is important to consider that NR can also have downstream implications for HR rates. NR results in the insertion of new stretches of DNA that lower the local sequence similarity at the conserved boundary sequences. The local decrease in sequence similarity has the effect of lowering local HR rates and this might result in propagating fronts of divergence as described by Vetsigian and Goldenfeld (2005). The propagating front hypothesis provides a mechanism that could promote divergence in highly recombining populations by creating barriers to gene exchange. Further research on the interplay of both types of recombination is necessary and in the future it should be possible to modify bactsimDF to simulate the effects of both HR and NR on the core and auxiliary genome and to evaluate the role of propagating fronts in lineage diversification.

The existence of a cohesive recombination threshold that circumscribes clonal and recombining populations has been predicted previously, and evidence for this threshold has previously been tested in several computer simulations (Majewski and Cohan 1999b; Vetsigian and Goldenfeld 2005; Falush et al. 2006; Fraser et al. 2007, 2009). These simulations have considered several scenarios: one population with or without temporary division (Falush et al. 2006; Fraser et al. 2007, 2009), local genomic effects of NR (Vetsigian and Goldenfeld 2005), and multiple ecotypes with selective sweeps (Majewski and Cohan 1999b). The simulation we describe is different because it evaluates how the core genome is expected to evolve in sympatric populations under the strong assumption of niche isolation between the two populations. In other words, we predict the effect of HR on any two populations that are unable to drive each other to extinction as a result of drift or selection. Our intention is to provide a quantitative framework based upon theory that can be used to make predictions about microbial populations without the need for computationally intensive simulation. For example, a species which falls below the curve in figure 4 can encompass multiple ecologically distinct populations, but cohesive recombination will prevent divergence across the loci of the core genome. Examples of species that have ecologically divergent populations that are not genetically resolved across the loci of the core genome include S. pneumonia (Hanage et al. 2009) and Vibrio cholera (Boucher et al. 2011). As a result, we would not expect MLST data to reveal ecological differentiation within these species. In contrast, MLST data could be sufficient for defining ecological differentiation for those species, such as Bacillus spp., that are not subject to the cohesive effects of recombination.

This theory also provides a measure to assess the completion of speciation, allowing one to conclude whether the core genomes of two genetically divergent lineages could converge due to recombination without being driven by selection. For example, we can consider the case of Campylobacter coli and Campylobacter jejuni in which interspecies HR is hypothesized to be driving species merger (Sheppard et al. 2008). From estimates made using MLST data, it is possible to estimate intraspecies HR rates for these species. Interpreting these rates in the context of our framework (fig. 4) indicates that recombination is unlikely to drive cohesion across the core genome of these species (fig. 4). Because sequence similarity between species is lower than that within species, we can further predict that although interspecies recombination is free to occur, merger across the core genome is unlikely between these species. Recent genomic analysis of C. jejuni and C. coli suggest that although interspecies recombination has occurred, the two species remain clearly distinct (Caro-Quintero et al. 2009; Lefebure et al. 2010). Analysis of 96 genome sequences indicates that interspecies recombination is relatively rare between the core genomes of these species (Lefebure et al. 2010). The framework we describe provides a tool for making prediction about whether a given level of recombination would be expected to promote lineage cohesion.

The availability of a null model built on a theoretical foundation has great utility when investigating bacterial population dynamics as it provides some expectations as to how populations should behave under simplifying assumptions. The model we describe provides a productive framework for generating and testing hypotheses about the evolutionary dynamics of specific populations.

Supplementary Material

Supplementary figure S1 and table S1 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).