Mixture theory-based poroelasticity as a model of interstitial tissue growth

Abstract

This contribution presents an alternative approach to mixture theory-based poroelasticity by transferring some poroelastic concepts developed by Maurice Biot to mixture theory. These concepts are a larger RVE and the subRVE-RVE velocity average tensor, which Biot called the micro-macro velocity average tensor. This velocity average tensor is assumed here to depend upon the pore structure fabric. The formulation of mixture theory presented is directed toward the modeling of interstitial growth, that is to say changing mass and changing density of an organism. Traditional mixture theory considers constituents to be open systems, but the entire mixture is a closed system. In this development the mixture is also considered to be an open system as an alternative method of modeling growth. Growth is slow and accelerations are neglected in the applications. The velocity of a solid constituent is employed as the main reference velocity in preference to the mean velocity concept from the original formulation of mixture theory. The standard development of statements of the conservation principles and entropy inequality employed in mixture theory are modified to account for these kinematic changes and to allow for supplies of mass, momentum and energy to each constituent and to the mixture as a whole. The objective is to establish a basis for the development of constitutive equations for growth of tissues.

1. Introduction

The purpose of this contribution is to present an alternative approach to mixture theory-based poroelasticity by transferring some poroelastic concepts developed by Maurice Biot (1935, 1941, 1956a,b; 1957, 1962a,b) to mixture theory. The long-term objective of this study is facilitating the mixture modeling of biological growth phenomena. Since mixture theory was first presented by Truesdell (1957) its relationship to the previously established Biot’s poroelasticity theory (1941) has been a subject of discussion. In this contribution the overlap in the two theories is increased. In several important ways the mixture model of saturated porous media is more general than the Biot (1941) model of poroelasticity; Bowen (1980, 1982) recovered the model of Biot (1941) from the mixture theory approach. The most important way in which the mixture model is more general than the Biot poroelastic model is that the mixture model admits the possibility of following many solid and fluid constituents and it admits the possibility of having chemical reactions occurring. Thus some constituents might vanish and others might be created. (Ateshian (2007) has suggested ways to model this within mixture theory.) The contrast with Biot theory is that Biot theory considers the single solid and fluid components to be chemically inert. In several important ways the poroelastic model of Biot (1941, 1957, 1956a,b; 1962a,b) offers better conceptual mechanisms for relating the elements of the physical situation to their mathematical representations, a principal example being a hierarchical structure that permits the distinction between the matrix, the drained and the undrained elastic constants. It is the objective of this contribution to transfer the selected Biot conceptual mechanisms to a mixture theory formulation of poroelasticity, thus combining the advantages of Biot’s ideas with mixture theory.

2. Mixture theory

A mixture is a material with two or more ingredients, the particles of which are separable, independent, and uncompounded with each other. If the distinct phases of a mixture retain their identity, the mixture is said to be immiscible; if they lose their identity, the mixture is said to be miscible. The constituents include a porous solid of possibly a number of constituents, as well as solvents and solutes. The theory of mixtures is based on diffusion models and stems from a fluid mechanics and thermodynamics tradition and goes back to the century before last. Fick (1855) and Stefan (1871) suggested (Truesdell and Toupin 1960, sections 158 and 295) that each place in a fixed spatial frame of reference might be occupied by several different particles, one for each constituent of the mixture. Truesdell and Toupin (1960) assigned to each constituent of a mixture in motion a density, a body force density, a partial stress, a partial internal energy density, a partial heat flux and a partial heat supply density.

Truesdell and Toupin postulated equations of balance of mass, momentum and energy for each constituent and derived the necessary and sufficient conditions that the balance of mass, momentum and energy for the mixture be satisfied. Bowen (1967) summarized the formative years of this subject. A readable history of the subject and its applications in the period 1957–1975 is given by Atkin and Craine (1976a, b). De Boer (1996, 2000) has presented more up-to-date histories. Of key importance in the development of the mixture theories is the application by Bowen (1967, 1976, 1980, 1982) of a thermodynamically-based analytical approach developed by Coleman and Noll (1963) to restrict the form of constitutive equations.

There have been many notable contributions of the mixture theory approach to the modeling of tissue growth that are not cited here, as this is not a review of that broad subject. Others have employed some of the modifications of mixture theory employed here, but one would have to trace each modification through the literature to determine which authors first employed it. Such a review is not the objective of this contribution.

3. Poroelasticity

Poroelasticity is a theory that models the interaction of deformation and fluid flow in a fluid-saturated porous, elastic medium. The deformation of the medium influences the flow of the fluid and vice versa. The theory was proposed and developed by Biot (1941, 1957, 1956a,b; 1962a,b) as a theoretical extension of soil consolidation models for calculating the settlement of structures placed on fluid-saturated porous soils. The theory has been widely applied to geotechnical problems beyond soil consolidation, most notably problems in rock mechanics and wave propagation in porous media. There are thousands of papers, and a singular, but notable, book on the subject is that of Coussy (2005). The governing equations for anisotropic poroelasicity for quasi-static and dynamic poroelasticity were developed and extended to include the dependence of the constitutive relations upon a pore structure fabric tensor F as well as the porosity (Cowin 1985, 2004; Cowin and Cardoso, 2010; Cardoso and Cowin, 2011).

4. The alternative formulation of mixture theory-based poroelasticity

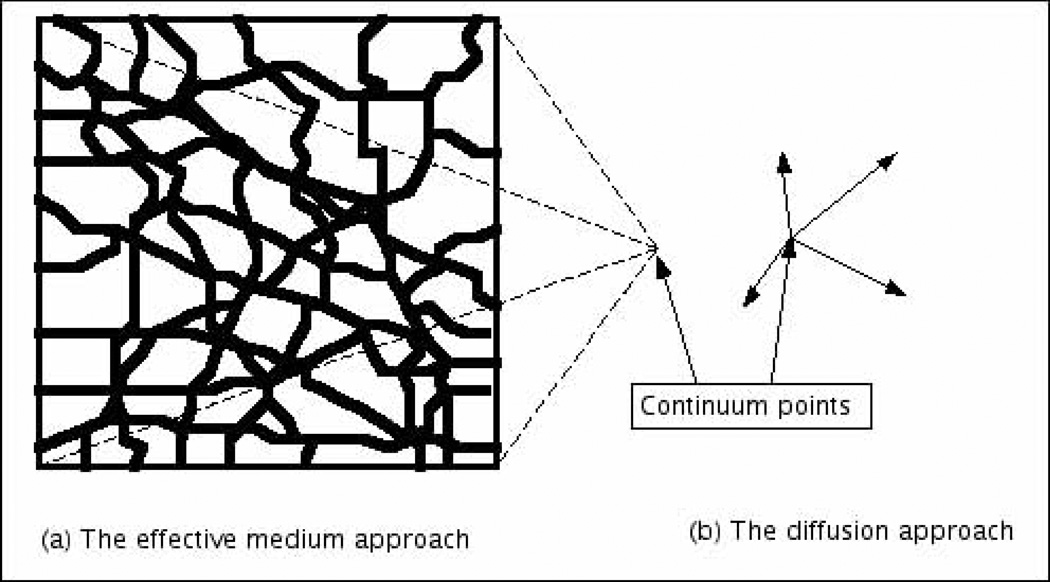
In this alternative formulation of mixture theory-based poroelasticity, the Eulerian point used in mixture theory as a model of the continuum point (Figure lb) is replaced by a larger RVE introduced by Biot as the model of the continuum point (Figure la). Further, Biot’s concept of the RVE level representation of the fluid velocity as a function of the pore fluid velocities in the sub RVE pores is employed. Finally, the mixture theory concept of the mean velocity of the solid and fluid constituents is replaced by reference to the velocity of the solid and the diffusion velocities relative to a solid constituent.

Figure 1.

(a) is a schematic version of the representative volume element (RVE) viewpoint described in Biot (1941). (b) Illustrates the averaging process for the mixture theory approach. In this Eulerian approach the flux of the various species toward and away from a spatial point is considered. The spatial point is shown in (b) and the vectors represent the velocities of various species passing through the referenced spatial point.

This formulation of mixture theory is directed toward the modeling of biological growth, that is to say changing mass and changing density of an organism. Growth is slow, acclerationless from a mechanics viewpoint and therefore, although formulas for the acceleration will be obtained, accelerations will be neglected in the applications. The formulas for acceleration are obtained so that what is neglected is specially specified. This presentation of the theory of mixtures is further restricted to the situation in which all the mixture constituents are compressible, immiscible, reacting (chemical reactions) and all are at the same temperature θ. It is assumed that terms proportional to the square of diffusion velocities will be negligible. Bowen (1976, see page 27) considers the case where they are not negligible. Interstitial flow is slow through a particular tissue because it is 8 liters per day or 5.55 cubic centimeters per minute for the entire human body (Levick, 1995; Cowin, 2011). The exact velocity ranges of this flow are unknown but measurements in limb tissue have suggested they are on the order of 0.1 to 2 microns per second (.03 to .57 feet per day) (Levick, 1995; Cowin, 2011). Deformation-driven interstitial flows, such as those that occur in bone tissue, are greater, on the order of tens of microns per second. No tissue has a mass always composed of the same proteins and fluids; they are always changing, however slowly. Thus tissues form open systems. It is also assumed that the stress tensor associated with each constituent is symmetric and that there are no action-at-a-distance couples, as there would be, for example, if the material contained electric dipoles and was subjected to an electrical field. The restrictions associated with each of these assumptions may be removed; they are imposed to restrict this presentation to an economical path for the development of a tissue-appropriate model for normal physiological growth phenomena.

4.1 Open and closed system models at the constituent and mixture levels

Open systems permit the transport of mass, momentum and energy across their boundaries, closed system do not. Bertalanffy (1950) pointed out that “From the physical point of view the characteristic state of the living organism is that of an open system.” Thus an open system model is desired to model growth. In traditional mixture theory (Truesdell and Toupin, 1960), each constituent is considered to be an open system, but the entire mixture is considered to be a closed system. In this development the mixture is also considered to be an open system as a mechanism by which growth may be modeled. This means that the statements of the balance principles for the mixture may have supply terms as well as the statements of the balance principles for each constituent.

An alternative attractive approach to achieving an open system by allowing supply terms in the balance equations for the mixture is to, instead, allow the mixture to be viewed as existing within a reservoir that is capable of supplying more mass of any constituent or a being capable of resorbing some of the mass of any constituent. This was the approach taken in Cowin and Hegedus (1976) in the development of a growth model for bone tissue.

4.2 The Biot RVE for poroelasticity and the mixture theory approach

A key difference between the Biot effective parameter approach and the Eulerian point approach to mixture poroelastic models is the averaging process employed. The effective parameter approach illustrated in Figure 1a is a schematic version of the viewpoint described in Biot (1941). He wrote, “Consider a small cubic element of soil, its sides being parallel with the coordinate axes. This element is taken to be large enough compared to the size of the pores so that it may be treated as homogeneous, and at the same time small enough, compared to the scale of the macroscopic phenomena in which we are interested, so that it may be considered as infinitesimal in the mathematical treatment.” This prose written by Biot appears to be the first statement of what later came to be called the representative volume element (RVE) concept. In Biot’s proposal a small but finite volume of the porous medium is used as a model for a continuum point in the development of constitutive equations for the fluid-infiltrated porous solid. These constitutive equations are then assumed to be valid at a point in the continuum. The length or size of the RVE is assumed to be many times larger than the length scale of the microstructure of the material, say the size of a pore. The length of the RVE is the length of the material structure over which the material microstructure is averaged or "homogenized" in the process of forming a continuum model. The homogenization approach is illustrated in Figure 1a by the dashed lines from the four corners of the RVE to the continuum point. The material parameters or constants associated with the solid phase are more numerous and difficult to evaluate compared to those associated with the fluid phase. The Biot - effective modulus approach provides a better understanding of the effective solid mechanical parameters like effective solid moduli than does the mixture theory approach.

The averaging process for the mixture approach is illustrated in Figure 1b. This is a Eulerian approach in that the flux of the various species toward and away from a spatial point is considered. The spatial point is shown in Figure 1b and the vectors represent the velocities of various species passing through the referenced spatial point. In neither approach is a length scale specified, but an averaging length is implied in the Lagrangian or material, Biot - effective modulus, approach because a finite material volume is employed as the domain to be averaged over. On the other hand the mixture theory is Eulerian and considers a fixed spatial point through which different materials pass and, as with the Biot approach, no length scale is suggested. It is difficult to imagine a length scale for the mixture theory approach other than one based on the mean free paths associated with the constituents. The significantly different averaging lengths in the two approaches reflect the difference in the averaging methods.

4.3 The larger RVE hypothesis

The larger RVE for mixture theory-based poroelasticity is considered to have a length or size many times larger than the length scale of the pores (Figure 1a). It is assumed that the pores represent a lesser length scale that is sub RVE. The length of the RVE is the length of the material structure over which the porous microstructure is averaged or "homogenized" in the process of forming a continuum model. The RVE is of sufficient size so that three sets of elastic constants (the drained and the undrained and those of the matrix material) may be represented as well as the porosity and the pore structure fabric tensor, F. Pore structure fabric is a quantitative stereological measure of the degree of structural anisotropy in the pore architecture of a porous medium (Hilliard, 1967; Whitehouse 1974a; Whitehouse and Dyson, 1974b; Oda, 1976, Oda et al, 1980, 1985; Cowin and Satake, 1978; Satake, 1982; Kanatani, 1983, 1984a,b, 1985; Harrigan and Mann, 1984; Odgaard, 1997a, 2001; Odgaard et al, 1997b, Matsuura et al., 2008). The governing equations for anisotropic poroelasticity were developed and extended to include the dependence of the constitutive relations upon pore structure fabric (Cowin 1985, 2004). Dynamic poroelasticity was extended by Cowin and Cardoso (2010) and Cardoso (2011) to include the pore structure fabric tensor as a variable. The pore structure of the RVE is assumed to be characterized by porosity and a pore structure fabric tensor F.

5. Kinematics of mixtures

In the traditional approach to the theory of mixtures each place x in a fixed spatial frame of reference might be occupied by several different particles. In this non-traditional approach a spatially fixed RVE that particles enter and leave is considered. Each constituent particle X_(a), a = 1, 2, …, N, of the mixture is followed.

This representation is a direct generalization of the single constituent continuum, thus the material description of motion is generalized to a description that recognizes all the constituents of the mixture:

$$\mathbf{x}=\mathbf{\chi }({\mathbf{X}}_{(\mathrm{a})},\mathrm{t})\text{ for all }{\mathbf{X}}_{(\mathrm{a})}\subset {\mathrm{O}}_{(\mathrm{a})}(0).$$ (1)

The inverse of the motion (1) is given by

$${\mathbf{X}}_{(\mathrm{a})}={\mathbf{\chi }}_{(a)}^{-1}(\mathbf{x},\mathrm{t})\text{ for all }{\mathbf{X}}_{(\mathrm{a})}\subset {\mathrm{O}}_{(\mathrm{a})}(0).$$ (2)

Similar generalizations to multi-component mixtures of the formulas for the deformation gradient and its inverse are straightforward. The deformation gradient tensor for the a^th constituent F_(a) is defined by

$${\mathbf{F}}_{(\mathrm{a})}={[{\nabla }_{(\mathrm{a})}\otimes \mathbf{\chi }({\mathbf{X}}_{(\mathrm{a})},\mathrm{t})]}^{\mathrm{T}}\text{ for all }{\mathbf{X}}_{(\mathrm{a})}\subset {\mathrm{O}}_{(\mathrm{a})}(0),$$ (3)

and the inverse deformation gradient tensor ${\mathbf{F}}_{(a)}^{-1}$ is, from (2), defined by

$${\mathbf{F}}_{(a)}^{-1}={[\nabla \otimes {\mathbf{\chi }}_{(a)}^{-1}(\mathbf{x},\mathrm{t})]}^{\mathrm{T}}\text{ for all }\mathbf{x}\subset {\mathrm{O}}_{(\mathrm{a})}(\mathrm{t}),$$ (4)

where O_(a)(t) is the continuum representation of phase a. The determinant of the tensor of deformation gradient for the a^th constituent, J_(a), is the Jacobian of the transformation from x to X_(a), thus

$${\mathrm{J}}_{(\mathrm{a})}\equiv \text{Det}{\mathbf{F}}_{(\mathrm{a})}=1/\text{Det}{\mathbf{F}}_{(a)}^{-1},$$ (5)

where it is required that

$$0<{\mathrm{J}}_{(\mathrm{a})}<\mathrm{\infty },$$ (6)

so that a finite continuum volume always remains a finite continuum volume. The velocity v_(a) and acceleration $\frac{D^{(a)}{\mathbf{v}}_{(a)}}{\mathit{\text{Dt}}}$ of a particle of the a^th constituent, X_(a), are defined by formulas that are generalizations of the definition for the velocity v and acceleration $\frac{D\mathbf{v}}{\mathit{\text{Dt}}}$ in a single component continuum,

$${\mathbf{v}}_{(a)}=\frac{D^a{\mathbf{x}}_{(a)}}{\mathit{\text{Dt}}}={\frac{\partial {\chi }_{(a)}({\mathbf{X}}_{(a)},t)}{\partial t}|}_{{\mathbf{X}}_{(a)}\mathit{\text{fixed}}},$$ (7)

$$\frac{D^a{\mathbf{v}}_{(a)}}{\mathit{\text{Dt}}}={\frac{{\partial }^2{\chi }_{(a)}({\mathbf{X}}_{(a)},t)}{\partial t^2}|}_{{\mathbf{X}}_{(a)}\mathit{\text{fixed}}},$$ (8)

where X_(a) is held fixed because it is the velocity or acceleration of the particle X_(a) that is being determined. The spatial description of motion of the particle X_(a) (as opposed to the material description of motion of the particle X_(a) represented by (1)) is obtained by substituting (2) into the expressions (7) for the velocity; thus ${\mathbf{v}}_{(a)}=\frac{D^a}{\mathit{\text{Dt}}}{\chi }_{(a)}({\mathbf{X}}_{(a)},t)$ becomes

$${\mathbf{v}}_{(a)}=\frac{D^a}{\mathit{\text{Dt}}}{\chi }_{(a)}({\chi }_{(a)}^{-1}(\mathbf{x},t),t)={\mathbf{v}}_{(a)}(\mathbf{x},t).$$ (9)

The material time derivative of the a^th constituent is the time derivative following the material particle X_(a); it is denoted by $\frac{D^a}{\mathit{\text{Dt}}}$ and is defined as the partial derivative with respect to time with X_(a) held constant. If Γ(x, t) represents a function of x and t, the material time derivative of the a^th constituent is given by:

$$\frac{D^a\mathrm{\Gamma }}{\mathit{\text{Dt}}}={\frac{\partial \mathrm{\Gamma }({\chi }_{(a)}({\mathbf{X}}_{(a)},t),t)}{\partial t}|}_{{\mathbf{X}}_{(a)}\mathit{\text{fixed}}}.$$ (10)

This definition is a generalization of (7) to an arbitrary function Γ(x, t). It then follows the formula for the material time derivative in an Eulerian reference frame that

$$\frac{D^a\mathrm{\Gamma }}{\mathit{\text{Dt}}}=\frac{\partial \mathrm{\Gamma }(\mathbf{x},t)}{\partial t}+{\mathbf{v}}_{(a)}·\nabla [\mathrm{\Gamma }(\mathbf{x},t)].$$ (11)

The modeler may select one component of the mixture as special because, from the viewpoint of the modeler, that constituent serves as a key reference relative to which the movement of all the other constituents may be referred. This constituent of the mixture is denoted by s. The motion of the selected constituent is, from (1), given by x = χ(X_s, t) for all X_s ⊂ O_s(0). The material time derivative following the selected constituent is given by (11) with the label a replaced by the label s. A relationship between the time derivative following the selected constituent s and the time derivative following the generic constituent a is obtained by subtracting the two formulas for the time derivatives:

$$\frac{D^a\mathrm{\Gamma }}{\mathit{\text{Dt}}}=\frac{D^s\mathrm{\Gamma }}{\mathit{\text{Dt}}}+{\mathbf{v}}_{(a/s)}·\nabla [\mathrm{\Gamma }(\mathbf{x},t)]$$ (12)

where v_(a/s) is the diffusion velocity of the a^th constituent relative to constituent s,

$${\mathbf{v}}_{(a/s)}={\mathbf{v}}_{(a)}-{\mathbf{v}}_{(s)}.$$ (13)

The tensor of velocity gradients for the a^th constituent L_(a) is formed by taking the spatial gradient of the velocity field for the a^th constituent v_(a) = v_(a)(x, t), thus

$${\mathbf{L}}_{(a)}=\nabla \otimes {\mathbf{v}}_{(a)}.$$ (14)

Please note that this definition is completely analogous to the definition of the tensor of velocity gradients for a single constituent material, L. Using the chain rule it is easy to show that L_(a) also has the representation

$${\mathbf{L}}_{(a)}=\frac{D^a{\mathbf{F}}_{(a)}}{\mathit{\text{Dt}}}·{\mathbf{F}}_{(a)}^{-1}.$$ (15)

If ρ_(a) denotes the density of the a^th constituent, then the density of the mixture may be defined by

$$\rho (\mathit{x},t)={\displaystyle \sum _{a=1}^N}{\rho }_{(a)}(\mathbf{x},t).$$ (16)

Physically ρ_(a) represents the mass of the a^th constituent per unit volume of the mixture. The true material density for the a^th constituent is denoted by γ_(a) and represents the mass of the a^th constituent per unit volume of the a^th constituent. The quantity ρ_(a) is sometimes called the bulk density as opposed to the true material density, γ_(a). The volume fraction of the a^th constituent, ϕ_(a), that is to say the volume of the a^th constituent per unit volume of the mixture, is defined by

$${\varphi }_{(a)}(\mathbf{x},t)=\frac{{\rho }_{(a)}(\mathbf{x},t)}{{\gamma }_{(a)}(\mathbf{x},t)},$$ (17)

and it is assumed that the sum of all volume fractions divided by the total volume is equal to one,

$${\displaystyle \sum _{a=1}^N}{\varphi }_{(a)}(\mathbf{x},t)=1.$$ (18)

If the a^th constituent is incompressible, then γ_(a) is a constant. Observe from (17) that the bulk density ρ_(a) need not be constant even if the a^th constituent is incompressible since the concentration ϕ_(a) may change. The mixture is only incompressible when all the γ_(a), a = 1, 2, …, N, are incompressible. If less than N constituents are incompressible, (18) is a constraining relationship between the densities. Note that the mixture density ρ given by (16) may be variable, even when all the constituents are incompressible, that is to say all the γ_(a)‘s are constant, because the volume fractions (17) of the constituents present at a point x are variable. The concentration of the a^th constituent, ρ_(a), is defined by

$$c_{(a)}=\frac{{\rho }_{(a)}}{\rho }=\frac{{\varphi }_{(a)}{\gamma }_{(a)}}{{\displaystyle \sum _{b=1}^N}{\varphi }_{(b)}{\gamma }_{(b)}}.$$ (19)

6. The hypothesis for representing microflows at the RVE level

Let ${\mathbf{v}}_{(a/s)}^m$ denote the fluid sub RVE velocity of constituent “a” relative to the selected (solid) constituent “s.” This is a velocity that exists only in the small pores of the solid matrix. The general hypothesis for representing microflows at the RVE level is that a homogenization process over the RVE may be constructed to determine the RVE level fluid velocity v_(a/s) from the fluid sub RVE velocity ${\mathbf{v}}_{(a/s)}^m$. This homogenization process will depend on the pore structure fabric tensor F of the RVE since the process is accomplished over the porous structure of the RVE.

The precise homogenization process employed is likely to depend upon the particular problem being studied so no general mathematical formulation is proposed here. For this presentation the Biot hypothesis (1956a) for representing sub RVE flows at the RVE scale is adopted.

$${\mathbf{v}}_{(a/s)}=\mathbf{J}·{\mathbf{v}}_{(a/s)}^m,$$ (20)

where J is the subRVE-RVE velocity average tensor; Biot (1962a) uses the term micro-macro velocity average tensor. J functions like a density distribution function that relates relative micro-solid-fluid velocity to its RVE level bulk volume average, v_(a/s). The subRVE-RVE velocity average tensor J is related to the pore structure fabric tensor A by (Cowin and Cardoso, equation (62))

$$\mathbf{J}=j_1\mathbf{1}+j_1\mathbf{A}+j_1{\mathbf{A}}^2,$$ (21)

where j₁, j₂, and j₃ are functions of ϕ, II and III, where II and III are the second and third invariants of A; the first invariant is normalized to one. In earlier work the governing equations for quasi-static (Cowin, 2004) and dynamic (Cowin and Cardoso, 2010) linear theories of anisotropic poroelastic materials were developed and extended to include the dependence of the constitutive relations upon pore structure fabric (Cowin 1985, 2004). It is assumed there that any mixture theory growth model based on the present formulation will assume that all the constitutive equations will depend upon pore structure fabric. However, in the present contribution, the pore structure fabric tensor will only appear in (21) above for the purpose of explaining the nature of the subRVE-RVE velocity average tensor J. It was noted above that J functions like a density distribution function; that density distribution is determined by the pore structure fabric tensor A. It is possible that growth models will, in the future, include fabric tensors associated with particular constituents (e.g., collagen) as well as pore structure fabric.

7. The mean velocity of a mixture

In mixture theory it is customary to define the mean velocity of the mixture as the density-weighted average of the velocities of all the constituents,

$$\mathbf{v}=\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a)}.$$ (22)

There are two reasons why the concept of mean velocity (22) is not employed in a significant way in this development. The first is its dubious physical significance when averaging over solid and fluid velocity components. The second is that its meaning as the mean velocity (22) is compromised when some of the RVE fluid velocities v_(a/s) are determined from the sub RVE fluid velocities ${\mathbf{v}}_{(a/s)}^m$ by a homogenization process. Given that the computation of the mean velocity employs RVE fluid velocities v_(a/s), which are determined from a homogenization process, renders the dubious physical significance of the mean velocity (22) more obscure. Here the velocity of the solid is used for reference velocity and the mean velocity of the mixture is generally avoided as has been assumed by a number of earlier mixture theory authors, although we have not seen in previous publications all the consequences of that assumption that we record here. This option results in some complicated formulas for the acceleration of constituents, but the biological growth processes of interest are accelerationless.

8. The conservation laws for mixtures

In this section equations are postulated for the balance of mass, momentum and energy for each constituent and then the necessary and sufficient conditions are obtained so that the usual global balance of mass, momentum and energy for the entire mixture is satisfied. In order to postulate equations for the balance of mass, momentum and energy for each constituent X_(a), a = 1, 2, …, N, each constituent of the mixture is assigned a density ρ_(a), an action-at-a-distance force density d_(a), a partial stress T_(a), a partial internal energy density ε_(a), a partial heat flux, and a partial heat supply density, r_(a).

The local statement of mass conservation for a single constituent continuum may be written for each constituent a = 1, 2, …, N as

$$\frac{\partial {\rho }_{(a)}}{\partial t}+\nabla ·({\rho }_{(a)}{\mathbf{v}}_{(a)})={\stackrel{⌣}{s}}_{(a)},$$ (23a)

where s̆_(a) represents the mass supply to a constituent from other constituents and from external sources. The local statement of mass conservation for a single constituent continuum rewritten in terms of the selected velocity becomes

$$\frac{\partial {\rho }_{(a)}}{\partial t}+\nabla ·({\rho }_{(a)}[{\mathbf{v}}_{(s)}+{\mathbf{v}}_{(a/s)}])={\stackrel{⌣}{s}}_{(a)}.$$ (23b)

The sum of all mass supplies to a constituent from other constituents is denoted by s̆(t), thus

$${\displaystyle \sum _{a=1}^{a=N}}{\stackrel{⌣}{s}}_{(a)}=\stackrel{⌣}{s}(t).$$ (24)

(As noted at the end of section 4.1 an alternative approach to allowing supply terms in the balance equations for the mixture in order to achieve an open system is to allow the mixture to be viewed as existing within a reservoir that is capable of supplying more mass of any constituent or a being capable of resorbing some of the mass of any constituent. This was the approach taken in Cowin and Hegedus (1976) in the development of a growth model for bone tissue. Thus one could set the sum in (24) equal to zero and employ the reservoir concept.)

The summation of (23b) over all constituents and the use of (24) yields

$$\frac{\partial \rho }{\partial t}+\nabla ·(\rho {\mathbf{v}}_{(s)}+{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)})=\stackrel{⌣}{s}(t).$$ (25)

When the selected point (s) for velocity reference is the point where the velocity is equal to the mean velocity the statement of the conservation of mass above reduces to the traditional formula below involving the mean velocity,

$$\frac{\partial \rho }{\partial t}+\nabla ·(\rho \mathbf{v})=\stackrel{⌣}{s}(t).$$ (26)

It is known that a point where the velocity is equal to the mean velocity exists because of the mean value theorem. The term s̆(t) in the two representations of mass balance above represents a mass supply or mass loss in the mixture; it has the dimensions of density over time. Since the mixture consists only of constituents, the mass supply or mass loss in the mixture is distributed in some fashion over the constituents. The existence of this term is a consequence of assuming the mixture to be an open system, an assumption that may be made to model growth (see section 4.1).

The conservation of momentum for a single constituent continuum may be written as

$${\rho }_{(a)}\frac{D^{(a)}{\mathbf{v}}_{(a)}}{\mathit{\text{Dt}}}=\nabla ·{\mathbf{T}}_{(a)}+{\rho }_{(a)}{\mathbf{d}}_{(a)}+{\stackrel{⌣}{\mathbf{p}}}_{(a)},$$ (27)

where T_(a) is the partial stress, d_(a) is the action-at-a-distance force density and p̆_(a) is the momentum supply associated with constituent a. The momentum supply p̆_(a) represents the transfer of momentum from the other constituents and external sources to constituent a. In this presentation it is assumed that all the partial stress tensors T_(a) are symmetric. The assumption is consistent with the mixture theory applications that are to be considered here, but it is an assumption that may be avoided if necessary (Bowen 1976, 1980). The conservation of energy for constituent a is a similar generalization of the single constituent continuum

$${\rho }_{(a)}\frac{D^a{\epsilon }_{(a)}}{\mathit{\text{Dt}}}={\mathbf{T}}_{(a)}:{\mathbf{D}}_{(a)}-\nabla ·{\mathbf{q}}_{(a)}+{\rho }_{(a)}{r}_{(a)}+{\stackrel{⌣}{\epsilon }}_{(a)},$$ (28)

where ε_(a) is the partial internal energy density, q_(a) is the partial heat flux vector, r_(a) is the heat supply density, ε̆_(a) is the energy supply and D_(a) = (1/2) (L_(a)+ (L_(a))^T). The energy supply ε̆_(a) represents the transfer of energy from the other constituents to constituent “a.”

It is a basic hypothesis of mixture theory (Truesdell, 1957, 1961; Truesdell and Toupin, 1960) that the constituent forms of the balance of mass (23b), the balance of momentum (27) and the balance of energy (28), summed over all the constituents, produce the customary single constituent continuum forms of the balance of mass, the balance of momentum and the balance of energy, respectively. This assumption is equivalent to assuming that the mixture is a closed system. As noted in section 4.1 here the mixture is considered to be to be an open system and this basic hypothesis is not followed and supply terms are allowed at the mixture level.

However, in the case when the summation over all constituents involves the density-weighted time derivatives of specific quantities following the generic constituent as, for example, on the left hand side of (27) and (28), the result is difficult to interpret. Let ϖ_(a) denote the generic component specific property such as v_(a) or ε_(a) and we seek a simple formula for ${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}$ to be used in determining the continuum level form of the conservation laws by summing over the single constituent continuum forms of the conservation laws. Thus a formula relating the density-weighted sum of the time derivatives of the selected components to the sum of the density-weighted time derivatives has been developed. The sum of generic constituent-specific quantity per unit mass ϖ_(a) is related to its density-weighted sum ϖ by

$$\varpi =\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\varpi }_{(a)}.$$ (29)

The desired formula relating the sum of the density-weighted, constituent-specific, time derivatives to the time derivative following the selected component is given by

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+{\displaystyle \sum _{b=1}^{N-s}}\nabla ·({\varpi }_{(b)}{\rho }_{(b)}{\nu }_{(b/s)})-\varpi \nabla ·{\displaystyle \sum _{b=1}^{N-s}}{\rho }_{(b)}{\mathbf{v}}_{(b/s)}+\{\varpi \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\},$$ (30)

where v_(a/s) is the diffusion velocity relative to the selected component. The derivation of this result is given in the Appendix. The derivation involves the relationship

$$\rho (\mathbf{v}-{\mathbf{v}}_{(s)})={\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}={\displaystyle \sum _{b=1}^{N-s}}{\rho }_{(b)}{\mathbf{v}}_{(b/s)},$$ (31)

which is obtained using (13), (22) and (16). The last equality in (31) follows from the fact that, from (13), v_(s/s) must be zero. Please recall that, in this development, terms of order of the diffusion velocity v_(a/s) squared are to be neglected. The derivation of (30) involves the expressions for the time derivatives (11) and (12), the constituent-specific mass balance (18) and the definition of the density-weighted sum ρϖ in terms of the constituent-specific quantity per unit mass denoted by ϖ_(a), (29). The result (30) coincides with equation (13.23) in Cowin and Doty (2007) when the last two mass supply rate terms are neglected and (31) is employed. When ϖ_(a) is assumed not to have a dependence upon the index “a,” the result (30) takes the simplified form

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a\varpi }{\mathit{\text{Dt}}}=\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+\rho (\mathbf{v}-{\mathbf{v}}_{(s)})·\nabla \varpi =\rho \frac{D\varpi }{\mathit{\text{Dt}}}.$$ (32)

Application of the formula (30) relating the sum of the density-weighted, constituent-specific time derivatives to the time derivative following the selected component to the special case of the velocity v_(a) yields the following representation:

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\mathbf{v}}_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\mathbf{v}}{\mathit{\text{Dt}}}+{\displaystyle \sum _{a=1}^N}\nabla ·[{\rho }_{(a)}{\mathbf{v}}_{(a/s)}\otimes {\mathbf{v}}_{(a/s)}]-\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}\nabla ·({\rho }_{(a)}{\mathbf{v}}_{(a/s)})\{{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}\}+\{\mathbf{v}\stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\mathbf{v}}_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}$$ (33)

which reduces to

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\mathbf{v}}_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\mathbf{v}}{\mathit{\text{Dt}}}+\{\mathbf{v}\stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\mathbf{v}}_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}$$ (34)

when terms of order of the diffusion velocity v_(b/s) squared are neglected.

With the results (30) and (34) in hand it is now possible to return to the development of the sums of the constituent-specific balance equations. Recall that it is required that the summation of the forms of the balance of mass (23), the balance of momentum (26) and the balance of energy (27) for each constituent over all the constituents is required to produce again the single constituent continuum forms of the balance of mass, the balance of momentum and the balance of energy, respectively. The summation of the component-specific form of the conservation of linear momentum (26), employing the representation (34) for the sum of the density-weighted, component-specific, time derivatives of the component-specific velocities, one obtains a result that is similar to the single component form,

$$\rho \frac{D^s\mathbf{v}}{\mathit{\text{Dt}}}=\nabla ·\mathbf{T}+\rho \mathbf{d}+\stackrel{⌣}{\mathbf{p}}(t),$$ (35)

where the total stress T is defined by

$$\mathbf{T}={\displaystyle \sum _{a=1}^N}{\mathbf{T}}_{(a)},$$ (36)

the sum of the action-at-a-distance forces by

$$\mathbf{d}=\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}({\rho }_{(a)}{\mathbf{d}}_{(a)}),$$ (37)

and the sum of the constituent momentum supplies p̆_(a) is denoted by p̆,

$${\displaystyle \sum _{a=1}^N}\{{\stackrel{⌣}{\mathbf{p}}}_{(a)}+{\mathbf{v}}_{(a)}{\stackrel{⌣}{s}}_{(a)}\}-\mathbf{v}\stackrel{⌣}{s}(t)=\stackrel{⌣}{\mathbf{p}}.$$ (38)

The existence of the momentum supply term for the mixture, p̆, is a consequence of assuming the mixture to be an open system, an assumption made to model growth (see section 4.1). The growth processes are so slow, however, that this term is likely to be negligible. If the velocity of the selected component is equal to the mean velocity of the mixture, v_(s) = v and the mass supply terms are neglected, the result (35) will coincide with results that appear in Bowen (1967, 1976, 1980, 1982).

The summation of the constituent-specific form of the balance of energy (28) over all the constituents, and subsequently employing the formula (30) with ϖ_(a) replaced by ε_(a), yields

$$\rho \frac{D^s\epsilon }{\mathit{\text{Dt}}}=\rho r+\stackrel{⌣}{\epsilon }(t)+{\displaystyle \sum _{a=1}^N}{\mathbf{T}}_{(a)}:{\mathbf{D}}_{(a)}-\nabla ·{\displaystyle \sum _{a=1}^N}\{{\mathbf{q}}_{(a)}+({\epsilon }_{(a)}-\epsilon ){\rho }_{(a)}{\mathbf{v}}_{(a/s)}\},$$ (39)

where ε is the specific internal energy density for the mixture and r is the heat supply density for the mixture given by

$$\epsilon =\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\epsilon }_{(a)},r=\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{r}_{(a)}={\displaystyle \sum _{a=1}^N}{c}_{(a)}{r}_{(a)},$$ (40)

and where the sum of the energy supplies ε̆_(a) is denoted by ε̆(t),

$$\stackrel{⌣}{\epsilon }(t)={\displaystyle \sum _{a=1}^N}\{{\stackrel{⌣}{\epsilon }}_{(a)}+{\epsilon }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}-\epsilon \stackrel{⌣}{s}(t).$$ (41)

The key results of this section are the statements of the conservation of mass, momentum and energy for each constituent and the summation of these component forms to yield statements of these conservation principles for the mixture.

9. The entropy inequality

The approach undertaken for development of the conservation principles for mass, momentum and energy was to sum the forms of each of the constituent-specific conservation equations over all constituents to obtain statements of those principles that applied to the mixture as whole. It will be recalled that the development of this argument began with constituent-specific forms of the conservation equations. In this development it will not be assumed that there were constituent-specific forms of the entropy inequality. The literature is somewhat divided on the use of constituent-specific forms of the entropy inequality (Bowen, 1976, section 1.7). The conservative position is to assume only the mixture level inequality. Thus the entropy inequality employed here only makes a statement for the entire mixture, not for any particular constituent.

Let E denote the strain in the solid portion of the mixture, then the thermodynamic state of a particle X in an object is completely specified by the thermodynamic substate {E, ρ_(a)}and the entropy η of the (RVE associated with the) particle. The basic assumption of thermodynamics is that the thermodynamic state completely determines the (specific) internal energy ε independent of time, place, motion and stress, thus ε = ε(η, E, ρ_(a), X). Choice of the exact functional form of ε defines different thermodynamic substances. If X does not appear in the form of ε chosen, the substance is said to be thermodynamically simple.

The Clausius Duhem inequality for internal entropy production is written as

$$\rho \frac{D^s\eta }{\mathit{\text{Dt}}}+\nabla ·(\frac{\mathbf{h}}{\theta })-\frac{\rho r}{\theta }\ge 0,$$ (42)

where h is the heat flux vector and θ, r and η were defined earlier. The temperature, θ, the stress tensor, T, and electrochemical (or chemical) potential, μ_(a), may be defined, in terms of the internal energy ε(η, E, ρ_(a), X), as the derivatives of ε(η, E, ρ_(a), X) with respect to entropy, η, strain, E, and concentration, ρ_(a), respectively:

$$\theta ={\left(\frac{\partial \epsilon }{\partial \eta }\right)}_{\mathbf{E},{\rho }_{(a)}},\mathbf{T}={\left(\frac{\partial \epsilon }{\partial \mathbf{E}}\right)}_{\eta ,{\rho }_{(a)}},{\mu }_{(a)}={\left(\frac{\partial \epsilon }{\partial c_{(a)}}\right)}_{\mathbf{E},\eta }.$$ (43)

The time derivative of the internal energy ε may then be expressed as follows:

$$\frac{D^s\epsilon }{\mathit{\text{Dt}}}=\theta \frac{D^s\eta }{\mathit{\text{Dt}}}+\mathbf{T}\mathbf{:}\mathbf{D}+{\displaystyle \sum _{a=1}^N}{\mu }_{(a)}\frac{D^s{c}_{(a)}}{\mathit{\text{Dt}}}.$$ (44)

The Helmholtz free energy is defined by

$$\psi (\theta ,\mathbf{E},c_{(a)},\mathbf{X})=\epsilon (\eta ,\mathbf{E},c_{(a)},\mathbf{X})-\eta \theta ,$$ (45)

and the derivatives of the free energy ψ with respect to temperature, strain and concentration yield the entropy, stress and electrochemical (or chemical) potential, respectively:

$$\eta =-{\left(\frac{\partial \psi }{\partial \theta }\right)}_{\mathbf{E},{\rho }_{(a)}},\mathbf{T}={\left(\frac{\partial \psi }{\partial \mathbf{E}}\right)}_{\theta ,{\rho }_{(a)}},{\mu }_{(a)}={\left(\frac{\partial \psi }{\partial c_{(a)}}\right)}_{\mathbf{E},\theta }.$$ (46)

The time derivative of the free energy ψ may then be expressed as follows:

$$\frac{D^s\psi }{\mathit{\text{Dt}}}=\eta \frac{D^s\theta }{\mathit{\text{Dt}}}+\mathbf{T}\mathbf{:}\mathbf{D}+{\displaystyle \sum _{a=1}^N}{\mu }_{(a)}\frac{D^s{c}_{(a)}}{\mathit{\text{Dt}}}.$$ (47)

It is assumed that each constituent of the mixture has the regular properties of a thermodynamic substance, thus the Helmholtz free energy of each constituent ψ_(a) is related to the temperature θ and constituent-specific internal energy ε_(a) and entropy η_(a) by the component-specific form of (45)

$${\psi }_{(a)}={\epsilon }_{(a)}-\theta {\eta }_{(a)},$$ (48)

where

$$\psi =\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\psi }_{(a)}.$$ (49)

In order to generalize the inequality (42) to a mixture, three substitutions into (42) are made. First the η in (42) is replaced by the density-weighted average of the constituent-specific internal entropy η_(a), thus

$$\eta =\frac{1}{\rho }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\eta }_{(a)},$$ (50)

and, second, a similar replacement, the second of (40) is made for ρr. The third substitution employs equation (51) to eliminate $\rho \frac{D^s\eta }{\mathit{\text{Dt}}}$ from (42). Equation (51) is obtained from the formula (30) by replacing ϖ_(a) by η_(a), thus

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\eta }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\eta }{\mathit{\text{Dt}}}+{\displaystyle \sum _{b=1}^{N-s}}\nabla ·({\eta }_{(b)}{\rho }_{(b)}{\nu }_{(b/s)})-\eta \nabla ·{\displaystyle \sum _{b=1}^{N-s}}{\rho }_{(b)}{\mathbf{v}}_{(b/s)}+\{\eta \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\eta }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}.$$ (51)

The entropy inequality for a mixture may now be formulated using the entropy inequality for the single component continuum (42) as the guide. The term $\rho \frac{D^s\eta }{\mathit{\text{Dt}}}$ in (42) is eliminated using (51). The heat supply density r in (42) is replaced by that for the mixture given by the second of (40), thus entropy inequality for a mixture takes the form

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\eta }_{(a)}}{\mathit{\text{Dt}}}+{\displaystyle \sum _{a=1}^N}\nabla ·(\frac{{\mathbf{h}}_{(a)}}{\theta }-{\eta }_{(a)}{\rho }_{(a)}{\nu }_{(a/s)})+\eta \nabla ·{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}-\frac{1}{\theta }{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{r}_{(a)}-\{\eta \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\eta }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}\ge 0,$$ (52)

where the constituent-specific flux vectors, h_(a), are introduced using $\mathbf{h}={\displaystyle \sum _{a=1}^N}{\mathbf{h}}_{(b)}$.

The remainder of this section presents the development of an alternate form of the entropy inequality (52). First, the product ρ_(a)r_(a) is eliminated between (28) and (52) and then, second, the result is multiplied by θ. Third, it is assumed that the constituent-specific flux vectors, h_(a) and q_(a), are related by

$${\mathbf{h}}_{(a)}={\mathbf{q}}_{(a)}+{\rho }_{(a)}\theta {\eta }_{(a)}{\mathbf{v}}_{(a/s)},$$ (53)

thus

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\{\theta \frac{D^a{\eta }_{(a)}}{\mathit{\text{Dt}}}-\frac{D^a{\epsilon }_{(a)}}{\mathit{\text{Dt}}}\}+\theta \nabla ·\{{\displaystyle \sum _{a=1}^N}\frac{{\mathbf{q}}_{(a)}}{\theta }\}+\theta \eta \nabla ·{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}+\stackrel{⌣}{\epsilon }(t)+{\displaystyle \sum _{a=1}^N}\{{\mathbf{T}}_{(a)}:{\mathbf{D}}_{(a)}-\nabla ·{\mathbf{q}}_{(a)}\}-\theta \{\eta \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\eta }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}\ge 0.$$ (54)

Substituting (48) into (53) it follows that

$$-{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\{\frac{D^a{\psi }_{(a)}}{\mathit{\text{Dt}}}\}-\rho \eta \frac{D^a\theta }{\mathit{\text{Dt}}}-\frac{1}{\theta }\mathbf{q}·\nabla \theta +\theta \eta \nabla ·{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}+\stackrel{⌣}{\epsilon }(t)+{\displaystyle \sum _{a=1}^N}\{{\mathbf{T}}_{(a)}:{\mathbf{D}}_{(a)}\}-\theta \{\eta \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\eta }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}\ge 0,$$ (55)

where the definition

$$\mathbf{q}={\displaystyle \sum _{a=1}^N}{\mathbf{q}}_{(a)},$$ (56)

has been employed. This expression for the heat flux is an approximation that neglects several terms associated with diffusion velocities. This point is discussed on page 27 of Bowen (1976). The expression relating the terms in (55) containing the time derivatives of the specific free energy density for the mixture ψ_(a) is replaced by

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\psi }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\psi }{\mathit{\text{Dt}}}+{\displaystyle \sum _{b=1}^{N-s}}\nabla ·({\psi }_{(b)}{\rho }_{(b)}{\nu }_{(b/s)})-\psi \nabla ·{\displaystyle \sum _{b=1}^{N-s}}{\rho }_{(b)}{\mathbf{v}}_{(b/s)}+\{\psi \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\psi }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\},$$ (57)

a result that was obtained by substituting ψ_(a) for ϖ_(a) in (30); thus (55) becomes

$$-\rho \frac{D^s\psi }{\mathit{\text{Dt}}}-\rho \eta \frac{D^s\theta }{\mathit{\text{Dt}}}-\frac{1}{\theta }\mathbf{q}·\nabla \theta +\epsilon \nabla ·{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}-\nabla ·{\displaystyle \sum _{b=1}^{N-s}}({\psi }_{(b)}{\rho }_{(b)}{\nu }_{(b/s)})+{\displaystyle \sum _{a=1}^N}\{{\mathbf{T}}_{(a)}:{\mathbf{D}}_{(a)}\}+\stackrel{⌣}{\epsilon }(t)-\{\epsilon \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\epsilon }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}\ge 0,$$ (58)

where use of been made of (54) in setting ψ + ηθ = ε. Using again the relation ψ + ηθ = ε the form of the inequality of interest could also be written entirely in terms of ε, thus

$$-\rho \frac{D^s\epsilon }{\mathit{\text{Dt}}}+\rho \theta \frac{D^s\eta }{\mathit{\text{Dt}}}-\frac{1}{\theta }\mathbf{q}·\nabla \theta +\epsilon \nabla ·{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\mathbf{v}}_{(a/s)}-\nabla ·{\displaystyle \sum _{b=1}^{N-s}}({\epsilon }_{(b)}{\rho }_{(b)}{\nu }_{(b/s)})+\nabla ·{\displaystyle \sum _{b=1}^{N-s}}\theta ({\eta }_{(b)}{\rho }_{(b)}{\nu }_{(b/s)})+{\displaystyle \sum _{a=1}^N}\{{\mathbf{T}}_{(a)}:{\mathbf{D}}_{(a)}\}+\stackrel{⌣}{\epsilon }(t)-\{\epsilon \stackrel{⌣}{s}(t)-{\displaystyle \sum _{a=1}^N}{\epsilon }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)\}\ge 0.$$ (59)

10. Incompleteness

The material that has been presented represents an incomplete theory because constitutive equations and the supply terms for each constituent as a whole have not been specified. The constitutive equations and terms that need to be specified depend upon the particular growth problem being considered. In addition, the particular growth problem should specify how the materials to be deposited are transported to their point of deposition. For the growth of soft tissue it is reasonable to assume that the blood supply to the tissue will deliver the proteins and the supply of energy. If these proteins carried by the blood are not employed or deployed by the liver in their first pass through the tissue in need they will likely be transported across the blood vessel walls to pass into the interstitial fluid of another tissue. The interstitial fluid will then pass through the tissue to a collecting lymph node and then pass into the lymphatic system. The lymphatic system collects the lymph from all the tissues, concentrates the proteins and passes them back into the circulatory system at the left subclavian vein before it enters the heart. The tissue building proteins are then recirculated again and again before they find deployment in a tissue or are passed out of the body (Levick, 1995). The coupling of these related transport problems to growth problems is not difficult due to very slow transport velocities involved (see section 4.1).

11. Summary

This contribution presented an alternative approach to mixture theory-based poroelasticity by transferring some poroelastic concepts developed by Biot to mixture theory. These concepts were a larger RVE and the subRVE-RVE velocity average tensor, which was assumed to depend upon the pore structure fabric. The formulation of mixture theory presented was directed toward the modeling of interstitial growth, that is to say changing mass and changing density of an organism by the addition of mass to each constituent and to the total mixture. Traditional mixture theory considers constituents to be open systems, but the entire mixture is a closed system. In this development the mixture was also considered to be an open system as one possible mechanism for modeling growth. Growth is slow and accelerations are neglected in the applications. The standard kinematics of mixture theory was modified to account for the fact that pore fluid velocities generally occur at a scale below those of the solid velocities in poroelastic materials. Use of the velocity of the main solid constituent is employed as the main reference velocity in preference to the mean velocity concept from traditional mixture theory. The standard development of statements of the conservation principles and entropy inequality employed in mixture theory were modified to account for these kinematic changes and to allow for supplies of mass, momentum and energy to each constituent and to the mixture as a whole. The basis for the development of constitutive equations for growth of tissues was thus partially established. There still remain the problems of specifying the supply terms for each constituent and for the mixture as a whole as well as the specification of how the building materials to be deposited are transported to their point of deposition.

Appendix

The purpose of this appendix is to record the derivation of equation (30) and some related auxiliary results. Recall that ϖ_(a) denotes a generic component-specific property such as v_(a) or ε_(a) and we seek a simple formula for ${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}$ to be used in determining the continuum level form of the conservation laws by summing over the single constituent continuum forms of the conservation laws. A formula relating the density-weighted sum of the time derivatives of the selected components to the sum of the density-weighted time derivatives is desired. Recall that the sum of generic constituent-specific quantity per unit mass ϖ_(a) is related to its density-weighted sum ϖ by (29). The time derivative of (29) with respect to the selected component is given by

$$\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+\varpi \frac{D^s\rho }{\mathit{\text{Dt}}}={\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^s{\varpi }_{(a)}}{\mathit{\text{Dt}}}+{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}\frac{D^s{\rho }_{(a)}}{\mathit{\text{Dt}}},$$ (A1)

which may be solved for ${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}$, thus

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^s{\varpi }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+\varpi \frac{D^s\rho }{\mathit{\text{Dt}}}-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}\frac{D^s{\rho }_{(a)}}{\mathit{\text{Dt}}}.$$ (A2)

The relationship between the time derivatives with respect to the selected component and with respect to the “a” component is obtained using (12)

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^s{\varpi }_{(a)}}{\mathit{\text{Dt}}}={\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}+{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\nu }_{(s)}·\nabla {\varpi }_{(a)}-{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\nu }_{(a)}·\nabla {\varpi }_{(a)};$$ (A3)

this is used to rewrite (A2) as

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+\varpi \frac{D^s\rho }{\mathit{\text{Dt}}}-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}\frac{D^s{\rho }_{(a)}}{\mathit{\text{Dt}}}-{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\nu }_{(s)}·\nabla {\varpi }_{(a)}+{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\nu }_{(a)}·\nabla {\varpi }_{(a)}.$$ (A4)

The following relationships, the first obtained from the conservation of mass for the mixture (25),

$$\frac{D^s\rho }{\mathit{\text{Dt}}}=\frac{\partial \rho }{\partial t}+{\nu }_{(s)}·\nabla \rho =\stackrel{⌣}{s}(t)-\nabla ·(\rho \nu )+{\nu }_{(s)}·\nabla \rho$$ (A5)

and the second obtained from the conservation of mass for the constituent (23)

$$\frac{D^s{\rho }_{(a)}}{\mathit{\text{Dt}}}=\frac{\partial {\rho }_{(a)}}{\partial t}+{\nu }_{(s)}·\nabla {\rho }_{(a)}={\stackrel{⌣}{s}}_{(a)}(t)-\nabla ·({\rho }_{(a)}{\nu }_{(a)})+{\nu }_{(s)}·\nabla {\rho }_{(a)}$$ (A6)

will now be used in (A4). However, before using (A6) it is multiplied by and summed over all values of “a,” thus

$${\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}\frac{D^s{\rho }_{(a)}}{\mathit{\text{Dt}}}={\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}\nabla ·({\rho }_{(a)}{\nu }_{(a)})+{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}{\nu }_{(s)}·\nabla {\rho }_{(a)}.$$ (A7)

These relationships, (A5) and (A7), obtained from the mass conservation equations for the mixture and for the constituent are substituted into (A2), thus

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+\varpi (\stackrel{⌣}{s}(t)-\nabla ·(\rho \nu )+{\nu }_{(s)}·\nabla \rho )-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)+{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}\nabla ·({\rho }_{(a)}{\nu }_{(a)})-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}{\nu }_{(s)}·\nabla {\rho }_{(a)}-{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\nu }_{(s)}·\nabla {\varpi }_{(a)}+{\displaystyle \sum _{a=1}^N}{\rho }_{(a)}{\nu }_{(a)}·\nabla {\varpi }_{(a)}.$$ (A7)

The second line of the result above is condensed

$${\displaystyle \sum _{a=1}^N}{\rho }_{(a)}\frac{D^a{\varpi }_{(a)}}{\mathit{\text{Dt}}}=\rho \frac{D^s\varpi }{\mathit{\text{Dt}}}+\varpi (\stackrel{⌣}{s}(t)-\nabla ·(\rho \nu )+{\nu }_{(s)}·\nabla \rho )-{\displaystyle \sum _{a=1}^N}{\varpi }_{(a)}{\stackrel{⌣}{s}}_{(a)}(t)+{\displaystyle \sum _{a=1}^N}\nabla ·({\varpi }_{(a)}{\rho }_{(a)}{\nu }_{(a)})-{\displaystyle \sum _{a=1}^N}{\nu }_{(s)}·\nabla {\varpi }_{(a)}{\rho }_{(a)}.$$ (A8)

and then the entire equation is algebraically reduced to (30).