Quantifying density fluctuations in volumes of all shapes and sizes using indirect umbrella sampling

Abstract

Water density fluctuations are an important statistical mechanical observable that is related to many-body correlations, as well as hydrophobic hydration and interactions. Local water density fluctuations at a solid-water surface have also been proposed as a measure of it’s hydrophobicity. These fluctuations can be quantified by calculating the probability, P_v(N), of observing N waters in a probe volume of interest v. When v is large, calculating P_v(N) using molecular dynamics simulations is challenging, as the probability of observing very few waters is exponentially small, and the standard procedure for overcoming this problem (umbrella sampling in N) leads to undesirable impulsive forces. Patel et al. [J. Phys. Chem. B, 114, 1632 (2010)] have recently developed an indirect umbrella sampling (INDUS) method, that samples a coarse-grained particle number to obtain P_v(N) in cuboidal volumes. Here, we present and demonstrate an extension of that approach to volumes of other basic shapes, like spheres and cylinders, as well as to collections of such volumes. We further describe the implementation of INDUS in the NPT ensemble and calculate P_v(N) distributions over a broad range of pressures. Our method may be of particular interest in characterizing the hydrophobicity of interfaces of proteins, nanotubes and related systems.

1 Introduction

Quantifying density fluctuations in a condensed phase is interesting from a statistical physics perspective. For example, the probability P_v(N) of finding N fluid particles in a probe volume v contains information about many-body correlations in the fluid. Calculations of P_v(N) in liquid water have significantly enhanced our understanding of hydrophobicity. In particular, as the hydration of an idealized solvent-excluding hydrophobic solute is equivalent to the creation of a cavity with the same size and shape as that of the solute, the excess free energy, μ^ex, of solute hydration is [1]

$${\mu }^{\text{ex}}=-k_{\text{B}}Tlog{P}_v(0),$$ (1)

where k_B is the Boltzmann constant, T is the temperature, and ‘log’ represents the natural logarithm. In 1996, Hummer et al. showed that in bulk water, P_v(N) distributions are gaussian for small spherical volumes containing fewer than ten water molecules on average [2]. This simplicity formed the basis for an information theoretic model that could predict the thermodynamics of hydrophobic hydration and the association of small solutes over a range of conditions, using only the readily available information on the average density and the water radial distribution function [2–4]. Gaussian statistics of density fluctuations [5] also underlies the Pratt-Chandler theory [6], which employs the same information to estimate pair correlation functions for small hydrated hydrophobic species.

While small solutes can be accommodated in cavities that are formed spontaneously by thermal fluctuations in bulk water, solvating large solutes requires forming a liquid-vapor-like interface [7–9]. As a result, the nature of density fluctuations in large volumes is more complex. The Lum-Chandler-Weeks (LCW) theory captures the lengthscale dependence of hydration quantitatively by combining the physics of gaussian density fluctuations and that of interface formation [8]. Specifically, it predicts that while P_v(N) for large volumes is gaussian around the mean, the low-N wings of the distribution are enhanced substantially [10,11]. Quantifying these rare water fluctuations in large volumes is essentially impossible in equilibrium molecular simulations, and requires non-Boltzmann or umbrella sampling methods [12]. Straightforward umbrella sampling of N, is further complicated by the fact that N is a discontinuous function of particle coordinates, resulting in impulsive forces, which are difficult to treat in typical molecular dynamics (MD) simulations. To circumvent this difficulty, Patel et al. recently introduced an indirect umbrella sampling (INDUS) method in which N is sampled indirectly, by biasing a coarse-grained variable, Ñ, which is strongly correlated with N but varies continuously with particle coordinates [13]. Some elements of this formalism have also been used previously by Andreev et al. in their study of deformed carbon nanotubes [14].

The original implementation of INDUS, which is suitable only for cuboidal volumes, showed that for large volumes in bulk water, P_v(N) indeed deviates significantly from gaussian behavior at low N, reflecting the underlying physics of interface formation [13]. Application of INDUS to sample density fluctuations in large volumes in interfacial environments showed that fluctuations near hydrophilic surfaces are similar to those in bulk, but near hydrophobic interfaces, the probability of density depletion is significantly enhanced [13]. The ability to calculate P_v(N), and especially μ^ex using Eq. 1, in large volumes near interfaces also allowed us to calculate the binding free energies of hydrophobic cuboids to surfaces with a range of chemistries, and these binding free energies were shown to correlate with the macroscopic wetting properties of the surfaces [15]. Thus, P_v(N) is a potential molecular measure of hydrophobicity, which may enable the characterization of surfaces of proteins and biomolecules that exhibit nanoscale roughness and chemical heterogeneity.

Here, we extend INDUS such that it can be used to umbrella sample probe volumes of other regular shapes, e.g., with cylindrical and spherical symmetry, as well as intersections and unions of collections of such regular volumes and their complements. While the ideas underlying the extension are simple, they considerably widen the scope of the method. For example, they allow umbrella sampling of arbitrarily shaped volumes, enabling faithful characterization of fluctuations in the hydration shells of ions, nanoparticles, nanotubes, as well as rugged proteins surfaces.

We also extend the method to work in the NPT ensemble. Previous applications of INDUS were performed in the NVT ensemble with a buffering vapor-liquid interface. While the two schemes yield indistinguishable results at low pressures, the present extension allows access to a much broader range of pressures. We begin by describing the INDUS method of Ref. [13], which is suitable for cuboidal probe volumes, and introduce the pertinent equations, which lays down the framework for extending the method to other regular volumes. We then generalize these equations to volumes of more general shapes and to collections of such volumes, and describe how INDUS affects the calculation of system pressure. Finally, we demonstrate these generalizations by calculating P_v(N) in various noncuboidal shapes and at high pressures.

2 The INDUS Method

The number of particles, N, in a specific probe volume, v, changes discontinuously as the center of any particle crosses the surface of v. Hence, if the biasing potential, U, were chosen to be a function of N, it would result in impulsive forces. Instead, we choose U to be a function of a closely related coarse-grained particle number, Ñ, that is a continuous function of the positions, {r_i}, of all M particles in the system as,

$$\stackrel{\sim }{N}=\sum _{i=1}^M\stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}}),$$ (2a)

where

$$\stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}})\equiv {\int }_v\mathrm{\Phi }(\mathbf{r}-{\mathbf{r}}_{\mathbf{i}})\text{d}\mathbf{r}.$$ (2b)

The integral in Eq. 2b is over the probe volume v, and the integrand is a coarse-graining function, Φ(r), which we choose to be

$$\mathrm{\Phi }(\mathbf{r})=\phi (x)\phi (y)\phi (z),$$ (3a)

where

$$\phi (\alpha )=k^{-1}[e^{-{\alpha }^2/2{\sigma }^2}-e^{-{\alpha }_{\text{c}}^2/2{\sigma }^2}]\mathrm{\Theta }({\alpha }_{\text{c}}-\mid \alpha \mid ).$$ (3b)

The function φ(α), shown in Fig. 1, is a gaussian that is truncated at |α| = α_c, shifted down, and then scaled, so as to make it continuous and normalized. The normalization constant, k, is equal to $\sqrt{2\pi {\sigma }^2}\text{erf}({\alpha }_{\text{c}}/\sqrt{2{\sigma }^2})-2{\alpha }_{\text{c}}exp(-{\alpha }_{\text{c}}^2/2{\sigma }^2)$ and Θ(α) is the Heaviside step function. As the width of the gaussian, σ, approaches 0, the function φ(α) approaches the Dirac delta function δ(α) and Ñ approaches N. The correlation between Ñ and N is thus strongest when σ is smallest, but if σ is chosen to be too small, the resulting biasing forces may be too large to handle correctly in typical MD simulations.

Fig. 1.

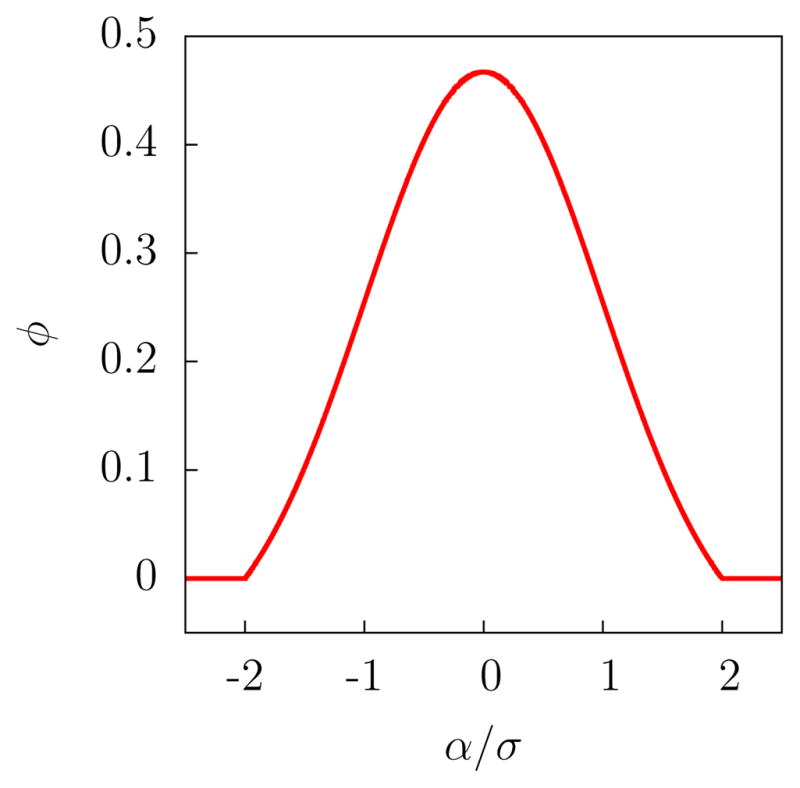
The coarse-graining function, φ(α), as defined in Eq. 3b, for α_c = 2σ.

For a cuboidal volume v, the integral in Eq. 2b can be performed independently in the x, y and z directions. The result is

$$\stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}})={\stackrel{\sim }{h}}_x(x_i){\stackrel{\sim }{h}}_y(y_i){\stackrel{\sim }{h}}_z(z_i),$$ (4a)

where

$${\stackrel{\sim }{h}}_x(x_i)={\int }_{x_{min}}^{x_{max}}\phi (x-x_i)\text{d}x,$$ (4b)

and x_min and x_max are the coordinates of the faces of v perpendicular to the x-axis. The functions h̃_y(y_i) and h̃_z(z_i) are defined analogously.

Fig. 2a shows the function h_x(x_i) (equal to 1 for x_min ≤ x_i ≤ x_max, and 0 otherwise), which can be thought of as the x contribution to h(r_i); that is, h(r_i) = h_x(x_i)h_y(y_i)h_z(z_i) and N = Σ_i h(r_i). Fig. 2a also shows the function h̃_x(x_i), which varies continuously across the boundary of v, unlike h_x(x_i). The coarse-graining function h̃_x(x_i) differs from h_x(x_i) only in the thin boundary region of thickness 2x_c. Thus, by ensuring that Ñ and N are strongly correlated, we are able to influence N indirectly by biasing Ñ.

Fig. 2.

The functions h_α (α_i), h̃_α (α_i) and its derivative, ${\stackrel{\sim }{h}}_{\alpha }^{\prime }({\alpha }_i)$, for coordinates that have (a) two (α → x), (b) one (α → r) or (c) zero (α → θ) boundaries.

For a cuboidal probe volume, the x-component of the force on particle i due to the biasing potential, U(Ñ), is given by

$$f_{x,i}\equiv -\frac{\partial U}{\partial x_i}=-\frac{\partial U}{\partial \stackrel{\sim }{N}}\frac{\partial \stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}})}{\partial x_i}=-\frac{\partial U}{\partial \stackrel{\sim }{N}}{\stackrel{\sim }{h}}_x^{\prime }(x_i){\stackrel{\sim }{h}}_y(y_i){\stackrel{\sim }{h}}_z(z_i),$$ (5)

where the derivative of h̃_x(x_i), obtained by differentiating Eq. 4b and shown in Fig. 2a, is

$${\stackrel{\sim }{h}}_x^{\prime }(x_i)=-[\phi (x_{max}-x_i)-\phi (x_{min}-x_i)].$$ (6)

It follows that the biasing forces act only on particles near the boundary of v, are finite, and are continuous functions of particle positions.

To obtain P_v(N) using INDUS, we perform n_w simulations with different biasing potentials, U_j(Ñ) (j = 1, …, n_w), chosen such that the range of interest of N is well sampled. During each simulation, we collect n_j samples of N and Ñ, denoted by N_j,l and Ñ_j,l (l = 1, …, n_j), in essence, sampling the biased joint distribution function, P_v(N, Ñ). We then unbias and stitch together the n_w biased joint distribution functions by using the weighted histogram analysis method (WHAM) [16, 17]. Finally, we integrate out the unbiased joint distribution function to obtain P_v(N), which is given by

$$P_v(N)=C\sum _{j=1}^{n_w}\sum _{l=1}^{n_j}\frac{{\delta }_{N,N_{j,l}}}{{\sum }_{i=1}^{n_w}{n}_i{e}^{-\beta [U_i({\stackrel{\sim }{N}}_{j,l})-c_i]}},$$ (7)

where β⁻¹ = k_BT is the thermal energy, δ_n,m is the Kronecker delta function, and C and {c_j} are normalization constants, determined self-consistently through the standard WHAM equations,

$$C^{-1}=\sum _{j=1}^{n_w}\sum _{l=1}^{n_j}\frac{1}{{\sum }_{i=1}^{n_w}{n}_i{e}^{-\beta [U_i({\stackrel{\sim }{N}}_{j,l})-c_i]}},$$ (8a)

and

$$e^{-\beta c_k}=C\sum _{j=1}^{n_w}\sum _{l=1}^{n_j}\frac{e^{-\beta U_k({\stackrel{\sim }{N}}_{j,l})}}{{\sum }_{i=1}^{n_w}{n}_i{e}^{-\beta [U_i({\stackrel{\sim }{N}}_{j,l})-c_i]}}.$$ (8b)

3 Extension of INDUS to noncuboidal volumes

While several coarse-graining schemes are possible for defining Ñ, a practically useful definition must satisfy the following three conditions: (i) Ñ must be a continuous function of particle positions, (ii) Ñ and N must be strongly correlated, and (iii) the calculation of Ñ and its derivatives should be straightforward. The choice of the form of Eq. 3a for cuboid volumes allows h̃(r_i) to be expressed as a product of independent contributions from x, y, and z coordinates (as in Eq. 4a). While this formulation is particularly convenient for cuboidal volumes, the integral (Eq. 2b) that defines h̃(r_i) would not be independent in the three coordinates for other regular volumes, such as spheres or cylindrical shells. Thus, calculating h̃(r_i) and its gradient efficiently at every MD step would not be straightforward. To circumvent this complication, we bypass defining h̃(r_i) via a coarse-graining function Φ as in Eq. 2b, and instead, define it directly as a product of independent contributions from the three co-ordinates (as in Eq. 4a) in the relevant co-ordinate system (e.g., cylindrical, spherical, etc.) as,

$$\stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}})=\prod _{\alpha }{\stackrel{\sim }{h}}_{\alpha }({\alpha }_i).$$ (9)

Here α represents the coordinate component index (e.g., x, y or z in Cartesian coordinates; r, θ or z for cylindrical ones, etc.) and h̃_α (α_i) may be defined in a manner analogous to h̃_x(x_i) (Eq. 4b and Fig. 2a).

However, unlike cuboidal volumes, where each coordinate component has two boundaries (e.g., x_min and x_max), the components in spherical or cylindrical systems may have either one boundary (e.g., the r coordinate for a spherical v), or no boundaries (e.g., the θ coordinate for a cylindrical v). These cases are illustrated in Fig. 2 and the expressions for h̃_α(α_i) and ${\stackrel{\sim }{h}}_{\alpha }^{\prime }({\alpha }_i)$ in each case are as follows:

• Two boundaries: α_min ≤ α ≤ α_max.

  $$\begin{array}{l}{\stackrel{\sim }{h}}_{\alpha }({\alpha }_i)=\left[k_1\text{erf}\left(\frac{{\alpha }_{max}-{\alpha }_i}{\sqrt{2}\sigma }\right)-k_2({\alpha }_{max}-{\alpha }_i)-\frac{1}{2}\right]\mathrm{\Theta }({\alpha }_{\text{c}}-\mid {\alpha }_{max}-{\alpha }_i\mid )\\ +\left[k_1\text{erf}\left(\frac{{\alpha }_i-{\alpha }_{min}}{\sqrt{2}\sigma }\right)-k_2({\alpha }_i-{\alpha }_{min})-\frac{1}{2}\right]\mathrm{\Theta }({\alpha }_{\text{c}}-\mid {\alpha }_i-{\alpha }_{min}\mid )\\ +\mathrm{\Theta }\left({\alpha }_{\text{c}}+\frac{1}{2}({\alpha }_{max}-{\alpha }_{min})-\left|{\alpha }_i-\frac{1}{2}({\alpha }_{min}+{\alpha }_{max})\right|\right),\end{array}$$ (10a)
  and

  $${\stackrel{\sim }{h}}_{\alpha }^{\prime }({\alpha }_i)=-[\phi ({\alpha }_{max}-{\alpha }_i)-\phi ({\alpha }_{min}-{\alpha }_i)],$$ (10b)

  where $k_1=k^{-1}\sqrt{\pi {\sigma }^2/2}$ and $k_2=k^{-1}exp(-{\alpha }_{\text{c}}^2/2{\sigma }^2)$.

• One boundary: α ≤ α_max.

  $${\stackrel{\sim }{h}}_{\alpha }({\alpha }_i)=\left[k_1\text{erf}\left(\frac{{\alpha }_{max}-{\alpha }_i}{\sqrt{2}\sigma }\right)-k_2({\alpha }_{max}-{\alpha }_i)-\frac{1}{2}\right]\mathrm{\Theta }({\alpha }_{\text{c}}-\mid {\alpha }_{max}-{\alpha }_i\mid )+\mathrm{\Theta }({\alpha }_{\text{c}}+{\alpha }_{max}-{\alpha }_i),$$ (11a)
  and

  $${\stackrel{\sim }{h}}_{\alpha }^{\prime }({\alpha }_i)=-\phi ({\alpha }_{max}-{\alpha }_i).$$ (11b)
• No boundaries:

  $${\stackrel{\sim }{h}}_{\alpha }({\alpha }_i)=1,$$ (12a)
  and

  $${\stackrel{\sim }{h}}_{\alpha }^{\prime }({\alpha }_i)=0.$$ (12b)

  The forces are then given by

  $$f_{x,i}=-\frac{\partial U}{\partial \stackrel{\sim }{N}}\frac{\partial \stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}})}{\partial x_i},$$ (13a)

  with
  $$\frac{\partial \stackrel{\sim }{h}({\mathbf{r}}_{\mathbf{i}})}{\partial x_i}=\sum _{\alpha }\left[{\stackrel{\sim }{h}}_{\alpha }^{\prime }({\alpha }_i)\frac{\partial {\alpha }_i}{\partial x_i}\prod _{\gamma \ne \alpha }{\stackrel{\sim }{h}}_{\gamma }({\gamma }_i)\right],$$ (13b)

  where ∂α_i/∂x_i is an element of the Jacobian for the coordinate transformation.

4 Generalization to collections of probe volumes

The above approach can be generalized to calculate P_v(N) in a probe volume v that is constructed from unions (v_A ∪ v_B) and intersections (v_A ∩ v_B) of regular subvolumes (v_A, v_B) and their complements (v̄_A, v̄_B). The subvolumes need not be of the same size or shape. When v is constructed from subvolumes using the complement, intersection and union operations, the corresponding definition of h̃(r_i) is constructed by noting that,

$${\stackrel{\sim }{h}}^{(\overline{A})}=1-{\stackrel{\sim }{h}}^{(A)},$$ (14a)

$${\stackrel{\sim }{h}}^{(A\cap B)}={\stackrel{\sim }{h}}^{(A)}{\stackrel{\sim }{h}}^{(B)},$$ (14b)

and

$${\stackrel{\sim }{h}}^{(A\cup B)}=1-{\stackrel{\sim }{h}}^{(\overline{A})}{\stackrel{\sim }{h}}^{(\overline{B})}.$$ (14c)

Here, the superscript (A) indicates that the function is evaluated with respect to the boundaries of sub-volume v_A. For the special case of a probe volume v that is a union of G non-overlapping sub-volumes {v_k} (k = 1, …, G), the above prescription yields,

$$\stackrel{\sim }{h}({\mathbf{r}}_i)=\sum _{k=1}^G{\stackrel{\sim }{h}}^{(k)}({\mathbf{r}}_i),$$ (15a)

where

$${\stackrel{\sim }{h}}^{(k)}({\mathbf{r}}_{\mathbf{i}})=\prod _{\alpha }{\stackrel{\sim }{h}}_{\alpha }^{(k)}({\alpha }_i).$$ (15b)

Once again, the force on particle i resulting from a biasing potential, U, is finite and continuous everywhere, and is given by

$$f_{x,i}=-\frac{\partial U}{\partial \stackrel{\sim }{N}}\frac{\partial \stackrel{\sim }{N}}{\partial x_i},$$ (16a)

where

$$\frac{\partial \stackrel{\sim }{N}}{\partial x_i}=\sum _{k=1}^G\frac{\partial {\stackrel{\sim }{h}}^{(k)}({\mathbf{r}}_{\mathbf{i}})}{\partial x_i}.$$ (16b)

The recipe given in Eqs. 10–13, when applied to v_k can be used to evaluate ${\stackrel{\sim }{h}}_{\alpha }^{(k)}$ and ∂h̃^(k)/∂x_i in Eqs. 15b and 16b.

5 INDUS in the NPT ensemble

When calculating P_v(N) using simulations in the NVT ensemble, as was done in Ref. [13], it is important to have a vapor bubble or a vapor-liquid interface in the simulation box. This vapor bubble can be nucleated, e.g., by applying a particle excluding field far from v, and can grow or shrink to accommodate water molecules pushed into or out of v. The resulting effective pressure of the system is close to the saturation vapor pressure of the fluid. Alternatively, we can perform simulations in the NPT ensemble without such a bubble, as long as the forces resulting from the umbrella potential are included in the calculation of the system pressure, . If v is fixed in space and does not move, grow or shrink as the simulation box dimensions fluctuate, then the contribution of the umbrella potential to is

$${\mathcal{P}}^{\text{umb}}\equiv -\frac{\partial U}{\partial V}=\frac{1}{3V}\sum _{i=1}^M{\mathbf{r}}_i•{\mathbf{f}}_i^{\text{umb}},$$ (17)

where ${\mathbf{f}}_i^{\text{umb}}$ is the umbrella force on particle i, calculated as described in the preceding sections, and V is the system volume.

6 Results

We illustrate the extension of the INDUS method by calculating P_v(N) distributions for volumes of different shapes in bulk water. Biased MD simulations of bulk water were performed using the MD simulation packages LAMMPS [19] and GROMACS [20], modified in-house to implement INDUS. For the parameters of the coarse-graining function φ(α) in Eq. 3b, we used σ = 0.1 Å and α_c = 0.2 Å (NVT ensemble) or α_c = 0.3 Å (NPT ensemble). Each simulation box contained several thousand water molecules, modeled with the extended simple point charge water model (SPC/E) [21], and was periodic in all directions.

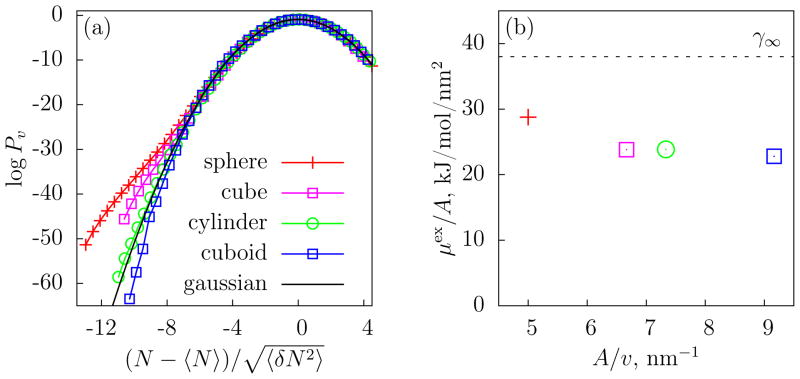
We selected volumes of four different shapes (a sphere, a cube, a cylinder, and a cuboid; see Figure 3), each with an average number of water molecules, 〈N〉, between 25 and 30. For these large volumes, INDUS allows us to measure probabilities for rare water fluctuations that are rather small (P_v(0) ≈ 10⁻³⁰), whereas calculations using straightforward equilibrium simulations [2] provide accurate estimates only for much smaller volumes (〈N〉 ≈ 8 with corresponding P_v(0) ≈ 10⁻⁸). Although the volumes of the shapes that we have selected are similar to each other, they are not identical, and contain slightly different number of waters on average. Therefore, to compare them with each other as well as with a gaussian distribution, in Fig. 3a, we plot P_v as a function of $(N-\langle N\rangle )/\sqrt{\langle \delta N^2\rangle }$, where 〈δN²〉 is the variance of N. Near the mean, the distributions are gaussian for all shapes, as expected. However, there are significant deviations from gaussian behavior in the low-N tails of P_v(N). Specifically, the smaller a shape’s surface-area to volume ratio, the fatter the low-N tail.

Fig. 3.

(a) log P_v as a function of $(N-\langle N\rangle )/\sqrt{\langle \delta N^2\rangle }$ for volumes of four different shapes: a sphere of radius 0.6 nm, a cube of side 0.9 nm, a ylinder of radius 0.3 nm and length 3 nm, and a thin cuboid of dimensions 0.3 nm × 1.6 nm × 1.6 nm. (b) The ratio of μ^ex to surface area A, as a function of A/v for the four different shapes. The dashed line represents the surface tension, γ_∞, of a vapor-liquid interface of SPC/E water [18].

In the large lengthscale limit, interface formation governs the free energy of cavity formation. LCW theory [8] predicted, and subsequent simulation studies verified [15,22–24], that the gradual crossover from small to large lengthscale physics occurs around 1 nm, which is roughly the length-scale of volumes selected here. Thus, we expect that shapes with smaller surface areas will have lower free energies of cavity formation and correspondingly fatter low-N tails, as observed in Fig. 3a. Fig. 3b further confirms that the free energy is governed by the physics of interface formation: the ratio of μ^ex to the surface area of the probe volume, A, which can be interpreted as an apparent surface tension, γ̃, is approximately constant, independent of the shape of v. For nanoscopic objects, γ̃ depends on solute size and curvature, and is expected to be lower than the macroscopic surface tension of a vapor-liquid interface, γ_∞ [13,22,25,26], in agreement with the results in Fig. 3b.

In Figure 4, we demonstrate the generalization of the INDUS method to collections of probe volumes by calculating P_v(N) in an arbitrarily shaped volume. The volume that we have chosen spells, ‘I N D U S’, using a collection of 156 non-overlapping cubic sub-volumes, each with a side of 0.25 nm.

Fig. 4.

P_v(N) obtained by umbrella sampling a probe volume that spells, ‘I N D U S’. The volume is composed of 156 cubic subvolumes of side 0.25 nm. The inset shows a superposition of five independent configurations, taken from an MD simulation with a strong biasing potential that empties the probe volume. The red spheres represent water oxygens. The letter ‘I’ in the inset is 0.5 nm wide and 2.0 nm tall.

In Fig. 5, we show that for a cube of side 0.9 nm, the P_v(N) distribution calculated in the NPT ensemble at a pressure, = 1 bar, is identical to that obtained in the NVT ensemble with a buffering vapor-liquid interface. This is expected since ≪ k_BT ≪ γA, so the energetics of emptying v is governed almost entirely by the cost of forming an interface (Figure 3b). The effective pressure in the NVT system is the coexistence pressure, , at T = 300 K, which is close to 0.06 bar. Since, < ≪ k_BT, our simulations in the NVT ensemble are an excellent approximation to those in the NPT ensemble at 1 bar.

Fig. 5.

Comparing P_v(N) for a cubic v of side 0.9 nm, obtained using NPT ensemble simulations ( = 1bar), with that obtained from NVT ensemble simulations having a buffering vapor-liquid interface located far from v.

The ability to calculate P_v(N) in the NPT ensemble allows us to study its pressure dependence systematically. In Fig. 6a, we show P_v(N) distributions in a cube of side 1.2 nm over a broad range of pressures. For pressures of 1 kbar and higher, the term is no longer negligible, and opposes emptying v. Correspondingly, the low-N fat tail disappears gradually with increasing pressure. We also show in Fig. 6b that the free energy of hydrating the cubic cavity increases roughly linearly with pressure. The slope of μ^ex versus is the excess volume for solvating the cavity, and is equal to 0.67v for this cubic probe volume.

Fig. 6.

(a) log P_v as a function of $(N-\langle N\rangle )/\sqrt{\langle \delta N^2\rangle }$ for a cube of side 1.2 nm, calculated in the NPT ensemble, over a range of pressures at T = 300 K. (b) Free energy, μ^ex, of the same cube as a function of pressure. A linear fit yields the excess volume of the cavity, v^ex ≈ 0.67v.

7 Conclusions

Given the importance of density fluctuations in understanding a range of solvation phenomena [3, 4,27–31], we anticipate that the INDUS method will be of broad interest. For instance, the size of density fluctuations at interfaces has been proposed recently as a measure of interface hydrophobicity [15,32–34]. The extended INDUS method is capable of characterizing hydrophobicity in complex environments that exhibit chemical heterogeneity [33,35–37], complex topography [25,38,39], and confinement [35,40–46]. The ability to calculate P_v(N) over a range of pressures using the NPT ensemble will be useful in studying the effect of pressure on biomolecular structure, and especially in quantifying the hydration contribution to the pressure denaturation of proteins [47]. Finally, quantifying P_v(N) in a region surrounding a solute molecule constitutes an important contribution in the quasichemical theories of solvation [48,49], and our extension of INDUS can be readily applied to quantify that contribution for a solute of arbitrary shape and size.