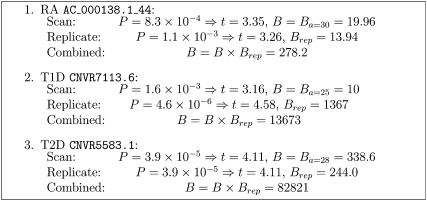Abstract
In genome-wide association studies hundreds of thousands of loci are scanned in thousands of cases and controls, with the goal of identifying genomic loci underpinning disease. This is a challenging statistical problem requiring strong evidence. Only a small proportion of the heritability of common diseases has so far been explained. This “dark matter of the genome” is a subject of much discussion. It is critical to have experimental design criteria that ensure that associations between genomic loci and phenotypes are robustly detected. To ensure associations are robustly detected we require good power (e.g., 0.8) and sufficiently strong evidence [i.e., a high Bayes factor (e.g., 106, meaning the data are 1 million times more likely if the association is real than if there is no association)] to overcome the low prior odds for any given marker in a genome scan to be associated with a causal locus. Power calculations are given for determining the sample sizes necessary to detect effects with the required power and Bayes factor for biallelic markers in linkage disequilibrium with causal loci in additive, dominant, and recessive genetic models. Significantly stronger evidence and larger sample sizes are required than indicated by traditional hypothesis tests and power calculations. Many reported putative effects are not robustly detected and many effects including some large moderately low-frequency effects may remain undetected. These results may explain the dark matter in the genome. The power calculations have been implemented in R and will be available in the R package ldDesign.
THE goal of genome-wide association studies (GWAS) is to understand the genetic basis of quantitative traits and complex diseases, by relating genotypes of large numbers of SNP markers to observed phenotypes. Results of GWAS to date suggest that the traits of interest are governed by many small effects (e.g., Wellcome Trust Case Control Consortium 2007; Diabetes Genetics Initiative of Broad Institute of Harvard and MIT 2007; Gudbjartsson et al. 2008; Lettre et al. 2008; Weedon et al. 2008; Lango Allen et al. 2010). Previously, we gave Bayesian power calculations for genome-wide association studies for quantitative traits (Ball 2005). This approach ensures power to detect effects of a specified size with a given Bayes factor, where the Bayes factor is chosen large enough to overcome the low prior odds for effects. These were the first results showing that much larger sample sizes were needed (e.g., thousands, even for a modest Bayes factor) than had been used at the time (cf. Luo 1998). However, these calculations do not apply to a binary phenotype such as presence or absence of a disease, e.g., coronary artery disease or type II diabetes, or case–control studies. Case–control studies, where a fixed (e.g., approximately equal) number of cases and controls are sampled, are used to study diseases that may not have high prevalence in the general population. This approach has higher power than a random population sample that may otherwise have only a small number of cases. In this article, we extend Bayesian power calculations for genome-wide association studies to case–control studies. Power calculations are given for dominant, recessive, and additive genetic models for biallelic observed marker loci in linkage disequilibrium with biallelic causal loci.
Genome-wide association studies
GWAS aim to understand the genetic basis of quantitative traits and complex diseases by detecting and locating SNPs in linkage disequilibrium (LD) with causal loci or, alternatively, developing models predictive of phenotype.
Experimental design is a key component to any study. Without sufficient power, effects may not be detected, and those that are detected may not be robustly detected. Effects may be subject to selection bias (Miller 1990; Ball 2001) where overestimated effects are overrepresented among the selected (or “significant”) effects, inflating the variance explained. Selection bias is a problem whenever the power to detect the true size of effect is not high. The fact that we observe only the estimated size of effect that may be subject to selection bias represents an additional difficulty. Selection bias can be overcome using Bayesian methods that allow for model uncertainty (e.g., Ball 2001; Sillanpää and Corander 2002).
The power of an experiment to detect effects of various sizes is an important consideration when interpreting the results of GWAS, since it bears on the proportion of undetected effects.
Spurious associations
The measure of statistical evidence is also critical in consideration of spurious associations. There have been many published spurious associations (reviewed in Terwilliger and Weiss 1998; Altshuler et al. 2000; Emahazion et al. 2001; Ball 2007a). In many of these, p-values were used, and it would have been apparent from a Bayesian analysis that the evidence was weak, e.g., with a Bayes factor <1 meaning that the data were more likely to be observed under the null hypothesis, H0, of no effect than under the alternative hypothesis, H1, that there is a real effect.
Even in larger studies (e.g., Diabetes Genetics Initiative of Broad Institute of Harvard and MIT 2007; Wellcome Trust Case Control Consortium 2007), using the apparently highly stringent threshold (P = 5 × 10−7, the then de facto standard), evidence for effects near the threshold (about half of the most significant effects reported), while strong, was not strong enough to overcome prior odds of, e.g., 1/50,000 that might apply to SNPs in a genome scan (cf. the scenario in Figure 1 below). Even (in fact, especially) with large sample sizes, power and spurious associations are important considerations. While larger and larger samples will eventually detect any effect of given size, there will be more and more possibly spurious effects “detected” at or near the threshold of significance.
Figure 1 .
Example parameters leading to prior odds and Bayes factor required.
There are two main approaches to power calculations for GWAS: frequentist (e.g., Purcell et al. 2003; Menashe et al. 2008) and Bayesian (Ball 2004, 2005). We briefly review frequentist and Bayesian measures of evidence with reference to recent GWAS. We start from first principles to make a clear and coherent argument and address common misconceptions.
Frequentist measures of evidence
In the traditional (frequentist) approach to experimental design, a threshold α (often α = 0.05) is selected, and the sample size chosen so that the experiment has good power, i.e., the probability of detecting effects of a specified size or greater is reasonably high (e.g., 0.8).
This approach relies on the efficacy of the p-value as a measure of evidence. Implicit in the approach is the belief that a p-value P < α represents good evidence. This may not be the case. A number of authors have pointed out the problems with using p-value for testing scientific hypotheses (e.g., Berger and Berry 1988; Ball 2007a).
Yet the common misconception persists that P < 0.05 represents good evidence among users of frequentist methods. For example, “Posterior odds of 10:1 seem acceptable which justifies the use of P < 0.05 for testing provided that the prior odds are close to evens” (Dudbridge and Gusnato 2008, p. 233). This does not consider the fact that the Bayes factor (discussed below), when P = 0.05, may not even be greater than one. The value of the conditional alpha (αc) (Sellke et al. 2001), which is a more appropriate value of α to use when P = p is observed, would be
| (1) |
| (2) |
which is substantially >0.05.
With this approximation, a p-value of 0.05 corresponds to a Bayes factor of only ∼3, or 3:1 odds and not 19:1 as the value 0.05 might suggest. A p-value of 0.05 may represent weak evidence regardless of the prior used (cf. Berger and Berry 1988), and the problem gets worse with larger sample sizes (Table 3 in Ball 2005); e.g., for a t-test with n = 100, a p-value of 0.05 may correspond to a Bayes factor of ≤1.
Table 3. Reduced genotype frequencies and penetrances for the APOE locus.
| aa | Aa | AA | |
|---|---|---|---|
| Frequency | 0.746 | 0.237 | 0.019 |
| Penetrance | 0.052 | 0.122 | 0.600 |
The p-value has some of the desired characteristics of a measure of evidence. From a given experiment, smaller p-value correspond to stronger evidence. This monotonicity property also holds for other statistics, e.g., the t- or F-statistics. The p-value represents a standardization of these statistics, at least under H0, to a uniform random variable. The p-value does not, however, successfully standardize evidence across different experiments that may have different experimental designs, sample sizes, allele frequencies, etc. The p-value is not the probability of being wrong and is not similar to the Bayesian posterior probability Pr(H0 | data). The latter probabilities are generally considerably higher regardless of the prior used (Berger and Berry 1988). The reason the p-value is difficult to relate to quantities of direct interest, such as the probability of a real effect, is that the p-value is the probability of an unobserved event; e.g.,
| (3) |
where T is a test statistic, tobs is its observed value, and Trep is the value of T in a hypothetical replicate of the experiment. Summarizing the data by the observed p-value amounts to conditioning on this unobserved event. The event that was observed is {T = tobs}.
Many authors have provided sophisticated adjustments to p-values (see, e.g., Dudbridge and Gusnato 2008 and references therein). However, the key problem of what threshold to use remains unresolved. A comparison-wise threshold of α = 0.05 is clearly (in hindsight) too weak, but there is no reason why an experimentwise α = 0.05 is the right or optimal choice, even after adjustments for the effective number of comparisons or a permutation test. A lower, more stringent, threshold eliminates more false positives, but also reduces power to detect the true positives. Underestimating the threshold needed means that many experiments are underpowered to detect effects with sufficient evidence. An apparently low p-value often does not represent strong evidence. This often becomes apparent only when Bayes factors or posterior probabilities are calculated.
In early association studies there were many spurious associations, some with apparently low p-values. Around the time of the Wellcome Trust Case Control Consortium (2007) and Diabetes Genetics Initiative of Broad Institute of Harvard and MIT (2007) studies, P = 5 × 10−7 became a de facto standard. Such associations from three large sample meta-analyses for human height (Gudbjartsson et al. 2008; Lettre et al. 2008; Weedon et al. 2008) have been termed “robustly detected” yet of the 54 “significant” associations only 3 were replicated across all three studies. A probable explanation is low power (Visscher 2008), suggesting these effects have not been robustly detected.
Since then, lower and lower thresholds are being used, representing an admission of the inadequacy of previous thresholds. For example, Dudbridge and Gusnato (2008) argue that an experimentwise P = 0.05 threshold should be used, after adjusting for the equivalent number of independent comparisons leading to a recommended threshold P = 5 × 10−8 for individual comparisons in a Western European population. This coincides with the current de facto standard for genome-wide significance of P = 5 × 10−8 generally required for journal publications (P. Visscher, personal communication) although the National Human Genome Research Institute catalog of genome-wide association studies (Hindorff et al. 2011) admits associations with P < 1 × 10−5.
Dudbridge and Gusnato (2008, p. 233) note that “at the time of writing the WTCCC reported successful replication of 10 associations from 11 attempts” but that this does not contradict the need for a lower threshold, because only a few of the 10 successfully replicated associations had p-values near the threshold.
Bayesian measures of evidence
Bayesian statistics are statistics soundly based on probability theory. Despite centuries of use, no better alternative has been found for making decisions under uncertainty. Bayes’ theorem is used to combine prior information, data, and a statistical model (likelihood), to obtain information about model parameters. Where more than one model is considered, e.g., corresponding to two hypotheses, H0, H1, the Bayes factor represents the strength of evidence in the data, for H1 over H0, while posterior probabilities for models (or odds) represent our probabilities after combining prior information with data.
The advantages of Bayesian measures of evidence are that prior knowledge is incorporated transparently and that the posterior distributions of parameters and posterior probabilities of alternate hypotheses are directly relevant for making a decision. Bayesian measures include Bayes factors and posterior probabilities. Posterior probabilities represent our knowledge about unknown parameters after analyzing the data. Posterior odds are the ratio of posterior probabilities for two models or hypotheses.
Let y denote the observed data. From Bayes’ theorem, it follows that the posterior odds are given by
| (4) |
The Bayes factor is defined as the ratio
| (5) |
Comparing (4) and (5), we see that
| (6) |
From (6), we see that the Bayes factor is clearly interpretable as the strength of evidence, in the data, for a real effect. This interpretation is valid regardless of sample size, statistical model, or experimental design. Increased posterior odds can be obtained either by getting a larger Bayes factor (e.g., by using a more powerful experiment) or by increasing prior odds (e.g., utilizing knowledge of candidate genes and pathways, results from other studies, etc.). Prior odds represent the scientist’s prior judgement of the odds before the experiment was carried out. Observers with different prior odds can easily compute their posterior odds using (4).
A quasi-Bayesian approach to setting the threshold
A quasi-Bayesian argument has been used to justify the threshold of 5 × 10−7 used in the Wellcome Trust Case Control Consortium (2007) study: “for a class of tests significant when a statistic T > t, the posterior odds may be expressed in terms of the prior odds as
| (7) |
where α, β are the type-I and type-II error rates…Assuming 106 independent regions of the genome, 10 disease-causing genes and average power 50% to detect an associated gene, posterior odds of 10:1 in favor of association would be achieved by a nominal p-value of 5 × 10−7 …” (Dudbridge and Gusnato 2008, p. 228).
Note that 1 − β is the power, denoted by below.
This recognizes the importance of prior odds, and the implied “Bayes factor” Bfreq of
| (8) |
is of the right order of magnitude for recent GWAS. However, effects detected at or near the specified threshold (P ≈ α = 5 × 10−7 rather than P < α) will have a significantly lower Bayes factor. For example, using the approximate Bayes factor formula below with a conservative default prior, we obtain a Bayes factor of B = 4318.6. This is a substantially lower Bayes factor and not high enough to obtain posterior odds greater than one in a genome scan in the absence of additional prior information.
The problem with the argument above is that α is a valid error rate only if set pre-experimentally. Once P has been observed, it is an error to set α = P. Regardless of whether α was set pre-experimentally, once P has been observed for an association it is an error to replace the observation {T = tobs} by the unobserved event {T > tobs}. According to Fisher (1959, p. 55), we must use all the information. From a Bayesian perspective, effects at differing loci are a priori exchangeable but once differing values of T have been observed they are not a posteriori exchangeable, and hence they cannot be treated collectively as in (7) above.
The argument given in the Wellcome Trust Case Control Consortium (2007, Box 1, p. 664) was that (7) applies if all effects are assumed to of the same size; however, this works only if the p-value are in some sense an “average” of a distribution of p-values with P ≤ α and not if P = α. A more appropriate value of α to use in (7) would be αc, leading to
| (9) |
which is still somewhat higher than the approximate Bayes factor with prior information equivalent to a sample of size a = 1 and approximately equal to the approximate Bayes factor with prior information equivalent to a sample of size a = 43.
Power
In the Bayesian context we define the power, , as the probability of detecting an effect with at least the specified Bayes factor.
When designing experiments with power to detect effects with a given type-I error rate, frequentists are specifying the maximum p-value among effects considered detected. When designing experiments with power to detect effects with a given Bayes factor, we are specifying the minimum Bayes factor among effects considered detected.
To robustly detect effects, we design experiments with power to detect effects with a given Bayes factor, where the Bayes factor is large enough to overcome prior odds for the expected number of effects of the given detectable size, to obtain reasonable posterior odds.
For illustration, we consider the scenario shown in Figure 1, suggesting that a Bayes factor of the order of 1 × 106 would be required. This scenario would apply for recent GWAS with a population with the extent of LD similar to that of a diverse human population. The Bayes factor required, and also the number of markers required, increases and the prior odds decrease as the extent of LD decreases or the expected number of causal loci decreases.
In the Methods section we derive the Bayesian power calculation for case–control studies. The key to the power calculation is a closed-form expression for an (asymptotic) approximate Bayes factor, which we derive using the Savage–Dickey density ratio, i.e., the ratio of prior to posterior densities at zero. Approximate Bayes factors of this type for testing genetic associations were first given in Ball (2007a) and subsequently by Wakefield (2007) (reviewed in Stephens and Balding 2009).
Note that formulas for Bayes factors can also be obtained using the method of Bayes factors based on test statistics (Johnson 2005, 2008) by assuming a prior for the test statistic values and treating the test statistic as data. However, here we use a prior for the effect being tested (i.e., the log-odds ratio at the causal locus), rather than a prior for the test statistic (a statistic at the marker locus), and our approximate Bayes factors are based on an asymptotic normal approximation to the posterior.
In the Results section we show retrospective power calculations for associations from several previous studies, including power of case–control studies for detecting the APOE locus for Alzheimer’s disease and the Wellcome Trust Case Control Consortium (2007) GWAS SNP associations. Power curves for a range of values of minor allele frequency, odds ratio, and allele frequency are shown graphically. R functions have been written to enable users to carry out the power calculations without needing to understand the technical details. R examples are shown in Appendix B.
Methods
We first derive a generic form for the approximate Bayes factor. The generic approximate Bayes factor is given in terms of a normalized test statistic (Zn), sample size (n), and equivalent number of sample points in the prior (a). We assume biallelic loci. For each genetic model (dominant, recessive, and additive) for a case–control study we solve for the expected value of Zn for the specified size of effect in terms of the log-odds ratio and its standard error, disease prevalence, allele frequencies, and linkage disequilibrium coefficient. For simplicity, we first consider the dominant or recessive models, where the causal locus is observed, deriving the generic form of the Bayes factor (Equation 21).
Further details are given in Appendix A, including derivations for the additive model, expressions for the sampling variance of the odds ratio at the observed locus in terms of the linkage disequilibrium coefficient and allele frequencies, and an expression for a in terms of a prior for the log-odds ratio at the causal locus.
Contingency tables for the observed counts and corresponding row probabilities are shown in Tables 1 and 2, where pij are the probabilities within rows. For the dominant model, X = 0 for genotype aa, and X = 1 for genotypes Aa, AA. For the recessive model, X = 0 for genotypes aa, Aa, and X = 1 for genotype AA. For the additive model, we need to consider 2 × 3 contingency tables (Appendix A).
Table 1. Contingency table for a case–control study with two genotypic classes.
| Counts | |||
|---|---|---|---|
| X = 0 | X = 1 | ||
| Control | n11 | n12 | n1 |
| Case | n21 | n22 | n2 |
Table 2. Row probabilities for a case–control study with two genotypic classes.
| Row probabilities | ||
|---|---|---|
| X = 0 | X = 1 | |
| Control | p11 | p12 |
| Case | p21 | p22 |
The Savage–Dickey density ratio (Dickey 1971) estimate of the Bayes factor for comparing nested models (e.g., H0: θ = 0 vs. H1: θ ≠ 0) is given by the ratio of prior to posterior densities at 0,
| (10) |
where θ is the parameter being tested, and π(θ), g(θ |y) are the prior and posterior distributions for θ. The formula is exact in nested models (i.e., θ = 0 vs. θ ≠ 0) with a common prior for “nuisance parameters” (i.e., parameters not being tested) (not shown), if we integrate over nuisance parameters to obtain π(θ), g(θ |y). The formula is approximate if we condition on nuisance parameters.
In a case–control study the parameter we wish to test is the log-odds ratio. The test statistic and sampling distribution are given by
| (11) |
| (12) |
| (13) |
where
| (14) |
| (15) |
The normalized test statistic and variance are given by
| (16) |
| (17) |
where c is the proportion of controls in the sample.
The generic form of the approximate Bayes factor is calculated as follows. Assume a prior, with information equivalent to a sample points,
| (18) |
The posterior density is given by
| (19) |
and the Bayes factor is given by
| (20) |
| (21) |
Note the following:
In (19) we use zn to represent the observed value of Zn, which is considered fixed in the posterior calculation, but we use Zn in (20) and (21) to represent a random future value.
From (20) it is apparent that the effect of the prior is not negligible asymptotically. It is not recommended to use a noninformative prior, but a = 1, i.e., a prior with information equivalent to a single sample point, is often a good conservative “default”.
From (21), it is apparent that, for fixed a, the Bayes factor for a given p-value [] depends on sample size n and prior information a. As n → ∞, the value of the “noncentrality parameter” () needs to go to infinity (albeit slowly due to the exponential) to maintain a fixed value of B. This is in essence Lindley’s paradox (Lindley 1957). A corollary is that we should use prior information if available. In practice, before considering extremely large sample sizes, smaller experiments should be done (e.g., a series of geometrically increasing sample sizes) in which case prior information would be increasing, e.g., a may be O(n).
When considering linkage disequilibrium (Appendix A), a is replaced by the corresponding value ax at the marker, which is larger, depending on allele frequencies and disequilibrium. Hence, even for the same sample size, Bayes factors and p-values may give different rankings of effects (cf. Ball 2005; Stephens and Balding 2009).
In the absence of prior estimates of location, since the sign of effects is unknown, it is natural to use a symmetric prior centered at 0. Where prior estimates of location are available, such as from a previous study, (19) and (21) can be adjusted accordingly.
The normal prior is convenient and allows a range of prior variances.
Let ZB be the solution to (21) for Zn:
| (22) |
The power is given by
| (23) |
To apply (22) and (23) we need expressions for in terms of η, a. To incorporate linkage disequilibrium between the observed and causal loci, we need expressions for the log-odds ratio (denoted by ηx) at the observed locus in terms of the log-odds ratio (η) at the causal locus. Additionally, we need expressions for a in terms of the prior variance, of η. The required expressions are calculated in terms of the prior variance for η, disease prevalence, linkage disequilibrium coefficients, and allele frequencies at the causal locus in Appendix A. Examples and power curves are shown in the next section. Example power calculations in R are shown in Appendix B.
Results
Example 1: Alzheimer’s/APOE
We consider the APOE locus associated with Alzheimer’s disease (Strittmatter and Roses 1996). This was a previously detected locus that was used to illustrate the potential of a GWAS approach. Previous calculations used simulations (Nielsen and Weir 2001; Ball 2007a, Example 8.6). To illustrate the deterministic power calculations of this article, we reduce to a biallelic locus by amalgamating the low-risk alleles ε2, ε3, reducing the genotypes to aa, Aa, AA corresponding to zero, one, or two copies of the high-penetrance ε4 allele, respectively. Reduced genotype frequencies and penetrances are shown in Table 3.
For the marker SNP2 considered by Nielsen and Weir (2001), the minor allele frequency is P = 0.15 and for the reduced APOE locus the minor allele frequency is q = 0.137. The coefficient of linkage disequilibrium between SNP2 and ε4 is D = 0.0717. The maximum LD for these allele frequencies is Dmax = 0.1164. We calculate the power of detecting the association at the SNP marker locus SNP2 with the observed level of disequilibrium (D = 0.0717) and also at the APOE locus itself (D = Dmax).
Results of power calculations for detecting the APOE–Alzheimer’s association with Bayes factors B = 1, 106 are shown in Table 4. The marker is assumed to be in partial LD (D = 0.0717) similar to SNP2 or in complete LD (D = 0.1164). Despite the large odds ratio, a sample of size n = 200, which had been suggested by the frequentist calculations, is sufficient only for power ≈ 0.5 to detect associations with a Bayes factor 1, while a sample of size of the order of 1000 is necessary to obtain a Bayes factor of 106 with power = 0.8. Despite the odds ratio being much higher for the recessive model, the power is similar to that of the dominant model. For similar odds ratios, power would be much lower for the recessive model (cf. power curves in Figures 5–9 below). Results are qualitatively similar to the results from simulations (Ball 2007a), which indicated a slightly higher sample size of 1200 for power of 0.95 to obtain B = 106.
Table 4. Power () of case–control studies to detect associations between APOE and Alzheimer’s disease with a given Bayes factor.
| Model | D | D′ | na | B | |
|---|---|---|---|---|---|
| Additive | 0.0717 | 0.61 | 100 | 1.0 | 0.83 |
| 0.1164 | 1.00 | 100 | 1.0 | 0.94 | |
| 0.0717 | 0.61 | 200 | 1.0 | 0.96 | |
| 0.1164 | 1.00 | 200 | 1.0 | 0.998 | |
| 0.0717 | 0.61 | 1000 | 106 | 0.96 | |
| 0.1164 | 1.00 | 1000 | 106 | 0.999 | |
| Dominant | 0.1164 | 1.00 | 100 | 1.0 | 0.70 |
| 0.1164 | 1.00 | 200 | 1.0 | 0.93 | |
| 0.1164 | 1.00 | 800 | 106 | 0.999 | |
| Recessive | 0.1164 | 1.00 | 100 | 1.0 | 0.50 |
| 0.1164 | 1.00 | 200 | 1.0 | 0.76 | |
| 0.1164 | 1.00 | 800 | 106 | 0.999 |
n = ncases + ncontrols.
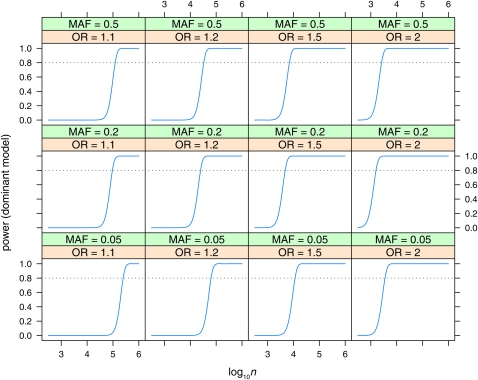
Figure 5 .
Power to detect effects in the dominant model with Bayes factor B = 106. Power is plotted vs. sample size (log10n) for various values of minor allele frequency (MAF = 0.05, 0.2, 0.5) and odds ratio (OR = 1.1, 1.2, 1.5, 2). Linkage disequilibrium is assumed to be the maximum possible for the given allele frequencies (D′ = 1).
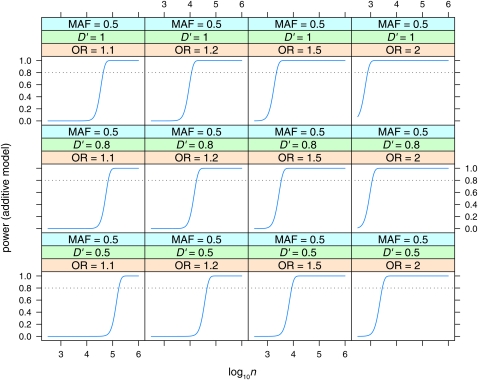
Figure 9 .
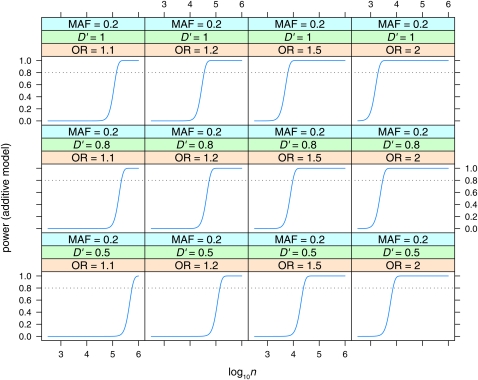
Power to detect effects in the additive model with Bayes factor B = 106. Power is plotted vs. sample size (log10n) for MAF = 0.5, for various values of linkage disequilibrium (D′ = 0.5, 0.8, 1) and odds ratio (OR = 1.1, 1.2, 1.5, 2).
Note that the odds ratio for the additive model is the increase in odds per copy of the risk allele (Q), or the square root of the increase from qq to QQ, while the odds ratio for the dominant or recessive model is the full increase in odds ratio from qq to QQ.
Example 2: Wellcome Trust Case–Control Consortium SNPs
P-values, odds ratios, and approximate Bayes factors for three Wellcome Trust Case–Control Consortium (WTCCC) loci are shown in Table 5. The diseases are rheumatoid arthritis (RA) and Crohn’s disease (CD). The very low p-value for SNP rs6679677 corresponds to a very large Bayes factor: >2.1 × 1022. Evidence for the other two effects with p-values around the WTCCC threshold of 5 × 10−7 while quite strong (B > 1000) is not enough to overcome the low prior odds for associations (e.g., B > 106), unless there is other evidence or prior knowledge.
Table 5. p-values, odds ratios, and approximate Bayes factors for 3 WTCCC loci (3 of ∼24 reported).
| Disease | Locus | SNP | Trend P | ORhet | ORhom | MAF | Ba |
|---|---|---|---|---|---|---|---|
| RA | 7q32 | rs11761231 | 3.9 × 10−7 | 1.44 | 1.64 | 0.370 | 5488 |
| RA | 1p13 | rs6679677 | 4.9 × 10−26 | 1.98 | 3.32 | 0.096 | 2.1 × 1022 |
| CD | 10q21 | rs10761659 | 1.7 × 10−6 | 1.23 | 1.55 | 0.460 | 1329 |
Approximate Bayes factor (Equation 21) with a = 1, n = 5000.
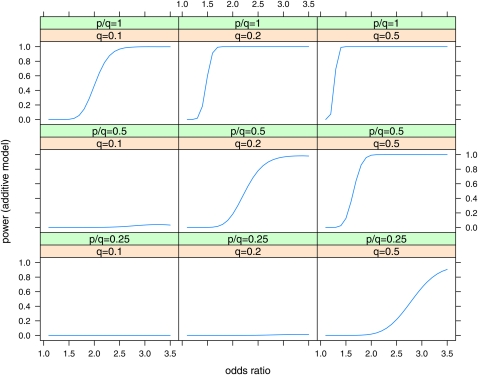
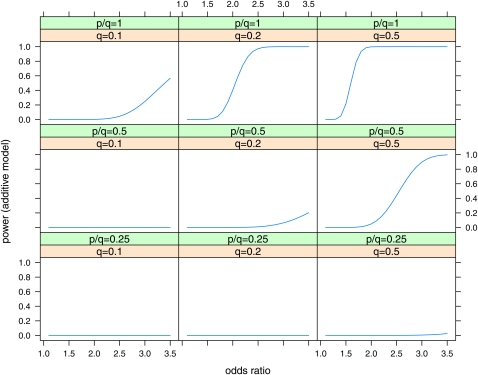
Plots of power vs. odds ratio for the Wellcome Trust Case Control Consortium (2007) case–control studies are shown in Figure 2 for the effects at maximum LD (D′ = 1) and in Figure 3 for D′ = 0.5 for effects at half the maximum LD (D′ = 0.5). The size of the odds ratio that can be detected with power 0.8 is shown in Table 6. While effects with odds ratio (OR) = 1.3 are detectable at the maximum LD with P = q = 0.5, the detectable odds ratios increase substantially at lower LD, lower q, and lower p/q.
Figure 2 .
Power of case–control studies with ncases = 2000, ncontrols = 3000 to detect effects in the additive model with a Bayes factor B = 106. Power is plotted vs. odds ratio for various values of minor allele frequency at the causal locus (q = 0.1, 0.2, 0.5) and ratio of minor allele frequency at the marker to minor allele frequency at the causal locus (p/q = 0.25, 0.5, 1). Linkage disequilibrium is assumed to be the maximum possible for the given allele frequencies (D′ = 1).
Figure 3 .
Power of case–control studies with ncases = 2000, ncontrols = 3000 to detect effects in the additive model with a Bayes factor B = 106. Power is plotted vs. odds ratio for various values of minor allele frequency at the causal locus (q = 0.1, 0.2, 0.5) and ratio of minor allele frequency at the marker to minor allele frequency at the causal locus (p/q = 0.25, 0.5, 1). Linkage disequilibrium is assumed to be half the maximum possible for the given allele frequencies (D′ = 0.5).
Table 6. Minimum odds ratio detectable with power = 0.5, 0.8 to obtain a Bayes factor B ≥ 103, 106 in case–control studies with ncases = 2000, ncontrols = 3000, for the additive model.
| B = 1000 | B = 106 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| D′ = 0.5 | D′ = 1 | D′ = 0.5 | D′ = 1 | ||||||
| q | p/q | = 0.5 | = 0.8 | = 0.5 | = 0.8 | = 0.5 | = 0.8 | = 0.5 | = 0.8 |
| 0.5 | 1.00 | 1.45 | 1.56 | 1.22 | 1.27 | 1.61 | 1.72 | 1.27 | 1.34 |
| 0.2 | 1.00 | 1.78 | 1.96 | 1.37 | 1.45 | 2.05 | 2.25 | 1.48 | 1.57 |
| 0.1 | 1.00 | 2.68 | 3.12 | 1.76 | 1.93 | 3.39 | a | 2.02 | 2.22 |
| 0.5 | 0.50 | 2.14 | 2.42 | 1.50 | 1.60 | 2.59 | 2.89 | 1.67 | 1.79 |
| 0.2 | 0.50 | 3.16 | a | 1.91 | 2.13 | a | a | 2.26 | 2.54 |
| 0.1 | 0.50 | a | a | a | a | a | a | a | a |
| 0.5 | 0.25 | a | a | 2.34 | 2.68 | a | a | 2.87 | 3.28 |
| 0.2 | 0.25 | a | a | a | a | a | a | a | a |
| 0.1 | 0.25 | a | a | a | a | a | a | a | a |
Minimum detectable odds ratio is shown for various values of minor allele frequency at the causal locus (q = 0.1, 0.2, 0.5) and ratio of minor allele frequency at the marker to minor allele frequency at the causal locus (p/q = 0.25, 0.5, 1) and linkage disequilibrium (D′ = 0.5, 1).
Minimum OR > 3.5.
In contrast, Wellcome Trust Case Control Consortium (2007, p. 662) claimed “The power of this study … averaged across SNPs with minor allele frequencies above 5% is estimated to be 43% for alleles with a relative risk of 1.3 increasing to 80% for a relative risk of 1.5, for a p-value threshold of 5 × 10−7. ”
On the face of it this suggests the study can detect effects with minor allele frequency (MAF) > 5%; however, alleles at MAF = 5% are included in an average over a population of alleles at higher frequencies. Moreover, this population of SNPs may not be representative of actual causal loci (cf. Yang et al. 2010).
The power to detect effects when the MAF is actually 5% is shown in Table 7. For the dominant model, effects with relative risk r = 1.3 are detected only with ≈ 0.5 with Bayes factor B = 1. Good power at higher Bayes factors is obtained only for the higher values of relative risk, e.g., r = 2.0 for = 0.98 for B = 106.
Table 7. Power of case–control studies with ncases = 2000, ncontrols = 3000 to detect effects in the dominant model with minor allele frequency of 0.05, with Bayes factors B ≥ 1000, 106 for various values of relative risk (r), at maximum LD (D = Dmax = 0.0475).
| r | OR | B = 1 | B = 1000 | B = 106 |
|---|---|---|---|---|
| 1.3 | 1.34 | 0.61 | 0.06 | 2.5 × 10−3 |
| 1.5 | 1.58 | 0.99 | 0.67 | 0.20 |
| 2.0 | 2.25 | 1.00 | 1.00 | 0.98 |
| 2.5 | 3.00 | 1.00 | 1.00 | 1.00 |
Odds ratios (OR) were calculated from relative risk assuming a baseline risk q0 = 0.1.
Note that at low allele frequencies and high odds ratios the odds ratio estimator (Equations 11 and A6) may be inefficient, particularly for the additive model, due to small probabilities in the denominator. For the additive model, the genotypes Aa, AA (or Qq, QQ) can be amalgamated (assuming A is the low-frequency allele), giving a more efficient estimator. Since the genotype AA is at a low frequency (2.5 × 10−3), this is approximately equivalent to the dominant model with the same odds ratio.
Example 3: WTCCC CNVs
Wellcome Trust Case Control Consortium (2010) tested 3432 copy number variant (CNV) polymorphisms for associations with eight diseases in the Wellcome Trust Case Control Consortium (2007) case–control population. Of the 12 replicated associations (Wellcome Trust Case Control Consortium 2010, Table 2) reported, 6 were from the HLA region. Some of these had very high Bayes factors, but, given the high LD in the HLA region these cannot definitively be attributed to a CNV. Two others were from the IRGM locus used as a positive control.
Bayes factor calculations for 3 of the 12 (non-HLA, non-IRGM) “replicated” CNV associations from Wellcome Trust Case Control Consortium (2010, Table 2) are shown in Figure 4. The diseases are RA, type I diabetes (T1D), and type II diabetes (T2D). Since Bayes factors were already given, we set the value of the prior variance parameter, a, in the generic Bayes factor (Equation 21) so that the approximate Bayes factors agreed with those published (except for the T2D association where a much higher value of a was indicated, so we used a value of a = 28, similar to the other two associations), used the same value of a in calculating the Bayes factor for the replication (p-value only published), and then calculated a combined Bayes factor as the product of the original Bayes factor and the Bayes factor from the replication.
Figure 4 .
Combined Bayes factor calculations for three Wellcome Trust Case Control Consortium (2010) CNVs.
The highest combined Bayes factor for the non-HLA, non-IRGM loci was ∼13,000. Thus, even after replication, there were no new associations definitively attributable to CNVs, with Bayes factors high enough to obtain respectable posterior odds.
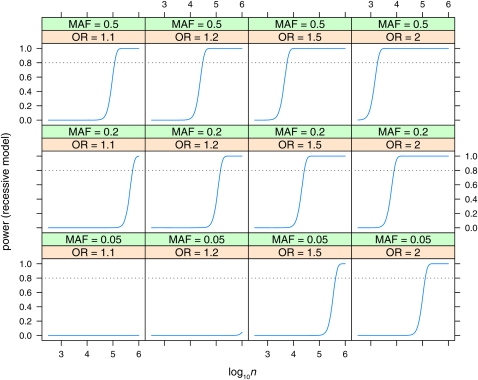
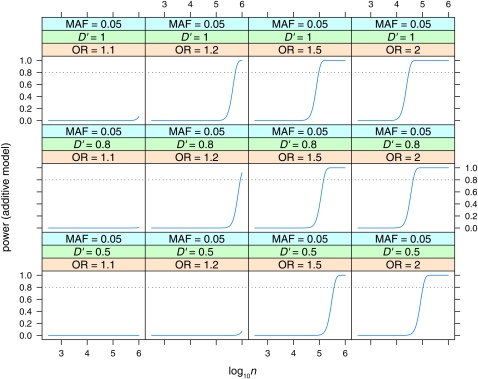
Power curves
Power is plotted vs. sample size (log10n, n = ncases + ncontrols) for the dominant (Figure 5), recessive (Figure 6), and additive (Figure 7, Figure 8, and Figure 9) models. Power is plotted at the maximum LD for the given allele frequencies (D′ = 1), for various values of odds ratio and minor allele frequencies, for the dominant and recessive models. For the additive model the effect of various values of LD (D′ = 0.5, 0.8, 1) is also shown. As expected, power increases with increasing n, and odds ratio, and decreases with decreasing D′. Power is low at lower allele frequencies, particularly for the recessive model; e.g., n = 100,000 is required to detect an effect with OR = 2 when the minor allele frequency is at 0.05. A sample size approaching n = 100,000 is also required to detect the lower odds-ratio effects (OR = 1.1) even at intermediate allele frequencies. Even at maximum LD, recessive effects at low allele frequencies (MAF = 0.05) and lower odds ratios are not detectable even with n = 106.
Figure 6 .
Power to detect effects in the recessive model with Bayes factor B = 106. Power is plotted vs. sample size (log10n) for various values of minor allele frequency (MAF = 0.05, 0.2, 0.5) and odds ratio (OR = 1.1, 1.2, 1.5, 2). Linkage disequilibrium is assumed to be the maximum possible for the given allele frequencies (D′ = 1).
Figure 7 .
Power to detect effects in the additive model with Bayes factor B = 106. Power is plotted vs. sample size (log10n) for MAF = 0.05, for various values of linkage disequilibrium (D′ = 0.5, 0.8, 1) and odds ratio (OR = 1.1, 1.2, 1.5, 2).
Figure 8 .
Power to detect effects in the additive model with Bayes factor B = 106. Power is plotted vs. sample size (log10n) for MAF = 0.05, for various values of linkage disequilibrium (D′ = 0.5, 0.8, 1) and odds ratio (OR = 1.1, 1.2, 1.5, 2).
Discussion
The goal of GWAS to understand the genetics of quantitative traits and complex diseases and to predict the phenotypes has not yet been achieved. To date, only a small percentage of the variation has been explained by putative SNP associations.
We have demonstrated, with conservative assumptions, the sample size required to detect SNP effects with respectable posterior probabilities. We have derived power calculations for the power as a function of sample size, effect size, allele frequencies, linkage disequilibrium between marker and causal locus, and Bayes factor required. The number of markers required depends on the extent of linkage disequilibrium and genome size. The Bayes factor required depends on the expected number of causal loci.
We have seen that much larger sample sizes may be needed, particularly with lower allele frequencies, disparate allele frequencies between markers and causal loci, incomplete LD, and/or recessive inheritance. Lack of power to detect such effects may explain the large unexplained variance—the so-called “dark matter in the genome”, from GWAS to date.
Although the proportion of variance explained by putative loci to date is small, a model with random SNP effects explains nevertheless ∼50% of the variance in human height (Yang et al. 2010). Yang et al. showed, by simulations, that [as was known from power calculations (Ball 2004, 2005)], if the set of causal loci were at lower minor allele frequencies than the set of SNPs used, the proportion of variance explained decreases. Extrapolating from the variance explained by current SNPs, they showed that the random-effects model could potentially explain all the additive genetic variance for human height, hence explaining the “dark matter” in the genome. Their simulations consider the regression of genetic covariance (Gij) for the causal loci on that for the SNP loci (Aij). This rests on the statement “The effects of the SNPs are treated statistically as random, and the variance explained by all the SNPs together is estimated. This approach … does not attempt to test the significance of individual SNPs but provides an unbiased estimate of the variance explained by the SNPs in total” (Yang et al. 2010, p. 565).
However, accuracy of predictions on independent data was not demonstrated. When fitting a large number of random SNP effects, the “variance explained” is not necessarily attributable to individual causal loci in LD with the SNPs. The variance explained by the random-effects model pertains to the data to which the model is fitted and not to predictions on independent samples. Although close relatives were removed, the random-effects model, with large numbers of SNPs (many more than population sample points), may nevertheless be detecting relatedness between individuals. Despite a high variance explained, the model may nevertheless have poor predictive accuracy (possibly less than due to putative associations found from GWAS to date) on independent individuals in a diverse population.
The extent of linkage disequilibrium (effective population size) is critical to the efficacy of the random-effects model. In an animal population of low effective population size reasonable prediction accuracy may be obtained, reflecting the regression of Gij on Aij. In such a population it is not necessary to detect the marker closest to a causal locus; rather, the effect would be shared among markers in a region, giving an effective increase in power. In contrast, in a diverse human population (with a fairly small number of markers within extent of LD of a given locus), the additive variance Aii itself may be low, e.g., if there were a relatively small number of causal loci poorly tagged by the SNPs (due to low power). Moreover, the actual distribution of SNP effect sizes may be quite different from the random-effects model assumptions, in which case the random-effects model theory would not apply.
Without sufficient power and high enough Bayes factors, a number of putative associations may not be robustly detected. They may be spurious and/or their effects overestimated. The good news is that this means there may still be large-effect SNPs of moderate to low MAF remaining to be discovered.
Replication is important, but replication by itself does not imply effects are “real”. Even after replication, the evidence still needs to be quantified, e.g., in terms of Bayes factors and posterior probabilities. The need to quantify evidence after replication is exemplified by the Wellcome Trust Case Control Consortium (2010) CNVs, where, after excluding the high-LD HLA region and the positive control locus IRGM, no new CNVs with combined Bayes factors B ≥ 14,000 were found from >24,000 disease–CNV associations tested.
The reader may have noted the appearance of similar quantities in Bayes factor calculations to frequentist calculations. For example, the classical F-statistic in the Spiegelhalter and Smith (1982) Bayes factor and in the factor in the exponent of the expression for the approximate Bayes factor (Equation 21) is similar to the noncentrality parameter in the chi-square test. Where the likelihood is characterized by a sufficient statistic, this statistic will feature in both the Bayes factors and the frequentist statistics. This does not, however, mean that the Bayesian and frequentist approaches are equivalent. The statistic values and interpretation are different.
We have seen there are substantial differences between frequentist and Bayesian methods in interpretation of evidence and sample sizes required. What threshold to use is unresolved in the frequentist domain and is likely to remain so because the threshold needed for a given Bayes factor depends on sample size and allele frequencies.
Experimentwise thresholds can be computed with permutation tests; however, there is no reason an experimentwise threshold should apply. We are not searching for a single effect vs. no effect; rather, we are searching for the set of causal loci, of which there are expected to be a number. Hence, although testing single markers along the genome involves multiple tests, the problem of determining which set of loci is causal is, intrinsically, a model selection problem. This has been considered in the QTL mapping context (Ball 2001; Sillanpää and Corander 2002), where LD is generated by recombinations within a family. The same considerations apply in association studies when LD is generated in a population. The “model” is a regression on the set of causal loci, or nearby markers, and probabilities need to be evaluated for alternative models. Typically many models are consistent with the data. In association studies the method is best applied to a “window” of markers corresponding roughly to the extent of linkage disequilibrium.
An alternative to using p-values is the false discovery rate (Benjamini and Hochberg 1995). This is preferable since we are interested in the probability that effects are real. However, the false discovery rate (FDR) is in essence a poor man’s posterior probability—the false discovery rate (modulo complexities of “estimating the prior” and assumptions) is an estimate of 1 minus the average posterior probability for a set of effects. Like p-values, the FDR can be misleading in that the posterior probability for effects near the threshold will be considerably lower than the average. Moreover, it is suboptimal to replace the individual posterior probabilities by the average: individual posterior probabilities for effects below the threshold will differ; hence the effects are not a posteriori exchangeable, and the individual posterior probabilities contain more information. According to Fisher (1959, p. 55), we must use all the information.
Dudbridge and Gusnato (2008) estimate the equivalent number of independent tests and propose adjusting for this number of multiple comparisons. This quantity is comparable to the total number of markers here since we consider marker spacing comparable to the extent of linkage disequilibrium. When there are substantially more markers, the natural generalization is to consider the power of detecting an association with one or more markers within a window of size comparable to the extent of linkage disequilibrium. Since there may be a number of markers in the window putatively associated with the trait, the analysis would necessarily use a multilocus approach (e.g., Ball 2001), estimating the posterior probability of all models with one or more markers in the window. Developing power calculations for this scenario is a topic for future research; however, we anticipate only a moderate increase in power for dense markers compared to markers spaced at about the extent of linkage disequilibrium, with most of the increase in power coming from a higher probability of a marker being near maximum LD (D′ = 1) with a QTL.
It has been stated that a “naive” Bayesian analysis would be similar to a frequentist analysis (Dudbridge and Gusnato 2008). This may be the case for estimation where estimates with a noninformative prior are similar to frequentist maximum-likelihood estimates. This is not the case for inference, where we need the probability that an effect is real, where it does not make sense to use a noninformative prior. The use of p-values is anticonservative; e.g., the use of the conditional α (αc) (Sellke et al. 2001) is more conservative than using α, and the use of the Bayes factor (Equation 21) with a = 1 is more conservative than using αc in (9).
This use of lower and lower thresholds in frequentist GWAS analyses represents a use of prior knowledge, e.g., based on experience from studies, e.g., considering what was “detected” and what previously reported associations were spurious with previous thresholds. This use of prior knowledge by frequentists is interesting, given that the frequentist rationale for using frequentist rather than Bayesian methods is to avoid use of prior distributions to be “objective”. Unlike Bayesian methods, this use of prior knowledge is not transparent and probably inefficient.
Part of the power calculation involves the prior number of causal effects and the sizes of effects, which are unknown. Nevertheless there is prior information. Since the heritability of the traits of interest is generally known, the number of effects greater than a given size can be bounded—e.g., if the heritability is 10%, there can be at most 10 loci each explaining ≥1% of the variance. At the same time, effects less than a detectable size in the given experiment can and should be neglected. Considering the size of effects detected in previous smaller studies and the power of these studies gives an upper bound on the size of effects, at least for similar minor allele frequencies.
Furthermore, prior information on effect sizes will be and is emerging as more results become available. Prior information can be obtained from other studies, e.g., of other traits or populations. Prior information can also be elicited from “experts”. Prior elicitation is an important but relatively neglected area (O’Hagan et al. 2006). Experts may consider evidence from similar or related experiments, traits, and populations; from bio-informatics; and from known gene-pathway relationships, etc. How much weight to give each type of evidence is, like any judgment, inevitably subjective (cf. Berger and Berry 1988). This sort of prior information is currently used by readers of journal articles—if there is a plausible biological explanation for an effect, it tends to be believed. Just how much weight is being given to prior information in such circumstances is, however, unclear.
We recommend interpreting results with posterior probabilities (shades of gray), rather than as significant or nonsignificant on the basis of a threshold, and using posterior probabilities as a basis for making a decision, using Bayesian decision theory (e.g., De Groot 1970; Ball 2007b). In decision theory, the expected utility (benefit) of any decision (e.g., to replicate or not to replicate or to carry out map-based cloning or functional testing) is the average over the posterior distribution of the benefit for given values of parameters. The optimal decision is the one that gives the maximum expected utility. Even if the Bayes factor is not high enough to give high posterior odds, an effect may be worth following up.
Effects without strong enough evidence to give respectable posterior odds (e.g., ≥0.8) include published effects with p-values near the thresholds of 5 × 10−7. A Bayes factor of the order of 106 is required for respectable posterior odds. Effects near the threshold, with Bayes factors of the order of 1000, require further evidence, e.g., replication and/or justification for higher prior odds before we believe they are probably real. For example, B ≥ 1000 in a genome scan may yield a posterior probability of 1/50 for an effect that would be worth following up, if the expected benefits, assuming the effect is real, are >50 times the cost of follow-up. Bayes factors B ≥ 1000 obtained in both the genome scan and replicate studies should (conservatively) combine to give B ≥ 106 and hence respectable posterior odds in the scenario above (Figure 1). Calculations using (21) with a = 1 (not shown) show that even the current de facto standard of 5 × 10−8 does not correspond to Bayes factors >105 for sample sizes >1000. For sample sizes of 100,000 as in recent meta-analyses of human height (Gudbjartsson et al. 2008; Lettre et al. 2008; Visscher 2008; Weedon et al. 2008) a threshold of 3.9 × 10−10 would be needed to obtain a Bayes factor of 106.
The scenario in Figure 1 is, of course, not the only possibility. A higher extent of linkage disequilibrium would result in lower Bayes factors being needed, while higher Bayes factors and more markers would be needed for a more diverse African population. Lower Bayes factors may be needed if there was more prior information either on the size of possible effects or on their number. Candidate genes mapping into QTL regions may have higher prior probability (Ball 2007b).
R functions for the calculations used in this article will be made available in a future version of the R package ldDesign (Ball 2004).
Acknowledgments
The author thanks Tony Merriman, Peter Visscher, and Bruce Weir for useful comments. This work was funded by a grant from the New Zealand Foundation for Research, Science, and Technology to the New Zealand Virtual Institute of Statistical Genetics through a contract with the New Zealand Forest Research Institute Limited (trading as Scion).
Appendix A: Equations for Dominant, Recessive, and Additive Models Allowing for LD
To incorporate LD, consider biallelic marker and causal loci with allele frequencies 1 − q, q for alleles {a, A}, and 1 − p, p for alleles {q, Q}, respectively. Denote the row probabilities at the observed (marker) locus and causal locus by pij, qij, respectively (cf. Table 2 or for the additive model Table A2 below). Let D denote the linkage disequilibrium coefficient such that
| (A1) |
To distinguish between the marker and the causal locus let ηx denote the log-odds ratio at the marker locus and η the log-odds ratio at the causal locus. Similarly let ax, a denote the prior equivalent sample size at the observed and causal loci, respectively. When incorporating LD, the Bayes factor and power calculations are based on the estimates and standard errors at the observed locus, as above, but the assumed true effect size (log-odds ratio) and prior values are at the causal locus.
We assume a prior for η is given as
| (A2) |
Recall that is n times the sampling variance of the estimated log-odds ratio (Equation 16). If we wish to specify the prior in terms of the equivalent sample size, then
| (A3) |
and
| (A4) |
so that
| (A5) |
Since we still use the estimated log-odds ratio at the marker locus, our estimated odds ratio is still the same as (11) above; i.e.,
| (A6) |
| (A7) |
for the dominant or recessive models.
Expressions for , and involve the cell probabilities pij. To solve for the Bayes factors these will be expressed in terms of qij, which in turn will be solved for in terms of prevalence (ν), baseline risk (q0), and relative risk (r),
| (A8) |
| (A9) |
where the prevalence and baseline risk are related by
| (A10) |
and the log-odds ratio and relative risk are related by
| (A11) |
The prior variance for ηx is related to that for η by
| (A12) |
To incorporate LD into the power calculations (Equations 22 and 23) we need expressions for , and ax. For the dominant or recessive models these are given in terms of pij by Equations 11 and 16 with η replaced by ηx together with (A5). For the additive model these are given in terms of pij by (A46)–(A48) below together with (21)–(23) and (A5). To determine ax we also need to solve for (Equations A5 and A12). The partial derivatives will be taken regarding q0 as a function of r, given implicitly by (A10), with ν regarded as fixed. This also uses the partial derivative of η with respect to r given by
| (A13) |
The required equations for each model are given in the following subsections.
Equations for the Dominant Model with LD
Dominant model, expression for the partial derivative
| (A14) |
and hence
| (A15) |
Dominant model, equations for pij
| (A16) |
| (A17) |
| (A18) |
| (A19) |
Dominant model, equations for qij
| (A20) |
| (A21) |
| (A22) |
| (A23) |
Dominant model, equation for q0 in terms of q,r
| (A24) |
The partial derivatives can be read from the coefficients of qij in (A16)–(A19).
Dominant model, partial derivatives qij/r
| (A25) |
| (A26) |
| (A27) |
| (A28) |
Dominant model, partial derivative
| (A29) |
Equations for the Recessive Model with LD
Recessive model, expression for the partial derivative
| (A30) |
and hence
| (A31) |
Recessive model, equations for pij
| (A32) |
| (A33) |
| (A34) |
| (A35) |
Recessive model, equations for qij
| (A36) |
| (A37) |
| (A38) |
| (A39) |
Recessive model, equation for q0 in terms of q,r
| (A40) |
The partial derivatives can be read from the coefficients of qij in (A32)–(A35).
Recessive model, partial derivatives qij/r
| (A41) |
| (A42) |
| (A43) |
| (A44) |
Recessive model, partial derivative q0/r
| (A45) |
Equations for the Additive Model with LD
For the additive model (additive on the log-odds-ratio scale) we have the 2 × 3 contingency tables (Table A1 and Table A2).
Table A1. Contingency table for a case–control study with three genotypic classes.
| Counts | ||||
|---|---|---|---|---|
| aa | Aa | AA | Total | |
| Control | n11 | n12 | n13 | n1 |
| Case | n21 | n22 | n23 | n2 |
Table A2. Row probabilities for a case–control study with three genotypic classes.
| Row probabilities | |||
|---|---|---|---|
| aa | Aa | AA | |
| Control | p11 | p12 | p13 |
| Case | p21 | p22 | p23 |
For the additive model, let ηx be the log-odds ratio for aa vs. Aa. By assumption this is the same as the odds ratio for Aa vs. AA. Averaging the estimates for these two comparisons gives
| (A46) |
| (A47) |
where the terms in p12, p22 cancel, and
| (A48) |
Note that for low allele frequencies the estimator (A46) may be inefficient due to low probabilities for the genotype AA. Our software uses a weighted average of the two odds ratios, where the weighting is chosen to maximize the noncentrality parameter.
Additive model, expression for the partial derivative
| (A49) |
and hence
| (A50) |
Additive model, equations for pij
| (A51) |
| (A52) |
| (A53) |
| (A54) |
| (A55) |
| (A56) |
Additive model, equations for qij
| (A57) |
| (A58) |
| (A59) |
| (A60) |
| (A61) |
| . | (A62) |
Additive model, equation for q0 in terms of q,r
| (A63) |
The partial derivatives can be read from the coefficients of qij in (A51)–(A56).
Additive model, partial derivatives q0/r
| (A64) |
| (A65) |
| (A66) |
| (A67) |
| (A68) |
| (A69) |
Additive model, partial derivative q0/r
| (A70) |
Appendix B: Example Power Calculations Using ldDesign
Literature Cited
- Altshuler D., Hirschhorn J. N., Klannemark M., Lindgren C. M., Vohl M.-C., et al. , 2000. The common PPARγ Pro12Ala polymorphism is associated with decreased risk of type 2 diabetes. Nat. Genet. 26: 76–80 [DOI] [PubMed] [Google Scholar]
- Ball R. D., 2001. Bayesian methods for quantitative trait loci mapping based on model selection: approximate analysis using the Bayesian information criterion. Genetics 159: 1351–1364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball R. D., 2004. ldDesign—Design of experiments for detection of linkage disequilibrium. Available at: http://cran.r-project.org/web/packages/ldDesign/index.html. Accessed November 2, 2011
- Ball R. D., 2005. Experimental designs for reliable detection of linkage disequilibrium in unstructured random population association studies. Genetics 170: 859–873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball R. D., 2007a. Statistical analysis and experimental design, pp. 133–196 Association Mapping in Plants, edited by Oraguzie N. C., Rikkerink E. H. A., Gardiner S. E., DeSilva H. N. Springer-Verlag, New York [Google Scholar]
- Ball R. D., 2007b. Quantifying evidence for candidate gene polymorphisms—Bayesian analysis combining sequence-specific and QTL co-location information. Genetics 177: 2399–2416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y., 1995. Controlling the false discovery rate a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57: 159–165 [Google Scholar]
- Berger J., Berry D., 1988. Statistical analysis and the illusion of objectivity. Am. Sci. 76: 159–165 [Google Scholar]
- De Groot M. H., 1970. Optimal Statistical Decisions. McGraw-Hill, New York [Google Scholar]
- Diabetes Genetics Initiative of Broad Institute of Harvard and MIT, 2007. Genome-wide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science 316: 1331–1336 [DOI] [PubMed] [Google Scholar]
- Dickey J. M., 1971. The weighted likelihood ratio, linear hypothesis on normal location parameters. Ann. Math. Stat. 42: 204–223 [Google Scholar]
- Dudbridge F., Gusnato A., 2008. Estimation of significance thresholds for genomewide association scans. Genet. Epidemiol. 32: 227–234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emahazion T., Feuk L., Jobs M., Sawyer S. L., Fredman D., et al. , 2001. SNP association studies in Alzheimer’s disease highlight problems for complex disease analysis. Trends Genet. 17: 407–413 [DOI] [PubMed] [Google Scholar]
- Fisher R. A. 1959. Statistical Methods and Scientific Inference, Ed. 2 Oliver and Boyd, Edinburgh and London [Google Scholar]
- Gudbjartsson D. F., Walters G. B., Thorleifsson G., Stefansson H., Halldorsson B. V., et al. , 2008. Many sequence variants affecting diversity of adult human height. Nat. Genet. 40: 609–615 [DOI] [PubMed] [Google Scholar]
- Hindorff L., Junkins H., Hall P., Mehta J., Manolio T., 2011. A Catalog of Published Genome-Wide Association Studies. Available at: http://www.genome.gov/gwastudies. Accessed: May 16, 2011
- Johnson V., 2005. Bayes factors based on test statistics. J. R. Stat. Soc. Ser. B Stat. Methodol. 67: 689–701 [Google Scholar]
- Johnson V., 2008. Properties of Bayes factors based on test statistics. Scand. J. Stat. 35: 354–368 [Google Scholar]
- Lango Allen H., Estrada K., Lettre G., Berndt S. I., Weedon M. N., et al. , 2010. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature 467: 832–838 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lettre G., Jackson A. U., Geiger C., Schumacher F. R., Berndt S., et al. , 2008. Identification of ten loci associated with height highlights new biological pathways in human growth. Nat. Genet. 40: 584–591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindley D. V., 1957. A statistical paradox. Biometrika 44: 187–192 [Google Scholar]
- Luo Z. W., 1998. Linkage disequilibrium in a two-locus model. Heredity 80: 198–208 [DOI] [PubMed] [Google Scholar]
- Menashe I., Rosenberg P., Chen B., 2008. PGA: power calculator for case-control genetic association analyses. BMC Genet. 9: 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller A., 1990. Subset Selection in Regression (Monographs on Statistics and Applied Probability 40) Chapman & Hall, London [Google Scholar]
- Nielsen D., Weir B., 2001. Association studies under general disease models. Theor. Popul. Biol. 60: 253–263 [DOI] [PubMed] [Google Scholar]
- O’Hagan A., Buck C., Daneshkhah A., Eiser J. R., Garthwaite P. H., et al. , 2006. Uncertain Judgements: Eliciting Experts’ Probabilities. Wiley, Hoboken, NJ [Google Scholar]
- Purcell S., Cherny S. S., Sham P. C., 2003. Genetic Power Calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics 19: 149–150 Available at: http://pngu.mgh.harvard.edu/∼purcell/gpc/cc2.html. Accessed: November 2, 2011 [DOI] [PubMed] [Google Scholar]
- Sellke T., Bayarri M. J., Berger J. O., 2001. Calibration of p-values for testing precise null hypotheses. Am. Stat. 55: 62–71 [Google Scholar]
- Sillanpää M. J., Corander J., 2002. Model choice in gene mapping: what and why. Trends Genet. 18: 301–307 [DOI] [PubMed] [Google Scholar]
- Spiegelhalter D., Smith A. F. M., 1982. Bayes factors for linear and log-linear models with vague prior information. J. R. Stat. Soc. B 44(3): 377–387 [Google Scholar]
- Stephens M., Balding D. J., 2009. Bayesian statistical methods for association studies. Nat. Rev. Genet. 10: 681–690 [DOI] [PubMed] [Google Scholar]
- Strittmatter W., Roses A., 1996. Apolipoprotein E and Alzheimer’s disease. Annu. Rev. Neurosci. 19: 53–77 [DOI] [PubMed] [Google Scholar]
- Terwilliger J., Weiss K., 1998. Linkage disequilibrium mapping of complex disease: Fantasy or reality? Curr. Opin. Biotechnol. 9: 578–594 [DOI] [PubMed] [Google Scholar]
- Visscher P., 2008. Sizing up human height variation. Nat. Genet. 40: 489–490 [DOI] [PubMed] [Google Scholar]
- Wakefield J., 2007. A Bayesian measure of the probability of false discovery in genetic epidemiology studies. Am. J. Hum. Genet. 81: 208–227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weedon M., Lango H., Lindgren C., Wallace C., Evans D., et al. , 2008. Genome-wide association analysis identifies 20 loci that influence adult height. Nat. Genet. 40: 575–583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellcome Trust Case Control Consortium, 2007. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447: 661–678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellcome Trust Case Control Consortium, 2010. Genome-wide association study of CNVs in 16,000 cases of eight common diseases and 3,000 shared controls. Nature 464: 713–722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Beben B., McEvoy D., Gordon S., Henders A., et al. , 2010. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 42: 565–569, 608 [DOI] [PMC free article] [PubMed] [Google Scholar]