Quantitative Trait Locus Analysis of Stage-Specific Inbreeding Depression in the Pacific Oyster Crassostrea gigas

Abstract

Inbreeding depression and genetic load have been widely observed, but their genetic basis and effects on fitness during the life cycle remain poorly understood, especially for marine animals with high fecundity and high, early mortality (type-III survivorship). A high load of recessive mutations was previously inferred for the Pacific oyster Crassostrea gigas, from massive distortions of zygotic, marker segregation ratios in F₂ families. However, the number, genomic location, and stage-specific onset of mutations affecting viability have not been thoroughly investigated. Here, we again report massive distortions of microsatellite-marker segregation ratios in two F₂ hybrid families, but we now locate the causative deleterious mutations, using a quantitative trait locus (QTL) interval-mapping model, and we characterize their mode of gene action. We find 14–15 viability QTL (vQTL) in the two families. Genotypic frequencies at vQTL generally suggest selection against recessive or partially recessive alleles, supporting the dominance theory of inbreeding depression. No epistasis was detected among vQTL, so unlinked vQTL presumably have independent effects on survival. For the first time, we track segregation ratios of vQTL-linked markers through the life cycle, to determine their stage-specific expression. Almost all vQTL are absent in the earliest life stages examined, confirming zygotic viability selection; vQTL are predominantly expressed before the juvenile stage (90%), mostly at metamorphosis (50%). We estimate that, altogether, selection on vQTL caused 96% mortality in these families, accounting for nearly all of the actual mortality. Thus, genetic load causes substantial mortality in inbred Pacific oysters, particularly during metamorphosis, a critical developmental transition warranting further investigation.

INBREEDING depression, the detrimental fitness consequences associated with consanguineous mating, has been observed for well over a century in domesticated as well as natural populations of plants and animals (Darwin 1876; Charlesworth and Charlesworth 1987; Charlesworth and Willis 2009). In normally outcrossing populations, inbreeding may decrease the mean of metric characters, such as body size, decrease fitness components, such as fecundity and survival, and increase the risk of extinction for small populations (Wright 1977; Charlesworth and Charlesworth 1987, 1999; Hedrick and Kalinowski 2000). Despite the significance of inbreeding depression, much of the foregoing research has focused on population-level differences in trait means, so that details of its genetic basis remain poorly understood. Whether the genetic load underlying inbreeding depression is maintained by dominance, overdominance, or epistasis is still debated, for example. Although many accept dominance as the major cause of inbreeding depression (Roff 2002; Charlesworth and Willis 2009), evidence exists for overdominance (e.g., Mitchell-Olds 1995; Williams et al. 2003) and epistasis (e.g., Li et al. 2001). Why genetic load varies among organisms with different life histories (Lynch and Walsh 1998, Tables 10.4 and 10.6) and why the number of lethal mutations might be uniform among vertebrates that apparently differ in mutation rate, genome size, and number of essential loci (McCune et al. 2002) are fundamental questions that will remain unanswered until detailed studies of the genetic basis of inbreeding depression are carried out in a variety of organisms.

Another aspect of inbreeding depression that bears detailed investigation is its developmental timing. If mutations in early-acting genes tend to be highly detrimental or lethal, as often assumed, and mutations in late-acting genes mildly detrimental, then mating system (inbred vs. outbred) should affect the life stages at which inbreeding depression and natural selection against harmful mutations are manifested. In support of this notion, inbreeding depression is detected in both the very early and late life stages of outcrossing plants but is generally shifted solely to the later stages in selfing plants, because early-acting mutations have been purged (Husband and Schemske 1996; Koelewijn et al. 1999). A similar temporal pattern of inbreeding depression exists in selfing vs. outcrossing species of the ascidian Corella (Cohen 1992). Animals are generally outcrossing, so substantial inbreeding depression is expressed early in development [Drosophila (Rizski 1952; Seto 1954, 1961), the European flat oyster (Bierne et al. 1998), the bluefin killifish (McCune et al. 2002), the snail Physia acuta (Escobar et al. 2008), and the purple sea urchin Stronglyocentrotus purpuratus (Anderson and Hedgecock 2010)]. This pattern of early inbreeding depression might be particularly exaggerated in highly fecund organisms, such as trees (Koelewijn et al. 1999) and the majority of marine animals (Thorson 1950; Winemiller and Rose 1992), because a high mutational load is generated as a by-product of germ-cell division (Williams 1975).

Using a molecular marker-based approach, Launey and Hedgecock (2001) showed that the Pacific oyster Crassostrea gigas carries a large number of highly deleterious, recessive mutations (∼12 per genome), which not only confirmed Williams’s (1975, p. 80) specific prediction of a high genetic load in oysters but also simultaneously explained a suite of long-standing observations about the genetics of bivalve molluscs, including segregation distortion in inbred crosses, heterosis in crosses between inbred lines, and heterozygosity–fitness correlations in the wild (reviewed by Launey and Hedgecock 2001). By comparing marker segregation ratios in the earliest swimming larval stage, which were Mendelian, to those in 2- to 3-month-old juveniles, which were significantly distorted, Launey and Hedgecock (2001) demonstrated conclusively that inbreeding depression was caused by zygotic, genotype-dependent selection against deleterious recessive mutations. Yet, this study left unresolved the number and genome distribution of these mutations, their contribution to mortality, and the timing of their expression during the complex life cycle of the oyster, which comprises a microscopic, free-swimming planktonic larva that metamorphoses into a sessile, benthic, filter-feeding form (Kennedy et al. 1996). Following up on the Materials and Methods of Launey and Hedgecock (2001), Bucklin (2003) showed that these highly deleterious mutations were heritable, not “synthetic lethals” (Dobzhansky 1946), and that individuals homozygous for these mutations died sometime during the larval or early juvenile stages. Unfortunately, temporal sampling in this study was sparse, so details about the expression of deleterious mutations during larval development, metamorphosis, and the juvenile and adult stages remain unknown. Understanding the developmental expression of deleterious alleles is an important step in uncovering the genetic basis of mutational load and should shed light on the causes and consequences of the substantial early mortality of highly fecund marine animals.

In this study, we again examine segregation of microsatellite markers across the genome in F₂ families of the Pacific oyster to characterize deleterious loci responsible for genetic load. Improving upon the single-marker or linked-marker approach used previously (Hedrick and Muona 1990; Launey and Hedgecock 2001), we use a quantitative trait locus (QTL) interval mapping model (Vogl and Xu 2000; Luo and Xu 2003) to integrate all marker segregation information, to localize viability loci of major effect in the Pacific oyster genome, and, with the aid of two-locus models, to characterize the degree of dominance of alleles at these viability loci. In a second, larger part of the study, we determine, for the first time in any nonhuman species, the stage-specific expression of major viability loci. This is accomplished by examining marker segregation ratios in samples taken at subdaily and daily time points during the larval period, at 30 days (juvenile stage), and at 700 days (adult stage) postfertilization. We test whether the timing of viability selection on deleterious alleles is focused on transitions in larval development, from the trochophore to the veliger stage, from the late umbo to the pediveliger stage, or at metamorphosis (Kennedy et al. 1996). Finally, after testing for synergistic interactions between loci in their effect on viability (epistasis), we estimate the total selective mortality attributable to genetic load and examine the magnitude and temporal pattern of mortality associated with inbreeding depression in the Pacific oyster.

Materials and Methods

Biological material and molecular methods

Crosses and culturing:

Families 46, 10, 51, and 35 were established by pair crosses of wild C. gigas from Dabob Bay, Washington, in 1996 (G₀) (Langdon et al. 2003). In 1998, inbred lines (G₁, f = 0.25) were created by a full-sib mating within each of the four families. In 2001, F₁ families 46×10 and 51×35 were produced by pair crosses between inbred lines (sire × dam) (Hedgecock and Davis 2007). In 2004, we crossed full siblings from each of the 46×10 and 51×35 F₁ hybrid families at the University of Southern California (USC), Wrigley Marine Science Center (WMSC) on Catalina Island, California, to produce the F₂ families used in these experiments (f = 0.25 × 1.25 = 0.3125, where 0.25 represents the inbreeding expected from a full-sib mating and the factor 1.25 accounts for inbreeding of the G₁ common ancestors). Gamete collection, fertilization, and standard larval rearing methods for the Pacific oyster follow Breese and Malouf (1975), as detailed in Hedgecock et al. (1996). Pedigrees of these families were verified with microsatellite DNA markers (Hedgecock and Davis 2007).

Sampling:

The study comprised two components: (1) mapping of QTL with major effects on viability followed by characterization of their mode of gene action and (2) determination of the life stages at which viability selection and mortality occurred. The first part of the study was done with samples taken in May 2006, when the F₂ oysters were ∼700-day-old adults (n = 96 for 46×10, n = 49 for 51×35); these adult oysters had been reared, since 2005, under the WSMC dock in Vexar^® mesh cages (19 mm² Aquapurse). Since the adult samples were the basis for viability QTL mapping and identifying nearest markers for the temporal study, power analyses were conducted to determine an adequate sample size for detecting major viability genes, as described by Launey and Hedgecock (2001). This analysis (see supporting information, File S1 for details) revealed good power with n = 49 (0.65–0.8) and excellent power with n = 96 (>0.9) to reject the null hypothesis of Mendelian segregation ratios in favor of the alternative hypothesis of strong viability selection.

For the temporal part of the study, samples of 96 larvae were taken from each family at 6 h, 12 h, and 24 h postfertilization and daily thereafter until larvae were ready to settle at approximately day 18. When competent for settling, larvae were screened off, treated with epinephrine to promote settlement without attachment (Coon et al. 1986), and set at low density in a downwelling/upwelling nursery system (Hedgecock and Davis 2007). A sample of 96 juvenile oysters (spat) was taken at day 30 for genotyping, and the remaining oysters were reared in the nursery system until large enough for deployment in Aquapurses. Allocation of genotyping effort across these samples is discussed below, in Stage-specific expression of vQTL. Sampling days are abbreviated as d1, d2, etc. Oysters sampled for the temporal study were classified into five life stages: trochophore larvae (6–24 hr), veliger larvae (d1–d13), pediveliger larvae (d14–d18), spat or recently settled juveniles (d30), and adults (d700) (Kennedy et al. 1996).

DNA extraction, PCR, and electrophoresis:

Adult tissues (both from the parents and from d700 progeny samples) were preserved in 70% ethanol prior to extraction. Larvae from each time point and the d30 juvenile samples were killed with three drops of household bleach in 15 ml of seawater and then rinsed and stored in bulk in 70% ethanol. DNA from parents of the F₂ crosses and from the F₂ adult progeny was extracted using the DNeasy animal tissue kit (Qiagen, Valencia, CA). Larval F₂ progeny were extracted in 40-µl volumes of 1× PCR buffer (Promega, Madison, WI), 1 mM EDTA, and 1 µl of 20 mg/ml proteinase K (Shelton Scientific, Shelton, CT). Digestion of the larvae was carried out at 56° for 3 hr followed by 10 min at 95° to denature the proteinase K.

Over 80 microsatellite markers cloned from the Pacific oyster were tested for use in this study (Magoulas et al. 1998; Huvet et al. 2000; McGoldrick et al. 2000; Li et al. 2003; Sekino et al. 2003; Yamtich et al. 2005), most of which were on published linkage maps (Hubert and Hedgecock 2004; Hubert et al. 2009). Markers were named as in the source publication, except for those developed in this laboratory (McGoldrick et al. 2000; Li et al. 2003; Yamtich et al. 2005), which were abbreviated from their original description, e.g., ucdCgi195 abbreviated to Cg195. Polymerase chain reactions were carried out in two phases, the first to amplify the target microsatellite marker and the second to incorporate a fluorescently labeled dye attached to a “zip” sequence that is complementary to the 3′ tail of the forward primer (Shuelke 2000). PCR cycle conditions consisted of an initial denaturing step at 94° for 2 min and then 20 phase-one cycles (30 sec at 94°, 45 sec at T_m, and 45 sec at 72°), followed by 10 zip cycles (30 sec at 94°, 45 sec at 59°, and 45 sec at 72°) and a final 10-min elongation step at 72°. The number of zip cycles was often increased to 30 or 40 when using larval DNA as template. T_m (the optimum annealing temperature) and the MgCl₂ concentration varied, depending on the locus (Magoulas et al. 1998; Huvet et al. 2000; McGoldrick et al. 2000; Li et al. 2003; Sekino et al. 2003; Yamtich et al. 2005). PCR products were electrophoresed on a 4% denaturing PAGE gel (acrylamide:bisacrylamide 19:1, 3 M urea) using 1× Tris(base), boric acid, and EDTA disodium salt (TBE) on the ABI Prism 377 DNA Sequencer (Perkin-Elmer, Waltham MA). Gel images were used to score the fluorescently labeled microsatellites by eye, comparing progeny alleles to adult alleles along with fluorescently labeled size standards (Dewoody et al. 2004).

Data analyses

Segregations and null alleles:

Because the grandparents of experimental crosses were not completely inbred, parental cross types have two alleles (symbolically, AA×AB or AB×AB), three alleles (AB×AC), or four alleles (AB×CD). Nonamplifying or null alleles, which are common in the Pacific oyster (McGoldrick et al. 2000; Launey and Hedgecock 2001; Hedgecock et al. 2004), require modification of classical segregation ratios only for cross type AØ×AB, since AA cannot be distinguished from AØ and the resultant progeny genotypes, A−, AB, and BØ have expected frequencies of 2:1:1, respectively. Under the null hypothesis of no viability selection, progeny genotypes should conform to an expected Mendelian ratio (1:1, 1:2:1, 1:1:1:1, or 2:1:1 for the null allele case). Deviations from expected Mendelian proportions were tested with goodness-of-fit chi-square tests, with the level of significance adjusted for multiple simultaneous tests within each type of segregation (Rice 1989; Launey and Hedgecock 2001). Adjustment for multiple tests increases type-II error, so statistical significance at both nominal α = 0.05 and Bonferroni-adjusted α-levels is reported (Rice 1989).

Mapping viability QTL:

Linkage maps for the two experimental families were constructed with the d700 genotype data, using the cross-pollinator (CP) population type in JoinMap 3.0 (Van Ooijen and Voorrips 2001). The Kosambi mapping function with a minimum likelihood of the odds (LOD) score of 2.0 was used for linkage group assignments. Because distortions of Mendelian segregation ratios may affect linkage mapping (Lorieux et al. 1995; Zhu et al. 2007), we compared marker orders and distances with previously published linkage maps constructed from samples with little segregation distortion (Hubert and Hedgecock 2004; Hubert et al. 2009). When markers that should have mapped failed to map (only one or two per family), we used locations from published maps (Hubert and Hedgecock 2004). Linkage phase was determined by JoinMap from the frequencies of parental and recombinant types. Percentages of the genome covered by these maps were estimated by GC = 1 − e^−2*dn/L, where d is mean intermarker distance, n is the total number of markers assigned to linkage groups, and L is map length estimated by adding twice the average intermarker interval to the sum of all intervals per linkage group (LG) and then summing the lengths of all LGs (Bishop et al. 1983).

The linkage map, parental linkage phases, and parent and progeny genotypes were input to the viability QTL model of Luo and Xu (2003), as implemented in PROC QTL (Hu and Xu 2009), a user-defined procedure for SAS (version 9.2) (SAS Institute 2000–2004). Four markers with ambiguous AA/AØ genotypes were dropped from the linkage map used for family 46×10, and two markers, one that was not known to be linked and did not link and another with ambiguous genotypes, were dropped from the map used for family 51×35. Genomes were scanned in 1-cM increments, under the maximum-likelihood QTL framework, and a likelihood-ratio test (LRT) statistic and estimates of genotype proportions were obtained for each increment (Luo and Xu 2003) (all cross types are interpreted by the model as AB×CD, yielding progeny genotypes AC, AD, BC, and BD). Since we could not use permutation tests to set QTL significance thresholds—because there is no phenotype to permute—we used an approximate method, on the basis of the LRT profile, to establish thresholds at the α = 0.05 level (Piepho 2001). We calculated genome- and chromosomewise significance thresholds for viability QTL (vQTL). Multiple QTL on a single linkage group were identified when the LRT statistic fell by at least 4.60 (∼1 LOD) between two QTL peaks (Lander and Botstein 1989).

Mortality:

In the absence of selection, one expects genotypic proportions in a family to be in Mendelian ratios at all positions in the genome, whereas, at a vQTL, these ratios are distorted by genotype-dependent mortality. We can calculate the magnitude of this mortality from the relative survival of genotypes at each QTL peak. The relative survival of each genotype at a QTL is $w_{ij}/w_{\text{max}}$, where w_max is the proportion of the highest-frequency genotype (Luo and Xu 2003). Average relative survival, S, at a QTL is thus

$$\overline{S}=\frac{\left(w_{11}/w_{\max }+w_{12}/w_{\max }+w_{21}/w_{\max }+w_{22}/w_{\max }\right)}{4}=\frac{1}{4w_{\max }}.$$ (1)

Average relative mortality at this QTL, M, is 1 − $\overline{S}$ or $1-1/4w_{\max }$.

In finite samples, chance fluctuations in genotype numbers will produce a nonzero estimate of mortality by this equation, even in the absence of selection, so to correct for this sampling error, we randomly generated 1000 data sets of progeny genotypes (i.e., no selection), using the parental genotypes and sample sizes specific to each family. We then ran each of the 1000 simulated data sets through the QTL model to obtain the average maximum genotype frequency in the absence of selection, w_maxØ. The correction for sampling error was then applied to the estimate of average survival at a vQTL, by adjusting the maximum frequency of the four genotypes,

$${\overline{S}}_{\text{adj}}=\frac{1}{4\left(w_{\max V}-\left(w_{\max \text{Ø}}-0.25\right)\right)},$$ (2)

where w_maxV is estimated from the data by the QTL model and 0.25 is the Mendelian expectation in a sufficiently large sample without selection (code for the simulations is available from the first author on request).

Selection, dominance, and epistasis of viability QTL:

We adapted the two-locus selection model of Hedrick and Muona (1990; see also Launey and Hedgecock 2001) to estimate jointly the selection coefficient (s) and the dominance deviation (h) for each viability locus, given the value of c, the recombination distance between a vQTL peak and the nearest microsatellite DNA marker. In each case, we took the estimates of s and h that maximized the ratio of the likelihood of genotype data, with selection, to the likelihood of the data, without selection. We produced 95% confidence intervals for estimates of s and h, by subtracting one from the LOD score of the maximized model. Only markers of cross type AB×AB, AB×AC, and ØA×ØB that were deficient for one homozygote could be used in the two-locus model; otherwise, gene effects were evaluated by inspection of genotypic proportions at the nearest marker and by modified chi-square goodness-of-fit tests (e.g., for AB×AB markers that were deficient for both homozygotes, we tested the fit of AB:AA or AB:BB to a 2:1 ratio).

Epistatic interactions were assessed in two ways, first, using the regression method of Fu and Ritland (1996) and, second, using contingency chi-square tests of genotypic associations across all pairs of markers. Under the univariate model of recessive viability selection (Equation 2d in Fu and Ritland 1996) the frequency of individuals homozygous for i markers linked to viability alleles, divided by its binomial expectation, is log transformed and regressed on i. This relationship is expected to be linear if there are no interactions between loci. Because this regression model assumes that deleterious alleles are recessive, we used 10 and 11 unlinked markers, for families 46×10 and 51×35, respectively, which appeared to have completely or nearly completely recessive mutations and to be associated each with a different viability QTL. Regression analysis was carried out in the R statistical package, version 6.2.2. Contingency chi-square tests for pairwise associations between all mapped markers were also carried out in R (code for pairwise test among markers with varying numbers of genotypic classes is available from the first author on request), with the significance level adjusted to control for the false discovery rate (Benjamini and Hochberg 1995).

Stage-specific expression of vQTL:

To estimate the life stage at which selection acted on each vQTL, we determined the first culture day or interval, when the marker closest to a vQTL became distorted. As most genotype-dependent mortality occurs by the juvenile stage (Launey and Hedgecock 2001; Bucklin 2003), we examined those markers that were significantly distorted at d700, at successively earlier time points, to determine when the distortion first appeared. When multiple genotypes at a distorted marker were deficient (e.g., both AA and BB genotypes deficient in AB×AB crosses), we tracked the timing of distortion for each homozygote separately (see Discussion). To reduce genotyping effort, we focused on samples from days 18, 10, 5, and 2, to locate when the P-value of the goodness-of-fit test went, retrospectively, from significant to nonsignificant. Gaps in the time series were filled by genotyping samples from intervening days, as needed, to place vQTL expression into a particular life stage. To test for the stability of segregation ratios at a marker, on days before and after the day on which genotypic ratios became significantly distorted, we performed R×C contingency tests, using the Chirxc program (Zaykin and Pudovkin 1993).

Results

Analysis of segregation ratios in F₂ adults

Testing >80 microsatellite markers in the F₁ parents of families 46×10 and 51×35 revealed 49 and 56 informative markers, respectively (Table 1). Typing of informative markers in the adult (d700) samples for each of the F₂ families yielded a total of 7024 genotypes, which constitute the “end-point” data set used to assess and map viability selection in this study (File S2, Table S1, and Table S2). Significantly distorted segregation ratios at the α = 0.05 level were found at 29 (60%) markers in 46×10 and 37 (66%) markers in 51×35; after adjustment for multiple tests within segregation types, 24 (50%) and 22 (39%) remained significant (Table 1). These distorted ratios were distributed broadly across the genome, on 9 of the 10 LGs, with many instances of multiple markers exhibiting distorted segregation ratios on the same linkage group (Table S1 and Table S2). Some markers showed distorted ratios in both families (e.g., Cg140, Cg212), but segregation ratios of many markers and regions of the genome were distorted in only one family, suggesting that different viability loci were segregating in each family.

Table 1. Day 700 segregation results for two F₂ families.

Family	Cross type	Markers scored	Distorted markers	Linkage group
46×10
	AA×AB	5	3 (3)	1, 4, 6, 7, 10
	AB×AB	20	12 (8)	2, 4, 5–8, 10
	AB×BC	11	6 (6)	1–7, 10
	AB×CD	2	1 (1)	1, 2
	AB×CØ	1	1 (1)	1
	AØ×CØ	6	4 (4)	1, 2, 4, 6
	AØ×AB	4	2 (1)	1, 6, 9
	Total	49	29 (24)
51×35
	AA×AB	5	3 (2)	1, 4, 7, 9
	AB×AB	27	19 (13)	1–10
	AB×BC	17	11 (6)	1, 3, 5–7, 8, 10
	AB×CD	2	1 (0)	4
	AB×CØ	3	3 (1)	1, 3
	AB×AØ	1	0	2
	Total	55	37 (22)

Numbers in parentheses represent significant tests (α = 0.05) after correction for multiple comparisons.

Inferences about the causes of these distortions were made after the vQTL analysis (see below), but we note here that the majority of segregation-ratio distortions (18 of 29 for 46×10 and 29 of 37 for 51×35) were attributable to deficiencies of homozygous genotypes (Table S1 and Table S2). For some AB×AB cross types (4 in 46×10 and 11 in 51×35), both homozygotes were deficient in the progeny. A minority of segregation-ratio distortions from three- or four-allele cross types (7 for 46×10 and 5 for 51×35) yielded deficiencies of heterozygous but not homozygous genotypes (e.g., “AB” in Cg162, family 46×10, Table 2; see also Table S1 and Table S2). Many of these cases of heterozygote deficiency were observed in crosses with null alleles, with AØ, BØ, or both being deficient (e.g., cmrCg02 in family 51×35 and Cg194 in family 46×10; Table S1 and Table S2).

Table 2. Viability QTL and the selection, dominance, and timing of selection at nearest markers, in families 46×10 and 51×35.

Family	Viability locus	Linkage group	Location (cM)	LRT	Nearest marker	Cross type	Progeny genotypes				Two-locus model results			Inferred dominance	Timing
							1	2	3	4	s (95% C.I.)	h (95% C.I.)	LOD
46×10
	1	1	0	27.5	cmrCg005	AB×CD	7	32	19	29	—	—	—	—	d18–30
	2	3	33	48.3	Cg162	AB×AC	46	29	3	12	—	—	—	—	d12–13, d18–30a
	3	4	0	31	Cg198	AB×AC	11	9	31	35	0.77 (0.42–0.95)	0.65 (0.02–1.0)	2.94	PD	d18–30
	4	4	20	23	cmrCg001	AB×AB	10	46	33		1.0 (0.82–1.0)	0.29 (0.0–0.63)	2.78	R	d18–30
	5	4	70	23	Cg178	ØA×ØB	7	15	28	38	0.83 (0.61–0.94)	0.53 (0.1–0.83)	5.10	PD	d15–16
	6	5	5	25	Cg164	AB×AB	5	55	21		0.89 (0.6–1.0)	0.01 (0.0–0.33)	4.25	R	<d18
	7	6	4	15.8	Cg14	ØA×ØB	8	29	27	29	0.79 (0.47–0.96)	0.01 (0.0–0.53)	3.60	R	d18–30
	8	7	0	28	Cg131	AA×AB	32	60			—	—	—	—	d14, d18–30b
	9	7	18	30	Cg155	AB×AB	37	52	3		0.92 (0.76–0.98)	0.33 (0.0–0.6)	7.75	R	<d1
	10	10	7	34	Cg129	AB×AB	36	51	2		1.0 (0.88–1.0)	0.32 (0.0–0.61)	8.27	R	d18–30
	11	10	43	72	Cg212	AB×AB	17	76	0		—	—	—	OD/R	d8–9
	12	10	45	70	Cg189	AB×AB	8	73	10		—	—	—	OD/R	>d30
51×35											—	—	—
	1	1	4	59	Cg126	AB×AB	0	42	6		—	—	—	R	d18–30, d5–7, >d30c
	2	3	33	23.9	Crgi26	AB×AB	0	35	13		0.99 (0.85–0.99)	0.01 (0.0–0.35)	5.91	R	d17
	3	3	67	23.9	Cg148	AB×AC	0	18	16	11	1.0 (0.85–1.0)	0.01 (0.0–0.32)	5.58	R	d10–12
	4	5	1	16	Cg112	AA×AB	11	36			—	—	—	—	<d2
	5	5	79	13	Cg138	AB×AB	7	34	6		—	—	—	OD/R	d18–30
	6	6	0	28	Cg141	AB×AB	0	40	8		—	—	—	R	d18–30, <d4d
	7	7	5	36	Cg156	AB×AC	3	13	22	8	—	—	—	—	d18–30
	8	7	24	15	Cg197	AB×AC	3	20	13	9	—	—	—	—	d18–30
	9	8	7	15.4	Cg196	AB×AB	3	26	18		1.0 (0.85–1.0)	0.35 (0.0–0.71)	4.96	R	d18–30
	10	9	6	28.5	Cg184	AB×AB	0	39	7		—	—	—	OD/R	NA
	11	10	39	19.1	Cg140	AB×AC	3	14	9	20	0.86 (0.53–0.98)	0.5 (0.0–0.58)	3.05	R	d18–30
	12	10	48	21.3	Cg212	AB×AC	14	0	12	19	—	—	—	—	d18–30

Order of progeny genotypes for cross type AA×AB is AA, AB; that for AB×AB is AA, AB, BB; that for AB×AC is AA, AB, AC, BC; that for AB×CD is AC, AD, BC, BD; and that for ØA×ØB is ØØ, ØB, ØA, AB. Degrees of dominance: R, recessive; D, dominant; OD, overdominant; PD, partially dominant. Additional viability loci not detected by the QTL model were added on the basis of their distinct timing of segregation distortion, relative to the marker nearest to the QTL peak, listed in footnotes a–d.

^aum2L48.

^bCg156.

^cCg126 and Cg208.

^dCg186.

Mapping of vQTL

Linkage maps were constructed from 45 and 52 markers scored in adult samples for families 46×10 ($\overline{n}$ = 89.8 per locus) and 51×35 ($\overline{n}$ = 46.9 per locus), resulting in estimated genome coverages of 80.0% and 81.3%, respectively. Four previously unmapped markers (Crgi26, Cg9, Crgi010, and cmrCg02) were added to the map for family 51×35 (Table S1 and Table S2). For both families, JoinMap grouped markers previously assigned to LG 1A or LG 10 (Hubert and Hedgecock 2004) into one linkage group (designated as LG 1 in this study), a finding supported by gene–centromere mapping (Hubert et al. 2009). With the joining of previously assigned LGs 1A and 10, numbers of the remaining linkage groups were shifted by one (e.g., LG 1B became LG 2, the previously assigned LG 2 became LG 3, etc.). Linkage maps consisted of 10 LGs for each family, with markers assigned to the same LG (adjusted by one) and in the same orders as reported previously (Hubert and Hedgecock 2004; Hubert et al. 2009). Only LG 10 in family 46×10 exhibited marker orders and distances that differed from previous data; however, Hubert and Hedgecock (2004) also found significant heterogeneity in marker order and distances across families for this linkage group. Overall, the large numbers of distorted markers linked to viability loci did not appear to affect linkage mapping severely.

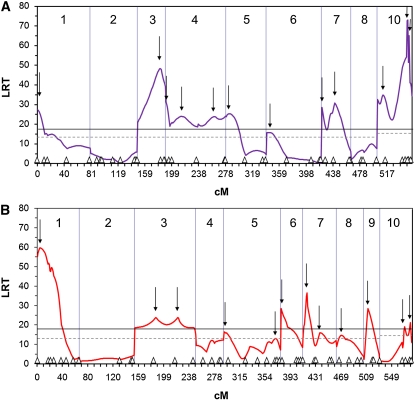
Eleven significant vQTL were identified in family 46×10 and 8 vQTL in family 51×35 by peak likelihood ratios above genomewise thresholds of 17.5 and 18.2 for families 46×10 and 51×35, respectively (Figure 1). Additional vQTL (1 in 46×10 and 4 in 51×35) were identified by peaks above the chromosomewise thresholds, which were ≤13 for all LGs in both families, except for LG 10, which had a threshold of 14.2 for family 46×10 and 14.4 for family 51×35 (Figure 1). LRT peaks below the genomewise threshold but above the chromosomewise threshold were associated with significant distortions of nearby markers. Thus, a total of 12 vQTL were found in each of the families (Table 2; Figure 1), and these were distributed across 7 of the 9 linkage groups studied in family 46×10 (LG 9 was dropped because it had only two markers with ambiguous AA/AØ genotypes) and 8 of the 10 linkage groups in family 51×35; neither family had a significant vQTL on LG 2. Multiple vQTL were found on over half of the linkage groups in each family.

Figure 1.

QTL mapping results for families 46×10 and 51×35. Shown are likelihood-ratio test statistic vs. map distance (cM) for F₂ families 46×10 (A) and 51×35 (B). Long vertical lines mark the ends of linkage groups, which are numbered 1–10. Small triangles along the x-axis indicate the position of markers used in the mapping procedure. Downward arrows mark the location of vQTL peaks. The solid black line indicates the genomewise threshold value for significance at the α = 0.05 level (17.5 for 46×10 and 18.2 for 51×35) and the dotted black line indicates the chromosomewise threshold value for α = 0.05; all chromosomes have a threshold of ≤13, except for chromosome 10, which is 14.2 for 46×10 and 14.4 for 51×35.

Selection and dominance of vQTL

Gene action was inferred from results of the two-locus model and inspection of segregation ratios at markers nearest to vQTL (Table 2). Selection coefficients (s), for the 11 markers that could be fit to the two-locus model, ranged from 0.77 to 1.0, with six above 0.9. Nine markers yielded mid- to low-dominance (h) estimates, with 95% confidence intervals that included zero (Table 2). For two markers (Cg198 and Cg178 in 46×10), 95% confidence intervals for h did not include zero, indicating partial dominance. Of the 13 cases that could not be fit to the two-locus model, six AB×AB cross types were significantly deficient for both homozygotes (Cg212 and Cg189 in 46×10 and Cg126, Cg138, Cg141, and Cg184 in 51×35), suggesting potentially overdominant gene action. Overdominance was subsequently called into question for all but two of them, on the basis of temporal data (see next section). Two markers with cross types AA×AB were significantly deficient for homozygous genotypes; the deleterious alleles at the linked vQTL were provisionally classified as recessive. Finally, 5 markers could not be fit to either the two-locus model or the chi-square framework, because they were not deficient for homozygous genotypes (cmrCgi005 and Cg162 in 46×10 and Cg156, Cg197, and Cg212 in 51×35); however, in these cases, heterozygotes sharing an allele were deficient, suggesting a dominant viability effect of the shared allele.

We found no evidence for epistasis among viability loci, using the regression method of Fu and Ritland (1996). Linear regression fitted the observed data well in both families (r² = 0.999, P = 0, for family 46×10; r² = 1.0, P = 0, for family 51×35), and adding a quadratic term did not significantly improve the model for either family (F-test, P = 0.212 for 46×10, P = 0.20 for 51×35). Tests of epistasis between all pairwise combinations of closely linked markers showed significant contingency chi-square values, as expected; otherwise, only a handful of interactions among unlinked markers (3 of 879 combinations for 46×10 and 4 of 1192 combinations for 51×35) were nominally significant and none after correction by the Benjamini and Hochberg (1995) method.

Temporal changes in marker genotypic proportions

Temporal segregation data were obtained for 21 of 29 adult-distorted markers in family 46×10 and for 28 of 37 adult-distorted markers in family 51×35 (Table S3 and Table S4). Altogether, 10,017 genotypes were determined in this portion of the study (i.e., not counting d700); on average, 2.8 and 2.4 temporal samples per locus, with average sizes of 79.4 and 78.4 individuals, were examined for families 46×10 and 51×35, respectively.

With the exception of two markers (Cg155 in 46×10 and Cg112 in 51×35), all marker segregation ratios became distorted after d2. Within the same linkage group, markers separated by large distances displayed different temporal patterns; however, tightly linked markers often showed the same or very similar timing of segregation-ratio distortion (e.g., Cg162 and Cg160, LG 3 in 46×10, Table S3). For all three of the two-allele cases (AB×AB) in 46×10, for which both homozygotes were deficient and temporal information was available, all on LG 10, the two homozygous genotypes became deficient at different time points (Table S3). Likewise, for four of seven such cases in 51×35, all on LG 1, the two homozygous genotypes became deficient at different time points (e.g., at Cg126, in 51×35, AA was deficient after d5, but BB became deficient only after d18; Table S4). However, temporal data for Cg138 were inconclusive and both homozygous genotypes became deficient at the same time for Cg141 and Cg184 (Table S4).

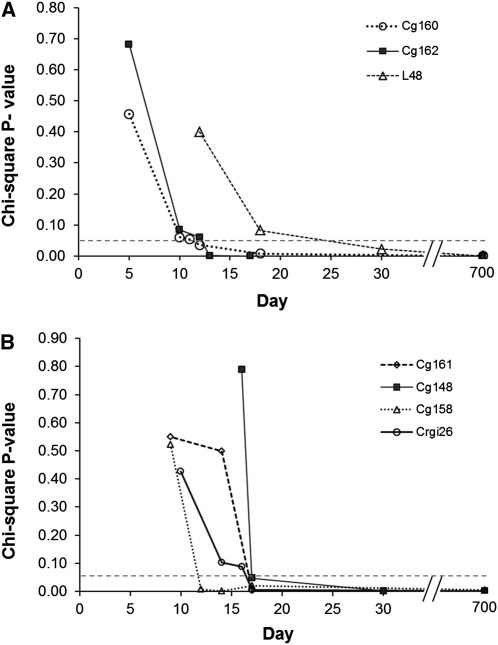
Statistical tests of heterogeneity among segregation ratios of pre- and postdistortion samples were generally not significant. Only 8 of 30 tests of postdistortion samples (both families) demonstrated significant heterogeneity among time points at the nominal α = 0.05 level, but after correction for multiple tests, none of these cases remained significant. Similarly, only 1 of the 13 predistortion cases was significant at the nominal α = 0.05 level (Crgi26, P = 0.025), but it was not significant after correction for multiple tests. In none of the 9 nominally significant cases, in which there was some heterogeneity among segregation ratios, did the ratios switch from being distorted to fitting Mendelian expectation or vice versa. Stability of genotypic proportions, before and after the onset of segregation distortion, is illustrated by chi-square P-values for markers on LG 3, in both families (Figure 2).

Figure 2.

Goodness-of-fit chi-square P-values vs. time for markers on linkage group 3, (A) 46×10 and (B) 51×35.

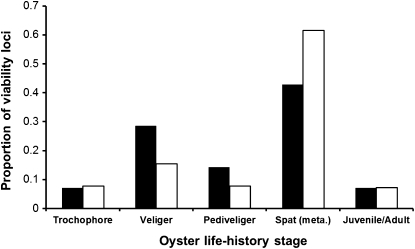
The timing of marker segregation-ratio distortions (Table S3 and Table S4) implied more viability loci than were detected by the QTL model (Table 2). For example, on LG 7 in family 46×10, 3 markers were significantly distorted, each with a distinct onset: days 0–1 (Cg155), day 14 (Cg131), and days 18–30 (Cg156), suggesting 3 different viability loci (Table 2). These 3 viability loci fall, however, under two peaks in the LRT profile on the basis of QTL analysis of adult data alone (Figure 1A, LG 7). Altogether, we resolved 5 more viability loci than the QTL model for the two families, on the basis of distinct timing of marker segregation-ratio distortion. All 5 fall under significant peaks in the LRT profile. For 46×10, these additional viability loci were suggested by markers um2L48 on LG 3 (distorted at days 18–30) and Cg156 on LG 7 (days 18–30) and for 51×35, by LG 1 markers Cg126 (two instead of one viability locus, days 5–7 and days 18–30) and Cg208 (days 30–700) and LG 6 marker Cg186 (before day 4; Table 2, Table S3, and Table S4). Thus, the total numbers of viability loci detected were 14 and 15 for families 46×10 and 51×35, respectively.

These additional viability loci were incorporated with identified vQTL (except for Cg164 in family 46×10 and Cg184 in family 51×35, which lacked sufficient temporal data) into a plot of stage-specific expression of viability loci (Figure 3). The distribution of viability loci across life stages did not differ between families (Fisher’s exact test, P = 0.30), so family results were pooled to test whether viability loci were evenly distributed across life stages. Viability loci were not evenly distributed in expression across life stages (chi-square goodness-of-fit, 4 d.f., P = 0.0007). About half of the viability loci were detected around metamorphosis, between the day-18 larval sample and the day-30 juvenile (spat) sample, and another quarter were expressed at the veliger stage. Only a few viability loci (<10%) appeared during the longest stage, from juvenile to adult, between days 30 and 700.

Figure 3.

Distributions of viability loci across life stages of the Pacific oyster. Bars represent the proportion of viability loci expressed at each stage and sum to 1.0 for each family (solid bars correspond to family 46×10 and open bars to family 51×35). Stages are, approximately, 0–24 hr (trochophore), 1–14 days (veliger), 15–18 days (pediveliger), 18–30 days (spat/metamorphosis), and 30–700 days (juvenile/adult).

Genotype-dependent mortality

The selective mortality required to explain distorted genotypic proportions was calculated from the relative fitnesses of genotypes at each vQTL. Because no evidence of epistasis was found, we assumed that vQTL separated by >50 cM were independent and had multiplicative effects on survival. When two QTL were separated by ≤50 cM, we took the more lethal of the two to estimate mortality. We calculated combined mortality attributable to i vQTL in each family as $1-{\displaystyle \prod {\overline{S}}_{i_{\text{adj}}}}$ (Table 3). Average relative survival in this calculation was adjusted for sampling error through simulation, as described in Materials and Methods. Relative survival in simulations with no selection averaged 0.80 and 0.68 for families 46×10 and 51×35, respectively (cf. the theoretical expectation of 1.0), leading to substantial upward adjustments of average relative survival at vQTL. Still, selective mortality at individual vQTL ranged from 1% (vQTL 9, LG 8, family 51×35) to 67% (vQTL 1, LG 1, family 51×35). Combined mortality from the multiplicative fitness effects of viability QTL was estimated as 96.4% in both families (Table 3).

Table 3. Selective mortality estimates for each family based on viability QTL results.

Family	Viability QTL	Linkage group	Position (cM)	wmax	Adjusted survival	Selective mortality
46×10	1	1	0	0.377	0.795	0.205
	2	3	33	0.506	0.564	0.436
	3	4	0	0.429	(0.682)	0.318
	4	4	20	0.459	0.631	0.369
	5	4	70	0.536	0.528	0.472
	6	5	5	0.418	0.703	0.297
	7	6	4	0.322	0.963	0.037
	8	7	0	0.401	0.739	0.261
	9	7	18	0.397	(0.747)	0.253
	10	10	7	0.585	0.478	0.522
	11	10	43	0.531	(0.534)	0.466
	12	10	45	0.525	(0.541)	0.459
	Cumulative				0.036	0.964
51×35	1	1	4	0.871	0.333	0.667
	2	3	33	0.385	(0.943)	0.057
	3	3	67.2	0.394	0.912	0.088
	4	5	1	0.386	0.940	0.060
	5	5	79	0.397	0.903	0.097
	6	6	0	0.408	0.868	0.132
	7	7	5.6	0.752	0.396	0.604
	8	7	24.6	0.449	(0.760)	0.240
	9	8	7	0.370	0.990	0.010
	10	9	6	0.408	0.868	0.132
	11	10	50	0.651	0.471	0.529
	12	10	60	0.432	(0.801)	0.199
	Cumulative				0.036	0.964

Estimates of cumulative survival use only QTL that are unlinked (>50 cM apart) or the more deleterious of QTL that are linked (≤50 cM apart; survival at the less deleterious QTL is shown in parentheses). Selective mortality is calculated as one minus the adjusted survival described in Equation 2; w_max is the maximum genotype frequency at each QTL (compared to the theoretical 0.25).

Discussion

In this study, we found substantial distortion of segregation ratios—at over half of the microsatellite markers tested in adult F₂ oysters—in agreement with previous documentation of high genetic load in the Pacific oyster (Launey and Hedgecock 2001; Bucklin 2003). This load largely comprises recessive mutations under strong viability selection, having large effects on early mortality. Specific aspects of selection, dominance, and early mortality are addressed later; we turn, first, to the novel documentation of the life stage at which genotype-dependent mortality appears.

Stage-specific expression of genetic load

Temporal segregation data and QTL mapping revealed a large number of viability loci, 90% of which were “expressed” during the larval stage, over half around metamorphosis and another quarter during the veliger stage. (We infer that the stage-specific appearance of genotype-dependent mortality reflects the expression or, more likely, lack of expression of a mutation in a functionally critical gene that is normally expressed at this point in development.) Genotype-dependent mortality occurred over a short period of time, generally a matter of days, and produced grossly distorted genotypic proportions that remained stable thereafter. All but two viability loci (one in each family) were expressed after day 2, which demonstrates that viability selection occurs predominately during the zygotic stage, not during the gametic stage. These results falsify meiotic drive or gametic selection as an explanation for segregation distortion in the Pacific oyster (cf. McCune et al. 2002) and affirm that this bivalve mollusc has many early-acting mutations that are lethal or highly deleterious.

Few studies have documented the ontogeny of genetic load in animals. Rizski (1952) and Seto (1954, 1961) showed that selection on most lethal or semilethal chromosomes acted during the larval stages in Drosophila. Bierne et al. (1998) were the first to show that viability selection occurred at the larval stage of inbred crosses of the European flat oyster, and Launey and Hedgecock (2001) confirmed these results in F₂ crosses of the Pacific oyster. Escobar et al. (2008) demonstrated, for a freshwater snail, that inbreeding depression for early survival was substantial. Almost all other studies of stage-specific inbreeding depression have been carried out on plants. These studies also generally find substantial, early-stage, inbreeding depression in outcrossing species, in line with theoretical predictions (Charlesworth et al. 1990; Husband and Schemske 1996). Interestingly, results from studies in outcrossing plants, particularly conifers (e.g., Savolainen et al. 1992; Remington and O’Malley 2000), show substantial embryonic-stage inbreeding depression, while we find evidence for only one or two mutations affecting survival during the embryonic stage of the oyster, from fertilization through the nonfeeding trochophore stage (∼0–24 hr).

We hypothesized that viability loci would affect fitness disproportionately around times of developmental transitions, when essential genes are turned on and expressed. For example, in plants one might expect to observe inbreeding depression during embryogenesis because of the many genes first expressed at this critical stage (e.g., Thomas 1993; Meinke 1995). In Drosophila, significant changes in gene expression are observed across different life stages, with spikes in gene expression leading up to or during the transition from one pupal stage to the next and during metamorphosis (White et al. 1999; Arbeitman et al. 2002). We did observe a disproportionate number of viability loci expressed around metamorphosis, which highlights this stage as a potentially important developmental transition in terms of selection and mortality. The induction of metamorphosis in invertebrates is well known to involve a complex array of signaling mechanisms and morphogenetic changes, which radically alter the biology and ecology of individuals as they transition to the juvenile stage (Williams et al. 2009). For a marine bivalve, like the Pacific oyster, the transition from a free-swimming larva, with a ciliated velum, to a sessile, filter-feeding juvenile, with gills, involves a complete rearrangement of the body plan and feeding apparatus, during which many new genes are most likely expressed for the first time (Kennedy et al. 1996; Heyland and Moroz 2006). We infer that mutations in these genes cause the many segregation-ratio distortions observed between day 18 and day 30 of development in the Pacific oyster. Ultimately, families, in which such “natural knockouts” of critical genes are segregating, could facilitate genomic dissection of oyster metamorphosis.

Estimating the number of viability loci

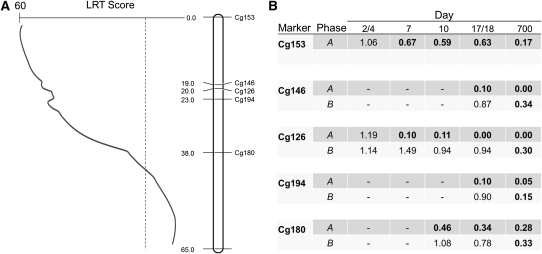
Temporal observations of segregation ratios and phase information suggested the presence of more viability loci than the 12 vQTL identified in each family by the QTL mapping procedure. Viability loci are not fully counted by the QTL model on linkage groups that have many severely distorted markers and high LRT values (>30) across most of their length (e.g., the one, broad LRT peak on linkage group 1, in 51×35). In these cases, markers are often deficient for both homozygous genotypes (AB×AB cross type; marker proportions of AA:AB:BB are expected to be 1:2:1 in progeny, but ratios approaching 0:1:0 are observed), and the A and B alleles are linked to mutations that exhibit different stage-specific patterns of selection (e.g., at Cg126, in 51×35, marker proportions are ∼0:2:1 at day 7 but are ∼0:1:0 at day 700, Table S4). Furthermore, phase analysis reveals that, across markers, the A alleles reside on one haplotype, while the B alleles all reside on the other haplotype (i.e., alleles are linked to mutations in repulsion phase; Figure 4). The most parsimonious explanation for the combined QTL, temporal, and phase information is two viability loci, each with a deleterious recessive mutation that was expressed at a specific time during development. While the QTL viability model marks an advance from the two-locus model used previously to map deleterious loci (e.g., Hedrick and Muona 1990; Launey and Hedgecock 2001), it clearly underestimates the number of viability loci, when multiple viability loci are linked in repulsion phase.

Figure 4.

(A) Distribution of distorted markers underlying the QTL peak on linkage group 1 for F₂ family 51×35. The dashed line indicates the genome-wide threshold of significance. (B) The proportions of affected homozygous genotypes, relative to their expectations, at distorted markers on linkage group 1, 51×35, arranged by phase and sampling time. Expected ratios are 1:2 for AA or BB homozygotes relative to AB for all markers (cross type AB×AB), except for Cg153, which has an expected ratio of 1:1 for AA relative to AB (cross type AA×AB; phase information available for the “A” haplotype only at Cg153). Dashes represent missing data. Frequencies in boldface type represent significant differences from those expected; a value close to 1.0 indicates the genotype is close to its Mendelian expectation. The timing of selection against individuals homozygous for the A-phase alleles (∼day 5) relative to the timing of “B”-phase alleles (days 18–700) suggests two different deleterious alleles acting on this linkage group, although the QTL model shows only one broad peak indicating one viability QTL.

Our estimate of 14–15 viability loci is slightly higher than the previous estimate for the Pacific oyster (∼12; Launey and Hedgecock 2001) and similar to molecular marker-based estimates from plants [e.g., 19 viability loci in Loblolly pine (Remington and O’Malley 2000) and 17 loci in rice (Xu et al. 1997)]. Genome-wide, marker-based estimates of the number of deleterious loci are rare for other animals [an early estimate of 15–38 detrimental genes for the European flat oyster was based on only four microsatellite markers (Bierne et al. 1998), and three transmission ratio distortions (TRD) were found in interspecific backcrosses of mice (Eversley et al. 2010)]. On the other hand, there are many estimates of lethal equivalents (LE), using the method of Morton et al. (1956), and these average three to four LE per genome (Lynch and Walsh 1998, Table 10.4). The number of lethal equivalents for egg to adult viability in the Pacific oyster is likely to be close to the tally of viability loci detected by the marker-based method, since many marker genotypes appear to be lethal, and results of the two-locus model show high selection coefficients (Table 2, discussed below). Thus, the Pacific oyster likely harbors a greater genetic load than any animal species thus far studied.

Selection, dominance, and epistasis of viability loci

Estimates of selection coefficients at most vQTL-associated markers are high, while estimates of dominance are low (Table 2). These results are consistent with previous studies in the Pacific oyster (Launey and Hedgecock 2001; Bucklin 2003). Two viability loci show strong evidence of partial dominance (Cg178 and Cg198), a finding supported by significant deviations from expected 1:1:1 ratios for nonhomozygous genotypes at these markers (AB×AC cross type; Table 2, Table S1, and Table S2). Again, this is consistent with the results of Launey and Hedgecock (2001), who attributed 3 of 20 cases to partially dominant viability loci. Heterozygote deficiencies and segregation distortion in molecular markers have been widely reported in pair crosses of wild bivalves (e.g., Mallet et al. 1985; see references in Launey and Hedgecock 2001), and partially dominant deleterious mutations may in part account for these observations. For a minority of vQTL, genotype deficiencies do not fit any of the classic gene-effect models and are not interpretable. Some vQTL appear to be overdominant, but most of these are resolved by temporal and phase data into separate, recessive deleterious alleles (see above; Figure 4). Thus, the dominance theory continues to be the best explanation of inbreeding depression and genetic load for the Pacific oyster.

Remington and O’Malley (2000) also found that most viability loci were recessive or nearly recessive, finding only one potentially overdominant locus in a selfed family of loblolly pine. However, in another study of a selfed family of Loblolly pine, Williams et al. (2003) found overdominance for four of seven lethal factors, using single-marker and two-locus interval mapping procedures. Williams et al. (2003) used only 17 microsatellite markers, so it is possible that their inference of overdominance at individual loci may be biased by the presence of multiple lethal factors linked in repulsion phase to these markers (i.e., pseudo-overdominance). Higher-density mapping with linkage phase information may, therefore, provide better resolution of gene action of viability loci.

No evidence of epistatic interactions between viability loci was detected in our experiments, using the regression method of Fu and Ritland (1996), which fits the linear expectation of noninteracting loci extremely well. There were, moreover, no significant contingency chi-square tests between any pair of markers, except those that were closely linked. These results support those from a previous study of Pacific oysters that looked at transmission of microsatellite marker alleles linked to lethal loci across two generations and showed that deleterious recessive alleles were heritable and were not “synthetic lethals” (Bucklin 2003). Mukai et al. (1972) also found synergism to be relatively weak or nonexistent in fitness-based inbreeding studies of Drosophila, and Remington and O’Malley (2000) found no evidence for epistasis, also using the regression method of Fu and Ritland (1996). Other molecular studies of the genetic basis of heterosis and inbreeding depression QTL in rice and Arabidopsis have found epistasis to be common (e.g., Li et al. 2001; Melchinger et al. 2007). Epistasis has also been demonstrated through nonlinear decreases in log fitness with increasing inbreeding level (e.g., Whitlock and Bourguet 2000; Salathe and Ebert 2003); although in many cases not all fitness traits exhibit epistasis within an experiment (Willis 1993; Carr and Dudash 1997; Kelly 2005). The marker-based regression analysis and the pairwise chi-square tests are perhaps more direct methods to evaluate epistasis compared with biometrical approaches that analyze trait means across levels of inbreeding. Epistasis may still play a role in the expression of inbreeding depression in the Pacific oyster, but we did not detect it using molecular marker-based methods.

Genetic load and its role in early mortality

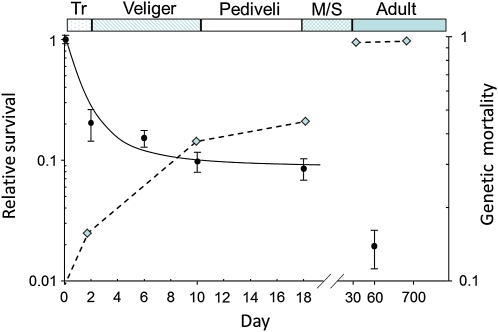
We show that viability selection at deleterious loci is stage specific and strong enough to require that 96% of the individuals in our experimental families must have died to generate the severe distortions of Mendelian ratios observed at marker loci. Do the magnitude and pattern of genetic mortality fit with actual mortality in experimental oyster cultures? Oysters, in general, show high early mortality (type-III survival) both in the wild (Korringa 1946) and in culture (Guo and Allen 1994). In an experiment with a 51×35 F₂ family related to the one reared in this study, observed mortality, from fertilization through day 60 (early juvenile or spat stage), was 98% (Figure 5; L. V. Plough, unpublished data); this level of mortality is typical of commercial hatchery cultures (J. P. Davis, Taylor Shellfish Farms, Quilcene, Washington, personal communication). Thus, the genotype-dependent mortality measured here is nearly as high as observed mortality to the juvenile stage. Moreover, the stage-specific pattern of genetic mortality is similar to the actual survival curve, at least after day 2. In particular, the substantial decrease in observed culture survival during the metamorphosis/early spat stage is matched by the cumulative mortality attributable to vQTL (Figure 5). Thus, the magnitude and pattern of cumulative genetic mortality do indeed closely match those observed in larval cultures, so that nearly all of the post-day-2 mortality in F₂ populations may be explained by genetic load. Since, as we have shown, genetic load is mostly caused by recessive deleterious mutations, much of it would probably not be expressed in natural populations, unless population sizes were reduced—owing, for example, to overfishing or environmental degradation—and the probability of inbreeding thereby increased.

Figure 5.

Mean relative log survival to day 60 of a replicated F₂ cross of Pacific oysters (solid circles correspond to primary y-axis; error bars represent one standard error) and cumulative genetic mortality inferred from relative fitness estimates at viability QTL, averaged over families 51×35 and 46×10 (diamonds and dashed line correspond to the secondary y-axis, also log transformed). The bottom x-axis is broken between day 18 and day 30 and points are not to scale thereafter. The top x-axis displays the life history stages (Tr, trochophore; Veliger; Pediveli, pediveliger; M/S, metamorphosis/setting stage).

Genetic mortality cannot account for the 50–80% mortality observed between day 0 and day 2 (Figure 5), since very few viability loci are observed during that time period in our study (Figure 3). One possible explanation is that fertilization success is much lower than we expect, perhaps ∼50%, so that much of the apparent mortality between fertilization and day 2 might be attributable to fertilization failure. However, fertilization was monitored closely in our experiments, and there was no indication of substantial fertilization failure for either of the crosses in this study. Another explanation could be dominant de novo germ-line mutations, which were predicted by Williams (1975) as a by-product of highly fecundity and would not be detected by linkage to marker loci. More data on the causes of early larval mortality, particularly at metamorphosis, should shed light on the role of genetic mortality over the entire Pacific oyster life cycle.