Prediction of in situ root decomposition rates in an interspecific context from chemical and morphological traits

Abstract

Background and Aims

We quantitatively relate in situ root decomposition rates of a wide range of trees and herbs used in agroforestry to root chemical and morphological traits in order to better describe carbon fluxes from roots to the soil carbon pool across a diverse group of plant species.

Methods

In situ root decomposition rates were measured over an entire year by an intact core method on ten tree and seven herb species typical of agroforestry systems and were quantified using decay constants (k values) from Olson's single exponential model. Decay constants were related to root chemical (total carbon, nitrogen, soluble carbon, cellulose, hemicellulose, lignin) and morphological (specific root length, specific root length) traits. Traits were measured for both absorbing and non-absorbing roots.

Key Results

From 61 to 77 % of the variation in the different root traits and 63 % of that in root decomposition rates was interspecific. N was positively correlated, but total carbon and lignin were negatively correlated with k values. Initial root traits accounted for 75 % of the variation in interspecific decomposition rates using partial least squares regressions; partial slopes attributed to each trait were consistent with functional ecology expectations.

Conclusions

Easily measured initial root traits can be used to predict rates of root decomposition in soils in an interspecific context.

INTRODUCTION

The global carbon cycle has been intensely studied for a long time because of its importance in climate regulation and ecosystem functioning. A key part of this cycle is the link between the carbon pools in the vegetation and soil. This link can be further divided into above- and below-ground components of the vegetation pool. To incorporate knowledge of root decomposition into more general models of carbon cycling we need to be able to estimate in situ rates of mass loss during root decomposition in natural soils. For efficient generalizations, estimations should be made across as many different species and environments as possible.

The methodological challenge

Unfortunately, the decomposition of above-ground litter and its subsequent incorporation into the soil carbon pool is much better studied than the decomposition of below-ground plant tissues despite the fact that root biomass represents a substantial, often dominant, proportion of plant biomass. In fact, about 98 % of decomposition experiments are related to leaves, and the remaining 2 % to roots (Zhang et al., 2008). Roots play a hidden role in the carbon cycle, one that is still poorly understood, with methodological challenges that put into question much of the existing research concerning root decomposition rates in natural soils. Naturally decomposing roots are constantly and intimately interacting with their surrounding rhizosphere at a very fine spatial scale. While living, most roots are associated with mycorrhizal fungi and other symbionts. Not only do these symbionts strongly influence resource acquisition (Marschner and Dell, 1994; Clark and Zeto, 2000) of living roots but they also influence the carbon budgets of both living and dying roots (Rygiewicz and Andersen, 1994; Wright et al., 1998), including decomposition rates of dead roots (Langley et al., 2006) and protection against soil toxicity (Van Tichelen et al., 2001). The act of removing the root from the soil, washing and drying it, and then placing it inside a litterbag largely destroys this root–rhizosphere interaction and thus puts into question estimates of root decomposition using litterbags.

Dead roots from the same plant vary greatly in morphology, especially with respect to diameter, which is another potential source of bias in root decomposition studies (Pritchard and Strand, 2008) unless the roots placed in the litterbag have the same diameter distribution as the natural root system. Most studies define fine roots as an absolute diameter class (e.g. below 2 mm in diameter). However, if we focus on a particular function of roots (e.g. water absorption, sap conduction, physical and biological protection), diameter classes can be extremely variable among species for this particular function. Morpho-anatomical studies are very informative for such comparisons (Valenzuela-Estrada et al., 2008). In the present study, we chose the absorbing function to functionally compare our tree species, and tested whether it improves the predictions of our models.

Unlike leaves, dying roots will undergo a progressive death of their cells and tissues (Comas et al., 2000) while remaining attached to still-living roots, and some root functions of the dying root can persist while others are already lost (Spaeth and Cortes, 1995; Dubrovsky et al., 1998; Lo Gullo et al., 1998). The act of excising a root and placing it in the litterbag changes this natural phenology of root death and decomposition.

For all these methodological reasons, comparative studies testing similarities between leaf and root decomposition (Hobbie et al., 2010; Wang et al., 2010) are controversial and we do not really know to what extent one can extrapolate from the rich literature on leaf litter decomposition to the processes of root decomposition. In this study we instead use an intact-core method adapted from Dornbush et al. (2002) that maintains the decomposing roots in their natural rhizosphere environment while allowing us to follow and quantify the process of mass loss during decomposition. We use this method with 17 species of crops, forage herbs and trees, including fast-growing poplar hybrids and highly conservative conifers.

The Olson exponential decomposition model

Classical decomposition kinetics (expressed as total or carbon mass remaining) describe an exponential loss of mass through time, M(t) = M(0) e^−kt, in which M(0) is the initial mass and k is a constant measuring the proportional mass loss per unit time (Olson, 1963). With this model, the k value is unique to each species and environmental condition. Plant communities in both natural and agro-systems encompass many species and their composition varies among locations. Given the difficulty in studying roots it is impossible to estimate these rates for every species and environment. We therefore investigate the use of initial root chemical traits (e.g. N and C concentrations, fibre content) and functional classifications (bulk root system versus absorbing roots only) to generalize Olson-based decomposition rates beyond taxonomic identities. Second, if decomposition depends on the chemical properties of roots, then the decomposition rate will change as these chemical properties change during decomposition, yet the Olson model assumes a constant specific decomposition rate (i.e. the ‘k’ parameter). To address this possibility we express the k values as a function of root chemical and morphological traits affecting decomposition. In this way, interspecific differences in k values will be predicted by these traits, and k values can also change over time according to temporal changes in the proportion of different carbon fractions during decomposition. Finally, as temperature is an environmental factor regulating root decomposition, at least for initial stages (Berg et al., 1998; Cusack et al., 2009), time (t in the exponential model) will be expressed in degree-days.

A comparative approach

Because the general goal is to incorporate knowledge of root decomposition into more general models of carbon cycling, it is necessary to link the k values of the Olson model to easily measured traits of roots before decomposition begins. Comparative statistical analyses across a broad range of species consistently show rates of leaf litter decomposition to increase with increasing litter nitrogen concentration and to decrease with increasing concentrations of cellulose and lignin as well as with increasing dry matter contents (Cornelissen and Thompson, 1997; Melillo et al., 1982; Kazakou et al., 2009). Such chemical and morphological characteristics are called functional traits, more precisely defined in Lavorel and Garnier (2002). As with leaves, root traits such as lignin contents, C : N ratios and calcium concentrations seem to influence root decomposition rates (Silver and Miya, 2001; Jalota et al., 2006). Conversely, root function also influences its chemistry, as previously shown when comparing different root orders (Pregitzer et al., 2002; Guo et al., 2004; Fan and Guo, 2010). Similarly, as found for leaf litter (Minderman, 1968), Larsson and Steen (1988) noted that decomposition rates of soluble carbohydrates, cellulose and lignin in roots decrease in that order. However, it is important to interpret these correlational patterns with care. As reported in Prescott (2005), the effect of N on litter decomposition rate is controversial. In this study we quantify initial root traits and follow the mass loss dynamics of roots from ten tree and seven herbaceous species typically used in agroforestry systems from initially intact roots over 401 d of in situ and root-adapted decomposition. We investigate three specific questions.

• (1) How variable are the initial root traits, and the in situ measured root decomposition rates, among species?

• (2) Is our ability to predict interspecific variation in root decomposition rates (k values) improved by the explicit inclusion of species-specific carbon fraction decay rates over that of models including a generalized decay rate for each carbon fraction, and how do these model results compare with observed k rates?

• (3) As root diameter class has previously been shown to be a poorer predictor than root morphology or functional class for predicting root traits and decomposition, is our ability to predict interspecific variation in root decomposition rates (k values) improved by including traits measured on functionally classified roots rather than on fixed diameter classes?

MATERIALS AND METHODS

The measurement of root decomposition rates consisted of three steps: (1) obtaining soil cores containing newly dead roots of a single species at a time, (2) placement of these cores in situ during decomposition while preventing invasion by new roots, and (3) sampling and extraction of decomposing roots. Each of these steps were performed on ten species of trees and seven herbaceous species (Tables 1 and 2).

Table 1.

List of the ten sampled tree species at the Saint-Nicolas site

Species	Family	Abbreviation	Year of plantation	Density (trees ha−1)
Betula alleghaniensis Britton	Betulaceae	Ba	1992	700
Fraxinus americana L.	Oleaceae	Fa	2003	1200
Juglans cinerea L.	Juglandaceae	Jc	1992	700
Juglans nigra L.	Juglandaceae	Jn	1992	700
Larix × marschlinsii Coaz (L. decidua × L. kaempferi)	Pinaceae	Lx	1997	1200
Picea abies L.	Pinaceae	Pa	1997	1800
Pinus strobus L.	Pinaceae	Ps	1995	1200
Populus × canadensis Moench (P. deltoides × P. nigra)	Salicaceae	Px	1998	700
Quercus macrocarpa Michaux	Fagaceae	Qm	1992	700
Quercus rubra L.	Fagaceae	Qr	1992	700

Table 2.

List of the seven herbaceous species grown in an open field on the Sherbrooke University campus

Species	Family	Abbreviation
Agropyron cristatum L.	Poaceae	Ac
Bromus inermis Leyss.	Poaceae	Bi
Festuca rubra L.	Poaceae	Fr
Lolium multiflorum Lam.	Poaceae	Lm
Poa pratensis L.	Poaceae	Po
Phleum pratense L.	Poaceae	Ph
Trifolium pratense L.	Fabaceae	Tp

Tree root collection

Soil cores containing the tree roots were from a study site in Saint-Nicolas (Quebec, Canada – 46°41′21″N, 71°27′55″W). This site is organized as a mosaic of 13 small monospecific tree plantations of approximately 2000 m² on marine deposits within an area of 6 ha. The drainage, which is performed by a network of pipes and underground agricultural drains, and soil properties are similar among the plantations.

We randomly chose five trees within each of the ten monospecific stands (Table 1). We established a 50 × 50-cm sampling square at each of the four cardinal directions and 1 m from the trunk of each tree in early June 2008. Each square was trenched to a depth of 30 cm and a geotextile was placed in the trench both to start the senescence of living roots within the square and to prevent new roots from growing into it. This was performed to maximize the proportion of newly senescent roots at harvest. At the end of September 2008 we took twinned soil cores (15 cm long, 5 cm diameter and taken at 5 cm below soil surface) from the centre of each square. One of the twinned soil cores was returned to the laboratory to get an estimate of the initial amount of roots in the other core. The second core was placed in a polyethylene terephtalate glycol (PETG) tube whose ends were covered in a 50-μm mesh plastic cloth. The mesh allowed water, gases and the microflora and fauna in the surrounding soil and atmosphere to interact naturally with the soil core while preventing roots from growing into the cores. We used four pairs of cores per tree, three trees per species and ten species, i.e. 200 cores in situ and their 200 twin cores.

To determine the likely level of error in our estimates of initial root mass per core, we also performed a preliminary sampling to test how the mass and length variability was spread among our different hierarchical levels (i.e. among species, among individual trees of the same species, among paired cores of the same individual and between twin cores of the same pair). We found that 16·6 % (mass) and 11·7 % (length) of the total variation of initial values for the tree cores existed between twinned cores and this level of error was therefore incorporated into the estimation of decomposition kinetics.

The tubes containing the soil cores for in situ measurements were returned in autumn to the University of Sherbrooke campus (Quebec, Canada – 45°22′48″N, 71°55′34″W, 260 m a.s.l.) with mean annual temperature of 4·1 °C and precipitation of 1144 mm. Each tube containing the soil core was placed vertically into the ground in a common garden that had previously been a lawn while respecting a randomized block design. There were 20 blocks of ten cores (one from each species). Five blocks were harvested on each of days 228, 282, 341 and 401 (i.e. 724, 1490, 2548, 3050 °Cd).

Herbaceous root collection

Soil cores containing roots of each of the seven herbaceous species were obtained as follows. Each species was grown from seed as a monoculture in plastic containers (40 × 30 × 35 cm high) from 19 June 2008. Soil was a commercial homogenized topsoil. We planted five replicate containers per species and the containers were placed in a full randomized block design in an open field on the University campus. Sufficient seeds were sown to produce a continuous canopy by mid-August. As with the tree species, four twinned cores were harvested in early September 2008 from each container. The root mass in one of the randomly chosen twins was immediately extracted while the other twin was placed in the same PETG tube as described above. All these in situ tubes were then placed into holes in one common garden site on the University of Sherbrooke campus in a randomized block design: 20 blocks of seven cores (one from each species). Five blocks were harvested on each of days 228, 282, 341 and 401 (i.e. 724, 1490, 2548 and 3050 °Cd).

As for trees, a preliminary sampling was performed to test how the mass and length variability was spread among our different hierarchical levels (i.e. among species, among individuals of the same species and among cores of the same container). The twinned cores for the herbaceous species provided more precise estimates of initial mass than those of trees as only 2·5 % of the total variance existed between twinned cores but 23 % of the initial variance in root length of the herbaceous roots existed at this level.

Upon removal from the common garden the sampled cores were stored at 3 °C in a cold room for up to 30 d. Roots from a core were then gently hand-washed and separated from soil particles in a 0·85-mm sieve. Washed roots were spread in a water tray and digitalized for morphological measurements with WinRHIZO software (Regent Instruments Inc., Québec, Canada). Because the cores containing the tree roots came from monocultures with a geotextile on the ground to prevent growth of herbs there were few herbaceous roots found and these were easily detected and removed. Total root length inside each sampled core was collected to calculate specific root length values (root length per tissue dry mass). Roots were then dried at 50 °C until constant dry weight was reached, and then weighed. Samples were ground to a 1-mm particle size in a ball mill and then used for the measurement of biochemical traits.

Root biochemical trait measurements

Roots of less than 3 mm in diameter were considered as ‘all roots’. The following traits were measured on ‘all roots’ of each tree soil core (herb samples were too small and did not allow such analyses): total carbon and nitrogen (mg g⁻¹), neutral detergent extractables (simple sugars, amino acids, peptides, water-soluble phenolics), acid detergent extractables (here considered to be mostly hemicelluloses), acid-hydrolysable carbohydrates (mostly cellulose) and acid-unhydrolysable residues (mostly lignin, and less soluble condensed tannins). These were measured using Fourier-transformed near-infrared spectrophotometry (FT-NIRS; Antaris II, FT-NIR Analyzer, Thermo Fisher Scientific Inc., MA, USA) after obtaining calibration curves of each chemical trait from proximate analyses. FT-NIRS calibrations were performed because of the time efficiency of the subsequent FT-NIRS measurements, and second because of the ability to measure smaller samples than with proximate analyses.

Proximate analyses for the calibration curves of the FT-NIRS were performed on 96 randomly chosen root samples from intact roots (neighbour cores). Carbon and nitrogen concentrations were analysed with an Elementar Vario Macro Analyzer (Elementar Analysensysteme GmbH, Hanau, Germany). We actually had sufficient dry mass to directly measure C and N for all but about 10 % of samples and so we constructed separate calibration curves for each harvest date. However, this was not possible for fibre analyses as larger sample masses were needed, and so we constructed a single calibration curve by sampling equally across both species and harvest dates. The various fibre fractions were determined according to the extraction protocol of Van Soest (1963) using a fibre analyser (Fibersac 24; Ankom, Macedon, NJ, USA). Four complementary fractions are sequentially separated with this method. (1) Neutral detergent extractables (hereafter ‘water solubles’) included simple sugars, amino acids, peptides and water-soluble phenolics, but also some cell-wall components, such as β-glucans and pectins, mucilage and some storage polysaccharids (Van Soest et al., 1991). The remaining fraction, neutral detergent fibre, is separated into the three following fractions: (2) acid detergent extractables (‘hemicellulose’), (3) acid-hydrolysable carbohydrates (‘cellulose’) and (4) acid-unhydrolysable residues (‘lignin’).

The NIR spectrum (12 000–3800 cm⁻¹, equivalent to 833–2630 nm) over each 0·6 nm, averaged over 32 individual scans, was acquired for each sample using the Omnic software (Thermo Fisher Scientific Inc., Waltham, MA, USA). Calibration curves for each biochemical trait were constructed using the TQ-Analyst software (Thermo Fisher Scientific) using the samples which had also been analysed using proximate analyses. Partial least squares (PLS) regression was used for these multivariate calibrations. The PLS method is a multivariate linear calibration technique that reduces large sets of raw data into coordinates within an n-dimensional space comprising a small number of orthogonal (non-correlated) factors so that they minimize the error sum of squares among the values to be predicted. Cross-validation was used to estimate the optimal number of factors used in the calibration: two-thirds of the samples in each calibration set were randomly chosen to construct the model and the remaining third was used for validation. No outliers were detected using Mahalanobis distances. The number of factors to be used for the model was chosen using the root mean square error (RMSE, below) calculated over the validation set:

with n the number of sample spectra in the validation set. The number of terms used should be the highest, but the validation RMSE should not be higher than that of the calibration, to avoid over-fitting.

Determination of root functional diameter classes

Most studies define fine roots as an absolute diameter class, regardless of the growth strategy (e.g. below 2 mm in diameter). However, if we focus on a particular function of roots (e.g. water absorption, sap conduction, physical and biological protection), diameter classes can be extremely variable among species for this particular function. Morpho-anatomical studies are very informative for such comparisons (Valenzuela-Estrada et al., 2008). In this work, we chose the absorbing function to functionally compare our tree species, and will test whether it improves the predictions of our models.

Fresh fine roots of each tree species were obtained from additional soil cores taken 1 m from the tree trunk on three randomly chosen trees per species. In the laboratory, ten root fragments 10 mm in length, and from 0·1 to 3 mm in diameter (at 0·3-mm increments), were collected from each soil core, quickly dipped in formalin-aceto-alcohol (FAA) 4 % fixative solution, embedded in Agar and sliced to a 100 µm thickness with a McIlwain microtome (Stoelting Co., IL, USA). This gave a total of 900 slides: three transverse cuts of each diameter, three sampled trees per species, ten diameter classes per species and ten species. The root on each slide was digitalized with a camera-equipped binocular microscope (Olympus Co., Tokyo, Japan). Functional classes were defined depending on the absorbing function. Absorbing roots were defined as still having a living cortical layer. The remaining fresh roots from each of these additional soil cores were analysed for the same chemical and morphological traits as described above.

Statistical methods

Specific decomposition rates of each species, i.e. the k constant in the Olson model, were estimated using least squares regression of the natural logarithm of dry root mass at each harvest on the degree-days. To build well-fitting and parsimonious models between root decomposition rates and the different carbon fraction decomposition rates, we used backward multiple linear regressions. Given the problem of multicollinearity between the initial root traits that are used as independent variables to predict root decomposition rates, we first performed principal component analyses (PCAs), followed by partial least squares regression (PLSR), allowing more quantitative predictions. PLSR is particularly well suited to avoid over-fitting and unstable slope estimates in such situations (Höskuldsson, 1988).

We performed linear mixed models [maximum-likelihood (ML) estimation] using either root mass or length as fixed effect, in order to estimate the variance components at each hierarchical level of our experimental design.

RESULTS

Interspecific variation in root traits and decomposition rates

Table 3 presents the mean values and coefficients of variation of the initial root traits of both trees and herbs. These initial mean values differed significantly among trees and herbs for all traits except for hemicellulose and lignin. Tree roots tended to have less nitrogen per mass and more carbon per mass than did the herbs. The types of carbon also differed between tree and herb roots. Tree roots tended to have higher lignin and cellulose per mass than those of herbs, but lower hemicellulose and carbon in the water-soluble fraction. Carbon per root mass was the least variable among species for both trees and herbs but the interspecific variation of this trait relative to the intraspecific variation was the largest of all chemical traits (i.e. 77·4 % of total variation). Ranges of interspecific, interindividual and individual variation of chemical traits for all species were 61·4–77·4, 14·1–25·4 and 6·8–13·2 %, respectively.

Table 3.

Specific mean initial morphological and chemical traits of total roots and their corresponding decomposition rates

Species	SRL (m g−1)	N (mg g−1)	C (mg g−1)	Water solubles (mg g−1)	Hemicellulose (mg g−1)	Cellulose (mg g−1)	Lignin (mg g−1)	Global k (×10−4 mg g−1)
Betula alleghaniensis	22·7	9·6	463·1	280·2	164·2	227·1	328·4	2·24
Fraxinus americana	18·6	13·0	436·4	351·7	229·6	232·8	185·9	5·25
Juglans cinerea	27·7	16·1	447·7	475·4	186·5	182·0	156·1	4·06
Juglans nigra	23·5	13·9	444·6	464·0	210·2	210·5	115·3	4·8
Larix × marschlinsii	15·5	10·3	466·9	270·8	143·6	263·4	322·3	3·58
Picea abies	12·7	8·1	464·5	247·2	178·3	269·1	305·4	2·51
Pinus strobus	4·4	11·5	436·7	282·7	153·4	242·5	321·4	3·17
Populus × canadensis	110·2	6·3	455·2	238·1	191·8	322·7	247·4	1·82
Quercus macrocarpa	59·1	8·1	453·2	380·3	182·9	232·7	204·1	1·54
Quercus rubra	28·8	7·1	459·8	291·4	214·0	289·0	205·6	2·59
Tree species average ± s.d.	32·3 ± 30·9	10·4 ± 3·2	452·8 ± 11·2	328 ± 86	185 ± 27	247 ± 40	239 ± 77	3·15 ± 1·2
Trees CV	95·7	30·8	2·5	26·3	14·7	16·3	32·2	39·6
Agropyron cristatum	88·6	19·3	380·6	330·3	295·1	224·4	143·9	5·27
Bromus inermis	107·6	19·5	378·2	366·8	266·5	209·0	152·8	4·23
Festuca rubra	102·5	18·6	380·9	323·1	252·9	210·8	186·6	2·98
Lolium multiflorum	99·4	20·2	381·6	314·0	319·3	227·8	112·5	8·59
Poa pratensis	122·2	20·0	370·1	356·3	282·7	208·9	142·8	0·91
Phleum pratense	91·5	18·4	372·9	349·9	253·6	210·7	170·9	7·59
Trifolium pratense	100·9	23·6	365·2	414·8	225·3	190·9	186·2	5·92
Herb species average ± s.d.	101·8 ± 11·1	19·9 ± 1·7	375·7 ± 6·4	351 ± 34	271 ± 31	212 ± 12	157 ± 27	5·07 ± 2·6
Herb species CV	10·9	8·7	1·7	9·7	11·5	5·7	17·1	52·2
All species average ± s.d.	60·9 ± 42·8	14·3 ± 5·5	421·0 ± 40·2	337 ± 69	221 ± 52	233 ± 36	205 ± 73	3·94 ± 2·1
All species CV	70·2	38·4	9·6	20·4	23·4	15·4	35·7	52·1
Trees vs. herbs comparison	F1,51  =  5·64	F1,51  =  6·78	F1,51  =  131·5	F1,51  =  24·7	F1,51  =  14·9	F1,51  =  1·58	F1,51  =  3·31	F1,451  =  13·01
	P  =  0·021	P  =  0·012	P < 0·0001	P < 0·0001	P  =  3e–4	P  =  0·21	P  =  0·075	P  =  3e–4

SRL specific root length; N, nitrogen content; C, carbon content.

The most variable initial root trait among the ten tree species was specific root length (Table 3). Root traits of trees appeared to be more variable than those of herbaceous species. The specific root length of the tree roots was also much more variable among species but this was primarily due to Populus canadensis. Among tree species, all root traits of absorbing roots differed from those of ‘all roots’ but hemicellulose content (Table 4).

Table 4.

Mean initial morphological and chemical traits of absorbing tree roots

Species	SRL (m g−1)	N (mg g−1)	C (mg g−1)	Water solubles (mg g−1)	Hemicellulose (mg g−1)	Cellulose (mg g−1)	Lignin (mg g−1)
Betula alleghaniensis	36·1	20·1	416·2	350·8	180·5	137·9	288·9
Fraxinus americana	21·9	24·0	399·4	365·4	238·9	173·0	204·5
Juglans cinerea	34·0	22·1	399·2	494·3	198·1	125·5	168·5
Juglans nigra	23·6	20·7	394·0	512·5	184·1	137·4	175·0
Larix × marschlinsii	27·7	16·8	417·0	305·6	176·5	159·7	318·9
Picea abies	24·0	16·4	413·6	308·9	176·4	159·3	293·2
Pinus strobus	13·6	17·8	406·5	319·7	200·5	157·8	252·9
Populus × canadensis	59·1	17·6	414·3	316·5	159·1	189·3	287·3
Quercus macrocarpa	34·9	15·0	421·3	395·5	136·2	133·0	297·8
Quercus rubra	31·8	12·9	428·7	400·0	109·2	123·4	334·2
Tree species average ± s.d.	30·7 ± 12·2	18·3 ± 3·4	411·0 ± 11·0	377 ± 75	176 ± 36	150 ± 22	262 ± 59
Tree species CV	42·5	19·4	2·8	20·8	21·6	14·9	24·0
Absorbing vs. all root comparison	F1,31  =  10·1	F1,31  =  370·1	F1,31  =  326·9	F1,31  =  83·2	F1,31  =  3·4	F1,31  =  204·0	F1,31  =  4·7
	P  =  0·003	P  =  0·0001	P < 0·0001	P < 0·0001	P  =  0·076	P < 0·0001	P  =  0·037

Prediction of root decomposition rates

The decomposition rate of total roots differed by a factor of five among the tree species (Table 3), with Fraxinus americana decomposing the most quickly and Quercus macrocarpa most slowly. Among herb species, these interspecific differences reached a factor of almost ten. Also, 63·3 % of total variation in root mass loss rate was interspecific. Rates of decomposition of single carbon fractions also differed among species in every case. We could not estimate the decomposition rates of the carbon types for the herbaceous species because the remaining root masses were not sufficient to perform either proximate analyses or FT-NIRS sample predictions.

Given this interspecific variation in decomposition rates and in initial types of carbon in the tree roots, we first determined the degree to which the interspecific variation in the overall decomposition rates (k_mass) of root mass could be predicted from the decomposition rates and initial proportions of each carbon type (k_type). The simplest hypothesis is that k_mass is an additive function of the k value of each carbon type weighted by the initial proportion of that carbon type in the root. This model is formulated as follows where [X]₀ is the percentage of the initial mass represented by carbon type X, and where k_i (y) is the decay rate of type y for species i:

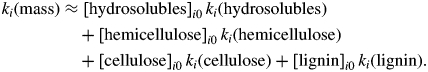The predicted and observed k_mass values were closely correlated (R²  =  0·97; RSE = 2·26e⁻⁵; P = 2·1e⁻⁷). The slope and intercepts between observed and predicted values was 1·05 and –1·7e⁻⁵ °Cd, respectively, and these values were not significantly different from 1 (t₈ = 0·74, P = 0·48) and 0 (t₈ = 0·79, P = 0·45). Thus, the decomposition rate of total mass is a simple linear function of the decomposition rates of each carbon component.

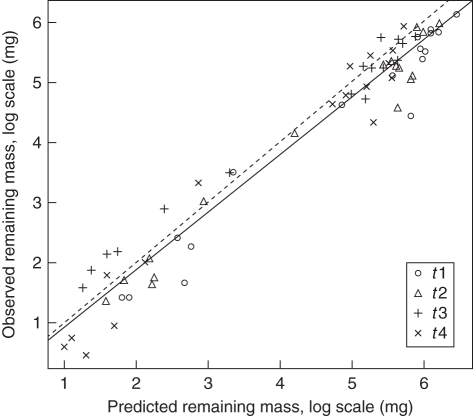
Because we could not measure the actual initial root mass per core and had to rely on the value estimated from its twin, we next attempted to predict the actual loss of root dry mass during decomposition using this initial estimate and a simple exponential decay function: M(dd)_i = M(0)_ie^–k·dd where M(dd)_i is the remaining root mass of species i at a given degree-day (dd), M(0)_i is the average initial root dry mass in the soil core of species i and k_i is the observed specific k value. The observed and predicted dry masses were highly correlated (Fig. 1, R² = 0·95, RSE = 0·39), with a slight overestimation of the highest values. The probability that the slope of the linear regression is different from 1 is P = 0·13 (t = 1·529, d.f. = 65) and the probability that the intercept is different from 0 is P = 0·73 (t = 0·35, d.f. = 65).

Fig. 1.

Relationship between the predicted specific root remaining mass and the observed specific root remaining mass of trees and herbs (log–log scale). Each species is represented by four points corresponding to the four sampling dates; the four symbols correspond to the four sampling dates (t1, 724; t2, 1490; t3, 2548 and t4, 3050 degree-days). The bottom-left cluster is formed of the seven herbaceous species, the upper-right one contains the ten tree species.

Thus, interspecific root mass loss over time could be accurately predicted from the initial root masses and the species-specific root decomposition rates. Furthermore, the species-specific decomposition rates could be accurately predicted from the masses of the initial carbon fractions and the species-specific decomposition rates of these fractions.

Initial root traits and decomposition rates

Figure 2 shows the results of PCAs involving the initial root traits and the global decomposition rates based on (1) all tree and herb roots (Fig. 2A), (2) all tree roots (Fig. 2B), (3) all herb roots (Fig. 2C) and (4) absorbing tree roots (Fig. 2d). In these four PCAs the first two principal components accounted for about 80 % of the total variance.

Fig. 2.

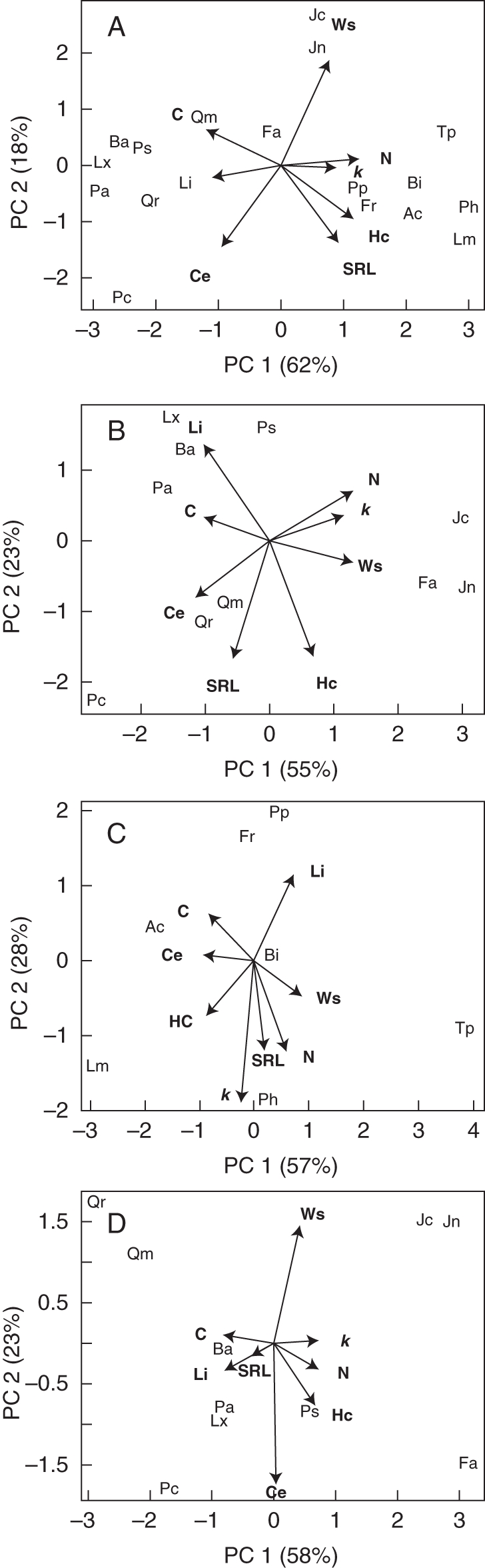
Principal component analyses of specific decomposition rates and initial root traits of (A) trees and herbs roots, (B) tree roots from all diameter classes, (C) herbaceous roots, and (D) absorbing tree roots. Abbreviations: C, carbon; N, azote; Ws, water solubles; Hc, hemicellulose; Ce, cellulose; Li, lignin; SRL, specific root length; for species' abbreviations see Tables 1 and 2.

Root decomposition rates (k values in °Cd⁻¹) were positively correlated with N content, and negatively with C and lignin content in the first two axes of all PCA plots. Hemicellulose and water-soluble fractions were either independent of or slightly positively correlated with k values. Cellulose content ranged from not correlated (in herbaceous species and in absorbing tree roots) to negatively (in absorbing tree roots) and highly negatively (in total tree roots) correlated with k values. Specific root length was positively correlated with k values in the PCA of herbaceous species but was negatively correlated in the PCA of tree species, regardless of the diameter class (all roots or absorbing roots).

To get a more quantitative measure of the relative importance of the initial morphological and chemical root traits in determining root mass decomposition rates we performed a series of simple regressions of k as a function of each trait. As proposed by Burnham and Anderson (2002) we used the change in the Akaike information criterion (AIC) to compare models; Δ_AIC = AIC_i – AIC_min was calculated as an index of support of each regression model with the corresponding trait. Although initial root traits, which are best correlated with root decomposition rates, depend on the category of roots considered (Table 5), nitrogen, hemicellulose, total carbon (except for herbs) and lignin contents appear as good predictors regardless of the root category. Let us consider a gradient of root coarseness as follows: herbs < absorbing tree roots < total tree roots. With respect to this gradient, the water-soluble fraction and cellulose appear better correlated with k values for coarser than for finer roots. The opposite trend was observed for hemicellulose and lignin.

Table 5.

Pearson product-moment correlation coefficients between root decomposition rate (°Cd) and the initial root traits

Independent variable	Tree roots						Herbaceous roots			Tree and herbaceous roots
	All roots			Absorbing roots			All roots			All roots
	r	AIC	ΔAIC	r	AIC	ΔAIC	r	AIC	ΔAIC	r	AIC	ΔAIC
SRL	–0·53	–149·8	7·9	–0·56	–149·8	7·0	0·43	–92·0	2·8	0·30	–236·3	7·1
Nitrogen	0·82	–157·7	0	0·73	–154·2	2·6	0·49	–92·4	2·4	0·63	–243·4	0·0
Carbon	–0·55	–150·2	7·5	–0·80	–156·8	0·0	–0·03	–90·5	4·3	–0·50	–239·6	3·8
Water solubles	0·54	–149·9	7·8	0·43	–148·6	8·2	–0·03	–90·6	4·2	0·29	–236·2	7·2
Hemicellulose	0·38	–148·1	9·6	0·73	–154·1	2·7	0·57	–93·3	1·5	0·61	–242·7	0·7
Cellulose	–0·52	–149·8	7·9	0·04	–146·6	10·2	0·22	–90·9	3·9	–0·39	–237·5	5·9
Lignin	–0·46	–148·9	8·8	–0·75	–154·8	2·0	–0·68	–94·8	0·0	–0·54	–240·5	2·9

Independent variables were classified into three categories, depending on the level of support of the model (in bold, italics and standard body in decreasing order of significance), based on their respective Δ_AIC values.

Table 6 summarizes the multiple regressions (PLS and ML) used to predict root decomposition rates given initial root traits. These regressions had good predictive ability. R², AIC and residual standard errors suggested that ML models prevail over PLS for the same two datasets (global tree roots). However, the biological interpretation of the signs of the partial regression coefficients associated with the initial root traits was more consistent with expectations using the PLS regression.

Table 6.

Coefficients and characteristics of multiple linear regressions (MLR) and partial least squares regressions (PLSR) using initial tree root traits from either all diameter classes or absorbing roots to predict the specific root decomposition rates

Model	Root category	k0	[N]0	[C]0	SRL	[water solubles]0	[hemicellulose]0	[cellulose]0	[lignin]0	R2	RSE	P	AIC
MLR	All roots	–0·0009	4·6e-05		–1e-06		0·00001438	0·00002126		0·93	4·5e-05	0·0048	–166·7
MLR	Absorbing roots	–0·0007			–7e-06	0·0000148		0·0000444		0·79	7e-05	0·0190	–158·1
PLSR	All roots	–0·0003	2·9e-05				0·0000159			0·75	7e-05	0·0020	–160·3
PLSR	Absorbing roots	0·0015		–3e-06		0·00000248	0·00000875		-0·00000542	0·66	7·6e-05	0·0041	–157·5

DISCUSSION

The main motivation of our study was to assess the potential of a comparative approach to predict in situ plant root decomposition rates. If successful this would be a quicker, more efficient and generalizable way of assessing root turnover and would be an important tool to better appraise carbon fluxes from plant roots to the soil organic carbon pool during the decomposition process. We specifically wanted to assess this potential in an agronomic context of sylviculture and crop production. However, this will require us to quantify carbon fluxes from roots. As many species and life forms can be cultivated in such agrosystems, it is necessary to generalize beyond taxonomic barriers. The comparative approach we used is based on morphological and chemical root traits, as it has been shown to give consistent predictions of leaf litter decomposition rates with above-ground traits (Melillo et al., 1982; Cornelissen and Thompson, 1997; Kazakou et al., 2009).

As the choice of herbaceous species was based on their use in North American agrosystems, our herbaceous species probably underestimate the natural range of root traits found in this group of plants. Indeed, variability in N content and specific root length in our species was lower than in the grassland species described in Roumet et al. (2006). As expected, the root N contents followed a pattern of herbaceous species > broadleaved trees > conifers. Within tree species, N content in absorbing roots was significantly higher than in diameter classes altogether.

As found by Silver and Miya (2001), herbaceous lignin concentrations were lower than in trees. But in contrast to Silver and Miya (2001), who found a lignin content pattern of broadleaved trees > conifers > graminoids for roots from all size classes, we found that conifer lignin was always higher than in broadleaved trees in every diameter class. This difference in lignin content between broadleaved and conifer trees seems to increase with root diameter and is already significant for the finest size classes (i.e. absorbing roots), which had a maximum mean diameter of 0·6 mm. However, because our study only considers three conifer species, we do not know to what degree this difference compared with Silver and Miya (2001) is real. Lignin control of decomposition rates is not unanimously supported (Alexander, 1977; Taylor et al., 1991). It has been reported that lignin concentrations would not be high enough to significantly inhibit decomposition (Taylor et al., 1991), or that correlations are not significant at a global scale (Silver and Miya, 2001). In this study, the correlations of lignin content with root decomposition rates follow the pattern of absorbing tree roots > herbaceous species > total tree roots. It seems that the coarser the diameter classes, the weaker the correlation. It would probably take very long-term studies to still detect a strong effect of lignin on higher diameter classes of tree roots (Berg, 1984).

Our results support the fact that interspecific variation in global root decomposition rates is predictable given the decomposition rates of each carbon fraction, weighted by their initial proportions. Unfortunately, although this model fits well, we also detected interspecific variation in the decomposition rates of the different carbon fractions. This means that interspecific variation in the total root mass decomposition rates are not only due to differences in the initial proportions of these carbon fractions among species but also to species-specific differences in the decomposition rates of the different carbon fractions themselves and this limits the generality of the result. What might cause such interspecific differences in decomposition rates of a single carbon type? One possibility is that the fibre analysis results in our carbon types are too heterogeneous; for instance, different types of lignin, whose proportions vary among species, could have different decomposition rates. Another possibility is that decomposition rates of a given carbon fraction might non-linearly depend on the proportions of other fractions. Such non-additive effects might arise, for instance, if the access of micro-organisms to the carbon fraction they are able to mineralize can be altered by other forms of carbon (e.g. cellulose fibres included in the lignin matrix of secondary cell walls).

Although the interspecific variation in k values for a given carbon type reduces the generality of our results, they still show that root mass during decomposition can be accurately predicted given the initial dead root mass and the measured k value of the corresponding species and point to the importance of finding those functional traits of roots that allow for interspecific generalization. This last predictive model appeared helpful as a test of the intact soil core sampling method. The standard error found at the lowest hierarchical level (i.e. between twin cores) is still high enough to be a significant source of error when estimating initial root mass and yet good predictive ability was observed using only the average initial root mass estimates rather than the actual initial root masses. The residual errors in the predicted remaining mass values of Fig. 1 reflect the cumulated errors of initial root mass estimates and imperfect fits of mass loss kinetics of each species with the Olson exponential model. Nevertheless, these predictions remained very satisfactory (R² = 0·95, RSE = 0·39), regardless of the method set-up (i.e. in the controlled experiment for herbaceous species or in the field for trees). Although our method of estimating initial root biomass first appeared as a potentially substantial drawback, this sampling method seems promising considering the many advantages.

An unexpected result probably arose from this in situ decomposition technique. In our PCA plots between tree root decomposition rates and their initial traits, specific root length is weighted negatively (i.e. the finer the roots, the longer their decomposition). Although specific root length is not significantly correlated to tree root decomposition rates when taken separately, this unexpected result might be influenced by greater mycorrhizal colonization of fine roots, also meaning slower decomposition for these colonized roots (Langley et al., 2006). Indeed, mycorrhizae, and especially ectomycorrhizal sheaths around their host root, are efficient in protecting the root from external physico-chemical attack. However, little is known about this phenomenon and the crucial factor is probably the survival of the fungi. Ectomycorrhizal enzymes can remain active for several weeks after the fungus is cut off from its root host (J. Garbaye, INRA, Nancy, France, pers. comm.), and this is probably proportional to the remaining carbon reserves in the excised root network. It is perhaps for this reason that Langley et al. (2006) found that mycorrhizal colonization slowed root decomposition, as they only harvested fine mycorrhizal roots that were dried before being put in litterbags. However, in the field, mycorrhizae probably live weeks or months after root death, and thus mineralize root organic carbon. As mycorrhizal colonization of roots occurs in the fine roots, mycorrhizal colonization probably plays a dominant role in fine root mineralization. This may be a reason why specific root length was not correlated with tree root decomposition rates.

Our initial motivation of proposing general equations predicting specific total root mass decomposition rates with initial root traits was compromised by the relatively small number of species. This was mostly due to the issue of multicollinearity between initial traits, revealed in the signs of four out of seven of the partial regression coefficients associated with the independent variables of the multiple linear regression (MLR) equations, which were contrary to global plant economic expectations. When strong collinearity among independent variables is encountered, or when the number of observations is modest relative to the number of variables, PLSR is expected to perform better than MLR (Höskuldsson, 1988) and this was the case in our study. Although MLR accounted for more of the variance (R² = 0·93 for total tree roots, and R² = 0·79 for absorbing tree roots) than PLSR (R² = 0·75 for total tree roots, and R² = 0·66 for absorbing tree roots) the coefficients of the independent variables from the PLSR analyses were consistent with typical expectations from functional trade-offs, with decomposition rates decreasing with increasing amounts of lignin and cellulose and increasing with increasing specific root length and amounts of soluble carbon and nitrogen. This issue of collinearity also comes out in the meta-analysis of Silver and Miya (2001), where lignin, lignin : N and C : N ratios have been used in the same multiple regression model. Their regression model had a positive lignin : N coefficient, where it is expected to be negative. As functional ecology is based on plant strategies defined by selected traits, which are strongly correlated with each other, this PLS method seems promising for these fields of biology where explanatory variables are not truly independent.

In interpreting the partial regression coefficients of our final regression model it is important to note that the effect of N on litter decomposition rate is controversial (Prescott, 2005). To better understand the underlying N-controlled mechanisms, we must distinguish between two factors: (1) the intrinsic tissue N content and the extrinsic soil inorganic nutrient availability, and (2) the early as opposed to later stages of decomposition. Unlike the external soil inorganic N, the intrinsic litter N is highly correlated with C chemistry and levels of polyphenols. However, artificial external N additions to the soil are more prone to stimulate the decomposition of lignin-poor litters and suppress that of lignin-rich ones (Carreiro et al., 2000) because N addition inhibits fungal lignolytic activity (Waldrop and Zak, 2006). In contrast to lignolitic activity, cellulase activity would be stimulated by increased soil N availability (Carreiro et al., 2000). Early stages of decomposition mostly driven by low-recalcitrance compounds would be stimulated, whereas it would be suppressed at later stages. In this study, we consider N root content as a specific chemical trait, used as an integrating index of root biochemistry.

There now exist large trait databases covering many thousands of plant species. Because our root traits are static measurements made on easily obtained roots and using standard chemical methods it should be possible to measure them on many species and incorporate the results in these pre-existing trait databases. If the results reported here can be replicated in a larger set of species and environmental conditions it should then be possible to use the resulting regressions in more general ecosystem models of carbon cycling. Besides determining the generality of our results, it will also be important to decompose the mass-loss kinetics reported here into the mass-loss kinetics of different carbon fractions as the temporal dynamics of carbon cycling in the soil is also profoundly affected by the recalcitrance of different carbon fractions in the root tissue.