Bayesian multiple-instance motif discovery with BAMBI: inference of recombinase and transcription factor binding sites

Abstract

Finding conserved motifs in genomic sequences represents one of essential bioinformatic problems. However, achieving high discovery performance without imposing substantial auxiliary constraints on possible motif features remains a key algorithmic challenge. This work describes BAMBI—a sequential Monte Carlo motif-identification algorithm, which is based on a position weight matrix model that does not require additional constraints and is able to estimate such motif properties as length, logo, number of instances and their locations solely on the basis of primary nucleotide sequence data. Furthermore, should biologically meaningful information about motif attributes be available, BAMBI takes advantage of this knowledge to further refine the discovery results. In practical applications, we show that the proposed approach can be used to find sites of such diverse DNA-binding molecules as the cAMP receptor protein (CRP) and Din-family site-specific serine recombinases. Results obtained by BAMBI in these and other settings demonstrate better statistical performance than any of the four widely-used profile-based motif discovery methods: MEME, BioProspector with BioOptimizer, SeSiMCMC and Motif Sampler as measured by the nucleotide-level correlation coefficient. Additionally, in the case of Din-family recombinase target site discovery, the BAMBI-inferred motif is found to be the only one functionally accurate from the underlying biochemical mechanism standpoint. C++ and Matlab code is available at http://www.ee.columbia.edu/~guido/BAMBI or http://genomics.lbl.gov/BAMBI/.

INTRODUCTION

Gene expression underlies most essential cellular processes and is typically controlled by complex networks of regulatory interactions. Two of the basic mechanisms directly involved in regulating gene expression are transcription factor binding and site-specific recombination (1). In both cases, the proteins involved often attach to highly specific nucleic acid sequences, which leads to the activation or repression of gene expression either through epigenetic interactions between transcription factors and components of RNA polymerase machinery or via recombinase-mediated genetic and genomic modifications of relevant DNA regions.

As individual binding sites are subject to context-specific optimizations of protein affinities as well as neutral alterations by random mutagenesis, nucleotide sequences of various site instances can display a significant degree of heterogeneity. Even so, each instance may be expected to preserve certain core sequence features—such as nucleotide patterns responsible for the specificity of transcription factor binding or relative positions of bases where recombinase-induced DNA strand breaks can occur—making them identifiable as a motif. A key question in understanding the genomic organization and gene-regulatory network structure of biological systems thus comprises the discovery of conserved motifs within available sequence data. Still, although nucleic acid motif discovery (whereby one attempts to infer the identity and locations of conserved patterns in a given set of nucleotide sequences) has been the subject of much research in recent years, it remains a highly multifaceted and computationally challenging problem (2).

The principal subject of this work is further development of basic methodology for motif discovery within nucleic acid sequences. Following the discussion in Tompa et al. (2), we focus on analyzing primary sequence data—in the absence of any auxiliary information. Notably, this does not preclude but rather encourages the subsequent integration of our method with other heterogeneous approaches—such as those involving comparative sequence analysis, expression level data, chromatin immunoprecipitation results, and others—that synergistically complement each other by identifying interactions across different scales and domains of system organization. [For example, the cMonkey scheme successfully combines motif discovery by the antecedent MEME algorithm (3) with novel developments in biclustering of expression data to generate cumulative improvements in gene regulatory network predictions (4).]

Along with performance, one of the essential requirements for a biologically useful discovery algorithm is its broad applicability—both with respect to the lack of constraints on motif features as well as the universality of supported sequence databases. For instance, while a number of techniques have been developed for identifying a motif that appears only once in each sequence of a database, the same motif may and often has to be present at multiple sites in the genome. This is particularly significant in the case of recombinases, like those of the Din family, that require two or more separate sites to provide counterparts for strand exchange as well as in the case of primary regulon mediators, like cAMP-CRP, that must have multiple genomic targets in order to enable the sophisticated control patterns observed (1)—thus demanding that the motif discovery algorithm be able to identify several instances of the same motif in a given sequence. Furthermore, based on the extent of experimental evidence, the method should also accommodate scenarios where a priori knowledge of such motif features as length or composition is likely to either be incomplete, uncertain or even entirely absent. The algorithm also needs to be versatile and scalable to be of meaningful practical utility. For example, since motif instances may be located near as well as far from any gene transcriptional start site, the technique must be capable of handling long sequences as well as short ones.

Many previously proposed solutions have been pattern-driven exhaustive searches, with the motif discovery question stated as an (l, d)-motif problem (5). In this approach, the motif is assumed to be of length l and have at most d mismatches between the true/empirical consensus sequence and its individual instances. Examples are WINNOWER (5), where the solution reduces to finding large cliques in multipartite graphs; and CONSENSUS (6), which uses a greedy technique to solve the problem. Another variant of this methodology is a sample-driven search that trades off sensitivity for computational efficiency by looking for patterns hidden in data subsets—such as employed by YMF (7), an enumerative algorithm that looks for motifs with highest z-scores; and Weeder (8), which uses extended enumeration that is better adapted to longer patterns. While potentially highly accurate, the main shortcoming of such methods is that they do not scale well with the size of the site, effectively limiting pattern-driven approaches to motifs no longer than 10–12 nt (9).

An alternative is offered by profile-based methods that model motifs in statistical terms. A motif is then described by a position weight matrix (PWM), where each column relates to the distribution of all possible nucleotides at a given position. That is, in the case of DNA-drawn sequences and a motif of length M, the PWM is typically a 4 × M matrix (often graphically represented as a logo), whose columns correspond to probability vectors of finding A, T, C or G at the corresponding nucleotide position. This matrix is not known a priori and is usually estimated before or jointly with the discovery of locations of individual motif instances. Examples of such technique are MEME (Multiple EM for Motif Elicitation) (3,10,11), which utilizes expectation-maximization (EM) framework to discover an unknown number of different motifs that appear an unknown number of times; several algorithms—including BioProspector (12), AlignACE (13), Gibbs Motif Sampler (14), MotifSampler (15) and SeSiMCMC (16)—that rely on Gibbs sampling; and Liang et al.'s approach (17), where a deterministic sequential Monte Carlo-based method is developed.

In this work, we present a Bayesian Algorithm for Multiple Biological Instances of motif discovery (BAMBI), which is able to detect an unknown motif of an unknown length with an unknown number of instances in a sequence database. The algorithm uses a profile-based approach—modeling a motif via PWM, which is estimated concurrently with the discovery task—and can work solely on the basis of nucleotide sequence data. (However, if additional experimental evidence, results of alternative motif discovery algorithms, or other sources of prior knowledge regarding any PWM components are available, BAMBI is flexible-enough to be able to include this information in its analysis.) Unlike earlier works, such as Liang et al. (17) that has developed a deterministic sequential Monte Carlo algorithm, our approach is able to independently estimate the putative motif size as well as to discover its multiple instances or to establish their absence in each of the database sequences—all within the Bayesian framework. The resulting method, BAMBI, displays better statistical performance than MEME, BioProspector (which is augmented with BioOptimizer (18) wherever there is uncertainty about motif length), SeSiMCMC and Motif Sampler in three diverse settings, including being the only algorithm that leads to a biochemically meaningful result in the recombinase binding site discovery case.

MATERIALS AND METHODS

This section provides an overview of basic methodology and a general description of the implementation used by the BAMBI algorithm—with specific mathematical details being provided in the Supplementary Data.

We are seeking to discover nucleotide motifs, which are sets of patterns conserved when compared to a collection of non-specific genomic segments. A database of nucleotide sequences—where each sequence may contain one, several, or no instances of motif—along with an upper limit on the total number of such instances in each sequence serve as problem inputs. For example, in the case of the CRP database (discussed later in further detail) the supplied input is a set of 105 nt-long DNA segments from non-coding regions upstream of 18 Escherichia coli genes. The desired output is the number, length and locations of CRP-binding sites within each sequence.

Overview

As noted earlier, the innate heterogeneity observed among instances of individual binding sites—which is driven by local context optimization requirements, mutagenesis, fluctuations in measurement fidelity, etc.—makes the determination of motif sequences a statistically uncertain problem. While these variations may be ascribed to an amalgamation of random processes, the ensuing probabilistic nature of the motif discovery problem can be captured through the use of the hidden Markov model (HMM) framework. That is, given a database of nucleic acid strand segments, we consider the information in question—namely, the number, length and locations of individual motif instances in each sequence—to be unobservable directly (i.e. ‘hidden’). Instead, the available data consists solely of base sequences themselves, wherein motif patterns of interest—which remain to be ‘discovered’—may (or may not) be embedded. The approach used for the discovery process is based on Bayesian inference—a powerful and flexible technique able to utilize a broad range of data toward elucidating various hidden/unknown system parameters—which, in our case, focuses on motif lengths, logos and instance locations. (Therein, one starts with a probabilistic model that reflects the knowledge regarding parameter values of interest as available a priori, if any. This ‘prior’ distribution is then updated to the ‘posterior’ one by conditioning on any additionally obtained information through the use of Bayes' probability formula, which results in a posteriori estimates of parameters that are progressively more constrained with each new observation.)

Significantly, although Bayesian techniques have been previously applied to the problem of identifying patterns in nucleic acid sequences, BAMBI implements this approach by treating entire sequences contained in the database (rather than single bases or smaller segments within them) as individual observations. This potentially allows an algorithm to better capture the more subtle structural features present within individual motif logos, which may account for the improved results demonstrated by BAMBI in discovering the binding motif of Din-family recombinases as discussed below.

However, while generally more informative, the use of such larger data elements comes with substantial additional computational costs, which inhibit efficient model estimation. Here, we overcome this impediment through the use of a sequential Monte Carlo technique. This approach generates estimates of hidden variables by finding approximations of their posterior distribution given observations. Ideally, one might have liked to approximate this posterior distribution by obtaining samples from it, but this is generally impossible—e.g. due to the referenced computational complexity. Instead, samples (called ‘particles’) are first drawn from an alternative distribution (called ‘importance distribution’) and a weight is then attached to each sample in such a way as to compensate for any mismatch between the true posterior and the importance distribution, which completes the method. (Given the broad freedom in choosing the importance distribution, here we have selected one that is suitable for a sequential method—that is, it enables processing of each observation individually—see Supplementary Data for more detail.)

Bayesian algorithm for multiple biological instances

As outlined in the previous section, when using BAMBI to identify the motif and find all of its instances, we look to process one sequence from the input database at a time in a sequential manner. To this end, we represent the system as a HMM, where the hidden state corresponds to the ‘state vector’, x_t, which is the concatenation of the number of motifs in the current sequence and their locations. (Note that the dimension of the state vector differs across individual sequences in the database due to the varying numbers of motif instances they contain.) The t-th sequence is considered to be the observation at step/time t, for which the corresponding state vector is to be estimated. The transition probability from the state at time t − 1 to the state at time t depends on the unknown distribution of the number of instances of the motif in a sequence, which we described by a vector: λ = [λ₀ … λ_N], where N is the upper bound on the number of motif instances in the sequence database. Similarly, for a given state, the emission probability is considered to be dependent on an unknown PWM, which describes the distribution of nucleotides at each position of the motif. These nucleotides are regarded as being denoted by letters drawn from a given alphabet, which is typically taken to be: {A, C, G, T/U} (although accounting for methylation, other nucleoside modifications, or experimental use of non-standard bases may lead to alternative representations). We let the probability of finding any specific letter at the j-th position of an M-long motif be denoted by θ_j. Taken across all positions in the motif, j = 1, … , M, this information can be represented as a PWM: θ = [θ₁, … , θ_M]. Finally, while more complicate models can be utilized when necessary, in this article nucleotides not belonging to a motif are assumed to be independent and identically distributed according to a given background distribution: θ₀, which is estimated in a problem-specific manner by collecting statistics over the embedding DNA segments, employing results of other methods as input, using uniform or other heuristics, etc.

BAMBI looks to estimate the number and position of motif instances in each sequence without prior knowledge of λ or the PWM. Given all sequences from first to t-th and the background distribution of nucleotides outside of motifs, θ₀, this information is encapsulated by the (hidden) state vector, x_t. Here, we propose to infer these hidden states, within a Bayesian framework, that is, we use prior distributions to model and handle the unknown parameters of the system. In particular, we assume the PWM θ consists of M independent random vectors (one for each position of the motif), which are distributed according to a Dirichlet distribution (19). The Dirichlet distribution is the multivariate generalization of the beta distribution, which is a univariate distribution notable for being able to assume a broad variety of shapes—from uniform to unimodal to bimodal—depending on the values of its two parameters, thus allowing for characterization of a broad variety of probabilistic systems. The Dirichlet distribution is defined for non-negative variables that sum to one—a condition satisfied by each column of the PWM. Moreover, this distribution has the advantage of being the conjugate prior of the categorical (discrete) distribution, that is, both prior and posterior distributions of θ_i will be distributed according to the same distribution. The Dirichlet distribution has previously been used for modeling the PWM (17). The distribution of the number of instances λ of the motif in each sequence is also represented as a random vector following a Dirichlet distribution.

Within the context of this model, a sequential Monte Carlo method is then used to approximate the distribution of the hidden states up until time step t given observations, which is the distribution of the quantity of interest conditional on the sequences from first to t-th. However, as the measurement model depends on an unknown vector θ and the state transition depends on an unknown vector λ, we modify the approximation procedure to average out the influence of these two unknown parameters. To this end, we show in the Supplementary Data how the resulting set of expressions can be computed in closed forms to enable a highly efficient solution for the problem of finding instances of a motif in a set of unaligned sequences.

The class-based resampling scheme presented in (20) is employed to estimate the unknown length of the motif, M, jointly with the number and location of motif instances for each sequence by using the augmented hidden state vector to include the length of the motif. As the length of the motif is not expected to change from sequence to sequence, a static dynamics is used for M. Finally, to avoid letting the algorithm be stuck with one potentially incorrect motif length, this scheme is applied to each of the possible considered motif lengths.

As the complexity of the sequential estimation process increases with the dimension of the state vector, we propose a fast version of the method that divides the inference process in two stages. In the first stage, we use the sequential Monte Carlo method in order to decide whether there is at least one or no instance of the motif in each sequence, and to obtain an estimate of the PWM θ. The number of instances of the motif in each sequence is then determined by the second stage, where the estimate of the PWM is used as a prior for a sequence of binary hypothesis (21) as shown in the Supplementary Data.

Notably, the Bayesian framework proposed here can be easily adapted for use with and/or refinement of results arising from other motif discovery algorithm by modifying the PWM prior based on this information. (If no such algorithm is available, estimation of the PWM is initiated with an uninformative prior.)

RESULTS

We have applied BAMBI to several motif discovery problems, using both empirical as well as synthetic data, and evaluated its performance on the basis of the nucleotide-level correlation coefficient (nCC)—a robust measure that captures both the sensitivity and the specificity of a method (22). While there are a number of alternative statistics that can potentially be used to compare performances of various bioinformatics algorithms, greatest nCC score has been suggested by Tompa et al. after an extensive study (2) as the reportable metric for subsequent assessment of motif discovery tools. It is defined as:

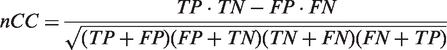where TP/TN are the total number of nucleotides in the input database that are estimated to be true positives/negatives and FP/FN are the total number of nucleotides estimated to be false positives/negatives, based on an empirically established baseline standard.

In all instances, the performance of the presented algorithm has been further compared against four popular nucleic acid motif discovery methods: BioProspector, MEME, SeSiMCMC and Motif Sampler.

In all the applications, BAMBI was initialized by setting the parameters of the corresponding Dirichlet distribution at each position in the PWM to be 1. This transforms the Dirichlet distribution into a uniform distribution, as no information about the motif is assumed. Similarly, the parameters of the Dirichlet distribution corresponding to the distribution of the number of instances of the motif in each sequence is initialized as follows. The parameter corresponding to the case of no instance of the motif is set to 1, and the parameter corresponding to the case of having one instance is set to be equal to the average length of the input sequences. This allows the algorithm to have a good number of particles with an instance of the motif while having some with no instance as well when processing the first sequences. Finally, the number of particles is set to be 20 times the average length of the input sequences.

Synthetic database

Synthetic data was used to test each algorithm for different motif lengths. For every considered motif length, 10 databases were generated, each containing 25 sequences of 200 nucleotides. All sequences were seeded with 0, 1 or 2 instances of the motif with probabilities 0.1, 0.3 and 0.6, respectively. When a sequence has one or two instances of the motif, their locations are randomly selected using a uniform distribution. Nucleotides belonging to an instance of the motif were drawn from a distribution that has 0.7 probability for a dominant nucleotide and 0.1 for the remaining three nucleotides. The identity of the dominant nucleotide for each position was chosen randomly. For the positions in the sequence not belonging to a motif, the nucleotides are equiprobable, i.e. there is a probability of 0.25 for each nucleotide. The total nCC is computed for each motif lengths between 14 and 20.

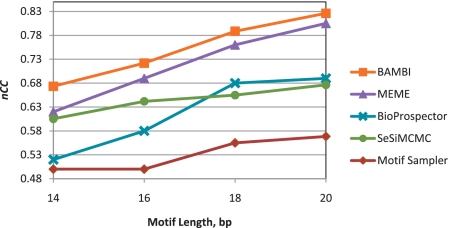
The results produced by the BAMBI algorithm have been compared with those generated by MEME, BioProspector, SeSiMCMC and Motif Sampler. All five algorithms have been given the exact motif length in each test. When applying Motif Sampler, the true background distribution is supplied as an input to the algorithm. The resulting values of nucleotide-level correlation coefficients are given as a function of motif length in Figure 1. It is seen that the algorithm proposed here achieves higher performance than the other four methods for all tested motif lengths.

Figure 1.

Performance comparison of different methods using synthetic data with varied motif length.

Real databases

We have analyzed two types of empirical DNA sequence data and compared the performance of BAMBI to that of MEME, BioProspector, SeSiMCMC and Motif Sampler. The first application is a transcription factor binding site data set, which consists of 18 short sequences that contain zero to two motif instances. The second is a site-specific recombinase binding data set, which comprises only 10 sequences, but of considerably greater length (see Table 1) that contain two instances of the motif. This represents two completely different experimental scenarios where the Bayesian motif discovery is tested and compared with other approaches.

Table 1.

Statistics of the recombinase database

Number of Sequences	10
Shortest Sequence (nucleotides)	546
Longest Sequence (nucleotides)	4335
Average Sequence Length (nucleotides)	2436.4
Total Data set Size (nucleotides)	24364

For these two data sets, we set Motif Sampler to estimate the background distributions as an order 1 Markov model from the input sequences. When analyzing the synthetic data set, the true background distribution was supplied, but in the case of the real data sets, such distributions are unknown.

cAMP receptor protein database

Site-specific cAMP-CRP binding to DNA represents the prototypical model of gene regulation by a transcription factor (1,23). In large part, this may be attributed to cAMP receptor protein (CRP) being an essential component of catabolite repression system, with research history in E. coli dating back to Monod's investigation of the ‘glucose effect’ (23). It also constitutes an example of a regulon, which plays a major role in directing bacterial energy metabolism (1) and whose significance has been recently further brought to fore by bioremediation and bioenergy applications (23,24). In fact, the identity of both CRP binding sites and amino-acid residues responsible for interacting with them have been so well-understood as to allow novel in silico-designed and in situ-engineered protein–DNA pairs binding with sufficient specificity to enable transcription factor activity (25). Here, we apply BAMBI as well as MEME, BioProspector with BioOptimizer, SeSiMCMC and Motif Sampler algorithms to identify the presence of CRP regulatory binding sites in 18 DNA sequences—each 105 nt in length. It has been experimentally determined that there are 23 instances of the motif of length 22 in the set (26).

For the purposes of our analysis, the length m of the motif is considered to be unknown, requiring the use of respective procedures noted earlier. We impose a lower and upper bound on m of 17 and 27—respectively—and set the number of possible instances of the motifs to be between 0 and 2. (If another algorithm supplies more than two instances of a motif in a sequence, only the two highest scoring ones are kept to facilitate the comparison.) In the case of Motif Sampler, the length of the motif is supplied as an input to the method, as it cannot deal with uncertainty regarding this parameter.

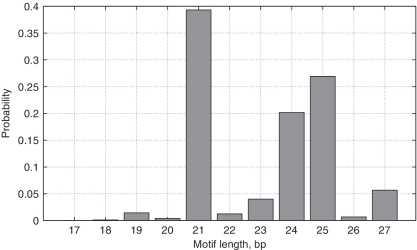
Figure 2 shows the estimated probability mass function of the different values of m after applying BAMBI to the entire database. As can be seen from the results, the BAMBI algorithm has estimated the most likely motif length to be 21 bp long, whereas the true motif length is considered to be 22 bp, as noted earlier. By comparison, both MEME and BioProspector with BioOptimizer have estimated the length of the motif to be 24 bp, with SeSiMCMC yielding 19 bp.

Figure 2.

Length PDF estimated by BAMBI for the CRP binding site motif.

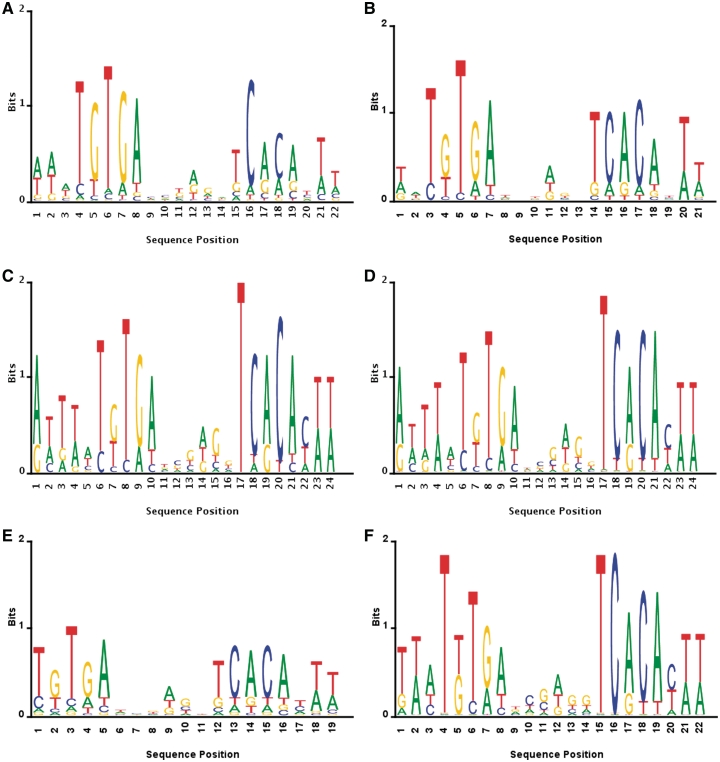
The estimated PWM logos for different motif discovery algorithms along with the one inferred from measured data are shown in Figure 3. The CRP motif contains two highly conserved inverted repeat sub-structures: ‘TGTGA’ and ‘TCACA’, which are likewise shown to be present in all of the logos.

Figure 3.

Logos of the CRP binding site motif. Empirical (‘True’) versus those inferred by the different algorithms. (A) True motif logo, (B) BAMBI's motif logo, (C) MEME's motif logo, (D) BioProspector's motif logo, (E) SeSiMCMC's motif logo and (F) Motif Sampler's motif logo.

The net results achieved by the BAMBI algorithm—as compared with those of MEME as well as BioProspector with BioOptimizer, SeSiMCMC and Motif Sampler (with the latter having been supplied with known motif length)—are given in Table 2, where 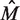is the estimated motif length. It can be seen that BAMBI is performing better by both the statistical significance criterion (nCC) as well as based on the estimated motif length 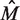, for which BAMBI gives an estimate closest to the experimentally determined value.

Table 2.

Performance comparison using the CRP database

	BAMBI	MEME	BioProspector (+BioOptimizer)	SeSiMCMC	Motif Sampler
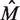	21	24	24	19	–
nCC	0.6763	0.5358	0.5745	0.63633	0.5590

The value of M was found to be 22 empirically.

Din-family of site-specific serine recombinases database

Site-specific recombination is a process by which well-defined sequences (‘recombination sites’) on the same or two different DNA molecules come together and undergo strand exchange, usually catalyzed by specialized enzymes called recombinases (sometimes contextually referred to as ‘invertases’ or ‘integrases’). Based on the location/orientation of sites and other conditions, a recombination reaction results either in the inversion or excision/integration of the intervening DNA segment (27). The latter generally contains promoters, alternative coding sequences, or other elements regulating gene expression; so that a recombination event causes initiation/cessation of transcription or/and synthesis of a different message RNA. Thus, site-specific recombination offers an organism or a virus an ability to generate mutually exclusive genetic states through ‘programmed’ DNA rearrangements. This type of gene regulatory mechanism has the advantage of being absolute—i.e. expression is impossible when the gene is lacking a correctly oriented promoter or is physically separated into several non-functional pieces—which may be critically important should presence of even one copy of the wrong protein become highly disadvantageous as, for example, might be the case for a pathogen targeted by antibodies directed against that protein (1,28). Recombination may also have a further advantage of facilitating rapid and optimized adaptation to such critical environmental conditions without the need to rely on slow and frequently deleterious process of random mutagenesis (29). Indeed, gene regulatory networks driven by site-specific recombination appear to be particularly enriched among pathogens, including uropathogenic E. coli—the predominant cause of urinary tract infections—and Salmonella Typhimurium (28,29).

Importantly, such environmental conditions may often be rare or difficult to reproduce in the lab—e.g. when they involve intra-host pathogen dynamics (28)—causing potentially critical genomic rearrangements to remain phenomenologically undetected. One alternative could be to analyze genomic sequences directly for the presence of recombination sites through bioinformatics means. This approach may be further enabled by the fact that virtually all identified site-specific recombinases belong to one of just two basic families, named serine or tyrosine after the amino acid residue that forms the covalent protein–DNA linkage in the reaction intermediate (27). The serine family comprises three primary subfamilies characterized by sequence, structural and recombination site homology (29,30). Here, we use motif discovery algorithms to infer the DNA recombination site (dix) of Din serine subfamily, which includes such notable recombinase examples as Hin (responsible for flagellar phase variation in Salmonella), Gin (determination of phage Mu host specificity) as well as a number of other bacterial and phage systems.

All known Din family members recognize a 26 bp-long minimal recombination sites (29,31), with the list used in this study given in Table 3. Specific sequence sources employed to assemble the segment database used for site motif discovery comprised: Salmonella enterica serovar Typhimurium D23580 (GenBank FN424405); Bacteriophage Mu (GeneBank AF083977); Enterobacteria phage P1 (GenBank AF234172); prophage e14 of E. coli K12 (GenBank K03521); E. coli plasmid p15B (GenBank X62121); Dichelobacter nodosus VCS1001 (A198) (GenBank U02462); and Shigella sonnei [GenBank D00660 – revised from S. boydii, but functional in S. sonnei A. Tominaga (personal communication)]. To generate the standardized data set, seven sequences listed above were further cut, making sure two instances of the motif remained inside each segment. As there are 20 instances of the motif, this resulted in 10 sequences being used as the input to the algorithm (see Supplementary Data). Specific details of the so obtained database are shown in Table 4.

Table 3.

Target sites of Din-family recombinases

dix (consensus)	TTC———AAAC–	–A	–GTTT———GAA
hixL	TTCTTGAAAACC	AA	GGTTTTTGATAA
hixR	TTTTCCTTTTGG	AA	GGTTTTTGATAA
gixL	TTCCTGTAAACC	GA	GGTTTTGGATAA
gixR	TTCCTGTAAACC	GA	GGTTTTGGATAA
cixL	TTCTCTTAAACC	AA	GGTTTAGGATTG
cixR	TTCTCTTAAACC	AA	GGTATTGGATAA
pixL	TTCTCCCAAACC	AA	GGTTTTCGAGAG
pixR	TTCTCCCAAACC	AA	CGTTTATGAAAA
mixMI′′L′	TTCCCCCAAACC	AA	CGTTTTAGTCTT
mixMr′′N′	TTCCCCTAAACC	AA	CGTTTTTATGCC
mixN′′O′	TTCCCCCAAACC	AA	CGTTTTTATGTG
mixO′′P′	TTCCCCTAAACC	AA	CGTTTTTATGCC
mixP′′Q′	TTCCCCTAAACC	AA	CGTTTTTATGCC
mixQ′′R′	TTCCCCCAAACC	AA	GGTAATCAAGAA
nix1	TTTCCCAGAAGC	AA	CCTTAAGTAAAA
nix2	TTTCGCAGAAGC	AA	CCTTACGTCAAA
nix3	AGACGAAGAAGC	AA	CCTTAAGTCAAA
nix4	TTTCCCAGAAGC	AA	CCTTAAGTCAAA
bixL	TTCCTGTAAACC	GA	GGTATTCGATAA
bixR	TTCCTGTAAACC	GA	GGTTTTAGATAA

Recombination sites for Din subfamily members: Hin (hixL and hixR), Gin (gixL and gixR), Cin (cixL and cixR), Pin (pixL and pixR), Min [mixMI′′L′, mixMr′′N′, mixN′′O′, mixO′′P′, mixP′′Q′ and mixQ′′R′—labeled according to the convention used in (32)], D. nodosus [nix1, nix2, nix3 and nix4—with sequences taken from the updated GenBank record rather than as specified in Moses et al. (31)], and PinB (bixL and bixR) (29,31–34). Din palindromic consensus binding site (dix) is as discussed in (35). The two core residues at the centers of the sites where strand breakage and exchange occur are highlighted in bold.

Table 4.

Database of recombination sites

GenBank accession number	Start sequence	End sequence	Recombination sites
FN424405	2907699	2908805	hixL, hixR
AF083977	31913	35084	gixL, gixR
NC_005856	32206	36541	cixL, cixR
X01805	21	1929	pixL, pixR
X62121	2743	4447	mixR′M1′′, mixMr′′N′
X62121	4848	5465	mixN′′O′, mixO′′P′
X62121	5868	6414	mixP′′Q′, mixQ′′L′
U02462	182	4049	nix1, nix2
U02462	4489	8411	nix3, nix4
D00660	600	3788	bixL, bixR

Sequence start and end labels are given by the nucleotide number in the corresponding GenBank record.

The number of nucleotides previous to the first instance of the motif is chosen from a uniform distribution between 0 and 50. The number of nucleotides to keep after the second instance of the motif was chosen analogously. Note that the two instances of the motif present in each sequence are often oriented in opposite directions, so the analysis has been extended in a straightforward manner to account for characteristics specific to double-stranded DNA by searching for sites located on the reverse complement as well. This is implemented within the context of the BAMBI hidden Markov model by replacing each double-stranded entry in the sequence database with one that is a concatenation of the corresponding forward and reverse strands (both in the 5′-to-3′ orientation). As BAMBI is able to discover both the number and locations of multiple motif instances, running the algorithm over the modified database identifies sites located on either strand.

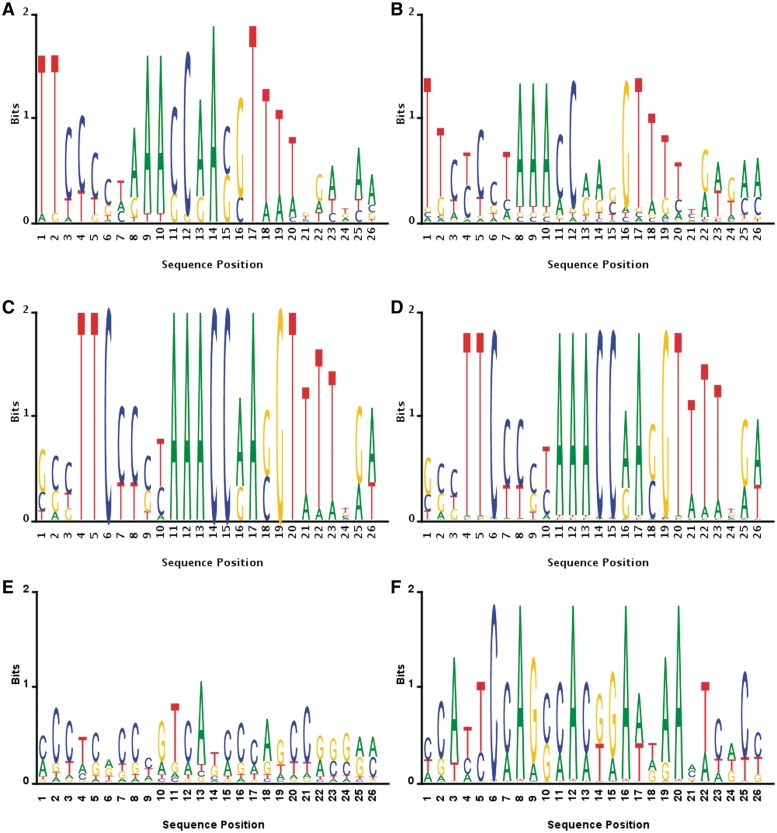
The logos estimated by the different algorithms are presented in Figure 4. It can be seen that BAMBI, MEME, and BioProspector find similar consensus sequences, while SeSiMCMC and Motif Sampler do not. A quantitative significance comparison of the results—given in Table 5—shows that the BAMBI algorithm achieves the best statistical performance, and that both SeSiMCMC and Motif Sampler were not able to find the motif.

Figure 4.

Logos of the Din recombinase binding site motif. Empirical (‘True’) versus those inferred by the different algorithms. (A) True motif logo, (B) BAMBI's motif logo, (C) MEME's motif logo, (D) BioProspector's motif logo, (E) SeSiMCMC's motif logo and (F) Motif Sampler's motif logo.

Table 5.

Performance comparison using the recombinase database

	BAMBI	MEME	BioProspector	SeSiMCMC	Motif Sampler
nCC	0.7711	0.7618	0.7618	−0.0153	−0.0182

MEME, BioProspector, SeSiMCMC and Motif Sampler did not produce a functionally correct site.

Furthermore, only the BAMBI algorithm has been able to identify a functionally meaningful and biochemically correct recombination site. This is because, while for a transcription factor the inferred site only needs to specify preferred binding locations, in the recombinase case the DNA sequence itself has a functional role in gene expression regulation and so requires accurate identification of both the motif as well as strand breakage/exchange positions within it. As a result, any spatial shifts in the binding motif location away from the true sequence are likely to have a dramatic and deleterious effect on the product of site-specific recombination—e.g. by either putting an alternative coding sequence out of frame, removing a portion of the promoter region in the course of an inversion/excision or inhibiting strand exchange altogether. Thus, a shifted sequence prediction—no matter how close to the true motif in the statistical sense—cannot be deemed correct or acceptable in the biochemical sense as it undermines either bioengineering/synthetic biological implementation or systems biological analysis of the recombination products and their function.

In the case of the Din subfamily recombinase sites, the strand breakage/exchange reaction occurs through a staggered cut between the two ‘core’ residues, which necessarily have to be symmetrically and centrally located within the recombinase binding motif [see Table 3 and, for example, (29)]. As may be seen by comparing the inferred logos (Figure 4) among themselves or with the empirically established consensus Din binding site (Table 3), only the motif discovered by BAMBI accurately identifies the spatial location of the dix sequence, while the predictions of both MEME and BioOptimizer are shifted right by 3 bp. Given that the overall length of the motif is 26 bp, such a difference may not appear to be particularly significant statistically (e.g. as reflected by the nCC performance measure, Table 5). However, this is not the case biochemically, because such shifts generally lead to the incorrect determination of the identity of the two middle residues—the location of strand exchange—and so result in a non-functional recombinase site. For instance, outside of the two central residues, the rest of the motif must largely be palindromic in order to accommodate the symmetric binding of two recombinase molecules, whose dimerization is generally required for strand exchange. However, in MEME- and BioOptimizer-discovered binding motifs, the lateral shift relative to the true empirically known sequence substantially breaks this critical symmetry. Furthermore, the 2 bp central residue pair found via both MEME and BioOptimizer is a definitive AC (logo positions 13 and 14). However, the absence of complementary cores in the database as well as the presence of a ‘C’ (instead of the strongly conserved ‘A’, see Table 3) in the second position render such binding sites largely unable to support wild-type Din recombination, i.e. they are essentially non-functional (29). These problems are notably not present in the BAMBI's motif prediction, which is spatially aligned with the dix sequence and assigns the most weight to either AA or GA core pairs that are biochemically permissible.

DISCUSSION

In this article, we have proposed a BAMBI algorithm for the discovery of motifs, which solves the motif discovery problem where the location of motif instances in a sequence, their number, and length are unknown. The solution is based on representing the problem as a HMM with the sequential Monte Carlo method being used to estimate the unknown characteristics of the motif and the locations of its instances. Such a solution resides within the Bayesian framework that also allows the algorithm to use experimental or other motif discovery algorithm results as prior information and to refine their estimations.

The algorithm was tested in applications using both synthetic data as well as two empirical DNA sequence databases: one containing cAMP-CRP transcription factor and the other—Din recombinases binding sites. In all examples BAMBI has been shown to perform better than MEME, BioProspector with BioOptimizer, SeSiMCMC and Motif Sampler by the statistical measure of the nucleotide-level correlation coefficient. Furthermore, BAMBI was the only algorithm to provide a biochemically meaningful result for the Din recombinase binding motif.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

U.S. National Science Foundation (NSF) (under grant DBI-0850030, in part); U.S. National Science Foundation (NSF) (under grant CMMI-1028112 to X.W.); and ENIGMA-Ecosystems and Networks Integrated with Genes and Molecular Assemblies supported by the U. S. Department of Energy, Office of Science, Office of Biological and Environmental Research through contract No. DE-AC02-05CH11231. Funding for open access charge: The Columbia Open-Access Publication (COAP) Fund.

Conflict of interest statement. None declared.