Electrophysiological Imaging of Brain Activity and Connectivity – Challenges and Opportunities

Abstract

Unlocking the dynamic inner workings of the brain continues to remain a grand challenge of the 21^st century. To this end, functional neuroimaging modalities represent an outstanding approach to better understand the mechanisms of both normal and abnormal brain function. The ability to image brain function with ever increasing spatial and temporal resolution utilizing minimal or non-invasive procedures has made a significant leap over the past several decades. Further delineation of functional networks could lead to improved understanding of brain function in both normal as well as diseased states. This article reviews recent advancements and current challenges in dynamic functional neuroimaging techniques, including electrophysiological source imaging, multimodal neuroimaging integrating fMRI with EEG/MEG, and functional connectivity imaging.

I. Introduction

Functional neuroimaging has shown tremendous promise in better understanding the brain functions and dysfunctions [1]. It has established itself as a major tool for neuroscience research and clinical applications. Of importance is to map the spatially distributed and temporally dynamic neural activity with high resolution in space and time domains. The spatiotemporal mapping of brain activity and, more recently, connectivity is now an essential tool for the investigation of the brain, in terms of functional segregation and coordination. Noninvasive high resolution imaging of spatio-temporal patterns of neural information processing would greatly benefit the investigation of how the “Mind” is implemented in the brain, better understanding the mechanisms of perception, attention, learning, etc. Furthermore, such high resolution spatio-temporal neuroimaging would reveal the mechanisms of origination and propagation of dynamic epileptic activities, aiding various management options for intractable epilepsy which affects millions of population worldwide. Our knowledge thus far has been determined by the capability of the imaging technology. An ideal technology would be able to directly record neuronal activities, i.e. electrophysiological signals, in high spatial and temporal resolution, high specificity and coverage, and particularly, non-invasively for studying human brains. Among the neural recording technologies listed in Fig. 1, the intracranial recordings (SUA, MUA, LFP and ECoG) have higher spatial/temporal resolution, specificity but limited coverage, and unfortunately, are invasive techniques that can be only applied to animal models or limited patient populations (e.g. epilepsy patients with implanted electrodes). Alternatively, the other imaging modalities based on hemodynamic measurements, such as the functional magnetic resonance imaging (fMRI), provide high spatial resolution in imaging brain activity but are limited in their low temporal resolution and interpretation in terms of the underlying neuronal activities. The other electrophysiological modalities, electroencephalography (EEG) and magnetoencephalography (MEG), which are non-invasive and share the superior temporal resolution of the invasive recordings, have been attractive for studying cognitive functions and assessing brain states in humans since Berger [2] first reported topographic features of alpha rhythm. However, EEG and MEG are compromised with limited spatial resolution/specificity, due to the volume conduction effect [3]. It has therefore been a major challenge to enhance the spatial precision of EEG/MEG to achieve high spatiotemporal mapping of the electromagnetic brain signals and to image the coordinated brain networks noninvasively.

Fig. 1.

Schematic illustration of the ranges of spatial and temporal resolution of various noninvasive (in blue) imaging techniques and invasive (in red) experimental techniques (adapted from [5], with permission).

In this context, electrophysiological source imaging (ESI) has been pursued in a hope to image underlying brain activity with a significantly enhanced spatial precision as compared with EEG and MEG measurements. Various attempts including the advancement of recording techniques (e.g. high-resolution EEG or dense array EEG) and the development of imaging methodologies (e.g. dipole localization and distributed source imaging) have led to great strides in improving the EEG/MEG spatial resolution to a centimeter scale or even smaller. Recently, integration of EEG/MEG and fMRI has shown great promise to further improve the spatial resolution of EEG/MEG. The advancement of the non-invasive functional imaging techniques has significantly broadened our capability to study “where”, “when” and “how” our brain functions. Such imaging ability is vital for a variety of neuroscience research and clinical applications. One example is to image the “imagined” brain activity, which are widely used in motor-imagery based brain computer interfaces. Another example is to localize and track the dynamic epileptogenic sources from EEG/MEG to guide surgical planning. A number of studies, including methodological developments and clinical investigations have suggested critical information provided by EEG/MEG imaging (with or without the integration of fMRI) for aiding pre-surgical planning in patients with intractable epilepsy. However, invasive intracranial recordings are still often used in order to precisely define and determine the epileptic brain. A further enhancement in spatial resolution of ESI would play a significant role in enhancing management of epilepsy and greatly promote the cognitive neuroscience studies including perception, attention and learning.

As opposed to source imaging that aims for the identification of functional segregation, connectivity analysis provides an important tool for understanding brain networks through which our brain functions under a highly interconnected organization. Studies have suggested the definition of connectivity through anatomical connections that are based on brain structures, and functional and effective connectivity that is instead based upon the functional properties of the various cortical regions. Functional connectivity patterns have been estimated from fMRI using the correlation mapping, revealing coherence and correlations among various brain regions. Intracranial EEG (iEEG), EEG/MEG, and the source signals reconstructed by EEG/MEG source imaging techniques have been proven efficient for measuring brain functional connectivity between various regions. Functional connectivity measures, such as coherence or causal directions, have been used to study brain networks associated with cognitive functions, spontaneous activities and neurological disorders. However, currently such noninvasive functional connectivity mapping is only available at the scale of intra-lobe. Significantly enhanced resolution in mapping functional and effective connectivity of dynamic brain networks would allow us to better understand the brain network characteristics at a sub-lobe scale.

In this perspective paper, we will critically review the most recent advancements and address the challenges in electrophysiological source imaging, multimodal neuroimaging integrating fMRI and EEG/MEG, and electrophysiological functional connectivity imaging. The merits, limitations, and needs for future development will be discussed.

II. Electrophysiological Imaging of Brain Activity

A. EEG/MEG Source Imaging

Fundamental principles

It has been widely accepted that EEG/MEG signals are mainly generated from synchronized activation of cortical pyramidal neurons. Neurons of this type have their cell bodies located within the cortical gray matter and their apical dendrites projected parallel to surrounding neurons [4, 5] (Fig. 2A). When pyramidal neurons are excited, the synaptic currents flowing across the cell membranes induce local excitatory postsynaptic potentials as well as magnetic fluxes, which collectively form the sources for EEG and MEG, respectively. When cortical neurons in columnar vicinity are in synchronized activation, the synaptic current flow, at a macroscopic level, approximates a current dipole located on cortical surface and oriented perpendicular to the local cortical surface (Fig. 2B). The configuration (e.g. location, magnitude, and orientation) of such current dipole can be related with EEG or MEG signals through the modeling of head volume conduction (Fig. 2C).

Fig 2.

When cortical pyramidal neurons (A) are excited, the synaptic currents flowing across the cell membranes induces local excitatory postsynaptic potentials as well as magnetic fluxes. The synchronized activity of cortical neurons in a columnar vicinity can be approximated by a current dipole located on cortical surface and oriented perpendicular to the local cortical surface (B). Through the forward modeling of brain source and head volume conductor (C, e.g. Finite element model and Boundary element model), the relationship between the EEG/MEG (D) measurements and underlying dipolar sources can be approximated through a linear system.

Direct electric measurements of neural activation within the brain offer high resolution, signal-to-noise ratio (SNR) and specificity, as achieved in iEEG for human subjects. However, the invasiveness of the intracranial technique limits the recording to a certain patient population (e.g., epilepsy patients) and restricted brain areas (e.g., epileptogenic regions). In this context, EEG/MEG source imaging techniques have been developed in an attempt to quantitatively localize and image brain activity from noninvasively recorded EEG or MEG. Such noninvasive approach is appealing due to its wide applicability to a larger population of healthy or diseased human subjects. Electrophysiological source imaging (ESI) is a model-based approach for imaging electrical sources associated with brain activation from noninvasive EEG or MEG measurements. ESI entails 1) forward modeling of brain sources and head volume conduction to establish a linear source-to-measurement relationship, and 2) inverse imaging of brain electrical sources from measured EEG/MEG, via various strategies, most commonly dipole localization and distributed source imaging.

Solving the forward problem - modeling of head volume conductor

The electromagnetic signals generated by the activations of cortical pyramidal neurons propagate through the head volume conductor to the EEG/MEG sensors sitting on or out of the scalp. Thus, an accurate modeling of the head volume conductor model, i.e. how the geometries and electrical properties of the head tissues can be computationally represented, is important for accurate imaging of brain sources. Historically, the simplest model uses a single or multiple spherical shells to represent different head compartments. Such a spherical model fits the shape of the frontal and parietal lobes well, but inadequately represents the complexity of the infero-occipital, temporal and orbitofrontal surfaces [6], which are important for cognitive functions and are also common locations for epileptogenic activities. More realistic head models were later developed, including the boundary element model (BEM) [7, 8] and the finite element model (FEM) [9–11]. The BEM uses realistically shaped layers constructed from structural MRI (e.g. the skin, skull and brain) to constitute the head volume and assumes piece-wise homogeneous conductivity in each layer. The BEM modeling has been shown to be computationally efficient and provides reasonably accurate solutions for many applications of ESI. The FEM, which is so far the best approximation to the real head volume conductor, divides the head into small elements of which the geometry and conductivity can be defined individually. The FEM modeling allows handling of conductivity inhomogeneity and also tissue anisotropy, however, restricted by complexity of model construction and computation.

Regardless of head models adopted, the relationship between EEG/MEG signals Y and cortical current source dipoles X can be represented by a linear system Y = LX, where L is a transfer matrix which describes how a unit dipole of a certain location and orientation is related to the EEG/MEG measurements. The head geometry and tissue conductivity are embedded in the transfer matrix L. The complexity and computational efficiency of constructing L are the topics of many researches in order to optimize the system for accurate and rapid imaging of brain sources from EEG/MEG measurements.

Solving the inverse problem – dipole source localization

Dipole source localization, which aims at quantitatively estimating one or more source dipoles that can be located anywhere within the brain from externally recorded EEG or MEG, has received considerable attention in the past decades. A dipole fitting problem [7, 12] assumes a pre-determined number of dipoles (equivalent current dipole model, ECD) as equivalent generators of scalp signals and estimates the locations and moments of the dipoles through non-linear optimization or subspace scanning methods [13–16]. Since only synchronized neuronal excitation will contribute, collectively, to EEG/MEG recordings, equivalent current dipoles represent reasonable models of neural activation in a sense that un-synchronized neuronal activities will be cancelled each other. Thus the estimated ECDs would represent locations of focal brain sources or centers of activities in the brain. Dipole source localization has been found useful in delineating neural origins of evoked potentials/fields, or event related EEG/MEG, and localizing focal epileptiform activity, mostly associated with interictal spikes. Studies conducted in epilepsy centers world-wide have yielded reasonably good source detection rates of the epileptic foci, and have converged to the conclusion that EEG/MEG dipole localization would provide critical additional information for the presurgical planning in epilepsy patients [6, 17–19]. Dipole localization techniques have also been used to obtain information with regard to distributed source activities, such as the sensorimotor rhythms in the alpha (8–13 Hz) band [20], occipital alpha activities [21] and sleep spindles [22]. An ECD model with a single or few discrete dipoles might be oversimplified for the representation of activity expanding over a large area of the cortex. The center of mass of the cortical activity might be localized, whereas the distribution and extension of the activity remain to be determined. This feature of dipole source localization represents the major limitation of the equivalent dipole model that, meaningful physiological correlates can only be established if the source is focal in nature.

Solving the inverse problem – imaging of distributed sources

Distributed source imaging has shown great promises to address the above problems of equivalent dipole modeling by assuming a source model consisting of a large number of unit dipoles evenly positioned in the brain volume [23, 24] or over the cortical sheet of gray matter (e.g. cortical current density model, CCD) [25]. Such a distributed source model approximates the biophysical organization and distribution of pyramidal neurons as discussed above (Fig. 2 A–B). The distributed source imaging has the merits of solving a linear inverse problem since the locations of dipoles are fixed. Various imaging strategies have been developed to obtain an “optimal” source estimation by adding biophysical and/or physiological constraints to the distributed source imaging inverse problem. The minimum norm estimate (MNE), which identifies an optimal solution by L-2 norm optimization in the sense of most energy efficiency, was first introduced to handle such “constraint” imaging [23]. Variants of MNE includes weighted-MNE (WMN) that compensates for the disfavored deep sources [26], low-resolution brain electromagnetic tomography (LORETA) that further considers spatial smoothness of the neural activity [24], and their statistical analysis [27]. However, the L-2 norm based techniques produce blurred images spreading over multiple cortical sulci and gyri, which lack spatial resolution to separate spatially focal sources. Non-linear techniques based on L-p norm (p<2) have then been developed in an attempt to make distributed source imaging applicable to image distributed yet focal source activities, such as the FOcal Underdetermined System Solver (FOCUSS) [28] and sparse source imaging based on L-1 norm [29–31].

Source imaging techniques of this type are generally applicable to image distributed brain sources underlying event-related potentials or continuous oscillatory activities, emerging from extended cortical areas or large-scale functional networks [32–34]. In the clinical realm, imaging distributed current or potential sources has been used to localize and image the epileptogenic zone [35–37]. It assists the determination of the location, and more importantly, provides information about the extension and boundary of the problematic regions, which cannot be easily achieved through dipole localization. In addition, temporal information reconstructed from source imaging has also been shown to further characterize the brain function, such as the connectivity, which will be discussed in details in a following section.

Remaining challenges in EEG/MEG source imaging

As reviewed above, the choice of source models and inverse methods can be different depends on the nature of brain activations in various conditions. Dipole fitting methods may accurately localize focal activation, but, as restricted by the model assumptions, cannot reconstruct an extended source distribution and cannot localize multiple sources without enough a priori knowledge. Distributed source imaging methods, on the other hand, can achieve good estimation of both source location and extension. L-2 norm based methods are suited to image extended sources whereas L-1 norm based methods are suited to image sparse and focal sources. In this situation, it is hard to find a universal inverse method to accurately image all kinds of brain activations under various experimental settings. The choice of inverse methods and the understanding of the nature of brain activations in different applications become important for the interpretation of EEG or MEG data [38]. A recent study [39] tested multiple distributed source imaging methods in well-controlled simulations. In a large range of spatial extents (10 mm² ~ 40 cm²), the study showed good performance of LORETA-based and MEM (maximum entropy on the mean)-based methods, but also suggested that the combination of different inverse methods may provide additional information for the accurate source localization. For focal sources, a study [40] compared source imaging results of somatosensory evoked potentials with intracranial EEG and found that L1-norm based methods provide better specificity than L2-norm based methods. Although the relative merits and limitations of different inverse methods have been widely discussed, systematic studies testing their performance in different source configurations (e.g., anatomical locations, spatial extents) and in different tasks (e.g., focal source induced by somatosensory stimulation vs. distributed source in cognitive tasks or spontaneous states) would be important for the wide application of ESI in various research fields or clinical applications.

EEG and MEG have been widely used to study evoked potentials or evoked rhythmic activities. However, recent findings of the resting state brain networks through the use of fMRI and PET have suggested that the human brain is fluctuating spontaneously even without any external input [41]. Studies using iEEG [42] and integrated EEG-fMRI [43] provide supporting evidence that the electrophysiological signals of the brain might also fluctuate spontaneously during rest. Pathological conditions also induce spontaneous activities that may last through a period of time. For example, epileptic seizures are characterized by rhythmic discharges in the brain that may evolve through time, space and frequency [44]. In these situations, continuous imaging of brain activity is desired in a search for the electrophysiological correlates of such normal or pathological spontaneous fluctuations.

Continuous imaging from EEG or MEG has been attempted through the spatiotemporal dipole fitting. A recent study, for example, reconstructed short period of ictal activity through sub-space scanning technique [16], the spatial precision and temporal resolution of which allows for the identification of causal relationship between epileptic sources. Although dipole fitting techniques have been successful in many situations, fMRI and EEG-fMRI studies suggested that spontaneous fluctuations are usually organized as diffused networks [41, 43]. One or a few discrete dipoles might not be adequate to represent such large-scale activity. Alternatively, EEG/MEG distributed source imaging serves well for this purpose. A straightforward strategy is to estimate the source distribution instant-by-instant to image brain activity spanning a continuous time period. Such a strategy has been applied to identify large-scale resting state rhythms [34], but it is challenged by the low SNR of continuous EEG/MEG signals and is computationally demanding.

Compared to a number of studies on dipole localization and distributed source imaging at selected time instants, only a few spatiotemporal imaging algorithms have been demonstrated to efficiently reconstruct the continuous distributed activity. In contrast to the instant-by-instant source imaging strategies, a rhythmic imaging technique [45, 46] has been proposed to target the sources in the frequency domain by transforming the windowed time course into Fourier space, showing the time-varying or condition-dependent modulation of distributed rhythmic sources. Also, recent findings suggested that continuous resting state EEG can be classified into a limited number of micro states with each spanning for a time window of about 100 ms [47]. These techniques image continuous rhythmic activities at the cost of temporal resolution. Beamforming techniques, which were originally designed for radar and sonar detection, have also been used for the reconstruction of fine temporal dynamics from regions of interest (ROIs). A beamformer [48, 49] uses spatial filtering to selectively pass brain activity from a certain region while attenuates the interference originated from other locations. The reconstruction of ROI waveforms, however, is dependent on the extent of the activated brain areas and the mutual correlation between spatially distinct sources [50].

In this context, although a few techniques have been developed for continuous source imaging, challenges remain to develop source imaging techniques, which can image large-scale evoked or spontaneous activity in healthy and diseased human brains. A major challenge of continuous source imaging is the low SNR of EEG or MEG signals. Conventional EEG/MEG analysis commonly uses a strategy of averaging to cancel out noise across hundreds of repeated trials. In the case of continuous imaging, the noise can significantly affect the accuracy of source imaging, especially during the periods with lower amplitudes of brain oscillations. Such a SNR-sensitive characteristic of source imaging significantly restricts further interpretations of estimated source waveforms. For example, while computing the connectivity between different source voxels, it is hard to eliminate the possibility that the connectivity can be induced by a global noise or artifact. While using source waveforms to build fMRI regressors, it is also difficult to remove the noise component.

Another challenge of electrophysiological source imaging lies in the limited sensitivity to deep brain structures, e.g. the thalamus, which are suggested to be involved in the resting-state networks from fMRI studies [43, 51]. The activities from deep brain activations are poorly represented in EEG/MEG signals, and their electromagnetic fields drop rapidly with distance. As such, it remains to be developed for a source imaging technique, which can efficiently provide whole brain coverage imaging brain activities. Integration with fMRI has been attempted in order to image deep brain activity, which will be discussed below.

B. Integration of EEG/MEG with fMRI

As a way of noninvasively measuring the electrophysiological signals accompanying brain activation, the EEG or MEG captures the electric potentials or magnetic fluxes (respectively) induced by synaptic activity virtually instantaneously, with a high temporal resolution on the order of milliseconds. Meanwhile, the spatial resolution of such electromagnetic recordings is subdued by the fact that a single electrode records a weighted average of brain activity from a large number of neurons and thus it is difficult to directly relate the measurements to a defined anatomical brain substrate. In contrast, another set of neuroimaging modalities, e.g. fMRI which measures the hemodynamic signals, are complementary to the strengths and limitations of EEG/MEG. FMRI based on the blood-oxygen-level-dependent (BOLD) contrast [52–55] measures the three-dimensional signal from the brain on a voxel-by-voxel basis, with a high spatial resolution up to the order of millimeters for a clinically available MRI scanner. However, the BOLD fMRI does not directly measure the neural signal, instead is a cascading response of associated cerebral blood flow and metabolism, which also limits the effective temporal resolution of the BOLD response to the order of seconds. In combination, these two complementary noninvasive methods would lead to an integrated neuroimaging technology with high resolution in both space and time domains that cannot be achieved by any modality alone. Such superior joint spatial and temporal resolution would be highly desirable to delineate complex neural networks related to cognitive function, such as error processing [56], learning [57] and decision making [58], allowing answering the question of “where” as well as the question of “when”. It can also permit delineation about the hypotheses of top-down versus bottom-up processing with the temporal resolution provided by electrophysiology [59]. The rich spatiotemporal information will ultimately be critical for inferences about the systematic organization of functional connectivity, for both the resting state and the task condition.

Multimodal integration approaches

As illustrated in Fig. 3, integration of fMRI with EEG/MEG has been pursued in two directions, which either relies on (1) the spatial correspondence or (2) the temporal coupling of fMRI and EEG/MEG signals. The first approach of spatial integration typically utilizes the fMRI maps as a priori information to inform the locations of the electromagnetic sources, including methods known as the fMRI-constrained dipole fitting [60, 61] and the fMRI-constrained/weighted source imaging [62–64]. In these methods, fMRI analysis yields statistical parametric maps with several fMRI hotspots, which each constrains the location of an equivalent current dipole or collectively produces weighting factors to evenly distributed current sources. With the spatial constrains, the ill-posedness of the original inverse problem is moderated and continuous time course of electromagnetic waveforms can be resolved from the fMRI hotspots, thus allowing inferences about the underlying neural processes [64].

Fig. 3.

Illustration of multimodal imaging approaches based on the spatial and temporal integrations. Waveforms of a typical EEG event-related potential and a block-designed BOLD change are shown. Notice the disparate temporal scales of the responses in the EEG and BOLD signals. Also, responses of both modalities are widely distrusted in the brain.

A major limitation of the spatial integration approach is due to the fact that fMRI yields relatively static maps compared to dynamic evolution of electromagnetic signals, owing to the highly different temporal scales in which data of these two modalities are generated and collected. Also, the spatial difference between the vascular and electrophysiological responses may lead to fMRI displacement. Thus the mismatch between a single static fMRI map and consecutive snapshots of EEG/MEG during the same period can lead to biased estimates as the fMRI extra sources (seen in fMRI but not EEG/MEG), the fMRI invisible sources (seen in EEG/MEG but not in fMRI), and the displacement sources (detailed discussion in [5]). New methods have been proposed towards overcoming this limitation, by means of a time-variant spatial constraint estimated from a combination of quantified fMRI and EEG responses [65] or estimating regionally fMRI-informed models by allowing model parameters jointly computed from electrophysiological source estimates and fMRI data rather than exclusively dependent on fMRI [66]. Examples of applying EEG/MEG-fMRI integration in the investigation of visual processing function have demonstrated how the subtle spatiotemporal dynamics revealed from electrophysiological imaging were able to delineate the hypotheses in regard to the underlying neural processes [59, 65, 67].

On the other hand, the second approach of temporal integration utilizes the EEG/MEG dynamic signatures in the time or frequency domain to inform the statistical mapping of fMRI. The structures derived from the electromagnetic signals include the single-trial task-induced modulations [57], responses at a specific timing [58], and spontaneous modulation in a specific frequency band [51, 68]. These quantities obtained from electromagnetic recordings are typically convolved with a canonical hemodynamic response function and then correlated to BOLD signals on a voxel-by-voxel basis to identify the statistical fMRI maps corresponding to the electromagnetic temporal signatures of interests. In this way, the integration method can recover the neural substrates by answering the question of “where” in joint with the question of “when”. An intriguing example is the study of nonrepeatable effects in epileptic patients, i.e. the inter-ictal activities. Correlates of the dynamics of inter-ictal discharges with the BOLD have led to insights into the problem of localizing the epileptic foci from fMRI [69].

Despite its attractive advantage of pinpointing the spatiotemporal signatures, the temporal integration approach so far has been exclusively focused on the temporal aspect of the electromagnetic signal. As discussed above the different temporal scales of the two modalities may lead to mismatches in the integration. Likewise, the difference in spatial scales can potentially bias the estimation as well. Previous studies employing the BOLD correlates of the EEG/MEG signals have mainly derived the temporal information at a mass level – either from one electrode [70], sum of a few channels [43, 51], or the sum of all channels [71]. In most of the cases reported, the electromagnetic signal under investigation appeared to be dominated by a single source and thus was well captured by one or a few electrodes. However, due to the effect of volume conduction, a single electrode records a weighted average of brain activity, which may contain distributed and diverse neuronal processes and therefore complicates the one-on-one relationship with BOLD signals from a much finer defined structure. A possible solution to such challenge can be achieved by restricting the dynamics of the EEG source signal from localized cortical regions before deriving the temporally integrated maps of fMRI and EEG.

What we can do and cannot do with multimodal imaging

With the promise of unprecedented spatiotemporal information, multimodal imaging has become increasingly attractive and been aggressively pursued since the invention of fMRI. A number of studies have continued to examine the basic hypothesis about whether or how these two modalities are related to each other. Those studies were driven by the search for a neurophysiological interpretation of the BOLD signal [72] and inevitably have taken the approach of multimodal imaging to compare one modality against another independent one, or to integrate data obtained from multiple imaging modalities.

The relationship between the hemodynamic and electrophysiological signals, termed as the neurovascular coupling, has been investigated by a number of investigators. Basically, literature from animal and human studies has increasingly converged to the understanding that the elevation of BOLD signals in response to tasks is tightly coupled to local changes in the concurrent neuronal activities [72]. Particularly, the relationship appears to be stronger for the synchronized synaptic activities, which are commonly reflected in the local field potentials and scalp-recorded EEG/MEG signals. This coupling relationship forms the basic principle for the integration of the fMRI with EEG/MEG.

Another important aspect of the neurovascular relationship is the linearity (or nonlinearity) of both BOLD and neural responses. In order to infer neural activities from fMRI, the relationship between hemodynamic and neural signals is most frequently modeled as a linear convolution system. A prediction of BOLD signals therefore results from local neural activations convoluted with a time-invariant hemodynamic response function (HRF). Such a linear HRF serves as an approximation for the cascading interplay between neuronal cellular activities and a complex of the metabolic demand, blood flow, and oxygen [73, 74], with influences from the astrocytes [75]. It is worthy to note that in the chain of responses, the linearity or nonlinearity can be present at the nodes between (1) tasks and BOLD, (2) tasks and neural activity, or (3) neural activity and BOLD. To address each aspect a number of studies have compared the responses of one or both modality signals against a linear function of varying task conditions, and the nonlinearity to a certain extent is acknowledged in the relationships, particularly between task and BOLD/neural activity. However, a critical concern lies in the variety of methods for quantifying the multimodal signals, which might have led to some of the nonlinearity. Additionally challenges may be further appreciated by considering the highly different temporal/spatial scales of the hemodynamic and electrophysiological responses. Nevertheless, two recent studies have led insights into this issue by co-registering the two modality signals [76, 77]. While the parametric variation of stimuli showed nonlinear effect on the responses of EEG or BOLD signal individually, the relationship between EEG and BOLD was found to be strongly linear across the variations to a large extent, especially when the EEG responses was quantified from the source domain that was co-localized with the regions of BOLD responses. Such experimental observations on the co-registered cross-modal relationship between fMRI and EEG thus provide a theoretical basis for the integration of these two modalities.

Resting-state and task-related rhythmic activity

One area of rapid development using multimodal imaging is using the endogenous BOLD and/or electrophysiological signals to study the resting-state network. This fluctuation of BOLD signals at resting state was first discovered when images were collected from subjects performing no task in the scanner [78]. The recorded spontaneous BOLD signals were not some randomly distributed noise but instead have been demonstrated to be organized covariantly within large-scale functional brain networks associated with visual, auditory, sensorimotor and attention functions as well as the default networks [41]. However, the neurophysiological mechanism of the resting-state signal or their physiological meaning are still under investigation, while an increasing number of studies have explored the application of resting-state network towards neuroscience questions and clinical conditions. Multimodal approach will be an important strategy to address such question by searching for the correlates of the electromagnetic signatures in the resting-state BOLD signals. In the meanwhile the high resolution spatio-temporal information obtained from multimodal imaging can permit inferences about resting-state networks under normal or pathological conditions. However, most of the existing multimodal imaging methods are developed in the task-related context, and thus there is a need to evaluate those methods, or to develop new multimodal techniques for imaging large-scale spontaneous brain activity. In a recent study by de Pasquale et al. [34], they recorded the MEG signals from subjects under resting state and reconstructed the continuous and endogenous source signals of the magnetic fluxes that were distributed across the entire cortical surface. Then the resting state network was imaged from the magnetic source signals alone using the seed-based correlation mapping, in a similar way with the BOLD signals. Comparison between the maps independently derived from MEG or BOLD signals revealed similarity between these two sets of images, while also showing the spectral and temporal dynamics of the MEG-derived networks. In another effort to estimate the distributed and spontaneous electromagnetic signals, Yang et al. have developed a new method by means of reciprocal integration of the EEG-fMRI temporal and spatial information [79], as illustrated in Fig. 4. The technique decomposes the spatiotemporal EEG signal into multiple components and integrates the EEG components and fMRI in the time domain and spatial domain subsequently. The components when recombined in the source space forms a spatiotemporal imaging of continuous brain activities (Fig. 4A). This study imaged long-term modulation of large-scale alpha rhythms and reconstructed the alpha-band synchronization and de-synchronization in the occipital and parietal regions in eyes-open versus eyes-closed conditions (Fig. 4B) [79].

Fig. 4.

In an effort to image continuous rhythmic activity, a recent study developed an EEG-fMRI integrated imaging methodologies (A). The technique was used to reconstruct spatial distribution and temporal modulation of alpha-band oscillation in an eyes-open-eyes-closed task. (From [79] with permission)

While the task-free paradigm opened a new horizon to study the resting state brain, investigations continue to search for better ways to image the task-related activities, particularly by combining the BOLD with the rhythmic activities. The task-related rhythms have been shown to be functionally relevant [80] and studies so far suggest their tight coupling with the BOLD responses [46, 81]. Furthermore, some recent studies have indicated new signatures of the task-related rhythms that may be functionally coupled. Another study by Busch et al. investigated the influence of oscillatory phase on visual perception. EEG signals were recorded when brief flashes of light at the individual luminance threshold were presented to subjects [82]. Examination on the phases shortly before stimulus onset revealed segregated distribution of phases for the trials of hits and misses, particularly in the theta and alpha frequency band. Interestingly, in another study on the somatosensory perception using fMRI, the BOLD signal immediately preceding the delivery of stimuli was found to be correlated with behavior performance of the conscious perception at a distributed network [83]. These evidences project new insights into the coupling between BOLD and neurophysiological signals and have implications on the interaction between the baseline activities (the preceding resting state) with the task-related responses.

C. Mapping Functional Brain Connectivity

Cortical connectivity and anatomy

Over the past several decades, our collective understanding of the activity within the brain has evolved from the identification of discrete loci of brain activity to the identification and characterization of the disparate brain networks involved in information processing and task performance. In particular, it is known through anatomic and experimental studies that there are a plethora of highly interconnected cortical networks, which allow for the rapid communication between spatially distinct brain regions [84]. Analyses of these networks have furthermore revealed disruptions of their normative function in a variety of disease states.

In the current description of cortical interactions, there are presently three definitions for connectivity: anatomic, functional and effective connectivity. Anatomic connectivity, as indicated by its name, refers to the physical neural connections between various regions of interest (ROIs). These connections can either be on the micro- or macroscopic level. On the microscopic level, anatomic connectivity can include dendritic sprouting and the forming of new synaptic connections [85] while, on a larger scale, anatomic connectivity encompasses the large white matter fiber tracts, which connect spatially disparate brain regions.

There are a variety of methods used to assess the anatomic connectivity using both in vitro and in vivo methodology. Diffusion tensor imaging (DTI) is one such non-invasive technique that has been developed in order to image white matter tracts in the brain [86]. DTI identifies these fiber tracts using a type of magnetic resonance imaging, which measures the diffusion of water particles. These fiber tracts correspond to myelinated axonal projections and maps of the anatomic cortical connectivity can be obtained in this matter [87]. Similar maps can be obtained by in vitro experiments such as the use of molecular probes [88] or through post-mortem studies.

DTI has recently emerged as a promising technique in the presurgical treatment planning of neurosurgical patients. These techniques are useful in their ability to identify functionally important white matter tracts and their relationship to intracranial pathology. The neurosurgeon can utilize this information in planning the surgical approach and, in the future, such techniques may aid in the identification of surgical versus nonsurgical patients. While DTI has been utilized in some limited clinical settings, further exploration applying this anatomic imaging technique to the clinical realm is needed [89].

As DTI utilizes the anisotropic properties of fiber tracts in the creation of the imaging results, anatomic variations or abnormalities such as locations of fiber tract crossings or areas of inflammation and edema may serve to reduce the quality of the DTI results. In the setting of patients undergoing resection of tumor or intracranial mass lesions, the intracranial pathology may serve to reduce or eliminate the utility of the DTI results in these situations. Several techniques have been developed in order to address these challenges [90, 91]. While these studies exploring the anatomic connectivity are useful from the standpoint that they identify interconnected cortical regions, they do not, however, provide information concerning the function of the regions and the relationship of such between them.

Functional and effective connectivity

As opposed to anatomic connectivity, the other two definitions of connectivity, functional and effective connectivity, are instead based upon the functional properties of the various cortical regions rather than the analysis of specific physical connections between them. Functional connectivity is defined as the temporal correlations between spatially remote neurophysiological events [92, 93] whereas effective connectivity is defined as the influence that one neural system exerts over another either directly or indirectly [93, 94]. In general, functional connectivity is a statistical property, which measures the amount of correlation in the activity of distinct cortical regions.

Functional connectivity measurements often take the form of covariance or coherence measures. The spectrum coherence for a pair of signals is given as:

$$C_{\mathit{\text{xy }}}(f)=\raisebox{1ex}{${|S_{\mathit{\text{xy }}}(f)|}^2$}\!\left/ \!\raisebox{-1ex}{$S_{\mathit{\text{xx }}}(f)S_{\mathit{\text{yy }}}(f)$}\right.$$

where S_xy (f) is the cross-spectral density between x and y and S_xx (f) and S_yy (f) are the autospectral density of x and y respectively. As can be seen from the above equation, there is no directionality affiliated with the spectral coherence measure. That is, for a given frequency, the interaction from x to y is equal to that of y to x, in other words C_xy (f) = C_yx (f). Functional connectivity measures, in general, identify regions, which are functionally linked by finding those which have greater statistical coupling than a normative distribution of coupling indices. Functional connectivity methods, however, do not indicate the directionality of these couplings.

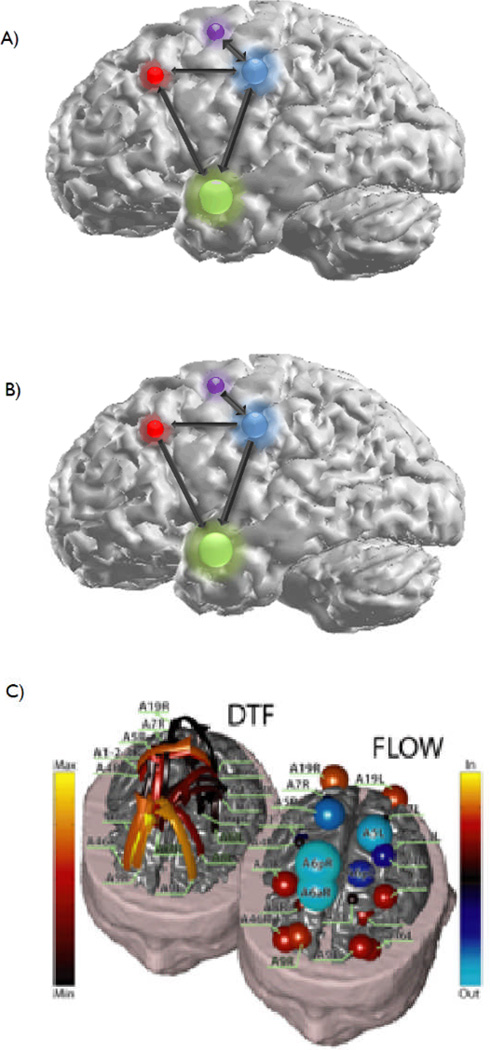
Effective connectivity, on the other hand, describes the direction of the functional interactions between brain regions. These directional interactions can be either pre-defined as used in structural equation modeling (SEM) or derived from the data (“model free”) as with Granger causality measures. The difference between functional and effective connectivity measures is shown graphically in Fig. 5.

Fig. 5.

Model depicting functional (A) and effective (B) connectivity metrics. As can be observed from the figure, functional connectivity denotes regions which are linked, but does not specify the direction of this coupling, a property which is provided by effective connectivity methods. A type of effective connectivity measure, the DTF, is shown in (C) during a motor task. From the directionality information provided by the DTF, the degree to which each cortical region acts as either a source or sink of cortical activity during the task can be calculated

Granger causality

In the late 1960’s, Granger described a method to evaluate the causal influences within bivariate systems [95]. This method identifies the causal influence between pairs of ROIs based upon the historic values, which compose each time series. Using this method, a time series is modeled as a linear combination of the previous values of the time series in an autoregressive model. One time series is said to Granger-cause a second time series if inclusion of the historic values of the first into the modeling of the second significantly reduces the variance of the modeling error.

Given this definition, it can be observed that if one time series has a causal influence on a second, it does not necessarily hold that the second similarly holds a causal influence on the first. In this sense, this method provides a measure of the directed interaction between two time series while this information cannot be obtained through more traditional bivariate measures, such as the coherence between a pair of time series. Since this definition of causality provides a picture of the interactions between a time series pair based upon their functional properties rather than a known physical linkage between them, it became known as Granger causality to avoid confusion with traditional direct cause-effect relationships. Granger causality was initially broadly applied to the field of econometrics in the study of relationships between economic indices [96] although it has become widely utilized in the neuroscience community to study the cortical interactions during both diseased and normative states.

Analysis of directed cortical interactions

There are a variety of connectivity estimators based upon the principle of Granger causality. A shortcoming of bivariate causality, however, is that the estimation of the connectivity is limited to pairwise systems and may incorrectly estimate the causal interactions in a multivariate setting [97]. Several techniques have been developed to provide estimates of connectivity in multivariate systems. Many of these techniques, such as the directed transfer function (DTF) and partial directed coherence (PDC), are based upon the spectral characteristics of the physiologic signals and are able to differentiate causal interactions within specific frequency bands of interest [98, 99]. These methods have been successfully applied to data obtained from a variety of sources including both invasive (ECoG) and noninvasive (fMRI, EEG, MEG) modalities.

fMRI-based connectivity estimation

fMRI measures the cerebral hemodynamic changes which arise from the neuronal activity. The major advantages of this method are the non-invasive basis of the imaging modality as well as the ability to image the entire cerebral volume including deep sources of activity. As opposed to connectivity estimation based upon electrophysiological data, which arises from direct neural activity, connectivity techniques utilizing hemodynamic changes are calculated using an indirect measure of the neuronal activity. The limiting factor regarding the application of connectivity techniques to fMRI data lies in the inherent poor temporal resolution of the modality. This prevents exploration of the cortical connectivity from fMRI results on a temporal resolution comparable with EEG/MEG studies. Despite these differences, many studies have shown a tight correlation between the hemodynamic responses and electrophysiological results [100].

One of the most commonly utilized connectivity tools in fMRI data, SEM, has been widely used by the fMRI community in order to identify the directional interactions between ROIs identified from the fMRI paradigms [101–103]. In SEM, the connections between the nodes are predicted in such a way that the functional data is used to determine if each selected connection constitutes a statistically significant causal link. As such, a priori information or calculated assumptions regarding the network structure must be made prior to these calculations. In fMRI datasets, such analyses are manageable due to the typically limited amount of analyzed ROIs. Alternatively, other model-free estimators of effective connectivity such as Granger causality do not require statistical testing of a predefined model. Using these techniques, the causal network connections are derived from the data itself. However, a cautionary note for the fMRI-based connectivity using the Granger causality is that the interaction it reflects are calculated from the signal across multiple time points and hemodynamic delays may override the actual causal relationship between them, if there is any [104].

Electrophysiological connectivity estimates

The fMRI-based connectivity analyses utilize the hemodynamic properties to determine causal interactions between selected ROIs. While the hemodynamic changes act as surrogates of the cortical activity, causal interactions can also be obtained from direct neuronal activity through the use of electromagnetic measurements such as EEG/MEG. The major benefit which EEG/MEG holds over fMRI is the significantly higher temporal resolution of the modalities. As these modalities measure the electrodynamics, as opposed to the slower transient hemodynamic response, they are able to capture the rapid changes in neuronal states. The drawback, however, is that they often lack the spatial resolution of fMRI measurements with the quality of EEG/MEG data, in particular, suffering in the cases of deep sources. Improving imaging techniques to reconstruct the neuronal activity with both high temporal and spatial resolution remains an important challenge. The connectivity imaging will benefit from advancements in the resolution and precision of imaging techniques.

Through the utilization of EEG/MEG-based high resolution non-invasive source imaging techniques, it is possible to reconstruct the cortical neural activity with a high degree of fidelity. The network connectivity can then be directly estimated from cortical ROIs [64, 105]. These types of connectivity estimation approximate the macroscopic causal interactions between functionally distinct brain regions. Still other recently developed techniques, such as dynamic causal modeling [106], aim to explain the local network dynamics at the neural level.

Clinical applications of electrophysiological connectivity

Aside from mapping cortical networks during normal physiologic activities, cortical connectivity tools have been utilized in the study of a variety of diseased states. Functional connectivity measures were successfully used to localize epileptogenic zones in patients suffering from intractable epilepsy [107, 108] using DTF, adaptive DTF and graph theory. Several methods have also been developed and applied to the analysis of functional brain networks in order to differentiate physiologic and pathologic conditions. Disruptions of these functional networks have been observed in a host of neurologic diseases including Parkinson’s [109], Huntington’s [110], autism [111], and other psychiatric disorders. In the near future, these methods could potentially lead to improved diagnosis of neurocognitive disorders even before their clinical manifestations become apparent. Such improved diagnostic techniques could allow for earlier treatment and enhanced measurement of treatment efficacy.

In addition to congenital or acquired neurocognitive disorders, cortical functional connectivity networks have been shown to be disrupted by focal brain lesions. In a study by Guggisberg et al [112], the resting state connectivity was shown to be decreased in patients with cortical lesions versus healthy controls. As this measure provides an estimate of cortical communication, regions with decreased resting state connectivity were observed to be correlated with dysfunctional cortical locations. Such connectivity-derived methods could therefore be utilized to better guide neurosurgical interventions and predict post-operative outcome and neurologic function through careful pre-operative evaluation of these cortical networks. These studies have demonstrated tremendous potential for connectivity-derived methods in the diagnosis and treatment of neurological disorders, however, continued evaluation is necessary before these methods become adapted to routine clinical care.

Challenges in mapping human brain connectivity

The interpretation of cortical network activity obtained from functional and effective connectivity estimates may not be entirely straightforward. While the relationship between anatomic connectivity measurements, such as DTI, and the physiologic cortical networks is easily discernable, the precise anatomic relationship between functionally coupled disparate brain regions is less obvious. Granger causality and other similar connectivity-based techniques do not provide information regarding the underlying physical connections between functionally coupled ROIs. Currently, as a result of this disconnect between structure and function measures, the identification of the precise neural networks which denote how functionally coupled brain regions interact is not trivial. Imaging modalities and connectivity techniques which are able to incorporate the structural neural network information into the causal interactions are needed to improve the accuracy and precision of the calculated cortical network activity. An effort has been made to first estimate brain sources using anatomically realistic head models and then functional connectivity among selected ROIs are assessed (Fig. 5C) [16, 64]. Such approach represents an initial albeit important direction to integrate anatomic and functional information to estimate the causal interactions within the brain networks.

The combination of high resolution anatomic and functionally-coupled measures would have a significant impact in the clinical setting. In the surgical treatment of epilepsy, the seizure onset zone (SOZ) is defined as the extent of cortical area whose removal is required for seizure cessation. Unfortunately, if during the presurgical evaluation, the SOZ is determined to be too large or overlap with eloquent cortex, the patient is deemed to not be a candidate for definitive surgical therapy. Combined high resolution anatomic and functional measures could theoretically benefit this group of patients by identifying the sites of activation and the neural pathways by which the seizure propagates. Potentially these pathways could serve as targets for therapeutic intervention and disruption, rather than complete surgical excision, of the fiber tracts conducting the seizure activity could be utilized. This could result in more targeted surgical techniques and better prediction of post-surgical outcome. Recent efforts to apply the Granger causality estimates to ECoG data revealed the potential for accurate localization of SOZ in epilepsy patients [107, 108]. Statistical approaches are needed to quantitatively assess the functional connectivity patterns of spontaneous brain networks. Recently Graph theory has been demonstrated to provide excellent performance in characterizing and identifying SOZ from ECoG data in a cohort of epilepsy patients [108].

In addition to the linkage of anatomic and functional measures, another area for substantial innovation lies in improved temporal resolution of Granger-type connectivity measures. The majority of Granger-causality techniques are based upon the framework of the autoregressive model. There are several limitations with the use of linear autoregressive models, namely the requirement that the selected data segment be quasi-stationary in nature. In practice, this is accomplished by careful selection of the appropriate data segment from the electrophysiologic recording. The connectivity pattern among the ROIs is then calculated over the duration of this selected interval. While some forms of cortical activity, such as the initiation and propagation of highly regular seizure waveforms, may satisfy this quasi-stationary assumption, others, such as short bursts of epileptiform activity or event related potentials with short latencies, may not. Given this limitation placed upon the analysis of cortical connectivity due to the modeling constraints, further development and refinement of connectivity algorithms during non-stationary data segments is warranted.

In addition to the requirements of quasi-stationarity previously mentioned, an inherent assumption in the calculation of connectivity using autoregressive-based methods such as the DTF or PDC is that the connectivity pattern among the ROIs is static during the analyzed epoch. A number of Granger causality measures calculate the connectivity over a time window typically several seconds in length. The implicit assumption in this calculation is that the connectivity pattern among the ROIs does not significantly change during the selected time window. In highly dynamic systems, such as the human cerebral cortex, this assumption may not necessary uniformly hold true. As a result, transient neural activity may be missed through the application of traditional connectivity metrics. Previous studies have shown that temporally short changes in the connectivity pattern of simulated systems may produce an erroneous picture of the network connectivity when traditional time-invariant connectivity methods are utilized [113]. Due to the dynamic properties of cortical-based neural networks, time-invariant connectivity methods such as the DTF and PDC may not sufficiently represent the full spectrum of causal activity in these networks.

The ability to capture these brief changes in network architecture remains an important challenge and requires advancement in not only improved neuroimaging modalities, but advances in the modeling of such data. To solve this problem, several techniques have been developed to provide time-variant connectivity estimation [113–115]. These techniques utilize time-variant Granger causality to provide estimates of changes in connectivity patterns over temporally short windows. The application of these and related methods to cortical recordings may help to provide a more thorough understanding of the underlying network dynamics. The utility of these methods has been shown to produce more accurate representations of the network architecture in both physiologic and pathologic states [107, 113, 115]. While a significant amount of research has been conducted on cortical networks in a variety of conditions, relatively less is known regarding the transient network characteristics and their function in both normative function and their role in disease. Further advancements and investigation into these changes in temporally short network dynamics is warranted.

III. Concluding Remarks

Numerous efforts have been made in an attempt to noninvasively image brain activity and connectivity with high spatial and time resolution. A high resolution spatio-temporal functional brain imaging methodology will not only provide an extremely useful tool for neuroscience research, but also directly benefit a number of patients suffering from various neurological disorders such as epilepsy. EEG and MEG are currently the only noninvasive modalities, which can provide high temporal resolution information assessing dynamic brain activity. Thanks to the collective efforts to significantly enhance the spatial resolution of these techniques, electrophysiological neuroimaging methods are increasingly being used in neuroscience research and rapidly entering into the clinical arena. Integration of EEG/MEG with fMRI represents an important advancement in seeking of new imaging modalities, which promises to provide complementary benefits of both electromagnetic and hemodynamic measurements. These advancements in electrophysiological source imaging and multimodal neuroimaging have great promise for the characterization and imaging of brain functional networks at increasingly fine spatial and temporal scales.

These improvements in spatial and temporal precision of neuroimaging modalities over the past two decades have led to the ability to analyze cortical networks over a variety of normal activities and pathologic states. While cortical activity has historically been viewed as a series of spatially discrete processes, exploration into the role of functional brain networks has witnessed an explosion within the past decade. In addition to providing further insight into the function of physiologic brain activity, disruptions in the cortical-based networks have been observed in a wide variety of neurological disorders. In the future, these network disruptions could be used to diagnose a spectrum of neurodegenerative and neurocognitive disorders possibly even prior to outward disease manifestation. As brain imaging and connectivity mapping techniques are further developed and refined, analysis of cortical networks could lead to not only improved diagnostic tools, but earlier and more focused interventions as well.

Looking to the future, a diverse development of new approaches as well as associated experimental studies are needed to fully address the challenges encountered in brain activity and connectivity imaging. Fundamental studies investigating the neural substrates of different imaging modalities, developing novel imaging techniques of better spatial or temporal resolution, and improved mathematical modeling which approximate realistic neuron-to-measurement relationships would further advance our capability to image the underlying neural activity on very fine time and spatial scales. Significant work remains to be done to correlate neural network activity discerned utilizing these methods with in vivo neurophysiologic findings. Through utilizing the electrophysiological and hemodynamic modalities, further needed are the development of analysis tools for investigating the brain connectivity networks of resting state and other task conditions. Such a development of noninvasive high-resolution spatio-temporal neuroimaging techniques would have significant impact over basic neuroscience and cognitive science, to better understand the mechanisms of perception, attention, learning, etc., and to improve substantially our understanding on how the “Mind” is implemented in the brain. These functional neuroimaging techniques would also significantly impact the diagnosis and treatment of neurodegenerative diseases and psychiatric disorders. The emergence of improved electromagnetic imaging techniques (e.g. EEG and MEG) as well as functional MRI techniques has contributed to thousands of research articles each year. More importantly, the development of functional neuroimaging techniques and connectivity analysis tools that are adapted to the clinical realm has provided additional information regarding the cortical mechanisms of brain disorders and in the near future may also serve to guide therapeutic interventions. Functional brain imaging of brain activity and connectivity promises to tremendously advance our understanding of the human brain and promises to offer innovations in the management of various neurological and psychiatric disorders.