Neural Correlates of Object-in-Place Learning in Hippocampus and Prefrontal Cortex

Abstract

Hippocampus and prefrontal cortex (PFC) process spatiotemporally discrete events while maintaining goal-directed task demands. Although some studies have reported that neural activities in the two regions are coordinated, such observations have rarely been reported in an object-place paired-associate (OPPA) task in which animals must learn an object-in-place rule. In this study, we recorded single units and local field potentials simultaneously from the CA1 subfield of the hippocampus and PFC as rats learned that Object A, but not Object B, was rewarded in Place 1, but not in Place 2 (vice versa for Object B). Both hippocampus and PFC are required for normal performance in this task. PFC neurons fired in association with the regularity of the occurrence of a certain type of event independent of space, whereas neuronal firing in CA1 was spatially localized for representing a discrete place. Importantly, the differential firing patterns were observed in tandem with common learning-related changes in both regions. Specifically, once OPPA learning occurred and rats used an object-in-place strategy, (1) both CA1 and PFC neurons exhibited spatially more similar and temporally more synchronized firing patterns, (2) spiking activities in both regions were more phase locked to theta rhythms, and (3) CA1–medial PFC coherence in theta oscillation was maximal before entering a critical place for decision making. The results demonstrate differential as well as common neural dynamics between hippocampus and PFC in acquiring the OPPA task and strongly suggest that both regions form a unified functional network for processing an episodic event.

Introduction

Prefrontal cortex (PFC) and hippocampus function as a unified network for certain cognitive processes (O'Reilly and Norman, 2002; Lee and Kesner, 2003; Jones and Wilson, 2005; Lee and Solivan, 2008; Benchenane et al., 2010). Hippocampus is known for representing spatiotemporal events (Morris et al., 1982; Pearce et al., 1998; Lee and Kesner, 2004) and remembering objects with their associated locations (Gilbert and Kesner, 2002; Day et al., 2003; Lee and Solivan, 2008). PFC plays significant roles in various cognitive processes such as temporal organization of behavior (Chiba et al., 1997; Fuster, 2000; Shima et al., 2007) and representing motivationally salient events (Pratt and Mizumori, 2001; Hok et al., 2005). Although some goal-directed memory tasks seem to require intact functions of both hippocampus and PFC and their interactions (Lee and Kesner, 2003; Jones and Wilson, 2005; Wang and Cai, 2006; Lee and Solivan, 2008), the nature of neural information processing that needs to occur simultaneously in both structures in such tasks remains largely unknown.

A goal-directed event memory task requires an animal to form and retrieve specific memory representations and organize some critical behaviors tightly around significant events in the task. With its capability for representing discrete locations (O'Keefe and Dostrovsky, 1971; Muller et al., 1987) and its autoassociative function for binding individual items with spatial locations (Treves and Rolls, 1994; Kesner et al., 2005; Rajji et al., 2006; Lee and Solivan, 2008; Jo and Lee, 2010a; Lee and Solivan, 2010), the hippocampus is considered as the major area through which discrete event memories are formed and retrieved. Successful performance in such a task not only requires discrete memory representations but also requires a system that learns sequential and procedural rules for leading an animal successfully to reward and decision making. Many studies suggest that PFC plays a crucial role in this cognitive function (Tomita et al., 1999; Fuster, 2000; Miller, 2000; Dobbins et al., 2002).

Despite several reports of the coordinated activities between hippocampus and PFC (assessed mainly in reference to theta rhythms) (Hyman et al., 2005; Jones and Wilson, 2005; Siapas et al., 2005), it is difficult to come across a study that directly compares the representational properties of single-unit spiking activities that are recorded simultaneously between the two regions in an event memory task. To compare qualitative differences in information processing between the two structures directly, we trained rats in an object-place paired-associate (OPPA) task for several days while continuously recording single units simultaneously from both regions throughout the acquisition period. We showed previously that making either area unavailable yielded profound deficits in this task (Lee and Solivan, 2008). We hypothesize that the hippocampus represents discrete spatial events, whereas PFC represents procedural task demands, and the two regions should coordinate their activities at critical times for proper decision making. Here we report significant representational differences and commonalities between hippocampus and PFC for the first time in the OPPA task.

Parts of this paper have been published previously (Lee and Kim, 2010).

Materials and Methods

Subjects

Three male Long–Evans rats (300–400 g) were used in the study. Food was controlled for maintaining their body weights at around 85% of free-feeding weights, but water was available ad libitum. A 12 h light/dark cycle was used, and all the behavioral testing and recording was done during the light phase. All of the protocols for animal care and surgery followed the guidelines of the National Institute of Health and the Institutional Animal Care and Use Committee.

Behavioral apparatus

A radial-arm maze made of black Plexiglas was located at the center of a circular curtained area (Lee and Solivan, 2008). Seven arms (each 8 × 80 cm and separated 25.7° from each other) radiated from the center of the maze where a start box (20 × 25 × 30 cm) was located. Each arm was numbered incrementally from left to right (when viewed from the top), and only the third arm (Arm 3) and the fifth arm (Arm 5) were used in the current study. The two arms were separated by 51.4°. At the distal end of each arm, a rectangular platform (23 × 30 cm, the “choice platform”) was attached (see Fig. 1A). In the choice platform, there were three food wells separated from each other by a transparent Plexiglas divider (6 × 13 cm) to encourage a targeted and discrete choice. In the OPPA task, two toy objects occupied the left and right food wells (center food well not used and not illustrated in Fig. 1A). Two toy objects were a toy girl figure (Obj_G) or a cylindrical junk object (Obj_C). A pair of an infrared emitter and detector was installed in the center of each food well for detecting the moment of displacement of an object: once the rat pushed an object, a transistor–transistor logic pulse was sent immediately to the neural data acquisition machine (Digital Lynx; Neuralynx) as a time-stamped event. A digital CCD camera on the ceiling recorded behavioral sessions, and white noise was provided through a loud speaker placed under the center platform of the maze.

Figure 1.

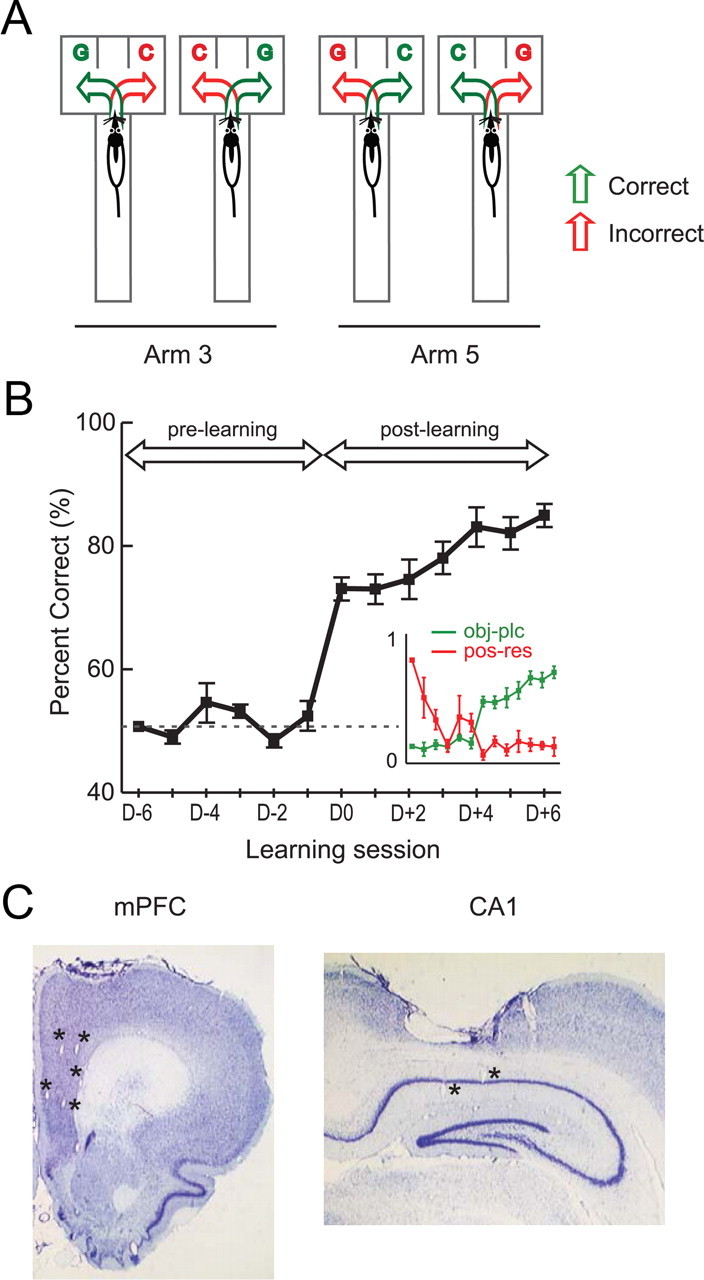
A. Schematic illustration of the OPPA task. In each trial, a rat was required to choose between two objects (toy girl and dummy cylindrical object denoted by G and C, respectively) arranged in a choice platform at the end of either Arm 3 or Arm 5 in a radial maze. Four possible conditions (2 object configurations by 2 arms) are illustrated here. In each condition, two possible choices (green arrow, correct choice; red arrow, incorrect choice) are shown. B, Learning curve in the OPPA task. Overall performance of animals averaged across arms (mean ± SEM) through the acquisition period of the task. The day on which rats performed better than 75% in both arms for the first time was marked as D0 and was used as the boundary for dividing prelearning and postlearning periods. The dotted line represents the chance-level performance (50%). Inset, A crossover of object-in-place strategy index (green) and position-response bias (red) near the acquisition day. The abscissa and ordinate represent learning session and strategy index (scaled from 0 to 1), respectively. C, Histological verifications of recording sites. Representative examples of recording electrode positions in mPFC and CA1 within the same animal are presented. Asterisks indicate tetrode tip positions in mPFC and CA1.

Presurgical training

All rats were handled individually for 1–2 weeks. Each rat was tamed until no defecation or urination was observed when placed in an open space (a lab cart). Afterward, the rat was placed in the maze for familiarization and was allowed to explore the entire maze while consuming some cereals scattered throughout the maze. Once the rat foraged comfortably in the maze, a shaping procedure began. For this, the rat was first placed in the start box, and, when the guillotine door was opened, it entered an opened arm (Arm 3 or Arm 5) that had already been chosen randomly by the experimenter. During the pretraining period, a black junk object (not used for the main OPPA task) was placed over the center food well (which was not used in the main task) in the choice platform with a cereal reward given in the food well. After the rat learned to displace the object to obtain food reward, a multitetrode recording device (hyperdrive) was surgically implanted.

Surgical implantation of hyperdrive

A hyperdrive carrying 18 tetrodes was used for the electrophysiological recording of single units. Nichrome wires (12 μm in diameter; Kanthal) were twisted and bonded with heat to make a tetrode. Final impedance of each wire was adjusted to 150–300 kΩ (measured in gold solution at 1 kHz with an impedance tester; IMP-1; BAK Electronics). Sixteen tetrodes were used for recording and two other tetrodes were used as reference electrodes. The hyperdrive was composed of two stainless-steel cannulae (each cannula carrying eight recording tetrodes and one reference electrode), one targeting the hippocampal CA1 region (3.0 mm posterior to bregma and 1.7 mm lateral to midline) and the other targeting the medial PFC (mPFC; i.e., prelimbic and infralimbic PFC; 3.0 mm anterior to bregma, 1.0 mm lateral to midline). For surgery, the animal was initially anesthetized with the injection of ketamine (55 mg/kg) and xylazine (6 mg/kg) before being placed in a stereotaxic frame, and the anesthesia was maintained using isoflurane (1–2% isoflurane with 100% O2) until the surgery was finished. One week was given for recovery afterward.

Recording setup

After a week of recovery, the rat was placed in a custom-built booth located outside the experimental room. While the rat slept in the booth, tetrodes were lowered individually to the target regions over several days. Neural activities were amplified (1000–10000 times) and digitized (sampled at 32 kHz, filtered at 300–6000 Hz) using a Digital Lynx data acquisition system (Neuralynx). In the experimental room, neural signals were transferred through a slip-ring commutator (Neuralynx) to the data acquisition system. To verify the stability of recording, unit activities were recorded for 30 min before and after the behavioral session. The rat's position in the apparatus was tracked through a digital ceiling camera, and the camera's signal was fed to a frame grabber (sampling rate, 30 Hz) for monitoring the position of an array of red and green LEDs (attached to the preamplifier that was connected to the hyperdrive) to measure the position and head directional information. Spiking data from single units and position information were time stamped and stored by the data acquisition machine for off-line analyses. The entire maze area was mapped to a 640 × 480 pixel space (0.31 cm² per pixel²).

Acquisition of the OPPA task

Once the majority of tetrodes were placed in the target regions, the acquisition of the OPPA task began. A trial started as the experimenter opened the guillotine door of the start box. Either Arm 3 or Arm 5 had already been opened by the experimenter before releasing the rat from the start box, and the two objects (Obj_G and Obj_C) had been placed in the choice platform (see Fig. 1A). The objects were placed only in the arm to be visited in a given trial but not in the closed arm. The configuration of the object positions in the choice platform and the arm information changed pseudorandomly in a counterbalanced manner throughout the session. In the OPPA task, a particular object was always rewarded in association with a certain arm, and whether the object occupied the left or right food well (i.e., object's position) in the choice platform did not matter (see Fig. 1A). The rat was trained to grab the cereal reward after displacing the correct object and return to the start box for consuming the reward. If the rat pushed a wrong object, a further attempt to displace the other object was blocked by the experimenter using a small plastic panel, and the rat was gently guided back to the start box without being rewarded. A single trial ended when the animal returned to the start box and the guillotine door was closed. Trial types in the task were defined by the combination of arm information (Arm 3 and Arm 5) and object configuration information (Obj_G–Obj_C and Obj_C–Obj_G) (four trial types in Fig. 1A). The four trial types were repeated pseudorandomly for 16 times within a recording session. Overall, 64 trials (intertrial interval, 20–30 s) were given in a behavioral session in a day.

Histological verification of electrode positions

After the completion of all recording sessions, positions of individual tetrodes were marked by electrolytic lesions (10 μA current for 10 s). The rat was then killed by injecting a lethal dose of Nembutal, and the brain was perfused transcardially with physiological saline followed by 10% formalin. The frozen brain was sectioned (30 μm) later using a sliding microtome. Cut sections were stained with thionin, and photomicrographs were taken under a digital microscope. The series of photomicrographs of tissues were used along with the physiological recording profile to reconstruct tetrode tracks and recording sites in the hippocampus and mPFC.

Unit isolation and criteria

Spikes from single units were isolated off-line using a Windows-based custom software as described previously (Lee et al., 2004a,b; Lee and Kim, 2010). Multiple parameters such as peak, width, height, and energy associated with the waveforms from four wires of a tetrode were compared for the unit isolation. Single units recorded from the tetrodes whose tips were located in the mPFC and CA1 of the hippocampus (see Fig. 1C) only were used. Interspike interval histograms were also examined for ensuring single unit activity. Only complex spike neurons (average spike width, 260.6 μs), but not theta cells (judged based on spike width and autocorrelogram), were used for hippocampal analysis (Kubie et al., 1990). No attempt was made to distinguish fast-spiking and regular-spiking neurons in the mPFC (Jung et al., 1998; Baeg et al., 2001), and no distinction was made between the neurons recorded from the prelimbic and infralimbic cortices (average spike width, 295.7 μs). A unit was not analyzed further if its stability during recording was not confirmed when comparing the data recorded before and after the behavioral session. The isolated units were used in final analyses only if the following conditions were met: (1) the number of spikes exceeded 100, (2) the average firing rate was >1 Hz in association with a single arm (including the choice platform) during outbound journeys in a recording session, and (3) the firing field's location (measured by center of mass) was identified within the arm or choice-platform area. An outbound journey started when the rat entered the arm and ended at the moment when the rat displaced one of the objects. The inbound journey following the object choice was excluded from the analyses because behaviors during inbound journeys were confounded by the interactions between the animal and the experimenter as the rat was guided to return to the start box by the experimenter in most trials.

Data analysis

Measuring object-in-place strategy and position-response bias.

In the current OPPA task, during the initial learning stage, rats typically started with a tendency to choose an object on a particular side (e.g., any object on the left food well) when entering a choice platform in a given arm (Lee and Solivan, 2008; Jo and Lee, 2010a,b; Lee and Solivan, 2010). This is a maladaptive strategy and was measured as a position-response bias index (I_pos-res). We prefer the term position-response bias to the conventional term “response bias” because it is unclear whether the rat chose an object on a particular side (e.g., left) during the early learning stage in the OPPA task because of its movement bias to one side or whether the animal was biased to visit the food-well position on that side (e.g., left food-well position) or both. In contrast, the animal's tendency to choose a particular object regardless of its associated food-well position was measured as an object-in-place index (I_obj-plc) (Lee and Solivan, 2008; Lee and Kim, 2010). Briefly, I_obj-plc was calculated by taking the absolute value of the difference between the number of trials in which Obj_G was chosen and the number of trials in which Obj_C was chosen, and then dividing the resulting value by the total number of trials. The index for measuring I_pos-res was calculated similarly using the number of trials in which left and right food wells were chosen.

Measuring spatial firing pattern.

For generating a rate map, the entire maze area was scaled down to a 64 × 48 pixel space. Two-dimensional spatial firing rate maps were calculated by dividing the number of spikes with the total time spent by the rat in each pixel. Then, an “adaptive binning method” (Skaggs et al., 1993) was applied to smooth the firing rate map. Spatial information conveyed per spike was measured by calculating spatial information score (Skaggs et al., 1993). An arm-specificity score was calculated to measure the differential firing rates between the two arms (Lee and Kim, 2010). Briefly, the average firing rate associated with each arm was calculated, and the absolute value of the difference between the two arms was divided by the overall firing rate for both arms. Thus an arm-specificity score closer to 1 indicates that the cell fired exclusively in a particular arm, whereas a score closer to 0 means that the neuron fired equivalently in both arms.

Perievent time histogram.

To test whether neuronal firing was significantly modulated by the occurrence of a spatial event, a perievent time histogram (PETH) was generated for each single unit as follows. Spikes were binned (10 ms/bin) within a time window of 500 ms before and after the occurrence of a target event. PETHs were generated for the following three significant events in the OPPA task: (1) Event 1, entrance into an arm from the center stage (measured off-line by detecting the rat's position crossing of a virtual boundary overlaid with the arm entrance area); (2) Event 2, entrance into the choice platform (measured off-line by detecting the rat's position crossing of a virtual boundary overlaid with the choice-platform entrance area); and (3) Event 3, displacement of an object (measured by the infrared optic sensor underneath the food well). A Wilcoxon signed-rank test was conducted between pre-event and postevent spiking bins in the following cases to test whether the unit's firing was significantly modulated with the occurrence of the target event: (1) a number of spikes ≥100 was observed in arm and choice-platform areas, (2) there were >10 spikes within a 1 s temporal window (500 ms pre-event and postevent, respectively), and (3) there were more than three consecutive bins containing spikes above 150% of the baseline spiking activity (estimated on the basis of the average firing rates in the start box before each trial commenced). The contrast in firing rates before and after the occurrence of a target event was measured by dividing the absolute difference between the numbers of spikes between the two periods by the sum of the two.

Population PETH analysis.

For the units showing modulations in firing rate in an event-dependent manner (at least for one event), a population PETH (pop-PETH) was constructed. Individual spike trains associated with outbound journeys (from arm entrance to object choice) were used for constructing the pop-PETH. Specifically, different temporal lengths associated with the time periods for outbound journeys in a single trial were scaled to 300 bins (150 bins from arm entrance to choice-platform entrance and 150 bins from choice-platform entrance to object choice), and neuronal spike trains for individual trials were scaled accordingly and averaged, which resulted in a single spike train that occupied a single row in the pop-PETH. On average, the size of a single bin was 14.8 ± 0.7 ms (mean ± SEM). This method eliminates the issue of confounding statistical analyses when applied to a series of individual PETHs because no event period is included multiple times in different PETHs. The pop-PETHs for correct and incorrect trials were constructed separately for each arm. When arranging individual average spike trains in a pop-PETH, the neurons were ordered according to the temporal location of the maximal firing rate in the event-time dimension in a given arm. The degree of similarity between pop-PETHs was determined by calculating a pixel-by-pixel Pearson's correlation coefficient (r). Correlation coefficients underwent Fisher's r-to-z transformation (z = ½ × ln[(1 + r)/(1 − r)]) for further statistical analyses throughout the study. To examine whether noncognitive behavioral differences might have significantly influenced the results, running speed and head direction were calculated and compared across animals and also among different conditions (e.g., arm, correctness, and learning stage).

In a PETH, spikes may occur at particular times reliably across trials because a neuron fires at a particular location (i.e., position locked) or because the neuron fires at a fixed temporal distance from an event (i.e., event locked) or both. We sought to differentiate the two possibilities and, within a neuron, calculated the variability (i.e., SD of x–y position coordinates of spikes in reference to the mean position coordinate) in position correlates from arm entrance to object choice (normalized by the average traveling distance). We also calculated the variability in the temporal distance of a spike train (measured by the mean temporal distance in the spike train) from the moment of object choice (normalized by the average latency to object choice) across trials in a session. The normalized SDs measured separately for spatial and temporal domains were then compared in a scatter plot (Baeg et al., 2003).

Cross-correlation between spatial firing rate maps.

Similarity in spatial firing pattern was examined by calculating a pixel-by-pixel cross-correlation coefficient between rate maps. Trials were sorted into different trial types based on arm (Arm 3 or Arm 5), configuration of object positions in the choice platform (Obj_G–Obj_C or Obj_C–Obj_G), and the position or direction associated with the choice response (left or right). Then, the average firing rate maps associated with the trial types were paired according to whether a given pair of conditions conforms the object-in-place strategy or position-response bias (both left- and right-turn pairs were analyzed, and the bigger correlation coefficient of the two was taken as a conservative measure, as illustrated in Fig. 6A) (Lee and Kim, 2010). The spatial similarity of firing rate maps was measured by Pearson's correlation coefficient (r). The correlation coefficient was calculated only for the pixels with overlapping trajectories between trials (Lee and Kim, 2010). Once calculated, the correlation coefficient underwent Fisher's r-to-z transformation (z = ½ × ln[(1 + r)/(1 − r)]) for further statistical analysis.

Figure 6.

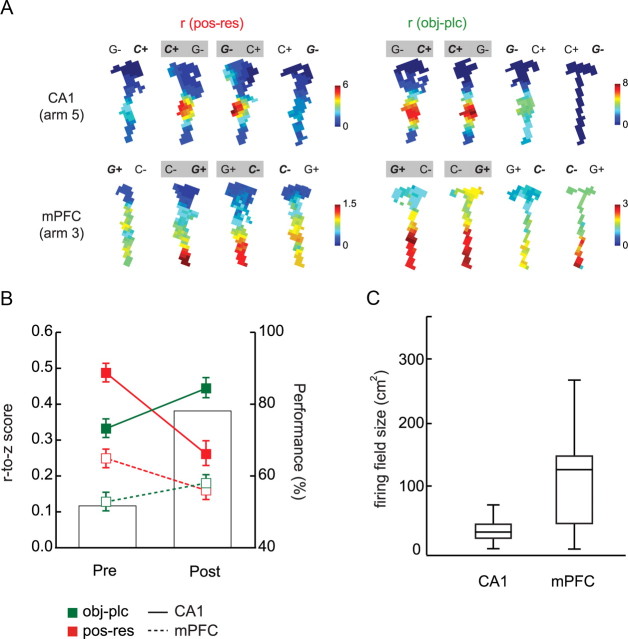
Common changes in strategy-related firing correlates in CA1 and mPFC across learning. A, Representative examples of firing rate maps associated with four trial types in the OPPA task. Each example shows how a pair of trial types (marked with gray boxes; for pos-res, only the pair with higher similarity in spatial firing was marked) can be categorized for calculating strategy-based, pixel-by-pixel cross-correlation. r(pos-res), Position-response bias; r(obj-plc), object-in-place strategy. The rate-map examples for CA1 and mPFC were drawn from Arm 5 and Arm 3 conditions, respectively. G and C denote the toy girl and dummy cylindrical objects, respectively. A plus sign indicates the correct object that needs to be chosen in a given condition, and bold, italic font indicates the objects actually chosen by the rat. B, The degree of similarity between firing rate maps from both position-response bias and object-in-place strategy pairs were r-to-z transformed and plotted (mean ± SEM) for comparison between prelearning and postlearning in CA1 and mPFC. Bar graphs indicate the average performance across learning stages. C, The distribution of firing field sizes for CA1 and mPFC. CA1 neurons exhibited smaller and more spatially localized firing fields, whereas mPFC neurons showed more broadly tuned spatial firing fields. Error bars denote the range of the firing field size, and the bar in the box indicates the median.

Bootstrap analysis.

To check whether changes in spatial firing patterns during learning were affected by inequality in sampling across trial conditions, parametric bootstrap was conducted (Lee and Kim, 2010). Specifically, firing rate maps were built using randomly resampled trials (repeated sampling allowed) in both object-in-place and position-response strategy conditions within a session and the r-to-z transformed cross-correlation coefficients were calculated based on the firing rate maps. This procedure was repeated for 1000 times per condition in each session, and an average correlation coefficient was obtained as a result. If the original results were mainly driven by the condition with larger number of trials, the parametric bootstrapping would negate the originally observed effects at a significance level of α = 0.001. In addition, shuffling bootstrap was conducted to test the possibility that a particular pattern of firing rate map was obtained by chance (Lee and Kim, 2010). To test this, briefly, the locations of pixels in each firing rate map were randomly shuffled among themselves within the map and the correlation coefficients recalculated using the firing rate maps with shuffled pixels. This procedure was repeated 1000 times, and an average r-to-z transformed correlation coefficient was obtained. If a specific spatial firing pattern were obtained by chance, this procedure should produce the same results.

Phase relationship of neuronal spiking with simultaneously recorded theta rhythm.

Since the phase relationships of spiking with theta rhythm depend heavily on the recording site (Bragin et al., 1995), the electrode that was adjusted minimally and recorded the largest number of putative pyramidal neurons (Burke et al., 2011) was chosen and used throughout the entire analyses. Raw local field potentials (LFPs) were downsampled from 32 to 2 kHz, bandpass filtered between 4 and 12 Hz, and parsed according to individual trials. Theta phases were detected by applying Hilbert transform to the previously bandpass-filtered (4–12 Hz) LFPs (Le Van Quyen et al., 2001). A theta cycle was excluded from analysis if its peak or trough fell within confidence limits (i.e., mean ± 1 SD based on all LFP recordings in a given session). For each neuron, a phase histogram (20° per bin) was built, and Rayleigh's test was used to determine whether the neuron was significantly phase locked to the theta rhythm. The proportion of neurons associated with the object-in-place strategy and the neuronal proportion associated with the position-response bias passing the statistical criteria were compared across the learning stages. All calculations and statistical tests were performed using a circular statistics toolbox for Matlab (Berens, 2009).

Calculation of temporal synchrony between CA1 and mPFC spike trains.

The amount of temporal synchrony in spiking between CA1 and mPFC was measured by cross-correlating spike trains recorded simultaneously from the two regions (bin size, 10 ms). A CA1 spiking train was always used as a reference. The cross-correlation was calculated for each trial in the time window (500 ms before object choice) critical for making a decision in the OPPA task, and the resulting individual cross-correlation coefficients (after r-to-z transformations) were used toward statistical analysis. At the beginning of the 500 ms time window, the positions of the rat were localized within the choice platform in 99.7% cases of the trials used in the analysis. In addition, running speed and traveling distance were measured and compared to test the influence of other noncognitive behavioral differences that might have affected the results. The cross-correlation was calculated only for the trial in which at least three spikes were identified within the 500 ms time window in both CA1 and mPFC spike trains. The time lag between the spike trains from CA1 and mPFC was calculated by measuring the location of the peak in the cross-correlogram. Throughout the analyses, parameters (i.e., correlation coefficient and time lag) associated with the cross-correlograms were used only when at least 10% of the continuous bins in the correlogram exceeded the 99% confidence interval. Correlation coefficients were normalized using Fisher's r-to-z transformation (z = ½ × ln[(1 + r)/(1 − r)]) for further statistical testing. The parametric bootstrap method used for verifying the results from the spatial correlation analysis was also applied to the data sets for temporal cross-correlation analysis between spikes trains.

Theta power spectrum and coherence analyses for LFPs.

Theta power spectrograms and coherograms were generated for LFPs in CA1 and mPFC using Chronux Toolbox (http://www.chronux.org) and custom-written programs in Matlab. Specifically, we used mtspecgramc and cohgramc functions with the following parameters: window size, 300 ms; time step, 150 ms; tapers, [3 5]; and fpass (bandwidth), [4 12]. Power spectrum and coherence were computed across five different time blocks (Fig. 9, b1 to b5; 300 ms window for each time block, 150 ms time lag between adjacent blocks) in reference to both the choice-platform entrance and the object-choice event. Each spectrogram and coherogram was normalized by the mean of all sessions.

Figure 9.

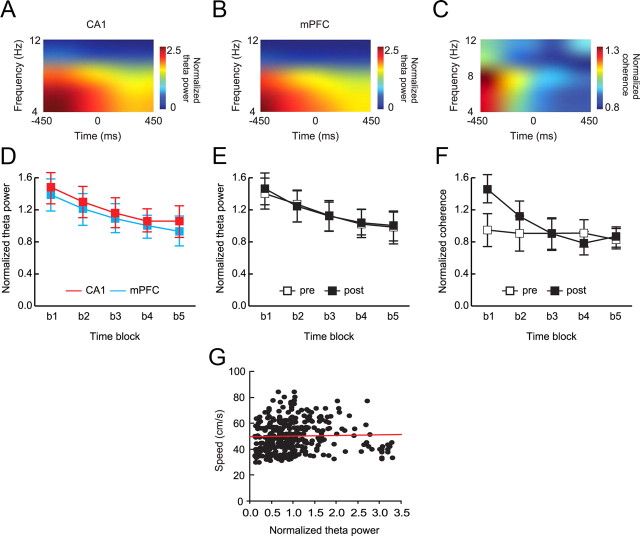
Coherence between CA1 and mPFC theta around the choice-platform entrance event. A, B, Representative spectrograms of CA1 LFP (A) and mPFC LFP (B) in reference to choice-platform entrance. Spectrograms were built by shifting a 300 ms time block by 150 ms. The moment of entering a platform was set as time 0. Prominent power in the theta frequency range (4–12 Hz) was observed in both CA1 and mPFC. C, A representative coherogram between hippocampal and mPFC LFPs simultaneously recorded in a recording session. Note the strong coherence before, but not after, entering the choice platform. D, E, Decrease in average theta power across time blocks (b1 to b5) occurred similarly in CA1 and mPFC regions (D) and between prelearning and postlearning stages (E) as the rat passed the choice-platform entrance. F, Decrease in coherence between CA1 and mPFC LFPs across the choice-platform entrance occurred only during the postlearning stage. Mean ± SEM. G, Scatter plot for showing the relationships between speed and normalized theta power measured across the choice-platform entrance event. No significant correlation was found between the two factors.

Results

Acquisition of the OPPA task with object-in-place strategy

In the OPPA task, rats entered one of two arms (Arm 3 and Arm 5) in a seven-arm radial maze in each trial and must choose an object (either a toy girl, Obj_G, or a cylinder, Obj_C) associated with reward in the currently visiting arm (Fig. 1A). Since the same pair of objects was used across trials, the rat should pay attention to both spatial information (i.e., arm) and object identity information to obtain a reward reliably. As reported previously (Lee and Solivan, 2008; Jo and Lee, 2010a,b; Lee and Kim, 2010; Lee and Solivan, 2010), rats learned the task in approximately 2 weeks and showed a sharp transition from chance performance (prelearning stage) to a learned state (>75% correct; postlearning stage) from the seventh day of acquisition (Fig. 1B, D0). An ANOVA using acquisition day as a factor showed that there was a significant main effect (F_{(12, 22)} = 12.59, p < 0.001) and the performance in the postlearning stage was significantly different from that of the prelearning stage (t₍₃₃₎ = 11.75, p < 0.001; independent sample t test).

During prelearning or when the hippocampus or other critical structures (e.g., mPFC or perirhinal cortex) were damaged (Lee and Solivan, 2008; Jo and Lee, 2010a,b; Lee and Solivan, 2010) in the OPPA task, rats typically adopted a task-irrelevant strategy (i.e., position-response bias) presumably because they could not process the OPPA demand of the task. The rat acquired the object-in-place rule in ∼1 week with a dramatic decrease in the position-response bias at the same time (Fig. 1B, inset). Such a shift in strategy observed previously in the OPPA task (Lee and Solivan, 2008; Jo and Lee, 2010a,b; Lee and Kim, 2010; Lee and Solivan, 2010) was also verified in the current study and was quantified by calculating a position-response index (I_pos-res) as well as an object-in-place index (I_obj-plc). I_pos-res would be high if the rat chose one side (or position) more than the other, and likewise for I_obj-plc if the rat selected the correct object more than the incorrect one. A repeated-measures ANOVA with acquisition day and strategy as main factors confirmed the strategy-shifting phenomenon because there was a significant two-way interaction between the strategy and acquisition day (F_{(12, 22)} = 12.30, p < 0.001) with significant main effects of both strategy (F_{(1, 22)} = 15.17, p < 0.05) and acquisition day (F_{(12, 22)} = 2.68, p < 0.05). An independent sample t test on both strategies confirmed that the object-in-place strategy was more prevalent significantly in the postlearning stage than in the prelearning stage (all p values < 0.001), thus predicting the performance in the OPPA task.

Recording sites in CA1 and mPFC and unit classification

After the completion of all experiments, recording sites were verified histologically (Fig. 1C). Tetrode-tip positions were verified by electrolytic lesion marks, and the physiological properties of neuronal firing recorded during tetrode adjustments were also used in the verification process. After cluster cutting (Lee et al., 2004a,b; Lee and Kim, 2010), the isolated units (n = 656 in CA1 and n = 403 in mPFC) that met several criteria (see Materials and Methods) were used in final data analysis (n = 357 in CA1 and n = 263 in mPFC). A summary of the neurons used for final analysis and their firing characteristics (per single session) are provided in Table 1. On average, 27 units in CA1 and 20 units in mPFC were used for analysis per single recording session.

Table 1.

The number of units used for analysis and their firing properties in a single session across acquisition days

	Learning Session
	D−6	D−5	D−4	D−3	D−2	D−1	D0	D+1	D+2	D+3	D+4	D+5	D+6
Number of cells
CA1	20	48	33	26	15	38	45	33	19	30	20	20	10
mPFC	7	19	22	24	12	23	25	22	23	23	25	26	12
Max firing rate (Hz)
CA1	7.7	7.7	5.6	4.5	7.6	5.7	5.5	6.4	5.4	6.7	6.5	7.8	4.9
mPFC	7.3	11.1	3.9	10.1	14.6	6.6	5.8	10.1	6.4	9.5	6.4	6.3	2.9
Spike width (μs)
CA1	256.7	254.9	259.2	276.0	261.8	260.0	258.9	262.4	256.0	269.1	250.2	251.5	271.6
mPFC	302.2	300.0	298.6	298.6	292.9	288.0	302.7	288.0	290.4	293.3	310.4	288.0	290.9

Neurons in CA1, but not in mPFC, convey arm-specific spatial information

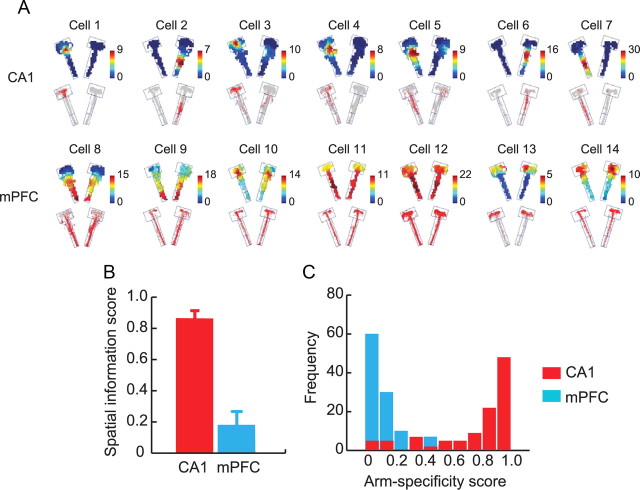
We first applied conventional spatial analytical methods to both regions to examine spatial firing patterns of hippocampal and mPFC neurons. As known in the literature (O'Keefe and Dostrovsky, 1971; Muller et al., 1987), CA1 neurons showed well-isolated spatial firing fields (i.e., place fields) associated with a specific arm in the maze (Fig. 2A). The spatial firing patterns of neurons recorded from mPFC, however, were not as localized in space as those from CA1 but showed more globally distributed firing patterns throughout the maze (Fig. 2A). Some mPFC neurons fired locally in the maze (Fig. 2A, cells 10, 13, 14), but interestingly, their localized firing occupied similar locations in both arms (e.g., near or within choice platform in these examples) as opposed to the single arm-specific firing of CA1 neurons. The diffused firing patterns of mPFC neurons in space (Poucet, 1997; Jung et al., 1998) were confirmed by poor spatial information scores (Skaggs et al., 1993) associated with mPFC units (mean, 0.24 ± 0.01) in contrast to the higher spatial information conveyed by hippocampal cells (mean, 0.82 ± 0.02) (Fig. 2B). An independent samples t test between the brain regions showed that CA1 neurons exhibited significantly higher spatial information than mPFC cells (t₍₆₁₁₎ = 22.18, p < 0.001). When the degree of specificity in firing for a particular arm was measured as an index (arm-specificity score) (Lee and Kim, 2010), the majority of CA1 neurons showed high arm specificity, whereas most mPFC neurons displayed low arm specificity (Fig. 2C). By simultaneously monitoring single units from CA1 and mPFC in a common task, our study thus confirms that the hippocampal neuronal firing is spatial in nature (O'Keefe and Dostrovsky, 1971; Muller et al., 1987) and such spatial firing characteristics are not displayed by neurons in mPFC (Poucet, 1997; Jung et al., 1998). The differences in spatial firing characteristics between CA1 and mPFC were observed consistently across the learning stages (F values > 2.20, p values > 0.14; one-way ANOVA).

Figure 2.

Spatial firing patterns of CA1 and mPFC neurons. A, Representative firing rate maps (top) and raw spiking positions (bottom) of neurons in CA1 and mPFC. Color bars represent firing rates (in hertz). B, Comparisons of spatial information content (bits per spike) between CA1 and mPFC. Note the contrast between the two areas. Mean ± SEM. C, Histograms showing the distributions of arm specificity scores of neuronal populations in CA1 and mPFC.

Neurons in mPFC, but not in CA1, represent a common “event type” associated with different spatial locations

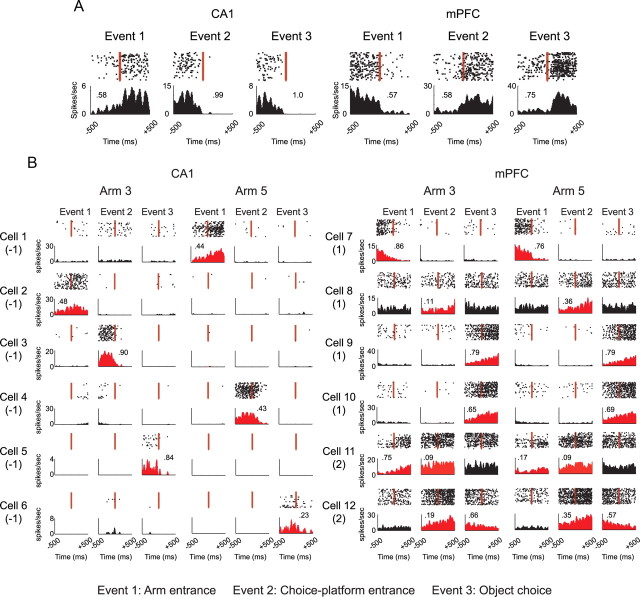
The poor spatial firing properties of mPFC units suggest that the conventional spatial analysis may not be ideal for capturing the nature of information represented by mPFC units. Since the literature suggests that the firing patterns of neurons in both mPFC and hippocampus are modulated by the occurrence of significant events in a goal-directed task (Hampson et al., 1999; Wood et al., 2000; Hok et al., 2005; Hyman et al., 2005; Jones and Wilson, 2005), we next examined whether the neuronal activity was significantly modulated by the occurrences of the following three event types (for details, see Materials and Methods): Event 1, arm entrance; Event 2, choice-platform entrance; Event 3, object choice. A PETH for each event type was constructed (±500 ms from the onset of the event with 10 ms binning) separately for each arm for individual units (Fig. 3A). Approximately similar proportions of neurons represented the three event types within mPFC and CA1, although there was a bigger proportion of neurons representing the choice-platform entrance event in CA1 than in mPFC (χ²₍₁₎ = 10.72, p < 0.01), and more neurons in mPFC represented the object-choice event than in CA1 (χ²₍₁₎ = 14.76, p < 0.001). As shown in Figure 3B, hippocampal unit firing was significantly modulated with a particular event associated with a specific arm only, whereas mPFC units showed multiple examples in which the firing rates were significantly modulated by the occurrence of an event (or multiple events) relatively independent of the arm in which the event occurred. For example, the firing of Cell 1 in CA1 was significantly modulated by Event 1 (arm entrance) only in Arm 5, but not in Arm 3, whereas the firing rate of Cell 7 in mPFC was modulated by arm entrance regardless of whether the rat entered Arm 3 or Arm 5. Similar examples were found for other event types (Fig. 3B). It appears that mPFC neurons, unlike CA1 neurons, tended to fire when a certain type(s) of event occurred regardless of its associated spatial location(s). This may explain why some mPFC neurons fired in similar locations in both arms when their spatial firing patterns were examined using conventional firing rate maps (Fig. 2A).

Figure 3.

Event-related modulation of firing in CA1 and mPFC. A, Raster plots and PETHs were constructed for three significant event types (arm entrance, choice-platform entrance, and object choice) in the OPPA task. Each PETH (bin size, 10 ms) was generated with spikes that occurred within 500 ms before and after the onset of an event, marked by the vertical red arrows. The number in the PETH indicates the absolute contrast in firing (scaled from 0 to 1) between the pre-event and postevent occurrences. B, PETHs generated for both arms for the three event types. The PETHs in red indicate the cases in which significant firing modulations were detected in Wilcoxon signed-rank tests, and at least three consecutive bins were above the baseline firing level. Numbers in parentheses below cell number indicate the event-type-specificity index. Positive numbers indicate that the cell fired for a particular type (or types) of event commonly across arms, whereas negative numbers denote the opposite. Note that mPFC neurons fired more arm independently for common event types.

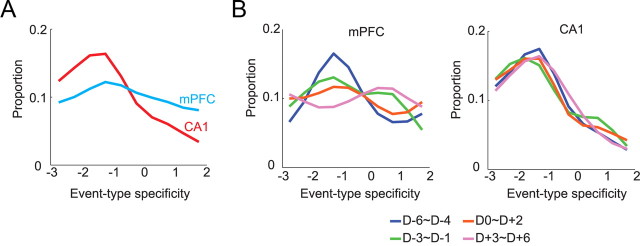
To measure the above differences between the two areas, we calculated event-type specificity for a single cell as follows. First, the pattern of significance levels (determined by the signed-rank test in each PETH) across six events (three events by two arms) was represented using a binary coding scheme in the following format: Arm 3 [x1, x2, x3] and Arm 5 [y1, y2, y3] with the variables inside the brackets being either 0 or 1 (depending on the statistical significance of the Wilcoxon signed-rank test for the PETH for each event). For example, Cell 1's firing pattern (Fig. 3B) was coded as Arm 3 [0, 0, 0] and Arm 5 [1, 0, 0] because only the PETH for Event 1 in Arm 5 was significant, and Cell 7's firing pattern could be likewise coded as Arm 3 [1, 0, 0] and Arm 5 [1, 0, 0]. Event-type specificity was then defined as [<x1, y1> + (x1 * y1)] + [<x2, y2> + (x2 * y2)] + [<x3, y3> + (x3 * y3)], where angle brackets indicate that the bigger value of the two was subtracted from the lesser (or equal) value. The resulting event-type-specificity scores ranged from −3 to 3. However, the cells with event-specificity index of 3 were removed from the analysis because firing for all the event types significantly may indicate no specificity in a sense. A positive index score indicates that the neuronal firing was modulated by a certain type of event across different arms, whereas a negative value denotes that a certain event type was represented as an orthogonal event tied to a specific arm. When the overall distributions of event-type-specificity scores were compared between CA1 and mPFC (Fig. 4A), a larger proportion of neurons in mPFC showed higher event-type specificity, and the trend was reversed between the two regions in the lower event-type-specificity range. The two distributions were significantly different from each other (Pearson χ² test; χ²₍₅₎ = 41.27, p < 0.001), and post hoc comparisons showed significant differences at all levels of event-type specificity (all p values < 0.05, except at −3 due to insufficient sampling).

Figure 4.

Interregional differences in representing common types of events across arms. A, Event-type specificity (abscissa) indicates the degree to which neurons represent comment event types regardless of arms as in Figure 3. Compared to CA1, mPFC contained a significantly bigger proportion of neurons showing higher event-type specificity. B, Changes in event-type specificity across learning sessions. Three sessions were binned into a block. In mPFC (left), the proportions on the positive side of the event-type specificity increased across days, while the ones on the negative side decreased. In CA1 (right), however, the proportional distributions remained unchanged throughout the acquisition period.

As the overall graph in Figure 4A was broken down using a 3 d moving window across acquisition, however, a gradual development of more positive event-type specificity and decrease in negative event-type specificity were observed in mPFC, but not in CA1 (Fig. 4B). The proportional distributions for different day blocks were not significantly different from each other in CA1 (χ²₍₁₅₎ = 18.30, p = 0.25), whereas a significant difference was found in mPFC (χ²₍₁₅₎ = 30.88, p < 0.01). The significant difference in mPFC was attributable to the difference between the first (D−6 to D−4) and the last (D+3 to D+6) acquisition blocks (χ²₍₅₎ = 17.92, p < 0.01).

These results suggest that the representation of an event is more spatially bound in the hippocampus than in mPFC throughout learning. There was no change in the event-type-specificity distribution in CA1 in which the proportions of negative index scores were maintained at high levels across learning. In contrast, the mPFC neuronal activity was more concerned with representing a particular type (or types) of event relatively independent of its associated spatial location, and such coding for event-types gradually developed over time during learning.

Event-related firing characteristics of neurons in CA1 and mPFC at the population level

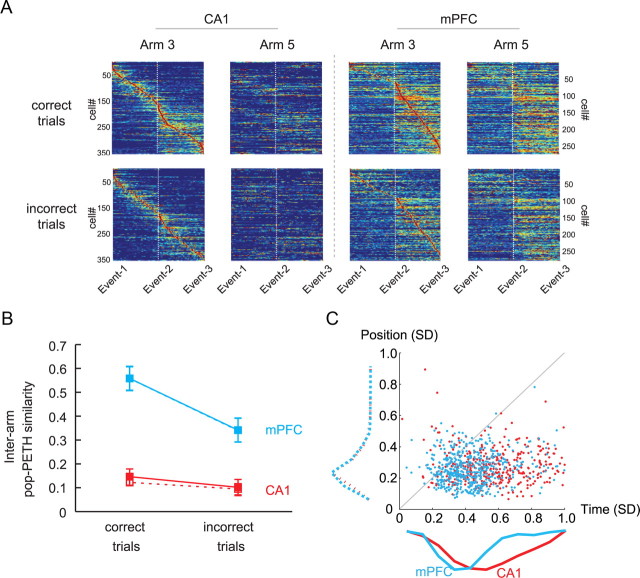
The differences in representation observed in individual neurons (Fig. 3B) between hippocampus and mPFC were further examined at the population level. For this purpose, a pop-PETH was constructed (Fig. 5A) for all the units that showed significant modulations in firing rates in association with at least one of the three event types (Fig. 3; for details, see Materials and Methods). Briefly, a single row in a pop-PETH shown in Figure 5A represents the firing rates of a single unit at different time points along the temporal dimension between arm entrance (Event 1) and choice-platform entrance (Event 2) as well as between choice-platform entrance and object choice (Event 3). The individual units of the population along the column were ordered sequentially according to the locations of their maximal firing rate in the temporal dimension between arm entrance and object-choice events. A sequential alignment of active firing (i.e., diagonal band) along the event-time dimension was noticeable in the pop-PETHs for both CA1 and mPFC (Fig. 5A).

Figure 5.

Temporal firing patterns of neuronal populations in CA1 and mPFC in relation to the occurrence of events in the OPPA task. A, A pop-PETH was generated (separately for each arm and for correct versus incorrect trials) by aligning the population of neurons (ordinate) by the temporal positions of maximal firing peak from arm entrance (Event 1) to object choice (Event 3) via choice-platform entrance (Event 2). Only cells showing significant modulations of firing across the events were used. Only the pop-PETHs using Arm 3 as the reference arm are shown here. In CA1, the linearly aligned patterns of peak firing locations across time were clearly visible, whereas such a linear arrangement of firing patterns was mostly associated with the second period (choice-platform entrance to object choice) in mPFC. Note the linear alignment of firing disappeared in CA1 when the same sequence of neurons was used for constructing the pop-PETH for the other arm, whereas a relatively similar level of firing could be still observed in mPFC. B, Comparison of the degree of similarity between pop-PETHs for Arm 3 and Arm 5 in correct trials and incorrect trials in CA1 and mPFC. Ordinate, r-to-z-transformed correlation coefficient. Solid lines and filled squares are based on the Arm 3-based alignment, and dotted lines and open squares are from the Arm 5-based alignment. Mean ± SEM. C, Comparison of the spatial and temporal variances in spiking activities between CA1 and mPFC. The spatial variance (ordinate) measured how reliably spikes were fired at a particular location in the maze, whereas the temporal variance (abscissa) measured how well timed the spike trains were from the onset of the object-choice event. The majority of data points were located below the 45° line, indicating that overall spiking activity was spatially bound similarly in both regions (see the dotted histograms along the y-axis). However, mPFC spikes were also fairly well timed from the object-choice event, as shown by the narrower distribution of the histogram (cyan) compared to the broad distribution of CA1 histogram (red) along the x-axis.

As observed in spatial analysis (Fig. 2) and individual PETHs (Fig. 3), in CA1, the linearly arranged sequential firing pattern in the pop-PETH for one arm (e.g., Arm 3) completely disappeared when the pop-PETH was constructed for the other arm (e.g., Arm 5) using the same set of neurons while preserving the same ordering scheme for the original arm (e.g., Arm 3). In contrast, albeit seemingly reduced in similarity, the overall firing patterns of mPFC neurons at the population level seemed relatively preserved between different arms compared to CA1 (Fig. 5A). To quantify the similarities between the pop-PETHs for different arms as stated above, correlation coefficients between the two pop-PETHs were calculated separately for correct and incorrect trials (Fig. 5B). Afterward, a repeated-measures ANOVA was performed with the region (CA1 vs mPFC) and correctness (correct vs incorrect trials) as main factors. There were significant effects of both factors (region, F_{(1, 4)} = 37.47, p < 0.01; correctness, F_{(1, 4)} = 226.51, p < 0.001) and a significant interaction between the two factors (F_{(1, 4)} = 98.22, p < 0.01). As observed in the pop-PETHs (Fig. 5A), similarity was higher in mPFC than CA1 in both correct and incorrect trials. The significantly higher similarity between pop-PETHs for different arms in mPFC is attributable to the firing characteristics of mPFC neurons for representing common event-type information across arms. Within mPFC, however, a significant drop was observed in the similarity between pop-PETHs for the incorrect trials compared to those for the correct trials (but not in CA1; all p values < 0.001). The results further suggest that the decrease in event type-related firing properties of mPFC neurons, but not CA1 neurons, is related to incorrect choices in the OPPA task.

Since it is possible that the differences between hippocampal and mPFC neuronal populations shown above (Fig. 5B) were due to generic differences in behavior, we examined the rat's running speed (in centimeters per second) and head direction (in degrees) information in matching conditions. The average running speeds were 20.45 ± 0.48 (mean ± SEM) in correct trials and 21.45 ± 0.61 in incorrect trials for the Arm 3-based alignment condition, and 22.82 ± 0.64 in correct trials and 23.99 ± 0.63 in incorrect trials when Arm 5 was used as a reference. The head directions were, on average, maintained at 285.77 ± 2.93 (mean ± SEM) in correct trials and 283.62 ± 2.87 in incorrect trials when using Arm 3 as a reference, and at 248.37 ± 1.75 in correct trials and 248.79 ± 1.81 in incorrect trials for the Arm 5-based alignment. Regardless of the arm used for alignment, statistical tests showed that both behavioral factors were comparable between correct and incorrect conditions (running speed, t values ≤ 1.29, p values ≥ 0.20, paired-sample t test; head direction, F values ≤ 0.27, p values ≥ 0.61, Watson–Williams F tests for circular statistics). The results indicate that it is unlikely that the differences in representation in neuronal populations between CA1 and mPFC were due to behavioral differences in the OPPA task.

An important trend that was noticeable in the pop-PETHs was that all event time bins from arm entrance to object choice were uniformly distributed in CA1 (as manifested by the red diagonal band of maximal firing), whereas the mPFC neuronal population's maximal firing was mostly distributed between choice-platform entrance and object choice. This phenomenon was easily captured when the center points of individual firing fields were fitted with polynomial curves (order, 2) in the pop-PETHs for CA1 and mPFC (data not shown). This trend indicates that mPFC neurons showed biased firings toward choice platform, so it raises the possibility that high firing similarity between arm conditions in mPFC stemmed from the firings from Event 2 to Event 3. To examine a possibility that the bigger similarity between pop-PETHs in mPFC than CA1 (Fig. 5B) might be due to the differences in homogeneity of field distributions in the maze between the two regions, interarm pop-PETH similarities were calculated for the Event 1 to Event 2 period and the Event 2 and Event 3 period, separately. Then, a three-way repeated-measures ANOVA was performed with brain region, correctness, and interevent period (Event 1 to Event 2 vs Event 2 to Event 3) as main factors. The results showed significant main effects of correctness (F_{(1, 8)} = 28.18, p < 0.01) and brain region (F_{(1, 8)} = 111.31, p < 0.001), but there were no significant effect of interevent period (F_{(1, 8)} = 1.76, p = 0.22) and no significant interaction effects involving the same factor [F values < 1, not significant (ns)], indicating that the interarm pop-PETH similarity in mPFC was not significantly affected by the biased firing in the choice platform (between Event 2 and Event 3). In post hoc comparisons, there were significant drops in firing similarity between correct and incorrect conditions in mPFC, but not in CA1, when aligned by either arm (all p values < 0.001).

To determine whether the orderly firing patterns observed in PETHs were more associated with positional consistency or event-related temporal consistency (i.e., time locked to the object-choice event), we calculated the variances associated with spatial positions and temporal distances (from the object-choice event). If spike trains occurred reliably across trials more associated with a particular position in space and less tied to the occurrence of the target event, a bigger variance in the latter domain should be observed than in the spatial domain. The opposite should be true when spike trains were more associated with the timing of occurrence of the target event. The spatial and temporal variances were compared with each other (Baeg et al., 2003). As clearly visible in Figure 5C, most data points for both CA1 and mPFC are located below the 45° line, implying that the neuronal spikes in both regions were correlated with spatial positions more reliably than with the occurrences of the object-choice event. A repeated-measures ANOVA with the type of variances and brain region as main factors showed significant effects of the type of variance (F_{(1, 871)} = 560.20, p < 0.001), brain region (F_{(1, 871)} = 98.56, p < 0.001), and the interaction between the two (F_{(1, 871)} = 89.42, p < 0.001). The main effect of the type of variance verified the observation that neuronal spikes were more reliably associated with spatial positions than the moments of object choice in the OPPA task. For both CA1 and mPFC, significant differences between positional and temporal variances were observed (all p values < 0.001). The positional variance ranged narrowly from 0 to 0.3 in both areas and, on the basis of post hoc comparisons, no significant difference was found between CA1 and mPFC (p > 0.05). The temporal variance was significantly bigger than the spatial variance in both regions (all p values < 0.01). Interestingly, with respect to the temporal variance of spiking in relation to object choice, the mean spiking timing was significantly more variable in CA1 than mPFC (p < 0.05) as illustrated by the narrower range of mPFC data points than CA1 points along the time dimension in Figure 5C, whereas no significant difference was found between the two regions for positional variance. The results suggest that spatial location information associated with an event was a more reliable predictor in the task for the occurrence of spiking activities in both regions.

Transition from position-response bias to object-in-place strategy occurs in both CA1 and mPFC during learning

After observing some differential firing characteristics between the two areas in the OPPA task, we next sought some commonalities in learning-related neural dynamics between hippocampus and mPFC. We reported previously that the spatial firing patterns of CA1 neurons became more similar as learning progressed in the OPPA task between the trial types associated with the object-in-place strategy, whereas the firing patterns became more dissimilar between the trial types associated with the task-irrelevant strategy (i.e., position-response bias) (Lee and Kim, 2010). We sought to identify the same neural correlates for strategy shifting in mPFC in the current study. Specifically, individual trials in the OPPA task were sorted into four trial types (Fig. 6A) according to the configuration of objects in the choice platform as well as the rat's response to an object in a given trial (e.g., in Fig. 6A, G− C+ indicates a trial type in which Obj_G and Obj_C occupy the left and right food wells, respectively, and the rat chose Obj_C, which was a correct choice in Arm 5). When the rat chose different objects (Obj_G and Obj_C) in the same arm across trials to obtain rewards in a given arm (Fig. 6A), we categorized those trials as position-response trial types (because food-well position or response direction, but not object identity, was a common factor in those trials). In contrast, once the rat chose the same object (Fig. 6A, Obj_C for CA1 neuron) across trials in a given arm, we categorized those trial types as object-in-place trial types. The degree of similarity between spatial firing rate maps associated with the strategy-specific trial types was measured by calculating the correlation coefficient between associated rate maps as illustrated in Figure 6A [r(pos-res) for the position-response bias and r(obj-plc) for object-in-place strategy]. As shown with some examples in Figure 6A, neurons showing higher similarities between spatial rate maps for either strategy were commonly identified both in CA1 and mPFC throughout learning.

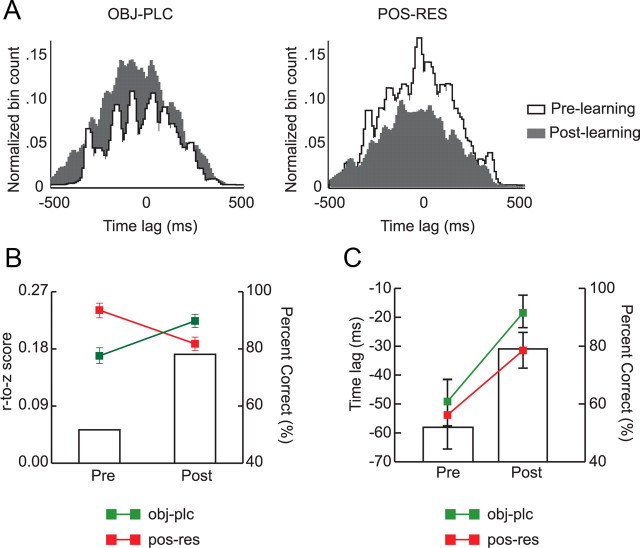
When the rate-map similarities were examined separately for the two conflicting strategies (or trial types) across learning stages, significant drops were observed in spatial correlation for the position-response bias in both hippocampus and mPFC after the acquisition of the task (postlearning) as shown in Figure 6B. In contrast, increases in rate-map similarity were identified for the object-in-place strategy as rats experienced the acquisition of the OPPA task in both hippocampus and mPFC. A repeated-measures ANOVA on r-to-z-transformed correlation coefficients using the strategy, learning stage, and brain region as factors confirmed the above observations: there were significant main effects of learning stage (F_{(1, 406)} = 4.15, p < 0.05) and region (F_{(1, 406)} = 119.55, p < 0.001). Furthermore, there was a significant three-way interaction among the main factors (F_{(1, 406)} = 13.57, p < 0.001), two-way interaction between strategy and learning stage (F_{(1, 406)} = 80.76, p < 0.001), and two-way interaction between strategy and region (F_{(1, 406)} = 4.15, p < 0.05). Post hoc comparisons showed that the decreases in rate-map similarity for the position-response bias after learning were significant in both regions (all p values <0.05). The increase in rate-map similarity for the object-in-place strategy from prelearning to postlearning in CA1 was statistically significant (p < 0.05), whereas the similar trend was observed in mPFC without statistical significance (p = 0.07).

Using bootstrap methods, we demonstrated previously that sampling bias does not play a significant role in producing dissociations presented in Figure 6 for hippocampal neurons (Lee and Kim, 2010). The same parametric bootstrap was applied to the CA1 and mPFC data sets, and a repeated-measures ANOVA on average r-to-z-transformed correlation coefficients (based on bootstrap) showed that there were still significant main effects of region (F_{(1, 1324)} = 116.85, p < 0.001) and strategy (F_{(1, 1324)} = 92.51, p < 0.001). There were also significant interactions of strategy and learning stage (F_{(1, 1324)} = 271.10, p < 0.001), strategy and region (F_{(1, 1324)} = 5.24, p < 0.05), region and learning stage (F_{(1, 1324)} = 5.79, p < 0.05), and strategy, region, and learning stage (F_{(1, 1324)} = 38.11, p < 0.001). A bootstrap method with pixel-shuffled rate maps (Lee and Kim, 2010) showed no significant effects (all p values > 0.05). The statistical tests using bootstrap methods thus suggest that the effects in Figure 6B were not due to inequality of sampling across different conditions during learning. The bigger differences observed both in prelearning and postlearning stages in CA1 than in mPFC are rather likely due to the differences in firing field size between the two regions. Specifically, we measured the size of a spatial firing field (Fig. 6C) as originally proposed by Muller et al. (1987), and the results confirm that the field size of mPFC was significantly bigger, on average, than that of CA1 (F_{(1, 618)} = 403.36, p < 0.001). There was no effect of learning stage on field size (F_{(1, 616)} < 1, ns), and no interaction of brain region and learning stage (F_{(1, 616)} < 1, ns) was observed either. The more spatially localized firing patterns of CA1 neurons could make the cross-correlation coefficient measure more sensitive to even small changes in the field, whereas the broadly tuned spatial firing patterns of mPFC neurons may make the same measure less sensitive to similar changes in mPFC.

In rule-relevant trials, more neurons in CA1 and mPFC become phase locked to theta rhythms after learning

To understand the functional interactions between CA1 and mPFC for learning the OPPA task, we examined whether spiking activities of CA1 neurons maintained a significant phase relationship with CA1's own theta rhythm and also with the simultaneously recorded theta rhythm in mPFC. The same analysis was performed for the mPFC spiking data for the simultaneously recorded theta rhythms from both CA1 and mPFC. To capture functional interactions between the two areas around the time of choosing an object in the choice platform, we calculated spiking phases in relation to the theta rhythm during the period between entering the choice platform and displacing an object. Phases of individual spikes were first calculated against the theta rhythms that were recorded simultaneously from CA1 pyramidal cell layers (Fig. 7A). The same phase calculations were performed in reference to mPFC theta rhythm. The resulting phase histogram of a neuron from a recording session (Fig. 7B) showed whether spiking activities were significantly modulated by certain phases of the theta rhythm (p < 0.05, Rayleigh's test). Most neuronal spikes were phase locked to the troughs of theta (mean phase, 357.8 ± 0.2°). Overall, a bigger proportion of neurons in CA1 (44.9%) were phase locked to theta rhythms than in mPFC (27.3%). Within CA1, more cells were phase locked to CA1 theta rhythms (50.9%) than to mPFC theta rhythms (39.0%), whereas similar proportions of neurons (28.0 and 26.8% to CA1 and mPFC theta rhythms, respectively) were phase locked to theta in mPFC. An ANOVA with the spiking region (CA1 and mPFC) and theta region (CA1 and mPFC) as factors showed that there were significant main effects of both factors (F values ≥ 6.6, p values < 0.05), and there was a significant two-way interaction between the factors (F_{(1, 1239)} = 4.1, p < 0.05).

Figure 7.

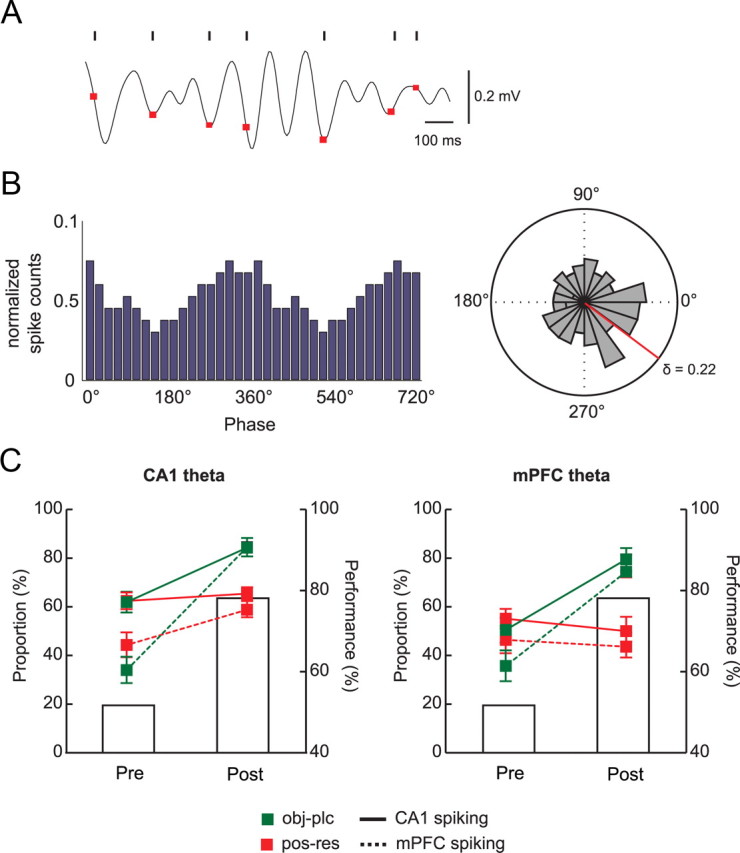
Phase relationships between neuronal spikes and simultaneously recorded theta rhythms in the OPPA task. A, A representative example of theta rhythm recorded in CA1, and the simultaneously recorded CA1 spikes (black ticks) are shown for a single trial. The phase of each spike is directly marked over the theta oscillation as a red dot. Horizontal and vertical bars on the right denote the temporal scale and amplitude of theta, respectively. B, The distribution of spiking phases in the theta rhythm. Left, A representative histogram showing the distribution of spiking phases. Note the concentration of phases near the troughs (0 or 360°) of theta. Right, The same distribution is shown as a polar plot to show the mean vector (red line) and circular concentration coefficients (δ). C, Changes in the proportions of CA1 and mPFC neurons that showed significant modulations of spiking activity against theta rhythms recorded from CA1 (left) and from mPFC (right). Note that the proportions significantly increased after learning in both regions only when the object-in-place strategy was used. Bar graphs show the average performance. Pre, Prelearning; post, postlearning. Mean ± SEM.

We then examined whether the proportion of neurons significantly phase locked to the theta rhythm changed between prelearning and postlearning stages differentially in CA1 and mPFC. In both regions, there were strategy-specific increases across learning (Fig. 7C). Specifically, more neurons in CA1 and mPFC exhibited significantly phase-locked spiking activities against theta in the postlearning stage than in the prelearning stage when object-in-place strategy (Fig. 7C, green lines) was used compared to when position-response bias (Fig. 7C, red lines) was used. Approximately 60% of CA1 neurons were phase locked to CA1 theta in the trials categorized as position-response trials during the prelearning stage, and the proportion did not change after learning (Fig. 7C, left). There was a slight increase in the proportion of mPFC neurons significantly phase locked to CA1 theta between prelearning (∼42%) and postlearning (∼58%) stages in position-response bias trials. In contrast, when the object-in-place strategy was used, ∼60% of CA1 neurons were phase locked to CA1 theta during prelearning, but this proportion increased to ∼80% in the postlearning stage (Fig. 7C, left). Furthermore, there was a steeper increase (∼30 to ∼80%) in the proportion of mPFC neurons significantly phase locked to CA1 theta between the learning stages in object-in-place trials. A repeated-measures ANOVA with strategy, learning stage, and spiking region as three main factors showed significant effects of all three factors (F values > 14.91, p values < 0.001), strategy by learning stage interaction (F_{(1, 418)} = 42.78, p < 0.001), learning stage by spiking region interaction (F_{(1, 418)} = 8.53, p < 0.01), and a three-way interaction of strategy by learning stage by spiking region (F_{(1, 418)} = 3.94, p < 0.05). According to post hoc comparisons, the proportions of neurons phase locked to theta were significantly different between the learning stages in both CA1 and mPFC in object-in-place trials (p values < 0.001). No significant difference was found in CA1 between the learning stages when only position-response bias trials were considered (p > 0.05). The mPFC neuronal proportion phase locked to theta was significantly bigger, however, in the postlearning than in the prelearning stage (p < 0.05). In addition, in both CA1 and mPFC, there were significant increases in the proportion of neurons phase locked to theta in object-in-place trials compared to position-response trials in the postlearning stage (p < 0.001), whereas no such relationships were found in the prelearning stage (p values > 0.05).

Similar results were obtained when mPFC theta was used as reference LFP: the proportions of CA1 and mPFC neurons significantly phase locked to mPFC theta rhythms in both object-in-place and position-response trials ranged from ∼35% to ∼55% during the prelearning stage (Fig. 7C, right). However, the proportions in object-in-place trials jumped to almost 80% in both CA1 and mPFC during the postlearning stage, whereas no such increase was observed in position-response trials. A repeated-measures ANOVA revealed significant effects of three main factors (strategy, learning stage, and spiking region; F values > 5.47, p values < 0.05) and the interaction between strategy and learning stage (F_{(1, 306)} = 40.0, p < 0.001). Other interaction tests were not significant (F values < 1, ns). On the basis of post hoc comparisons, the proportions of phase-locked neurons in both CA1 and mPFC significantly increased in the postlearning stage compared to the prelearning stage in object-in-place trials (p values < 0.001), whereas no such increases were observed in position-response bias trials (p values > 0.05). Furthermore, the proportions of phase-locked neurons in the prelearning stage were not significantly different from each other between CA1 and mPFC for both strategies (p values > 0.05). However, in both CA1 and mPFC, there were significant differences in the proportion of phase-locked neurons between object-in-place and position-response conditions in the postlearning stage (p values < 0.001).

The above results strongly suggest a positive relationship between learning stage and the proportion of neurons whose spiking activities were significantly phase locked to theta oscillations across CA1 and mPFC. As the network activities in the two regions became more coordinated during the postlearning stage, we were more likely to observe a neuron in one network firing in sync with the other network's oscillating rhythm in a reciprocal manner.

CA1–mPFC coherence in spike timing associated with different strategies changes across learning stages

For the purpose of examining the strategy-dependent regional interactions in more detail, we measured the degree of temporal synchrony between CA1 and mPFC by constructing a cross-correlogram between the spike trains of a pair of single units recorded simultaneously from CA1 and mPFC 500 ms before the onset of the object choice (spikes were fired within the choice-platform area in 99.7% of trials in this time window). To examine the strategy-dependent differences in temporal correlations between CA1 and mPFC spiking activities, spike trains of a CA1–mPFC neuronal pair for individual trials were grouped according to trial types (Fig. 6A). Then, the cross-correlograms for the object-in-place strategy and the ones for the position-response bias were prepared separately for a given pair of spike trains from CA1 and mPFC (Fig. 8A). The maximal correlation coefficient of the cross-correlogram was detected to measure the amount of temporal synchrony between the two regions.

Figure 8.

Learning-related changes in spike-timing synchrony between CA1 and mPFC. A, Representative examples of cross-correlograms (bin size, 10 ms) constructed based on simultaneously recorded spike trains from CA1 and mPFC (CA1 as a reference) for object-in-place trials (left) and position-response bias trials (right) according to different learning stages. Note that the correlation coefficient was lower in prelearning (white) but increased after learning (gray) in object-in-place trials, whereas the pattern reversed in position-response trials. B, Average correlation coefficients between CA1 and mPFC in association with different strategies and learning stages. The correlation coefficients were r-to-z transformed. Note the increase in synchrony in rule-relevant trials between spike trains from the two regions as learning occurred and the decrease in synchrony when the position-response bias was used. C, The average time lag between CA1 and mPFC spike trains was measured by the peak location in the correlogram. Time lags between spike trains of the two regions were shortened after learning regardless of strategies used. pre, Prelearning; post, postlearning. Mean ± SEM. Bar graphs show the average performance levels.

When the average temporal cross-correlation coefficients were compared between prelearning and postlearning stages (Fig. 8B), the amount of CA1-mPFC spiking synchrony in object-in-place trials significantly increased after learning, whereas a significant drop was observed after learning in position-response trials. A repeated-measures ANOVA on r-to-z-transformed correlation coefficients with task strategy and learning stage as main factors showed significant effects of strategy (F_{(1, 1388)} = 34.28, p < 0.001) and strategy by learning stage interaction (F_{(1, 1388)} = 284.37, p < 0.001). Post hoc comparisons showed that the amount of synchronization was significantly higher in position-response trials than in object-in-place trials in the prelearning stage, whereas the trend was reversed in the postlearning stage (all p values < 0.01). The same analysis was conducted using the samples prepared by the parametric bootstrap method to rule out the influence of sampling bias. Repeated-measures ANOVA with strategy and learning stage as factors on transformed coefficients in the bootstrap analysis confirmed the main results: there were main effects of strategy (F_{(1, 1388)} = 42.87, p < 0.001) and a significant two-way interaction of strategy and learning stage (F_{(1, 1388)} = 297.56, p < 0.001). Post hoc comparisons showed that decreases in position-response and increases in object-in-place conditions were all significant (all p values < 0.001). The results suggest that the amount of synchronization between spike trains in CA1 and mPFC was dependent on the dominant strategy adopted in the course of learning in the OPPA task.

When the temporal lag (measured by the temporal position of the peak in the cross-correlogram) was examined between mPFC spiking and CA1 spiking (Fig. 8C), CA1 spiking activity preceded mPFC spiking by 32.8 ± 4.7 ms, on average. A repeated-measures ANOVA with strategy and learning stage as factors showed a significant effect of learning stage (F_{(1, 730)} = 8.70, p < 0.01) with no significant effect of strategy (F_{(1, 730)} = 2.88, p = 0.09). There was no significant interaction between strategy and learning stage (F_{(1, 730)} < 1, ns). Interestingly, CA1 spiking led mPFC spiking by a greater amount in the prelearning stage than in the postlearning stage. When the same analysis was performed using the samples prepared from the parametric bootstrap method, there were still significant main effects of strategy (F_{(1, 730)} = 164.71, p < 0.001) and learning stage (F_{(1, 730)} = 10.96, p < 0.01), but there was no significant interaction between the two factors (F_{(1, 730)} < 1, ns).

It is unlikely that the above effects were due to nonspecific behavioral differences, because when running speed and traveling distance were measured in the time window used in the cross-correlation analysis, both variables were not significantly different between strategies (F values > 2.45, p values > 0.12) and learning stages (F values > 0.18, p values > 0.67). No interaction (strategy by learning stage) was observed in both measures (F values > 0.23, p values > 0.63).

Theta coherence in CA1-mPFC networks increases significantly before the choice-platform entrance after learning

Since CA1 and mPFC spiking activities were significantly phase locked to theta rhythms (Fig. 7), we then examined whether there were significant differences in the amount of CA1 and mPFC theta (and the coherence between them) before and after the rat entered a critical space (i.e., choice platform) in the OPPA task. The choice-platform entrance event was checked first over the object-choice event because both hippocampal and mPFC spiking activities were more reliable in reference to the spatial event than to the temporal event (Fig. 5C). For this purpose, we built a spectrogram for each recording session using a time window of 300 ms, starting 450 ms before the moment of choice-platform entrance, moving by 150 ms steps, and ending 450 ms after the event (the moment of choice-platform entrance denoted by time 0 in Figs. 9A–C). This temporal moving-window scheme resulted in five different time blocks (Figs. 9D–F, b1–b5). To quantify theta powers associated with the time blocks during the critical learning stage (in which the sharp increase in performance was observed), spectrograms were constructed using the simultaneously recorded LFPs for CA1 (Fig. 9A) and mPFC (Fig. 9B) for the 3 d before and after learning (Fig. 1B). Coherograms (Fig. 9C) using the CA1 and mPFC LFPs were then built to visualize and quantify the amount of coherence between theta oscillations recorded simultaneously in CA1 and mPFC around the choice-platform entrance.

The spectrograms for both regions showed salient theta power bands. Specifically, theta oscillations in both CA1 and mPFC were strong before the rat entered the choice platform but decreased afterward (Fig. 9A,B), resulting in a gradually decreasing theta power across the time blocks (Fig. 9D). A repeated-measures ANOVA with brain region and time block as main factors showed a significant main effect for time block (F_{(4, 128)} = 27.21, p < 0.001). The effect of brain region was not significant, and there was no interaction between the two factors (F values < 1, ns). Post hoc comparisons between time blocks demonstrated significant differences with each other (all p values < 0.001) except for the b4–b5 pair (p > 0.05) for both CA1 and mPFC. Between learning stages, there was no significant difference between prelearning and postlearning stages (Fig. 9E), as a repeated-measures ANOVA revealed a significant effect of time block (F_{(4, 128)} = 27.05, p < 0.001) with no other effects being significant (F values < 1, ns).

The changing patterns of theta coherence across the platform entrance event, however, were different between the learning stages: coherence was maximal before the rat entered the choice platform and decreased as the animal passed the entrance in the postlearning stage (Fig. 9F), whereas such a pattern was not visible during prelearning (i.e., coherence remained at the same level throughout the time blocks). A repeated-measures ANOVA on coherence with learning stage and time block as main factors confirmed this by showing significant main effects of time block (F_{(4, 60)} = 4.35, p < 0.01) and two-way interaction of time block by learning stage (F_{(4, 60)} = 2.93, p < 0.05). The main effect of learning stage was not significant (F_{(1, 15)} < 1, ns). Post hoc comparisons revealed that coherence at time block b1 was significantly different from the other time blocks (p values < 0.01) in the postlearning stage. We applied the same analytical scheme as above for theta power and coherence in reference to the object-choice event instead of the choice-platform entrance event, but found no significant theta power changes across the time blocks between brain regions (F values < 1.06, p values > 0.05) and between learning stages (F values < 1, ns). The same was true for the coherence measure for the object-choice event (p values >0.05).

Since it has been suggested that hippocampal theta rhythms are related to motor movement (O'Keefe and Burgess, 1999), the rat's moving speed was measured across the time blocks before and after the choice-platform entrance. Despite the significant decrease in speed (F_(4,132) = 100.1, p < 0.001) across the choice-platform entrance, we found no significant relationship between speed and theta power (Fig. 9G; p values > 0.07, r² values > 0.02, linear regression). This is largely because the significant drop in speed occurred immediately after the rat's entrance into the choice platform, whereas the significant drop in theta power took place before the entrance (data not shown).

The similar amounts of theta between learning stages before the rat entered the choice platform suggest that the amount of theta oscillation itself may not be a good predictor for OPPA learning. The elevated coherence in CA1–mPFC theta oscillations before the rat experiences critical events, however, serves as a good indicator of learning instead.

Discussion

We have demonstrated that neurons recorded simultaneously in hippocampus and mPFC represent qualitatively different information in the OPPA task. Hippocampal neurons fired maximally only in their preferred firing fields associated with one arm, whereas neurons in mPFC fired more broadly in space and their maximal firing occurred in similar locations between the two arms in the OPPA task. Neuronal activity in mPFC was significantly modulated rather by the overall structure of the task because mPFC neurons fired for a particular type of event commonly associated with different arms. Such properties of mPFC neurons developed across learning and significantly correlated with the correctness of choice. Importantly, despite these differences, the hippocampus and mPFC operated as a common functional network in the OPPA task, showing learning-related coherence; that is, shift in strategy during learning was reflected in spatial firing patterns of both regions. Furthermore, both temporal synchrony in spike timing between neuronal pairs and the amount of phase locking of spiking to theta rhythm increased after learning. Overall, our study demonstrates both unique firing properties and functional interactions between the two regions in OPPA learning.

Firing properties of hippocampal neurons in purely spatial navigational settings have been well established (O'Keefe and Nadel, 1978; Muller et al., 1987). Although whether neurons in mPFC fire in a spatially selective manner has been relatively unclear, the literature implies that mPFC neuronal firing may not be fully understood in relation to location information only, and behavioral variables should also be considered (Poucet, 1997; Pratt and Mizumori, 2001; Gemmell et al., 2002; Jones and Wilson, 2005). The results from our study not only verify this, but also provide additional information that may explain why: in the OPPA task, a type of event (e.g., choice-platform entrance) can occur regularly across different spatial locations, whereas a spatially unique event of that type (e.g., choice-platform entrance in Arm 3) occurs only in a particular location. Firing in both arms for a common event type naturally decreased the spatial information content of mPFC neuronal firing. The lack of such components in a foraging task in an open space (e.g., cylinder) in prior studies (Poucet, 1997; Gemmell et al., 2002) must have made it harder to identify the source of low spatial information content in mPFC firing. The results from the studies that used behaviorally more structured tasks (Jung et al., 1998; Pratt and Mizumori, 2001; Jones and Wilson, 2005) have indicated the existence of some common firing patterns associated with different locations with respect to behavioral significance. Our study suggests that it would be misleading to interpret such neural firing in mPFC as spatially insensitive because the majority of neurons in both mPFC and CA1 showed spiking activities that were spatially bound to similar degrees (Fig. 5C). However, it is important to emphasize at the same time that mPFC neuronal spiking was more temporally bound to the object-choice event.

The OPPA task requires the rat to process a chain of regularly occurring, common types of events across arms. Representing such regularities in mPFC must be critical because incorrect trials were associated with a significant decrease in similarity between the pop-PETHs for different arms (Fig. 5B). It is possible that the population signal in mPFC for representing each type of event in behavioral sequence may provide other parts of the brain a boxcar-like framework within which a specific episodic event can be represented with specific times and locations. It is also possible that discrete spatial representation of the hippocampus may train mPFC to extract regularities of the task during learning because mPFC developed event-type specificity across learning (Fig. 4B). Direct projections of CA1 efferents to mPFC (Swanson, 1981; Jay and Witter, 1991) and the results from other prior studies support this line of reasoning (Milner et al., 1985; Fuster, 2000; Doeller et al., 2005; Bailey and Mair, 2007; Shima et al., 2007; Sigala et al., 2008). Considering that some mPFC neurons gradually increased or decreased firing across a given event (Fig. 3B, Cell 9 for Event 3) instead of showing a phasic shift in firing (Fig. 3B, Cell 7 for Event 1), one may argue that such a cell's firing was not necessarily modulated by the event used for the PETH analysis. However, even if the cell's firing was modulated by an unknown event (presumably not easily identifiable or internally generated, such as expectation of reward, etc.), that does not nullify our main conclusion that mPFC neurons fired similarly across different arms near a certain common event. In other words, we did not argue that the three events used for PETH analyses in the study were sole determinants of neuronal firing in the OPPA task. Instead, we used those events as tools whereby arm-dependent firing patterns could be quantified for neurons at different phases during the OPPA task.

It is suggested that the significant increase in the proportion of neurons whose spiking activities were temporally locked to the troughs of theta (Fig. 7) serves as a good indicator of the acquisition of the object-in-place rule. The increase in such neuronal proportions matched the amount of increase in performance between prelearning and postlearning stages (Fig. 7C) when the spiking phases were examined in CA1 and mPFC against theta rhythms from both regions. This suggests that spiking in CA1 and mPFC became more synchronized with the network oscillations in both regions after the OPPA task was learned. The fact that these relationships were not observed in trials in which the position-response bias was used (Fig. 7C) strongly suggests that the increase in the amount of phase locking to theta occurred as the two networks became more functionally integrated for optimal performance in the OPPA task. In addition, our results show that the amount of cross-correlation between spike trains of the two regions serves also as a functional indicator of the performance in the OPPA task (Fig. 8B). The hippocampal spiking activity always preceded the spiking in mPFC (Jones and Wilson, 2005; Siapas et al., 2005; Benchenane et al., 2010) but, compared to the analysis for coefficient changes, the spiking time lag between CA1 and mPFC does not seem to provide specific information in regard to learning in the OPPA task (Fig. 8C).

In the OPPA task, the synchrony between CA1 and mPFC theta rhythms was maximal before the rat entered the choice platform, and it decreased afterward (Fig. 9). It may be related to the speed of the rat, as the speed decreased when the rat approached the critical scene. However, the decreasing pattern of speed was not significantly correlated with the decreasing pattern of coherence. It may also be speculated that a coarse decision for choosing a correct object was made before the rat entered the choice platform, since the objects were visible before the choice-platform entrance. The decrease in CA1–mPFC theta coherence, however, was universally observed regardless of correctness of choice behavior in our study, suggesting that this pattern alone may not explain a significant portion of choice accuracy. Another possibility is that the CA1–mPFC networks may have critically communicated “where” information (i.e., arm) with each other while the rat traveled the arm area before the animal entered the choice platform, because it was a critical piece of information to resolve ambiguity in the OPPA task. Nevertheless, the results from our study suggest that the two regions must work as a unified functional network in a particular time window before final decision making in the OPPA task.

The OPPA task used in the current study requires multiple brain regions including the dorsal hippocampus, mPFC, and perirhinal cortex (Lee and Solivan, 2008; Jo and Lee, 2010a,b; Lee and Solivan, 2010). The results from the current study and our prior studies may allow the following speculations for the relative contributions of different brain regions in the OPPA task. The hippocampus represents a unique spatial context associated with a particular arm, which is essential in choosing an object in the task. We find no significant degradation of the spatial firing pattern of the CA1 population during incorrect trials compared to correct ones (Fig. 5B). This suggests that the capability of representing space is robustly maintained in the hippocampus regardless of correctness of upcoming choice behavior, and task-dependent information is reflected rather by rate modulation. The spatial representation in the hippocampus then may be critically communicated to mPFC before the rat enters a choice platform. The final decision driving a specific choice response is likely to be made once the rat recognizes objects and combines the object information with arm information. This critical information exchange and decision making may occur as the rat approaches the scene of object-place event.

The current study and a previous study (Lee and Solivan, 2008) suggest that the mPFC-hippocampal network is critical when ambiguous events need to be represented as discrete event memories within a common organizational scheme. Further investigation of the interactive dynamics between hippocampus and mPFC may elucidate how animals keep on track toward goals in a task while differentiating slight variations across events (e.g., person, object, smell, etc.) as discrete memories.