A common visual metric for approximate number and density

Abstract

There is considerable interest in how humans estimate the number of objects in a scene in the context of an extensive literature on how we estimate the density (i.e., spacing) of objects. Here, we show that our sense of number and our sense of density are intertwined. Presented with two patches, observers found it more difficult to spot differences in either density or numerosity when those patches were mismatched in overall size, and their errors were consistent with larger patches appearing both denser and more numerous. We propose that density is estimated using the relative response of mechanisms tuned to low and high spatial frequencies (SFs), because energy at high SFs is largely determined by the number of objects, whereas low SF energy depends more on the area occupied by elements. This measure is biased by overall stimulus size in the same way as human observers, and by estimating number using the same measure scaled by relative stimulus size, we can explain all of our results. This model is a simple, biologically plausible common metric for perceptual number and density.

It has long been known that observers can judge the number of objects within a scene (1) but only recently has it been proposed that this ability is directly supported by low-level visual mechanisms. Specifically, Burr and Ross (2) report that prolonged viewing of a dense field of elements (adaptation) causes the number of elements in a subsequently viewed pattern to appear drastically reduced. The notion of a visual sense of number has generated considerable excitement, not least because, for example, childrens’ mathematical ability correlates with their ability to make approximate estimates of number (3). However, when one varies the number of elements within a fixed region, one also varies the mutual separation or density of elements. Durgin (4) reported that stronger adaptation is induced by a small-dense patch than by a large-sparse patch (that actually contains more elements). This result is consistent with adaptation being determined by density and not number per se.

The notion that our sense of number might be linked to density is intuitive when one considers that there are only two ways to estimate number. The first is to explicitly count (item-by-item), a strategy ruled out by the finding that number estimation does not slow in proportion to number beyond around seven elements (5). The second way is by comparing measurements whose product is dimensionless, e.g., density × area = number. If we require only relative number (i.e., “Which is more numerous?” the judgment made in forced-choice experiments), then we can use a density estimate that need only scale with physical density (e.g., contrast). This is the approach adopted here: We sought to develop a computational model of approximate number estimation by identifying the measures used by the visual system to estimate density (and so encode approximate number).

A major constraint on any density estimate is whether it is dependent on number. Can we determine experimentally whether number and density estimations are independent? One approach is to show that manipulation of the notionally irrelevant dimension (say density) leaves estimation along the relevant dimension (say number) unaffected. For example, doubling element size (thereby doubling the ratio of occupied to unoccupied pixels in the pattern) has no effect on number discrimination (2). However, if one defines density not as pixels per unit area but as elements per unit area—the latter being widely used (6)—then this result is not diagnostic.

The most direct way to decouple number and density is to mismatch the area over which elements are distributed within two stimuli. Several previous studies have reported that this manipulation does not greatly influence the precision of number discrimination (6–8). However, in addition to expressing the usual concern about negative results, we note first that some studies have used relatively small numbers of elements (∼30) (6, 8), which are less effective at engaging approximate number processing. Furthermore, the study by Ross and Burr (7) required observers to make either number or density comparisons within different blocks of trials. In number blocks (for example) either area or density was held constant so that in trials when the area of the stimulus matched the standard, observers could report density whereas in trials when the density was matched, they could report area; subjects never needed to judge number. Critically, when observers are forced to make an explicit comparison—as in the experiment of Tokita and Ishiguchi (8)—a strong effect of size is evident (albeit on the appearance rather than discriminability of the patches). Larger patches are perceived as being ∼10% more numerous. Here we confirm this effect for number, find that it is magnified for judgments of density, and show how this result is critical for understanding the mechanism supporting number and density judgments.

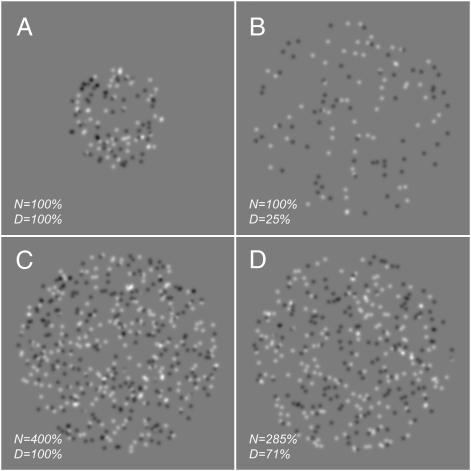
Fig. 1 A and B shows two patches containing 128 elements. The difference in patch size makes this equivalence difficult to confirm, and in Results, we show that this difference interferes with observers’ precision at discriminating number. Note that this result is contrary to the notion of a sense of number that operates independently of stimulus size or density. Fig. 1C further illustrates that density estimation is not immune to a similar manipulation of size or number. Fig. 1C has the same physical density as Fig. 1A but appears considerably denser. Fig. 1D is a typical perceptual match for the density of Fig. 1A and illustrates the results of our experiment. We show that observers typically require around a factor of 1.4 reduction in density (100%/1.4 = 71%) to achieve a reliable perceptual match for density across this difference in number or size.

Fig. 1.

Our sense of number and sense of density (element spacing) are entangled. (A) The small reference patch contains 128 elements. (B) Doubling the radius of the patch makes it difficult to tell that A and B contain the same numbers of elements. The size change disrupts our sense of number. (C) This patch has the same physical density as A, but the elements typically appear more closely spaced. D is perceptually matched to the density of A but has a much lower physical density—it contains 365 elements (i.e., 147 fewer than the physical match; C). Size change disrupts our sense of both density and number.

We experimentally quantified the impact of mismatching patch size on observers’ ability to discriminate which member of a pair of stimuli (a test and a reference, the latter containing 128 elements) was either more numerous or more dense. We did this using a 3 × 3 design measuring observers’ performance with all possible pairings of patches with radii of 2.0°, 2.8°, or 4.0° of visual angle.

Results

Analysis.

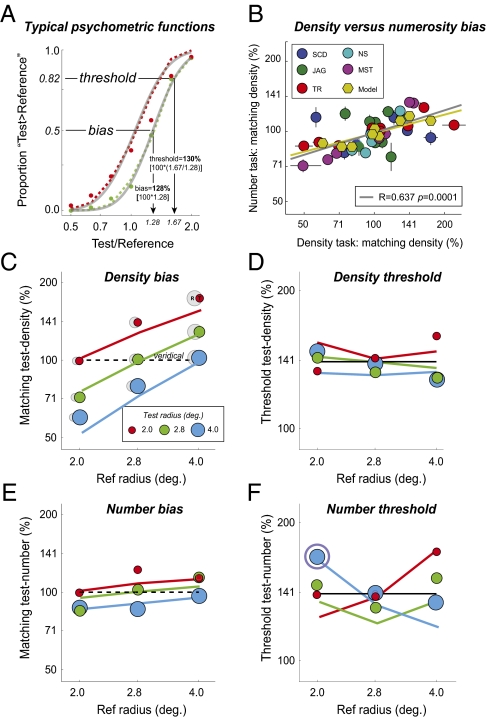
For density discrimination, responses were first plotted (Fig. 2A) as the proportion of times subjects said the test was denser than the reference, as a function of the ratio of the densities of the test and reference. Data were fitted with cumulative Gaussian functions (gray lines in Fig. 2A) to derive (i) bias (offset: the proportion of test density required to produce a subjective match between test and reference; i.e., so that the subject was 50% likely to say the test was denser than the reference) and (ii) threshold (the proportion of extra density required to raise performance from 50% to 82%). An analogous procedure was applied to number data (the full dataset is shown in Fig. S1).

Fig. 2.

(A) Psychometric functions for number and density discrimination. Symbols plot average proportion of times observers categorized a test as denser (green) or more numerous (red) than the reference as a function of the number of elements in the test compared with the reference. Gray lines are the best-fitting cumulative Gaussian functions, with the stimulus levels producing a perceptual match (bias) or a just noticeable difference (threshold) overlaid for the density task. Dashed colored lines are the predictions of the model using the relative activity (response ratio) of two filters tuned to low and high spatial frequencies. (B) Individual observers’ bias on number vs. density discrimination on comparable size-mismatched conditions. Note that bias is greater for density judgments and is correlated with bias on the number judgments in a manner predicted by the model (olive green line). (C–F) Matching (C and E) and discrimination (D and F) performance for density (C and D) and number (E and F). Biases indicate that subjects see larger objects as (C) denser and (E) more numerous. (D and F) Discrimination is broadly similar for both tasks [observers can spot a difference of ∼40% (i.e., ×140%) in either number or density], with both tasks being compromised by mismatching stimuli sizes. Solid lines are the predictions of the response ratio model.

Average Bias/Thresholds.

Fig. 2C shows how density bias varies with patch-size mismatch. Consider the small red symbols: Moving from left to right, they show that for a small test patch to be perceptually matched to a variable-size reference the test's density must increase as the reference grows. Conversely, a large test paired with a small reference (leftmost blue point) can be sparser (i.e., fall below the dashed horizontal line) and still be perceptually matched. Essentially these data indicate that larger/more-numerous patches appear denser than they are and that perception of number and density is veridical (i.e., points fall on the dashed horizontal line) only when test and reference are matched in size.

Fig. 2E indicates that number matching across differences in patch size is less biased than density matching (the slopes of data in Fig. 2E are shallower than the slopes of data in Fig. 2C), but that observers still make systematic errors such that larger test patches appear more numerous (replicating ref. 8). Thresholds for the two tasks are shown in Fig. 2 D and F. Observers require ∼40% difference in number or density to make a reliable discrimination between a test and a reference patch. This result is somewhat higher than previous estimates of Weber fractions for number discrimination (∼25%) (2) that we have identified (in control experiments) as being due to a combination of the larger element size and parafoveal presentation used here. We note that the largest size mismatches substantially elevate thresholds (e.g., circled data point in Fig. 2F).

Modeling.

We propose that shared effects on bias and precision arise from the use of a common metric for both number and density judgments. The colored lines in Fig. 2 are predictions from a model that estimates density and number using a pair of filters tuned to high and low spatial frequencies, specifically relying on the ratio of their responses to a full-wave rectified version of the stimulus. We predict density discrimination thresholds using these response ratios corrupted by multiplicative noise. Discrimination of number requires this estimate be scaled in proportion to the relative area of stimuli: To this end, we simply multiply a given response ratio by the ratio of the low spatial frequency (SF) filter responses (from the stimulus pair). This number estimate is corrupted by a second larger noise term (that we suppose originates from having to compare low SF response across space). Note that whereas number could be estimated directly from the output of high-spatial frequency filters, this method would fail to produce the moderate bias evident in Fig. 2E. Given the small number of free parameters (one for density and one for number), the model does a remarkably good job of capturing our main effects including the strong and weak nonveridical matching of density and number, respectively, and Weber fractions for discrimination.

Individual Differences.

Individual differences in bias provide an independent source of evidence that density and number use a common perceptual metric. Fig. 2B plots observer bias (percentage of reference number or density required for a match, where 100% is veridical/unbiased performance) on the density vs. the number task, for comparable size-mismatched conditions. Data from five observers indicate that these two biases are highly correlated (R = 0.64, P < 0.0001), but that the density bias is consistently higher than the number bias. The level of correlation and good agreement with the prediction of the model (olive-colored line) again suggests that the two tasks are tapping into a common mechanism.

Element Type/Arrangement.

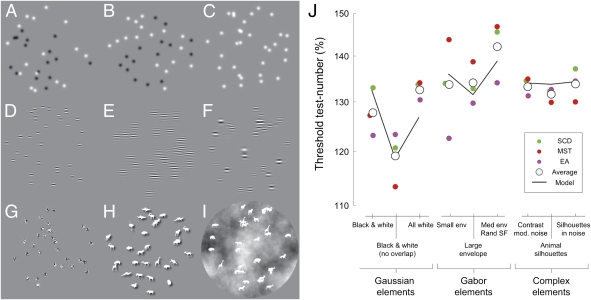
To test the wider relevance of the model we examined its ability to predict psychophysical discrimination of stimuli composed of different elements. Starting with a smaller number (32) of random contrast polarity Gaussian elements, as used above, we compared performance with a random spatial arrangement (Fig. 3A) vs. one that minimized element overlaps (Fig. 3B). We also tested single contrast-polarity elements (Fig. 3C), as well as SF narrowband Gabor elements (Fig. 3 D–F) with a small envelope (Fig. 3D), a large envelope (Fig. 3E), or a medium envelope with carrier SF jittered (σ = 0.5 octaves) (Fig. 3F). We compared this result to performance with another class of contrast-defined element (with an isotropic noise carrier) (Fig. 3G) or animal silhouettes presented against either a uniform gray (Fig. 3H) or a fractal noise background (Fig. 3I). These conditions challenge the model by manipulating element arrangement, cue type (contrast or luminance), element shape, surrounding context, and feature density within elements. Results from the experiment are presented alongside predictions from the response ratio model in Fig. 3J. Removing element overlap improves performance considerably, whereas thresholds are remarkably stable across variation in contrast polarity, envelope size, and envelope shape. This result is captured well by the density estimate from the response ratio model using the same filters as before, with only a single (multiplicative-noise) parameter varying (being set once for each of the three classes of stimuli). We note here that the connectedness of elements can also influence numerosity judgments (9, 10); in Fig. S2, we show that the response ratio model also predicts performance with such stimuli.

Fig. 3.

Manipulation of element type and configuration. (A–C) Gaussian elements of either (A and B) mixed or (C) single contrast polarity positioned either (A and C) randomly or (B) to avoid overlaps. (D–F) Gabor elements with (D) small, (E) large, or (F) medium envelopes and a (D and E) fixed or (F) variable carrier spatial frequency. (G–I) Complex elements made up of (G) patches of isotropic noise or (H and I) animal silhouettes in (H) isolation or (I) embedded in fractal noise. (J) Psychophysical discrimination performance (colored symbols) for the nine conditions compared with predictions of the simple filter model (solid line) described above.

Discussion

We have shown that observers’ difficulty in matching and discriminating both number and density across differences in stimulus size and element type is consistent with their using a simple perceptual metric based on the relative response of a pair of spatial-frequency tuned filters.

We note that our approach has something in common with Allik's “occupancy” model of numerosity (11), a major difference being that our model operates not on abstracted object locations but on raw images. That our model knows nothing of objects is critical because it predicts that systematic mismatching of element size should affect both number and density judgments, whereas contrast (and contrast polarity) should not (because response ratios do not change with overall contrast level). These predictions are broadly supported by existing literature; substantial differences in element size disrupt numerosity judgments (12, 13), whereas contrast manipulations do not (2, 13).

The predictions for density discrimination are based directly on noisy response ratios whereas for number discrimination these values were scaled by the ratio of low SF outputs, to compensate for the effect of difference in region size on response ratio. We do not suggest that this approach means density estimation can never compensate for size, but merely that this task did not promote such a strategy. It may be that, for density, a more natural compensation is for element size (which would give a scale-invariant representation of density; i.e., one that does not change with viewing distance). We suggest that such a computation could be achieved using the ratio of responses from a different (intermediate SF) filter pair. Because our experiment did not alter element size, it may not have revealed the behavioral consequences of such a computation.

Why then should judgments of number and density be so biased by stimulus size? Consider a comparison with the visual coding of luminance. For humans it is luminance difference (contrast) and not absolute luminance that drives our visually guided behavior. A predominantly contrast-based code might sacrifice veridical representation of luminance (e.g., through a center-surround receptive-field organization) to detect image structure under wild fluctuations in overall luminance. The price we pay is that our judgment of absolute luminance can be biased by context, a fact that is exploited by a variety of impressive brightness illusions. In analogy to luminance, we suggest that the visual system makes a similar sacrifice of accuracy for absolute number/density to preserve our sensitivity to relative number and relative density under fluctuation in absolute levels of these visual attributes. Producing estimates of number/density that are biased by overall size may be the price the visual system pays to preserve discriminability of visual attributes that are likely more functionally important.

Our work broadly fits with several recent suggestions that the representation of number is linked to other visual attributes (e.g., coding of duration) (14). It is inconsistent with the notion of a dedicated visual mechanism for approximate number (independent of density) as has been claimed (e.g., on the basis of psychophysical evidence from adaptation) (2). In terms of physiological mechanisms we note that the great majority of studies have used low numbers of elements (typically 1–7, never higher than 32). Although it is assumed that such mechanisms could deal with larger numbers, this assumption has not been explicitly demonstrated. In terms of modeling, the details of number channels (i.e., how one moves from images to predicted behavior) have yet to be described. That neural mechanisms tuned for small numbers have been located in parietal cortex (15–18) suggests that they may rely on resources such as attentional pointers. This result in turn is consistent with low-number discrimination (subitizing) placing a heavier attentional load on observers than estimation of larger numbers, suggesting that different mechanisms exist for both (19, 20). This result squares with earlier adaptation findings that the critical switch at higher numbers is toward a more density-dependent measure (21). The general idea is that statistical mechanisms like the response ratio are always available but that at lower numbers they may be unreliable compared with strategies that engage more attentional resources (like pointers).

We started out by pointing out several flaws in earlier studies of the influence of relative size on number/density judgment. Although the behavioral evidence relating to numerical cognition is frequently contentious, we believe our findings will generalize. First, we note that, because we are reporting a positive effect of our manipulation, we cannot have made a type II error. Second, since conducting these experiments, we have measured larger biases on both number and density discrimination under conditions of higher uncertainty and have further evidence for a close correspondence between these tasks under a wide range of manipulations (including variable attentional load, contrast manipulation, and element-size manipulation) (22). Finally, we have shown that the model can predict performance with other classes of stimuli (Fig. 3).

Inspecting Fig. 1, one could argue that it should come as no surprise that number and density are supported by a common mechanism, because both code the degree to which space is occupied. What is striking about our findings is that our sense of density (or feature spacing) is inconsistent with an explicit code for spatial position, beyond the influence that feature arrangement has on the spatial frequency structure of an image. We must be surprisingly poor at judging average feature spacing (which would unambiguously code density in our experiment) for us to rely on a measure that was so vulnerable to a simple manipulation of overall size. The idea that feature density might always be derived from filter activities (in a manner that is more akin to the processing of contrast) runs contrary to the notion that an explicit code for token position—the cornerstone of the primal sketch (23, 24)—is preserved throughout visual processing. Instead, either token positions are pooled or undersampled within clusters (25) in a manner consistent with some form of local spatial compression or the tokens did not exist in the first place. The latter view would be consistent with our sense of relative spatial position of features being illusory, manufactured after the fact on the basis of the spatial frequency structure of the scene.

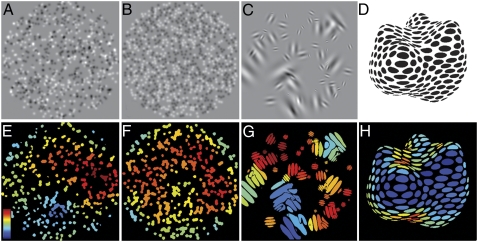
The model we have described computes a response ratio estimate at every location and then pools over the entire image. We now briefly consider the advantages of an explicit representation of local response ratio. We have already shown that element clustering increases overlaps and leads to poorer performance (Fig. 3) but it is also known that clustering reduces perceived number and/or density (26). Fig. 4 A and B shows an example of this phenomenon; note that more regularly spaced elements (Fig. 4B) appear more numerous, despite having the same number as the clustered stimulus (Fig. 4A). Below each image (Fig. 4 E and F) are response ratio maps based on the (Gaussian smoothed) local filter ratios. Note that the warmer/denser response to the more evenly spaced pattern predicts an ∼8% elevation in perceived number (in line with psychophysical estimates) (26).

Fig. 4.

(A–D) Original images and (E–H) heat maps of local response ratio (blue, low response ratio; red, high response ratio). (A and B) Both images contain similar numbers of elements but lack of “clustering” in B increases its perceived number by ∼8%. (E and F) Local response ratio reflects this difference. (C and D) Response ratio can also be mapped onto images as an estimate of (C and G) local size and (D and H) local surface gradient.

It is known that the visual system has access to statistical attributes such as mean element orientation (27) and element size (28), and although there is a candidate neural mechanism for orientation averaging (a population code based on the response of V1 neurons), the mechanism for size averaging is currently unclear. Fig. 4C shows a typical stimulus containing size-varying elements, and Fig. 4G shows how the corresponding response ratio map reflects local feature density. A pooled response ratio for this image could be used as a reliable proxy for mean-size estimation. We have noted that a curious feature of size averaging is that performance seems to depend on neither the diameter nor the area of stimuli, but on a measure closer to R^∼1.4 (29). We propose that this outcome arises from observers relying on a cue from a response ratio that rises slower than density with increasing stimulus diameter (Fig. 5C).

Fig. 5.

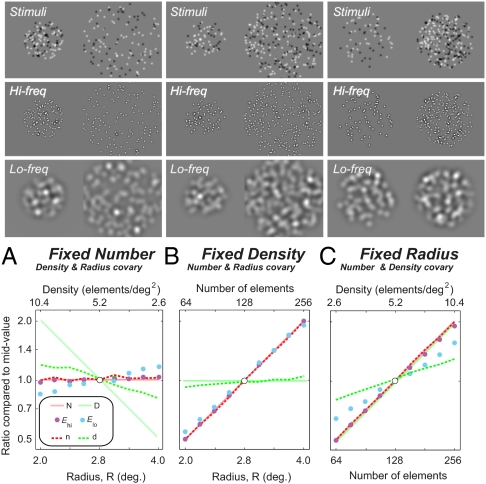
Stimuli with one parameter fixed—(A) number, (B) density, or (C) radius—and the other two allowed to covary. (Upper, row 1) Example stimuli and (Upper, row 2) high-SF and (Upper, row 3) low-SF filtered versions of rectified versions of the stimuli. (Lower) Graphs plot pooled energy from the high (purple circles) and low (blue circles) filters under conditions of fixed number, density, and radius, along with the estimated density (green dashed lines) and number (red dashed lines) based on response ratio. Units are a proportion relative to the value derived from the midvalue stimulus (so all lines pass through 1.0). An ideal estimate of number and density is shown as the solid red and green lines, respectively.

Finally, it is known that element size/density is a useful cue to surface shape. Fig. 4 D and H shows, respectively, a textured figure and a version of the same that has been labeled using local response ratio to indicate local surface density. Note how element color now reflects size/density of elements and that hotspots indicate regions of surface discontinuity.

In summary, our psychophysical evidence indicates that the abilities to judge number and density are both influenced by the size of stimuli in a manner that suggests they rely on a common visual mechanism. This mechanism, we propose, is based on the relative response of spatial filters tuned to high and low spatial frequencies. Such a simple mechanism may prove useful in uncovering the operation of a variety of additional tasks including size averaging and texture processing. Furthermore, we speculate that ratios of filter responses are the common currency of visual magnitude estimation (14). For example, duration estimation could similarly be based on the ratio of responses from a transient and sustained filter mechanism, a notion that squares with recent suggestions that our visual clock continuously compares the output of magnocellular and parvocellular channels (30) or is sensitive to the second-order temporal statistics of natural visual stimuli (31).

Materials and Methods

Stimulus and Task.

We presented pairs of stimuli (±6.0° left/right of central fixation)—a test and a reference patch—for 250 ms. Observers reported which patch was either more numerous or more dense (in separate blocks). No feedback was given. Patches were composed of a variable number of small 2D Gaussian patches (σ = 3.8 arc min; 50% contrast, random contrast polarity) falling within a circular region. We used a 3 × 3 design, independently varying the size of the test and reference patches (radii: 2.0°, 2.8°, or 4.0°). The (variable-size) reference always contained 128 elements (e.g., Fig. 1A is the smallest reference). The density or number of the (variable-size) test (e.g., Fig. 1B is the largest test patch) was set using a method of constant stimuli and varied over a range of 50–200% in seven steps (centered on 100%, i.e., a physical match to the density or number of the reference, according to run). Thus, for “number” runs, tests contained 64, 81, 102, 128, 162, 203, or 256 elements. For “density” runs, tests were 50, 63, 79, 100, 126, 159, or 200% of reference density (2.5, 5.2, or 10.4 elements per degree squared depending on reference size). Each run consisted of 112 trials (16 trials at seven stimulus levels) and five observers (two naive, all experienced in psychophysics, with normal or corrected-to-normal vision) performed one to two runs of each judgment type (number or density discrimination).

Modeling.

To reliably discriminate number (N) and density (D = N/A, where A is area) the visual system requires estimates (n and d) such that n ∝ N and d ∝ D. We propose that the responses of known visual mechanisms—SF band-pass filters—are combined to make these estimates. Specifically, we convolve stimuli with Laplacian of Gaussian, center-surround filters constructed from the combination of a Gaussian filter and a second derivative (Eq. 1),

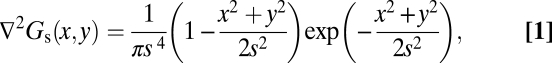to estimate the filter response to a rectified version of a given image (I_n; this nonlinear transform of the image confers subsequent filtering with sensitivity to second order or contrast-defined image structure) pooled across all image locations (Eq. 2):

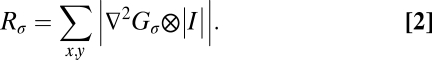Fig. 5 illustrates the logic of using this filter response to estimate density and number. Fig. 5, Upper presents stimuli similar to those used in our experiment and looks at the effects of number, density, and radius by fixing one of these parameters (Fig. 5 A, B, and C, Lower, respectively) and allowing the other two to covary. The example stimuli are from the extremes of the range tested and beneath each is the result of filtering a rectified version of it at two different scales. The graphs in Fig. 5 A–C plot the response from the high- and low-frequency filters (purple and blue symbols, respectively), averaged across all pixels in 32 image examples. For the purpose of illustration (and because we are interested in discrimination) we have normalized responses relative to the response to the midrange stimulus. Solid green and red lines show the ideal (normalized) responses of a mechanism tuned for density and number, respectively. Note that the purple symbols (high-frequency response) closely follow the pure number prediction (solid red line). That R_hi ∝ N should be unsurprising because small filters generate isolated responses to individual elements. Looking at blue symbols (low-frequency response), we note that although this measure rises as a function of (Fig. 5 B and C) number it also rises as a function of (Fig. 5A) patch radius when number is fixed. That R_lo ∝ A is a consequence of large filters responding to clusters of elements and their response ultimately being limited by the patch size elements fall within. On the basis of this observation, we propose that the ratio of two filter responses might be a useful correlate of density and number (Eq. 3),

a measure that we call response ratio (where γ_n is Gaussian random noise so that 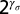is a multiplicative noise term). Response ratio is plotted as the green dashed line in Fig. 5 A–C. The slope of straight-line fits to response ratio is around (Fig. 5A) −0.30 and (Fig. 5C) +0.4 when density changes (with either fixed number or radius) but only (Fig. 5B) +0.08 when density is fixed. We selected the filters to use in this and the following simulations by averaging the magnitude of the slopes of the functions in Fig. 5 A and C for all possible pairings of filter spatial frequencies, selecting the filter pair that maximized the slope of the functions (i.e., maximizing sensitivity to density change). We then ran Monte Carlo simulations of our experimental procedure, generating stimulus image pairs (Fig. 5 A and B) the same way as in the real experiment, and then computed an estimate of relative density as (Eq. 4)

The denser stimulus was selected on the basis of whether d_a,b was less than or greater than 1.0, and this selection was used to derive psychometric functions. Because filter sizes had been set by the earlier simulation, this model has only one free parameter (the multiplicative noise level in Eq. 3 that was set to σ = 0.1).

How then to estimate number? The first possibility is that the visual system directly accesses R_hi (useful because R_hi ∝ N). This possibility is unlikely for two reasons: First, if this information were available, then mismatching region size would have little or no effect on performance (which it demonstrably does). For example, the purple symbols in Fig. 5A would indicate that density and radius have no effect of perceived number whereas our own bias data indicate that they do. Second, it would predict that observers’ estimate of number would increase with increasing contrast; if anything, the opposite is true. Instead we propose that number is derived from response ratio and that an explicit weighting for degree of size mismatch is applied to recover the high spatial frequency component. Because low spatial frequency is used as a proxy for area in computing density, the scaling is based on the ratio of the low SF response from the two stimuli (Eq. 5),

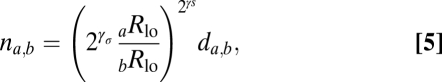which includes a second noise term (S = 1.9 in the simulations). In Fig. 5, the dashed red lines plot estimated number n and show that (Fig. 5A) the estimate is essentially flat when number is unchanging and increases with number at about the same rate when density is fixed (Fig. 5B) or increases (Fig. 5C), closely mirroring the predictions from high SF energy. Given that the slope of these functions indicates discriminability, it is interesting to note that reweighting of the response ratio estimates leads to similar slopes with either pure-number change or when number changes with density. Ross and Burr (3) took their finding that subjects could discriminate number equally well under both of these conditions as an indicator that number could not be mediated by density. This simulation shows that such performance does not rule out reliance on a common mechanism (based on neither number nor density but on a simple statistic based on the SF structure of the image).

Fig. S1 plots individual psychometric functions from the five observers for both tasks (red, density; green, number) along with the predictions of the model described above (solid lines) fitted to the mean psychometric function.