Mathematical modeling of prostate cancer progression in response to androgen ablation therapy

Abstract

Prostate cancer progression depends in part on the complex interactions between testosterone, its active metabolite DHT, and androgen receptors. In a metastatic setting, the first line of treatment is the elimination of testosterone. However, such interventions are not curative because cancer cells evolve via multiple mechanisms to a castrate-resistant state, allowing progression to a lethal outcome. It is hypothesized that administration of antiandrogen therapy in an intermittent, as opposed to continuous, manner may bestow improved disease control with fewer treatment-related toxicities. The present study develops a biochemically motivated mathematical model of antiandrogen therapy that can be tested prospectively as a predictive tool. The model includes “personalized” parameters, which address the heterogeneity in the predicted course of the disease under various androgen-deprivation schedules. Model simulations are able to capture a variety of clinically observed outcomes for “average” patient data under different intermittent schedules. The model predicts that in the absence of a competitive advantage of androgen-dependent cancer cells over castration-resistant cancer cells, intermittent scheduling can lead to more rapid treatment failure as compared to continuous treatment. However, increasing a competitive advantage for hormone-sensitive cells swings the balance in favor of intermittent scheduling, delaying the acquisition of genetic or epigenetic alterations empowering androgen resistance. Given the near universal prevalence of antiandrogen treatment failure in the absence of competing mortality, such modeling has the potential of developing into a useful tool for incorporation into clinical research trials and ultimately as a prognostic tool for individual patients.

The prostate is an accessory sex gland in the male reproductive system whose embryological development, growth, and function is dependent upon the primary male androgen, testosterone, produced primarily in the testes (1). Similarly, the etiology and progression of epithelial cancers arising in the prostate is strongly dependent upon the presence of testosterone (2, 3). Testosterone acts on the prostate epithelium via a highly orchestrated process integrated with multiple hormones and growth factors that continues to be elucidated (3). Testosterone, upon entering a prostate cell, is enzymatically converted to dihydrotestosterone (DHT) by the enzyme 5α-reductase (4). Although testosterone and DHT both bind to and activate androgen receptor (AR), DHT has 10-fold greater binding affinity and forms a more stable complex with AR than testosterone (5). Upon binding, the androgen-AR complex is phosphorylated and dimerizes. The complex is then translocated to the cell nucleus where specific binding to the DNA elicits transcriptional activity of genes associated with proliferation, survival, and differentiation (6).

Prostate cancer (CaP) remains a major public health problem striking nearly 200,000 American men annually and is responsible for 27,000 deaths (7). The majority of patients diagnosed with cancer localized to the prostate are primarily treated with surgery (prostatectomy) or radiation therapy with curative intent. Yet, men with recurrence or who present with metastatic disease need additional interventions that can act systemically. In the late 1930s, Huggins et al. demonstrated that surgical castration (removal of the testes) resulted in dramatic improvement in the status of men suffering from advanced prostate cancer (8). In subsequent decades, a number of pharmaceutical agents targeting testosterone production and signaling have been developed providing therapeutic benefits similar to surgical castration (9, 10). These agents act by different mechanisms, including: (i) inhibition of testicular testosterone production by down-regulation of gonadotropin-releasing hormone production by the pituitary, (ii) blocking the ability of testosterone to bind the androgen receptor, (iii) inhibition of the 5α-reductase enzyme responsible for testosterone conversion to DHT (11), and (iv) inhibition of enzymes involved in testosterone synthesis (12).

Unfortunately, despite maintenance of castrate levels of testosterone and inhibition of AR activity, cancer cells eventually develop castration resistance after a median duration of 18–24 months of treatment, evident by the rise of prostate-specific antigen (PSA) levels, followed by progressive disease. However, the duration of response to antiandrogen therapy and the development of resistance is very heterogeneous, ranging from a few months to over 10 years (13). The mechanistic basis for the development of castrate resistance is the result of genetic and epigenetic instability of the prostate cancer genome and the development of aberrant AR signaling pathways that allow the cancer to progress in the setting of low circulating testosterone (14, 15). With goals of reducing the decrements in quality of life and perhaps having a therapeutic advantage of prolonging disease sensitivity to pharmacologic intervention, clinical investigators are examining a role for intermittent, as opposed to continuous, antiandrogen therapy. Intermittent treatment is accomplished by discontinuing antiandrogen therapy once a predefined clinical objective or decline in PSA has been achieved, then restarting for disease progression, or a defined PSA threshold, or after a specific time period. This process would continue in cycles until resistance develops and the disease requires other interventions.

To enhance the therapeutic efficacy of androgen-deprivation therapy, we need improved prognostic and predictive tools such as the use of mathematical models that take into account key biological features that are unique to each individual. Earlier mathematical models such as those by Jackson (16, 17), Ideta et al. (18), and Potter et al. (19) have considered the dynamical interplay between cancer cells and their mutations from androgen-sensitive to androgen-resistant phenotypes; however, these remain limited in scope and ability account for the observed heterogeneity in patients. More recently, Eikenberry et al. (20) introduced a model of early cancer development with testosterone, DHT, and AR dynamics-driven CaP cell growth. Their results suggest that low androgen levels can increase selection for castration-resistant cancer cells with elevated AR expression. We will use this evolutionary concept as the basis for the mathematical progression model proposed here.

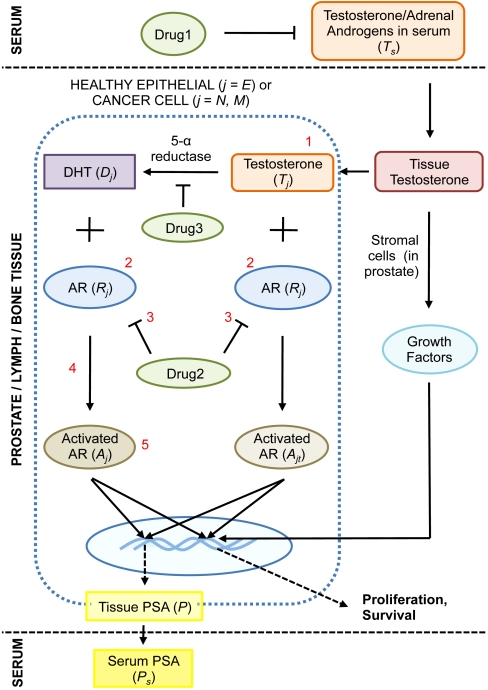
The objective of the present paper is to develop a comprehensive mathematical model of CaP progression, focused primarily on antiandrogen therapy of advanced disease, which could be applied to different antiandrogen interventions. We consider the case of a typical patient with advanced prostate cancer. We introduce three primary cell phenotypes—healthy prostatic epithelial cells (E), androgen-dependent CaP cells (N), and castration-resistant CaP cells (M). Here, E, N, and M represent total cell number, in millions. While E cells are limited to the prostate, N and M cells are typically systemic at metastatic sites, allowing for simulation of cases where patients present with metastatic disease or relapsed/recurrent disease post radical prostatectomy or radiation. To avoid overparameterizing our system, N and M represent total CaP burden in the body and are not compartmentalized to specific metastatic sites such as bone or lymph nodes. Driving the behavior of each cell is the intracellular signaling network presented in Fig. 1. Following Eikenberry et al. (20), this is translated into a system of differential equations using the law of mass action, the full details of which are presented in SI Text. Our model is designed to simulate the response to antiandrogen therapy of prostate cancer up to the emergence of castration resistance, defined as the progression of the disease in the presence of castrate concentrations of serum testosterone.

Fig. 1.

The dynamics of intracellular androgen biology governing prostate cancer (CaP) growth is shown. Briefly, testosterone is synthesized by the testes (not shown) and released into the circulation. From here, it enters the prostate and is taken up by prostatic epithelial cells (E), androgen-dependent cancer cells (N), and castrate-resistant cancer cells (M). Testosterone is converted into DHT by the action of 5α-reductase. Both testosterone and DHT subsequently bind and activate androgen receptors, a process mediated by additional cofactors, resulting in proliferative and survival signal modulation. PSA production is also androgen-dependent and related to cancer volume. Growth factors expressed by stromal cells at the site of tumor growth include: IGF-I, VEGF, bFGF, FGF7, TGF-β. However, given the paucity of data, we do not include the role of growth factors that might be secreted by the stroma on cancer cell survival or death explicitly in our model. Instead, it may be assumed that this is implicitly accounted for in the fits of prostate growth. In our model, castration-resistant cancer cells arise as a result of random mutations that occur when androgen-dependent cancer cells proliferate. Several mutations resulting in castration-resistance are numbered in red (1: local production of androgens, 2: up-regulated AR expression, 3: drug 2-induced activation of AR, 4: lowered AR activation threshhold, 5: constitutively activated AR). Finally, the actions of three types of drugs used to treat CaP are shown in green ovals.

Mathematical Model

We begin with a description of the equations describing the dynamics of the principle species in our model—namely, healthy epithelial and cancer cells, and intraprostatic and serum PSA concentration.

Cell Type E.

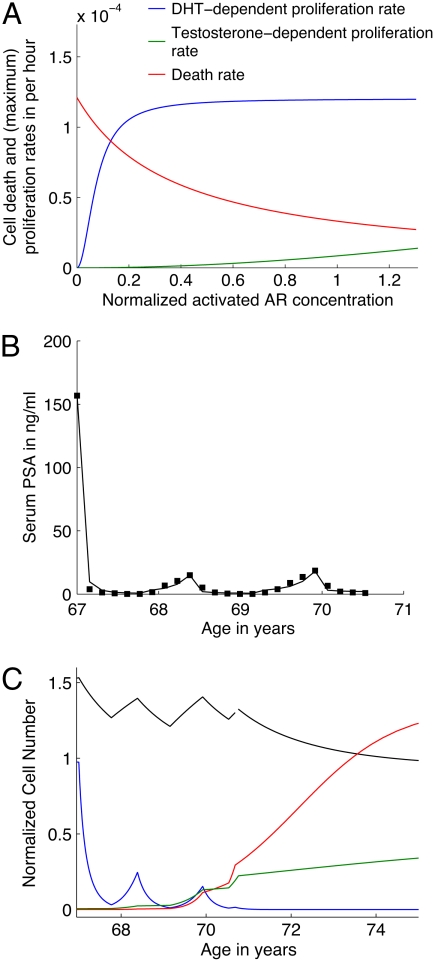
Healthy epithelial cells proliferate at a rate μ_E and have a natural death rate δ_E that is in balance and dependent on testosterone- and DHT-activated androgen receptors (A_Et and A_E, respectively; Fig. 2A). Competitive inhibition due to the presence of other cells is also incorporated in our model. The equation governing E is

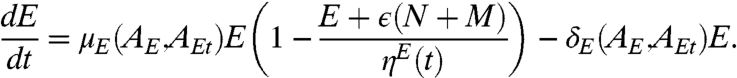[1]

Fig. 2.

(A) Androgen-dependent proliferation (DHT, blue and testosterone, green) and death (red) rates for human prostatic epithelial cells estimated from fitting experimental data. Activated AR concentration of 1 in dimensionless terms corresponds to homeostatic levels in the healthy prostate (see SI Text). (B) Fit to (averaged) patient PSA values as reported in literature (28) in response to intermittent androgen ablation therapy using an approach that treatment would be reinstituted arbitrarily with a PSA greater than 15 ng/mL, and applied for a period of about 40 weeks. (C) Numerical predictions of cancer response to therapy, in terms of normalized cell number. The experimental protocol as described in B is simulated. Healthy prostatic epithelial cells (E, black curve), androgen-dependent cancer cells (N, blue curve), and castration-resistant cancer cells (M) with average phenotype (green curve) and aggressive phenotype (red curve) are plotted versus time.

Prostate volume increases with age (21) by a process known as benign prostatic hypertrophy. By choosing the carrying capacity (η^E) in the cell proliferation term to be a function of time, we can capture this variability in prostate size accurately. The parameter ϵ is a measure of the competitive interaction between healthy and cancer cells. Because N and M include CaP cells from distant metastatic sites, ϵ is assumed to have a very small or negligible value in the setting of metastatic disease but could have a role in locally advanced nonmetastatic disease.

Cell Type N.

Because we are concerned with prostatic cancer that has its origins in the epithelia, the proliferation rate μ_N and the death rate δ_N of androgen-dependent cancer cells are significantly related to androgen-activated androgen receptors (A_Nt and A_N, respectively) signaling, as in the case of E. The equation for N is taken to be

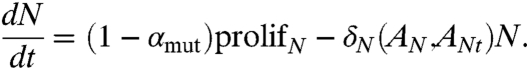[2]

Here, prolif_N = μ_N(A_N,A_Nt)N(1 - (ϵE + N + M)/η^C), and η^C is a measure of the maximum carrying capacity of the tissue in which the cancer resides. It has been suggested that mutations leading to castration resistance are an early event, independent of androgen ablation (22). This indicates the possibility of mutation acquisition occurring as a result of proliferation of aberrant cancer cells in N, which is accounted for by the parameter α_mut, which represents the probability of a cell with androgen-dependent phenotype N mutating to a castration-resistant phenotype M. This is an important parameter in our model, because it could account for significant heterogeneity, in addition to being a key predictor of treatment outcome. Note that the overall rate of mutation (= α_mut ∗ prolif_N) depends both on the number of proliferating N cells as well as how fast they proliferate.

Cell Type M.

The equation governing the rate of growth of castration-resistant cancer cells is similar to that for N above,

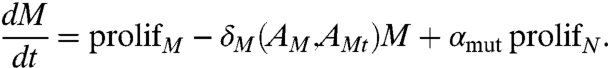[3]

Here, A_Mt and A_M are testosterone- and DHT-activated androgen receptors respectively, in M and prolif_M = μ_M(A_M,A_Mt)M(1 - (ϵE + N + M)/η^C).

PSA in Tissue, P.

Healthy and cancerous epithelial cells of the prostate produce PSA (23) in response to activated androgen receptors (24). However, in the noncancerous prostate the extravasation of the large PSA protein (35 kDa) into the bloodstream is hampered due to the presence of natural barriers, including the basal cell layer, prostatic basement membrane, prostatic stroma, and layers of the capillary walls (25). The equation governing PSA production in tissue is taken to be

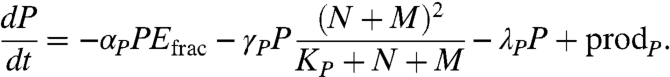[4]

PSA is produced by E, N and M, in response to activated androgen receptors, at a rate 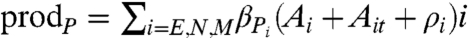, where β_Pi is a rate constant. We also account for the possibility of an independent production mechanism, via the constant ρ_i. PSA undergoes natural decay at a rate λ_P and is assumed to leak into blood serum at a rate dependent on the epithelial volume relative to stromal volume of the prostate. Consequently, this leakage rate is taken to be proportional to the epithelial fraction E_frac in the nonmalignant prostate—that is, the ratio of the epithelial volume to total prostatic volume.

In order to model the breakdown of natural barriers to the leakage of PSA into the blood in the presence of cancer cells, an additional leakage term is incorporated in Eq. 4. It is assumed that this additional leakage is negligible when the number of tumor cells is low, while for high numbers of tumor cells, this leakage is approximately linearly related to the number of tumor cells. This assumption is reasonable because it is to be expected that a comprehensive breakdown of the interstitial PSA barriers is more likely to occur for a higher number of tumor cells.

Serum PSA, P_S.

The equation governing the rate of change of serum PSA concentration is

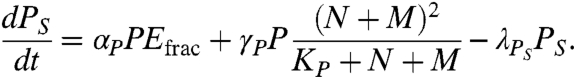[5]

The leakage terms in Eq. 4 correspond to source terms for serum PSA. Serum PSA is cleared from the body at a rate λ_PS.

Personalized Parameters.

We divide the parameters in our model into three categories: (i) parameter values from the literature, (ii) parameters derived from data fitting, and (iii) personalized parameters. The parameters in classes i and iiare derived from experimental data, humans when possible or experimental animal models as reported in ref. 26, and in vitro data on established CaP cells lines. A detailed description of the estimation of these parameters is presented in SI Text, sections S2 and S3. Data on the development of the human prostate, together with variations in its size and serum androgen levels with age, is taken into account while extrapolating parameter values for the human case.

It is commonly recognized that prostate cancer is a highly heterogeneous disease regarding response to antiandrogen therapy and rate of progression. In addition, serum testosterone and other androgens are known to vary widely from person to person. Furthermore, although PSA within a person is a useful marker of changing tumor burden in response to therapy, PSA is a poor predictor of tumor burden between patients. The model is equipped to deal with this heterogeneity by appropriately adjusting the relevant model parameters to match each patient profile; we refer to these parameters as “personalized parameters.”

Initially, cancer cells are assumed to be androgen-dependent. Following ref. 27, the transformed cells are assumed to differ from healthy epithelial cells in having a higher net turnover rate. This is the first of our personalized parameters, because this doubling rate is estimated from patient treatment data and can vary among individuals. The simulation is allowed to run, until our virtual patient’s PSA levels accumulate, at which time a screening event (screening PSA or digital rectal exam) is assumed to take place. However, in many men not undergoing screening or previously treated with local therapy that was too late, cancer cells have spread via the lymphatics or blood to metastatic sites. At this point antiandrogen therapy is the mainstay of treatment, and the various drugs and their actions are shown in Fig. 1. Because this is a proof-of-concept paper, we do not distinguish between the unique aspects of each drug’s action; instead we assume that the collective effect of the treatment is to reduce the bioavailability of DHT in the prostate by 60%, based upon the literature (14). From this point onward, we may simulate continuous or intermittent therapy. As mentioned earlier, we assume that mutations leading to M phenotype emerge spontaneously as a result of N cell proliferation. The hypothesis that application of androgen ablation therapy selects for these resistant cell lines is then investigated. M cells are allowed to have a different rate of turnover in terms of proliferation and apoptosis rates as compared to N cells. The type of mutation, frequency of mutation acquisition, and mutated-cell doubling time are also designated as personalized parameters. Given that one of the common mutations observed in hormonally refractive tumors is androgen receptor overexpression, we take this example, coupled with an increased stability of the receptors, to be the mutations in M cells. Then, by changing cell doubling time and frequency of mutation acquisition, we can simulate an aggressive versus a milder M phenotype and predict responses to continuous versus intermittent therapy (on various schedules).

Results

Case Study 1: Slow Cycling of Intermittent Therapy.

In 1995, Goldenberg et al. (28) published one of the first trials of intermittent androgen ablation therapy in prostate cancer patients. A group of 47 patients represented a wide range of cancer stage and grade and had an average age of 67 years. The mean follow-up time was 120 weeks and two cycles of treatment reported, lasting 73 and 75 weeks, with a mean time off therapy of 30 and 33 weeks, respectively. In seven patients with Stage D2 disease, the cancer was reported to progress to an androgen-independent stage in a mean time of 128 weeks. The treatment consisted of inhibiting pituitary gonadotropins with goserelin and androgen receptor blockade with flutamide. PSA concentrations (averaged across the entire patient dataset) were reported on an eight-week cycle from the onset of therapy. In order to fit this data to our model, we estimated the personalized parameters mentioned previously. Specifically, N and M turnover rates, probability of mutation α_mut, and CaP cell-dependent PSA leakage rate parameters (γ_P and K_P) are fit to the available data. It should be noted that CaP cell PSA production rate is fixed prior to performing fits at 30% of the level of healthy cells. This is essentially a free parameter in our model, and its effect on serum PSA concentration may be adjusted to required levels by correspondingly changing γ_P.

Fits to the PSA data reported in ref. 28 up to the end of the first cycle of therapy indicate a doubling time of 80 d for N. This implies that the patients on average had a neoplastic transformation in their prostatic epithelia at about age 60. In order to fit the PSA data for the second cycle of therapy, from week 72 onward, it is necessary to allow for the emergence of castration resistance. In fact, an entire continuum of castration-resistant phenotypes, ranging from a milder variant (with a high doubling time of 135 d) to a more aggressive variant (with a short doubling time of 75 d) gives a good fit to the data (Fig. 2B). Correspondingly, α_mut ranges from 1 in 10,000 to 1 in 10,000,000. In all cases, γ_P and K_P are taken to have the same values; that is, all CaP cells are taken to have an equal effect on PSA leakage from the prostate to the serum. In the following, we treat both extremes of M phenotypes in turn.

Consider first the case when the N cells mutate to a phenotype with a slower turnover rate. If we allow the model to run on a similar schedule beyond the two cycles reported in ref. 28 (so that each time a patient’s PSA levels rise above 15 ng/mL he is put on therapy for a period of 40 weeks, while the time off therapy is at most 32 weeks, with therapy reintroduced if PSA levels rise above 15 ng/mL before this time), the model predicts that intermittent treatment will fail within cycle 3. Treatment failure is defined by the inability of androgen ablation to reduce patient PSA levels below 4 ng/mL. As can be seen from Fig. 2C (green curve), we have emergence of castration-resistant cancer cells leading to intermittent therapy failure; in fact even continuous therapy applied at this point is unable to eradicate the M cells, while the N cell population has been rendered insignificant. However, the cancer is kept in check as M increases at slow rate, and the physician might recommend the patient for an alternative treatment course such as surgery and/or radiotherapy. It should be noted that further mutations in the M cell population leading to uninhibited cancer growth is possible; however, this possibility is not incorporated in our current model. For more details, see SI Text, section S4.

The model can be used to simulate the case where continuous treatment had been provided to the patient instead of intermittent therapy. Numerical simulations indicate that this leads to an apparent eradication of the cancer, based upon PSA decline, within a few months. Further, a disease-free period of up to 15 years is predicted, with PSA levels remaining at very low levels during this time. At about age 85, there is evidence of emergence of castration-resistant cancer, occurring from M cells generated possibly during age 60–67, when N cells were proliferating rapidly prior to treatment. This scenario reflects a cancer that is very sensitive to therapy and with a low rate of mutational adaption to low testosterone, which occurs in some men.

Next, we consider the case when the N cells mutate to a phenotype with a higher turnover rate. The model predicts that intermittent therapy will fail within the very next cycle of treatment, due to dominance of the castration-resistant phenotype. Fig. 2C shows the temporal evolution of the various cell populations corresponding to this schedule. As can be seen, even the application of continuous therapy at this point is unable to contain the rapidly proliferating M cells (red curve). In contrast, application of continuous therapy instead of intermittent therapy from the start of treatment is predicted to result in a disease-free survival period of up to five years; for more details, see SI Text, section 4.

Case Study 2: Rapid Cycling of Intermittent Therapy.

Here, we investigate the effect of competition between cells of type N and M on choice of treatment schedule. Both cell types may be competing for space and nutrients; and it is possible that in the process of mutation acquisition, cell type M becomes a poor competitor of cell type N. We quantify the competitive advantage of N over M by a parameter θ > 1, replacing (1 - (ϵE + N + M)/η^C) by (1 - (ϵE + N + (1/θ)M)/η^C) in Eq. 2, and by (1 - (ϵE + θN + M)/η^C) in Eq. 3.

In 2006, Feltquate et al. (29) reported on a study conducted to investigate the feasibility of rapid androgen cycling for men with progressive prostate cancer. The schedule included a 12-week induction of androgen deprivation, followed by four-week treatment cycles consisting of a gonadotropin-releasing hormone agonist analogue injection on day 1, coupled with testosterone repletion on days 1 to 7. This cycling was repeated until the cancer progressed to a castration-resistant stage. A number of PSA patterns were observed including patients whose PSA levels declined to an undetectable nadir, as well as PSA decline to a plateau, followed by eventual increase. A large subset of these patients had undergone radical prostatectomy previously and was thus being treated for metastatic disease. Although such a schedule is unlikely to be common in clinical practice we present it here to illustrate the wide scope of our model in terms of its ability to simulate a variety of treatment scenarios.

It is possible to repeat the fitting exercise described earlier for Case 1 for the various PSA patterns reported in ref. 29. This leads to results similar to those reported above. While this serves as good validation of our model—because we are able to reproduce a number of clinically observed outcomes for a variety of different treatment strategies—we use the experimental data to test a hypothesis of possibly vital importance in determining treatment strategies for advanced CaP patients. The question we wish to ask of the model is “What if M cell type is a poor competitor of N cell type?” This is a natural question to pose; it can be an important determinant of the success of intermittent therapy in comparison to continuous treatment in terms of delaying the onset of a hormonally refractive cancer. Note that under conditions of androgen ablation, N cells have a reduced rate of proliferation and undergo apoptosis at a high rate, thereby losing their competitive edge over M cells.

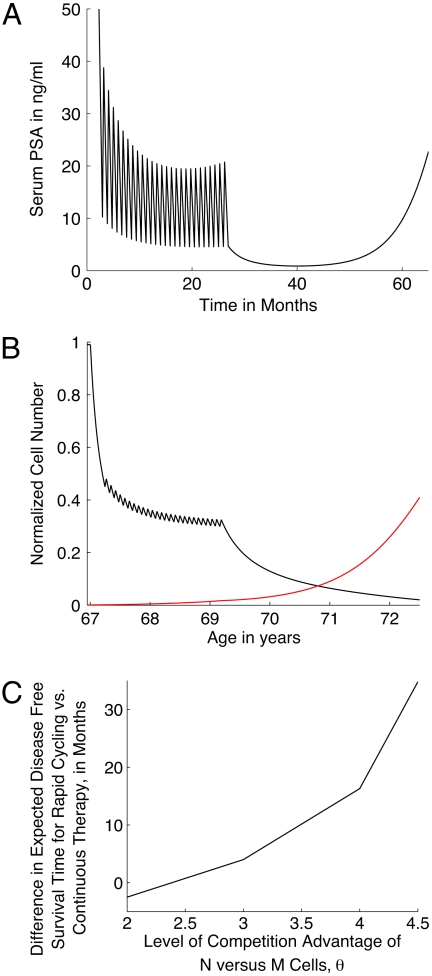
Fig. 3A shows a fit of our model to patient PSA data as reported in ref. 29 (compare to figure 2B in reference) for the case when PSA levels appear to decline to a stable plateau. Eventually the PSA levels start to rise again, at which point the patient is taken off the rapid cycling trial and put on continuous therapy. Fig. 3B shows corresponding normalized cell numbers. Note that as we are simulating a case where the patient is likely to have received a radical prostatectomy before enrollment in the study, the number of PECs has been set to zero. Prior to fitting, we make the assumption that the M phenotype has overexpression of androgen receptors coupled with an increased stability in these, as in case study 1. The personalized parameters being fit are the same as earlier.

Fig. 3.

(A) Fit to patient PSA values as reported in literature (29) (compare to figure 2b in reference) in response to rapid cycling intermittent androgen ablation therapy. (B) Numerical predictions of cancer response to therapy, in terms of normalized cell number. Following experimental protocol, therapy is provided for three weeks and stopped for one week, during which period testosterone is provided. The treatment schedule is continued for as long as PSA concentration decreases or remains stable (approximately 27 months from the start of therapy). At this point, patient is placed on continuous androgen ablation. Androgen-dependent cancer cells (N, black curve), and castration-resistant cancer cells (M, red curve) are plotted versus time. (C) Plot of the difference in predicted disease-free survival periods in patients on rapid cycling as described above and continuous therapy versus increasing levels of competitive advantage of N over M, represented by the nondimensional constant θ.

Taking a value of θ = 3, model simulations predict that the patient has an expected disease-free survival time of 28 months post rapid cycling therapy, after which PSA levels begin to rise again above a minimum threshold (taken to be 4 ng/mL for the purposes of illustration), due to emergence of castration resistance. In contrast, had continuous therapy been provided from the start of treatment, the expected recurrence of disease would have occurred four months sooner. We now increase the parameter θ and provide rapid cycling therapy for as long as it takes for PSA levels to start rising again. This is followed by continuous therapy, as in the therapy protocol reported in ref. 29. The time lag between disease recurrence in this case, versus providing continuous therapy from the outset, is predicted to increase exponentially (Fig. 3C). It should be noted that for θ ≤ 2, continuous versus intermittent therapy application is favored.

Discussion

Advanced CaP is treated with drugs that either inhibit androgen synthesis or block the ability of androgens to interact with its receptor in prostate cancer cells. It has been hypothesized that intermittent as opposed to continuous therapy may have advantages for some individuals through limiting impact of treatment on quality of life and metabolic or functional health outcomes as well as prolonging the duration of response to antiandrogen therapy. Intermittent scheduling may also reduce the rate of acquisition of mutations that contribute to the castration-resistant phenotype. Yet, at the present time we lack tools to help us tailor the appropriate therapy for each individual.

The paper develops a biochemically motivated mathematical model that begins to address heterogeneity of prostate cancer progression under different antiandrogen treatment regimes. The model is formulated by a system of differential equations where most of the parameters are based on experimental data. Due to the heterogeneous nature of the disease, several “personalized parameters” are to be adjusted based upon patient data. By fitting model predictions of serum PSA levels in response to androgen ablation therapy, we provide a quantitative confirmation of the clinically held view (14) that the selective pressure of androgen blockade is a stimulus for the emergence of hormonally refractive cancers.

The model was applied to two case studies (28, 29) of intermittent therapy representing two different intermittent treatment strategies. By adjusting the few personalized parameters, we were able to fit the model simulations to the “average” patients reported in the corresponding publications for these cases. We subsequently used the model to predict the future course of the disease for the next 5–10-year period under either intermittent or continuous therapy. Which of these two strategies yields a longer remission period depends on the personalized parameters, which quantify the competitive advantage of androgen-sensitive cancer cells over mutated androgen-independent cancer cells and on the “aggresiveness” of the mutated cancer cells.

The key to a model that is predictive and prognostic is the identification and quantification of the parameters that contribute to the variation or heterogeneity that is profound in the prostate cancer population. We have postulated these to be the following parameters: rate of acquisition of new mutations conferring resistance, competitive advantage of hormone-sensitive cells over androgen-independent cells, and overall sensitivity to androgen deprivation. Having shown that model simulations agree with medical data for the average patients, the model may be used in the future to examine individual cases and clinical trials, to further quantify the contribution of these factors to treatment failure in order to predict which men would benefit from continuous therapy or one of many different strategies of intermittent therapy, thus enhancing outcome through personalized therapy.