Applying Geostatistical Analysis to Crime Data: Car-Related Thefts in the Baltic States

Abstract

Geostatistical methods have rarely been applied to area-level offense data. This article demonstrates their potential for improving the interpretation and understanding of crime patterns using previously analyzed data about car-related thefts for Estonia, Latvia, and Lithuania in 2000. The variogram is used to inform about the scales of variation in offense, social, and economic data. Area-to-area and area-to-point Poisson kriging are used to filter the noise caused by the small number problem. The latter is also used to produce continuous maps of the estimated crime risk (expected number of crimes per 10,000 habitants), thereby reducing the visual bias of large spatial units. In seeking to detect the most likely crime clusters, the uncertainty attached to crime risk estimates is handled through a local cluster analysis using stochastic simulation. Factorial kriging analysis is used to estimate the local- and regional-scale spatial components of the crime risk and explanatory variables. Then regression modeling is used to determine which factors are associated with the risk of car-related theft at different scales.

Introduction

Quantitative analyses of area crime data often focus on the identification of areas of extreme criminality, such as areas with high rates or counts of offenses (crime hot spots). Hot spot detection is often undertaken using any one of a number of ad hoc techniques (e.g., Sherman, Gartin, and Buerger 1989) or statistical cluster detection methods drawn either from spatial epidemiology (e.g., Kulldorff 1997) or quantitative geography (e.g., Messner et al. 1999; Anselin et al. 2000; Haining 2003). Ecological modeling to explain spatial variation in counts or rates is usually undertaken using regression (e.g., Ceccato and Haining 2008; Haining, Law, and Griffith 2009).

Several authors suggest the use of geostatistical methods for the investigation of crime data (Anselin et al. 2000; Krivoruchko and Gotway 2003; Krivoruchko, Gotway, and Zhigimont 2003; Getis 2004), but we are aware of only one application. Camara et al. (2004) use ordinary kriging based on centroids of administrative units to produce a surface of homicide rates in Brazil and to identify clusters. However, recent advances in geostatistical methodology, such as area-to-area (ATA) and area-to-point (ATP) kriging (Kyriakidis 2004) and Poisson kriging (Goovaerts 2005; Monestiez et al. 2005), have opened up new opportunities.

We demonstrate in this article the application of geostatistical methods for analyzing the geography of offenses and for identifying significant clusters of crimes. Data about car-related thefts in the Baltic states (Estonia, Latvia, and Lithuania) in 2000, a data set previously analyzed by Ceccato and Haining (2008), are used. This article contrasts the insights obtained using geostatistical methodology with those reported by Ceccato and Haining.

Acquisitive crime in the Baltic states: an earlier study

A conceptual framework

Since the collapse of the Soviet Union in 1991, the three Baltic states of Estonia, Latvia, and Lithuania have undergone profound political change and associated social and economic change as their economies have become more market oriented. The conceptual framework developed by Ceccato and Haining (2008, p. 216) to explain the geography of acquisitive crime emphasizes the role of both medium- and short-term dynamics. In the medium term, citizens of countries experiencing profound socioeconomic change are subject to uncertainty and instability that create anomic conditions leading to increased rates of crime and violence (Durkheim 1897). However, effects are moderated where strong social institutions exist (Messner and Rosenfeld 1997; Kim and Pridemore 2005). Ceccato and Haining (2008) measure medium-term effects using “economic, social and welfare change” over the period 1993–2000. All the change variables were calculated so that more change (e.g., increasing unemployment) would be expected to produce more offenses.

In the short term, the incidence of acquisitive offenses at the area level reflects a rational choice theory trade-off made by a motivated offender in terms of current “risk and reward.” Motivated offenders not only assess an area’s attractiveness (reward to the offender) but also the probability of getting caught (risk to the offender). Geographical variation in rates of acquisitive crime depends on prevailing economic conditions, the social context (strength of social institutions; quality of welfare provision), and demographic structure. Periods of high unemployment may have more motivated offenders. A strong economy is more likely to have more targets for acquisitive crimes. If economic performance is geographically and sectorally uneven, motivated offenders may be more drawn to better-off regions than to poorer regions. However, the literature about social cohesion has long suggested the importance of strong social institutions in moderating the negative effects of economic problems in society (Sampson 1986) and in discouraging would-be offenders. Lack of social cohesion in an area reduces the risk to the offender to commit an offense there because fewer “capable guardians” are present. Demographic structure is important because areas with relatively large numbers of young males or with an overrepresentation of certain marginalized non-national ethnic groups (Lehti 2001) tend to experience higher rates of offending.

Although the three Baltic states have experienced the effects of transition, these effects have played out differently across the states and the subregions into which they are subdivided. Other place-specific variables were added to the set of covariates that are known to correlate with offense rates: whether areas are at national political borders (“border”) and whether they are urban or rural areas (“population density”). A list of the variables used is given in Table 1. For full details and a graphical representation of the conceptual framework used, see Ceccato and Haining (2008).

Table 1.

Summary of the Final Model for Spatial Regression Reported in Ceccato and Haining (2008) (66.8% of Variance Explained) and Variogram Parameters for Models Fitted to Experimental Variograms of the Areal Data for Car-Related Theft and Explanatory Variables

Variable	Ceccato and Haining (2008) results		Variogram parameters
	Estimate	t prob.	Model 1	Model 2	c0	c1	c2	a1 (km)	a2 (km)	c0: Sill	c1: Sill	c2: Sill
Car-related theft			Cubic	Cubic	0.26	325.1	69.23	142.4	738.5	0	0.82	0.18
Constant	2.85	<0.000
Border		NS	Spherical	*	0.06	0.18	*	150.7	*	0.26	0.74	*
Divorce rate	0.36	<0.000	Pure	Nugget	*	*	*	*	*	*	*	*
Economic change		NS	Cubic		0	0.82	*	125.2	*	0	1	*
FDI		NS	Spherical	*	21,587	823,051	*	413.3	*	0.03	0.97	*
GDP			Cubic	Cubic	340,548	484,848	774,830	674.2	674.3	0.21	0.30	0.49
GDP (Lithuania; Latvia)	7.9E-5	0.071
GDP (Estonia)	3.8E-4	<0.000
Hospital beds		NS	Cubic	Cubic	0	912.7	410.4	157.1	1255.6	0	0.69	0.31
Infant mortality	−0.08	0.001	Cubic	Spherical	0	18.39	5.97	115.0	348.2	0	0.75	0.25
Males aged 15–29		NS	Cubic	Cubic	0	1.17	0.51	135.9	431.9	0	0.70	0.30
Natural increase	0.46	0.004	Cubic	*	0.03	0.09	*	166.2	*	0.25	0.75	*
Net migration		NS	Cubic	Cubic	0	0.10	0.04	151.1	724.5	0	0.71	0.29
Non-national pop.		NS	Spherical	Spherical	7.27	150.6	257.6	178.7	422.8	0.02	0.36	0.62
Population density	3.0E-4	0.001	Cubic	*	0.004	129,274	*	130.7	*	0	1	*
Roads		NS	Spherical	*	0.035	0.20	*	118.7	*	0.15	0.85	*
Social change			Expo.	Cubic	0	0.006	0.006	77.9	657.3	0	0.50	0.50
Social change (Estonia; Lithuania)	−2.95	<0.000
Social change (Latvia)	1.75	<0.000
Unemployment		NS	Cubic	*	0	24.60	*	136.1	*	0	1	*
Voter participation		NS	Expo.	Cubic	6.29	22.02	214.9	801.6	861.3	0.03	0.09	0.88
Welfare change		NS	Cubic	Cubic	0	1.03	0.15	132.4	281.2	0	0.87	0.13

^*Parameter not applicable to this variable.

NS, not significant; FDI, foreign direct investment; GDP, gross domestic product.

Values in bold are significant at alpha = .05.

Ceccato and Haining’s methodology and findings

Using the statistical software package STATA, the negative binomial regression model was fitted to counts of car-related thefts for 107 administrative units (Osgood 2000; Osgood and Chambers 2000). Dummy variables were introduced to allow parameters to vary between the three countries. However, statistically significant spatial autocorrelation was identified in the generalized linear model (GLM) residuals (Lin and Zhang 2007). Because the counts for this offense were large, they were converted to standardized offense ratios, log transformed (Ceccato and Haining 2008, p. 227), and a normal linear regression model was fitted with first-order simultaneous autoregressive errors to model the residual spatial autocorrelation. Also, because the residuals from this model were not spatially autocorrelated (and other diagnostics were satisfactory), this was the model used for hypothesis testing.

The final model of Ceccato and Haining (2008), summarized in Table 1, explains just under 67% of the variation in the log-transformed dependent variable (pseudo-R²). Short-term dynamics dominate the final model and show the importance of target area attractiveness (higher levels of the variable gross domestic product [GDP], lower levels of “infant mortality” indicative of a higher standard of living, and higher levels of “population density”) and social disorganization associated with areas with high rates of family breakdown (higher “divorce rate”). Ceccato and Haining (2008) found no convincing evidence of medium-term effects being important except in Latvia, where “social change” is statistically significant and its coefficient has the “correct” (i.e., expected) sign, although in Lithuania and Estonia the coefficient for the same variable, while again statistically significant, has the “wrong” sign. Table 1 summarizes their main results.

As Ceccato and Haining (2008) observe, one of the problems with this type of small-area analysis is how to deal with the scale effects associated with different explanatory variables. Areas are not sealed units and “economic disadvantage in one region may trigger higher rates of offending and offence rates in other areas as motivated offenders travel or migrate to find suitable targets” (Ceccato 2007, p. 141). The identification and mapping of these scales of variability and their association with offense rates is not straightforward in the types of models used by Ceccato and Haining (2008), which is one of the reasons to investigate the use of geostatistical methods, including factorial kriging analysis (FKA). However, another important set of reasons is that geostatistics also provides an analyst with a much wider range of models for describing spatial structure in data, and recent developments now allow the analyst of area data to account for the spatial support of the measurements (i.e., size and shape of administrative units), as well as the population size, which can vary greatly among units.

Revisiting car-related thefts in the Baltic states: methods

Data

Car-related theft counts refer to the 107 administrative units in Estonia, Latvia, and Lithuania in 2000 (Fig. 1a). The average population size of the areas in 2000 was just under 70,000, making them large heterogeneous spatial units. Data about demographic, social, economic, and welfare variables refer to the same spatial units. Quality issues arise with this data, including underreporting of offenses (Del Frate and van Kesteren 2004; see also European Sourcebook of Crime and Criminal Justice Statistics 1996, 2003). (For an extended overview of database construction and data quality issues, see Ceccato and Haining (2008) and Ceccato (2008).)

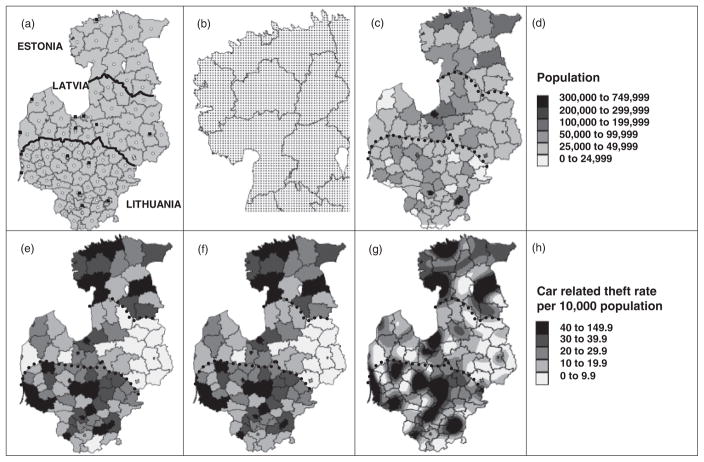
Figure 1.

(a) Municipal (white dot) and city (black dot) centroids. (b) Discretization grid (5km used for population weight set and 2 km grid used for area-to-point (ATP) kriging). (c) Population in 2000 weight dataset (5km grid). (d) Key for (c). (e) Crude car-related theft rate. (f) Area-to-area Poisson kriged car-related theft rate. (g) ATP Poisson kriged car-related theft rate per 10,000 population in 2000. (h) Key for (e)–(g).

Geostatistical methodology

Crime rates for an administrative unit v_α are the number of crimes in that unit d(v_α) divided by its population n(v_α) and then multiplied by 10,000. When n(v_α) is small, rates z(v_α) = d(v_α)/n(v_α) may appear unrealistically large or small (the small number problem). Variogram and spatial predictions need to be adapted to counter this source of noise.

Variogram computation

First, the usual variogram estimator (equation 4 in Haining, Kerry, and Oliver 2010), must be adapted to characterize the spatial variability in the data. The following population-weighted estimator adjusts for the small number problem:

$${\widehat{\gamma }}_{Rv}(\mathbf{h})=\frac{1}{2{\displaystyle \sum _{\alpha ,\beta }^{N(\mathbf{h})}}\frac{n(v_{\alpha })n(v_{\beta })}{n(v_{\alpha })+n(v_{\beta })}}\sum _{\alpha ,\beta }^{N(\mathbf{h})}\left\{\frac{n(v_{\alpha })n(v_{\beta })}{n(v_{\alpha })+n(v_{\beta })}{\left[z(v_{\alpha })-z(v_{\beta })\right]}^2-m^{\ast }\right\}$$ (1)

where N(h) is the number of pairs of areas (v_α, v_β) whose population-weighted centroids are separated by the vector h, and m* is the population-weighted mean of the N area rates. The usual squared differences, [z(v_α) − z(v_β)]², are weighted by a function of their respective population sizes, n(v_α)n(v_β)/[n(v_α) + n(v_β)], a term inversely proportional to their standard errors, thus giving more importance to more reliable data pairs (Monestiez et al. 2006). More importance is given to data values based on larger populations, which have smaller standard errors. In analyses where the areal units are small, this adjustment is particularly important but is not likely to make a major difference to the results here. This adjustment should also be made when considerable heterogeneity exists in population size across a set of areal units.

An important step in the application of the kriging techniques described in this article is inference about the point-support variogram γ_R(h) or, equivalently, the point-support covariance C_R(h) defined as C_R(0) − γ_R(h). The major difficulty here is that this function cannot be estimated directly from the experimental variogram [equation (1)] because the latter is computed from areal rate data. Therefore, the model fitted to (1) using weighted least squares (see, e.g., Haining, Kerry, and Oliver 2010) needs to be deconvoluted. We adopt an iterative deconvolution procedure whereby the point-support model is chosen that, once regularized, is the closest to the model fitted to the areal data. See Goovaerts (2006b, 2008) for more details about this approach and simulation studies that illustrate the reliability of this method in proceeding from areal to point support. Unlike conventional deconvolution methods developed for regular mining blocks, this approach takes into account the irregular shape and size of areal units, and the nonuniform distribution of population within those units if those data are available.

Spatial prediction

Adaptation of kriging as outlined by Haining, Kerry, and Oliver (2010) for use with crime data should proceed as follows. The crime count d(v_α) is interpreted as a realization of a random variable D(v_α) that is Poisson distributed with a parameter (expected number of crimes) that is the product of the population size n(v_α) and the local crime risk R(v_α). R(v_α) might be thought of as a noise-filtered crime rate for area v_α, which we also refer to as the crime risk. It is estimated by using a variant of kriging with nonsystematic errors, known as Poisson kriging (Monestiez et al. 2005). Choropleth mapping of crime rates creates visual bias as large units dominate. ATP kriging (Kyriakidis 2004; Goovaerts 2006b) is used to create isopleth maps of the estimated crime risk to reduce this bias.

The crime risk and the associated kriging variance for a unit X are estimated as

$$\widehat{r}(X)=\sum _{i=1}^K{\lambda }_{i}z(v_i)$$ (2)

and

$${\sigma }^2(X)={\overline{C}}_R(X,X)-\sum _{i=1}^K{\lambda }_i{\overline{C}}_R(v_i,X)-\mu (X)$$ (3)

where X represents either an area v_α (ATA kriging) or a point u_s within that area (ATP kriging). The kriging weights (λ_i) and the Lagrange parameter μ(X) are computed by solving the Poisson kriging system of equations:

$$\begin{array}{l}\sum _{j=1}^K{\lambda }_j\left[{\overline{C}}_R(v_i,v_j)+{\delta }_{ij}\frac{m^{\ast }}{n(v_i)}\right]+\mu (X)={\overline{C}}_R(v_i,X),\text{i}=1,\dots ,K,\\ \sum _{j=1}^K{\lambda }_j=1\end{array}$$ (4)

where δ_ij = 1 if i = j and 0 otherwise. The error variance term, m*/n(v_i), leads to smaller weights for rates measured over smaller populations. The ATA covariances C̄_R(v_i, v_j) and ATP covariances C̄_R(v_i, X = u_s) are approximated as the population-weighted average of the point-support covariance C_R(h) computed between any two locations discretizing the areas v_i and v_j, or v_i and u_s. An important property of the ATP kriging estimator is its coherence: the population-weighted average of the risk values estimated at the P_α points u_s discretizing a given entity v_α yields the ATA risk estimate for this entity:

$$\widehat{r}(v_{\alpha })=\frac{1}{n(v_{\alpha })}\sum _{s=1}^{P_{\alpha }}n({\mathbf{u}}_s)\widehat{r}({\mathbf{u}}_s)$$ (5)

where u_s∈ v_α with s = 1, …, P_α, and n(u_s) is the population count assigned to the interpolation grid node u_s (e.g., centroids of 25km² cells in this study). Constraint (5) is satisfied if the same K areal data are used for the ATA kriging of r̂(v_α) and the ATP kriging of the P_α risk values.

Local cluster analysis

A common task in crime analysis is the identification of regions where rates measured in adjacent geographical units are either significantly similar (i.e., positive autocorrelation that may produce local clusters) or different (i.e., negative autocorrelation that may produce local outliers). Similarity between the crime rate measured within area v_α and those recorded in the J(v_α) neighbouring areas v_β (e.g., which share a common border with v_α) can be quantified by the local Moran statistic (Anselin 1995):

$$I(v_{\alpha })=\left[\frac{z(v_{\alpha })-m}{s}\right]\times \left(\sum _{j=1}^{J(v_{\alpha })}\frac{1}{J(v_{\alpha })}\times \left[\frac{z(v_j)-m}{s}\right]\right)$$ (6)

where m and s are the mean and standard deviation of the set of N area rates.

This local indicator of spatial association (LISA) is simply the product of the kernel rate and the average of the neighboring rates. Camara et al. (2004) use it to identify significant clusters of crimes, (I(v_α) > 0), along with spatial outliers of high or low crime rates, (I(v_α) < 0). The distribution of the local Moran statistic under the null hypothesis of complete spatial randomness is usually derived by (repeatedly) randomly shuffling all the rates except at v_α, each time computing (6), thus obtaining the distribution of simulated LISA values. The empirical value of (6) is compared with this distribution to compute the P value for the test. This randomization ignores the population size associated with each areal unit (Goovaerts and Jacquez 2005). To address this, we randomly sample a Poisson distribution, Po(n(v_j) × m*), where n(v_j) is the size of the population at risk and m* is the population-weighted mean of the N rates.

The impact of population size on the reliability of crime rates also needs to be incorporated into the computation of the local Moran statistic. Although Poisson kriging provides a measure of rate uncertainty in the form of the kriging variance, this information cannot be used directly in (6) to derive a measure of uncertainty for the LISA statistic. Following Goovaerts (2006a), the uncertainty attached to crime rates is carried through a local cluster analysis by conducting this analysis with a set of L-simulated crime rate maps. Differences between the resulting L maps of LISA statistics illustrate how the uncertainty about crime rates impacts the results of a local cluster analysis. The correlation of each area with adjacent areas is tested L times, enabling the computation of the probability that an area either belongs to a local cluster or is a spatial outlier. Goovaerts (2006a) proposes the use of p-field simulation to circumvent the problem that no risk data, only risk estimates and thus no reference histogram, are available to condition the simulation. According to this procedure the lth realization of the crime rate for unit v_α is computed from the Poisson kriging estimate and the square root of the kriging variance σ²(v_α) as

$$r^{(l)}(v_{\alpha })=\widehat{r}(v_{\alpha })+\sigma (v_{\alpha })w^{(l)}(v_{\alpha })$$ (7)

and the L sets of random deviates, {w^(l)(v_α), α = 1, …N}, are generated using nonconditional sequential Gaussian simulation and the semivariogram of the risk, γ_R(h), rescaled to a unit sill; see Goovaerts (2006a) for a detailed description of the p-field simulation algorithm.

Scale dependent correlation and regression

Many factors explain the variation in crime rates in the Baltic states but over different time scales and probably at different spatial scales (Ceccato and Haining 2008). These scales could be distinguished from the variogram, which would then be modeled. For the variable “car-related thefts,” the point-support model uses the sum of two cubic models: γ_R(h) = γ_local(h) + γ_regional(h) or, equivalently, C_R(h) = C_local(h) + C_regional(h). The local model range of the autocorrelation estimate (140 km) is one order of magnitude smaller than for the regional model (1130 km). Based on the nested variogram model, the risk estimate can be decomposed into the sum of a local and a regional component, plus a trend component (TC)

$$\widehat{r}(v_{\alpha })={\widehat{r}}_{\text{local}}(v_{\alpha })+{\widehat{r}}_{\text{regional}}(v_{\alpha })+TC(v_{\alpha })=E_1(v_{\alpha })+E_2(v_{\alpha })+TC(v_{\alpha })$$ (8)

The spatial components are still estimated as linear combinations of crime rates recorded in neighboring counties (equation (2)), but the weights are computed by solving the following system of equations:

$$\begin{array}{l}\sum _{j=1}^K{\lambda }_j^{\text{local}}\left[{\overline{C}}_R(v_i,v_j)+{\delta }_{ij}\frac{m^{\ast }}{n(v_i)}\right]+\mu (v_{\alpha })={\overline{C}}_{\text{local}}(v_i,v_{\alpha })\text{i}=1,\dots ,K\\ \sum _{j=1}^K{\lambda }_j^{\text{local}}=0\end{array}$$ (9)

$$\begin{array}{l}\sum _{j=1}^K{\lambda }_j^{\text{regional}}\left[{\overline{C}}_R(v_i,v_j)+{\delta }_{ij}\frac{m^{\ast }}{n(v_i)}\right]+\mu (v_{\alpha })={\overline{C}}_{\text{regional}}(v_i,v_{\alpha })\text{i}=1,\dots ,K\\ \sum _{j=1}^K{\lambda }_j^{\text{regional}}=0\end{array}$$ (10)

The only differences between these two systems and (4) are the right-hand-side covariance terms that are approximated as the population-weighted average of the point-support covariances C_local(h) or C_regional(h) computed between any two locations discretizing the areas v_i and v_α. This decomposition is a generalization of FKA (Wackernagel 1998) to Poisson kriging. The kriging system for the trend component is similar to (4), except the right-hand-side covariance terms are set to zero (Goovaerts 1997).

The maps of spatial components can be used as visualization tools to discriminate between regional and local patterns in estimated crime risk. Spatial components are also helpful for exploring scale-dependent correlation patterns. Inferring scale-dependent correlations directly from FKA is less demanding in terms of assumptions than computing structural correlation coefficients from the parameters of a linear model of coregionalization fitted to a set of direct- and cross-variograms (Goovaerts and Webster 1994; Goovaerts 1997). Fitting normal linear regression models with first-order simultaneous autoregressive errors to each of the spatial components from FKA can also help indicate which variables are most important at each scale.¹

Results and discussion

Variogram analysis

Fig. 1a shows the location of centroids for the administrative units in the Baltic states. In several cases, a city municipality is found in the center of a district municipality (nested geographies). The two centroids are close together yet have very different crime rates. This arrangement of data creates a problem when quantifying spatial autocorrelation using the distance between centroids as the measure of geographic proximity. Most maps of the original variables (not shown) give visual evidence of spatial autocorrelation, as can be seen for “car-related theft” in Fig. 1e. But, because of the proximity of city and district centroid locations, the variograms for these variables appear to be pure nugget. Cities thus act as spatial outliers, creating a noisy effect superimposed on the underlying spatial autocorrelation of the regions. To address this data feature, city and district municipalities were merged (reducing the number of administrative units from N = 107 to = 89), and the total number of crimes in the new area were divided by the combined population. Note that this is only done for the purpose of estimating the variograms and that the original 107 rates are still used for kriging. This approach is comparable to the frequent practice in geostatistics of removing outliers when computing a variogram but returning them for interpolation so that their presence is not lost; however, the variogram portrayed in Fig. 2 is not erratic due to their presence. In the absence of fine-scale census data, population was assumed uniformly distributed within each of the 107 original administrative units, and population data for 2000 was disaggregated to a 5-km grid (Fig. 1b) to produce a population-weighted dataset (Fig. 1c) for population-weighted centroids. The population data from the original unmerged geography were disaggregated to create this data set so that the denser city populations were allowed for in the computation of the variogram from the merged geographies.

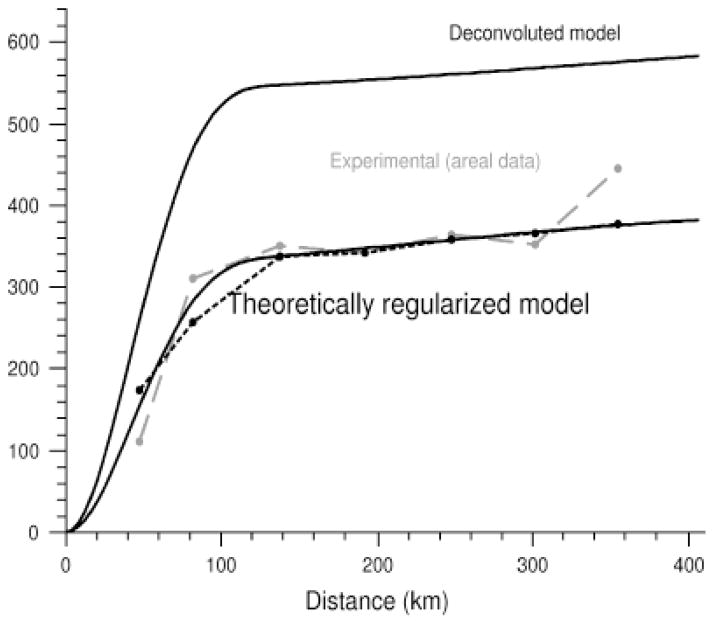
Figure 2.

Experimental variogram and model from areal data; and theoretically regularized variogram and deconvoluted model for car-related theft.

The dimensions of the study area are approximately 1000 km (N–S) by 750 km (E–W). Variograms of the areal data for the merged geography were computed for each of the variables using equation (1) and the population-weighted centroids. A spatial lag distance of around 55km was used, and variograms were computed to a maximum lag of about 450 km; the lag classes varied slightly to achieve a balance between having an erratic variogram and oversmoothing. Variogram models were fitted using weighted least squares with equal weight assigned to each lag because the number of comparisons for the first lag class was small and an accurate estimate of the nugget variance is important to obtain for kriging. This approach also tends to give a good indication of the range parameter, which is valuable for identifying different scales of variability. Models with nested structures were accepted as the best-fitting models only if clear evidence existed of more than one scale of variation in the experimental variogram.

Once computed and modeled, variograms were deconvoluted using an iterative procedure that returns the point-support variogram, which once regularized is closest to the variogram of the areal data (Goovaerts 2008). For this procedure, the 5-km grid was used as the discretization geography, with the population data as the weight data set. Fig. 2 shows that the experimental variogram for “car-related theft” constructed with the areal data and the theoretically regularized model are similar in form, as are the parameters. However, the sill of the point-support (deconvoluted) model is higher, showing that the a priori variance of the point process is greater than that of the spatially aggregated process. The Poisson variogram estimator and kriging equations were used for the variable “infant mortality” because it is the only explanatory variable that has a relatively rare outcome and as such could suffer from the small number problem. For all other explanatory variables a similar procedure was adopted using the traditional variogram estimator and kriging procedure (see Haining, Kerry, and Oliver 2010).

Table 1 shows the parameters of models fitted to the experimental variograms for “car-related theft” and all the explanatory variables. Some variograms exhibit one basic structure, whereas others exhibit two. The parameter c₀ is the nugget variance, which refers to the spatially unstructured or random variation; c₁ gives the amount of variance associated with patches with an average diameter of a₁ (local or short range variation); and c₂ gives the amount of variance associated with patches with an average diameter of a₂ (regional or large range variation). The parameters c₀:sill, c₁:sill, and c₂:sill give the proportion of the overall variance (sill = c₀ + c₁ + c₂) that is accounted for by each structure.

The variograms for most variables have two structures, and the majority of these have a first structure with a range of 110–150 km. This distance is about double the diameter of an average administrative unit, suggesting that most patterns for this shorter range structure cover a district plus its adjacent neighbours. However, where administrative units are larger (Estonia), this small range structure will reflect the presence of spatial outliers. Foreign direct investment (“FDI”), “GDP,” and “voter participation” have markedly larger ranges of autocorrelation for the first structure. The second basic structure shows a wide spread of range values, most of which are larger than the maximum lag used for the experimental variogram. These larger-scale structures may be identifying intercountry differences. The variables “border,” “economic change,” “FDI,” “natural increase,” “population density,” “roads,” and “unemployment” do not show variation at this scale.

The relative nugget effect, c₀: sill (Table 1), indicates that for most variables the proportion of variance accounted for by the nugget is near zero, and hence very little variation is spatially random. The only variables with marked nugget effects are “border,” “GDP,” “natural increase,” and “roads.” The variogram for “divorce rate” is pure nugget (Table 1) and hence the influence of this variable could not be investigated using geostatistical techniques. For most variables, the ratio c₁:sill shows that the first structure accounts for most of the variance; however, for “GDP,” “non-national population,” and “voter participation,” c₂ accounts for the largest proportion of the variance, suggesting that differences between countries are most important for these variables.

Analysis of patterns of crime

Kriged maps

Poisson kriging was applied to the crime data based on the original areal geography (N = 107) but using the point-support variogram model inferred from the merged geography (N = 89) (see the section on variogram analysis).

Two prediction supports were considered for Poisson kriging: the original areal geography (ATA Poisson kriging) and a grid of points with a spacing of 2km (ATP Poisson kriging). The aggregated ATP Poisson kriged predictions (not shown) are the same as the ATA Poisson kriged predictions, which demonstrates that the coherency constraint is met. Maps of the “car-related theft” data are shown in Figs. 1e–g. The map of the original rates and ATA Poisson kriged predictions are similar, although differences can be seen for three districts in the southeast of Estonia, one district on the Estonian border, one on the Baltic coast in Latvia, one in the central north, and one in the south of Lithuania (see Ceccato and Haining 2008 for names of these districts). Each of these districts is located near a country border or has a relatively small population (25,000–50,000 [Fig. 1c]). The similarities between Figs. 1e and 1f suggest, as anticipated, that the small number problem is not a serious issue for the crime data because of the large population sizes of the administrative units.

Fig. 1e shows that the expected rates of “car-related theft” are lower in Latvia, especially in the east. Large rates appear in the central areas of Lithuania. Administrative areas are artificial constructions, and crime rates should not be expected to be uniform within them. The ATP Poisson kriged map (Fig. 1g) indicates the broad underlying patterns of the crime risk that might be revealed if data were not aggregated by administrative unit.

Local cluster analysis

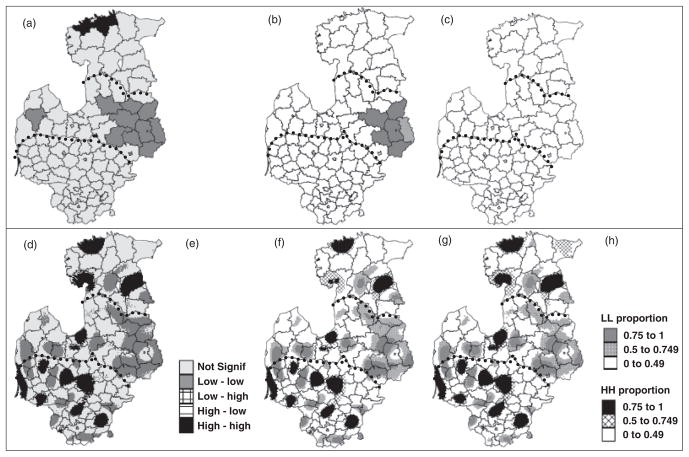
One hundred simulated rate maps were generated using p-field simulation. The LISA statistic was computed for each simulated map, and its significance was tested using two different randomization procedures: random shuffling of simulated rates ignoring population sizes (Model 1); and, accounting for population size differences by sampling from a Poisson distribution Po(n(v_j) × m*), where n(v_j) is the size of the population at risk and m* is the population-weighted mean of the N rates (global crime rate) (Model 2). In both cases, a significance level of .05 was used with correction for multiple testing utilizing Castro and Singer’s (2006) false discovery rate (FDR). These results were post-processed to retrieve for each administrative unit the category that occurred most frequently over the 100 simulated fields: not significant; LL (low-low cluster); LH (low-high outlier); HL (high-low outlier); and HH (high-high cluster). The frequency of occurrence of each category is used as a measure of the reliability of the categorization.

Using the original rates data with no adjustments for multiple testing or population size (Model 0), Fig. 3a and Table 2 show that several administrative units in eastern Latvia are significant LL clusters, and one unit in northern Estonia is a significant HH cluster of “car-related thefts.” Using the ATA Poisson kriged maps (which, as noted, are noise-filtered rates) and Model 1 reduces the number of significant LL clusters by half, and there are no significant HH clusters. The reductions in significant clusters compared with Model 0 are caused by the multiple testing correction. In Model 2, which accounts for population size, no units are identified as significant clusters (Fig. 3c and Table 2). When using ATP kriging (Figs. 3d–f) estimates, many significant clusters are found irrespective of model choice (Table 2). This result for ATP kriged estimates compared with ATA kriged estimates is to be expected based on the change in the scale of analysis. Because spatial autocorrelation decays with increasing distance, any given point on a 2-km grid is more likely to be surrounded by points with similar high or low crime rates than an administrative unit measuring 50 km in diameter. Accounting for multiple testing using the FDR method (Models 1 and 2, Figs. 3e–f) is now especially important. Many areas are identified as HH or LL clusters in Fig. 3d (Table 2) but are only classified as such with a 50–75% frequency once multiple testing is taken into consideration. For Model 2 (Fig. 3f), where population size is also taken into account, a larger area on the southwest coast of Estonia is considered to be a HH cluster with a frequency of more than 75%, and, compared with Fig. 3e, smaller areas in northeastern Latvia are identified as LL clusters with a frequency of 50– 75% (Table 2). In summary, the maps in Fig. 3 and LISA results (Table 2) provide a number of perspectives on the existence and location of “hot spots” and “cold spots” for the offense of “car-related theft.” Hot spots tend to occur at the local scale, whereas cold spots are a more regional phenomenon including most of eastern Latvia, perhaps related to lower “GDP” in this area. Given that law enforcement agencies are more interested in locating and policing the hot spot areas, this analysis also indicates the value of ATP Poisson kriging before cluster analysis to pinpoint more effectively where these clusters might be, which would be largely missed by an analysis using areal data.

Figure 3.

Local cluster analysis for car-related theft under different model test procedures: (a) crude rates and model 0. (b) ATA Poisson kriged rates and model 1. (c) ATA Poisson kriged rates and model 2. (d) ATP Poisson kriged rates and model 0. (e) key for (a) and (d). (f) ATP Poisson kriged rates and model 1. (g) ATP Poisson kriged rates and model 2. (h) key for (b), (c), (f), and (g).

Table 2.

Local cluster Analysis Results of Car-related Theft (Original Rates, Area-to-Area (ATA) and Area-to-Point (ATP) Poisson Kriged Rates) Under the Three Different Models for Hypothesis Testing

Classification	Proportion of areas (original and ATA) or points (ATP) in category (%)
	Original rate	ATA			ATP
Frequency of classification	Model 0	Model 0	Model 1	Model 2	Model 0	Model 1	Model 2
HH	2.8	2.8	0.0	0.9	13.6	14.7	19.1
LL	11.2	10.3	5.6	0.0	23.2	25.0	14.7
HH, 0	*	*	99.1	99.1	*	5.6	6.2
HH, 0.01–0.49	*	*	0.9	0.0	*	80.3	78.5
HH, 0.50–0.74	*	*	0.0	0.0	*	5.3	5.6
HH, 0.75–1	*	*	0.0	0.9	*	8.8	9.7
LL, 0	*	*	87.9	98.1	*	11.5	14.3
LL, 0.01–0.49	*	*	6.5	1.9	*	51.8	52.5
LL, 0.50–0.74	*	*	0.9	0.0	*	21.6	29.6
LL, 0.75–1	*	*	4.7	0.0	*	15.1	3.6

Proportions of areas or points classified as significant clusters (HH and LL).

^*No results given for Model 0 as uncertainty is not taken into account by this model.

Explaining patterns of car-related thefts

Scale-dependent correlations

Correlations were computed between the original values for “car-related theft” and the set of explanatory variables and also each of their spatial components (trend component = TC, local = E1 and regional = E2) obtained using factorial ATA (Poisson) kriging (hence noise-filtered measures of the variables). We discuss pairs of variables with a correlation coefficient >0.5 (a value chosen as indicative of a moderate relationship), and where the correlation based on a spatial component is greater than those based on the original data values. This selected threshold enables us to make some preliminary comparisons with the findings of Ceccato and Haining (2008).

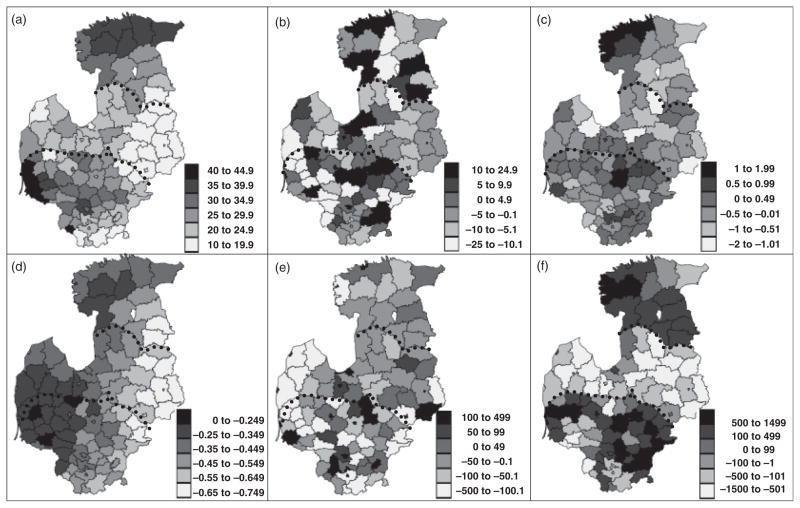
Correlations between “car-related theft” and the two variables “natural increase” and “roads” are 0.25 and 0.05, respectively, when based on the original data values, but 0.57 and −0.51, respectively, when based on the estimated trend components. Figs. 4a and 4d show the maps for the TCs of “car-related theft” and “natural increase.” Both maps show a general increase in the estimates from east to west and higher values in the north and south.

Figure 4.

(a) TC estimates for car-related theft. (b) E1 estimates for car-related theft. (c) E2 estimates for car-related theft. (d) TC estimates for natural increase. (e) E1 estimates for population density. (f) E2 estimates for GDP.

The correlations between “car-related theft” and “population density” for the original variables and E1 components are 0.47 and 0.59, respectively. Figs. 4b and 4e map these E1 components for the two variables, indicating a scale of variation of approximately 120–140km with aggregations of high or low values.

Finally, the correlations between “car-related theft” and “GDP” for the original variables and E2 components are 0.42 and 0.55, respectively, and the scale of variation is between 700 and 1130 km. Figs. 4c and 4f map these E2 components, revealing lower “GDP” and “car-related thefts” in Latvia.

The purpose of this analysis, similar to carrying out a correlation analysis before undertaking multivariate regression, is to identify associations among all the variables, only here the data are decomposed into different components of variation and associations are identified with respect to each component. The higher correlation between “GDP” and “car-related theft” at the E2 scale reflects the results of the Ceccato and Haining (2008) analysis, where an association reveals a differentiation between Estonia, Latvia, and Lithuania. The association between “car-related theft” and urbanization (“population density”)—identified at the administrative area level in Ceccato and Haining (2008)—appears to be strongest at the scale of each administrative area taken together with its nearest neighbor areas (E1).

The Ceccato and Haining (2008) analysis shows no significant relationship between road density (“roads”) and “car-related thefts,” but a negative relationship does appear significant in the trend component of variation. While their analysis reveals a significant relationship between “natural increase” and “car-related thefts,” the analysis here suggests that this association may be a product of larger-scale trends in both variables rather than an association at the administrative area level. The next stage of analysis, to which we now turn, allows a closer examination of these relationships while controlling for the effects of the other variables.

Scale-dependent regression

A multiple linear regression (MLR) model with first-order simultaneous autoregressive errors was fitted, using GeoDA. The dependent variable is “car-related thefts,” and in the first analysis the log of the original crime rates (z(v_α)) was used, and the original values were used for the independent variables. This implementation facilitates comparison with the results in Ceccato and Haining (2008). In the second analysis, ATA kriged estimates (KE)² of all the variables are used. In the third set of analyses, each of the spatial components from ATA FKA (TC, E1, and E2)³ for all the variables are analyzed in turn. The second and third analyses are not directly comparable with the Ceccato and Haining results because the variables have been constructed differently, as previously explained.

The specific MLR model was fitted because the earlier analysis by Ceccato and Haining (2008) and the results of the preceding spatial components analysis suggest the need to allow for spatial autocorrelation in the errors (see also note 1). Appropriate diagnostic tests demonstrated for all models the absence of residual spatial autocorrelation and the normality of the residuals.

Table 3 summarizes all of the MLR results. Note that the spatial error parameter is significant in all of the analyses. Although “divorce rate” is identified as statistically significant for the original data, it could not be included in the second and third analyses because its variogram is pure nugget. For the original variables, three other explanatory variables are significant at the 5% level: “GDP,” “voter participation,” and “social change” (which has the “wrong” sign). These results can be compared with those of Ceccato and Haining (2008) (Table 1), although in their analysis they allow for intercountry differences using dummy variables and the dependent variable is the log of the standardized “car-related crime” ratio. As with this earlier study, the results here show that a target area attractiveness variable is significant (“GDP”) as is a social disorganization variable (“divorce rate”). In addition a social cohesion variable is significant (“voter participation”). Ceccato and Haining (2008) also report that “social change” has the “wrong sign” for Estonia and Lithuania, but not Latvia. They attribute this result to measuring “social change” with changes in the “divorce rate” for the purpose of analysis. Interested readers should consult the original article for more details.

Table 3.

Regression Results for Car-Related Theft Using the Original Variables, ATA Poisson Kriged Estimates (KE), and the Spatial Components From ATA Factorial Poisson Kriging (TC; E1; E2)

CAR-RELATED THEFT	Log-transformed car-related theft rate		KE		TC		E1		E2
	Variance accounted for: 59.2%		Variance accounted for: 68.4%		Variance accounted for: 83.8%		Variance accounted for: 52.4%		Variance accounted for: 52.6%
Variable	Estimate	t prob.	Estimate	t prob.	Estimate	t prob.	Estimate	t prob.	Estimate	t prob.
Constant	1.34	<0.001	60.4	0.004	41.7	0.025	−0.133	0.944	−0.0440	0.634
Border	−0.0941	0.053	−4.37	0.081	−2.69	0.347	−7.77	0.018	†	†
Divorce rate	0.117	0.001	*	*	*	*	*	*	*	*
Economic change	−0.0121	0.759	1.50	0.521	3.01	0.319	2.68	0.218	†	†
FDI	9.14E-6	0.761	−6.60E-4	0.720	−9.40E-4	0.308	−6.80E-4	0.757	−5.20E-5	0.563
GDP	5.43E-5	0.019	0.00141	0.357	0.00200	0.056	0.00174	0.331	6.26E-4	<0.001
Hospital beds	6.04E-4	0.287	0.0515	0.155	0.0325	0.365	0.0328	0.380	0.0442	0.054
Infant mortality	−0.00288	0.434	−0.449	0.158	−0.953	0.004	−0.821	0.020	−0.876	0.002
Males aged 15–29	0.0109	0.538	2.01	0.063	−0.184	0.878	2.38	0.041	0.950	0.019
Natural increase	−0.0130	0.902	−4.37	0.524	−5.186	0.436	−7.73	0.316	−3.38	0.010
Net migration	−0.00697	0.877	3.97	0.066	−0.0768	0.975	5.00	0.081	0.0378	0.064
Non-national population	0.00118	0.390	0.193	0.039	−0.00258	0.971	0.0263	0.835	0.00930	0.259
Population density	4.13E-5	0.346	0.0141	<0.001	0.00466	0.267	0.0157	<0.001	0.00195	0.750
Roads	0.0163	0.688	1.31	0.613	−5.72	0.166	0.239	0.928	†	†
Social change	−0.867	0.001	−44.9	0.002	−49.2	0.003	−25.1	0.124	−3.00	0.280
Unemployment	5.39E-4	0.931	−0.154	0.674	−0.0816	0.848	0.0620	0.865	†	†
Voter participation	−0.0109	0.001	−1.123	<0.001	−0.155	0.029	†	†	0.0179 ( −0.0656)	0.114 (0.013)
Welfare change	0.00412	0.797	0.637	0.518	0.242	0.859	0.300	0.781	†	†
Spatial error term	0.484	<0.001	0.707	<0.001	0.900	<0.001	0.323	0.007	0.414	<0.001

Bold values show the variables that are significant at the α = 0.05 level. Numbers in brackets are for E1 for voter participation, which had a similar variogram range to E2 for voter participation and so are included in E2 regression.

^*Variogram was pure nugget so factorial kriging of spatial components was not possible.

^†No spatial component exists at this scale.

Modeling using KE increases the proportion of variance explained in the dependent variable from 59% to 68% (Table 3). The apparently better fit may be partly due to working with noise-filtered dependent and independent variables, which have lower overall variances. The significant variables explaining the Poisson kriged estimates of risk are “social change” (but again with the wrong sign), “voter participation,” “population density,” and “non-national population,” all with the expected signs. These results, from which divorce rate had to be excluded, are not directly comparable to those of Ceccato and Haining and draw particular attention to urbanization (“population density”) and social cohesion (“voter participation” and “non-national population”) variables in explaining crime risk.

We now turn to the results obtained from modeling the three scales of variation in crime risk using the corresponding scales of variation in the explanatory variables (excluding “divorce rate”). Modeling TC, the variables “infant mortality,” “social change,” and “voter participation” are significant at the 5% level and explain 84% of the variation (Table 3). Again the sign is wrong for “social change.” The percentage of variation explained in the E1 component is 52%, and the significant variables (Table 3) are “border,” “infant mortality,” “males aged 15–29,” and “population density.” The percentage of the variation explained in the E2 component is 53%, and the significant variables (Table 3) are “GDP,” “infant mortality,” “males aged 15–29,” “natural increase,” and “voter participation.”

The significant variables for explaining the variation in the risk of “car-related theft” at local and regional/national scales (E1 and E2) are those relating to demographic and economic conditions. This finding suggests that countries and subregions that are leading economically and with large proportions of young males tend to have the highest risk of this offense (and hence, are likely to have the highest rates). The association of car crime rates with these explanatory variables has a spatial reach that is both local (the spatial unit and its immediate neighbors) and regional. However, we can go further. Because over 80% of the spatial variation in “car-related theft” as described by its variogram (Table 1) is local, the most important variables explaining this variation are those identified by the MLR for E1. This in turn emphasizes the importance of demographics (proportion of “males aged 15–29”), urbanization (“population density”), social cohesion (“voter participation”), location (“border”), and the variable “infant mortality” (which may be capturing a measure of welfare provision) in explaining the geographical distribution of this offense in the Baltic states, where the association is not just between levels of these variables in the same administrative area but between levels of these variables in contiguous administrative areas. This finding about the importance of the E1 component of variation may be indicative of what are often termed local “spillover effects,” with certain criminogenic conditions in one administrative area spilling over into neighboring areas and affecting their crime rates as well. The negative sign for the coefficient parameter estimate for the “border” variable may be indicating the barrier effect that international borders have on these spillover effects, which is understandable.

The importance of the TC of variation for “car-related theft” is not captured in the variogram; however, its relative importance can be estimated by computing the variance of each set of kriged estimates (E1, E2, and TC) and dividing these by the variance of the kriged risk. When this calculation is done 71%of the variation can be explained by E1, 12% by E2, and 17% by TC. This result suggests that the variables identified as significant locally (E1) are by far the most important and that broad trends in “infant mortality,” “social change,” and “voter participation” are only slightly more important than regional patterns in “GDP,” “infant mortality,” “males aged 15–29,” “natural increase,” and “voter participation” for explaining patterns of “car-related theft.” Interestingly, some variables (“infant mortality,” “voter participation,” and “males aged 15–29”) are significant at more than one scale.

Conclusions

This study demonstrates the use of geostatistics for studying crime data. First, ATA Poisson kriging can be used to filter out the noise in rates caused by the small number problem, which is important for low volume crimes recorded in areas with small populations. Second, ATP Poisson kriging creates a continuous risk surface that reduces the visual bias associated with large administrative units. Third, local cluster analysis of simulated crime rates from ATA and ATP kriging, accounting for population size and multiple testing in the randomization and testing procedures, is helpful in more carefully identifying significant clusters of crimes and pinpointing the most likely clusters. Doing this analysis with ATP Poisson kriged estimates may also give insight into more localized potential “hot spots” that are not evident when areal rates are used.

Correlation and regression analyses using the spatial components obtained from ATA factorial Poisson kriging help to identify the most important spatial scales at which crime rates vary and which explanatory variables are significant at those scales. It also allows visualization of the patterns associated with these different scales, which can give further insight into the independent variables that are associated with high crime rates. The methodology described here provides a way to explore these different scales of spatial variation and associations and offers some advantages over methods that sweep unexplained spatial variation into a single spatially autocorrelated error term or into spatial dummies. A rich set of models also exists that can be called upon for describing the spatial structure in data.

The geostatistical methodology presented here is not without its challenges. First, it cannot circumvent the limitations that arise from the scale at which data have been collected. Any assumptions made about, for example, how population is distributed at a subunit scale need to be acknowledged and, if possible, their validity assessed and their effect on analysis considered. An additional challenge for the present application, which is not likely to be a problem in many other studies, is the existence of nested geographies, which creates an artifact nugget effect when geographical proximity is quantified using distance between centroids. Second, variables may not be amenable to geostatistical analysis if they have no spatial structure—as in the case for the variable “divorce rate.” Third, the methodology has not been widely tested on crime data sets, and the software used (Terraseer STIS) is currently available only as a beta product.