The impact of comparative effectiveness research on health and health care spending

Abstract

Comparative effectiveness research (CER) is thought to identify what works and does not work in health care. We interpret CER as infusing evidence on product quality into markets, shifting the relative demand for products in CER studies. We analyze how shifts in demand affect health and health care spending and demonstrate that CER may raise or lower overall health when treatments have heterogeneous effects, but payers respond with product-specific coverage policies. Among patients with schizophrenia, we calibrate that subsidy policies based on the clinical trial CATIE may have reduced overall health by inducing some patients to switch away from schizophrenia treatments that were effective for them towards winners of the CER.

1. Introduction

Driven by rising costs of health care and growing concern that much of this spending could be reduced without detriment to health, comparative effectiveness research (CER) has been offered as a means to identify what works and does not work in health care. Although not explicitly inclusive of costs, proponents of CER envision better value in health care by eliminating care which is no more effective than cheaper alternatives (FCCCER Report, 2009; IOM, 2009). Indeed, although public technology assessments in the US have been heavily debated in the past,¹ the last several years have witnessed unprecedented public support for CER, most notably through the 2009 American Recovery and Reinvestment Act which allocated about $1 billion towards this research and the 2010 Patient Protection and Affordable Care Act which established a national center to support CER (Clancy and Collins, 2010).

Although CER has been positioned as a means to improve health and potentially lower health care costs, how the market itself will respond to this information and what those responses will mean for health care spending and patient health has not been fully explored. At a first pass, the dissemination of CER may be viewed as an infusion of quality evidence into the market place with predictable market consequences. Winners and losers of CER studies would be expected to face higher and lower demand, respectively, with an impact on total spending that depends on the subsequent prices and quantities of the product and its competitors.

In addition, CER may not only impact market demand of patients and doctors, but may also affect payer coverage policy. For example, health plans may choose to cover only those treatments which are shown to be comparatively effective on average in CER studies, resulting in co-pay or coverage differences between treatments.² How producers of treatments evaluated by CER will respond to such coverage policies makes the expected market response to CER more complex than previously recognized.

The impact of CER on overall patient health, as opposed to health spending, is equally important to understand. By eliminating use of treatments which are ineffective, proponents of CER intuitively argue that health will be improved by CER, or at least not worsened. This seemingly straightforward point fails to consider, however, how overall patient health is affected when patients respond to treatments differently and coverage decisions are product-specific. Under some CER designs, coverage policies responding to average treatment responses may be useful in identifying which treatments to attempt first. However they may preclude important health benefits from accruing to patients for which the losing treatments of CER studies are most appropriate.

In this paper, we develop a quantitative framework to study the impact of CER on patient health and health care spending. Our main contributions are to recognize that the infusion of CER into health care markets will be met by market responses and to analyze the implications of those responses for health and health care spending. These responses will depend on how patients, doctors, and payers react to the new quality evidence generated by CER and whether coverage decisions are based on average effectiveness or other summary statistics that mask individual differences.

The paper may be briefly outlined as follows. Section 2 specifies the model that allows us to explore how the infusion of CER into health care markets will affect the prices, quantities, and spending associated with products evaluated by CER. We first consider responses by patients and doctors to new quality evidence generated by CER studies. Generally, sales of winners of CER studies are expected to rise and sales of losers expected to fall, implying unpredictable effects on total spending. While in competitive markets, new CER evidence will raise overall health by leading patients to substitute towards more effective treatments, the opposite may be true when there is monopoly power. New CER evidence may lead to increases in market power that result in restrictions in quantity that dominate the expansion in demand arising from favorable evidence.

Section 3 extends this analysis to the dissemination of CER in markets with third party payers, where the extent of coverage or co-pays is based on the results of CER. Treatments that fare better under CER would receive better coverage through either less strict formulary restrictions, fewer or no prior authorization requirements, or better tiering. CER now impacts the market in two ways: first, by affecting patients and doctors and second, by impacting third-party payers.

Section 4 explores how overall patient health is impacted when treatments have heterogeneous effects but coverage decisions are product-specific and based on averages which mask those differences. For example, a CER study may favor one treatment, deemed the “winner” by average effectiveness, even though the best treatment varies across patients. When coverage responds to new CER summary statistics, some patients may face higher prices for their best therapy while others will see price reductions. This can have an indeterminate effect on health outcomes which depends on how appropriately patients were matched to treatments prior to the new CER.

Section 5 provides an illustrative empirical simulation of spending and health responses to new CER in the market for anti-psychotic drugs, among the top spending classes overall and, in particular, in Medicaid. The 2006 Clinical Anti-psychotic Trials of Intervention Effectiveness (CATIE trial) generated considerable debate in Medicaid about coverage of second-generation (atypical) anti-psychotics which were shown in the trial to be as effective on average but not more so than cheaper first-generation (typical) anti-psychotics. Using the observed heterogeneity in treatment effects demonstrated by the CATIE trial, we simulate the impact on health outcomes and spending of a Medicaid policy which would cover only the most cost-effective anti-psychotic in the CATIE trial rather than allow patients and physicians to choose the anti-psychotic best suited for a given patient. In this case, we find that the negative impact on health of incorrectly matching patients to treatments outweighs the reduction in spending by an amount valued at 5% of class spending.

Section 6 concludes by discussing future research in quantitative evaluation of CER and how such analysis may inform the development of improved methods for CER.

2. Impact of comparative effectiveness research on doctors and patients

2.1. Basic framework

To illustrate ideas, this section specifies an economic framework for analyzing the impact of CER on health care spending and overall health when treatments are privately purchased and not subsidized by insurance. Our main result is that in competitive markets, CER will increase overall health but will have ambiguous effects on total health spending. In a subsequent section, we extend our theory to markets with insurance.

As a basic setup, consider two competing treatments (i = 1, 2) with effectiveness q₁ and q₂, where effectiveness is defined as average effectiveness (e.g. average increase in life-expectancy) associated with use of a treatment. These treatments may represent first and second generation treatments for a given clinical condition.

We initially assume that a treatment’s true effectiveness does not vary across patients, but that expectations of effectiveness do vary. For example, a treatment may lead to identical improvements in life expectancy across patients but may be perceived by both patients and physicians as having different effectiveness based on prior beliefs and new evidence.

In this framework, demand for a given treatment i can be depicted D_i(p, e) where p = (p₁, p₂) and e = (e₁, e₂) are price and evidence vectors. Market demand for a given treatment will depend not only on its own price and the price of its comparators, but on available quality evidence for all treatments. For example, new favorable evidence on the benefits of a treatment would be expected to increase its own demand while lowering that of its competitors, i.e. dD_i(p, e)/de_i > 0 and dD_j(p, e)/de_i < 0. The impact of favorable new evidence on treatment demand is analogous to the impact of shifts in quality on product demand more generally; demand for higher quality products will rise while demand for competitors will fall.

An example of such a demand function would be a Bayesian updating model of population mean treatment effects. In such a case, the expected effectiveness of treatment i is given by:

$$z_i=(1-w_i)z_i^0+w_i{e}_i$$ (1)

where z_i is expected effectiveness based on prior beliefs ( $z_i^0$), new evidence (e_i), and the weight placed on prior beliefs versus new evidence (w_i).³ New evidence may be CER demonstrating higher life expectancy associated with one treatment relative to its comparator in a randomized controlled trial. Eq. (1) states that new evidence (e) about a treatment will raise expectations about its effectiveness (if $e_i>z_i^0$) as would more precise evidence (higher w).

Consider when patients care about perceived effectiveness of a treatment net of price (p_i) when making a decision between two competing treatments. Assume effectiveness can be denominated in dollars. Treatment 1 would be chosen over treatment 2 whenever its expected effectiveness net of price is greater: z₁ – p₁ ≥ z₂ – p₂ or

$$(1-w_1)z_1^0+w_1{e}_1-p_1\ge (1-w_2)z_2^0+w_2{e}_2-p_2$$ (2)

Treatments are more likely to be chosen when the prior expected benefit is high (e.g. due to direct to consumer advertising or physician detailing), new evidence is more favorable (e) or more precise (w), or prices are low (p). We assume patients are always treated so that the total volume of treatment is fixed.

If there is a population of patients who differs in unobservable prior beliefs and weights according to the distribution H(z⁰, w), the utility maximizing treatment choices of patients in this population will generate market demands for each treatment given by D₁(p, e) and D₂(p, e), both a function of the observable price and evidence vectors.

2.2. Impact of CER on health care spending and health

The infusion of new quality evidence through CER shifts the demand for treatments, D(p, e), and these demand shifts in turn affect health care spending and overall health.⁴ As in any market, the impact of shifts in demand on total spending and quantity will depend on how equilibrium quantities and prices of treatments are affected. Thus, changes in prices and quantities depend not only on the demand response but also on the structure of supply. Importantly, the impact of shifts in demand for treatments that are competitively supplied at marginal cost (e.g. generic drugs) may be different than for treatments that are supplied by producers with potential market power (e.g. branded drugs or devices). We consider each of these cases below.

2.2.1. CER in competitive markets

Equilibrium prices and quantities will be determined by the intersection of supply and demand for each treatment. Recall we first consider the no-insurance case. Denoting equilibrium prices and quantities by (P₁, P₂) and (Y₁, Y₂), respectively, aggregate spending (S) and health (Q) will be given by:

$$\begin{array}{l}S=S_1+S_2=Y_1{P}_1+Y_{2}P2\\ Q=Q_1+Q_2=Y_1{q}_1+Y_2{q}_2\end{array}$$ (3)

Now suppose that the true quality of treatment 1 is greater than treatment 2 (q₁ > q₂) and that new CER evidence e′ is generated in relative favor of treatment 1 so that:

$$e_1^{\prime }\ge e_1\text{and}{e}_2^{\prime }\le e_2$$ (4)

This evidence is assumed valid in the sense that the newly generated evidence on the comparative effectiveness of treatments conforms with the true comparative effectiveness, though this was unknown to the market previously. The introduction of this CER will impact equilibrium quantities of treatments, total spending, and total health. By increasing the relative demand for treatment 1, both the equilibrium quantity of treatment 1 that is demanded ( $Y_1^{\prime }$) and spending on treatment 1 ( $S_1^{\prime }$) will rise, whereas quantity and sales of treatment 2 ( $Y_2^{\prime }$ and $S_2^{\prime }$, respectively) will fall:

$$\begin{array}{l}{Y}_1^{\prime }>Y_1\text{and}{Y}_2^{\prime }<Y_2\\ S_1^{\prime }>S_1\text{and}{S}_2^{\prime }<S_2\end{array}$$ (5)

This will have two general effects. First, because q₁ > q₂, aggregate health will rise (Q′ > Q) as patients switch from less effective treatment 2 to more effective treatment 1. Second, because sales of the winner of CER will rise while sales of the loser will fall, overall spending will be ambiguously affected.

If evidence is measured continuously, the total effect on aggregate health of new CER evidence will be⁵:

$$\text{d}Q=\sum _{i=1,2}{q}_i\sum _{j=1,2}\frac{{\text{d}Y}_i}{{\text{d}e}_j}{\text{d}e}_j=\sum _{i=1,2}{q}_i\sum _{j=1,2}\sum _{k=1,2}\left[\frac{\partial D_i}{\partial P_k}\frac{\partial P_k}{\partial e_j}+\frac{\partial D_i}{\partial e_j}\right]{\text{d}e}_j$$ (6)

In competitive markets, overall health will generally rise (dQ > 0), with the size of the impact depending on the relative qualities of treatments, the direct effects of new evidence on shifting relative demand (∂D/∂e), and the indirect effects of evidence on demand through changing equilibrium prices, (∂D/∂P)(∂P/∂e). When marginal costs are increasing, so that supply is upward sloping, demand shifts due to new evidence will be moderated. Consequently, the overall demand response to evidence should be lower in markets with less elastic supply.

Similarly, the total derivative of aggregate spending with respect to CER evidence will be:

$$\text{d}S=\sum _{i=1,2}{Y}_i\sum _{j=1,2}\frac{\partial P_i}{\partial e_j}{\text{d}e}_j+\sum _{i=1,2}{P}_i\sum _{j=1,2}\frac{\partial Y_i}{\partial e_j}{\text{d}e}_j$$ (7)

This implies CER will generally have an ambiguous effect on aggregate spending because the sales of winners rise and the sales of losers fall in response to new CER evidence. Under certain conditions, however, one can sign this effect. Consider when marginal costs are constant with free entry so that supply is perfectly elastic. Consequently, demand shifts due to new evidence will not have any price effects ∂P/∂e = 0. Thus if the first treatment is more expensive, aggregate spending will rise as patients switch to the more effective, but also more expensive, treatment. Similarly, when the winner of CER is also cheaper, the shift in demand towards the winner will reduce aggregate spending.

As a general rule, under perfectly elastic supply, when expensive treatments are shown to be more effective than previously believed (the first instance considered), total health will rise as will total spending. An illustration of this may be automated implantable cardiac defibrillators (AICDs), expensive devices which have been shown to improve mortality in patients with severe heart failure. Such devices are expensive and cost-effective, but not cost-saving. When treatments that are inexpensive are shown to be more effective than previously thought, total health will again rise but total spending will fall. Generic medications which demonstrate efficacy over expensive branded medications would be an example of treatments that are both effective and cost-saving.

2.2.2. CER in markets with differentiated products and market-power

When a producer of one treatment has market power, the introduction of new CER evidence will continue to have ambiguous effects on total spending but contrary to the competitive scenario, will have ambiguous effects on total health as well. This occurs when CER evidence increases demand for the winner of the CER, thereby potentially leading to restrictions in its quantity.

To illustrate, consider two treatments for a given disease, one of which is a second-generation medication under patent (treatment 2) and the other of which is a first-generation medication off patent (treatment 1). At equilibrium prices P₁(e) and P₂(e), the quantities are:

$$Y_1=D_1(P_1(e),e)\text{and}{Y}_2=D_2(P_2(e),e)$$ (8)

Here, equilibrium in the competitive market for treatment 1 is determined by the intersection of supply and demand, and equilibrium in the monopoly market for treatment 2 is determined by the intersection of marginal revenue and marginal cost.

Unlike the case in which treatment 2 is competitively supplied, new CER evidence favoring the treatment may lead to reductions in quantity if the effect on demand inelasticty generated by the CER (price effect) offsets the direct demand effect of new evidence:

$${\text{d}Y}_2=\sum _{j=1,2}\sum _{k=1,2}\frac{\partial D_2}{\partial P_k}\frac{\partial P_k}{\partial e_j}{\text{d}e}_j+\sum _{j=1,2}\frac{\partial D_2}{\partial e_j}{\text{d}e}_j<0$$ (9)

Intuitively, if new CER evidence confers additional market power for the producer of treatment 2 (thereby making demand for treatment 2 more inelastic and raising price through dP₂/de), the increase in market power may lead to restrictions in quantity that dominate the expansion due to the demand-shift from new favorable CER evidence.

A reduction in the equilibrium quantity of treatment 2 (dY₂ < 0) will reduce overall health according to:

$$\text{d}Q=q_1{\text{d}Y}_1+q_2{\text{d}Y}_2$$ (10)

as patients substitute from the more-effective treatment 2 towards the less-effective treatment 1 (dY₁ + dY₂ = 0 and q₁ < q₂).

This ambiguous impact of CER on aggregate health can be easily demonstrated under constant marginal costs c = (c₁, c₂) for each treatment, in which case equilibrium demand would be given by:

$$Y_1=D_1(c_1,e)\text{and}{Y}_2=D_2(m(e)c_2,e)$$ (11)

where m(e) is the mark-up of price above costs and could depend positively on own-evidence and negatively on cross-evidence.

New CER evidence supporting treatment 2 would shift out demand for treatment 2 and shift in demand for treatment 1, raising the price of treatment 2 and leaving the price of treatment 1 unchanged. If the mark-up were unchanged (i.e. not dependent on evidence), we would obtain our earlier result that the quantity of treatment 2 demanded would rise and the quantity of treatment 1 demanded would fall, thereby raising overall health as patients substitute towards the more effective treatment 2.

If, however, new evidence supporting treatment 2 makes demand more inelastic and raises the mark-up, the equilibrium quantity of treatment 2 may fall. Intuitively, the demand-expanding effect of CER may be dominated by the increase in the monopolist mark-up. In this case, new CER evidence would lower total health by shifting patients away from the more effective branded treatment (2) towards the less effective generic treatment (1).

3. Impact of comparative effectiveness research in markets with insurance

In most countries, including the US, health care is subsidized; producers of treatments receive supply prices that exceed the demand prices paid by patients (e.g. co-pays). In subsidized markets, CER may impact health care spending and health not only through the basic demand shifts of doctors and patients but also through changes in third party subsidies or coverage. For example, treatments that are shown to be more effective than others in CER may be subject to lower co-pays, fewer prior authorization requirements, or more generous reimbursement of manufacturers. Although the American Recovery and Reinvestment Act of 2009 generally discourages the use of CER in guiding Medicare coverage, it does not prohibit it completely (see footnote 4). Moreover, both state Medicaid programs and private insurers have routinely relied on current evidence and costs to determine drug formularies. More generally, the premise of value based insurance design (Fendrick et al., 2001) is to improve overall health by increasing access to proven effective therapies through lower co-payments or fewer restrictions. Such value based designs are therefore intimately linked to the impact of quality evidence generated on therapies.

3.1. CER in competitive markets with value based insurance design

When the ‘winners’ of CER are subsidized, the previously discussed impacts of CER on health care spending and health may be reinforced. For example, reconsider the perfectly competitive case from earlier but now allow for third-party payer subsidies s = (s₁, s₂) for each treatment. For given subsidy levels s(e) that may depend on CER, let the equilibrium quantity be denoted by Y(s(e),e), while supply and demand prices are denoted by P^S(s(e),e) and P^D(s(e),e), respectively. For each treatment, equilibrium is defined by demand and supply prices and quantity that satisfy:

$$\begin{array}{l}{P}^{\text{S}}(s(e),e)=P^{\text{D}}(s(e),e)+s(e)\\ Y(s(e),e)=D(P^{\text{D}}(s(e)),e)=S(P^{\text{S}}(s(e)))\end{array}$$ (12)

We here assume that supply does not depend on evidence as it does not alter the cost of production. It is well known that, ceteris paribus, increasing the subsidy raises the supply price, lowers the demand price, and raises the equilibrium quantity: dP^S/ds ≥ 0, dP^D/ds ≤ 0, dY/ds ≥ 0.

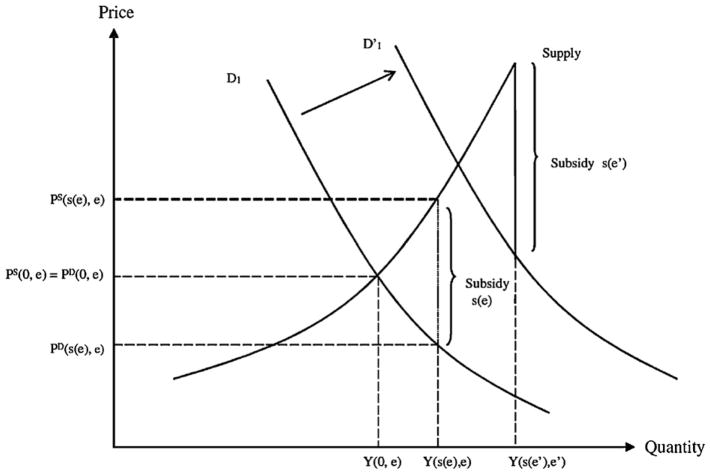
Now suppose that new CER evidence is published which demonstrates a greater effectiveness of treatment 1 over treatment 2. Responding to this information, suppose that third party payers increase the subsidy towards treatment 1 ( $s_1^{\prime }>s_1$) and lower the subsidy towards treatment 2 ( $s_2^{\prime }<s_2$) in attempt to steer patients towards the newly demonstrated more effective treatment 1. For treatment 1, the ‘winner’ of the CER, not only will demand shift outwards as before, but the subsidy for the treatment will also rise. Likewise, for the ‘losing’ treatment 2, not only will demand shift inwards as before, but the subsidy will also fall. These effects are illustrated in Fig. 1.

Fig. 1.

Impact of CER on treatment demand when insurance coverage responds to CER.

Fig. 1 demonstrates the impact on demand and supply for the ‘winning’ treatment of a CER study. Demand for the winning treatment shift outwards, thereby increasing price and quantity, and the subsidy level also increases, reinforcing the effect on price and quantity. More precisely, under common models of the supply side,⁶ the effect on the quantity and supply price of winning treatment 1 ( $Y_1^{\prime }-Y_1$ and ${P^{\prime }}_1^{\text{S}}-P_1^{\text{S}}$, respectively) will be larger when subsidies, in addition to demand, respond to CER evidence. Analogously, the fall in the quantity and supply price of the losing treatment 2 ( $Y_2-Y_2^{\prime }$ and $P_2^{\text{S}}-{P^{\prime }}_2^{\text{S}}$, respectively) will be larger with a negative subsidy response as well. Subsidies which respond to CER will therefore increase overall health compared to private responses alone.

Formally, the impact of CER-based subsidies on overall health can be represented as before:

$$\text{d}Q=\sum _{i=1,2}{q}_i\sum _{j=1,2}\sum _{k=1,2}\sum _{z=1,2}\left[\frac{\partial D_i}{\partial P_k^{\text{D}}}\left[\frac{\partial P_k^{\text{D}}}{\partial s_z}\frac{\partial s_z}{\partial e_j}+\frac{\partial P_k^{\text{D}}}{\partial e_j}\right]+\frac{\partial D_i}{\partial e_j}\right]{\text{d}e}_j$$ (13)

Here, the effect of new CER evidence on equilibrium demand prices is reflected by ∂P_D/∂e = (∂P_D/∂s)(∂s/∂e) + ∂P_D/∂e. In general, CER-based subsidies will lead the winner of CER to experience less of a rise in equilibrium demand price than in the absence of subsidies. Similarly, losers of CER will experience less of a fall, the overall effect being to reinforce the switch of patients towards more effective treatments and therefore greater overall health.

Aggregate spending in a subsidized market will be the sum of patient and third-party spending: S = S₁ + S₂, where $S_i=Y_i\times P_i^{\text{S}}$. With price and quantity responses discussed above, spending on the winners of CER will rise more than before while spending on the losers will fall by more, the overall impact on aggregate spending being indeterminate as before. Generally, the impact of CER evidence on aggregate spending will still depend on whether the ‘winners’ of CER are cheaper or more expensive than the ‘losers.’

Our argument that total health will rise further when the winners of CER are subsidized of course requires that spending on the winning treatment is cost-effective. Indeed, there are many instances in which treatments that are not cost-effective by traditional measures (i.e. costing greater than $100,000 per quality adjusted life year saved) are shown to be more comparatively effective than previously believed. For example, a cancer biologic with an estimated cost-effectiveness ratio of $500,000 per QALY (compared to chemotherapy) may be demonstrated to be more effective than previously believed, thereby lowering its cost-effectiveness ratio to $400,000 per QALY. If this treatment were then (inefficiently) subsidized in light of new and favorable CER, total health may fall if resources are drawn from more cost-effective options and instead devoted to a treatment with little value.

Our framework for studying the impact of CER and CER-based subsidies on health and health care spending shares obvious similarities to work on value based insurance design or VBID (Chernew et al., 2007; Goldman and Philipson, 2007; Pauly and Blavin, 2008). The assumption behind VBID is that patients may have perceptions of treatment effectiveness that differ from actual effectiveness, much like in our model. VBID proposes introducing differential cost-sharing as a way to steer individual patients towards treatments shown to be of value (determined either by cost-effectiveness or sometimes effectiveness alone) in other patients like them. For example, VBID would target patients with a select diagnosis such as congestive heart failure and lower co-payments for high-value treatments such as beta-blockers and angiotensin-converting enzyme inhibitors. In both VBID and our analysis, attempts to create value by steering patients to the most cost-effective treatments would be expected to improve health but not necessarily lower costs, depending on whether treatments that are favored are cost-saving or not. Additionally, Pauly and Blavin (2008) show that “ignorance” of true treatment effects can improve efficiency in the presence of insurance, analogous to our argument that increasing information might lower efficiency.

Beyond this similarity, our analysis of CER differs in important ways from the traditional analysis of VBID. First, VBID mainly concerns demand prices as opposed to payer responses to CER which concern both demand and supply prices. Second, VBID is a normative theory of demand prices whereas our analysis is a positive theory of the health and spending effects of CER under private and public pricing.

3.2. CER in differentiated product markets with market-power and insurance

Our analysis can be extended to the case in which one or more treatments have market power. For example, consider again the scenario in which there are two treatments for a given disease, one of which is a second-generation medication under patent (treatment 2) and the other of which is a first-generation medication off patent (treatment 1). As discussed earlier, in the absence of demand subsidization, new CER evidence favoring treatment 2 may lead to lower overall health if the reduction in demand elasticity induced by CER is enough to dominate the demand-expanding effect of CER. The presence of demand subsidies, however, may tilt the balance in favor of raising overall health by reinforcing the demand-expanding effect of CER. Intuitively, subsidies counteract the effect of market power on equilibrium quantity by lowering prices to patients.

4. Impact of comparative effectiveness research under heterogeneous treatment effects

This section extends the previous analysis of CER by allowing treatments to have heterogeneous effects across patients, so that a treatment may affect the health of individual patients differently. This is the norm in health care, ranging from blood pressure medications which have varying effects by race to targeted cancer drugs which work best in individuals with specific gene mutations. The biologic drug panitumumab, for example, was rejected in Europe in 2007 on the basis of similar average efficacy to pre-existing, less expensive chemotherapy to treat metastatic colorectal cancer. After reviewing initial submission data, however, it was later shown to be effective in patients with a specific normal gene type (known as KRAS) and the drug was ultimately approved for patients with this particular gene type.

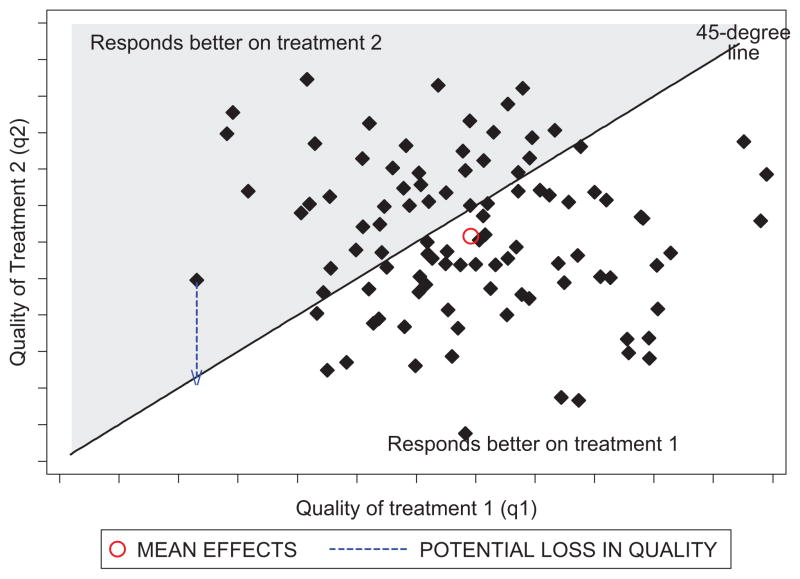
As compared to our earlier analysis, in which subsidies for winners of CER would be expected to further raise total health under perfect competition, such subsidies may adversely affect total health when there is heterogeneity in treatment effects. For example, consider the case when two treatments have a joint distribution of true effectiveness across patients given by F(q₁, q₂). This is illustrated in Fig. 2.

Fig. 2.

Distribution of treatment responses.

A given point in the figure corresponds to the two qualities (q₁, q₂) for a given patient and the distribution of points in the figure corresponds to the distribution F across all patients. The patients below the 45° line benefit relatively more from treatment 1, whereas those above the line benefit more from treatment 2. As revealed in the figure, treatment 1 would be the winner of a CER study based on its larger average treatment effect compared to treatment 2.

Now consider the impact of a policy which subsidizes treatments shown to be most effective on average through CER. The effect of such a policy would be substitution by patients towards treatment 1. Of course, if prior to this CER and subsidy, patients were randomly assigned to treatments, such a policy would raise total health since treatment 1 is more effective, on average, than treatment 2. If, however, patients were already correctly sorted to their most effective treatment (e.g. through trial and error by patients and their physicians), the overall impact on health would be negative as some patients who would benefit more from treatment 2 would switch to treatment 1 due to the subsidized price being lower. More generally, the overall impact on health will depend on the degree of correct self-selection that existed before the subsidy and the extent to which the subsidy leads to substitution away from more effective “losers” of CER studies.

An expression for how CER affects overall health when treatments favored by CER are subsidized and treatments have heterogeneous effects can be derived. As before, conditional on a set of true effects q = (q₁, q₂), demand for each treatment would be a function of price and evidence represented by D₁(p, e|q) and D₂(p, e|q). Patients themselves of course cannot condition on true quality but they are nevertheless faced with the implied treatment effect of their true quality. Aggregate demand of the population would be determined by aggregating the conditional demand functions over all true quality levels q. Thus, aggregate health for patients taking treatment 2 would then be given by:

$$Q_2=\int \int D_2(p,e\mid q)q_2\text{d}F(q\mid q_1\ge q_2)+\int \int D_2(p,e\mid q)q_2\text{d}F(q\mid q_1<q_2)$$ (14)

Aggregate health in the population would therefore be given by Q = Q₁ + Q₂ and the impact of CER on health would depend on how CER leads patients towards treatments that are more or less effective for them individually. In the expression above, the first term represents patients who would benefit from moving to treatment 1 and the second term represents those who would not.

Now consider a policy which subsidizes treatments (like treatment 1) that are demonstrated to be winners of CER studies according to some summary statistic such as an average. Subsidization based on CER will result in a lower relative price of treatment 1 and higher relative price of treatment 2. The impact of this change in relative price will be to induce a subset of patients consuming treatment 2 to switch over to treatment 1 because of the lower relative price. For those patients previously using treatment 2 but for whom q₁ > q₂, total health will be improved, whereas for those patients using treatment 2 for whom q₁ < q₂, the substitution towards treatment 1 will lower total health. The effect on overall health will depend on which of these opposing effects dominates, which in turn will depend on how efficiently allocations occurred prior to the CER and subsequent subsidy. If prior to the subsidy, all patients were matched to the treatments best for them, the unambiguous effect of the subsidy would be to lower total health by inducing substitution of a subset of patients towards treatments less effective for them.

The basic issue raised by our analysis of heterogeneity is that when coverage decisions are responsive to summary evidence produced by CER, price responses lead some patients to switch away from their best treatment and lead others to switch towards their best treatment. This has ambiguous effects on health because CER is used to form product-specific coverage policies, when indeed treatment effects may be patient-specific. Heterogeneity is necessary but not sufficient for this to occur; what is needed is that at least for some set of patients, one treatment is more effective than the other.

5. Calibrating the impact of CER-based coverage in the market for antipsychotics

Using the market for antipsychotic drugs to treat schizophrenia, this section calibrates the potential impact of CER-based subsidies when treatments have heterogeneous effects on patients.

5.1. Interpreting the CATIE trial CER in our framework

Antipsychotic medications represent the primary treatment for patients with schizophrenia and are among the largest drug classes in Medicaid (Bruen and Ghosh, 2004). Beginning in 1990, a second generation of antipsychotic drugs, also known as atypical antipsychotics (AA), was introduced. These drugs were believed to cause less side effects (such as movement disorders) compared to the first generation antipsychotics (also known as “typicals” or neuroleptics) (Kane, 2004; Meltzer, 2009) though more recently, some of the second generation antipsychotics have been linked to increased metabolic side-effects such as weight gain and diabetes (Meltzer, 2005).

Following a series of small comparative effectiveness studies (Polsky et al., 2006; Leucht et al., 2009), a large comparative effectiveness trial – the Clinical Anti-psychotic Trials of Intervention Effectiveness (CATIE trial) – was conducted to evaluate antipsychotics in the U.S. (Lieberman et al., 2005). The CATIE trial found equivalence between the effectiveness of first generation antipsychotic drugs (typical or FGA) and all second generation antipsychotics (atypicals or SGAs) (Lieberman et al., 2005; Rosenheck et al., 2006). Based on these results, many argued that Medicaid should preferentially subsidize FGAs over SGAs (Banthin and Miller, 2006; Rosenheck et al., 2007; NY Times, 2005; Soumerai and Law, 2007). Subsequent to the publication of the CATIE trial, approximately 40% of state-run Medicaid programs instituted prior authorization restrictions on some SGAs (Polinski et al., 2007).

Despite the large impact of the CATIE trial on coverage policies towards antipsychotics, little is known about the quantitative health and spending impacts of these policies. As such, we calibrate how the CER generated by the CATIE trial impacted the health of Medicaid beneficiaries and Medicaid spending on antipsychotics. Our calibration compares overall health and spending in a pre-CATIE environment in which patients and physicians together chose treatments felt to be most effective to a post-CATIE environment in which these same decisions were allowed to occur but atypical antipsychotics were provided either partial or no coverage.⁷

In the context of our prior framework, FGAs are represented by treatment 1 and SGAs are represented by treatment 2. Because SGAs were initially felt to be superior to FGAs on average, the results of the CATIE trial could be construed as FGAs being the ‘winners’ and SGAs the ‘losers’ of the CER. For simplicity and given the poverty of the Medicaid patient population, we assume that without subsidies for either FGAs or SGAs there would be no demand for these therapies, i.e. D₁(c, e) = D₂(c, e) = 0 where c is the vector of marginal costs (c₁, c₂). In this case, all utilization would be determined by subsidy policy and any viable Medicaid market for treatment i would need supply prices $p_i^{\text{S}}$ (provider reimbursement) at or above costs and demand prices $p_i^{\text{D}}$ (patient co-pays) at or below costs. i.e. $p_i^{\text{S}}\ge c_i\ge p_i^{\text{D}}=p_i^{\text{S}}-s_i$, where s_i is the subsidy for treatment i.

Given a set of subsidy levels s = (s₁, s₂) for both classes of antipsychotic treatments prior to the CATIE trial, suppose Medicaid were to respond to the new CER produced by the trial by only covering the winner (in this case, FGAs). This would raise demand prices for SGAs relative to FGAs, thereby reducing the market for the SGAs and expanding the market for the FGAs. Depending on how accurately patients were matched to treatments most effective for them prior to the CATIE trial, the expansion in the market for FGAs and the reduction in the market for SGAs could increase or decrease overall health. Specifically, if pre-CATIE, patients and physicians were at liberty to switch between drugs with ease so that patients could settle on the drug most cost-effective for them, subsidizing one drug over another could lower overall health by artificially lowering the price of a drug that is less effective for some patients. This negative impact on overall health relies, of course, on two assumptions: first, in a pre-CATIE environment, patients were matched with the treatment most effective for them (perhaps through repeated trials of medication options) and second, that the subsidized price would not attract new patients into the antipsychotic market who previously would have utilized no treatment at all.

5.2. Policy scenarios

We calibrate the impact on average health of Medicaid beneficiaries with schizophrenia of alternative CER-based subsidy policies. Based on our prior analysis, differences in overall health between alternative subsidy policies are determined by those Medicaid patients for whom SGA therapy was most effective pre-CATIE but who switched to FGA post-CATIE due to subsidies for this class.

The first policy that we consider is one in which both generations of antipsychotic drugs are fully reimbursed so that the demand prices faced by patients are zero (pre-CATIE environment).⁸ Since the supply price of second-generation drugs is higher, the size of the subsidy for this class is larger than for first generation drugs (s₂ ≥ s₁). Under this policy, demand for each class of drugs is fully determined by heterogeneity in treatment effects: with unrestricted coverage physicians and patients are able to try out alternative drugs and settle on a drug that appears to be most effective for an individual patient.

We compare overall health in this pre-CATIE scenario to two hypothetical post-CATIE scenarios: a partial coverage policy and no-coverage policy for the loser of the CATIE trial (SGAs). Under the partial coverage scenario, only risperidone (a SGA) is covered along with all FGAs, thereby allowing equilibrium quantity demanded for SGAs to be positive. All other second generation drugs are not included in the Medicaid formulary and are therefore not covered. We consider risperidone to be the only atypical reimbursed under the partial coverage policy as it is the only generic SGA available in the market and is consistently in the top tier of preferred drug lists across Medicaid programs.

Under the no-coverage scenario, none of the second generation drugs are covered, i.e. s₂ = 0. Given the low income of the Medicaid population, this is assumed to eliminate demand in this population so that the post-CATIE quantity of SGAs demanded is zero. We include this case not because of its likelihood of adoption, but to trace out the implications of a policy that reimburses only the most effective care. When care that is less effective is not reimbursed, poor individuals cannot access it and this has important health effects under heterogeneity.

5.3. Methods

We evaluate each policy described above over an 18-month period, corresponding to the length of the CATIE trial. We focus on three second generation antipsychotic drugs (risperidone, olanzapine, and quetiapine), as well as one first generation drug, perphenazine. These comprise nearly 70% of the market of antipsychotic prescriptions written in the United States. In order to calculate the number of Medicaid beneficiaries impacted by these alternative policies, we assume the prevalence of schizophrenia among non-elderly Medicaid patients to be 1.66% (Wu et al., 2006). We apply this estimate to the 15 million non-elderly adult Medicaid enrollees to obtain a total number of 250,000 non-elderly adult enrollees with schizophrenia.

In order to calculate overall health in the pre-CATIE era and in both policy scenarios, we begin with a baseline quality of life weight equal to 0.68 for patients with schizophrenia who are not under active relapse. If baseline status-quo could be maintained over the 18-month period considered, there would be an accrual of 1.02 (=0.68 × 1.5) QALYs per patient. Obviously, receipt of effective medications could help improve QALYs, while absence of such could result in decreases in QALYs (via relapse) during this period. We model changes in QALYs during the same 18-month period under alternative policies and add the additional QALYs gained or lost to this baseline accrual level. These additional gains or losses in QALYs are calculated using an area-under-the-curve (AUC) approach based on the time trajectory of quality of life weights under different scenarios. Specifically, we approximate this area with a triangle whose slope is determined by the rate of change in QOL weight over time in each scenario.

Total costs under each policy are calculated from monthly cost estimates from CATIE data and those reported by Rosenheck et al. (2006).

5.3.1. Pre-CATIE scenario

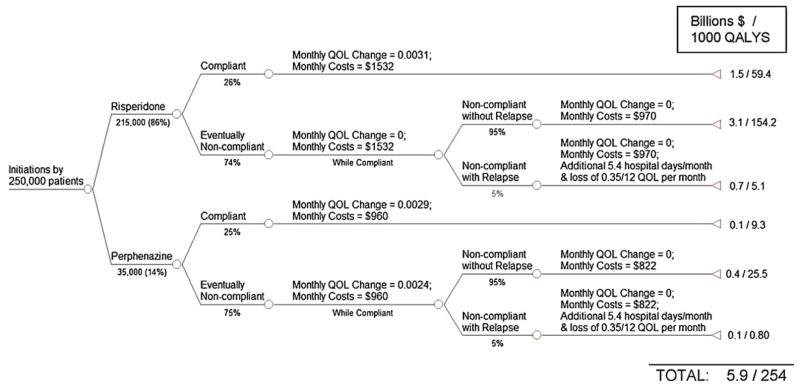
In the pre-CATIE environment, irrespective of the first drug a patient tries, physicians and patients are assumed to be able to switch to alternative drugs that may be more efficacious for that particular patient. We capture the overall effect of these switches using the intention-to-treat rate of change in QOL over time for specific drug initiations from CATIE data (shown in Fig. 3 and summarized in Table A1).⁹ We calculate the proportion of patients initiating antipsychotic treatment with a given drug in the pre-CATIE era using drug-specific prescription shares in 2005 (obtained from IMS Health), a year prior to the CATIE trial. For each drug, this proportion is multiplied by the 250,000 patients in our simulation to arrive at the number of patients initiating antipsychotic treatment with a given drug (Fig. 3).

Fig. 3.

Patterns of utilization and outcomes under the Pre-CATIE policy.

Table A1.

Intention-to-treat effectiveness and cost estimates from CATIE data used for pre-CER policy.

Initial assignment	Effect of initial assignment on average monthly changes in QOL	Effect of initial assignment on average monthly total costs (drugs and services)a	Effect of initial assignment on costs of antipsychotic drugs onlya
Quetiapine	0.0030 (0.0006)a	$1657	$415
Risperidone	0.0028 (0.0005)a	$1529	$440
Olanzapine	0.0030 (0.0005)a	$1428	$595
Perphenazine (typical)	0.0028 (0.0006)a	$1139	$196

^aBased on Rosenheck et al. (2006), Supplemental Table C.

The total health effect generated by a specific drug initiation is calculated by multiplying the number of patients initiated on the drug with the sum of: (1) the baseline QALYs (1.02 QALYs per patient) and (2) the AUC representing deviations in QALYs from baseline = 0.5 × (intention-to-treat monthly rate of change in QOL × 18) × 1.5 years. For example, the 90,000 patients initiated on quetiapine are expected to experience 90,000 × (1.02 + (0.5 × (0.003 × 18) × 1.5)) = 95,445 QALYs. Similar calculations are made for each drug initiation and the total benefits are summed across all the drug initiations.

Total costs in the pre-CATIE environment are calculated by multiplying the number of patients initiated on a drug with the corresponding intention-to-treat monthly costs of total drugs and services costs, as reported by Rosenheck et al. (2006) in their Supplemental Table C (reproduced here in Fig. 3 and Table A1), and summing over 18 months. Of these costs, about 18–34% is due to the use of the antipsychotic medications (Table A1) and the remainder due to utilization of psychiatric services.

5.3.2. Partial coverage scenario

The partial coverage scenario is illustrated in Fig. 4. We assume that all patients who had chosen a SGA to initiate their treatment in the pre-CATIE era would now choose to initiate treatment with risperidone as it is the only atypical covered.

Fig. 4.

Patterns of utilization and outcomes under a partial coverage policy for losers of CER.

Among patients initiating therapy with risperidone, 26% are assumed to find it efficacious and tolerable and continue to take it (estimated from CATIE). The remaining 74% are assumed to discontinue the drug after 5 months (median time to discontinuation estimated from CATIE). Patients initiating therapy with perphenazine are assumed to follow the same route; 25% of patients are assumed to stay on the drug for a full year and 75% discontinue after 6 months. Discontinuers of either perphenazine or risperidone are allowed to switch to the alternative and therefore have a lower relapse rate (we assume 5%) than the 11% reported when no such switching is possible (Weiden and Oltson, 1995).

We estimate separate mixed-effects models to estimate the effect of the initially assigned drug on monthly rate of changes in QOL. For those who continue their initial assignment, we sum QOL changes over the duration of the trial, and for those who do not, only until the time of discontinuation of the initially assigned drug. These estimates are shown in Fig. 4 and summarized in Table A2.

Table A2.

Estimated treatment effectiveness and costs stratified by continuers and discontinuers of initial treatment assignment, used for post-CER responsive policy.

Initial assignment	Effect of initial assignment on average monthly changes in QOL	Effect of initial assignment on average monthly total costsa
		All drugs and services	Services only
	Among those who continued on initial assignment
Quetiapine	0.0027 (0.0008)*	$1478	$962
Risperidone	0.0031 (0.0007)*	$1532	$970
Olanzapine	0.0030 (0.0009)*	$1404	$758
Perphenazine (typical)	0.0029 (0.0009)*	$960	$822
	Among those who discontinued on initial assignment
Quetiapine	0.0019 (0.001)	–
Risperidone	−0.0020 (0.001)	–
Olanzapine	0.0038 (0.001)*	–
Perphenazine (typical)	0.0024 (0.001)	–

Note: Joint test for treatment-time interaction for QOL effect among continuers not significant (p = 0.94); joint test for treatment-time interaction for QOL effect among discontinuers significant (p = 0.015).

^aBased on Rosenheck et al. (2006), Supplemental Table D, crossovers excluded.

^*p-Value < 0.05.

For continuers, we apply the same method as in the pre-CATIE environment, where total QALYs are calculated by multiplying the number of continuers with the sum of: (1) baseline QALY and (2) drug-specific AUC for deviations from baseline QALYs (Fig. 4 and Table A2). For discontinuers who do not relapse into schizophrenia, the deviations from baseline QOL are calculated only up to the month where discontinuation occurs. Thereafter, baseline QOL are assumed to persist (this allows us to obtain a conservative estimate of the adverse effects on health since no further deterioration is accounted for). Patients who relapse into schizophrenia after discontinuation are assumed to spend on average 5.4 additional days per month (valued at $1000/day) in psychiatric hospitals¹⁰ (Ascher-Svanum et al., 2010) and experience a loss in quality of life of 0.35/12 per patient per month over the remaining duration of the 18-month period (Lenert et al., 2004).¹¹

Costs for the compliant groups under each drug initiation are calculated based on estimates of total drugs and services reported by Rosenheck et al. (2006) in their Supplemental Table D, where treatment crossovers were excluded. The same monthly costs are applied to the noncompliant group during the months where they were compliant with the initial assignment. After discontinuation, patients are assumed to continue to accumulate assignment-specific average monthly service costs (but not any drug costs).¹²

Compared to the pre-CATIE scenario, overall health is lower when there is partial coverage because patients who discontinue initial assignments face limited options of alternative medications.

5.3.3. No-coverage scenario

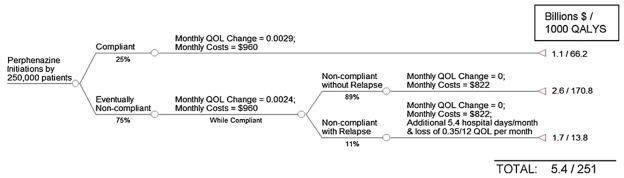
The no-coverage scenario is illustrated in Fig. 5. We assume that all schizophrenia patients initiate antipsychotic treatment with perphenazine and that 25% of these patients find the drug to be efficacious and tolerable and therefore continue on it (based on CATIE). The remaining 75% are assumed to discontinue perphenazine after six months (median time to discontinuation based on CATIE data) but are unable to switch to other drugs due to lack of coverage. These discontinuers are therefore without drug therapy for months following discontinuation of perphenazine. Monthly rates of change in QOL under perphenazine initiation are the same as under the partial-coverage policy (Fig. 5 and Table A2).

Fig. 5.

Patterns of utilization and outcomes under a no-coverage policy for losers of CER.

Calculation of total QALYs and costs are identical to the partial-coverage scenario except that under the no-coverage scenario, 11% of perphenazine discontinuers are assumed to relapse (Weiden and Oltson, 1995) and experience the associated costs as well as an additional loss of (0.35/12) QOL units per patient per month over the remaining duration of the 18-month period (Lenert et al., 2004).

5.4. Results

In the pre-CATIE environment, the added QALYs generated by all treatments over an 18-month period sums to 265,000 QALYs above baseline, while total costs sum to $6.7B (Table 1). Under partial coverage, patients initiating treatment with risperidone generate 218,500 QALYs above baseline and those starting with perphenazine generate 35,500 additional QALYs. This sums to 254,000 QALYs under this scenario at a cost of $5.9B. The no-coverage scenario produces a total of 251,000 QALYs at a cost of $5.4B, mainly due to the severe effect on the quality of life and psychiatric service utilization of those who relapse due to the unavailability of alternate drugs.

Table 1.

Net monetary benefits of various CER-based subsidization policies applied to 250,000 non-elderly adult patients with schizophrenia under Medicaid.

	Added QALYs over baseline	Value of additional QALYS (in $B)	Costs (in $B)	Net monetary benefit ($B)	Incremental net monetary benefit ($B)
Pre-CATIE	265,000	26.5	6.7	19.80
Partial coverage	254,000	25.4	5.9	19.30	−0.50 (vs pre-CATIE)
No coverage	251,000	25.1	5.4	19.70	0.40 (vs partial)

Notes: Partial coverage implies access only to first generation perphenazine or second generation risperidone. No coverage implies access only to first generation perphenazine. Net monetary benefits = Value of QALYs ($B) − Costs ($B).

Table 1 presents the net monetary benefits (Stinnett and Mullahy, 1998) of each of these alternative policies when a QALY is valued at $100,000. Compared to the pre-CATIE era in which drugs were readily substituted, the partial coverage scenario produces a loss in value worth $0.5B over the 18-month period we consider. Based on estimates from the CATIE trial (Table A1), class spending on antipsychotics by Medicaid was $2.0B in this time frame. Therefore, a partial coverage scenario, which most closely resembles the real restrictions placed by many Medicaid programs, would be calculated to generate losses worth 25% of overall class spending. The no-coverage policy, on the other hand, produces a calibrated loss of $0.1B (5% of class spending) compared to the pre-CATIE period. The calibrated loss of $0.1B draws from the monetized reduction in QALYs occurring in the no-coverage environment (14,000 QALYs valued at $1.4B in total) compared to the savings in cost ($6.7B − $5.4B = $1.3B).

Sensitivity analysis varying the QOL effect of relapse reveals that even if we assume the most conservative effect of relapse on QOL (i.e. loss of 0.25/12 QOL per month per patient), partial coverage would entail 255,000 added QALYs compared to baseline whereas no-coverage would entail 253,000 added QALYs. Compared to pre-CATIE, this would amount to a net loss of $0.2B under partial coverage and a net gain of $0.1B under no-coverage.

6. Conclusion

Despite the promise of comparative effectiveness research to improve health and lower cost, little conceptual and empirical understanding exists on how market responses to this research will impact health and health care spending. We analyzed the impact of CER on patient health and health care spending by interpreting new CER as shifting the relative demand for products demonstrated to be most effective. We demonstrated how the impact of CER may vary with both the presence of insurance in markets and market power among producers of treatments. In contrast to commonly held views, our analysis demonstrated instances in which CER may both increase spending and adversely impact overall health under plausible assumptions of how markets respond to the infusion of new quality information. In our analysis of treatment effect heterogeneity, we showed that product specific coverage policies may negatively impact health when they fail to account for patient-specific treatment effects. Illustrating these arguments for one of the largest drug classes in Medicaid, antipsychotics, we calibrated that if subsidies were eliminated for all but one atypical antipsychotic based on results from the landmark CATIE trial, a loss of value at 5% of class spending would be observed.¹³

Although the main conclusion we emphasize is that CER may have unexpected effects on health and health care spending under endogenous market responses, this does not mean that public technology assessments do not have a useful role to play. Our analysis suggests several future research issues that we list here to enable a better understanding of that role.

6.1. Decentralized versus centralized production of evidence

Our analysis of the impact of CER-based subsidies suggests that CER should be focused on obtaining the right treatments for the right sub-populations rather than on the “best” treatment for all patients. “One size fits all” treatment evaluations may be harmful and the main remedy used to account for this is sub-group analysis. However, simply performing sub-group analyses for many demographic groups neither solves the problem of within-group heterogeneity nor the practical bureaucratic issue of reimbursing separate sub-groups differently. More must be understood about how individual-level attempts to learn about treatment effects (e.g. through trial-and-error or “decentralized patient-controlled cross-over trials”) compare to centralized evidence such as publicly funded CER. Of critical importance is the understanding and assessment of how such nuanced comparative information translates to physicians’ and patients’ choices of treatments. Indeed, with efficient transmission of heterogeneity information, demand responses can become less sensitive to prices and consequently may require less stringent coverage (Basu, 2011).

6.2. CER for sequenced care

Traditional RCTs that focus on intention-to-treat effects may not be useful when treatment algorithms for a disease follow sequences, i.e. failure of first-line therapy leads to second-line therapy and so on. RCTs generate marginal distributions of treatment responses, when it would be more valuable to know distributions of second-line treatment responses conditional on failing first-line therapy. If there is dependence in treatment responses, as suggested by the data we considered from the CATIE trial, learning about the joint distribution is of great value (Basu, 2009). CER should be tailored to incorporate such dependence when finding the right treatment for a particular patient, perhaps through trial and error, is important and costly to do in a decentralized manner.

6.3. Procedures versus medical products as the domain for CER

The presence of intellectual property for medical products (drugs, biologics, or devices) provides strong incentive for manufacturers (or their competitors) to generate accurate evidence about the relative quality of their own products compared to others.¹⁴ The contrast is true of procedures which, without patents, have no owners with similar protective interests. In fact, many countries mandate quality evidence be produced for drugs and devices before marketing (e.g. the FDA in the US) though similar mandates are not true of procedural practices (e.g. aggressive procedural management of complications of coronary artery disease versus management by medicines alone). A useful role for public subsidies of CER may therefore be for procedures rather than for products. This is supported by evidence that the share of private funding for technology assessments is higher for patented medical products than for generic products or procedures. Indeed, although procedural CER may lower or raise total spending based on our earlier analysis, health care variations documented by the Dartmouth Atlas suggest that procedural spending could be reduced without sacrificing overall health.

6.4. Endogenous pricing when reimbursement policy is based on CER

Our analysis highlights how producers may respond to new information generated by CER by raising or lowering prices. Cost-effectiveness analysis based on this new information must also adapt to reflect these changes in prices (Jena and Philipson, 2008, 2009; Jena et al., 2010). For example, in response to new CER, manufacturers will likely re-price their products to become or remain eligible for reimbursement. In the case of antipsychotics, the debate about whether second-generation treatments should be reimbursed at par with first-generation treatments is therefore somewhat misguided. Producers of second-generation treatments may endogenously lower prices so that what was not cost-effective to payers before the CER may be cost-effective after. In this case, realized savings from new CER favoring first-generation antipsychotics may be less than anticipated if prices of second-generation antipsychotics were not to change.

6.5. Implications for R&D and product approval

Although we focus on how CER may affect reimbursement policy, a special case of our analysis is how CER affects the approval process. Certain treatments proposed to the FDA for approval may be less effective on average than pre-existing treatments, but may be effective in certain sub-groups. Just as the “one-size-fits-all” approach to CER may negatively impact health by lowering reimbursement for particular treatments, approval decisions based on average effectiveness may completely prevent certain patients from utilizing treatments that would be effective in them and them alone.

In summary, as a better understanding develops on these and related topics, improved evaluation can take place of the value of public technology assessments in general, and CER in particular. As it stands, there are no methods to quantitatively assess the impact of these activities and why they improve on private sector activities aimed at the same purpose. Quantitative frameworks similar to ours may help bridge that gap, making precise assessments of the value of public subsidies for technology assessments feasible and more common. Indeed, the indeterminate impact on health and health care spending of comparative effectiveness research suggests that the “CER of CER” needs to be better understood and deserves more attention by health economists.

Appendix A. Estimates from CATIE analysis

See Tables A1 and A2.