Simultaneous multiple non-crossing quantile regression estimation using kernel constraints

Abstract

Quantile regression (QR) is a very useful statistical tool for learning the relationship between the response variable and covariates. For many applications, one often needs to estimate multiple conditional quantile functions of the response variable given covariates. Although one can estimate multiple quantiles separately, it is of great interest to estimate them simultaneously. One advantage of simultaneous estimation is that multiple quantiles can share strength among them to gain better estimation accuracy than individually estimated quantile functions. Another important advantage of joint estimation is the feasibility of incorporating simultaneous non-crossing constraints of QR functions. In this paper, we propose a new kernel-based multiple QR estimation technique, namely simultaneous non-crossing quantile regression (SNQR). We use kernel representations for QR functions and apply constraints on the kernel coefficients to avoid crossing. Both unregularised and regularised SNQR techniques are considered. Asymptotic properties such as asymptotic normality of linear SNQR and oracle properties of the sparse linear SNQR are developed. Our numerical results demonstrate the competitive performance of our SNQR over the original individual QR estimation.

1. Introduction

Regression is central to statistics. Different from ordinary least squares regression, quantile regression (QR) tries to estimate the conditional quantile function. It was originally introduced by Koenker and Bassett (1978) and has been extensively studied afterwards. It has been applied in many different areas. Interested readers are referred to Koenker (2005) for a comprehensive review on QR.

Many real applications ask for a complete understanding of the conditional distribution of the response given covariates. One approach is to estimate multiple conditional quantile functions. A naive method is to individually estimate different conditional quantile functions. This individual estimation method is simple and easy to carry out. Theoretically different conditional quantile functions should not cross each other according to the basic principle of conditional distribution functions. However, the naive individual estimation may lead to estimated conditional quantile functions that cross each other. Thus, it is desirable to jointly estimate multiple QR with non-crossing constraints embedded. Another important motivation of joint estimation is that multiple quantile functions may share strength among them (Zou and Yuan 2008a). As a result, simultaneous estimation may help to improve the estimation accuracy of an individual quantile function.

In the literature, there exist some techniques addressing the crossing issue of multiple quantile function estimation. He (1997) proposed the location-scale shift model to impose monotonicity across the quantile functions. However, as noted by Neocleousa and Portnoy (2007), even for linear regression quantiles, corresponding models can be much more general. Thus, a more general development of the estimation of non-crossing regression quantiles is needed. Shim, Hwang and Seok (2009) also considered the location-scale model and proposed to estimate both location and scale functions simultaneously by doubly penalised kernel machines to achieve non-crossing of quantiles. Takeuchi, Le, Sears and Smola (2006) proposed to impose non-crossing constraints on the data points. Although their approach can help to reduce the chance of crossing, their data constraints may not ensure non-crossing in the entire covariate space. Takeuchi and Furuhashi (2004) further extended the method of Takeuchi et al. (2006) by using the ε-insensitive check function in the support vector machine framework. Recently, Wu and Liu (2009) proposed a stepwise procedure to perform the estimation of multiple non-crossing QR functions. Despite improvement over individually estimated quantile functions, the stepwise procedure does not produce a simultaneous estimation. In a recent paper, Bondell, Reich and Wang (2010) proposed an method for non-crossing quantile regression curve estimation using spline-based constraints.

For nonparametric non-crossing quantile estimation, several people have proposed to first estimate the conditional cumulative distribution function via local weighting and then invert it to obtain the quantile curve. Yu and Jones (1998) suggested a double kernel smoothing method with a minor modification of this estimate in a second step, so that the corresponding quantile curves are monotone. Hall, Wolff and Yao (1999) proposed an adjusted Nadaraya-Watson estimate, which modifies the weights of the Nadaraya–Watson estimate such that the resulting estimate of the conditional distribution function is monotone. Chernozhukov, Fernandez-Val and Galichon (2009) proposed to estimate non-crossing quantile curves via a monotonic rearrangement of the original non-monotone function. They also studied the asymptotic behaviour of their bootstrap-type method. Dette and Volgushev (2008) proposed a similar approach to achieve non-crossing quantile curves via solving the problem of inversion and monotonisation on the initial estimates. Although these indirect approaches are effective in obtaining nonparametric quantile curves without crossing, it can be difficult to quantify the effect of the predictors. For instance, if variable selection is a desirable goal, a direct approach is needed to estimate multiple non-crossing quantiles.

In this paper, we propose a new method to perform simultaneous estimation of multiple non-crossing conditional quantile functions. We call the method simultaneous non-crossing quantile regression (SNQR). We employ simple constraints on the kernel coefficients which can guarantee the estimated conditional quantile functions never cross each other. This kernel formulation covers both linear and nonlinear models. Furthermore, we demonstrate that through sharing strength among different quantiles, SNQR can produce better estimation than individually estimated quantile functions. We have also developed asymptotic normality of linear SNQR and oracle properties of the sparse linear SNQR.

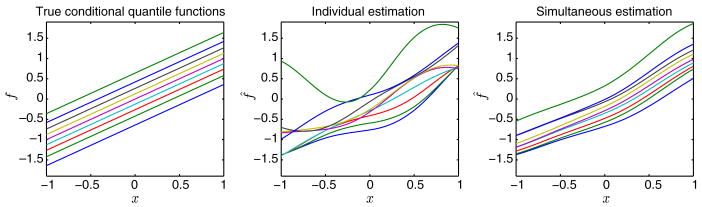
To illustrate the effect of quantile crossing and the benefit of joint estimation, we consider a simple illustrating one-dimensional toy example. Consider the underlying model Y = X + ε, where X ∼ Uniform[−1, 1] and ε ∼ N(0, 0.25) are independent of each other. Figure 1 displays the true and estimated quantile functions based on a simulated data set of size 40 using individual and joint estimations, respectively. The Gaussian kernel was used for the estimation. From the plots, we can clearly see that individual estimation has severe quantile crossing, while our SNQR does not. More importantly, it appears that the individual estimation performs poorly for small or large τ values such as 0.1 and 0.9. In contrast, through the joint estimation, our proposed SNQR gives much improvement on the estimation of all quantile functions.

Figure 1.

Illustration plot of quantile crossing of individual estimation and quantile non-crossing of the proposed SNQR estimation on the one-dimensional toy example. The left panel displays the true quantile functions for τ = 0.1, 0.2, …, 0.9. The middle and right panels display the estimation results of the original individual and proposed simultaneous estimation of the nine quantiles for one data realisation.

The rest of this article is organised as follows. In Section 2, we briefly review the standard QR and then introduce the proposed SNQR. In Section 3, we develop the asymptotic properties of a linear SNQR. We demonstrate the numerical performance of our proposed SNQR using simulations in Section 4 and the baseball data example in Section 5. Some final discussion is given in Section 6. Proofs of theoretical results are collected in the appendix.

2. Methodology

In this section, we first briefly review the standard QR and then introduce the proposed SNQR. In this paper, we use the kernel representation for quantile functions and embed non-crossing constraints on the kernel coefficients. Due to the use of kernel formulation, we first introduce the nonlinear version in Section 2.1, followed by the linear case in Section 2.2.

Suppose that we are given a sample {(x_i, y_i), i = 1, 2, …, n} with covariates x_i ∈ 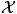⊂ ℝ^d and the response y_i ∈ ℝ. The conditional τth quantile function f_τ(x) is defined such that

$$P(Y\le f_{\tau }(\mathit{x})\mid \mathit{X}=\mathit{x})=\tau$$ (1)

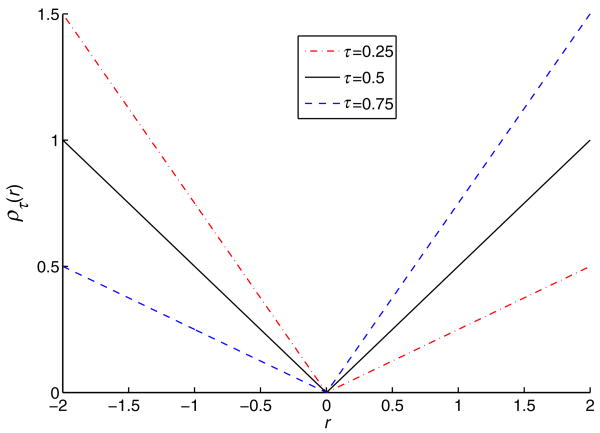
for 0 < τ < 1. By tilting the absolute loss function, Koenker and Bassett (1978) introduced the check function which is defined as ρ_τ (z) = z(τ − I(z < 0)) and illustrated in Figure 2. Here I(·) denotes the indicator function. Further they demonstrated in their seminal paper (Koenker and Bassett 1978) that the τth conditional quantile function can be estimated by solving

Figure 2.

Plot of the check function for three different values of τ.

$$\underset{f_{\tau }\in ℱ}{min}\sum _{i=1}^n{\rho }_{\tau }(y_i-f_{\tau }({\mathit{x}}_i)).$$ (2)

Depending on how large the function space 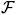is, a regularisation term may be necessary to avoid over-fitting and improve generalisation ability as considered in Koenker, Ng and Portnoy (1994) and Koenker (2004). Namely, we add a roughness penalty term J(f_τ) and solve

$$\underset{f_{\tau }\in ℱ}{min}\sum _{i=1}^n{\rho }_{\tau }(y_i-f_{\tau }({\mathit{x}}_i))+\lambda J(f_{\tau }),$$ (3)

where λ is a tuning parameter balancing the data fitting measured by the check function and the complexity of f_τ(·) measured by the roughness penalty J(f_τ). The kernel QR by Li, Liu and Zhu (2007) fits in the form of Equation (3).

Although QR works well for estimating a quantile function for any particular τ, in certain scenarios, it is desirable to estimate multiple conditional quantile functions simultaneously. For example, one may be interested in estimating K quantile functions for 0 < τ₁ < τ₂ < ⋯ < τ_K < 1. A naive way is to estimate f_τk(·) individually by solving Equation (2) or (3) one at a time to get estimates f̂_τk, k = 1, 2, …, K. Despite its simple implementation, there are some drawbacks with the naive approach. First of all, in theory, different quantiles should not cross each other. However, the naive estimates may suffer from quantile crossing for the finite sample case, especially when the sample size is small. Secondly, the naive estimation cannot share the strength of other quantile estimation due to the individual estimation scheme. Therefore, it is desirable to have a joint estimation technique which can ensure non-crossing of different quantiles and also improve the estimation accuracy of the quantile functions.

In this section, we propose a new general method that guarantees non-crossing of the estimated multiple quantile functions. Our method is based on the use of kernel representation of quantile functions. To introduce the proposed technique, we first discuss the nonparametric case using a Mercer kernel. Then we extend our method to the parametric linear case. For both cases, we assume that our input domain 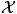is bounded. This bounded domain assumption is natural and necessary for our nonparametric technique. Even for the linear case, the bounded domain assumption is very reasonable due to the fact that two linear lines will eventually cross each other in ℝ^d unless they are parallel.

2.1. Nonlinear case

For a Mercer kernel function K(·, ·), the representer theorem (Kimeldorf and Wahba 1971) allows us to represent the τth quantile function by $f_{\tau }(\mathit{x})={\sum }_{i=1}^n{w}_{\tau ,i}K({\mathit{x}}_i,\mathit{x})+b_{\tau }$. Our key observation is that for two quantile functions f_τ1 and f_τ2, if the kernel function is non-negative with K(·, ·) ≥ 0, then we have f_τ1(x) ≤ f_τ2(x) for any x ∈ 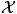if w_τ1,i ≤ w_τ2,i; i = 1, …, n and b_τ1 ≤ b_τ2. One typical example of non-negative kernels is the Gaussian kernel with K(x₁, x₂) = exp(−‖x₁ − x₂‖²/σ²), where σ² is the kernel parameter. Using this observation, we can use simple constraints on the kernel coefficients to jointly estimate K kernel-based quantile functions without crossing.

Using the additional constraints, our SNQR technique estimates the QR coefficients by solving the following joint optimisation problem

$$min\sum _{k=1}^K\sum _{i=1}^n{\rho }_{{\tau }_k}\left(y_i-\sum _{j=1}^n{w}_{{\tau }_{k,}j}K({\mathit{x}}_j,{\mathit{x}}_i)-b_{{\tau }_k}\right)+\lambda \sum _{k=1}^K{w}_{{\tau }_k}^{\mathrm{T}}{\mathit{Kw}}_{{\tau }_k},$$ (4)

$$\text{subject}\text{to}{b}_{{\tau }_k}\le b_{{\tau }_{k+1}}\text{for}k=1,2,\dots ,\mathit{K}-1,$$ (5)

$$w_{{\tau }_k,i}\le w_{{\tau }_{k+1},i}\text{for}i=1,2,\dots ,n;k=1,2,\dots ,K-1,$$ (6)

where w_τk = (w_τk,1, w_τk,2, …, w_τk,n)^T and K is a matrix of size n × n with its (i, j) element being K(x_i, x_j). Here the regularisation term for the kth quantile function is ${\mathit{w}}_{{\tau }_k}^{\mathrm{T}}{\mathit{Kw}}_{{\tau }_k}$ as a consequence of the representer theorem (Kimeldorf and Wahba 1971).

Note that the set of simple constraints (5) and (6) can guarantee the non-crossing of the estimated quantile functions as long as K(·, ·) ≥ 0. Here we want to note that the non-negativity assumption on the kernel K(·, ·) is not essential. According to Scholkopf and Smola (2002), K(·, ·) + C is a Mercer kernel as long as K(·, ·) is a Mercer kernel and C ≥ 0. Thus, for any Mercer kernel K(·, ·), we define K₊(·, ·) = K(·, ·) − K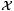, where K 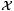= min{0, inf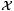_{x∈ ,x′∈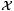} K(x, x′)}. Then the new kernel K₊ (·, ·) satisfies the non-negativity assumption. Denote the solution to Equation (4) by ${\widehat{w}}_{{\tau }_k,i}^{+}$ and ${\widehat{b}}_{{\tau }_k}^{+}$ when the new kernel K₊(·, ·) is used. Our estimated conditional quantile functions are given by ${\widehat{f}}_{{\tau }_k}(\mathit{x})={\sum }_{i=1}^n{\widehat{w}}_{{\tau }_k,i}^{+}{K}_{+}({\mathit{x}}_i,\mathit{x})+{\widehat{b}}_{{\tau }_k}^{+}={\sum }_{i=1}^n{\widehat{w}}_{{\tau }_k,i}^{+}K({\mathit{x}}_i,\mathit{x})-\left({\sum }_{i=1}^n{\widehat{w}}_{{\tau }_k,i}^{+}\right)K_{\mathcal{X}}+{\widehat{b}}_{{\tau }_k}^{+}$ for k = 1, 2, …, K. Note that our estimate f̂_τk(x) can still be expressed in terms of the original kernel K(·, ·) that we begin with.

As a remark, we note that the objective function (4) aggregates the check function losses for different τ's and treats them equally. However, the value of ${\sum }_{i=1}^n{\rho }_{{\tau }_k}(y_i-{\sum }_{j=1}^n{w}_{{\tau }_k,j}K({\mathit{x}}_j,{\mathit{x}}_i)-b_{{\tau }_k})$ may not be on the same scale for different τ's. Equal treatments of the loss function for different τ may be suboptimal. The following proposition gives the expected value of the check function when the error term is normally distributed.

Proposition 1

Let ε ∼ N(0, 1) and denote Φ⁻¹(τ) as the τth quantile of ε, where Φ(·) is the CDF of N(0, 1). Then, we have

$$E[{\rho }_{\tau }(\epsilon -{\mathrm{\Phi }}^{-1}(\tau ))]=\varphi ({\mathrm{\Phi }}^{-1}(\tau )),$$

where ϕ(·) is the density of N(0, 1).

Proposition 1 indicates that the expected value of the check function can vary greatly with different τ's. In the Gaussian case, the expected check function varies in the same way as the Gaussian density. In particular, the value for τ = 0.5 is the largest and it decreases as τ gets closer to 0 or 1. If we treat them equally, then those with τ around 0.5 will receive much larger emphasis than other quantiles. The quantiles with very small or large τ's tend to be ignored. To fix this problem, one can use weight adjustment for different quantiles. In particular, we can extend the objective function in Equation (4) to a weighted version as follows:

$$\sum _{k=1}^K{W}_k\sum _{i=1}^n{\rho }_{{\tau }_k}\left(y_i-\sum _{j=1}^n{w}_{{\tau }_{k,}j}K({\mathit{x}}_j,{\mathit{x}}_i)-b_{{\tau }_k}\right)+\lambda \sum _{k=1}^K{\mathit{w}}_{{\tau }_k}^{\mathrm{T}}{\mathit{Kw}}_{{\tau }_k},$$ (7)

where W_k is the weight for the τ_kth quantile. In this paper, we consider two different weight vectors: equal weights and Gaussian-induced weights with W_k = 1/ϕ(Φ⁻¹(τ)). The Gaussian-induced weight can help to correct the scale difference of the check loss function for different quantiles when the error is normal. Even when the error distribution is not normal, the Gaussian-induced weight provides a helpful adjustment for different quantile estimations. Furthermore, if some prior knowledge on the error distribution is available, then the corresponding weight can be adjusted accordingly.

2.2. Linear case

Different from nonlinear learning, we assume a parametric conditional quantile function f_τ = x^T β_τ + β_0τ in linear learning. However, the linear conditional quantile estimation can be achieved in the kernel representation framework using the linear kernel $L({\mathit{x}}_1,{\mathit{x}}_2)={\mathit{x}}_1^{\mathrm{T}}{\mathit{x}}_2$ and assuming $f_{{\tau }_k}(\mathit{x})={\sum }_{i=1}^n{w}_{{\tau }_k,i}L({\mathit{x}}_i,\mathit{x})+b_{{\tau }_k}$. These two representations are equivalent in the sense that ${\mathit{\beta }}_{{\tau }_k}={\sum }_{i=1}^n{w}_{{\tau }_k,i}{\mathit{x}}_i$ and β_0τk = b_τk.

Note that the linear kernel $L({\mathit{x}}_1,{\mathit{x}}_2)={\mathit{x}}_1^{\mathrm{T}}{\mathit{x}}_2$ does not satisfy the non-negativity assumption in general. As discussed above, we can define a new kernel L₊(·, ·) = L(·, ·) − L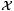, where $L_{\mathcal{X}}=min\{0,\underset{{\mathit{x}}_1\in \mathcal{X},{\mathit{x}}_2\in \mathcal{X}}{inf}L({\mathit{x}}_1,{\mathit{x}}_2)\}$. Then L₊(·, ·) is a well-defined Mercer kernel and also satisfies the non-negativity assumption. With the new kernel L₊(·, ·), we can formulate our linear QR by defining $f_{\tau }(\mathit{x})={\sum }_{i=1}^n{w}_{\tau ,i}{L}_{+}({\mathit{x}}_i,\mathit{x})+b_{\tau }$ with slight abuse of notations. In this way, linear QR without crossing can be achieved by solving

$$min\sum _{k=1}^{\mathit{K}}{W}_k\sum _{i=1}^n{\rho }_{{\tau }_k}\left(y_i-\sum _{j=1}^n{w}_{{\tau }_{k,}j}{L}_{+}({\mathit{x}}_j,{\mathit{x}}_i)-b_{{\tau }_k}\right),$$ (8)

$$\text{subject}\text{to}{b}_{{\tau }_k}\le b_{{\tau }_{k+1}}\text{for}k=1,2,\dots ,K-1,$$ (9)

$$w_{{\tau }_k,i}\le w_{{\tau }_{k+1},i}\text{for}i=1,2,\dots ,n;k=1,2,\dots ,K-1.$$ (10)

In terms of the original linear kernel $K({\mathit{x}}_1,{\mathit{x}}_2)={\mathit{x}}_1^{\mathrm{T}}{\mathit{x}}_2$ the linear quantile function can be rewritten as $f_{\tau }(\mathit{x})={({\sum }_{i=1}^n{w}_{\tau ,i}{\mathit{x}}_i)}^{\mathrm{T}}\mathit{x}-({\sum }_{i=1}^n{w}_{\tau ,i})L_{\mathcal{X}}+b_{\tau }$.

One interesting point is that our kernel representation of linear quantile functions is equivalent to the other parametric representation f_τ(x) =x^Tβ_τ + β_0τ via the connection ${\beta }_{\tau }=({\sum }_{i=1}^n{w}_{\tau ,i}{\mathit{x}}_i)$ and ${\beta }_{0\tau }=-({\sum }_{i=1}^n{w}_{\tau ,i})L_{\mathcal{X}}+b_{\tau }$. This connection allows us to apply techniques for linear QR. For example, we can incorporate various penalties in linear QR that are capable of variable selection.

Another approach to estimate linear non-crossing quantile functions is to use the parametric representation f_τ(x) = x^T β_τ + β_0τ directly. Suppose 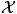= [0, ∞)^d. Then linear non-crossing QR functions can be obtained by solving

$$min\sum _{k=1}^K{W}_k\sum _{i=1}^n{\rho }_{{\tau }_k}(y_i-{\mathit{x}}_i^{\mathrm{T}}{\mathit{\beta }}_{{\tau }_k}+{\beta }_{0{\tau }_k}),$$ (11)

$$\text{subject}\text{to}{\beta }_{0{\tau }_k}\le {\beta }_{0{\tau }_{k+1}}\text{for}k=1,2,\dots ,K-1,$$ (12)

$${\beta }_{{\tau }_k,j}\le {\beta }_{{\tau }_{k+1},j}\text{for}j=1,2,\dots ,d;k=1,2,\dots ,K-1.$$ (13)

The constraints here ensure quantile functions with larger τ's to be always above of those with smaller τ's to prevent crossing.

As a remark, we note that the kernel representation (8) requires (K − 1)(n + 1) inequality constraints while the linear parametric representation (11) requires (K − 1)(d + 1) inequality constraints. For low-dimensional problems with d < n, the formulation (11) can be easier to solve as it involves fewer constraints. In contrast, the formulation (8) is more preferable for high-dimensional low sample-size problems with d > n.

2.3. Variable selection for linear quantile functions

Variable selection plays an important role in the model-building process. In practice, it is very common to have a large number of candidate predictor variables available. These variables can be included in the initial stage of modelling for the consideration of removing potential modelling bias (Fan and Li 2001). However, it is undesirable to keep irrelevant predictors in the final model since this makes it difficult to interpret the resulting model and may decrease its predictive ability.

In the regularisation framework, many different types of penalties have been introduced to achieve variable selection. The L₁ penalty was used in the least absolute shrinkage and selection operator (LASSO) proposed by Tibshirani (1996) for variable selection. Zou (2006) proposed the adaptive LASSO to improve the original LASSO. Fan and Li (2001) proposed the smoothly clipped absolute deviation (SCAD) function and also studied its oracle properties in the penalised likelihood setting. For the QR, Koenker (2004) applied the LASSO penalty to the mixed-effect QR model for longitudinal data to encourage shrinkage in estimating the random effects. One important special case of QR with τ = 0.5, the least absolute deviation regression, was studied by Wang, Li and Jiang (2007). Li and Zhu (2008) developed an algorithm to derive the entire solution path of linear L₁ QR. Wu and Liu (2008) studied both the adaptive L₁ and SCAD QR and developed the corresponding oracle properties. They also developed the difference convex algorithm (Liu, Shen and Doss 2005) for the SCAD penalised methods.

For variable selection in multiple quantile estimation, Zou and Yuan (2008b) proposed a hybrid of L₁ and L_∞ penalties to perform variable selection. The sup-norm is applied on the coefficients of the same variable for multiple quantile functions to encourage simultaneous sparsity. A similar sup-norm penalty was used by Zhang, Liu, Wu and Zhu (2008) for variable selection in multicategory support vector machines. To achieve simultaneous variable selection for multiple quantile functions, we also consider a sup-norm type of penalty to achieve simultaneous variable selection. One fundamental difference of our approach from the approach by Zou and Yuan (2008b) is that their approach cannot guarantee non-crossing of different quantile functions. Using the connection of ${\mathit{\beta }}_{\tau }={\sum }_{i=1}^n{w}_{\tau ,i}{\mathit{x}}_i$, we propose to solve the penalised version of Equations (8)–(10) as follows:

$$min\sum _{k=1}^K{W}_k\sum _{i=1}^n{\rho }_{{\tau }_k}\left(y_i-\sum _{j=1}^n{w}_{{\tau }_k,j}{L}_{+}({\mathit{x}}_j,{\mathit{x}}_i)-b_{{\tau }_j}\right)+\sum _{j=1}^d{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|\sum _{i=1}^n{w}_{{\tau }_k,i}{x}_{ij}\right|\right),$$ (14)

$$\text{subject}\text{to}{b}_{{\tau }_k}\le b_{{\tau }_{k+1}}\text{for}k=1,2,\dots ,K-1,$$ (15)

$$w_{{\tau }_k,i}\le w_{{\tau }_{k+1},i}\text{for}i=1,2,\dots ,n;k=1,2,\dots ,K-1,$$ (16)

where p_λ(·) is a general penalty function with the regularisation parameter λ. Similar to the nonlinear case in Section 2.1, constraints (15) and (16) can guarantee that our estimated linear conditional quantile functions do not cross each other in the bounded input space .

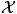Similar to the kernel version, we can also extend the parametric linear formulation in Equations (11)–(13) with penalties as follows:

$$min\sum _{k=1}^K{W}_k\sum _{i=1}^n{\rho }_{{\tau }_k}(y_i-{\mathit{x}}_i^{\mathrm{T}}{\mathit{\beta }}_{{\tau }_k}+{\beta }_{0{\tau }_k})+\sum _{j=1}^d{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_{{\tau }_k,j}|\right),$$ (17)

$$\text{subject}\text{to}{\beta }_{0{\tau }_k}\le {\beta }_{0{\tau }_{k+1}}\text{for}k=1,2,\dots ,K-1,$$ (18)

$${\beta }_{{\tau }_k,j}\le {\beta }_{{\tau }_{k+1},j}\text{for}j=1,2,\dots ,d;k=1,2,\dots ,K-1.$$ (19)

In this paper, we used the SCAD penalty (Fan and Li 2001); however, many other penalty functions can be adopted here. The SCAD penalty is mathematically defined in terms of its first-order derivative and is symmetric around the origin. For θ > 0, its first-order derivative is given by

$$p_{\lambda }^{\prime }(\theta )=\lambda \left\{I(\theta \le \lambda )+\frac{(a\lambda -\theta )+}{(a-1)}I(\theta >\lambda )\right\},$$ (20)

where a > 2 and λ > 0 are tuning parameters. Note that the SCAD penalty function is symmetric, non-convex on [0, ∞) and singular at the origin.

2.4. Computation

Computation of the proposed SNQR can be done in a similar way as the original unregularised and regularised QR. For example, problems (4) and (8) can be implemented using quadratic programming and linear programming (LP), respectively. For problem (14), in order to handle the SCAD penalty, we make use of the local linear approximation algorithm proposed by Zou and Li (2008). In particular, at each step with the current solution w̃_τk,i, we replace $p_{\lambda }({max}_{k=1}^K|{\sum }_{i=1}^n{w}_{{\tau }_k,i}{x}_{ij}|)$ by

$$p_{\lambda }^{\prime }\left(\underset{k=1}{\overset{K}{max}}\left|\sum _{i=1}^n{\stackrel{\sim }{w}}_{{\tau }_k,i}{x}_{ij}\right|\right)\left(\underset{k=1}{\overset{K}{max}}\left|\sum _{i=1}^n{w}_{{\tau }_k,i}{x}_{ij}\right|\right).$$ (21)

To simplify Equation (21), we introduce a slack variable η_j to simplify the max function. In particular, we modify Equation (21) as

$$p_{\lambda }^{\prime }\left(\underset{k=1}{\overset{K}{max}}\left|\sum _{i=1}^n{\stackrel{\sim }{w}}_{{\tau }_k,i}{x}_{ij}\right|\right){\eta }_j,$$ (22)

subject to

$${\eta }_j\ge \sum _{i=1}^n{w}_{{\tau }_k,i}{x}_{ij},{\eta }_j\ge -\sum _{i=1}^n{w}_{{\tau }_k,i}{x}_{ij};\text{for}k=1,\dots ,K.$$

Then using approximation (22), problem (14) can be solved using the iterative LP. Similarly, the parametric penalised version (17)–(19) can also be computed using the iterative LP.

3. Theoretical properties

In this section, we consider the theoretical properties of our non-crossing linear conditional quantile estimates presented above. To that end, we first consider the standard unpenalised and penalised linear QR without non-crossing constraints. Then we investigate the behaviour of the constraints as n grows to infinity to explore the theoretical properties of the new proposed technique.

3.1. Asymptotic normality of unconstrained and constrained linear QR

We first consider the unpenalised version by establishing asymptotic properties of the solution to Equation (8). Without the non-crossing constraints, it is equivalent to the naive individual estimate by solving

$$\underset{{\mathit{\beta }}_{{\tau }_k},{\beta }_{0{\tau }_k}}{min}\sum _{i=1}^n{\rho }_{{\tau }_k}(y_i-{\beta }_{0{\tau }_k}-{\mathit{x}}_i^{\mathrm{T}}{\mathit{\beta }}_{{\tau }_k})$$ (23)

one at a time for each k = 1, 2, …, K. Denote the optimal solution of Equation (23) by β̃_0τk and β̃_τk.

Define 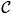_n to be an event that individually estimated conditional quantile functions, obtained by solving Equation (23) with a random sample of size n, cross each other, namely, there exist k and x ∈ 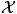such that ${\stackrel{\sim }{\beta }}_{0{\tau }_k}+{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}^{\mathrm{T}}\mathit{x}>{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}+{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}^{\mathrm{T}}\mathit{x}$. We prove that P( 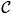_n) → 0 as n → ∞ by showing P( 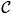_n) decays exponentially in n.

As in Koenker (2005, p. 120), we consider a general form of the linear quantile model. Let Y₁, Y₂, … be independent random variables with distribution functions F₁, F₂, … and suppose that the τth conditional quantile function is linear in the covariate vector x by assuming

$$Q_{Y_i}(\tau \mid \mathit{x})={\beta }_0(\tau )+{\mathit{x}}^{\mathrm{T}}\mathit{\beta }(\tau ).$$

The conditional distribution functions of the Y_i's will be written as P(Y_i < y∣x_i) = F_Yi(y∣x_i) = F_i(y), and then

$$Q_{Y_i}(\tau \mid {\mathit{x}}_i)=F_{Y_i}^{-1}(\tau \mid {\mathit{x}}_i)\equiv {\xi }_i(\tau ).$$

To proceed, we assume that the following two conditions are satisfied.

Condition A: The distribution functions {F_i} are absolutely continuous, with continuous densities f_i(·) uniformly bounded away from 0 and ∞ at points {ξ_i(τ₁), ξ_i(τ₂), …, ξ_i(τ_K)}, i = 1, 2, ….

Condition B: There exist positive-definite matrices Σ₀ and Σ₁ (τ_k) for k = 1, 2, …, K such that

1. $$\underset{n\to \infty }{lim}{n}^{-1}\sum _{i=1}^n{\stackrel{\sim }{\mathit{x}}}_i{\stackrel{\sim }{\mathit{x}}}_i^{\mathrm{T}}={\sum }_0.$$
2. $$\underset{n\to \infty }{lim}{n}^{-1}\sum _{i=1}^n{f}_i({\xi }_i({\tau }_k)){\stackrel{\sim }{\mathit{x}}}_i{\stackrel{\sim }{\mathit{x}}}_i^{\mathrm{T}}={\sum }_1({\tau }_k).$$
3. $$\underset{i=1,2,\dots ,n}{max}\frac{\Vert {\mathit{x}}_i\Vert }{\sqrt{n}}\to 0,$$

where ${\stackrel{\sim }{\mathit{x}}}_i={(1,{\mathit{x}}_i^{\mathrm{T}})}^{\mathrm{T}}$.

Recall that the naive individual estimate is denoted by β̃_0τk and β̃_τk. Denote the corresponding true parameters by β₀(τ_k) and β(τ_k). Our non-crossing estimates are denoted by β̂_0τk and β̂_τk.

Lemma 1

Under conditions A and B, as n → ∞, the naive individual estimates have the following asymptotic normality

$$\sqrt{n}\left[\left(\begin{array}{c}{\stackrel{\sim }{\beta }}_{0{\tau }_k}\\ {\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}\end{array}\right)-\left(\begin{array}{c}{\beta }_0({\tau }_k)\\ \mathit{\beta }({\tau }_k)\end{array}\right)\right]\to N(\mathbf{0},{\tau }_k(1-{\tau }_k){\sum }_1{({\tau }_k)}^{-1}{\sum }_0{\sum }_1{({\tau }_k)}^{-1}).$$ (24)

Proposition 2

When the domain 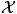is bounded, under the conditions of Lemma 1, there exists a constant c > 0 such that P( 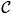_n) ≤ e^−nc asymptotically.

Proposition 2 shows that the quantile crossing phenomenon is only a finite sample behaviour. As the sample size n increases, the probability of quantile crossing decreases exponentially in n. Thus, we can expect that the non-crossing quantile technique shares the same asymptotic behaviour as the corresponding QR methods without non-crossing constraints if the constraints are necessary for non-crossing under certain cases.

As discussed earlier, constraints (9) and (10) or (12) and (13) are sufficient to ensure the non-crossing of the resulting estimated multiple quantile functions. The following proposition states the necessity of the constraints for non-crossing.

Proposition 3

Suppose $f_{{\tau }_k}(\mathit{x})={\beta }_{0{\tau }_k}+{\mathit{\beta }}_{{\tau }_k}^{\mathrm{T}}\mathit{x}$ with (β_0τk, β_τk); k = 1, …, K, bounded and x ∈ 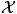= [0, ∞)^d. Then (i) constraints (12) and (13) are necessary and sufficient to ensure the non-crossing of f_τk in 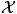; (ii) if d > n, constraints (9) and (10) are also necessary and sufficient to ensure the non-crossing of f_τk's in .

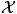Our next theorem states the same asymptotic normality of the non-crossing estimators as the unconstrained estimators. Since the probability of the crossing event goes to 0 asymptotically as shown in Proposition 2, the non-crossing estimators asymptotically behave the same as the unconstrained estimators if the constraints are sufficient and necessary for non-crossing.

Theorem 1

Assume that the non-crossing constraints are necessary and sufficient. Under the conditions of Proposition 2, then with the probability tending to 1, the simultaneous non-crossing estimates obtained by solving Equation (8) have the asymptotic normality

$$\sqrt{n}\left[\left(\begin{array}{c}{\widehat{\beta }}_{0{\tau }_k}\\ {\widehat{\mathit{\beta }}}_{{\tau }_k}\end{array}\right)-\left(\begin{array}{c}{\beta }_{0{\tau }_k}\\ {\mathit{\beta }}_{{\tau }_k}\end{array}\right)\right]\to N(\mathbf{0},{\tau }_k(1-{\tau }_k){\sum }_1{({\tau }_k)}^{-1}{\sum }_0{\sum }_1{({\tau }_k)}^{-1}).$$ (25)

3.2. Oracle properties of sparse constrained linear SNQR

In this section, we develop the oracle properties of our sparse penalised linear SNQR in the notion of Fan and Li (2001). With a non-concave penalty p_λ(·), similar to the development in Section 3.1, we first consider the version without non-crossing constraints by solving

$$min\sum _{k=1}^K{W}_k\sum _{i=1}^n{\rho }_{{\tau }_k}(y_i-{\mathit{x}}_i^{\mathrm{T}}{\mathit{\beta }}_{{\tau }_k}-{\beta }_{0{\tau }_k})+n\sum _{j=1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_{j{\tau }_k}|\right).$$ (26)

Without loss of generality, in this section, we set W_k = 1; k = 1, …, K. The results can be directly generalised to other weights W_k's. The corresponding optimiser is denoted by ${\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}^S$ and ${\stackrel{\sim }{\beta }}_{0{\tau }_k}^S$.

Recall that the true parameters are denoted by β(τ_k) = (β₁(τ_k), β₂(τ_k), …, β_p(τ_k))^T, β₀(τ_k) for k = 1, 2, …, K. Denote $u_{ik}=y_i-{\mathit{x}}_i^{\mathrm{T}}\mathit{\beta }({\tau }_k)-{\beta }_0({\tau }_k)$ for i = 1, 2, …, n and k = 1, 2, …, K.

The behaviour of $\sqrt{n}\{{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}^S-\mathit{\beta }({\tau }_k)\}$ and $\sqrt{n}\{{\stackrel{\sim }{\beta }}_{0{\tau }_k}^S-{\beta }_0({\tau }_k)\}$ follows from the consideration of the following objective function

$$Q({\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_K,a_1,a_2,\dots ,a_K)=Z_{nk}({\mathit{\alpha }}_k,a_k)+n\sum _{j=1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{jk}}{\sqrt{n}}\right|\right),$$ (27)

where α_k = (α_1k, α_2k, …, α_pk)^T and $Z_{nk}({\mathit{\alpha }}_k,a_k)={\sum }_{i=1}^n[{\rho }_{{\tau }_k}(u_{ik}-{\mathit{x}}_i^{\mathrm{T}}{\mathit{\alpha }}_k/\sqrt{n}-a_k/\sqrt{n})-{\rho }_{{\tau }_k}(u_{ik})]$. This minimiser of Equation (27) is given by $\sqrt{n}({\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}-\mathit{\beta }({\tau }_k))$ and $\sqrt{n}({\stackrel{\sim }{\beta }}_{0{\tau }_k}-{\beta }_0({\tau }_k))$.

By reordering if necessary, we assume without loss of generality that the first s predictors are important, which means that $\underset{1\le k\le K}{max}|{\beta }_j({\tau }_k)|>0$ for any j ≤ s. It also implies that β_j(τ_k) = 0 for j > s and k = 1, 2, …, K. Denote $\mathcal{A}=\{j:\underset{k=1,2,\dots ,K}{max}|{\beta }_j({\tau }_k)|\ne 0\}=\{1,2,\dots ,s\}$ to be the true active set. Note that the set 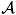includes all variables that have at least one non-zero coefficient among all quantile functions considered. We do not require all quantile functions to have the same non-zero coefficients. Denote $c_n=\underset{j\in \mathcal{A}}{max}{p}_{\lambda }^{\prime }(\underset{k=1,2,\dots ,K}{max}|{\beta }_j({\tau }_k)|)$. Set 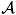^c = {s + 1, s + 2, …, p}, 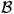= {1, 2, …, s + 1}, and 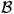^c = {s + 2, s + 3, …, p + 1}. Use β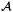_k to denote the subvector of β_k with indices in 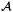and Σ_{1, 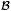, 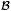^c} to denote the submatrix of Σ₁ with a row index in 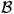and a column index in 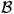^c.

Lemma 2

If λ = λ_n → 0, c_n = O(n^−1/2) and ${max}_{j\in \mathcal{A}}|p_{\lambda }^{″}({max}_{k=1,2,\dots ,K}|{\beta }_j({\tau }_k)|)|\to 0$ under conditions A and B, then there exits a local minimiser α̂_k and α̂_k, k = 1, 2, …, K, for Equation (27) such that ‖α̂_k‖ = O_p(n^−1/2) and α̂_k = O_p(n^−1/2).

Lemma 3

If $lim{inf}_{\lambda \to 0+}lim{inf}_{\theta \to 0+}{p}_{\lambda }^{\prime }(\theta )/\lambda >0$, under the conditions of Lemma 2, then with the probability tending to 1, for any a_k and α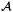_k satisfying $\sqrt{{\sum }_{k=1}^K({\Vert {\alpha }_{\mathcal{A}k}\Vert }^2+a_k^2)}=O_p(n^{-1/2})$ and for any constant C > 0,

$$Q\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}1}\\ \mathbf{0}\end{array}\right),\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}2}\\ \mathbf{0}\end{array}\right),\dots ,\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}K}\\ \mathbf{0}\end{array}\right),a_1,a_2,\dots ,a_K\right)=\underset{\sqrt{{\sum }_{k=1}^K\Vert {\mathit{\alpha }}_{{\mathcal{A}}^{c}k}\Vert }C{n}^{-1/2}}{min}Q\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}1}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}1}\end{array}\right),\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}2}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}2}\end{array}\right),\dots ,\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}K}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}K}\end{array}\right),a_1,a_2,\dots ,a_K\right).$$

Theorem 2

If λ → 0 and $\sqrt{n}\lambda \to \infty$, under the conditions of Lemma 3, then with the probability tending to 1, the $\sqrt{n}$ consistent local minimiser β̃_τk and β̃_0τk, k = 1, 2, …, K, of Lemma 2 satisfies that

1. β̃_jτk = 0 for j ∉ ,

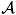2. the optimiser β̃_jτk for j ∈ 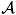and β̃_0τk has the same asymptotic property of the minimiser of the following objective function

$$min\sum _{k=1}^K\sum _{i=1}^n{\rho }_{{\tau }_k}\left(y_i-\sum _{j\in \mathcal{A}}{x}_{ij}{\beta }_{j{\tau }_k}-{\beta }_{0{\tau }_k}\right)+\sum _{j\in \mathcal{A}}p\lambda \left(\underset{k=1}{\overset{K}{max}}|{\beta }_{j{\tau }_k}|\right).$$ (28)

As a remark, we note that the absolute value of the true parameters may have a tie for some j ≤ s, namely, |β_j(τ_k)| = |β_j(τ_k′)| for some 1 ≤ k, k′ ≤ K and 1 ≤ j ≤ s. Thus, it is not easy to derive the asymptotic properties of the minimiser of Equation (28) for a general non-concave penalty. When the SCAD penalty by Fan and Li (2001) is used, we have the following result as stated in Proposition 4.

Proposition 4

When the SCAD penalty is used, under the conditions of Theorem 2, as n → ∞, with the probability tending to 1, we have that

1. β̃_jτk = 0 for j ∉ .

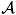2. the optimiser β̃_jτk for j ∈ 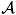and β̃_0τk satisfies

$$\sqrt{n}\left[\left(\begin{array}{c}{\widehat{\beta }}_{0{\tau }_k}\\ {\widehat{\mathit{\beta }}}_{\mathcal{A}{\tau }_k}\end{array}\right)-\left(\begin{array}{c}{\beta }_0({\tau }_k)\\ {\mathit{\beta }}_{\mathcal{A}}({\tau }_k)\end{array}\right)\right]\to N(\mathbf{0},{\tau }_k(1-{\tau }_k){\sum }_{1,ℬ,ℬ}{({\tau }_k)}^{-1}{\sum }_{0,ℬ,ℬ}{\sum }_{1,ℬ,ℬ}{({\tau }_k)}^{-1}).$$ (29)

The following theorem states the same oracle property of the constrained sparse SNQR with the unconstrained sparse SNQR.

Theorem 3

Assume that the non-crossing constraints are necessary and sufficient for non-crossing. With the probability tending to 1, asymptotic results in Theorem 2 and Proposition 4 apply to the proposed non-concave penalised non-crossing quantile estimation (14) under the same conditions.

As a remark, we note that model selection techniques that enjoy the oracle property may have unsatisfactory asymptotic behaviours in the ‘uniform sense’ with respect to the unknown parameter as one referee pointed out. The pointwise asymptotic distribution of the estimator may not be representative for the finite sample performance of the estimator (see, e.g. Leeb and Potscher 2008; Potscher and Leeb 2009; Potscher and Schneider 2010). We will not further explore this aspect on the proposed SNQR in this paper.

4. Simulations

In our simulated examples, our training sample size is denoted by n. An independent tuning set of size n and an independent test set of size 10n are generated in the same way to tune the regularisation parameter and calculate test errors, respectively. The tuning parameter λ is selected via a grid search by minimising ${\sum }_{k=1}^K{W}_k{\sum }_{i=1}^n{\rho }_{{\tau }_k}({\check{y}}_i-{\widehat{f}}_{{\tau }_k}({\check{\mathit{x}}}_i))$, where (x̌_i, y̌_i) denotes an pair of observations in our tuning set, f̂(·) denotes an estimate of the conditional quantile function and W_k is the weight for τ_k. We evaluate the test error, $\mathrm{TE}(\widehat{f})={\sum }_{k=1}^K{W}_k{\sum }_{i=1}^{10n}{\rho }_{{\tau }_k}({\stackrel{\sim }{y}}_i-{\widehat{f}}_{{\tau }_k}({\stackrel{\sim }{x}}_i))$, to compare the performance of our new method with competitive estimators, where (x̃_i, ỹ_i) denotes a pair of observations in our test set.

To examine the performance of the proposed SNQR, we compare it with the individual QR. For individual penalised QR as in Examples 4.1 and 4.2, we carry out two different tuning procedures. One is to separately tune λ for different QR functions. The other one is to jointly tune λ as in SNQR so that all different quantile terms use the same λ. Besides the unconstrained QR, we also compare SNQR with the QR with constraints on the training data only as suggested by Takeuchi et al. (2006). While comparing two different methods, we report the pairwise t-statistic between test errors over 100 repetitions for each example, namely $t_{\mathrm{M}2,\mathrm{M}1}=\sqrt{100}{\text{mean}(\mathrm{TE}}_i({\widehat{f}}_{\mathrm{M}2})-{\mathrm{TE}}_i({\widehat{f}}_{\mathrm{M}1})$, i = 1, 2, …, 100)/std(TE_i(f̂_M2) − TE_i(f̂_M1, i = 1, 2, …, 100). For the nonlinear quantile estimation, we use the Gaussian kernel $K(\mathit{x},{\mathit{x}}^{\prime })=exp(-{\Vert \mathit{x}-{\mathit{x}}^{\prime }\Vert }_2^2)$.

Example 1 (Nonlinear example with i.i.d. noise)

In this example, our predictor is univariate and uniformly distributed over [−1, 1], namely, X ∼ Uniform[−1, 1]. Conditional on X, Y = 2 sin(π X) + 0.5ε, where ε ∼ N(0, 1) denotes the independent noise. We set τ_k = 0.1k for k = 1, 2, …, 9. We compare different estimators with the Gaussian kernel. The training sample size is set to be n = 100. Results over 100 repetitions are given in Table 1, which reports the pairwise t-test statistics for comparing test errors of different methods. The weight and error options indicate the types of weight used in model-building and calculation of the testing error, respectively. The results show that the proposed SNQR (M3) gives the best performance among all methods considered here. When we use the joint tuning procedure for λ, the simultaneous method with data point restriction (M2) works better than the individually estimated QR (M1). Interestingly, when we perform separate tuning for individual multiple quantile estimation (M1′), the results are better than the simultaneous method with data point restriction (M2). Furthermore, the types of weights and errors do not appear to have much influence on the methods in this example.

Table 1.

Pairwise t-test for the test error of nonlinear i.i.d Example 1.

Weight	Error	M2 versus M1	M3 versus M2	M3 versus M1	M1 versus M1′	M2 versus M1′	M3 versus M1′
Uniform	Uniform	−2.9895	−11.3217	−10.4820	4.6798	3.1192	−9.7830
	Normal	−3.2488	−12.5514	−11.6472	6.1261	4.5797	−9.3860
Normal	Uniform	−2.8038	−12.3808	−11.2452	4.5684	3.4622	−10.4665
	Normal	−3.1294	−13.2998	−11.9478	5.7226	4.8629	−10.4114

Notes: M1, individual estimation with joint tuning; M1′, individual estimation with separate tuning; M2, simultaneous estimation with data point restriction; M3, SNQR.

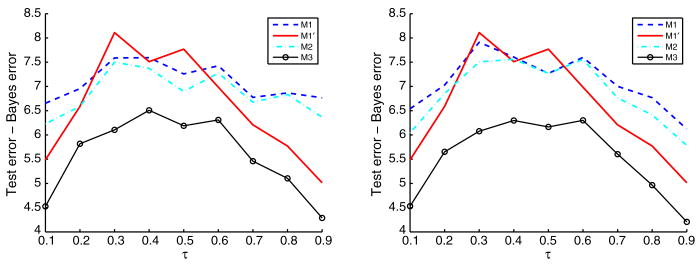
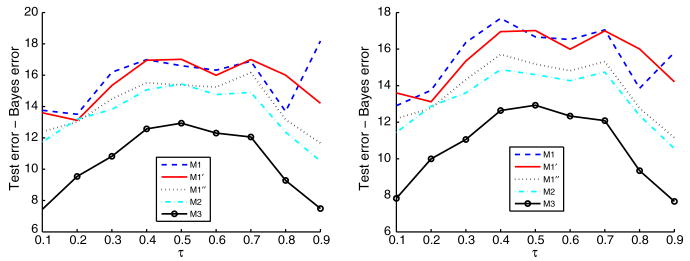
In Figure 3, we plot the average individual difference of the test error ${\sum }_{i=1}^{10n}{\rho }_{{\tau }_k}({\stackrel{\sim }{y}}_i-{\widehat{f}}_{{\tau }_k}({\stackrel{\sim }{\mathit{x}}}_i))$ and the Bayes error ${\sum }_{i=1}^{10n}{\rho }_{{\tau }_k}({\stackrel{\sim }{y}}_i-f_{{\tau }_k}({\stackrel{\sim }{\mathit{x}}}_i))$ with respect to individual τ_k's for different methods, where f_τk(·) denotes the true conditional quantile function. It clearly shows the improvement of our method.

Figure 3.

Plot of the average differences between the test errors and Bayes errors for Example 1. The left and right panels correspond to the uniform and normal weights respectively.

Example 2 (Nonlinear example with non-i.i.d. noise)

In this example, the predictor is the same as in the previous example, namely, X ∼ Uniform[−1, 1]. Conditional on X, Y = 2 sin(π X) + 0.5(1 + X²)ε, where ε ∼ N(0, 1) denotes the independent noise. The sample size is chosen to be n = 100. Results over 100 repetitions are reported in Table 2. The results are similar to that of Example 1, although the differences among methods are smaller in this example. In particular, the proposed SNQR (M3) works the best, followed by individual estimation with separate tuning (M1′), simultaneous estimation with data point restriction (M2) and individual estimation with joint tuning (M1).

Table 2.

Pairwise t-test for the test error of Example 2.

Weight	Error	M2 versus M1	M3 versus M2	M3 versus M1	M1 versus M1′	M2 versus M1′	M3 versus M1′
Uniform	Uniform	−1.6692	−5.4152	−5.4005	2.7011	1.6137	−3.6387
	Normal	−1.4907	−5.0432	−4.9881	3.9332	2.9301	−2.4405
Normal	Uniform	−2.6016	−5.4650	−6.6603	2.8115	0.2473	−5.0223
	Normal	−3.0040	−4.6702	−6.0799	3.7212	0.8714	−3.8507

Notes: M1, individual estimation with joint tuning; M1′, individual estimation with separate tuning; M2, simultaneous estimation with data point restriction; M3, SNQR.

Example 3 (Linear example with i.i.d. noise)

Data are generated from

$$Y=X_1+X_2+0.5\epsilon ,$$

with X₁ ∼ Uniform[0, 1], X₂ ∼ Uniform[0, 1], ε ∼ N(0, 1) being independent of each other We set n = 100, d = 2 and τ_k = k/10 for k = 1, 2, …, 9. For this example, we compare unpenalised QR methods, i.e. individual estimation (M1), simultaneous estimation with data point restriction (M2) and SNQR (M3). Results over 100 repetitions are reported in Table 3. The results show that SNQR (M3) works the best, then followed by the data restriction method (M2). The individual estimation (M1) gives the worst estimation accuracy.

Table 3.

Pairwise t-test for test errors of linear i.i.d of Example 3.

Weight	Error	M2 versus M1	M3 versus M2	M3 versus M1
Uniform	Uniform	−4.3214	−6.6111	−7.2070
	Normal	−4.3348	−5.3270	−6.0527
Normal	Uniform	−3.9829	−7.4806	−8.0344
	Normal	−3.9335	−6.3636	−7.0218

Notes: M1, individual estimation; M2, simultaneous estimation with data point restriction; M3, SNQR.

Example 4 (Linear example with non-i.i.d. noise)

Consider the following location-scale model

$$Y=1+X_1+X_2+\left(1+\frac{1+X_3}{2}\right)\epsilon ,$$

where X_j ∼ Uniform[−1, 1], j = 1, 2, 3, and ε ∼ N(0, 1) are independent of each other. Similar to Example 3, we compare three unpenalised QR methods: individual estimation (M1), simultaneous estimation with data point restriction (M2) and SNQR (M3). We set n = 100, d = 3 and τ_k = k/10 for k = 1, 2, …, 9. Results over 100 repetitions are reported in Table 4. The results once again demonstrate that SNQR (M3) works the best, followed by the data restriction method (M2) and then the individual estimation (M1).

Table 4.

Pairwise t-test fortest errors of linear non-i.i.d Example 4.

Weight	Error	M2 versus M1	M3 versus M2	M3 versus M1
Uniform	Uniform	−6.8340	−10.9368	−12.2511
	Normal	−6.6010	−10.4753	−11.8933
Normal	Uniform	−6.4172	−10.7988	−11.7562
	Normal	−6.2999	−10.7351	−11.9027

Notes: M1, individual estimation; M2, simultaneous estimation with data point restriction; M3, SNQR.

Example 5 (SCAD linear example with i.i.d. noise)

In this example, we simulate predictors X ∼ N(0, Σ) with Σ = (σ_ij), where σ_ij = 0.5^{|i − j|} for 1 ≤ i, j ≤ p. Data are generated from the model

$$Y={\mathit{X}}^{\mathrm{T}}\mathit{\beta }+\epsilon ,$$

where ε ∼ N(0, 1) is the independent error. Here we consider two settings, β = (3, 1.5, 0, 0, 2, 0, 0, 0)^T as in Tibshirani (1996) and β = (1.5, 0.75, 0, 0, 1, 0, 0, 0)^T which has a lower signal level. Among the eight covariates, three are important variables and the remaining five are noise variables. We use this example to examine the performance of sparse penalised QR.

For comparison, we consider five different methods: the individual QR estimation with joint tuning on λ (M1), the individual QR estimation with separate tuning on λ (M1′), the simultaneous SCAD-max QR estimation without non-crossing constraints (M1″), the simultaneous SCAD-max QR estimation with non-crossing restrictions on training data (M2) and the simultaneous SCAD-max SNQR (M3). Tables 5 and 6 report the pairwise t-statistics for the comparison of these five methods. For example, the first entry 1.0840 in Table 5 is the pairwise t-statistic t_M1′,M1 which shows that M1 gives a smaller test error than that of M1′. Overall, we can conclude that the simultaneous SCAD-max SNQR (M3) works the best in terms of test errors. Between the uniform and normal weights, the results are similar although the improvement of SNQR over other methods appears to be larger when we use the normal weight than that of the uniform weight.

Table 5.

Pairwise t-tests for test errors of Example 5 with β = (3, 1.5, 0, 0, 2, 0, 0, 0)^T.

	Uniform error				Normal error
Weight	M1	M1′	M1′′	M2	M1	M1′	M1′′	M2
Uniform
M1′	1.0840				1.9523
M1′′	−3.6614	−4.6880			−4.0600	−4.9097
M2	−6.9470	−7.8040	−5.6231		−7.7608	−8.2131	−5.7375
M3	−12.1945	−13.1992	−11.9942	−9.5200	−12.9902	−13.9023	−12.7855	−10.3205
Normal
M1′	0.4965				1.4542
M1′′	−3.3025	−3.8849			−3.3873	−4.4074
M2	−6.5717	−6.6360	−4.4325		−7.4641	−7.3642	−4.7444
M3	−12.5578	−13.5503	−13.0412	−11.0871	−13.7023	−14.6033	−14.5311	−11.9845

Notes: M1, individual estimation with joint tuning; M1′, individual estimation with separate tuning; M1′′, simultaneous SCAD-max estimation without constraints; M2, simultaneous SCAD-max estimation with data point restriction; M3, simultaneous SCAD-max SNQR.

Table 6.

Pairwise t-tests for test errors of Example 5 with β = (1.5, 0.75, 0, 0, 1, 0, 0, 0)^T.

	Uniform error				Normal error
Weight	M1	M1′	M1′′	M2	M1	M1′	M1′′	M2
Uniform
M1′	−0.8772				−1.3600
M1′′	−4.1814	−4.5246			−4.3181	−4.6945
M2	−5.0955	−5.8740	−1.8677		−5.0897	−6.0284	−2.1718
M3	−12.3679	−15.9101	−10.8048	−8.7489	−11.7193	−16.1446	−12.1681	−9.6643
Normal
M1′	−0.4428				−0.4475
M1′′	−4.6602	−5.4521			−4.7435	−5.8945
M2	−5.7025	−7.2761	−3.7704		−5.5784	−7.4678	−3.6670
M3	−10.9239	−13.0084	−10.0445	−8.1136	−10.8430	−13.5719	−11.3901	−9.3674

Notes: M1, individual estimation with joint tuning; M1′, individual estimation with separate tuning; M1′′, simultaneous SCAD-max estimation without constraints; M2, simultaneous SCAD-max estimation with data point restriction; M3, simultaneous SCAD-max SNQR.

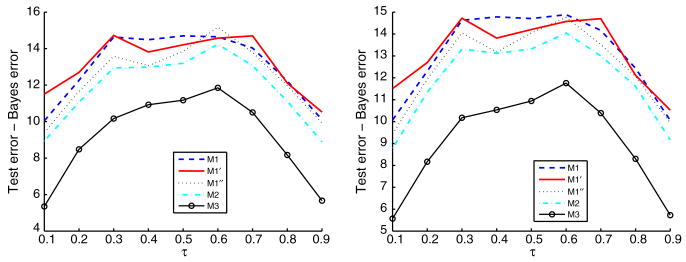
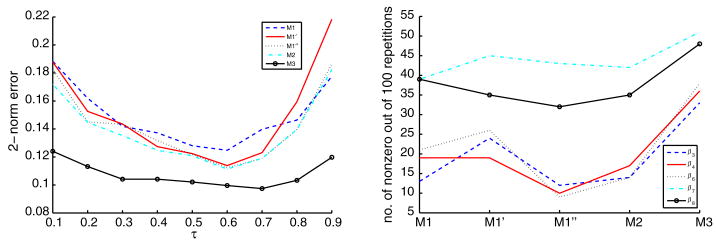
Similar to Example 1, in Figures 4 and 5, we plot the individual average differences of test errors and the Bayes errors with respect to individual τ_k for five different methods. Once again, the plot clearly demonstrates the competitiveness of the proposed SNQR for both settings of β.

Figure 4.

Plot of the average differences between the test errors and Bayes errors for Example 5 with β = (3, 1.5, 0, 0, 2, 0, 0, 0)^T. The left and right panels correspond to the uniform and normal weights, respectively.

Figure 5.

Plot of the average differences between the test errors and Bayes errors for Example 5 with β = (1.5, 0.75, 0, 0, 1, 0, 0, 0)^T. The left and right panels correspond to the uniform and normal weights, respectively (lower signal- to-noise ratio).

Tables 7 and 8 show the results on variable selection of Example 5. We report the average correct and wrong zero coefficients across all quantiles. Since there are three important variables and five noise variables, the true model has five zero coefficients and three non-zero coefficients for each QR function. As expected, the performance for the weaker signal setting is worse than that of the stronger signal setting. For the individual estimation, joint tuning appears to work better than separate tuning in terms of variable selection. Interestingly, for simultaneous estimation methods, the method M1″ without non-crossing constraints works better in variable selection than the methods with constraints. Nevertheless, in view of the big advantage of SNQR in terms of test errors, SNQR is more preferable for multiple QR estimation.

Table 7.

Variable selection results of Example 5 with β = (3, 1.5, 0, 0, 2, 0, 0, 0)^T.

Weight	M1	M1′	M1′′	M2	M3
Uniform
Average wrong 0	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
Average correct 0	3.41 (0.14)	1.00 (0.12)	4.49 (0.08)	4.40 (0.09)	3.91 (0.15)
Normal
Average wrong 0	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
Average correct 0	3.45 (0.14)	1.00 (0.12)	4.42 (0.09)	4.31 (0.10)	3.69 (0.15)

Notes: M1, individual estimation with joint tuning; M1′, individual estimation with separate tuning; M1′′, simultaneous SCAD-max estimation without constraints; M2, simultaneous SCAD-max estimation with data point restriction; M3, simultaneous SCAD-max SNQR.

Table 8.

Variable selection results of Example 5 with β = (1.5, 0.75, 0, 0, 1, 0, 0, 0)^T.

Weight	M1	M1′	M1′′	M2	M3
Uniform
Average wrong 0	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
Average correct 0	2.76 (0.16)	0.64 (0.11)	4.39 (0.09)	4.27 (0.10)	3.35 (0.19)
Normal
Average wrong 0	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
Average correct 0	2.84 (0.15)	0.64 (0.11)	4.26 (0.10)	4.16 (0.11)	3.54 (0.17)

Notes: M1, individual estimation with joint tuning; M1′, individual estimation with separate tuning; M1′′, simultaneous SCAD-max estimation without constraints; M2, simultaneous SCAD-max estimation with data point restriction; M3, simultaneous SCAD-max SNQR.

One reviewer suggested another setting of the parameter vector β = (3, 1.5, 0, 0, 2, 0, 0.1, 0.1)^T. In this case, the last two parameters are replaced by small non-zero values, $1/\sqrt{n}=0.1$ with n = 100. A similar example was considered by Leeb and Potscher (2008). Since the last two parameters are close to 0, it can be more difficult to select them compared with other non-zero parameters. On the other hand, a model with only X₁, X₂, X₅ could be a reasonable model as well in terms of prediction and interpretability.

We examine the performance of five different methods, M1, M1′, M1″, M2 and M3, on this example with the new parameter setting. The results with normal weights are displayed in Figure 6. The left panel shows the average squared differences between β̂ and β, ${{\sum }_{j=0}^8({\widehat{\beta }}_j-{\beta }_j)}^2$, based on 100 replications. Similar as before, our proposed SNQR works the best in terms of parameter estimation. The right panel shows the number of non-zero estimates of β₃, β₄, β₆, β₇, and β₈ for the quantile function with τ = 0.4 among these 100 replications. Notice that all methods have higher percents of non-zero estimates for β₇, β₈ than those of β₃, β₄ and β₆. This is expected since β₇ and β₈ are non-zero while the other three are zero. Due to the small values of these two parameters, all methods estimate β₇ and β₈ as zero over 50% times. We do not plot the selection results for β₁, β₂ and β₅ since the corresponding estimates are non-zero for all replications. Overall, the performance of the proposed SNQR is very reasonable compared with other methods.

Figure 6.

The left panel shows the average squared differences between β̂ and β for five different methods using normal weights. The right panel shows the corresponding number of non-zero estimates of β₃, β₄, β₆, β₇ and β₈ for the quantile function with τ = 0.4 based on 100 replications.

5. Real data

In this section, we apply our proposed SNQR to analyse the Annual Salary of Baseball Players Data provided by He, Ng and Portnoy (1998). This data set consists of n = 263 North American major league baseball players for the 1986 season. Following He et al. (1998), we use the number of home runs in the latest year (performance measure) and the number of years played (seniority measure) as predictor variables. The response variable is the annual salary of each player (measured in thousands of dollars). We first standardise both predictor variables to have mean zero and variance one. We apply the nonlinear QR using the Gaussian kernel with data width parameter σ chosen to be the median pairwise Euclidean distance of the standardised predictor variables. Similar recommendation on data width parameter selection was previously provided by Brown et al. (2000). We use 10-fold cross-validation to select the regularisation parameter λ.

The conditional quantile function is estimated at τ = 0.1, 0.2, …, 0.9. In Figure 7, we plot the individually estimated median function and the Gaussian weighted SNQR estimated median function on the top left and right panels, respectively. To visualise quantile crossing, we plot the difference f̂_0.8(x) − f̂_0.7(x) on the bottom row. The one from the individual estimation is shown on the bottom left panel, and the one from SNQR is displayed on the bottom right panel. Several interesting remarks can be made from the plots. First of all, the conditional median plots suggest that players with large numbers of home runs and moderate numbers of years played have the highest median salaries. This matches our expectation since that group of players have relatively better skills than other players and are possibly in the peak time of their Baseball career. Between the individually estimated median function and the SNQR median function, the shapes are quite similar although the SNQR median function appears to be slightly more peaked. As to quantile crossing, we can see from the bottom left panel of Figure 7 that the individually estimated 70% quantile function can be higher than that of the 80% quantile function. This undesirable phenomenon disappears when the SNQR is applied. Furthermore, due to the joint estimation, the difference curve of our SNQR is smoother than that from the individual estimation.

Figure 7.

Plots for the Baseball data example. Top left panel: individually estimated median function; top right panel: SNQR estimated median function; bottom left panel: the difference between the individually estimated quantile functions of τ = 0.8 and τ = 0.7; bottom right panel: the difference between the SNQR estimated quantile functions of τ = 0.8 and τ = 0.7.

6. Discussion

In this paper, we study the problem of multiple conditional quantile function estimation. When individual optimisation is performed, the obtained quantile functions may cross each other and as a result violate the basic property of quantiles. A new method SNQR, which avoids quantile crossing via simple constraints, is proposed. We demonstrate that SNQR can not only help to obtain more interpretable quantile functions, it can also help to improve the estimation efficiency.

As in other regularisation problems, the choice of the regularisation parameter λ is very important for the performance of QR. It is common for one to select a finite set of representative values for λ and then use a separate validation data set or certain model selection criterion to select a value for λ. In this article, we have used separate validation sets for simulation and cross-validation for the real data analysis. As an alternative, one can use certain model selection criterion to choose λ. Two commonly used criteria are the Schwarz information criterion (Schwarz 1978; Koenker et al. 1994) and the generalised approximate cross-validation criterion (Yuan 1978). These criteria are well studied for unconstrained QR and require further developments for our constrained methods.

Our asymptotic study is restricted to the linear SNQR. It will be interesting to explore the asymptotic behaviour of the nonlinear SNQR as well. The existing asymptotic results (e.g. Yu and Jones 1998; Hall et al. 1999; Dette and Volgushev 2008; Chernozhukov et al. 2009) can shed some light here. Further investigation is needed.

Appendix

Proof of Proposition 1

The result can be shown directly using integration by parts. The details are not included here to save space.

Proof of Lemma 1

The result is straightforward by applying Theorem 4.1 of Koenker (2005) to each τ_k.

Proof of Proposition 2

In theory, it is guaranteed that

$$d_k\triangleq \underset{\mathit{x}\in \mathcal{X}}{inf}\{[{\beta }_0({\tau }_{k+1})-{\beta }_0({\tau }_k)]+{\mathit{x}}^{\mathrm{T}}[\mathit{\beta }({\tau }_{k+1})-\mathit{\beta }({\tau }_k)]\}>0$$

due to Condition A. Using the triangle inequality, we have

$$\begin{array}{ll}\underset{\mathit{x}\in \mathcal{X}}{inf}\{{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}-{\stackrel{\sim }{\beta }}_{0{\tau }_k}+{\mathit{x}}^{\mathrm{T}}({\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k})\}\hfill & \ge \underset{\mathit{x}\in \mathcal{X}}{inf}\{{\mathit{x}}^{\mathrm{T}}[{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-\mathit{\beta }({\tau }_{k+1})]\}+({\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}-{\beta }_0({\tau }_{k+1}))+({\beta }_0({\tau }_{k+1})-{\beta }_0({\tau }_k))+\underset{\mathit{x}\in \mathcal{X}}{inf}\{{\mathit{x}}^{\mathrm{T}}[\mathit{\beta }({\tau }_{k+1})-\mathit{\beta }({\tau }_k)]\}+({\beta }_0({\tau }_k)-{\stackrel{\sim }{\beta }}_{0{\tau }_k})+\underset{\mathit{x}\in \mathcal{X}}{inf}\{{\mathit{x}}^{\mathrm{T}}[\mathit{\beta }({\tau }_k)-{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}]\}\hfill \\ \hfill & \ge -\underset{\mathit{x}\in \mathcal{X}}{sup}|{\mathit{x}}^{\mathrm{T}}[{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-\mathit{\beta }({\tau }_{k+1})]|-|{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}-{\beta }_0({\tau }_{k+1})|+({\beta }_{0{\tau }_{k+1}}-{\beta }_{0{\tau }_k})+\underset{\mathit{x}\in \mathcal{X}}{inf}\{{\mathit{x}}^{\mathrm{T}}[\mathit{\beta }({\tau }_{k+1})-\mathit{\beta }({\tau }_k)]\}-|{\beta }_0({\tau }_k)-{\stackrel{\sim }{\beta }}_{0{\tau }_k}|-\underset{\mathit{x}\in \mathcal{X}}{sup}|{\mathit{x}}^{\mathrm{T}}[\mathit{\beta }({\tau }_k)-{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}]|.\hfill \end{array}$$

Another application of the triangle inequality leads to

$$\underset{\mathit{x}\in \mathcal{X}}{sup}|{\mathit{x}}^{\mathrm{T}}[{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}-\mathit{\beta }({\tau }_k)]|\le \left(\underset{\mathit{x}\in \mathcal{X}}{sup}\Vert \mathit{x}\Vert \right)\Vert {\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}-\mathit{\beta }({\tau }_k)\Vert .$$ (A1)

Denote M = sup_x∈ 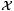‖x‖. Consequently, we have

$$\begin{array}{ll}P\left(\underset{\mathit{x}\in \mathcal{X}}{sup}\{{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}-{\stackrel{\sim }{\beta }}_{0{\tau }_k}+{\mathit{x}}^{\mathrm{T}}({\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k})\}<0\right)& \le P\left(\underset{\mathit{x}\in \mathcal{X}}{sup}|{\mathit{x}}^{\mathrm{T}}[{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-\mathit{\beta }({\tau }_{k+1})]|>\frac{d_k}{4}\right)+P\left(\underset{\mathit{x}\in \mathcal{X}}{sup}|{\mathit{x}}^{\mathrm{T}}[{\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}-\mathit{\beta }({\tau }_k)]|>\frac{d_k}{4}\right)+P\left(|{\beta }_0({\tau }_k)-{\stackrel{\sim }{\beta }}_{0{\tau }_k}|>\frac{d_k}{4}\right)+P\left(|{\beta }_0({\tau }_{k+1})-{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}|>\frac{d_k}{4}\right)\\ & \le P\left(\Vert {\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-\mathit{\beta }({\tau }_{k+1})\Vert >\frac{d_k}{2M}\right)+P\left(\Vert {\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_k}-\mathit{\beta }({\tau }_k)\Vert >\frac{d_k}{2M}\right)+P\left(|{\beta }_0({\tau }_k)-{\stackrel{\sim }{\beta }}_{0{\tau }_k}|>\frac{d_k}{4}\right)+P\left(|{\beta }_0({\tau }_{k+1})-{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}|>\frac{d_k}{4}\right).\end{array}$$ (A2)

Based on Lemma 1, the sum of probabilities in Equation (A2) decays exponentially. Thus, we have P(sup_x∈ 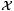{β̃_0τk+1 − β̃_0τk +x^T(β̃_τk+1 − β̃_τk)} < 0) < e^−nak asymptotically for some a_k > 0. This completes the proof by noting that

$$P({\mathcal{C}}_n)\le \sum _{k=1}^{K}P\left(\underset{\mathit{x}\in \mathcal{X}}{sup}\{{\stackrel{\sim }{\beta }}_{0{\tau }_{k+1}}-{\stackrel{\sim }{\beta }}_{0{\tau }_k}+{\mathit{x}}^{\mathrm{T}}({\stackrel{\sim }{\mathit{\beta }}}_{{\tau }_{k+1}}-{\mathit{\beta }}_{{\tau }_k})\}<0\right).$$

Proof of Proposition 3

The sufficiency of the constraints is straightforward. For necessity, we prove parts (i) and (ii) separately. For(i), the necessity of constraint (12) can be shown by letting x* = (0, …, 0) for f_τk (x). For Equation (13), let x* = (0, …, 0, M, 0, …, 0), i.e. all elements are 0 except the jth element being M > 0. Then f_τk (x*) = β_0τk + β_τk,j M and f_τk+1 (x*) = β_0τk+1 + β_τk+1,j M. Since β_0τk and β_0τk+1 are bounded, the constraint β_τk,j ≤ β_τk+1,j is necessary to ensure f_τk (x*) ≤ f_τk+1 (x*) for arbitrarily large M. The conclusion in (i) then follows.

For (ii), $f_{{\tau }_k}(\mathit{x})={\sum }_{i=1}^n{w}_{{\tau }_k,i}\langle {\mathit{x}}_i,\mathit{x}\rangle +b_{{\tau }_k}$. Without loss of generality, assume that the design matrix is of rank n. Since d > n, there exists x* ∈ 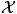such that x* ⊥ x_i for ∀i ≠ i′ and 〈x*, x_i′〉 = M. Then f_τk (x*) ≤ f_τk+1 (x*) implies that w_τk,i^′ M + b_τk ≤ w_{τk+1, i^′} M + b_τk+1. When M = 0, we have b_τk ≤ b_τk+1. Moreover, we have w_τk,i^′ ≤ w_τk+1,i^′ with M being arbitrarily large. Then part (ii) follows.

Proof of Theorem 1

The desired result is straightforward by combining Lemma 1 and Proposition 2.

Proof of Lemma 2

It is enough to show that for any δ > 0, there exists a large constant C such that

$$P\left(\underset{{\sum }_{j=1}^p({\Vert {\mathit{\alpha }}_j\Vert }^2+a_j^2)=C}{inf}Q({\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_K,a_1,a_2,\dots ,a_K)>Q(\mathbf{0},\mathbf{0},\dots ,\mathbf{0},0,0,\dots ,0)\right)>1-\delta .$$

This will imply that with probability at least 1 − δ there exists a local minimum inside the ball of $\mathit{\beta }({\tau }_k)+{\mathit{\alpha }}_k/\sqrt{n}$, ${\beta }_0({\tau }_k)+a_k/\sqrt{n}$, k = 1, 2, …, K with α_k and a_k satisfying ${\sum }_{k=1}^K({\Vert {\mathit{\alpha }}_k\Vert }^2+a_k^2)=C$.

Note that

$$\begin{array}{cc}Q({\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_K,a_1,a_2,\dots ,a_K)-Q(\mathbf{0},\mathbf{0},\dots ,\mathbf{0},0,0,\dots ,0)& =\sum _{k=1}^K{Z}_{\mathit{nk}}({\mathbf{\alpha }}_k,a_k)+n\sum _{j=1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{jk}}{\sqrt{n}}\right|\right)-n\sum _{j=1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\\ & \ge \sum _{k=1}^K{Z}_{\mathit{nk}}({\mathit{\alpha }}_k,a_k)+n\sum _{j\in \mathcal{A}}\left[p_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{jk}}{\sqrt{n}}\right|\right)-p_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\right],\end{array}$$

where the last inequality is due to the fact that ${max}_{k=1}^K|{\beta }_j({\tau }_k)|=0$ for j ∉ A and p_λ (·) is non-decreasing on [0, ∞).

Note further that

$$\begin{array}{ll}n\sum _{j\in \mathcal{A}}\left[p_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{\mathit{jk}}}{\sqrt{n}}\right|\right)-p_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\right]\hfill & \le n\sum _{j\in \mathcal{A}}\left[p_{\lambda }^{\prime }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\sum _{k=1}^K\frac{|{\alpha }_{jk}|}{\sqrt{n}}\right]+n\frac{1+o(1)}{2}\sum _{j\in \mathcal{A}}\left[p_{\lambda }^{″}\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\sum _{k=1}^K\frac{|{\alpha }_{jk}^2|}{n}\right]\hfill \\ \hfill & \le \sqrt{n}{c}_n\sum _{j\in \mathcal{A}}\sum _{k=1}^K|{\alpha }_{jk}|+\frac{1+o(1)}{2}\left[\sum _{j\in \mathcal{A}}\sum _{k=1}^K{\alpha }_{jk}^2\right]\underset{j\in \mathcal{A}}{max}|p_{\lambda }^{″}\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)|.\hfill \end{array}$$

According to Koenker (2005), we have

$$Z_{\mathit{nk}}({\mathit{\alpha }}_k,a_k)\to -(a_k,{\mathit{\alpha }}_k^{\mathrm{T}}){\mathit{W}}_k+\frac{1}{2}(a_k,{\mathit{\alpha }}_k^{\mathrm{T}}){\sum }_1({\tau }_k){(a_k,{\mathit{\alpha }}_k^{\mathrm{T}})}^{\mathrm{T}}\text{in}\text{distribution},\text{as}n\to \infty ,$$ (A3)

where W_k ∼ N(0, τ_k(1 − τ_k)Σ₀).

Recall that we assume that c_n = O(n^−1/2) and ${max}_{j\in \mathcal{A}}|p_{\lambda }^{″}({max}_{k=1}^K|{\beta }_j({\tau }_k)|)|\to 0$. Thus asymptotically,

$$Z_{\mathit{nk}}({\mathit{\alpha }}_k,a_k)+n\sum _{j\in \mathcal{A}}\left[p_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{jk}}{\sqrt{n}}\right|\right)-p_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\right]$$

is dominated by the quadratic term $\frac{1}{2}{{\sum }_{k=1}^K(a_k,{\mathit{\alpha }}_k^{\mathrm{T}}){\sum }_1({\tau }_k)(a_k,{\mathit{\alpha }}_k^{\mathrm{T}})}^{\mathrm{T}}$ when C is large enough. This completes the proof.

Proof of Lemma 3

Note that

$$Q\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}1}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}1}\end{array}\right),\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}2}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}2}\end{array}\right),\dots ,\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}K}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}K}\end{array}\right),a_1,a_2,\dots ,a_K\right)-Q\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}1}\\ \mathbf{0}\end{array}\right),\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}2}\\ \mathbf{0}\end{array}\right),\dots ,\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}K}\\ \mathbf{0}\end{array}\right),a_1,a_2,\dots ,a_K\right)=\sum _{k=1}^K{Z}_{\mathit{nk}}\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}k}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}k}\end{array}\right),a_k\right)+n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{\mathit{jk}}}{\sqrt{n}}\right|\right)-\sum _{k=1}^K{Z}_{\mathit{nk}}\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}k}\\ \mathbf{0}\end{array}\right),a_k\right)+n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right).$$

Note that

$$Z_{\mathit{nk}}\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}k}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}k}\end{array}\right),a_k\right)-Z_{\mathit{nk}}\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}k}\\ \mathbf{0}\end{array}\right),a_k\right)\to -{\mathit{\alpha }}_{{\mathcal{A}}^{c}k}^{\mathrm{T}}{\mathit{W}}_{{ℬ}^{c}k}+(a_k,{\mathit{\alpha }}_{\mathcal{A}k}^{\mathrm{T}}){{\sum }_{1,ℬ,{ℬ}^c}\mathit{\alpha }}_{{\mathcal{A}}^{c}k}.$$

Recall that β_j(τ_k) = 0 for j > s. Thus

$$\begin{array}{ll}n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{\mathit{jk}}}{\sqrt{n}}\right|\right)-n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)\hfill & =n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|\frac{{\alpha }_{\mathit{jk}}}{\sqrt{n}}\right|\right)\hfill \\ \hfill & \ge n\sum _{j=s+1}^p\lambda \left(\underset{\lambda \to 0}{liminf}\underset{\theta \to 0+}{liminf}\frac{p_{\lambda }^{\prime }(\theta )}{\lambda }\right)\left(\underset{k=1}{\overset{K}{max}}|\frac{{\alpha }_{\mathit{jk}}}{\sqrt{n}}|\right)(1+o(1))\hfill \\ \hfill & =(1+o(1))\sqrt{n}\lambda \sum _{j=s+1}^p\left(\underset{k=1}{\overset{K}{max}}|{\alpha }_{\mathit{jk}}|\right)\left(\underset{\lambda \to 0}{liminf}\underset{\theta \to 0+}{liminf}\frac{p_{\lambda }^{\prime }(\theta )}{\lambda }\right).\hfill \end{array}$$

This completes the proof by noting that $\sqrt{n}\lambda \to \infty$ and as a result

$$n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}\left|{\beta }_j({\tau }_k)+\frac{{\alpha }_{jk}}{\sqrt{n}}\right|\right)-n\sum _{j=s+1}^p{p}_{\lambda }\left(\underset{k=1}{\overset{K}{max}}|{\beta }_j({\tau }_k)|\right)$$

dominates

$$\sum _{k=1}^K\left(Z_{\mathit{nk}}\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}k}\\ {\mathit{\alpha }}_{{\mathcal{A}}^{c}k}\end{array}\right),a_k\right)-Z_{\mathit{nk}}\left(\left(\begin{array}{c}{\mathit{\alpha }}_{\mathcal{A}k}\\ \mathbf{0}\end{array}\right),a_k\right)\right)$$

asymptotically as n → ∞.

Proof of Theorem 2

This is straightforward due to Lemmas 2 and 3.

Proof of Proposition 4

Note for the SCAD penalty, p_λ(θ) is flat as long as |θ| > aλ. Lemma 2 implies that β̃_jτk is consistent. Thus we are solving Equation (28) in a neighbourhood of true β_j(τ_k) and, consequently, when n is large enough, $p_{\lambda }({max}_{k=1}^K\mid {\beta }_{j{\tau }_k})$ is flat by noting that λ → 0 as n →∞. Then the asymptotical normality (29) is valid.

Proof of Theorem 3

This can be proved in the same way as how Theorem 1 is proved using Proposition 2.