Skip to main content
PMC home page
Annals of Advances in Automotive Medicine / Annual Scientific Conference logoLink to Annals of Advances in Automotive Medicine / Annual Scientific Conference
. 2010 Jan;54:3–14.

The Tolerance of the Nasal Bone to Blunt Impact

Joseph Cormier 1, Sarah Manoogian 1, Jill Bisplinghoff 2, Steve Rowson 2, Anthony Santago 2, Craig McNally 2, Stefan Duma 2, John Bolte IV 3
PMCID: PMC3242551  PMID: 21050587

Abstract

The nasal bone is among the most frequently broken facial bone due to all types of trauma and is the most frequently fractured facial bone due to motor vehicle collisions. This study reports the results of anterior-posterior impacts performed on male cadavers using a free-falling impactor with a flat impacting surface. The force at fracture onset was determined using an acoustic emission sensor. These non-censored data were utilized in parametric and non-parametric techniques to determine a relationship between applied force and fracture risk. Based on these analyses a 50% risk of fracture corresponded to an applied force of approximately 450 to 850 N. There was no correlation between fracture force and anthropometric measures of the nasal bone. Interestingly, age had a statistically significant relationship with the risk of nasal bone fracture. This study demonstrates the need for a non-censored measure of fracture occurrence when evaluating structures that can continue to support load after fracture onset.

INTRODUCTION

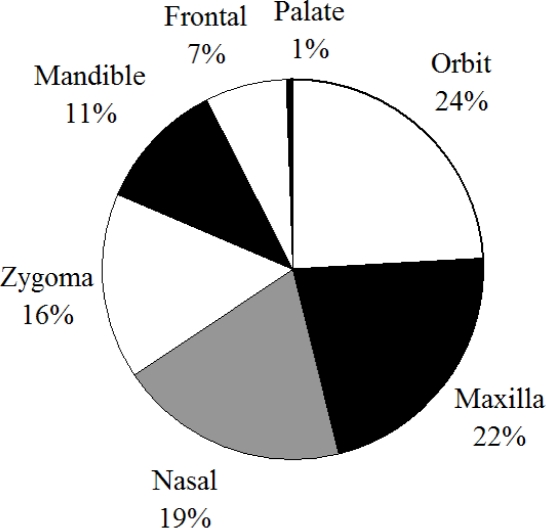
The nasal bone is a relatively weak structure and due to its prominence on the face it is one of the most frequently broken structures due to facial trauma [Muraoka et al., 1995; Hackle et al., 2001; Alvi et al., 2003] (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Distribution of facial fractures from hospital data (Alvi 2003).

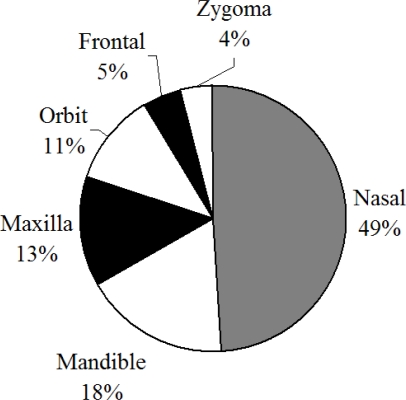
In hospital data nasal bone fractures tend to result from Motor Vehicle Collisions (MVC) violence, sports and falls [Lim et al., 1993; Muraoka et al., 1995; Jayamanne and Gillie 1996; Shapiro et al., 2001; Gassner et al., 2003]. Evaluating MVCs using NASS-CDS, it has been shown that the nasal bone is the most frequently fractured facial bone during frontal impacts [Cormier and Duma 2009] (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Distribution of facial fractures in frontal impacts within NASS-CDS.

The nasal bones are two small oblong bones which form a bridge across the frontal processes of the maxilla. Their superior surface borders with the frontal bone while the inferior surface is attached to the lateral cartilage of the nose (Figure 3).

Figure 3.

Figure 3

Open in a new tab

Basic facial anatomy demonstrating location of nasal bones.

The few studies that have examined the tolerance of the nasal bone have consisted of striking the face with the flat end, or the curved side of a cylindrical impactor. Striking the nasal bone with the end of a cylinder applies a more focal load on the nose without involving other structures of the face. This method was utilized in an undocumented number of tests by Nahum et al., (1975). The area of the impacting surface was 6.45 cm2 and was covered with a thin piece of nickel foam padding. Impact severity was not documented; however, a minimal tolerance of 111–334 N was estimated. A cylindrical impactor, representing a steering wheel rim was utilized in a separate study on the nasal bone [Nyquist et al., 1986]. A rigid, 25 mm diameter cylinder was oriented in the horizontal plane with the longitudinal axis aligned with the inferior orbital ridge. Impactor energy ranged from 241 to 815 J and resulted in peak forces of 2010 to 3890 N. All tests resulted in a nasal bone fracture at a minimum. Four of the eleven tests resulted in more extensive fractures involving the maxilla, frontal bone, zygoma and orbit. A second study using a horizontal bar aligned with the nasion at speeds of 2.3 to 4.8 m/s resulted in peak forces of 1790 to 3760 N [Cesari et al., 1989]. LeFort Type III fractures were generated at impact speeds of 3.86 and 3.67 m/s, indicating that the severity of these impacts exceed that necessary to cause a nasal bone fracture since LeFort III fractures consist of bilateral fractures of the frontal processes of the zygoma the zygomatic arch and a fracture through the nasal bones, posteriorly through the orbital walls.

The previous work provides some insight into the tolerance of the nasal bone, but more importantly it points to the ability of the facial structures behind the nasal bone to continue supporting load after nasal bone fracture. In previous works, Allsop et al., demonstrated that facial bones are capable of supporting load after fracture has occurred [Allsop et al., 1988; Allsop and Kennett 2002]. Instead of assuming peak force was the fracture tolerance, they utilized Acoustic Emission (AE) sensors to identify the time of fracture. AE sensors have been utilized by previous studies to determine a non-censored measure of injury tolerance on other bones as well [Wells and Rawlings 1985; Funk et al., 2002; Rudd et al., 2004; Kent et al., 2008]. Using data from the current study, a previous paper was published demonstrating the use of AE to determine the onset of facial fracture [Cormier et al., 2008]. In that study and others, a voltage threshold to determine the magnitude of AE consistent with fracture onset was established [Funk et al., 2002; Rudd et al., 2004; Cormier et al., 2008]. In the study by Cormier et al. (2008) additional validation was obtained by demonstrating that high magnitude AE occurred when striking bones with pre-existing fractures at low energy levels. This suggests that the high magnitude AE was due to the propagation of pre-existing fractures and not the result of the impact itself.

The high peak forces obtained in the studies by Cesari et al., (1989) and Nyquist et al., (1986), along with the occurrence of maxilla and frontal bone fractures demonstrate the continued structural support after nasal bone fracture. This suggests that nasal bone fracture occurs prior to peak force and, furthermore, the tolerance of the nasal bone is unrelated to the peak forces reported in the previous studies. The goal of this study is to utilize AE sensors to determine the onset of nasal bone fracture and develop a statistical measure of fracture risk based on these non-censored data.

METHODS

The data for this study were obtained by performing nasal bone impacts on male cadaveric subjects using the flat face of an unpadded, cylindrical impactor, along with the use of acoustic emission sensors to determine the time of fracture onset. All heads were frozen and thawed prior to testing. A total of 24 male subjects ranging in age from 41 to 94 years were included in the study. Pre-test CT imaging was performed on 13 subjects and post-test CT imaging was performed on two specimens.

Anthropometry

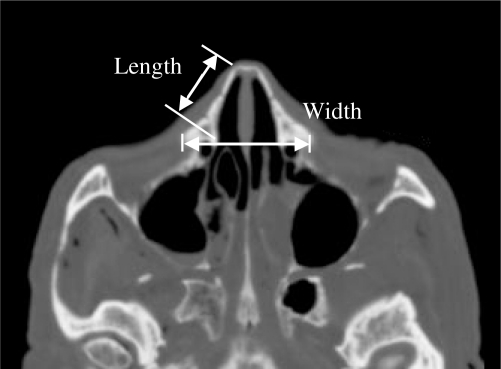
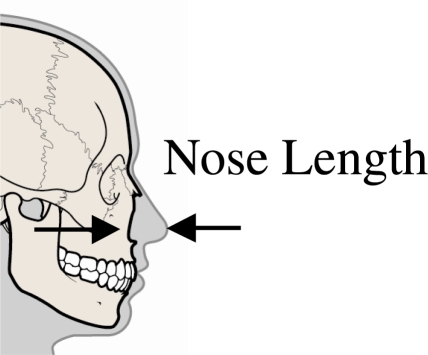
Prior to testing CT imaging was performed on 13 of the subjects. Due to differences in testing locations, CT imaging was not available for all subjects. From these images, the length and width of the nasal bone was measured along with the thickness of the nasal bone (Figure 4). An additional measurement was taken to determine the maximum length of the nose (Figure 5) in the horizontal plane. A regression analysis was performed to evaluate the potential relationship between the nasal geometry and fracture tolerance for these specimens.

Figure 4.

Figure 4

Open in a new tab

Measurements of nasal bone taken using pre-test CT images.

Figure 5.

Figure 5

Open in a new tab

Demonstration of nose length measurement.

Specimen Preparation

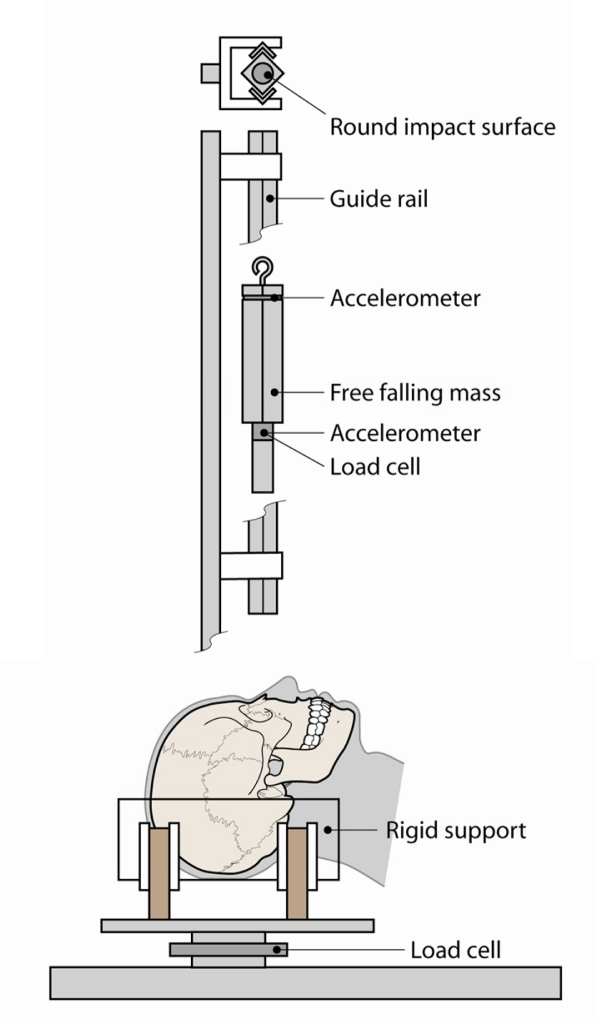
The specimens were removed from the body and prepared by removing the scalp overlying the occipital region. Metal screws were inserted into the occiput to provide additional structure for the casting material to adhere to. Each head was then rigidly mounted to a semi-circular, polycarbonate support using Bondo (Figure 6). The influence of the mounting procedure on the stiffness of the skull was minimized by limiting the lateral support provided by the casting material to the posterior aspect of the skull. This ensured that there was no lateral constraint anterior of the occipital region of the skull. Consistent orientation between subjects was obtained by vertically aligning the Frankfort plane prior to mounting.

Figure 6.

Figure 6

Open in a new tab

Schematic of test apparatus to be used in the current study.

Test Conditions

Each impact was performed using a cylindrical, free-falling rigid aluminum impactor (3.2 kg) with a steel tip. The flat impacting surface had an area of 6.45 cm2 (1 in2) and was machined with a slight bevel to reduce edge effects. The impactor was centered over the palpated inferior surface of the nasal bones. Impactor energy ranged from 4 to 16 J. Dissections were performed after testing to evaluate fracture patterns.

Instrumentation

The rigid impactor was instrumented with two single-axis accelerometers (Endevco 7264B-2000, Endevco Corp., San Juan Capistrano, CA). A load cell (Denton, 8617JTF, Rochester Hills, MI) was attached to behind the tip of the impactor which was also instrumented with a single axis accelerometer (Endevco 7264B-2000, Endevco Corp., San Juan Capistrano CA) (Figure 6). A load cell (Denton 1968, Rochester Hills, MI) was mounted to the head support to measure reaction forces. Impact force was obtained using the impactor load cell along with the inertially compensated tip mass. The secondary accelerometer mounted at the top of the impactor was a redundant sensor to help ensure data were obtained for each test and to compare to other sensors. Data obtained using the load cell and accelerometers were well correlated. All data were filtered to CFC 300. Previous studies have utilized CFC 180; however the use of CFC 300 did not significantly alter the measured peak forces and was chosen to increase the likelihood of capturing small changes in impactor force during fracture [Nyquist et al., 1986; Bermond et al., 1989; Bruyere et al., 2000]. Fuji Film (Fuji Film, Valhalla, NY) pressure film was placed on the surface of the impactor prior to each test. Impactor displacement was calculated by double-integrating the acceleration data. Contact between the impactor and subject was defined based on an impactor force of 10 N. Once the impactor force reached a level above 10 N, the displacement with respect to the face was set to zero and further motion was calculated by double integration. Additionally, high-speed video was also recorded at a frame rate of approximately 4,000 fps.

Acoustic Emission

In all cases an AE sensor (Micro30S, Physical Instruments, NJ) was mounted to the frontal bone, just posterior to the apex of the frontal bone. The AE sensor was mounted directly to the bone by removing the soft tissue and periosteum and gluing the sensor in place with cyanoacrylate adhesive. Mounting of the AE sensor is not expected to cause any change in the fracture mechanics of the bone due to its location away from the impact location and the lack of a structural effect on the skull. In this study, an AE voltage threshold was established by comparing the AE amplitude between fracture and non-fracture tests. This threshold is used to define the time at which the fracture processes begins and differentiates between low-amplitude AE occurring during non-fracture tests and the higher amplitude AE measured during fracture tests. Essentially, the maximum value of the AE signal for fracture and non-fracture tests was compared and a threshold that distinguished between the two was created. Since this study is part of a larger analysis of other facial bones, additional data were available for validating the AE threshold. Additional details can be found in a previously published paper [Cormier et al., 2008].

Risk Function Analysis

Survival analyses were performed utilizing parametric and non-parametric techniques. For the parametric analysis, a Weibull model was assumed and fit to the data which contained fracture and non-fracture observations. The advantage of using a Weibull model is that the method used to determine the model parameters accounts for the fact that non-fracture tests are right-censored. The LIFEREG procedure within SAS (SAS Institute, Cary, NC) accounts for left and right censoring as well as non-censored data and was used to determine the parameter estimates for the Weibull model [Allison 1995; Cantor 2003]. The Weibull distribution is advantageous because it is not forced to be symmetric, so it can accommodate risks that do not increase in the same way throughout the set of input variables. The Weibull Cumulative Distribution Function (CDF) is given by,

CDF=1−exp−(λ⋅F)γ (Equation 1)

Where, λ and γ are the scale and shape parameters, respectively, and F is the applied force. This function will provide an estimate of risk of injury using the maximum likelihood estimates of the scale and shape parameters. A non-parametric model was also created using the Kaplan-Meier method. The Kaplan-Meir method assumes the data are only right or non-censored and determines the risk of fracture based on the number of subjects at risk which sustain a fracture for a given force [Kleinbaum and Klein 2005]. Measurements obtained using CT imaging as well as subject age were also included as covariates to assess their potential for predicting the risk of fracture.

RESULTS

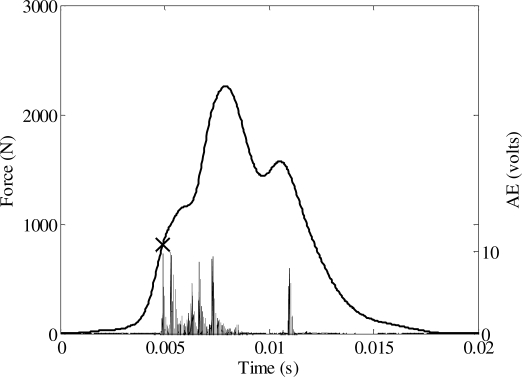
A total of 24 tests were performed to determine the tolerance of the nasal bone to blunt impact (Appendix). The peak force during each impact ranged from 784 to 2260 N. A nasal fracture was produced in 23 tests. An Acoustic Emission (AE) signal was measured in every test using a sensor mounted on the frontal bone. A threshold voltage was established based on the magnitude of AE during fracture (Figure 7, Figure 8) and non-fracture (Figure 9) tests. Therefore, the force corresponding to an AE above the threshold was utilized as the force to initiate fracture in the statistical analysis. A threshold voltage was established based on the magnitude of the AE during fracture and non-fracture tests. The threshold was exceeded in all fracture tests and was not exceeded in the single non-fracture test. The force at fracture onset ranged from 106 to 1767 N.

Figure 7.

Figure 7

Open in a new tab

Acoustic emission and force during an impact resulting in a nasal fracture.

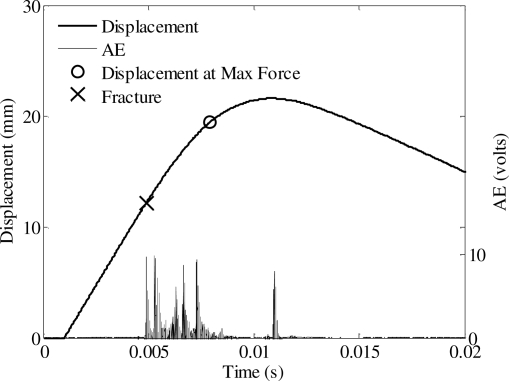
Figure 8.

Figure 8

Open in a new tab

Force-displacement response from nasal impact shown in Figure 7.

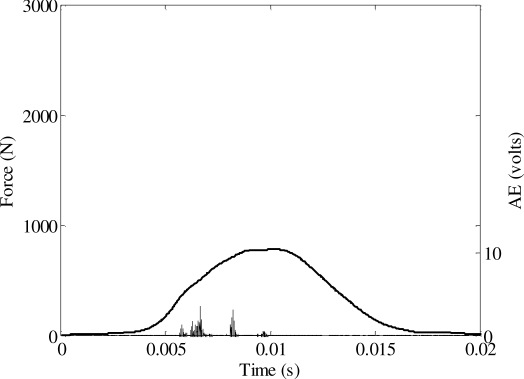
Figure 9.

Figure 9

Open in a new tab

Impact force and AE during nasal impact resulting in no fracture.

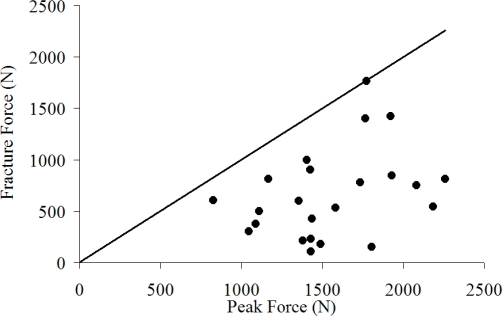
The relationship between fracture force and various impact and subject descriptors was investigated using Pearson product-moment correlations. On average, fracture force was 43% of the peak force and there was no correlation between the two (r = 0.35, p = 0.1) (Figure 10). Fracture force had no statistical correlation between impactor energy and, consequently impactor velocity (p = 0.59).

Figure 10.

Figure 10

Open in a new tab

Relationship between peak force and fracture force.

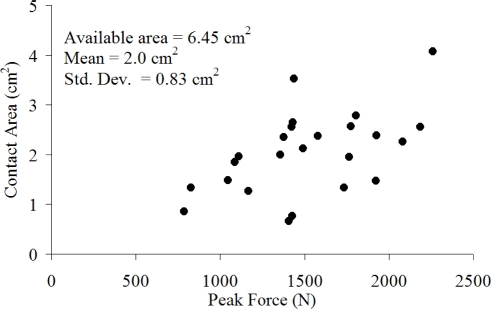
Fuji film placed on the impactor surface prior to impact was used to estimate contact area during the event. The area obtained through this analysis represents the maximum area of contact and not necessarily the contact area at fracture. The average contact area was 2 cm2 (std. dev. = 0.83 cm2) and had a weak correlation with peak force (r = 0.53, p = 0.007) (Figure 11). This area is less than half of the available contact area of 6.45 cm2. Peak pressure calculated using the estimated area was not related to impactor energy (r = 0.09, p = 0.66).

Figure 11.

Figure 11

Open in a new tab

Relationship between contact area and peak force during nasal bone impacts.

Anthropometry

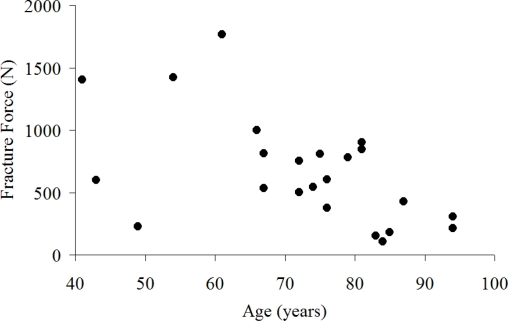
Pre-test CT imaging was used to measure head width and depth, nasal bone width, length and nose length in 13 of the tested subjects (Figure 4). The average nasal bone length in the horizontal plane was 2.3 cm (SD = 0.31) with a maximum of 2.9 cm and a minimum of 2.0 cm. The width of the base of the two nasal bones was 2 cm on average (SD = 0.44) with a maximum of 2.8 cm and a minimum of 1.3 cm. The maximum length of the nose in the horizontal plane was 3.4 cm on average (SD = 0.38) with a maximum of 4.2 cm and a minimum of 2.65 cm. The length of the nose measured in the horizontal plane was statistically correlated with head width (r = 0.62, p = 0.023). There was a weak positive correlation between the maximum force in each test and the width of the nasal bone (r = 0.55, p = 0.05). With respect to fracture force, none of the nasal measurements were statistically correlated to fracture force, including nasal bone length (p = 0.45) and width (p = 0.24) and head depth and width. There was a negative, statistically significant (r = – 0.54, p = 0.006) correlation between age and fracture force (Figure 12) which was illustrated further in the risk of nasal bone fracture.

Figure 12.

Figure 12

Open in a new tab

Relationship between subject age and nasal bone fracture force.

Risk of Nasal Bone Fracture

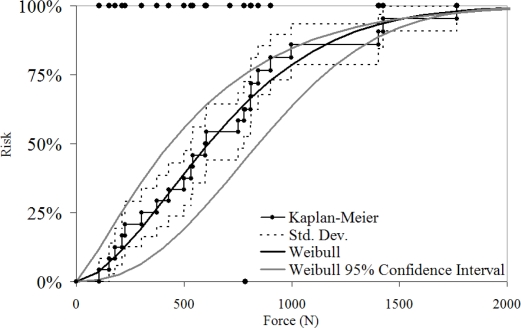
The risk of fracture was estimated using a Kaplan-Meir non-parametric estimate and a two-parameter Weibull distribution (Figure 13). The 50% risk of fracture was 600 and 540 N respectively. The anthropometric measures were included in the model to evaluate their utility in predicting nasal bone fracture. None of the measures were found to be a statistically significant parameter in predicting fracture within the reduced dataset (n=13). The model parameters derived can be used to recreate the Weibull estimates and confidence interval (Table 1).

Figure 13.

Figure 13

Open in a new tab

Risk of nasal bone fracture using parametric and non-parametric techniques.

Table 1.

Parameters for Weibull model of nasal bone fracture risk.

Parameter Estimate 95% Confidence Interval
Lower Upper
Scale - γ 0.0013 0.0017 0.0010
Shape - λ 1.65 1.20 2.26
Open in a new tab

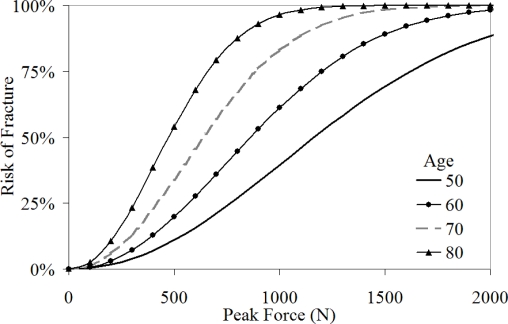
Age was available for the entire dataset and when added to the Weibull model as a covariate, it was found to be a statistically significant (p = 0.0003) parameter. The model with age as a covariate produced similar results to the overall model at an age of 70 years, which is the mean age for the subjects included in this study (Figure 14). Use of these curves should be limited to a qualitative sense until additional data can be added to improve the confidence in the estimates.

Figure 14.

Figure 14

Open in a new tab

Risk of nasal bone fracture with age as a covariate.

DISCUSSION

Using a total of twenty-four impacts, the tolerance of the nasal bone to blunt impact was estimated and its relationship to various anthropometric measures was assessed. Using acoustic emission sensors to detect the onset of fracture, it was found that fracture occurred prior to peak force. It should be noted that during fracture tests, the force-displacement response exhibited an initial peak, followed by a higher secondary peak [Cormier et al., 2010]. This is consistent with the idea that following nasal bone fracture, the impactor continues to translate toward the face and begins to interact with additional facial structures. These structures can include the frontal process of the maxilla and the frontal bone. The acoustic emission data indicated that fracture occurred prior to the lower initial peak. This phenomenon illustrates the importance of acoustic emission sensors in determining fracture onset rather than relying on peak forces, since additional structures (the frontal bone and maxilla) can support higher loads after the nasal bone has fractured and become structurally unstable. These structures are stronger and therefore capable of generating higher reaction forces following nasal bone fracture.

Parametric and non-parametric models were used to estimate the risk of fracture as a function of impactor force. Using the non-parametric model, the 50% risk of nasal bone fracture corresponded to a force of 530 to 780 N. The 95% confidence interval of the Weibull model at a risk of 50% corresponded to a force of 400 to 800 N. The fit of the Weibull model can be assessed using the size of the 95% confidence interval and through comparison to the Kaplan-Meier method which does not assume a distribution to which the data must fit. The resulting Weibull model fits well within the Kaplan-Meier estimate indicating that the Weibull model is a good estimate of the risk of fracture. The relatively small confidence intervals is a result of the higher statistical power associated with the non-censored data obtained in this study. If only peak force was known for the fracture tests, the left-censored nature of those data would have reduced the accuracy of the risk prediction through the parametric and non-parametric techniques.

The risk curves were developed based on the current study which utilized an impactor with an available area of 6.45 cm2 (1 in2). On average, the actual contact area was approximately 32% of the available impactor surface. This suggests that the risk curves can be applied to flat impactors with a smaller area as long as the nasal bones are allowed to interact with the impacting surface. The impactor in the current study is not padded and focal enough to apply loading directly to the nasal bone, making a more aggressive surface. The location of the impact may also influence the tolerance of the nasal bone. In this study, the impactor was aligned such that the palpated end of the nasal bone was located at the center of the impactor. Depending on the subject, this allowed for some interaction between the upper aspect of the nose (nasal septum) and the impactor prior to interaction with the nasal bones. Therefore, in some subjects, the nasal structures played a role in supporting the impactor force. Based on force-displacement data of these tests, the amount of impactor energy dissipated during the toe region of compression is less than approximately 3% of the initial impactor energy [Cormier et al., 2010]. After the toe region of the loading is completed, compression of the nasal bones is expected to dominate, however, the soft tissue will continue to be compressed which will contribute to the stiffness measured by the impactor. Therefore, it is difficult to assess the stiffness contribution of the nasal soft tissues during nasal bone loading; however, there is little change in impactor energy at the time the impactor interacts with the nasal bones. The response of the nose to the anterior-posterior impacts performed in this study will differ from an off-vertical impact which may result in more or less interaction with the soft tissues of the nose. In the case of a more downward directed impact, the impactor would strike the nasal bones prior to any interaction with the soft tissues of the nose. This could result in a lower tolerance depending on the shape of the impactor. It is felt that the impacts performed in this study represent the response expected due to anterior-posterior interaction with a flat object.

Fracture of the nasal bones was readily apparent due to an obvious change in shape and a laceration was usually created allowing visualization of the fracture. The severity of the fracture ranged from a posterior depression of the nasal bones to slight separation of the nasal bone at the frontal process of the maxilla. Comminution of the nasal bones occurred as well. Fractures of the orbital bones were not observed during the detailed autopsies performed post-test.

Two previous studies have reported peak forces resulting from nasal impacts [Nyquist et al., 1986; Cesari et al., 1989]. These studies struck the nasal region using the side of a cylindrical impactor to represent steering wheel impact. Peak forces measured during the studies by Cesari et al., (1989) and Nyquist et al., (1986) (Figure 15) were significantly higher than those of the current study. This is consistent with the higher range of impactor energies utilized in their tests as well as the relative size of the contact area available. The impactor energy utilized by Nyquist et al., (1986) was over an order of magnitude greater than that in the current study and over twice that used in the Cesari et al., (1989) study. Despite the larger impactor energy, the peak forces achieved in their study were less than twice those achieved in the current study and approximately equal to those obtained in the Cesari et al., (1989) study. The two no fracture tests observed in the Cesari et al., (1989) study are surprising considering they resulted in peak forces around 3,000 N. The lack of nasal bone fracture was explained by the authors in the test with a peak force of 3,403 N by stating that impactor struck the frontal bone. Therefore, it may be possible that the second test, having a peak force of 2,918 N interacted with other facial structures instead of the nasal bone. Nyquist et al., (1986) utilized an impactor similar to Cesari et al., (1989) with a lower alignment and reported fractures in every test with an average peak force of 2,889 N. This is in good agreement with the current risk estimate of practically 100% for forces greater than 2,000 N. The minimum tolerance estimated by Nahum et al., (1975) of 111–334 N corresponds to a risk of 3 to 20% using the current estimate.

Figure 15.

Figure 15

Open in a new tab

Nasal bone peak force with respect to impactor energy by study.

None of the anthropometric measures were found to be a statistically significant parameter in fracture prediction. These measures were available for thirteen of the 25 subjects; therefore, the lack of trends may be due to the lack of data. Age however, was available for each subject and was found to have a statistically significant influence on the risk of nasal bone fracture. The average age of the specimens in the current study was 72 (SD = 15). Using age as a covariate, the force corresponding to a 50% risk of fracture decreased approximately 250 N for a 10 year increase in age. Previous studies have not found a trend in facial tolerance with age and the lack of cancellous bones suggests minimal remodeling with age [Yoganandan et al., 1988], therefore, it is unlikely that the decrease in tolerance is solely related to a decrease in the strength of the nasal bone. The septal cartilage has been shown to exhibit a decrease in modulus with age [Rotter et al., 2002] and, therefore, it may also contribute to the age related changes observed in this study. During the impacts performed in this study, the septum will play a role in supporting the impactor and, therefore, a decrease in its stiffness will place a higher burden on the nasal bones. So, there may be a correlation between a known decrease in septal cartilage stiffness and the lower nasal bone tolerance with age.

Limitations

This study was able to demonstrate a relationship between nasal bone tolerance and age; however, the true extent of its influence should be estimated with a larger sample. The lack of statistical significance for the relationships between tolerance and anthropometric measures may also be due to the lack of a larger sample. The tolerance obtained in this study is based on a flat, unpadded impactor. The size and shape of an impactor may influence the tolerance of the nasal bone and should be considered when applying these data.

CONCLUSIONS

This study presents a statistical relationship between the force applied to the nasal bone and its risk of fracture. The fracture risk estimate is based on a survival analysis technique utilizing parametric and non-parametric models. Non-censored fracture data were obtained using acoustic emission sensors and these data were utilized in the survival analysis. In the majority of the tests performed peak force was much greater than the force necessary to initiate fracture. This is due to the structures posterior to the nasal bones which can support load after the nasal bone is fractured. This emphasizes the importance of a non-censored measure of fracture onset when determining the tolerance of the nasal bone. The 50% risk of nasal bone fracture corresponded to a force of approximately 450 to 850 N. Age was found to have a statistically significant influence on fracture risk. Using CT imaging, the width of the nasal bone was measured and found to have a statistically significant relationship with the maximum force achieved during impact. The force at fracture onset was not correlated with any anthropometric measure.

APPENDIX

Summary of cadaver characteristics and test results for nasal bone impacts. na = not available

Subject Age Height (cm) Weight (kg) Impactor Energy (J) Peak Force (N) Fracture Force (N) Nasal Bone Width (mm) Nasal Bone Length (mm) Nose Length (mm)
1 61 168 69 8 1774 1767 na na na
2 41 170 64 16 1764 1402 na na na
3 57 170 84 4 784 - na na na
4 75 165 65 16 2260 810 na na na
5 76 170 44 4 828 605 na na na
6 43 183 112 8 1355 598 na na na
7 66 na na 8 1406 1000 na na na
8 54 na na 8 1924 1426 na na na
10 72 na na 12 2081 752 na na na
12 49 na na 10 1429 228 na na na
13 79 na na 10 1734 781 na na na
14 83 175 73 8 1804 152 1.95 2.1 3.60
15 94 163 64 8 1378 214 2.52 2.89 3.76
17 67 180 82 8 1581 533 2.33 2.16 4.23
19 84 183 109 8 1431 106 1.7 2.24 3.09
21 76 152 91 8 1088 375 1.3 2.5 3.19
23 87 163 75 8 1438 428 2.02 2.78 3.30
24 94 165 54 8 1045 305 1.9 2 3.15
26 85 150 79 16 1490 182 1.8 2 3.50
27 72 163 59 16 1110 502 1.37 2.41 3.73
29 81 175 88 16 1927 845 2.08 2.23 3.43
31 67 na na 16 1167 813 2.4 2.1 2.65
33 81 177 79 16 1424 903 2.3 1.9 3.40
35 74 191 86 16 2185 542 2.8 2.5 3.40
Open in a new tab

REFERENCES

  1. Allison PD. Survival Analysis Using SAS: A Practical Guide Cary. SAS Press; 1995. [Google Scholar]
  2. Allsop D, Kennett K. Skull and Facial Bone Trauma. In: Nahum A, Melvin J, editors. Accidental Injury: Biomechanics and Prevention. 2nd Edition. New York: Springer-Verlag; 2002. pp. 254–76. [Google Scholar]
  3. Allsop D, Warner C, Wille M, Schneider D, Nahum A. Facial Impact Response – A Comparison of the Hybrid 3 Dummy and Human Cadaver. Society of Automotive Engineers. 1988 SAE 881719. [Google Scholar]
  4. Alvi A, Doherty T, Lewen G. Facial Fractures and Concomitant Injuries in Trauma Patients. The Laryngoscope. 2003;113 doi: 10.1097/00005537-200301000-00019. [DOI] [PubMed] [Google Scholar]
  5. Bermond F, Kallieris D, Mattern R, Ramet M, Bouquet R, Caire Y, Voiglio E. Human Face Response at an Angle to the Fore-aft Vertical Plane Impact. Proceedings of the IRCOBI. 1989:121–32. [Google Scholar]
  6. Bruyere K, Bermond F, Bouguet R, Caire Y, Ramet M, Voiglio E. Human Maxilla Bone Response to 30 degree Oriented Impacts and Comparison with Frontal Bone Impacts. Proceedings of the 44th Association for the Advancement of Automotive Medicine Conference; 2000. pp. 219–34. [PMC free article] [PubMed] [Google Scholar]
  7. Cantor AB. Analysis Techniques for Medical Research Cary SAS Press. 2003 [Google Scholar]
  8. Cesari D, Ramet M, Welbourne E. Experimental Evaluation of Human Facial Tolerance to Injuries. Proceedings of the IRCOBI. 1989 [Google Scholar]
  9. Cormier J, Duma S. Epidemiology of Facial Fractures in Automotive Collisions. Annals of Advances in Automotive Medicine. 2009;53:169–76. [PMC free article] [PubMed] [Google Scholar]
  10. Cormier J, Manoogian S, Bisplnghoff J, McNally C, Duma S. The Use of Acoustic Emission in Facial Fracture Detection. Biomed Sci Instrum. 2008;44:147–52. [PubMed] [Google Scholar]
  11. Cormier J, Manoogian S, Bisplnghoff J, Rowson S, Santago A, McNally C, Duma S, Bolte J. Biomechanical Response of the Human Face and Corresponding Biofidelity of the FOCUS Headform. Society of Automotive Engineers. 2010 No. 2010-01-1317. [Google Scholar]
  12. Funk J, Crandall J, Tourret L, MacMahon C, Bass C, Patrie J, Khaewpong N, Eppinger R. The Axial Injury Tolerance of the Human Foot/Ankle Complex and the Effect of Achilles Tension. Journal of Biomechanical Engineering. 2002;124 doi: 10.1115/1.1514675. [DOI] [PubMed] [Google Scholar]
  13. Gassner R, Tuli T, Hächl O, Rudisch A, Ulmer H. Cranio-Maxillofacial Trauma: A 10 Year Review of 9543 cases with 21067 Injuries. Cranial and Maxillofacial Surgery. 2003;31:51–61. doi: 10.1016/s1010-5182(02)00168-3. [DOI] [PubMed] [Google Scholar]
  14. Hackle W, Hausberger K, Sailer R, Ulmer H, Gassner R. Prevalence of Cervical Spine Injuries in Patients with Facial Trauma. Oral and Maxillofacial Surgery. 2001;92(4):370–376. doi: 10.1067/moe.2001.116894. [DOI] [PubMed] [Google Scholar]
  15. Jayamanne DGR, Gillie RF. Do Patients with Facial Trauma to the Orbito-Zygomatic Region also Sustain Significant Ocular Injuries? Coll Surg Eding. 1996;41:200–3. [PubMed] [Google Scholar]
  16. Kent R, Stacey S, Parenteau C. Dynamic Pinch Tolerance of the Phalanges and Interphalangeal Joints. Traffic Injury Prevention. 2008;9:83–88. doi: 10.1080/15389580701697112. [DOI] [PubMed] [Google Scholar]
  17. Kleinbaum D, Klein M. Survival Analysis: A Self-Learning Text. NewYork: Springer Science; 2005. [Google Scholar]
  18. Lim LH, Lam LK, Moore MH, Trott JA, David DJ. Associated Injuries in Facial Fractures: A Review of 839 Patients. British J Plast Surg Vol. 1993;46:365–38. doi: 10.1016/0007-1226(93)90191-d. [DOI] [PubMed] [Google Scholar]
  19. Muraoka M, Nakai Y, Nakagawa K, Yoshioka N, Nakaki Y, Yabe T, Hyodo T, Kamo R, Wakami S. Fifteen-year statistics and observation of facial bone fracture. Osaka City Med J. 1995;41(2):49–61. [PubMed] [Google Scholar]
  20. Nyquist GW, Cavanaugh JM, Goldberg SJ, King AI. Impact Tolerance and Response of the Face. Proceedings of the Advances in Bioengineering Conference; 1986. pp. 75–81. [Google Scholar]
  21. Rotter N, Tobias G, Lebl M, Roy AK, Hansen MC, Vacanti CA, Bonassar LJ. Age-related changes in the composition and mechanical properties of human nasal cartilage. Arch Biochem Biophys. 2002;403(1):132–40. doi: 10.1016/S0003-9861(02)00263-1. [DOI] [PubMed] [Google Scholar]
  22. Rudd R, Crandall J, Millington S, Hurwitz S, Hoglund N. Injury Tolerance and Response of the Ankle Joint in Dynamic Dorsiflexion. Proceedings of the 48th Stapp Car Crash Conference; 2004. SAE No. 2004--22-0001. [DOI] [PubMed] [Google Scholar]
  23. Shapiro AJ, Johnson RM, Miller SF, McCarthy MC. Facial Fractures in a Level I Trauma Centre: The Importance of Protective Devices and Alcohol Abuse. Injury Int J Care Injured Vol. 2001;32:353–56. doi: 10.1016/s0020-1383(00)00245-x. [DOI] [PubMed] [Google Scholar]
  24. Wells J, Rawlings R. Acoustic emission and mechanical properties of trabecular bone. Biomaterials. 1985;6 doi: 10.1016/0142-9612(85)90016-x. [DOI] [PubMed] [Google Scholar]
  25. Yoganandan N, Fintar F, Sances A, Myklebust J, Schmaltz D. Steering Wheel Induced Facial Trauma; Proceedings of the 32nd Stapp Car Crash Conference; SAE No. 881712, 1988. [Google Scholar]

Articles from Annals of Advances in Automotive Medicine / Annual Scientific Conference are provided here courtesy of Association for the Advancement of Automotive Medicine

RESOURCES