High rate of calculation errors in mismatch distribution analysis results in numerous false inferences of biological importance

One of the greatest challenges in unravelling the demographic history of populations is the lack of a universal molecular clock as first envisioned by Zuckerkandl and Pauling (1965) and our lack of certainty concerning even calibrated or local (within and between closely related species) molecular clocks (Hickerson et al., 2003). Evolutionary rates can vary widely within and among groups of organisms (for example, García-Moreno, 2004; Thomas et al., 2006). The hypothesised causes of this variation are diverse and include varying population sizes and selection pressures, different generation times and the influence of body size on metabolic rates (for example, Baer et al., 2007). The stochasticity of the coalescence process within lineages (Edwards and Beerli, 2000) adds even more complexity to simple uniform calibrations. Although attempts to overcome or account for these uncertainties remain at the forefront of evolutionary research, our focus in this study is on a much more mundane problem. Very simply, assuming a given substitution or divergence rate, are authors correctly applying it in standard algorithms in order to infer the timing of demographic events?

One approach in demographic analysis, which lends itself to easy re-calculation, is the so-called mismatch analysis (Slatkin and Hudson, 1991; Rogers and Harpending, 1992). Populations that have experienced a sudden or exponential growth or decline produce a smooth, uni-modal wave in the distribution of pairwise sequence differences (the mismatch distribution) corresponding to that event, whereby stable populations produce more steadily sloped (non-wave-like) distributions. For a uni-modal mismatch distribution, the mode is at the value of tau (τ), a moment estimator, which represents a unit of mutational time. Therefore, the time since population expansion (t) can be calculated by t=τ/2u, where u is the cumulative (across the sequence) probability of substitution. Note that the u in this formula is not the commonly used μ representing the substitution rate per nucleotide. A simple error, for example, would be to insert the divergence rate (between lineages) into the mismatch formula t=τ/2u. As the divergence rate is twice the substitution rate, the resulting estimation of the number of generations since population expansion will be half of the correct value, which would have a large effect on biological inferences. We observed such an error in our own work (Sušnik et al., 2007), as well as several other published studies and decided to evaluate the frequency and magnitude of such errors in the literature. Although we restrict our evaluation to the solving of the mismatch formula, the misuse or exchange of substitution and divergence rates will affect a large number of calculations concerning demographic inference.

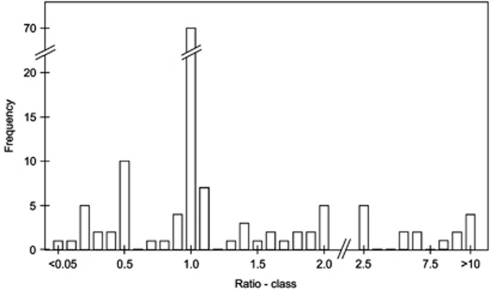
Of 137 publications analysed (see methods in Supplementary File I) only approximately half (N=70; 51.1%) reported a time-since-expansion value that matched our re-calculation or fell within a ±5% tolerance interval (Figure 1, Supplementary File II). We chose this tolerance interval as it represents rounding at the second decimal place of a typical substitution rate in scientific notation (μ). We excluded considering larger rounding errors as these would necessarily have significant influence on biological interpretations and thus should not under any circumstances have been undertaken. Thus, in 67 manuscripts (48.9%) errors greater than those, which could be attributed to an acceptable rounding error were found. Over half of the errors (N=36) involved a multiple of the true value (for example, one-half or double). There was no apparent temporal pattern in error rate across the study period.

Figure 1.

Distribution of the ratio of stated versus implied divergence rates stemming from our re-calculation of time-since-expansion. Stated divergence rate is the rate that the authors reported to use in the calculation. Implied divergence rate stems from our own calculation of time-since-expansion followed by a back calculation to arrive at divergence rate. A value of 1.0 stems from the correct application of the formula t=τ/2u. Bars just left and right of 1.0 represent a deviation >5%. The x-axis is not evenly scaled. Bars up to a value of 2.0 encompass a range of 0.10; bars from 2.5 to 10.0 encompass a range of 1.0 and the last bar (>10) ranges from 10.15 to 68.97.

Although a number of manuscripts presumably exchanged the substitution rate with the divergence rate (N=10, corresponding to the 0.5 class in Figure 1), there were a number of other relatively large and not so easily explained errors resulting in even larger deviations in biological inference. To gain insight on this effect, we plotted the stated time-since-expansion versus the newly calculated values (data not shown) and found differences up to an order of magnitude or more, relating to time periods up to nearly 10 million years. These errors do not consider several studies where a faulty τ (for example, 0.0025) or an unreasonable divergence rate (such as 1000%/million years) was given, rather only errors stemming from the misapplication of the formula t=τ/2u or a rate conversion error. The wide range of substitution rates reported or implied (evaluated through back-calculation using the reported τ and time-since-expansion) was a striking observation throughout the data set. After standardizing the substitution rates to ‘divergence per million years', values ranging from 0.03 up to 2000%/million years were implied. In our data set, a variety of different genes, including among others the mitochondrial DNA control region, 16S rRNA and genes from chloroplast DNA were used for mismatch calculations and therefore there can be no standard expected divergence rate. Nonetheless, authors should be obliged to either use calibrated rates or at least reasonable or commonly reported substitution rates for the genes in their study organism or some close relative.

Rather than bemoan the mistakes of the past, we urge authors to use more care in applying substitution rates reported in the literature and advocate a more explicit description of input parameters in demographic analysis. Such clarity would additionally aid researchers who apply rates in their own work that have been reported in the literature. We further offer a simple online spreadsheet tool for the application of the mismatch analysis or for converting among typical forms of reported substitution or divergence rates (http://www.uni-graz.at/zoowww/mismatchcalc/ index.php). The tool allows the mismatch calculation to be made using one of four different commonly reported forms of substitution rates, and also provides an overview of the span of estimated times since expansion for a range of rates, which can be set by the user. Values produced with this tool should be compared with those already reported in the literature in order to control for obvious anomalies.

The authors declare no conflict of interest.